Abstract
Proof-theoretic semantics explains meaning in terms of proofs. Two different concepts of proof are in question here. One has its roots in Heyting’s explanation of a mathematical proposition as the expression of the intention of a construction, and the other in Gentzen’s ideas about how the rules of Natural Deduction are justified in terms of the meaning of sentences. These two approaches to meaning give rise to two different concepts of proof, which have been developed much further, but the relation between them, the topic of this paper, has not been much studied so far. The recursive definition of proof given by the so-called BHK-interpretation is here used as an explication of Heyting’s idea. Gentzen’s approach has been developed as ideas about what it is that makes a piece of reasoning valid. It has resulted in a notion of valid argument, of which there are different variants. The differences turn out to be crucial when comparing valid arguments and BHK-proofs. It will be seen that for one variant, the existence of a valid argument can be proved to be extensionally equivalent to the existence of a BHK-proof, while for other variants, attempts at similar proofs break down at different points.
This is an elaborated version of a talk at the “Second conference on proof-theoretic semantics” at Tübingen in March 2013. Earlier versions have also been presented elsewhere and have been circulated among some colleagues, which has given me the benefit of several comments. I thank especially Per Martin-Löf, Peter Schroeder-Heister and Luca Tranchini for their suggestions, which have stimulated me to prove stronger results and to improve the presentation.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
1 Introduction
The term “proof-theoretic semantics” was introduced to stand for an approach to meaning based on what it is to have a proof of a sentence. The idea was, at least originally, that in contrast to a truth-conditional meaning theory, one should explain the meaning of a sentence in terms of what it is to know that the sentence is true, which in mathematics amounts to having a proof of the sentence.Footnote 1
There are in particular two different concepts of proof that have been used in meaning theories of this kind, but the relation between them has not been paid much attention to. They have their roots in ideas that were put forward by Arend Heyting and Gerhard Gentzen in the first part of the 1930s. Their approaches to meaning are quite different and result in different concepts of proof. Nevertheless there are clear structural similarities between what they require of a proof. The aim of this paper has been to compare the two approaches more precisely, in particular as to whether the existence of proofs comes to the same.
I shall first retell briefly how Heyting and Gentzen formulated their ideas and how others have taken them. In particular, I shall consider how the ideas have been or can be developed so that they become sufficiently precise and general to allow a meaningful comparison, which will then be the object of the second part of the paper.
2 Heyting’s Approach to Meaning
A mathematical proposition expresses according to Heyting the intention of a construction that satisfies certain conditions. He explained the assertion of a proposition to mean that the intended construction had been realized, and a proof of a proposition to consist in the realization of the intended construction (Heyting 1930 [5, pp. 958–959], 1931 [6, p. 247], 1934 [7, p. 14]). Thus, according to this explanation, to assert a proposition is equivalent with declaring that there is proof of the proposition. The notion of proof retains in this way its usual epistemic connotation: to have a proof is exactly what one needs in order to be justified in asserting the proposition.
As an important example, Heyting explained the meaning of implication, saying that “\(a \mathbin {\supset }b\) means the intention of a construction that takes any proof of a to a proof of b”.
There are several proposals for how to develop Heyting’s ideas more explicitly. One early proposal due to Kreisel (1959, 1962) [10, 11] suggests quite straightforwardly that the constructions intended by implications and universal quantifications are constructive functionals of finite type satisfying the conditions stated by Heyting.Footnote 2
The so-called BHK-interpretation stated by Troelstra and van Dalen (1988) [24], which is less developed ontologically, defines recursively “what forms proofs of logically compound statements take in terms of the proofs of the constituents”.Footnote 3 What is here called a proof corresponds rather to what Heyting calls an intended construction, but it has become common in intuitionism to speak about proofs in this way, and I shall follow this way of speaking.
For my purpose here it is sufficient to stay roughly at the level of precision of the BHK-interpretation. I assume that we are given a set  of proofs of atomic sentences of a first order language and an individual domain D. What it is to be a proof over
of proofs of atomic sentences of a first order language and an individual domain D. What it is to be a proof over
 of a closed compound sentence A in that language is then defined by recursive clauses like the ones below:
of a closed compound sentence A in that language is then defined by recursive clauses like the ones below:
-
(1)
\(\alpha \) is a proof over
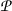 of \(A \mathbin {\supset }B\), if and only if, \(\alpha \) is an effective operation such that if \(\beta \) is any proof over
of \(A \mathbin {\supset }B\), if and only if, \(\alpha \) is an effective operation such that if \(\beta \) is any proof over  of A then \(\alpha (\beta )\) is a proof over
of A then \(\alpha (\beta )\) is a proof over  of B.
of B. -
(2)
\(\alpha \) is a proof over
 of \(\forall x A(x)\), if and only if, \(\alpha \) is an effective operation such that for any element e in the individual domain D, \(\alpha (e)\) is a proof over
of \(\forall x A(x)\), if and only if, \(\alpha \) is an effective operation such that for any element e in the individual domain D, \(\alpha (e)\) is a proof over  of the instance A(e).
of the instance A(e).
Instead of speaking of proofs of open sentences A(x) under assignments of individuals to variables, I have here assumed for convenience that each element e in the individual domain D has a canonical name, and understand by A(e) the closed sentence obtained by substituting in A(x) this canonical name of e for x. Furthermore, I assume that if \(\alpha \) is as stated in clause (2), then there is another effective operation \(\alpha ^*\), effectively obtained from \(\alpha \), such that for any closed term t, \(\alpha ^*(t)\) is a proof of A(t).
To distinguish proofs defined by recursive clauses of this kind, I shall sometimes refer to them as BHK-proofs.
3 Gentzen’s Approach to Meaning
Gentzen’s approach to meaning is commonly described by saying that he had the idea that the meaning of a logical constant is determined by its introduction rule in Natural Deduction, or as he put it himself: “the introductions present, so to speak, the ‘definitions’ of the symbols concerned” (Gentzen 1934–35 [4, p. 189]). However, this should not be confused with what has later become known as inferentialism, the view that the meaning of a sentence is given by the inference rules concerning the sentence that are in force, which was advocated by Carnap (1934) [1] at about the same time. For Gentzen only some of the inference rules are meaning constitutive, viz. the introduction rules. To indicate their special status, a proof or deduction whose last step is an introduction is now commonly called canonical or is said to be in canonical form.Footnote 4
Besides introduction rules there are elimination rules and about them Gentzen says “in an elimination we may use the constant only in the sense afforded to it by the introduction of that symbol”. What is intended is clearly that we may use the constant only in this sense, if we are to justify the elimination inference. Gentzen is obviously concerned with what justifies inferences: the introductions stipulate what the logical constants mean, and the eliminations are justified because they are in accord with this meaning.
He clarifies how his ideas are to be understood by giving one example, saying that given an implication \(A \mathbin {\supset }B\) as premiss, “one can directly infer B when A has been proved, because what \(A \mathbin {\supset }B\) attests is just the existence of a proof of B from A”.Footnote 5
Three important principles can be distinguished here. Firstly, what a sentence “attests” is the existence of a canonical proof. An introduction is therefore immediately justified: given proofs of its premisses, the conclusion is warranted, since what the conclusion attests is just that there is a canonical proof of it—the introductions are self-justifying, as one says, when they are taken to be what gives the meanings of the logical constants. Thus, in view of what a sentence attests, a canonical proof is in order, or is valid, provided only that its immediate sub-proofs are.
Secondly, the justification of an elimination consists more precisely in the fact that given that there are proofs of the premisses of the elimination and that the proof of the major premiss is of the kind attested to exist, that is, is in canonical form, a proof of the conclusion can be obtained from these proofs without the use of that elimination. For instance, as Gentzen points out, a proof of the conclusion B of an implication elimination can be obtained from proofs of the premisses if the proof of the major premiss \(A \mathbin {\supset }B\) is in canonical form, because then there is a proof of B from A, and by replacing the assumption A in that proof by the proof of the minor premiss A, one obtains a proof of B, as is illustrated by the following figure:

[A] stands for the set of assumptions that are discharged by the exhibited \(\mathbin {\supset }\)-introduction in the first figure and become replaced by the proof of A in the second figure. The operation by which the proof to the left is transformed to the one to the right, that is, substituting in the proof of B from A the proof of the minor premiss A for the occurrences of A that belong to [A], is what is called an \(\mathbin {\supset }\)-reduction. These kinds of reductions, which were introduced explicitly in the proof of the normalization theorem for natural deduction (Prawitz 1965 [16]), but which Gentzen was already quite aware of,Footnote 6 have in this way a semantic import in being what shows the eliminations to be justified. By this way of reducing a proof that ends with an elimination to another proof of the same conclusion, the conclusion of the elimination becomes warranted, provided of course that this other proof is valid. Thus, proofs that end with eliminations are valid, if the proofs that they reduce to by applying certain reductions are valid.
Thirdly, when saying that we get a valid proof of B by making the substitution just described, we are tacitly taking for granted that a valid proof from assumptions remains valid when making such substitutions.
We can in this way extract from Gentzen’s example three principles about what makes something a valid proof or a valid deduction, as I prefer to say (since when the term proof is used, it is normally taken for granted that the reasoning is valid, a convention not strictly adhered to in my informal explanations above). The principles are formulated more precisely below, where I have adopted the terminology that a deduction is open when it depends on assumptions and closed when all assumptions are discharged or bound.
-
Principle I.
Introductions preserve validity: a closed deduction in canonical form is valid, if its immediate sub-deductions are.
-
Principle II.
Eliminations are justified by reductions: a closed deduction not in canonical form is valid if it reduces to a valid deduction.
-
Principle III.
An open deduction is valid, if all results of substituting closed valid deductions for its free (undischarged) assumptions are valid.
Because of the fact that the premises of an introduction and the assumptions that an introduction may bind are of lower complexity than that of the conclusion, these principles can be taken as clauses of a generalized inductive definition of the notion of valid deduction, relative to a basic clause stating what is counted as valid deductions of atomic sentences. The effect of defining the notion inductively in this way is that no deduction is valid if its validity does not follow from I–III and that the converses of I–III hold true too.
When taking into account also inferences involving quantified sentences, we have to reckon with inferences that bind free individual variables: for instance, an \(\forall \text {I}\)-inference in which \(\forall x A(x)\) is inferred from A(a) is said to bind occurrences of the variable a that are free in sentences of the deduction of A(a); the occurrences are said to be bound in the deduction of \(\forall x A(x)\). A deduction is then said to be open/closed if it contains either/neither occurrences of unbound assumptions or/nor occurrences of unbound variables. Accordingly, in principle III the substitution referred to is also to replace all free individual variables by closed individual terms. We then arrive at a notion of validity for natural deductions in general.Footnote 7
Gentzen’s idea could be summarized by saying that the meaning of a sentence is determined by what counts as a canonical proof of it, which is to say among other things that non-canonical reasoning must be possible to transform to canonical form in order to be acceptable—spelled out in full, the idea is that the meaning of a sentence is determined by what is required from a valid deduction of it. Although this way of formulating Gentzen’s ideas goes beyond what he said himself, the three principles of validity formulated here are implicit in the example that he gave, as has been shown above.
Closed valid deductions may be seen as representing proofs, and I shall sometimes refer to them as Gentzen proofs.
4 A First Comparison Between Heyting’s and Gentzen’s Approaches
Both Heyting and Gentzen approached questions of meaning in relation to what it is to prove something, but as seen from the above, their approaches were still very different. Gentzen was concerned with what justifies inferences and thereby with what makes something a valid form of reasoning. These concerns were absent from Heyting’s explanations of mathematical propositions and assertions. The constructions that Heyting refers to in his meaning explanations, called proofs in the BHK-interpretation, are mathematical objects, naturally seen as belonging to a hierarchy of effective operations as suggested by Kreisel. They are not proofs built up from inferences. Nor does a proof in Heyting’s sense, the realization of an intended construction, constitute a proof built up of inferences, although it does constitute what is required to assert the proposition in question. As was later remarked by Heyting (1958) [8], the steps taken in the realization of the intended construction, in other words, in the construction of the intended object, can be seen as corresponding to inference steps in a proof as traditionally conceived.
These differences between what I am calling BHK-proofs and Gentzen proofs do not rule out the possibility that the existence of such proofs nevertheless comes materially to the same. For instance, a BHK-proof of an implication \(A \mathbin {\supset }B\) is defined as an operation that takes a BHK-proof of A into one of B, and a closed Gentzen proof of \(A \mathbin {\supset }B\) affords similarly a construction that takes a Gentzen proof of A into one of B; the latter holds because the validity of a closed deduction of \(A \mathbin {\supset }B\) guarantees a closed valid deduction in canonical form (by principle II when seen as a clause in an inductive definition) containing a valid deduction of B from the assumption A (principle I), which gives rise to a closed valid deduction of B when a closed valid deduction of A is substituted for the assumption (principle III). Such similarities may make one expect that one can construct a BHK-proof given a Gentzen proof and vice versa.
However, the ideas of Gentzen discussed above are confined to a specific formal system with particular elimination rules associated with reductions, while there is no comparable restriction of the effective operations that make up a BHK-proof. It is easily seen that for each (valid) deduction in that system there is a corresponding BHK-proof (provided that there are BHK-proofs corresponding to the deductions of atomic sentences), but the converse does not hold. For instance, there is a BHK-proof (over the set of proofs of arithmetical identities) of the conclusion obtained by an application of mathematical induction if there are BHK-proofs of the premisses, but there is no corresponding valid deduction unless we associate a reduction to applications of mathematical induction. If Gentzen proofs are to match BHK-proofs, Gentzen’s ideas have first to be generalized, making them free from any particular formal system.
5 Further Development of Gentzen’s Ideas
The generalization to be considered in this section will retain Gentzen’s ideas of explaining the meaning of sentences in terms of certain canonical forms of reasoning and of connecting the meaning so explained with the justification of inferences. It should be mentioned however that Gentzen’s and Heyting’s ideas have also been developed in another way, resulting in a certain fusion of their ideas. The explanations in the BHK-interpretation may be enriched by saying à la Gentzen how proofs of sentences of various forms can be constructed. To Gentzen’s introduction rules there then correspond canonical ways of forming BHK-proofs of compound sentences from BHK-proofs of the constituents, while to the elimination rules there correspond operations on BHK-proofs to BHK-proofs defined in essentially the same way as the reductions in natural deduction. These correspondences, which further develop the Curry-Howard isomorphism (Howard 1980 [9]), constitute cornerstones of Martin-Löf’s type theory (see especially Martin-Löf 1984 [15, p. 24]). In the other direction, I have suggested that a legitimate inference is to be seen as involving not only a transition from assertions to assertions but also an operation on grounds for the premisses that yields a ground for the conclusion, where grounds are BHK-proofs formed in the way just described (Prawitz 2015 [21]).
In this paper, I am not concerned with such fusions of Heyting’s and Gentzen’s ideas, but want to compare BHK-proofs with forms of reasoning that appear as valid in accordance with Gentzen’s ideas about the justification of inferences, sufficiently generalized.
In outline the general idea is this: We consider pieces of reasoning, which will be called argument structures, proceeding by arbitrary inferences, and possible justifications of these inferences in the form of a set of reductions. An argument structure paired with a set of reductions is called an argument, and we define what it is for an argument to be valid by essentially the same three clauses that defined the notion of valid deduction. I shall develop two new notions of validity, called weak and strong validity. They are variants of notions of valid arguments that have been proposed earlier,Footnote 8 and will be shown to have distinct features that are especially important when it comes to compare valid arguments and BHK-proofs.
At the end of the paper, I reflect upon the fact that all the variants of valid arguments considered so far deviate in one important respect from the intuitions connected with Gentzen’s approach as described above, and point to how the notion of justification may be developed in another way that stays closer to the original ideas.
5.1 Argument Structures
In order to extend the notion of validity defined for deductions so that it can be applied to reasoning in general that proceeds by making arbitrary inferences, I consider tree-formed arrangements of sentences of the kind employed in natural deduction, except that now the inference steps need not be instances of any fixed rules. They will be described by using common terminology from natural deduction, and are what will be called argument structures. A sentence standing at the top of the tree is to be seen either as an assumption or as asserted (inferred from no premisses). An occurrence of an assumption can be bound (discharged) by an inference further down in the tree. Indications of which sentences in the tree are assumptions and where they are bound (if they are bound) are to be ingredients of the argument structure.
An inference may also bind occurrences of a free variable (parameter) in sentences above the conclusion. Again it has to be marked how variables are bound by inferences. An argument structure is thus a tree of sentences with indications of these kinds, and can also be seen as a tree-formed arrangement of inferences chained to each other.
The notions of free assumption and free variable, of open and closed argument structure, and of a sentence or argument structure depending on a free assumption or parameter are carried over to the present context in the obvious way.
There are no restrictions on the argument structures except that an inference may not bind a variable that occurs in an assumption that remains free after the inference, that is, that the conclusion of the inference depends on (otherwise there would be a clash with the idea that an occurrence of a free assumption is free for substitution of closed argument structures, while bound variables are not free for substitution).
An argument structure may for instance look as follows

where the exhibited inference binds assumptions in the part  of the form A(a) marked (1) as well as variables a that are free in
of the form A(a) marked (1) as well as variables a that are free in  . The inference can be seen as representing an application of mathematical induction, where N stands for ‘natural number’ and s is the successor operation.
. The inference can be seen as representing an application of mathematical induction, where N stands for ‘natural number’ and s is the successor operation.
We keep open what forms of sentences are used in an argument structure in order to make the notion sufficiently general. However, when making comparisons with BHK-proofs of sentences in a first order language, we restrict ourselves to such languages. It is assumed that for each form of compound sentences there are associated inferences of a certain kind called introductions, for which we retain the condition from natural deduction that for some measure of complexity, the premisses of the inference and the assumptions bound by the inference are of lower complexity than that of the conclusion. For instance, we could allow the pathological operator tonk proposed by Prior and associate it with the introduction rule that he proposed.
We shall say that an argument structure is canonical or in canonical form if its last inference is an introduction.
5.2 Arguments
The inferences of an argument structure that are not introductions should be justified by reductions as in natural deduction. I shall now be following Schroeder-Heister (2006) [22] partially by taking a justification to be simply a set of reductionsFootnote 9 and a reduction to be a pair  of argument structures such that
of argument structures such that  is not canonical and
is not canonical and  ends with the same sentence as
ends with the same sentence as  and depends at most on what
and depends at most on what  depends on.
depends on.
An argument is a pair  , where
, where  is an argument structure and
is an argument structure and  is a justification. An argument is said to be closed, open, or canonical (or in canonical form), if the respective attribute is applicable to the argument structure.
is a justification. An argument is said to be closed, open, or canonical (or in canonical form), if the respective attribute is applicable to the argument structure.
 is said to reduce immediately to
is said to reduce immediately to  with respect to
with respect to  , if
, if  belongs to
belongs to  . A reduction sequence with respect to the justification
. A reduction sequence with respect to the justification
 is a sequence
is a sequence  \((n \ge 1)\) such that for each \(i < n\), either
\((n \ge 1)\) such that for each \(i < n\), either  reduces immediately to
reduces immediately to  with respect to
with respect to  or
or  is obtained from
is obtained from  by replacing an initial part
by replacing an initial part  of
of  by an argument structure
by an argument structure  such that
such that  reduces immediately to
reduces immediately to  with respect to
with respect to  . An argument structure
. An argument structure  is said to reduce to the argument structure
is said to reduce to the argument structure  with respect to the justification
with respect to the justification
 , if there is a reduction sequence with respect to
, if there is a reduction sequence with respect to  whose first element is
whose first element is  and last element is
and last element is  .
.
Justifications of deductions as described above (Sect. 3) and of argument structures as I originally defined them were effective operations assigned to inference schemata and differ in this respect from the notion that I am now adopting. The main difference is that the relation ‘to reduce immediately to’ becomes now one-many instead of one-one. The present notion of justification is of particular interest when we come to comparing valid arguments with BHK-proofs,Footnote 10 but as we shall see it has some unwanted consequences.
Schroeder-Heister remarks that to take justifications to be relations corresponds to the idea that there can be “alternative justifications” of the same argument structure. I think that this idea is somewhat doubtful; anyway, as we shall soon see, it can be taken in many ways.
Since a justification is just a set of reductions, it may not “really” justify the argument structure. We could say that what is called a justification is merely a proposed or possible justification, a justification candidate. What is required of a “real” justification gets expressed by the definition of what it is for an argument to be valid.
For instance, one can invent a justification of an argument structure using Prior’s elimination rule for tonk by assigning some reductions to applications of the rule, but this will never give rise to valid arguments that make creative uses of Prior’s rule.
An important example of justifications outside the standard ones for the elimination rules in natural deduction is one that can be associated with the argument structures exhibited in the preceding subsection as representing applications of mathematical induction. It consists of a pair  where thus
where thus  is an argument structure of this form. What
is an argument structure of this form. What  is depends on the form of the first premiss of the last inference, Nt, which may be called the major premiss of the inference. If the major premiss has the form N0 and the conclusion accordingly has the form A(0),
is depends on the form of the first premiss of the last inference, Nt, which may be called the major premiss of the inference. If the major premiss has the form N0 and the conclusion accordingly has the form A(0),  is to be
is to be  , the argument structure for A(0) that represents the induction base. If it has the form Ns(t) and stands as conclusion of an inference whose premiss is Nt, the conclusion accordingly having the form A(s(t)),
, the argument structure for A(0) that represents the induction base. If it has the form Ns(t) and stands as conclusion of an inference whose premiss is Nt, the conclusion accordingly having the form A(s(t)),  is to be argument structure
is to be argument structure

If the term t is a numeral n, the argument structure is finally transformed by successive reductions of this kind to an argument structure consisting of the induction base  followed by n applications
followed by n applications  of the induction step on top of each other. These reductions represent indeed the natural and commonly given justification for inferences by mathematical induction.
of the induction step on top of each other. These reductions represent indeed the natural and commonly given justification for inferences by mathematical induction.
5.3 Validity of Arguments
We can now define what it is for an argument to be valid by adopting three principles analogous to the ones stated for valid deductions:
-
I.
A closed canonical argument
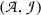 is valid, if for each immediate sub-argument structure
is valid, if for each immediate sub-argument structure
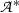 of
of 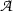 , it holds that
, it holds that
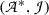 is valid.
is valid. -
II.
A closed non-canonical argument
 is valid, if
is valid, if
 reduces relative to
reduces relative to
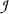 to an argument structure
to an argument structure
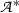 such that
such that
 is valid.
is valid. -
III.
An open argument
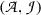 depending on the assumptions
\(A_1, A_2,\ldots ,A_n\)
is valid, if all its substitution instances
depending on the assumptions
\(A_1, A_2,\ldots ,A_n\)
is valid, if all its substitution instances
 are valid, where
are valid, where
 is obtained by first substituting any closed terms for free variables in sentences of
is obtained by first substituting any closed terms for free variables in sentences of
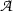 , resulting in an argument structure
, resulting in an argument structure
 depending on the assumptions
\(A_1^\circ ,A_2^\circ ,\ldots ,A_n^\circ \), and then for any valid closed argument structures
depending on the assumptions
\(A_1^\circ ,A_2^\circ ,\ldots ,A_n^\circ \), and then for any valid closed argument structures
 for
\(A_i^\circ \), \(i \le n\), substituting
for
\(A_i^\circ \), \(i \le n\), substituting
 for
\(A_i^\circ \) in
for
\(A_i^\circ \) in 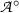 , and where
, and where
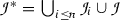 .
.
Because of the assumed condition on the relative complexity of the ingredients of an introduction inference, the principles I-III can again be taken as clauses of a generalized inductive definition of the notion of valid argument relative to a base
 , which is to consist of a set of closed argument structures containing only atomic sentences. If
, which is to consist of a set of closed argument structures containing only atomic sentences. If  is an argument structure of
is an argument structure of  , the argument
, the argument  , where \(\emptyset \) is the empty justification, is counted as canonical and outright as valid relative to
, where \(\emptyset \) is the empty justification, is counted as canonical and outright as valid relative to  . A base is seen as determining the meanings of the atomic sentences. An argument that is valid relative to any base can be said to be logically valid.
. A base is seen as determining the meanings of the atomic sentences. An argument that is valid relative to any base can be said to be logically valid.
If  is an argument structure representing mathematical induction as exhibited in Sect. 5.1,
is an argument structure representing mathematical induction as exhibited in Sect. 5.1,  is the justification associated with
is the justification associated with  as described in Sect. 5.2, and
as described in Sect. 5.2, and  is a base for arithmetic, say corresponding to Peano’s first four axioms and the recursion schemata for addition and multiplication, then the argument
is a base for arithmetic, say corresponding to Peano’s first four axioms and the recursion schemata for addition and multiplication, then the argument  is valid relative to
is valid relative to  (as was in effect first noted in a different conceptual framework by Martin-Löf (1971) [14]. This is an example of a valid argument that is not logically valid but whose validity depends on the chosen base. However, I shall often leave implicit the relativization of validity to a base.
(as was in effect first noted in a different conceptual framework by Martin-Löf (1971) [14]. This is an example of a valid argument that is not logically valid but whose validity depends on the chosen base. However, I shall often leave implicit the relativization of validity to a base.
Instead of saying that the argument  is valid it is sometimes convenient to say that the argument structure
is valid it is sometimes convenient to say that the argument structure  is valid with respect to the justification
is valid with respect to the justification  . But it is argument structures paired with justifications that correspond to proofs and that will be compared to BHK-proofs.
. But it is argument structures paired with justifications that correspond to proofs and that will be compared to BHK-proofs.
6 Weak and Strong Validity and Their Features
6.1. As is easily seen, it comes to the same if we in clause II of the definition of validity require instead that  reduces relative to
reduces relative to  to a canonical argument structure
to a canonical argument structure  that is valid with respect to
that is valid with respect to  .
.
An important question concerning valid arguments, especially crucial when comparing them with BHK-proofs, is whether this canonical argument  required by clause II can be found effectively.
required by clause II can be found effectively.
6.1.1. If the definition of validity is read constructively, or in other words, if the existential quantifier in clause II is understood intuitionistically, the answer is of course yes, the canonical argument  can be found effectively. If so, there is also an effective operation denoted by \(^*\) that is defined for every valid closed argument
can be found effectively. If so, there is also an effective operation denoted by \(^*\) that is defined for every valid closed argument  and yields a canonical argument structure
and yields a canonical argument structure  such that
such that  reduces to
reduces to  with respect to
with respect to  and
and  is valid.
is valid.
6.1.2. Otherwise, if the definition is not taken in a constructive sense, it is not guaranteed that  can be found effectively. Even if we require of a justification that it should be possible to generate its reductions effectively, it is still not guaranteed that
can be found effectively. Even if we require of a justification that it should be possible to generate its reductions effectively, it is still not guaranteed that  can be found effectively. It is true that when we are generating the reduction sequences with respect to a justification
can be found effectively. It is true that when we are generating the reduction sequences with respect to a justification  that start from a closed non-canonical argument structure
that start from a closed non-canonical argument structure  that is valid with respect to
that is valid with respect to  , we sooner or later hit upon a canonical argument structure
, we sooner or later hit upon a canonical argument structure  such that
such that  is valid. But since validity is not a decidable property, we may not be able to tell which one(s) of the canonical structures
is valid. But since validity is not a decidable property, we may not be able to tell which one(s) of the canonical structures  that we reach in this way is (are) the right one(s).
that we reach in this way is (are) the right one(s).
6.2. The situation was quite different when we were dealing with valid deductions based on the standard reductions in natural deduction. Given a closed valid deduction  , a valid canonical deduction
, a valid canonical deduction  as required by principle II can always be found effectively because of two facts: firstly, as already noted, the justifications consist of effective operations, which means that a deduction reduces immediately to at most one other deduction; and secondly, it can be shown that, regardless of the order in which the operations are applied, they will transform a closed deduction to a valid canonical one. This second feature can be called strong validity,Footnote 11 in analogy with how in proof theory one says that a natural deduction is strongly normalizable if all reduction sequences terminate in a normal deduction.
as required by principle II can always be found effectively because of two facts: firstly, as already noted, the justifications consist of effective operations, which means that a deduction reduces immediately to at most one other deduction; and secondly, it can be shown that, regardless of the order in which the operations are applied, they will transform a closed deduction to a valid canonical one. This second feature can be called strong validity,Footnote 11 in analogy with how in proof theory one says that a natural deduction is strongly normalizable if all reduction sequences terminate in a normal deduction.
Similarly, we can speak of strong validity of arguments when the canonical argument  is found regardless of the order in which the reductions are taken and regardless of which reductions in
is found regardless of the order in which the reductions are taken and regardless of which reductions in  are employed. More precisely, a definition of an argument structure
are employed. More precisely, a definition of an argument structure  being strongly valid (relative to a base
being strongly valid (relative to a base  whose argument structures are now counted outright as strongly valid) is obtained by clauses I\(^*\)-III\(^*\), where I\(^*\) and III\(^*\) are like I and III except that “valid” is replaced with “strongly valid” and the second clause reads:
whose argument structures are now counted outright as strongly valid) is obtained by clauses I\(^*\)-III\(^*\), where I\(^*\) and III\(^*\) are like I and III except that “valid” is replaced with “strongly valid” and the second clause reads:
- II\(^*\) :
-
A closed non-canonical argument
 is strongly valid, if each reduction sequence relative to
is strongly valid, if each reduction sequence relative to
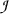 starting from
starting from
 can be prolonged to a reduction sequence that contains a canonical argument structure
can be prolonged to a reduction sequence that contains a canonical argument structure
 such that
such that  is strongly valid.
is strongly valid.
Henceforth, I shall refer to the notion of validity defined by I–III as weak validity.
6.3. Effectiveness is restored when going from weak validity to strong validity, in spite of the justification still being a relation instead of a set of operations, provided that we require that its reductions can be generated effectively. When we generate in some arbitrarily chosen order the reduction sequences with respect to  that start from a closed argument structure
that start from a closed argument structure  that is a strongly valid with respect to
that is a strongly valid with respect to  , the first canonical argument
, the first canonical argument  that we find is guaranteed to be strongly valid with respect to
that we find is guaranteed to be strongly valid with respect to  ; to verify this fact, note that reductions obviously preserve strong validity: if
; to verify this fact, note that reductions obviously preserve strong validity: if  reduces to
reduces to  with respect to
with respect to  and
and  is strongly valid, then so is
is strongly valid, then so is  .
.
6.3.1. That effectiveness is obtained can be seen as an aspect of the fact that strong validity requires all so-called “alternative justifications” to be “real” justifications, so to say—if a closed argument  is strongly valid and the reductions
is strongly valid and the reductions  and
and  both belong to
both belong to  , clause II\(^*\) requires that regardless of which one is used in a reduction sequence, it takes
, clause II\(^*\) requires that regardless of which one is used in a reduction sequence, it takes  a step towards a valid canonical argument. Clause II, in contrast, only requires that one of the reductions does so, which means that the other reduction may lead astray and may have no significance for the validity of the argument in question.
a step towards a valid canonical argument. Clause II, in contrast, only requires that one of the reductions does so, which means that the other reduction may lead astray and may have no significance for the validity of the argument in question.
6.3.2. An aspect of the last feature is that weak validity is obviously monotone with respect to justifications: if  is weakly valid and
is weakly valid and  , then
, then  is weakly valid too—whatever reductions we add to
is weakly valid too—whatever reductions we add to  , the argument remains weakly valid. In contrast, strong validity is not monotone with respect to justifications—added “alternative justifications” must be “real”, if validity is to be preserved.
, the argument remains weakly valid. In contrast, strong validity is not monotone with respect to justifications—added “alternative justifications” must be “real”, if validity is to be preserved.
6.3.3. Yet another aspect of essentially the same feature is that the property of an argument structure to be weakly valid with respect to some justification  is indeed a very weak property. In fact, there is a justification
is indeed a very weak property. In fact, there is a justification  for a given language such that any non-canonical argument structure
for a given language such that any non-canonical argument structure  for a sentence A in that language is weakly valid with respect to
for a sentence A in that language is weakly valid with respect to  , provided only that there exists a weakly valid closed argument
, provided only that there exists a weakly valid closed argument  in that language for
in that language for  . We can simply choose as
. We can simply choose as  the universal set of reductions in that language, call it
the universal set of reductions in that language, call it  . Since
. Since  , the argument
, the argument  is weakly valid by the monotonicity of weak validity, and since
is weakly valid by the monotonicity of weak validity, and since  reduces to
reduces to  with respect to
with respect to  ,
,  is weakly valid too in virtue of clause II.
is weakly valid too in virtue of clause II.
It must be said that this argument  may be quite far from an intuitively valid argument for A—the inferences in
may be quite far from an intuitively valid argument for A—the inferences in  may lack any significance for the validity of the argument, and the only relevant property of
may lack any significance for the validity of the argument, and the only relevant property of  for the validity is that the reduction
for the validity is that the reduction  is an element and that
is an element and that  is included.
is included.
6.4. It should be noted that strong validity does not entail weak validity; a strongly valid argument for an implication \(A \mathbin {\supset }B\) is also weakly valid if A does not contain implication, but as soon as implication becomes nested in the antecedent, this may cease to hold because of the third clause in the definitions of validity.
The features discussed here of the two variants of validity are essential when we are to compare the valid argument with the BHK-proofs, as will be seen in the next section.Footnote 12
7 Mappings of Valid Arguments on BHK-Proofs and Vice Versa
After having now made Gentzen’s approach free from ties to a specific formal system, we return to the question whether the two approaches come to the same thing extensionally. Let us assume that  is a set of BHK-proofs of atomic sentences, that
is a set of BHK-proofs of atomic sentences, that  is a base of valid arguments for atomic sentences, and that they have been mapped on each other. We shall try to extend these mappings to compound sentences.
is a base of valid arguments for atomic sentences, and that they have been mapped on each other. We shall try to extend these mappings to compound sentences.
In other words, we shall try to define one mapping called
-
 :
: -
which applied to a valid closed argument relative to
 for a sentence A gives as value a BHK-proof of A over
for a sentence A gives as value a BHK-proof of A over  ,
,
and a mapping in the other direction called
-
 :
: -
which applied to a BHK-proof over
 of a sentence A gives as value a valid closed argument relative to
of a sentence A gives as value a valid closed argument relative to  for A,
for A,
assuming as an induction assumption that we have been able to define such effective mappings for all sentences of complexity less than that of A.
If \(\alpha \) is a BHK-proof of a sentence A,  has to be a pair, which will be written
has to be a pair, which will be written  ; thus,
; thus,  is an argument structure for A and
is an argument structure for A and  is a justification.
is a justification.
I restrict myself to the cases when A is an implication or a universal quantification, and shall consider in parallel the problems that arise for different variants of validity of arguments.
7.1 Extending the Mapping  to Arguments for A
to Arguments for A
7.1.1. Consider first the case when A is an implication \(B \mathbin {\supset }C\).  is then to be defined for any valid closed argument
is then to be defined for any valid closed argument  for A, which is done by saying that
for A, which is done by saying that  is to be the operation \(\alpha \) defined for BHK-proofs \(\beta \) of B such that
is to be the operation \(\alpha \) defined for BHK-proofs \(\beta \) of B such that

I have to explain what operation  is and show—under the assumptions that
is and show—under the assumptions that  is a valid closed argument for A and that \(\beta \) is a BHK-proof of B and the induction assumption—that:
is a valid closed argument for A and that \(\beta \) is a BHK-proof of B and the induction assumption—that:
-
(i)
the operation
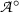 is an effective procedure for finding an argument structure for C, and
is an effective procedure for finding an argument structure for C, and -
(ii)
the pair to which
 is applied above in (a) is effectively obtained from
is applied above in (a) is effectively obtained from 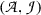 and \(\beta \), and is a valid closed argument for C.
and \(\beta \), and is a valid closed argument for C.
It then follows by the induction assumption that  is defined for this argument and that \(\alpha (\beta )\) as defined in (a) is a BHK-proof of C, which means that the operation \(\alpha \) is a BHK-proof of A.
is defined for this argument and that \(\alpha (\beta )\) as defined in (a) is a BHK-proof of C, which means that the operation \(\alpha \) is a BHK-proof of A.
If  is in canonical form, that is, has the form
is in canonical form, that is, has the form

we let  be the immediate sub-structure
be the immediate sub-structure  of
of  , which is an argument structure for C.Footnote 13
, which is an argument structure for C.Footnote 13
If  is not in canonical form, we want
is not in canonical form, we want  to be the immediate sub-structure of a closed canonical argument structure
to be the immediate sub-structure of a closed canonical argument structure  to which
to which  reduces with respect to
reduces with respect to  and that is valid with respect to
and that is valid with respect to  . Now it becomes important what kind of validity we are dealing with. If the argument
. Now it becomes important what kind of validity we are dealing with. If the argument  is strongly valid, then as noted in Sect. 6.3, there is an effective procedure for finding such an argument structure
is strongly valid, then as noted in Sect. 6.3, there is an effective procedure for finding such an argument structure  that is strongly valid with respect to
that is strongly valid with respect to  : Generating the reduction sequences with respect to
: Generating the reduction sequences with respect to  that start from
that start from  in some arbitrarily chosen order, we take the first canonical argument structure
in some arbitrarily chosen order, we take the first canonical argument structure  that we find. We then let
that we find. We then let  be its immediate sub-structure; that is,
be its immediate sub-structure; that is,  is again
is again  if
if  has the form shown above.
has the form shown above.
Note that if  is weakly valid, the procedure described above may result in an argument structure such that
is weakly valid, the procedure described above may result in an argument structure such that  is not weakly valid with respect to
is not weakly valid with respect to  , and that if
, and that if  is neither strongly nor weakly valid, the procedure may not give any result at all. But when
is neither strongly nor weakly valid, the procedure may not give any result at all. But when  is strongly valid and closed, the operation
is strongly valid and closed, the operation  is defined and is an effective procedure. Hence,
is defined and is an effective procedure. Hence,  is an effective procedure for finding an argument structure for C.
is an effective procedure for finding an argument structure for C.
If  is weakly valid and this is taken in a constructive sense, then as already noted (Sect. 6.1.1), there is an effective procedure \(^*\) defined for all weakly valid closed arguments
is weakly valid and this is taken in a constructive sense, then as already noted (Sect. 6.1.1), there is an effective procedure \(^*\) defined for all weakly valid closed arguments  which yields an argument structure
which yields an argument structure  such that
such that  reduces to
reduces to  with respect to
with respect to  and
and  is weakly valid with respect to
is weakly valid with respect to  . Letting
. Letting  be the immediate substructure of
be the immediate substructure of  , we have again explained the operation
, we have again explained the operation  as an effective procedure for finding an argument structure for C.
as an effective procedure for finding an argument structure for C.
Task (i) has thus been carried out for strong validity and for weak validity read constructively, but not for weak validity read non-constructively. In the two successful cases, task (ii) is now easy. That the pair to which  is applied in (a) is effectively obtained follows from the induction assumption and the effectiveness of the operation
is applied in (a) is effectively obtained follows from the induction assumption and the effectiveness of the operation  . The demonstration of the fact that the pair is a strongly or weakly valid closed argument for C follows the same pattern for the two cases of validity, so we may let valid mean either weakly or strongly valid: That
. The demonstration of the fact that the pair is a strongly or weakly valid closed argument for C follows the same pattern for the two cases of validity, so we may let valid mean either weakly or strongly valid: That  is a valid argument for C follows from the validity of
is a valid argument for C follows from the validity of  or of
or of  , as the case may be. By the induction assumption
, as the case may be. By the induction assumption  is a valid argument for B, and from these two facts it follows by clause III\(^*\) or III that the argument to which
is a valid argument for B, and from these two facts it follows by clause III\(^*\) or III that the argument to which  is applied in (a) is a closed valid argument for C, as was to be shown.
is applied in (a) is a closed valid argument for C, as was to be shown.
7.1.2. Let now A be the sentence \(\forall x B(x)\), and let  be a closed argument for \(\forall x B(x)\) that is strongly valid or is weakly valid taken in a constructive sense.
be a closed argument for \(\forall x B(x)\) that is strongly valid or is weakly valid taken in a constructive sense.
As in Sect. 2, it is assumed that the elements in the individual domain D have canonical names. I apply the conventions explained there, and define  to be the operation \(\alpha \) defined for the elements e in the individual domain D such that
to be the operation \(\alpha \) defined for the elements e in the individual domain D such that

The operation  is explained analogously to how it was explained in the preceding case. Thus, if
is explained analogously to how it was explained in the preceding case. Thus, if  is in canonical form,
is in canonical form,  has the form
has the form

and we let  be
be  , the immediate sub-structure of
, the immediate sub-structure of  .
.  is then the result of substituting for a in
is then the result of substituting for a in  the canonical name for e.
the canonical name for e.
If  is not in canonical form, we find effectively as in the preceding case a closed canonical argument structure
is not in canonical form, we find effectively as in the preceding case a closed canonical argument structure  to which
to which  reduces with respect to
reduces with respect to  such that
such that  has the same kind of validity as
has the same kind of validity as  . We let then
. We let then  be the immediate substructure of
be the immediate substructure of  and
and  the result of substituting for a in
the result of substituting for a in  the canonical name for e.
the canonical name for e.
Since by clauses I\(^*\) and III\(^*\) or by clauses I and III  is a closed valid argument for B(e), validity taken in one of the two forms here considered, it follows by the induction assumption in question, that
is a closed valid argument for B(e), validity taken in one of the two forms here considered, it follows by the induction assumption in question, that  is defined for this argument and that \(\alpha (e)\) as defined in (b) is a BHK-proof of B(e). Thus, \(\alpha \) is a BHK-proof of A.
is defined for this argument and that \(\alpha (e)\) as defined in (b) is a BHK-proof of B(e). Thus, \(\alpha \) is a BHK-proof of A.
7.2 Extending the Mapping  to BHK-Proofs of A
to BHK-Proofs of A
7.2.1. Now I first consider the easiest case when A is a universal sentence \(\forall x B(x)\). Let \(\alpha \) be a BHK-proof of A. I define  as follows:
as follows:

The line above the top sentence B(a) in the argument structure that  assumes as value is meant to indicate that B(a) is not an assumption but is inferred from zero premisses; thus, the parameter a does not occur in any assumption that the sentence at the bottom depends on, and it becomes therefore bound by the \(\forall \mathrm {I}\)-inference as usual.
assumes as value is meant to indicate that B(a) is not an assumption but is inferred from zero premisses; thus, the parameter a does not occur in any assumption that the sentence at the bottom depends on, and it becomes therefore bound by the \(\forall \mathrm {I}\)-inference as usual.
For the argument structure  to be valid with respect to a justification
to be valid with respect to a justification  , it is necessary and sufficient that
, it is necessary and sufficient that  contains a reduction such that any instance of the argument structure \(\overline{B(a)}\) reduces with respect to
contains a reduction such that any instance of the argument structure \(\overline{B(a)}\) reduces with respect to  to an argument structure
to an argument structure  that is valid with respect to
that is valid with respect to  . The problem is that it is not sufficient to find, for each closed term t, appropriate reductions for \(\overline{B(t)}\).Footnote 14 Instead we must find a set
. The problem is that it is not sufficient to find, for each closed term t, appropriate reductions for \(\overline{B(t)}\).Footnote 14 Instead we must find a set  of reductions such that it can be shown that, for each term t,
of reductions such that it can be shown that, for each term t,  contains appropriate reductions. I succeed in showing this only for the case of weak validity. The set
contains appropriate reductions. I succeed in showing this only for the case of weak validity. The set  defined above will be shown to be such a justification in that case. The same result could be obtained more easily by choosing the universal set of reductions for the language in question, but it may be of some interest to see that this smaller set will do.
defined above will be shown to be such a justification in that case. The same result could be obtained more easily by choosing the universal set of reductions for the language in question, but it may be of some interest to see that this smaller set will do.
For the understanding of the definition of  , recall that \(\alpha ^*\) is the effective operation assumed in Sect. 2 to be possible to obtain effectively from \(\alpha \) such that for each closed term t, \(\alpha ^*(t)\) is a BHK-proof of B(t). I also want to make clear that
, recall that \(\alpha ^*\) is the effective operation assumed in Sect. 2 to be possible to obtain effectively from \(\alpha \) such that for each closed term t, \(\alpha ^*(t)\) is a BHK-proof of B(t). I also want to make clear that  is the union of two sets (i) and (ii) where (i) is the union of all sets
is the union of two sets (i) and (ii) where (i) is the union of all sets  for closed terms t and (ii) is the set of all pairs
for closed terms t and (ii) is the set of all pairs  where t is a closed term. By the induction assumption,
where t is a closed term. By the induction assumption,  and
and  are both defined.
are both defined.
In order to show that  is a weakly valid argument for \(\forall x B(x)\), we have to show in view of principles I and III and since
is a weakly valid argument for \(\forall x B(x)\), we have to show in view of principles I and III and since  is a closed argument structure for \(\forall x B(x)\) in canonical form that the argument
is a closed argument structure for \(\forall x B(x)\) in canonical form that the argument  is weakly valid for each closed term t. To this end we must show in view of principle II that \(\overline{B(t)}\) for each closed term t reduces with respect to
is weakly valid for each closed term t. To this end we must show in view of principle II that \(\overline{B(t)}\) for each closed term t reduces with respect to  to an argument structure
to an argument structure  such that
such that  is weakly valid.
is weakly valid.
We shall now verify that for each closed term t,  is such an argument structure
is such an argument structure  . Firstly note that it has been arranged so that \(\overline{B(t)}\) reduces to
. Firstly note that it has been arranged so that \(\overline{B(t)}\) reduces to  with respect to
with respect to  for each closed term t by the defining
for each closed term t by the defining  as a union of two sets (i) and (ii) where (ii) is the set of all pairs
as a union of two sets (i) and (ii) where (ii) is the set of all pairs  for closed terms t. Secondly, note that by the induction assumption, for each closed term t,
for closed terms t. Secondly, note that by the induction assumption, for each closed term t,  is a closed weakly valid argument for B(t), since \(\alpha ^*(t)\) is a BHK-proof of B(t). Thirdly, we recognize that from the last fact follows the wanted result that
is a closed weakly valid argument for B(t), since \(\alpha ^*(t)\) is a BHK-proof of B(t). Thirdly, we recognize that from the last fact follows the wanted result that  is weakly valid, because
is weakly valid, because  is a subset of
is a subset of  (in virtue of being a subset of the set (i) described above) and weak validity is monotone with respect to justifications, as remarked in Sect. 6.3.2.
(in virtue of being a subset of the set (i) described above) and weak validity is monotone with respect to justifications, as remarked in Sect. 6.3.2.
As seen the monotonicity of weak validity with respect to justifications is used in establishing this mapping, and therefore a similar demonstration does not go through for strong validity, not being monotone with respect to justifications.
7.2.2. Let now A be an implication \(B \mathbin {\supset }C\) and let \(\alpha \) be a BHK-proof of \(B \mathbin {\supset }C\). The construction of  is similar to the preceding case. Clearly,
is similar to the preceding case. Clearly,  is to be the canonical argument structure
is to be the canonical argument structure

It is weakly valid with respect to  , if and only if, for each weakly valid, closed argument
, if and only if, for each weakly valid, closed argument  for B, the argument structure
for B, the argument structure

reduces with respect to  to an argument structure
to an argument structure  such that
such that  is weakly valid (as is seen by applying clauses I, III, and II in this order). To guarantee that there is such an
is weakly valid (as is seen by applying clauses I, III, and II in this order). To guarantee that there is such an  for each weakly valid closed argument
for each weakly valid closed argument  , I define
, I define

Assume now that  is a closed argument for B that is weakly valid. We shall verify that
is a closed argument for B that is weakly valid. We shall verify that  is the wanted
is the wanted  . Firstly, note that the argument structure (c) reduces with respect to
. Firstly, note that the argument structure (c) reduces with respect to  to
to  in virtue of the fact that the pair ((c),
in virtue of the fact that the pair ((c),  is a member of the second set in the union that by definition constitutes
is a member of the second set in the union that by definition constitutes  . Secondly, we note that by the induction assumption,
. Secondly, we note that by the induction assumption,  is a BHK-proof of B. Hence
is a BHK-proof of B. Hence  is a BHK-proof of C. Therefore, by the induction assumption in the other direction,
is a BHK-proof of C. Therefore, by the induction assumption in the other direction,

is a weakly valid argument for A. Thirdly, we recognize that from the weak validity of the argument (d) follows the wanted result that the argument  is weakly valid, because
is weakly valid, because  is a subset of
is a subset of  (in virtue of being a subset of the first set of the union that constitutes
(in virtue of being a subset of the first set of the union that constitutes  by definition) and weak validity is monotone with respect to justifications.
by definition) and weak validity is monotone with respect to justifications.
The demonstrations in 7.2.1 and 7.2.2 have been entirely constructive and thus show that the result that  is a closed weakly valid argument for A when \(\alpha \) is a BHK-proof of A holds even when the notion of weak validity is understood constructively.
is a closed weakly valid argument for A when \(\alpha \) is a BHK-proof of A holds even when the notion of weak validity is understood constructively.
8 Concluding Remarks
8.1. We have thus shown that the notion of a weak valid argument taken constructively is extensionally equivalent with the notion of a BHK-proof.
When weak validity is taken non-constructively, I have not been able to construct a BHK-proof of A from a weakly valid argument for A, but only in the other direction a weakly valid argument for A from a BHK-proof of A, given the induction assumption.
In contrast, from a strongly valid argument for A, I have constructed a BHK-proof of A, given the induction assumption and the assumption that the reductions can be generated effectively, but have not been able to construct in the other direction a strongly valid argument for A from a BHK-proof of A.
Since the mentioned constructions depend on the assumption that there are mappings in both directions for sub-sentences, nothing has been established about the relations between on the one hand BHK-proofs and on the other hand arguments that are weakly valid understood in a non-constructive sense or are strongly valid.
8.2. As has been seen above, when the notion of valid deduction is generalized to the notion of valid argument, the justifications come to play the major role and the inferences of the argument structures a correspondingly minor role. Some of the intuitions behind the notion of valid deduction are lost in this way. It would therefore be interesting to investigate a more restricted notion of reductions than the one used here in connection with arguments.
The standard reductions in natural deduction are all transformations of a given deduction by two kinds of very simple effective operations, possibly combined with each other. One kind consists of operations \(\varphi \) such that  is a sub-deduction of
is a sub-deduction of  . The other kind consists of operations \(\varphi \) such that
. The other kind consists of operations \(\varphi \) such that  is the result of substituting in
is the result of substituting in  an individual term occurring in a sentence of
an individual term occurring in a sentence of  for a free variable occurring in a sentence of
for a free variable occurring in a sentence of  or substituting in a sub-deduction of
or substituting in a sub-deduction of  for a free assumption (in that sub-deduction) another sub-deduction of
for a free assumption (in that sub-deduction) another sub-deduction of  . Also the reduction associated with mathematical induction (Sect. 5.2) is a transformation built up of these two kinds of operations.
. Also the reduction associated with mathematical induction (Sect. 5.2) is a transformation built up of these two kinds of operations.
By applying operations of these two kinds to a deduction or an argument structure one obtains an argument structure that is contained in the given deduction or argument structure; in case substitutions have been carried out, we should perhaps say that the result is implicitly contained. A reduction of this kind associated to an inference constitutes a justification of the inference in a much stronger sense than the reductions that have been considered in connection with argument structures: Given that the arguments for the premisses are acceptable, there is an acceptable argument for the conclusion, because an argument for the conclusion is already contained, at least implicitly, in the arguments for the premisses taken together. This is actually the kind of justification of Gentzen’s elimination rules that I have labelled the inversion principle, using a term from Lorenzen, and have presented as the intuition behind the normalization theorem for natural deductions [16].
An argument structure that is valid with respect to a justification that assigns such operations to occurrences of inferences would in itself have an epistemic force. Perhaps one could say that the function of the justifications would then be to verify that they have such a force, whereas valid arguments as they have been defined here often get their entire epistemic force from the justifications.
A notion of valid argument based on justifications of this kind would be a quite different concept from the variants of valid argument that have been dealt with in this paper. It would also be different from the notion of BHK-proof, it seems.
Notes
- 1.
Schroeder-Heister (2006) [22], who coined the term and used it as the title of a conference that he arranged at Tübingen in 1999, writes that proof-theoretic semantics “is based on the fundamental assumption that the central notion in terms of which meanings can be assigned to expressions of our language ... is that of proof rather than truth”.
- 2.
Kreisel was interested in this interpretation as a technical tool for obtaining certain non-derivability results. For a foundation of intuitionistic logic he suggested another interpretation that took a proof of an implication to consist of a pair \((\alpha , \beta )\) where \(\alpha \) is a construction satisfying the condition stated by Heyting and \(\beta \) is a proof of the fact that \(\alpha \) satisfies this condition (Kreisel 1962 [12]).
- 3.
BHK stands here for Brouwer-Heyting-Kolmogorov, but there is also another interpretation stated by Troelstra (1977) [23] that is called the BHK-interpretation, where BHK stands for Brouwer-Heyting-Kreisel. It is more akin to Kreisel’s second proposal mentioned in footnote 2.
- 4.
- 5.
“kann man ... aus einem bewiesenen A sofort B schließ[en]. Denn \(A \mathbin {\supset }B\) dokumentiert ja das Bestehen einer Herleitung von B aus A” (Gentzen 1934–35 [4, p. 189]).
- 6.
Although Gentzen never stated these reductions in any published work, it seemed clear already from his example quoted here that he was aware of them. This was later verified when finding an unpublished manuscript where Gentzen actually proved a normalization theorem for intuitionistic natural deduction with these reductions (see von Plato 2008 [25]).
- 7.
What was called “validity based on the introduction rules” by Prawitz (1971) [17] differs from the notion presented here in one substantial respect: in clauses corresponding to principle III, extensions of the set of valid deductions for atomic sentences were considered and it was required that substitutions preserved validity also relative to them; cf. footnote 12. In addition to this notion, I also defined a notion of “validity used in proofs of normalizability”, similar to Martin-Löf (1971) [14] notion of computability, but as pointed out by Schroeder-Heister (2006) [22], this notion of validity is quite different and should not be counted as a semantic notion explicating Gentzen’s idea of meaning, because normalizable deductions are defined outright as computable although (if open) they may not be reducible to canonical form.
- 8.
- 9.
I have dropped the requirement that the justifications should be closed under substitutions.
- 10.
It also offers one way to avoid a problem connected with my earlier definition of justification. When generalizing principle III in the definition of valid deduction to argument structures, the substitutions of valid argument structures
 in open arguments
in open arguments 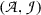 had to be restricted to ones where
had to be restricted to ones where 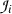 was consistent with
was consistent with 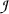 . The restriction is unwanted and may make the notion of validity too weak (essential also when comparing with BHK-proofs). A possible alternative in order to avoid this problem while keeping the relation ‘to reduce immediately to’ one-one is to take reductions to be assignments of effective operations to occurrences of inferences (instead of inference schemata or inferences).
. The restriction is unwanted and may make the notion of validity too weak (essential also when comparing with BHK-proofs). A possible alternative in order to avoid this problem while keeping the relation ‘to reduce immediately to’ one-one is to take reductions to be assignments of effective operations to occurrences of inferences (instead of inference schemata or inferences). - 11.
I have previously used the expression strongly valid for deductions and arguments in another way where it would be better to say strongly computable—cf. second part of footnote 7.
- 12.
As to the other variants of validity mentioned in footnote 8, Dummett defines validity directly for argument structures, thus leaving the justifications implicit. I have commented on this difference elsewhere [20], but then overlooked one important consequence of it, which is now taken up in footnote 14.
Schroeder-Heister’s notion of validity differs from weak validity as defined here by following my previous definition of valid deduction as regards extensions of the given base
 (see footnote 7). We get this notion by requiring in clause III that also for every extension
(see footnote 7). We get this notion by requiring in clause III that also for every extension  of
of 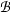 , it holds that all substitution instances
, it holds that all substitution instances 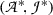 are valid relative to
are valid relative to  where
where 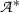 is obtained by substituting for
is obtained by substituting for  a closed argument structure
a closed argument structure  such that
such that 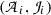 is valid relative to
is valid relative to 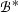 .
.To consider extensions of the given base in this way is natural when a base is seen as representing a state of knowledge, but is in conflict with the view adopted here that a base is to be understood as giving the meanings of the atomic sentences. For instance, the argument representing reasoning by mathematical induction presented in Sect. 5.3 ceases to be valid relative to the arithmetical base
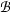 if we require in clause III that validity be monotone with respect to the base.
if we require in clause III that validity be monotone with respect to the base.Concerning my original notion of validity see remarks made in the text and in footnote 10.
- 13.
Note the difference between the two notations below, commonly used in natural deduction:

The left one stands for the same argument structure as
 and is used to indicate that the last sentence of
and is used to indicate that the last sentence of  is A. The right one stands for an argument structure formed by putting A under the structure
is A. The right one stands for an argument structure formed by putting A under the structure 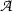 (and it is left open what the last sentence of
(and it is left open what the last sentence of  is).
is). - 14.
This is all that is required by Dummett’s notion of valid argument structure, which means that his notion is quite obviously extensionally equivalent to the notion of BHK-proof.
References
Carnap, R.: Logische Syntax der Sprache. Springer, Wien (1934)
Dummett, M.: The philosophical basis of intuitionistic logic. In: Rose, H.E., et al. (eds.) Logic Colloquium ’73, pp. 5–40. Amsterdam, North-Holland (1975)
Dummett, M.: The Logical Basis of Metaphysics. Duckworth, London (1991)
Gentzen, G.: Untersuchungen über das logische Schließen. Mathematische Zeitschrift 39, 176–210, 405–431 (1934–1935)
Heyting, A.: Sur la logique intuitionniste. Académie Royale de Belgique, Bulletin de la Classe des Sciences 16, 957–963 (1930)
Heyting, A.: Die intuitionistische Grundlegung der Mathematik. Erkenntnis 2, 106–115 (1931)
Heyting, A.: Mathematische Grundlagenforschung, Intuitionismus, Beweistheorie. Springer, Berlin (1934)
Heyting, A.: Intuitionism in mathematics. In: Klibansky, R. (ed.) Philosophy in the Mid-Century, pp. 101–115. La Nuova Italia, Florence (1958)
Howard, W.: The formula-as-types notion of construction. In: Seldin, J., et al. (eds.) To H. B. Curry: Essays on Combinatory Logic, Lambda Calculus and Formalism, pp. 479-490. Academic Press, London (1980)
Kreisel, G.: Interpretation of analysis by means of constructive functionals of finite types. In: Heyting, A. (ed.) Constructivity of Mathematics, pp. 101–128. North-Holland, Amsterdam (1959)
Kreisel, G.: On weak completeness of intuitionistic predicate logic. J. Symb. Log. 27, 139-158 (1962)
Kreisel, G.: Foundations of intuitionistic logic. In: Nagel, E., et al. (eds.) Logic, Methodology and Philosophy of Science, pp. 198-212. Stanford University Press, Stanford (1962)
Kreisel, G.: Book reviews, the collected papers of Gerhard Gentzen. J. Philos. 68, 238–265 (1971)
Martin-Löf, P.: Hauptsatz for the intuitionistic theory of iterated inductive definitions. In: Fenstad, J.E. (ed.) Proceedings of the Second Scandinavian Logic Symposium, pp. 179-216. North-Holland, Amsterdam (1971)
Martin-Löf, P.: Intuitionistic Type Theory. Bibliopolis, Napoli (1984)
Prawitz, D.: Natural Deduction: A Proof-Theoretic Study. Almqvist & Wicksell, Stockholm. (1965) (Republished, Dover Publications, New York (2006))
Prawitz, D.: Ideas and results in proof theory. In: Fenstad, J.E. (ed.) Proceedings of the Second Scandinavian Logic Symposium, pp. 235-307. North-Holland, Amsterdam (1971)
Prawitz, D.: Towards a foundation of general proof theory. In: Suppes, P., et al. (eds.) Logic, Methodology and Philosophy of Science IV, pp. 225–250. North-Holland, Amsterdam (1973)
Prawitz, D.: On the idea of a general proof theory. Synthese 27, 63–77 (1974)
Prawitz, D.: Meaning approached via proofs. Synthese 148, 507–524 (2006)
Prawitz, D.: Explaining deductive inference. In: Wansing, H. (ed.) Dag Prawitz on Proofs and Meaning, pp. 65–100. Springer, Cham (2015)
Schroeder-Heister, P.: Validity concepts in proof-theoretic semantics. Synthese 148, 525–571 (2006)
Troelstra, A.S.: Aspects of constructive mathematics. In: Barwise, J. (ed.) Handbook of Mathematical Logic, pp. 973–1052. North-Holland, Amsterdam (1977)
Troelstra, A.S., van Dalen, D.: Constructivism in Mathematics, vol. 2. North-Holland, Amsterdam (1988)
von Plato, J.: Gentzen’s proof of normalization for intuitionistic natural deduction. Bull. Symb. Log. 14, 240-257 (2008)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is distributed under the terms of the Creative Commons Attribution Noncommercial License, which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Copyright information
© 2016 The Author(s)
About this chapter
Cite this chapter
Prawitz, D. (2016). On the Relation Between Heyting’s and Gentzen’s Approaches to Meaning. In: Piecha, T., Schroeder-Heister, P. (eds) Advances in Proof-Theoretic Semantics. Trends in Logic, vol 43. Springer, Cham. https://doi.org/10.1007/978-3-319-22686-6_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-22686-6_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-22685-9
Online ISBN: 978-3-319-22686-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)





 of
of  of A then
of A then  of B.
of B. of
of  of the instance A(e).
of the instance A(e).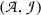 is valid, if for each immediate sub-argument structure
is valid, if for each immediate sub-argument structure
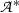 of
of 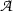 , it holds that
, it holds that
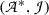 is valid.
is valid. is valid, if
is valid, if
 reduces relative to
reduces relative to
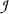 to an argument structure
to an argument structure
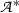 such that
such that
 is valid.
is valid.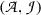 depending on the assumptions
depending on the assumptions
 are valid, where
are valid, where
 is obtained by first substituting any closed terms for free variables in sentences of
is obtained by first substituting any closed terms for free variables in sentences of
 , resulting in an argument structure
, resulting in an argument structure
 depending on the assumptions
depending on the assumptions
 for
for
 for
for
 , and where
, and where
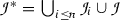 .
. is strongly valid, if each reduction sequence relative to
is strongly valid, if each reduction sequence relative to
 starting from
starting from
 can be prolonged to a reduction sequence that contains a canonical argument structure
can be prolonged to a reduction sequence that contains a canonical argument structure
 such that
such that  is strongly valid.
is strongly valid. :
: for a sentence A gives as value a BHK-proof of A over
for a sentence A gives as value a BHK-proof of A over  ,
, :
: of a sentence A gives as value a valid closed argument relative to
of a sentence A gives as value a valid closed argument relative to  for A,
for A, to Arguments for A
to Arguments for A
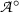 is an effective procedure for finding an argument structure for C, and
is an effective procedure for finding an argument structure for C, and is applied above in (
is applied above in (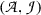 and
and  to BHK-Proofs of A
to BHK-Proofs of A
 in open arguments
in open arguments 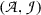 had to be restricted to ones where
had to be restricted to ones where  was consistent with
was consistent with  . The restriction is unwanted and may make the notion of validity too weak (essential also when comparing with BHK-proofs). A possible alternative in order to avoid this problem while keeping the relation ‘to reduce immediately to’ one-one is to take reductions to be assignments of effective operations to occurrences of inferences (instead of inference schemata or inferences).
. The restriction is unwanted and may make the notion of validity too weak (essential also when comparing with BHK-proofs). A possible alternative in order to avoid this problem while keeping the relation ‘to reduce immediately to’ one-one is to take reductions to be assignments of effective operations to occurrences of inferences (instead of inference schemata or inferences). (see footnote 7). We get this notion by requiring in clause III that also for every extension
(see footnote 7). We get this notion by requiring in clause III that also for every extension  of
of  , it holds that all substitution instances
, it holds that all substitution instances  are valid relative to
are valid relative to  where
where  is obtained by substituting for
is obtained by substituting for  a closed argument structure
a closed argument structure  such that
such that 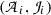 is valid relative to
is valid relative to 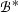 .
.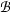 if we require in clause III that validity be monotone with respect to the base.
if we require in clause III that validity be monotone with respect to the base.
 and is used to indicate that the last sentence of
and is used to indicate that the last sentence of  is A. The right one stands for an argument structure formed by putting A under the structure
is A. The right one stands for an argument structure formed by putting A under the structure 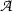 (and it is left open what the last sentence of
(and it is left open what the last sentence of  is).
is).