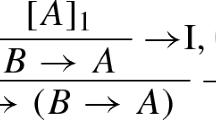Open Problems in Proof-Theoretic Semantics

Abstract

I present three open problems the discussion and solution of which I consider relevant for the further development of proof-theoretic semantics: (1) The nature of hypotheses and the problem of the appropriate format of proofs, (2) the problem of a satisfactory notion of proof-theoretic harmony, and (3) the problem of extending methods of proof-theoretic semantics beyond logic.

1 Introduction

Proof-theoretic semantics is the attempt to give semantical definitions in terms of proofs. Its main rival is truth-theoretic semantics, or, more generally, semantics that treats the denotational function of syntactic entities as primary. However, since the distinction between truth-theoretic and proof-theoretic approaches is not as clear cut as it appears at first glance, particularly if ‘truth-theoretic’ is understood in its model-theoretic setting (see Hodges [33], and Došen [10]). it may be preferable to redirect attention from the negative characterisation of proof-theoretic semantics to its positive delineation as the explication of meaning through proofs. Thus, we leave aside the question of whether alternative approaches can or do in fact deal with the phenomena that proof-theoretic semantics tries to explain. In proof-theoretic semantics, proofs are not understood simply as formal derivations, but as entities expressing arguments by means of which we can acquire knowledge. In this sense, proof-theoretic semantics is closely connected and strongly overlaps with what Prawitz has called general proof theory.

The task of this paper is not to provide a philosophical discussion of the value and purpose of proof-theoretic semantics. For that the reader may consult Schroeder-Heister [56, 61] and Wansing [72]. The discussion that follows presupposes some acquaintance with basic issues of proof-theoretic semantics. Three problems are addressed, which I believe are crucial for the further development of the proof-theoretic approach. This selection is certainly personal, and many other problems might be added. However, it is my view that grappling with these three problems opens up further avenues of enquiry that are needed if proof-theoretic semantics is to mature as a discipline.

The first problem is the understanding of hypotheses and the format of proofs. It is deeply philosophical and deals with the fundamental concepts of reasoning, but has important technical implications when it comes to formalizing the notion of proof. The second problem is the proper understanding of proof-theoretic harmony. This is one of the key concepts within proof-theoretic semantics. Here we claim that an intensional notion of harmony should be developed. The third problem is the need to widen our perspective from logical to extra-logical issues. This problem proceeds from the insight that the traditional preoccupation of proof-theoretic semantics with logical constants is far too limited.

I work within a conventional proof-theoretic framework where natural deduction and sequent calculus are the fundamental formal models of reasoning. Using categorial logic, which can be viewed as abstract proof theory, many new perspectives on these three problems would become possible. This task lies beyond the scope of what can be achieved here. Nevertheless, I should mention that the proper recognition of categorial logic within proof-theoretic semantics is still a desideratum. For the topic of categorial proof theory the reader is referred to Došen’s work, in particular to his programmatic statement of 1995 [6], his contribution to this volume [11] and the detailed expositions in two monographs [7, 12].

2 The Nature of Hypotheses and the Format of Proofs

The notion of proof from hypotheses—hypothetical proof—lies at the heart of proof-theoretic semantics. A hypothetical proof is what justifies a hypothetical judgement, which is formulated as an implication. However, it is not clear what is to be understood by a hypothetical proof. In fact, there are various competing conceptions, often not made explicit, which must be addressed in order to describe this crucial concept.

2.1 Open Proofs and the Placeholder View

The most widespread view in modern proof-theoretic semantics is what I have called the primacy of the categorical over the hypothetical [58, 60]. According to this view, there is a primitive notion of proof, which is that of an assumption-free proof of an assertion. Such proofs are called closed proofs. A closed proof proves outright, without referring to any assumptions, that which is being claimed. A proof from assumptions is then considered an open proof, that is, a proof which, using Frege’s term, may be described as ‘unsaturated’. The open assumptions are marks of the places where the proof is unsaturated. An open proof can be closed by substituting closed proofs for the open assumptions, yielding a closed proof of the final assertion. In this sense, the open assumptions of an open proof are placeholders for closed proofs. Therefore, one can speak of the placeholder view of assumptions.

Prawitz [46], for example, speaks explicitly of open proofs as codifying open arguments. Such arguments are, so-to-speak, arguments with holes that can be filled with closed arguments, and similarly for open judgements and open grounds [50]. A formal counterpart of this conception is the Curry-Howard correspondence, in which open assumptions are represented by free term variables, corresponding to the function of variables to indicate open places. Thus, one is indeed justified in viewing this conception as extending to the realm of proofs Frege’s idea of the unsaturatedness of concepts and functions. That hypotheses are merely placeholders entails that no specific speech act is associated with them. Hypotheses are not posed or claimed but play a subsidiary role in a superordinated claim of which the hypothesis marks an open place.

I have called this placeholder view of assumptions and the transmission view of hypothetical proofs a dogma of standard semantics. It should be considered a dogma, as it is widely accepted without proper discussion, despite alternative conceptions being readily available. It belongs to standard semantics, as it underlies not only the dominant conception of proof-theoretic semantics, but in some sense it also underlies classical truth-condition semantics. In the classical concept of consequence according to Bolzano and Tarski, the claim that B follows from A is justified by the fact that, in any model of A—in any world, in which A is true—, B is true as well. This means that hypothetical consequence is justified by reference to the transmission of the categorical concept of truth from the condition to the consequent. We are not referring here to functions or any sort of process that takes us from A to B, but just to the metalinguistic universal implication that, whenever A is true, B is true as well. However, as with the standard semantics of proofs, we retain the idea that the categorical concept precedes the hypothetical concept, and the latter is justified by reference to the former concept.

The concept of open proofs in proof-theoretic semantics employs not only the idea that they can be closed by substituting something into the open places, but also the idea that they can be closed outright by a specific operation of assumption discharge. This is what happens with the application of implication introduction as described by Jaśkowski [34] and Gentzen [25]. Here the open place disappears because what is originally expressed by the open assumption now becomes the condition of an implication. This can be described as a two-layer system. In addition to hypothetical judgements given by an open proof with the hypotheses as open places, we have hypothetical judgements in the form of implications, in which the hypothesis is a subsentence. A hypothetical judgement in the sense of an implication is justified by an open proof of the consequent from the condition of the implication. The idea of two layers of hypotheses is typical for assumption-based calculi and in particular for natural deduction, which is the main deductive model of proof-theoretic semantics.

According to the placeholder view of assumptions there are two operations that one can perform as far as assumptions are concerned: Introducing an assumption as an open place, and eliminating or closing it. The closing of an assumption can be achieved in either of two ways: by substituting another proof for it, or by discharge. In the substitution operation the proof substituted for the assumption need not necessarily be closed. However, when it is open then instead of the original open assumption the open assumptions of the substitute become open assumptions of the whole proof. Thus a full closure of an open assumption by means of substitution requires a closed proof as a substitute. To summarise, the three basic operations on assumptions are: assumption introduction, assumption substitution, and assumption discharge.

These three basic operations on assumptions are unspecific in the following sense: They do not depend on the internal form of the assumption, that is, they do not depend on its logical or non-logical composition. They take the assumption as it is. In this sense these operations are structural. The operation of assumption discharge, although pertaining to the structure of the proof, is normally used in the context of a logical inference, namely the introduction of implication. The crucial idea of implication introduction, as first described by Jaśkowski and Gentzen, involves that, in the context of a logical inference, the structure of the proof is changed. This structure-change is a non-local effect of the logical rule.

The unspecific character of the operations on assumptions means that, in the placeholder view, assumptions are not manipulated in any sense. The rules that govern the internal structure of propositions are always rules that concern the assertions, but not the assumptions made. Consequently, the placeholder view is assertion-centred as far as content is concerned. In an inference step we pass from assertions already made to another assertion. At such a step the structure of the proof, in particular which assumptions are open, may be changed, but not the internal form of assumptions. This may be described as the forward-directedness of proofs. When proving something, we may perform structural changes in the proof that lies ‘behind’ us, but without changing the content of what lies behind. It is important to note that we do not here criticise this view of proofs. We merely highlight what one must commit oneself to in affirming this view.

2.2 The No-Assumptions View

The most radical alternative to the placeholder view of assumptions is the claim that there are no assumptions at all. This view is much older than the placeholder view and was strongly advocated by Frege (see for example Frege [22]). Frege argues that the aim of deduction is to establish truth, and, in order to achieve that goal, deductions proceed from true assertions to true assertions. They start with assertions that are evident or for other reasons true. This view of deduction can be traced back to Bolzano’s Wissenschaftslehre [1] and its notion of ‘Abfolge’. This notion means the relationship between true propositions A and B, which obtains if B holds because A holds.

However, in view of the fact that hypothetical claims abound in everyday life, science, legal reasoning etc., it is not very productive simply to deny the idea of hypotheses. Frege was of course aware that ‘if ..., then ...’ statements play a central role wherever we apply logic. His logical notation (the Begriffsschrift) uses implication as one of the primitive connectives. The fact that he can still oppose the idea of reasoning from assumptions is that he denies a two-layer concept of hypotheses. As we have the connective of implication at hand, there is no need for a second kind of hypothetical entity that consists of a hypothetical proof from assumptions. Instead of maintaining that B can be proved from the hypothesis A, we should just be able to prove A implies B non-hypothetically, which has the same effect. There is no need to consider a second structural layer at which hypotheses reside.

For Frege this means, of course, that implication is not justified by some sort of introduction rule, which was a much later invention of Jaśkowski and Gentzen. The laws of implication are justified by truth-theoretic considerations and codified by certain axioms. That A implies itself, is, for example, one of these axioms (in Frege’s Grundgesetze, [21]), from which a proof can start, as it is true.

The philosophical burden here lies in the justification of the primitive axioms. If, like Frege, we have a truth-theoretic semantics at hand, this is no fundamental problem, as Frege demonstrates in detail by a truth-valuational procedure. It becomes a problem when the meaning of implication is to be explained in terms of proofs. This is actually where the need for the second structural layer arises. It was the ingenious idea of Jaśkowski and Gentzen to devise a two-layer method that reduces the meaning of implication to something categorically different. Even though this interpretation was not, or was only partly, intended as a meaning theory for implication (in Gentzen [25] as an explication of actual reasoning in mathematics, in Jaśkowski [34] as an explication of suppositional reasoning) it has become crucial in that respect in later proof-theoretic semantics. The single-layer alternative of starting from axioms in reasoning presupposes an external semantics that is not framed in terms of proofs.

Such an external semantics need not be a classical truth-condition semantics, or an intuitionistic Kripke-style semantics. It could, for example, be a constructive BHK-style semantics, perhaps along the lines of Goodman-Kreisel or a variant of realisability (see, for example, Dean and Kurokawa [4]). We would then have a justification of a formal system by means of a soundness proof. As soon as the axioms or rules of our system are sound with respect to this external semantics, they are justified. In proof-theoretic semantics, understood in the strict sense of the term, such an external semantics is not available. This means that a single-layer concept of implication based only on axioms and rules, but without assumptions, is not a viable option.¹

2.3 Bidirectionality

The transmission view of consequence is incorporated in natural deduction in that we have the operations of assumption introduction, assumption-closure by substitution and assumption-closure by discharge. There are various notations for it. The most common such notation in proof-theoretic semantics is Gentzen’s [25] tree notation that was adopted and popularised by Prawitz [44]. Alternative notations are Jaśkowski’s [34] box notation, which is the origin of Fitch’s [18] later notation. A further notation is sequent-style natural deduction. In this notation proofs consist of judgements of the form $A_1,\ldots ,A_n {{\mathrm{\vdash }}}B$, where the A’s represent the assumptions and B the conclusion of what is claimed. This can be framed either in tree form, in boxed form, or in a mixture of both. With sequent-style natural deduction the operation of assumption discharge is no longer non-local. In the case of implication introduction

(1)

we pass from one sequent to another without changing the structure of the proof. In fact, in such a proof there are no sequents as assumptions, but every top sequent is an axiom, normally of the form $A {{\mathrm{\vdash }}}A$ or $A_1,\ldots ,A_n,A {{\mathrm{\vdash }}}A$. However, this is not a no-assumptions system in the sense of Sect. 2.2: It combines assumption-freeness with a two-layer approach. The structural layer is the layer of sequents composed out of lists of formulas building up the left and right sides (antecedent and succedent) of a sequent, whereas the logical layer concerns the internal structure of formulas. By using introduction rules such as (1), the logical layer is characterised in terms of the structural layer. In this sense sequent-style natural deduction is a variant of ‘standard’ natural deduction.

However, a different picture emerges if we look at the sequent calculus LK or LJ that Gentzen devised. These are two-layer systems in which we can manipulate not only what is on the right hand side and what corresponds to assertions, but also what is on the left hand side and what corresponds to assumptions. In sequent-style natural deduction a sequent

$$\begin{aligned} A_1,\ldots ,A_n {{\mathrm{\vdash }}}B \end{aligned}$$

(2)

just means that we have a proof of B with open assumptions $A_1,\ldots ,A_n$:

(3)

In the symmetric sequent calculus, which is the original form of the sequent calculus, the $A_1, \ldots , A_n$ can still be interpreted as assumptions in a derivation of B, but no longer as open assumptions in the sense of the transmission view. Or at least they can be given an alternative interpretation that leads to a different concept of reasoning. In the sequent calculus we have introduction rules not only on the right hand side, but also on the left hand side, for example, in the case of conjunction:

This can be interpreted as a novel model of reasoning, which is different from assertion-centred forward reasoning in natural deduction. When reading a sequent (2) in the sense of (3), the step of $(\wedge {\text {L}})$ corresponds to:

This is a step that continues a given derivation $\mathscr {D}$ of C from A upwards to a derivation of C from $A \mathbin {\wedge }B$. Therefore, from a philosophical point of view, the sequent calculus presents a model of bidirectional reasoning, that is, of reasoning that, by means of right-introduction rules, extends a proof downwards, and, by means of left-introduction rules, extends a proof upwards.

This is, of course, a philosophical interpretation of the sequent calculus, reading it as describing a certain way of constructing a proof from hypotheses.² Since under this schema both assumptions and assertions are liable to application of rules, assumptions are no longer understood simply as placeholders for closed proofs. Both assumptions and assertions are now entities in their own right. Read in that way we have a novel picture of the nature of hypotheses. We can give this reading a format in natural-deduction style, namely by formulating the rule $(\wedge {\text {L}})$ as

where the line above $A \mathbin {\wedge }B$ expresses that $A \mathbin {\wedge }B$ stands here as an assumption. We may call this system a natural-deduction sequent calculus, that is, a sequent calculus in natural-deduction style. It is a system in which major premisses of elimination rules occur only as assumptions (‘stand proud’ in Tennant’s [70] terminology). The intuitive idea of this step is that we can introduce an assumption in the course of a derivation. If a proof of C from A is given, we can, by introducing the assumption $A \mathbin {\wedge }B$ and discharging the given assumption A, pass over to C. That $A \mathbin {\wedge }B$ occurs only as an assumption and cannot be a conclusion of any other rule, demonstrates that we have a different model of reasoning, in which assumptions are not just placeholders for other proofs, but stand for themselves. The fact that, given a proof of $A \mathbin {\wedge }B$ and a proof of the form

we obtain a proof of C by combining these two proofs is no longer built into the system and its semantics, but something that must be proved in the form of a cut elimination theorem. According to this philosophical re-interpretation of the sequent calculus, assumptions and assertions now resemble handles at the top and at the bottom of a proof, respectively. It is no longer the case that one side is a placeholder whereas the other side represents proper propositions.

This interpretation also means that the sequent calculus is not just a meta-calculus for natural deduction, as Prawitz ([44], Appendix A) suggests. It is a meta-calculus in the sense that whenever there is a natural-deduction derivation of B from $A_1,\ldots ,A_n$, there is a sequent-calculus derivation of the sequent $A_1,\ldots ,A_n {{\mathrm{\vdash }}}B$, and vice versa. However, this does not apply to proofs. There is no rule application in natural deduction that corresponds to an application of a left-introduction rule in the sequent calculus. This means that at the level of proof construction there is no one-one correspondence, but something genuinely original in the sequent calculus. This is evidenced by the fact that the translation between sequent calculus and natural deduction is non-trivial. Prawitz is certainly right that a sequent-calculus proof can be viewed as giving instructions about how to construct a corresponding natural-deduction derivation. However, we would like to emphasise that it can be interpreted to be more than such a metalinguistic tool, namely as representing a way of reasoning in its own right. We do not want to argue here in favour of either of these positions. However, we would like to emphasise that the philosophical significance of the bidirectional approach has not been properly explored (see also Schroeder-Heister, [59]).

2.4 Local and Global Proof-Theoretic Semantics

We have discussed the philosophical background of three conceptions of hypotheses and hypothetical proofs. Each of them has strong implications for the form of proof-theoretic semantics. According to the no-assumptions view (Sect. 2.2) with its single-layer conception there is no structural way of dealing with hypotheses. Therefore, there is no proof-theoretic semantics of implication, at least not along the common line that an implication expresses that we have or can generate a hypothetical proof. We would need instead a semantics from outside.

A proof-theoretic semantics for the placeholder view of assumptions (Sect. 2.1), even though it is assertion-centred, is not necessarily verificationist in the sense that it considers introduction rules for logical operators to be constitutive of meaning. Nothing prevents us from considering elimination rules as primitive meaning-giving rules and justifying introduction rules from them (see Prawitz [49], Schroeder-Heister [67]). However, the placeholder-view forces one particular feature that might be seen as problematic from certain points of view, namely the global character of the semantics.

According to the placeholder-view of assumptions, an open derivation $\mathscr {D}$ of B from A

would be considered valid if for every closed derivation of A

the derivation

obtained by substituting the derivation $\mathscr {D}'$ of A for the open assumption A is valid. This makes sense only if proof-theoretic validity is defined for whole proofs rather than for single rules, since the entity in which the assumption A is an open place is a proof. A proof would not be considered valid because it is composed of valid rules, but conversely, a rule would be considered valid if it is a limiting case of a proof, namely a one-step proof. This is actually how the definitions of validity in the spirit of Prawitz’s work proceed (Prawitz [48], Schroeder-Heister [56, 61]).

This global characteristic of validity has strong implications. We must expect now that a proof as a whole is well-behaved in a certain sense, for example, that it has certain features related to normalisability. In all definitions of validity we have as a fundamental property that a closed proof is valid iff it reduces to a valid closed proof, which means that validity is always considered modulo reduction. And reduction applies to the proof as a whole, which means that it is a global issue. As validity is global, there is no way for partial meaning in any sense. A proof can be valid, and it can be invalid. However, there is no possibility of the proof being only partially valid as reflected in the way the proof behaves.

This global proof semantics has its merits as long as one considers only cases such as the standard logical constants, where everything is well-founded and we can build valid sentences from the bottom up. However, it reaches its limits of applicability, if proof-theoretic semantics should cover situations where we do not have such a full specification of meaning. When dealing with iterated inductive definitions, we can, of course, require that definitions be well-behaved, as Martin-Löf [40] did in his theory. However, when it comes to partial inductive definitions, the situation is different (see Sect. 4).

Here it is much easier to say: We have locally valid rules, but the composition of such rules is not necessarily a globally valid derivation. In a rule-based approach we can make the composition of rules and its behaviour a problem, whereas on the transmission view the validity of composition is always enforced. Substitution becomes an explicit step, which can be problematised. It will be possible, in particular, to distinguish between the validity of rules and the effect the composition of rules has on a proof. In fact, it is not even mandatory to allow from the very beginning that each composition of (locally) valid rules renders a proof valid. We might impose further restriction on the composition of valid rules. This occurs especially when the composition of locally valid rules does not yield a proof the assumptions of which can be interpreted as placeholders, that is, for which the substitution property does not hold.

Therefore, the bidirectional model of proof allows for a local proof-theoretic semantics. Here we can talk simply of rules that extend a proof on the assertion or on the assumption side. There will be rules for each side, and one may discuss issues such as when these rules are in harmony or not. Whether one side is to be considered primary, and, if yes, which one, does not affect the model of reasoning as such. In any case a derivation would be called valid if it consists of the application of valid rules, which is exactly what local proof-theoretic semantics requires.

3 The Problem of Harmony

In the proof-theoretic semantics of logical constants, harmony is a, or perhaps the, crucial concept. If we work in a natural-deduction framework, harmony is a property that introduction and elimination rules for a logical constant are expected to satisfy with respect to each other in order to be appropriate. Harmony guarantees that we do not gain anything when applying an introduction rule followed by an elimination rule, but also, conversely, that from the result of applying elimination rules we can, by applying introduction rules, recover what we started with. The notion of harmony or ‘consonance’ was introduced by Dummett ([13], pp. 396–397).³

However, it is not absolutely clear how to define harmony. Various competing understandings are to be found in the literature. We identify a particular path that has not yet been explored, and we call this path ‘intensional’ or ‘strong’ harmony. The need to consider such a notion on the background of the discussion, initiated by Prawitz [45], on the identity of proofs, in particular in the context of Kosta Došen’s work (see Došen [6, 8, 9], Došen and Petrić [12]), was raised by Luca Tranchini.⁴ As the background to this issue we first present two conceptions of harmony, which are not reliant on the notion of identity of proofs.

3.1 Harmony Based on Generalised Rules

According to Gentzen “the introductions represent so-to-speak the ‘definitions’ of the corresponding signs” whereas the eliminations are “consequences” thereof, which should be demonstrated to be “unique functions of the introduction inferences on the basis of certain requirements” (Gentzen [25], p. 189). If we take this as our characterisation of harmony, we must specify a function $\mathscr {F}$ which generates elimination rules from given introduction rules. If elimination rules are generated according to this function, then introduction and elimination rules are in harmony with each other.

There have been various proposals to formulate elimination rules in a uniform way with respect to given introduction rules, in particular those by von Kutschera [36], Prawitz [47] and Schroeder-Heister [53]. At least implicitly, they all intend to capture the notion of harmony. Read [51, 52] has proposed to speak of ‘general-elimination harmony’. Formulated as a principle, we could say: Given a set $c\mathscr {I}$ of introduction rules for a logical constant c, the set of elimination rules harmonious with $c\mathscr {I}$ is the set of rules generated by $\mathscr {F}$, namely $\mathscr {F}(c\mathscr {I})$. In other words, $c\mathscr {I}$ and $\mathscr {F}(c\mathscr {I})$ are by definition in harmony with each other. If alternative elimination rules $c\mathscr {E}$ are given for c, one would say that $c\mathscr {E}$ is in harmony with $c\mathscr {I}$, if $c\mathscr {E}$ is equivalent to $\mathscr {F}(c\mathscr {I})$ in the presence of $c\mathscr {I}$. This means that, in the system based on $c\mathscr {I}$ and $c\mathscr {E}$, we can derive the rules contained in $\mathscr {F}(c\mathscr {I})$, and in the system based on $c\mathscr {I}$ and $\mathscr {F}(c\mathscr {I})$, we can derive the rules contained in $c\mathscr {E}$.

Consequently the generalised elimination rules $\mathscr {F}(c\mathscr {I})$ are canonical harmonious elimination rules ⁵ given introduction rules $c\mathscr {I}$. The approaches mentioned above develop arguments that justify this distinguishing characteristic, for example by referring to an inversion principle. The canonical elimination rule ensures that everything that can be obtained from the premisses of each introduction rule can be obtained from their conclusion. For example, if the introduction rules for $\varphi$ have the form

the canonical elimination rule takes the form

The exact specification of what the $\Delta _i$ can mean, and what it means to use the $\Delta _i$ as dischargeable assumptions, depends on the framework used (see Schroeder-Heister [63, 65]).⁶

While the standard approaches use introduction rules as their starting point, it is possible in principle, and in fact not difficult, to develop a corresponding approach based on elimination rules. Given a set of elimination rules $c\mathscr {E}$ of a connective c, we would define a function $\mathscr {G}$ that associates with $c\mathscr {E}$ a set of introduction rules $\mathscr {G}(c\mathscr {E})$ as the set of introduction rules harmonious to $c\mathscr {I}$. While the rules in $\mathscr {G}(c\mathscr {E})$ are the canonical harmonious introduction rules, any other set $c\mathscr {I}$ of introduction rules for c would be in harmony with $c\mathscr {E}$ if $c\mathscr {I}$ is equivalent to $\mathscr {G}(c\mathscr {E})$ in the presence of $c\mathscr {E}$. This means that, in the system based on $c\mathscr {E}$ and $c\mathscr {I}$, we can derive the rules contained in $\mathscr {G}(c\mathscr {E})$, and in the system based on $c\mathscr {E}$ and $\mathscr {G}(c\mathscr {E})$, we can derive the rules in $c\mathscr {I}$. For example, if the elimination rules have the form

then the canonical introduction rule takes the form

Here the conclusions of the elimination rules become premisses of the canonical introduction rules. Again, the exact specification of $\Delta _i$ depends on the framework used. For example, if, for the four-place connective $\mathbin {\wedge }\!\!\,\rightarrow \,\!$, the set $\mathbin {\wedge }\!\!\,\rightarrow \,\!\mathscr {E}$ consists of the three elimination rules

we would define $\mathscr {G}(\mathbin {\wedge }\!\!\,\rightarrow \,\!\mathscr {E})$ as consisting of the single introduction rule

In Schroeder-Heister [63] functions $\mathscr {F}$ and $\mathscr {G}$ are defined in detail.

3.2 Harmony Based on Equivalence

Approaches based on generalised eliminations or generalised introductions maintain that these generalised rules have a distinguished status, so that harmony can be defined with respect to them. An alternative way would be to explain what it means that given introductions $c\mathscr {I}$ and given eliminations $c\mathscr {E}$ are in harmony with each other, independent of any syntactical function that generates $c\mathscr {E}$ from $c\mathscr {I}$ or vice versa. This way of proceeding has the advantage that rule sets $c\mathscr {I}$ and $c\mathscr {E}$ can be said to be in harmony without starting either from the introductions or from the eliminations as primary meaning-giving rules. That for certain syntactical functions $\mathscr {F}$ and $\mathscr {G}$ the rule sets $c\mathscr {I}$ and $\mathscr {F}(c\mathscr {I})$, or $c\mathscr {E}$ and $\mathscr {G}(c\mathscr {E})$, are in harmony, is then a special result and not the definiens of harmony. The canonical functions generating harmonious rules operate on sets of introduction and elimination rules for which harmony is already defined independently. This symmetry of the notion of harmony follows naturally from an intuitive understanding of the concept.

Such an approach is described for propositional logic in Schroeder-Heister [66]. Its idea is to translate the meaning of a connective c according to given introduction rules $c\mathscr {I}$ into a formula $c^I$ of second-order intuitionistic propositional logic IPC2, and its meaning according to given elimination rules $c\mathscr {E}$ into an IPC2-formula $c^E$. Introductions and eliminations are then said to be in harmony with each other, if $c^I$ and $c^E$ are equivalent (in IPC2). The introduction and elimination meanings $c^I$ and $c^E$ can be read off the proposed introduction and elimination rules. For example, consider the connective&& with the introduction and elimination rules

Its introduction meaning is $p_1 \,\wedge \,(p_1 \,\rightarrow \,p_2)$, and its elimination meaning is $\mathord {\forall }r_1 r_2 r (((p_1 \,\rightarrow \,r_1) \,\wedge \,(p_2 \,\rightarrow \,r_2) \,\wedge \,((r_1 \,\wedge \,r_2) \,\rightarrow \,r)) \,\rightarrow \,r)$. As these formulas are equivalent in IPC2, the introduction and elimination rules for && are in harmony with each other. Further examples are discussed in Schroeder-Heister [66].

The translation into IPC2 presupposes, of course, that the connectives inherent in IPC2 are already taken for granted. Therefore, this approach works properly only for generalised connectives different from the standard ones. As it reduces semantical content to what can be expressed by formulas of IPC2, it was called a ‘reductive’ rather than ‘foundational’ approach. As described in Schroeder-Heister [63] this can be carried over to a framework that employs higher-level rules, making the reference to IPC2 redundant. However, as the handling of quantified rules in this framework corresponds to what can be carried out in IPC2 for implications, this is not a presupposition-free approach either. The viability of both approaches hinges on the notion of equivalence, that is, the idea that meanings expressed by equivalent propositions (or rules in the foundational approach), one representing the content of introduction-premisses and the other one representing the content of elimination-conclusions, is sufficient to describe harmony.

3.3 The Need for an Intensional Notion of Harmony

Even though the notion of harmony based on the equivalence of $c^I$ and $c^E$ in IPC2 or in the calculus of quantified higher-level rules is highly plausible, a stronger notion can be considered.⁷ Let us illustrate this by an example: Suppose we have the set $\mathbin {\wedge }\mathscr {I}$ consisting of the standard conjunction introduction

and two alternative sets of elimination rules: $\mathbin {\wedge }\mathscr {E}$ consisting of the standard projection rules

and $\mathbin {\wedge }\mathscr {E'}$ consisting of the alternative rules

It is obvious that $\mathbin {\wedge }\mathscr {E}$ and $\mathbin {\wedge }\mathscr {E'}$ are equivalent to each other, and also equivalent to the rule

which is the canonical generalised elimination rule for $\mathbin {\wedge }$. However, do $\mathbin {\wedge }\mathscr {E}$ and $\mathbin {\wedge }\mathscr {E'}$ mean the same in every possible sense? According to $\mathbin {\wedge }\mathscr {E}$, conjunction just expresses pairing, that is, a proof of $p_1 \mathbin {\wedge }p_2$ is a pair $\langle \Pi _1, \Pi _2\rangle$ of proofs, one for $p_1$ and one for $p_2$. According to $\mathbin {\wedge }\mathscr {E'}$, conjunction expresses something different. A proof of $p_1 \mathbin {\wedge }p_2$ is now a pair that consists of a proof of $p_1$, and a proof of $p_2$ which is conditional on $p_1$. Using a functional interpretation of conditional proofs, this second component can be read as a procedure f that transforms a proof of $p_1$ into a proof of $p_2$ so that, according to $\mathbin {\wedge }\mathscr {E'}$, conjunction expresses the pair $\langle \Pi _1,f \rangle$. Now $\langle \Pi _1, \Pi _2\rangle$ and $\langle \Pi _1,f \rangle$ are different. From $\langle \Pi _1,f \rangle$ we can certainly construct the pair $\langle \Pi _1,f(\Pi _1) \rangle$, which is of the desired kind. From the pair $\langle \Pi _1, \Pi _2\rangle$ we can certainly construct a pair $\langle \Pi _1,f' \rangle$, where $f'$ is the constant function that maps any proof of $p_1$ to $\Pi _2$. However, if we combine these two constructions, we do not obtain what we started with, since we started with an arbitrary function and we end up with a constant function. This is an intuition that is made precise by the consideration that $p_1 \mathbin {\wedge }p_2$, where conjunction here has the standard rules $\mathbin {\wedge }\mathscr {I}$ and $\mathbin {\wedge }\mathscr {E}$, is equivalent to $p_1 \mathbin {\wedge }(p_1 \,\rightarrow \,p_2)$, but is not isomorphic to it (see Došen [6, 9]). Correspondingly, only $\mathbin {\wedge }\mathscr {E}$, but not $\mathbin {\wedge }\mathscr {E'}$ is in harmony with $\mathbin {\wedge }\mathscr {I}$.

Unlike the notion of equivalence, which only requires a notion of proof in a system, the notion of isomorphism requires a notion of identity of proofs. This is normally achieved by a notion of reduction between proofs, such that proofs that are linked by a chain of reductions are considered identical.⁸ In intuitionistic natural deduction these are the reductions reducing maximum formulas (in the case of implication this corresponds to $\beta$-reduction), as well as the contractions of an elimination immediately followed by an introduction (in the case of implication this corresponds to $\eta$-reduction) and the permutative reductions in the case of disjunction and existential quantification. Using these reductions, moving from $p_1 \mathbin {\wedge }p_2$ to $p_1 \mathbin {\wedge }(p_1 \,\rightarrow \,p_2)$ and back to $p_1 \mathbin {\wedge }p_2$ reduces to the identity proof $p_1 \mathbin {\wedge }p_2$ (i.e., the formula $p_1 \mathbin {\wedge }p_2$ conceived as a proof from itself), whereas conversely, moving from $p_1 \mathbin {\wedge }(p_1 \,\rightarrow \,p_2)$ to $p_1 \mathbin {\wedge }p_2$ and back to $p_1 \mathbin {\wedge }(p_1 \,\rightarrow \,p_2)$ does not reduce to the identity proof $p_1 \mathbin {\wedge }(p_1 \,\rightarrow \,p_2)$. In this sense $\mathbin {\wedge }\mathscr {E}$ and $\mathbin {\wedge }\mathscr {E'}$ cannot be identified.

More precisely, given a formal system together with a notion of identity of proofs, two formulas $\psi _1$ and $\psi _2$ are called isomorphic if there are proofs of $\psi _2$ from $\psi _1$ and of $\psi _1$ from $\psi _2$, such that each of the combination of these proofs (yielding a proof of $\psi _1$ from $\psi _1$ and $\psi _2$ from $\psi _2$) reduces to the trivial identity proof $\psi _1$ or $\psi _2$, respectively. As this notion, which is best made fully precise in categorial terminology, requires not only a notion of proof but also a notion of identity between proofs, it is an intensional notion, distinguishing between possibly different ways of proving something. The introduction of this notion into the debate on harmony calls for a more finegrained analysis. We may now distinguish between purely extensional harmony, which is just based on equivalence and which may be explicated in the ways described in the previous two subsections, and intensional harmony, which requires additional means on the proof-theoretic side based on the way harmonious proof conditions can be transformed into each other.

However, even though the notion of an isomorphism has a clear meaning in a formal system given a notion of identity of proofs, it is not so clear how to use it to define a notion of intensional harmony. The notion of intensional harmony will also be called strong harmony in contradistinction to extensional harmony which is also called weak harmony.

3.4 Towards a Definition of Strong Harmony

For simplicity, take the notion of reductive harmony mentioned in Sect. 3.2. Given introduction rules $c\mathscr {I}$ and elimination rules $c\mathscr {E}$ of an operator c, it associates with c the introduction meaning $c^I$ and the elimination meaning $c^E$, and identifies extensional harmony with the equivalence of $c^I$ and $c^E$ in IPC2. It then appears to be natural to define intensional harmony as the availability of an isomorphism between $c^I$ and $c^E$ in IPC2. However, this definition turns out to be unsuccessful, as the following observation shows.

What we would like to achieve, in any case, is that the canonical eliminations for given introductions are in strong harmony with the introductions, and similarly that the canonical introductions for given eliminations are in strong harmony with the eliminations. The second case is trivial, as the premisses of the canonical introduction are exactly the conclusions of the eliminations. For example, if for the connective $\mathbin {\leftrightarrow }$ the elimination rules

are assumed to be given, then its canonical introduction rule has the form

Both the elimination meaning $\mathbin {\leftrightarrow }^I$ and the introduction meaning $\mathbin {\leftrightarrow }^E$ have the form $(p_1 \,\rightarrow \,p_2) \,\wedge \,(p_2 \,\rightarrow \,p_1)$, so that the identity proof identifies them. However, in the first case, where the canonical eliminations are given by the general elimination rules, the situation is more problematic.

Consider disjunction with the rules

Here the introduction meaning of $p_1 \mathbin {\vee }p_2$ is $p_1 \mathbin {\vee }p_2$, viewed as a formula of IPC2, and its elimination meaning is $\mathord {\forall }q (((p_1 \,\rightarrow \,q)\,\wedge \,(p_2 \,\rightarrow \,q))\,\rightarrow \,q)$. However, though $p_1 \mathbin {\vee }p_2$ and $\mathord {\forall }q (((p_1 \,\rightarrow \,q)\,\wedge \,(p_2 \,\rightarrow \,q))\,\rightarrow \,q)$ are equivalent in IPC2, they are not isomorphic. There are proofs

of $\mathord {\forall }q (((p_1 \,\rightarrow \,q)\,\wedge \,(p_2 \,\rightarrow \,q))\,\rightarrow \,q)$ from $p_1 \mathbin {\vee }p_2$ and of $p_1 \mathbin {\vee }p_2$ from $\mathord {\forall }q (((p_1 \,\rightarrow \,q)\,\wedge \,{} (p_2 \,\rightarrow \,q))\,\rightarrow \,q)$, so that the composition $\mathscr {D}_2 \circ \mathscr {D}_1$ yields the identity proof $p_1 \mathbin {\vee }p_2$, but there are no such proofs so that $\mathscr {D}_1 \circ \mathscr {D}_2$ yields the identity proof $\mathord {\forall }q (((p_1 \,\rightarrow \,q)\,\wedge \,{} (p_2 \,\rightarrow \,q))\,\rightarrow \,q)$. One might object that, due to the definability of connectives in IPC2, $p_1 \mathbin {\vee }p_2$ should be understood as $\mathord {\forall }q (((p_1 \,\rightarrow \,q)\,\wedge \,(p_2 \,\rightarrow \,q))\,\rightarrow \,q)$, so that the isomorphism between $p_1 \mathbin {\vee }p_2$ and $\mathord {\forall }q (((p_1 \,\rightarrow \,q)\,\wedge \,(p_2 \,\rightarrow \,q))\,\rightarrow \,q)$ becomes trivial (and similarly, if conjunction is also eliminated due to its definability in IPC2). To accommodate this objection, we consider the example of the trivial connective $+$ with the introduction and elimination rules

Here the elimination rule is the canonical one according to the general-elimination schema. In order to demonstrate strong harmony, we would have to establish the isomorphism of p and $\mathord {\forall }q((p \,\rightarrow \,q) \,\rightarrow \,q)$ in IPC2, but this fails. This failure may be related to the fact that for the second-order translations of propositional formulas, we do not have $\eta$-conversions in IPC2 (see Girard et al. [27], p. 85⁹). This shows that for the definition of strong harmony the definition of introduction and elimination meaning by translation into IPC2 is perhaps not the best device. We consider the lack of an appropriate definition of strong harmony a major open problem, and we provide two tentative solutions (with the emphasis on ‘tentative’).

First proposal: Complementation by canonical rules. In order to avoid the problems of second-order logic, we can stay in intuitionistic propositional logic as follows. Suppose for a constant c certain introduction rules $c\mathscr {I}$ and certain elimination rules $c\mathscr {E}$ are proposed, and we ask: When are $c\mathscr {I}$ and $c\mathscr {E}$ in harmony with each other? Suppose $\overline{{c}\mathscr {I}}$ is the canonical elimination rule for the introduction rules $c\mathscr {I}$, and $\overline{c\mathscr {E}}$ is the canonical introduction rule for the elimination rules $c\mathscr {E}$. We also call $\overline{c\mathscr {I}}$ the canonical complement of $c\mathscr {I}$, and $\overline{c\mathscr {E}}$ the canonical complement of $c\mathscr {E}$. We define two new connectives $c_1$ and $c_2$. Connective $c_1$ has $c\mathscr {I}$ as its introduction rules and its complement $\overline{c\mathscr {I}}$ as its elimination rule. Conversely, connective $c_2$ has $c\mathscr {E}$ as its elimination rules and its complement $\overline{c\mathscr {E}}$ as its introduction rules. In other words, for one connective we take the given introduction rules as complemented by the canonical elimination rule, and for the other connective we take the given elimination rules as complemented by the canonical introduction rule. Furthermore, we associate with $c_1$ and $c_2$ reduction procedures in the usual way, based on the pairs $c\mathscr {I}$/$\overline{c\mathscr {I}}$ and $c\mathscr {E}$/$\overline{c\mathscr {E}}$ as primitive rules. Then we say that $c\mathscr {I}$ and $c\mathscr {E}$ are in strong harmony, if $c_1$ is isomorphic to $c_2$, that is, if there are proofs from $c_1$ to $c_2$ and back, such that the composition of these proofs is identical to the identity proof $c_1$ or $c_2$, depending on which side one starts with.¹⁰ In this way, by splitting up c into two connectives, we avoid the explicit translation into IPC2.¹¹

Second proposal: Change to the notion of canonical elimination. As mentioned above, we do not encounter any problem in IPC2, if we translate the introduction meaning of disjunction by its disjunction-free second-order translation, as isomorphism is trivial in this case. In fact, whenever we have more than one introduction rule for some c then the disjunction-free second-order translation is identical to the second-order translation of the elimination meaning for the canonical (indirect) elimination. We have a problem in the case of the connective $+$, which has the introduction meaning p and the elimination meaning $\mathord {\forall }q((p \,\rightarrow \,q) \,\rightarrow \,q)$. However, for $+$ an alternative elimination rule is derivable, namely the rule

In fact, this sort of elimination rule is available for all connectives with only a single introduction rule. We call it the ‘direct’ as opposed to the ‘indirect’ elimination rule. For example, the connective $\mathbin {\mathord { \& }\mathord {\supset }}$ with the introduction rule

has as its direct elimination rules

If we require that the canonical elimination rules always be direct where possible, that is, whenever there is not more than one introduction rule, and indirect only if there are multiple introduction rules, then the problem of reduction to IPC2 seems to disappear. In the direct case of a single introduction rule, the elimination meaning is trivially identical to the introduction meaning. In the indirect case, they now become trivially identical again. This is because disjunction, which is used to express the introduction meaning for multiple introduction rules, is translated into disjunction-free second-order logic in a way that makes its introduction meaning identical to its elimination meaning.

This second proposal would require the revision of basic tenets of proof-theoretic semantics, because ever since the work of von Kutschera [36], Prawitz [47] and Schroeder-Heister [53] on general constants, and since the work on general elimination rules, especially for implication, by Tennant [69, 70], López-Escobar [37] and von Plato [43],¹² the idea of the indirect elimination rules as the basic form of elimination rules for all constants has been considered a great achievement. That said, the abandonment of projection-based conjunction and modus-ponens-based implication has received some criticism (Dyckhoff [15], Schroeder-Heister [66], Sect. 15.8). In fact, even the first proposal above might require this priority of the direct elimination rules. If we consider conjunction with $\mathbin {\wedge }\mathscr {I}$ and $\mathbin {\wedge }\mathscr {E}$ given by the standard rules

then $\overline{\mathbin {\wedge }\mathscr {I}}$ is the generalised $\mathbin {\wedge }$-elimination rule

whereas $\overline{\mathbin {\wedge }\mathscr {E}}$ is identical with $\mathbin {\wedge }\mathscr {I}$. This means that strong harmony would require that projection-based conjunction and conjunction with general elimination are isomorphic, but no such isomorphism obtains.¹³

4 Proof-Theoretic Semantics Beyond Logic

Proof-theoretic semantics has been occupied almost exclusively with logical reasoning, and, in particular, with the meaning of logical constants. Even though the way we can acquire knowledge logically is extremely interesting, this is not and should not form the central pre-occupation of proof-theoretic semantics. The methods used in proof-theoretic semantics extend beyond logic, often so that their application in logic is nothing but a special case of these more general methods.

What is most interesting is the handling of reasoning with information that is incorporated into sentences, which, from the viewpoint of logic, are called ‘atomic’. A special way of providing such information, as long as we are not yet talking about empirical knowledge, is by definitions. By defining terms, we introduce claims into our reasoning system that hold in virtue of the definition. In mathematics the most prominent example is inductive definitions. Now definitional reasoning itself obeys certain principles that we find otherwise in proof-theoretic semantics. As an inductive definition can be viewed as a set of rules the heads of which contain the definiendum (for example, an atomic formula containing a predicate to be defined), it is only natural to consider inductive clauses as kinds of introduction rules, suggesting a straightforward extension of principles of proof-theoretic semantics to the atomic case. A particular challenge here comes from logic programming, where we consider inductive definitions of a certain kind, called ‘definite-clause programs’, and use them not only for descriptive, but also for computational purposes. In the context of dealing with negation, we even have the idea of inverting clauses in a certain sense. Principles such as the ‘completion’ of logic programs or the ‘closed-world assumption’ (which logic programming borrowed from Artificial Intelligence research), are strongly related to principles generating elimination rules from introduction rules and, thus, to the idea of harmony between these rules.

4.1 Definitional Reflection

In what follows, we sketch the idea of definitional reflection, which employs the idea of clausal definitions as a powerful paradigm to extend proof-theoretic semantics beyond the specific realm of logic. It is related to earlier approaches developed by Lorenzen [38, 39] who based logic (and also arithmetic and analysis) on a general theory of admissible rules using a sophisticated inversion principle (he coined the term ‘inversion principle’ and was the first to formulate it in a precise way). It is also related to Martin-Löf’s [40] idea of iterated inductive definitions, which gives introduction and elimination rules for inductively defined atomic sentences. Moreover, it is inspired by ideas in logic programming, where programs can be read as inductive definitions and where, in the attempt to provide a satisfactory interpretation of negation, ideas that correspond to the inversion of rules have been considered (see Denecker et al. [5], Hallnäs and Schroeder-Heister [31]). We take definitional reflection as a specific example of how proof-theoretic semantics can be extended beyond logic, and we claim that such an extension is quite useful. Other extensions beyond logic are briefly mentioned at the end of this section.

A particular advantage that distinguishes definitional reflection from the approaches of Lorenzen and Martin-Löf and makes it more similar to what has been done in logic programming is the idea that the meaning assignment by means of a clausal or inductive definition can be partial, which means in particular that definitions need not be well-founded. In logic programming this has been common from the very beginning. For example, clauses such as

which defines p by its own negation, or related circular clauses have been standard examples for decades in the discussion of normal logic programs and the treatment of negation (see, e.g. Gelfond and Lifschitz [24], Gelder et al. [23]). Within mainstream proof-theoretic semantics, such circular definitions have only recently garnered attention, in particular within the discussion of paradoxes, mostly without awareness of logic programming semantics and developments there. The idea of definitional reflection can be used to incorporate smoothly partial meaning and non-wellfounded definitions. We consider definitional reflection as an example of how to move beyond logic and, with it, beyond the totality and well-foundedness assumptions of the proof-theoretic semantics of logic.

As definitional reflection is a local approach not based on the placeholder view of assumptions, we formulate it in a sequent-style framework. A definition is a list of clauses. A clause has the form

where the head a is an atomic formula (‘atom’). In the simplest case, the body B is a list of atoms $b_1,\ldots ,b_m$, in which case a definition looks like a definite logic program. We often consider an extended case where B may also contain structural implication¹⁴ ‘$\Rightarrow$’, and sometimes even structural universal implication, which essentially is handled by restricting substitution. Given a definition $\mathbb {D}$, the list of clauses with a head starting with the predicate P is called the definition of P. In the propositional case where atoms are just propositional letters, we speak of the definition of a having the form

However, it should be clear that the definition of P or of a is normally just a particular part of a definition $\mathbb {D}$, which contains clauses for other expressions as well. It should also be clear that this definition $\mathbb {D}$ cannot always be split up into separate definitions of its predicates or propositional letters. So ‘definition of a’ or ‘of P’ is a mode of speech. What is always meant is the list of clauses for a predicate or propositional letter within a definition $\mathbb {D}$.

Syntactically, a clause resembles an introduction rule. However, in the theory of definitional reflection we separate the definition, which is incorporated in the set of clauses, from the inference rules, which put it into practice. So, instead of different introduction rules which define different expressions, we have a general schema that applies to a given definition. Separating the specific definition from the inference schema using arbitrary definitions gives us wider flexibility. We need not consider introduction rules to be basic and other rules to be derived from them. Instead we can speak of certain inference principles that determine the inferential meaning of a clausal definition and which are of equal stance. There is a pair of inference principles that put a definition into action, which are in harmony with each other, without one of them being preferential. As we are working in a sequent-style framework, we have inferential principles for introducing the defined constant on the right and on the left of the turnstile, that is, in the assertion and in the assumption positions. For simplicity we consider the case of a propositional definition $\mathbb {D}$, which has no predicates, functions, individual variables or constants, and in which the bodies of clauses are just lists of propositional letters. Suppose $\mathbb {D}_a$ (as above) is the definition of a (within $\mathbb {D}$), and the $B_i$ have the form ‘$b_{i1},\ldots ,b_{i{k_i}}$’, as in propositional logic programming. Then the right-introduction rules for a are

and the left-introduction rule for a is

If we talk generically about these rules, that is, without mentioning a specific a, but just the definition $\mathbb {D}$, we also write $(\vdash \!{\mathbb D})$ and $({\mathbb D}\!\vdash )$. The right introduction rule expresses reasoning ‘along’ the clauses. It is also called definitional closure, by which is meant ‘closure under the definition’. The intuitive meaning of the left introduction rule is the following: Everything that follows from every possible definiens of a, follows from a itself. This rule is called the principle of definitional reflection, as it reflects upon the definition as a whole. If $B_1,\ldots ,B_n$ exhaust all possible conditions to generate a according to the given definition, and if each of these conditions entails the very same conclusion, then a itself entails this conclusion.

This principle, which gives the whole approach its name, extracts deductive consequences of a from a definition in which only the defining conditions of a are given. If the clausal definition $\mathbb {D}$ is viewed as an inductive definition, definitional reflection can be viewed as being based on the extremal clause of $\mathbb {D}$: Nothing else beyond the clauses given in $\mathbb {D}$ defines a. To give a very simple example, consider the following definition:

Then one instance of the principle of definitional reflection with respect to this definition is

Therefore, if we know $\text {anna} {{\mathrm{\vdash }}}\text {tall}$ and $\text {robert} {{\mathrm{\vdash }}}\text {tall}$, we can infer $\text {child}\_\text {of}\_\text {tom} {{\mathrm{\vdash }}}\text {tall}$.

Since definitional reflection depends on the definition as a whole, taking all definientia of a into account, it is non-monotonic with respect to $\mathbb {D}$. If ${\mathbb D}$ is extended with an additional clause

$$ a \ \mathbin {\Leftarrow }\ B_{n+1} $$

for a, then previous applications of the $({\mathbb D}\!\vdash )$ rule may no longer remain valid. In the present example, if we add the clause

$$ \text {child}\_\text {of}\_\text {tom} \ \mathbin {\Leftarrow }\ \text {john} $$

we can no longer infer $\text {child}\_\text {of}\_\text {tom} {{\mathrm{\vdash }}}\text {tall}$, except when we also know $\text {john} {{\mathrm{\vdash }}}\text {tall}$. Note that due to the definitional reading of clauses, which gives rise to inversion, the sign ‘$\mathbin {\Leftarrow }$’ expresses more than just implication, in contradistinction to structural implication ‘$\Rightarrow$’ that may occur in the body of a clause. To do justice to this fact, one might instead use ‘:-’ as in PROLOG, or ‘:=’ to express that we are dealing with some sort of definitional equality.

In standard logic programming one has, on the declarative side, only what corresponds to definitional closure. Definitional reflection leads to powerful extensions of logic programming (due to computation procedures based on this principle) that lie beyond the scope of the present discussion.

4.2 Logic, Paradoxes, Partial Definitions

Introduction rules (clauses) for logically compound formulas are not distinguished in principle from introduction rules (clauses) for atoms. The introduction rules for conjunction and disjunction would, for example, be handled by means of clauses for a truth predicate with conjunction and disjunction as term-forming operators:

In order to define implication, we need a rule arrow in the body, which, for the whole clause, corresponds to using a higher-level rule:

This definition requires some sort of ‘background logic’. By that we mean the structural logic governing the comma and the rule arrow $\Rightarrow$, which determine how the bodies of clauses are handled. In standard logic we have just the comma, which is handled implicitly. In extended versions of logic programming we would have the (iterated) rule arrow, that is, structural implication and associated principles governing it, and perhaps even structural disjunction (this is present in disjunctive logic programming, but not needed for the applications considered here).

It is obvious that $({{\mathrm{\vdash }}}\mathbb {D}_{ log })$ gives us the right-introduction rules for conjunction and disjunction or, more precisely, those for T(A), where A is a conjunction or disjunction. Definitional reflection $(\mathbb {D}_{ log }{{\mathrm{\vdash }}})$ gives us the left-introduction rules. The clause for $T(p \,\rightarrow \,q)$ gives us the rules for implication, where the precise formulation of these rules depends on the exact formulation of the background logic governing $\Rightarrow$.

Definitional reflection in general provides a much wider perspective on inversion principles than deductive logic alone. Using the definitional rule

$$ t \in \{x: a\} \ \mathbin {\Leftarrow }\ a[t/x] $$

we obtain a principle of naive comprehension, which does not lead to a useless theory in which everything is derivable, even if we allow a to be the formula $x \not \in x$ and t the term $\{x: x \not \in x\}$. A definition of the form

$$ p \ \mathbin {\Leftarrow }\ \mathord {\lnot }p $$

yields a paraconsistent system in which both ${{\mathrm{\vdash }}}p$ and ${{\mathrm{\vdash }}}\mathord {\lnot }p$ are derivable, without every other formula being derivable. Formally, this means that the rule of cut

is not always admissible. For special cases cut can be obtained, for example, if the definition is stratified, which essentially means that it is well-founded. So the well-behaviour of a definition in the case of logic, where we do have cut elimination, is due to the fact that it obeys certain principles, which in the general case cannot be expected to hold. This connects the proof theory of clausal definitions with theories of paradoxes, which conceive paradoxes as based on locally correct reasoning (Prawitz [44] (Appendix B), Tennant [68], Schroeder-Heister [62], Tranchini [71]).

For the situation that obtains here, Hallnäs [28] proposed the terms ‘total’ vs. ‘partial’ in analogy with the terminology used in recursive function theory. That a computable (i.e., partial recursive) function is total is not something required by definition, but is a matter of (mathematical) fact, actually an undecidable matter. Similarly, that a clausal definition yields a system that admits the elimination of cuts is a result that may or may not hold true, but nothing that should enter the requirements for something to be admitted as a definition. If it holds, the definition is called ‘total’, otherwise it is properly ‘partial’.

4.3 Variables and Substitution

The idea of proof-theoretic semantics beyond logic invites consideration of powerful inversion principles that extend the simple form of definitional reflection considered above. Although we mentioned clauses that contained variables, we formally defined definitional reflection only for propositional definitions of the form $\mathbb {D}_a$, where it says that everything that can be inferred from each definiens can be obtained from the definiendum of a definition. However, this is insufficient for the more general case which is the standard case in logic programming. We show this by means of an example. Suppose we have the following definition in which the atoms have a predicate-argument-structure:

$$ \ \left\{ \begin{array}{rcl} \text {child}\_\text {of}\_\text {tom(anna)} &{} {}\mathbin {\Leftarrow }{} &{} \text {daughter}\_\text {of}\_\text {tom(anna)} \\ \text {child}\_\text {of}\_\text {tom(robert)} &{} {}\mathbin {\Leftarrow }{} &{} \text {son}\_\text {of}\_\text {tom(robert)} \\ \text {tall(anna)} &{} {}\mathbin {\Leftarrow }{} &{} \text {daughter}\_\text {of}\_\text {tom(anna)} \\ \text {tall(robert)} &{} {}\mathbin {\Leftarrow }{} &{} \text {son}\_\text {of}\_\text {tom(robert)} \end{array} \right. $$

Given our propositional rule of definitional reflection, we could just infer propositional results such as $\text {child}\_\text {of}\_\text {tom(anna)} {{\mathrm{\vdash }}}\text {tall(anna)}$ or $\text {child}\_\text {of}\_\text {tom(robert)} {{\mathrm{\vdash }}}{} \text {tall}\text {(robert)}$. However, what we would like to infer is the principle

$$\begin{aligned} \text {child}\_\text {of}\_\text {tom}(x) {{\mathrm{\vdash }}}\text {tall}(x) \end{aligned}$$

with free variable x, since anna and robert are the only objects for which the predicate child_of_tom is defined, and since for them the desired principle holds.

In an even more general case, we have clauses that contain variables the instances of which match instances of the claim we want to obtain by definitional reflection. Consider the definition

$$ \mathbb {D}_1\left\{ \begin{array}{rll} p(y,a) &{} {}\mathbin {\Leftarrow }{} &{} q(y) \\ p(x,f(a)) &{} {}\mathbin {\Leftarrow }{} &{} q(f(x)) \end{array}\right. $$

According to the principle of general definitional reflection, we obtain, with respect to $\mathbb {D}_1$,

$$ p(a,z) {{\mathrm{\vdash }}}q(z) $$

The intuitive argument is as follows: Suppose p(a, z). Any, and in fact the only, substitution instance of p(a, z) that can be obtained by the first clause is generated by substituting a for y in the first clause, and a for z in p(a, z). We denote this substitution by [a / y, a / z] and call it $\sigma _1$. Any, and in fact the only, substitution instance of p(a, z) that can be obtained by the second clause is generated by substituting a for x in the second clause, and f(a) for z in p(a, z). We denote this substitution by [a / x, f(a) / z] and call it $\sigma _2$. When $\sigma _1$ is applied to the body of the first clause, q(a) is obtained, which is also obtained when $\sigma _1$ is applied to q(z). When $\sigma _2$ is applied to the body of the second clause, q(f(a)) is obtained, which is also obtained when $\sigma _2$ is applied to q(z). Therefore, we can conclude q(z).

In the propositional case we could describe definitional reflection by saying that every C that is a consequence of each defining condition is a consequence of the definiendum a. We cannot now even identify a single formula as a definiendum, as any formula which is a substitution instance of a head of a definitional clause is considered to be defined. Therefore we should now say: Suppose a formula a is given. If for each substitution instance $a\sigma$ that can be obtained as $b\sigma$ from the head of a clause $b \ \mathbin {\Leftarrow }\ C$, we have that $C\sigma$ implies $A\sigma$ for some A, then A can be inferred from a.

Formally, this leads to a principle of definitional reflection according to which, for the introduction of an atom a on the left side of the turnstile, the most general unifiers mgu(a, b) of a with the heads of all definitional clauses are considered:

$$ (\mathbb {D}\!\vdash )_\omega \ \frac{\{\Gamma \sigma ,C\sigma \,\vdash A\sigma : \sigma = mgu(a,b)\ \mathrm{for\ some\ clause\ } b \ \mathbin {\Leftarrow }\ C \mathrm{\ in\ } {\mathbb {D}}\}}{\Gamma ,a \,\vdash A} $$

with the proviso: The variables free in $\Gamma , a \mathbin {\vdash }A$ must be different from those in the $b\ \mathbin {\Leftarrow }\ C$ above the line. This means that we always assume that variables in clauses are standardised apart. We call this principle the $\omega$-version of definitional reflection, as it is in a certain way related to the $\omega$-rule in arithmetic, a point that we cannot elaborate on here (see Schroeder-Heister [55]).

This powerful principle is typical of applications outside logic. When we consider logical definitions such as $\mathbb {D}_{ log }$, we see that each formula T(a), where a is a compound logical formula, determines exactly a single head b in one or two clauses (two in the case of disjunction), such that T(a) is a substitution instance of b. This means that (1) there is just matching and no unification between b and T(a), and (2) there is just a single substitution for the main logical connective in T(a) involved due to the strict separation between the clauses for the different logical connectives, implying that there is no overlap between substitution instances of clauses.

The power of the $\omega$-version of definitional reflection is demonstrated, for example, by the fact that the rules of free equality can be obtained from the definition consisting of the single clause

$$ \mathbb {D}_=\left\{ \ x= x\ \mathbin {\Leftarrow }\ \right. $$

For example, the transitivity of equality is derived by a single inference step as follows:

Here we use that the substitution $[x_2/x_1, x_2/x]$ is an mgu of $x_1 = x_2$ with the head $x=x$ of the clause $x=x\ \mathbin {\Leftarrow }\$. In a similar way, all freeness axioms of Clark’s equational theory [35] can be derived.¹⁵

4.4 Outlook: Applications and Extensions of Definitional Reflection

We have not discussed computational issues here. Clausal definitions give rise to computational procedures as investigated and implemented in logic programming, and definitional reflection adds a strong component to such computation (see Hallnäs and Schroeder-Heister [31], Eriksson [17]). This computational aspect is important to proof-theoretic semantics. We should not only be able to give a definition of a semantically correct proof, where ‘semantically’ is understood in the sense of proof-theoretic semantics, we should also be interested in ways to construct such proofs that proceed according to such principles. Programming languages, theorem provers and proof editors based on inversion principles make important contributions to this task. Devising principles of proof construction that can be used for proof search is itself an issue of proof-theoretic semantics that is a desideratum in the philosophically dominated community. Theories that go beyond logic are of particular interest here, as theorems outside pure logic are what we normally strive for in reasoning.

If we want to deal with more advanced mathematical theories, stronger closure and reflection principles are needed. At an elementary level, clauses $a \ \mathbin {\Leftarrow }\ B$ in a definition can be used to describe function computation in the form

$$ f(x_1,\ldots ,x_k) \ \mathbin {\Leftarrow }\ (x_1,\ldots ,x_k) $$

which is supposed to express that from the arguments $x_1,\ldots ,x_k$ the value $f(x_1,\ldots ,x_k)$ is obtained, so that by means of definitional reflection $f(x_1,\ldots ,x_k)$ can be computed. More generally, one might describe functionals F by means of (infinitary) clauses the bodies of which describe the evaluation of functions f which are arguments of F (for some hints see Hallnäs [29, 30]). An instructive example is the analysis of abstract syntax (see McDowell and Miller [41]).

There are several other approaches that deal with the atomic level proof-theoretically, that is, with issues beyond logic in the narrower sense. These approaches include Negri and von Plato’s [42] proof analysis, Brotherston and Simpson’s [2] infinite derivations, or even derivations concerning subatomic expressions (see Więckowski [73]), and corresponding linguistic applications, as discussed by Francez and Dyckhoff [19] and Francez et al. [20]. Proof-theoretic semantics beyond logic is a broad field with great potential, the surface of which, thus far, has barely been scratched.