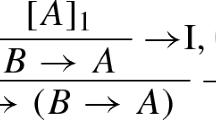It was very kind of Peter Schroeder-Heister to invite me to contribute to this meaty conference. He said:

(1)

That’s a fantastic invitation, and I went to the meeting resolved to disagree with as many people as possible.

In the event it was not so easy. Partly there was serious research being done in proof theory, and I am not a proof theorist. Partly there were a good number of entirely sensible and friendly people. But also I often found it hard to see what the issues were. I think this was not entirely my fault. Straw men were being set up and knocked down. I could see this most clearly when the straw men were described as model theorists, because I do know something about model theory, and some of the views being attributed to model theorists were not ones I recognised. This impression was strengthened when I read a recent paper of Peter’s in Synthese [14].

So I had plenty to disagree with, but not in a very satisfactory way. It’s more edifying to discuss substantive issues than to clear away misunderstandings. But the clearance work has to be done first. I will try to keep it both brief and profitable.

I thank Peter Schroeder-Heister and Kosta Došen for some valuable discussions.

1 Straw Model Theory

A good place to start will be an elegant paper of Dag Prawitz [11] from 1974. There is a lot that I agree with in the paper, but I was pulled up sharp when he said:

(2)

I can say with absolute confidence that I never met a model theorist who ‘concentrates on questions like what sentences are logically valid and what sentences follow logically from other sentences’. On his next page Prawitz discusses Alfred Tarski’s proposal for defining logical consequence, from his paper of 1936 [17]. So it seems likely that Prawitz reached the view stated in (2) by assuming that Tarski’s 1936 paper is of interest to model theorists. This is not in fact the case. Nothing in the paper is of any interest to model theorists, except perhaps those with an interest in the prehistory of their subject.

Peter Schroeder-Heister adds another ingredient to the mix in his recent paper [14], namely model-theoretic semantics. This is a discipline concerned with describing meanings, so Peter rightly connects it with questions about how one should describe the meanings of logical constants. But its origins are quite different from those of the model-theoretic truth definition, and it belongs to a different research community. Model theorists don’t do model-theoretic semantics either. I do know one person who contributes to model-theoretic semantics using techniques of model theory, namely Dag Westerståhl; but there are not many of him. In short, the three areas of research—model theory, the definition of logical consequence and model-theoretic semantics—are quite different and they have hardly anything in common beyond a connection with models in the sense associated with Alfred Tarski.

So now let me unpick the historical relations between these areas. (All the comments on Tarski below draw out material from my [10].)

There are some other research areas that connect with Tarski’s notion of models but not with each other. One is mental model theory as pursued by the cognitive scientist Ruth Byrne [2], and another is the model-theoretic syntax advocated by the linguists Geoffrey Pullum and Barbara Scholz [12].

1.1 Tarski’s Definition of Logical Consequence

During the years 1929–1933 Tarski put together a definition of the concept ‘\(\phi \) is a true sentence of the language L’ [16], which has become known as ‘Tarski’s definition of truth’. Tarski stated some very strict conditions that his definition had to meet. All symbols of the language L (apart from punctuation—we ignore this below) must be fully meaningful. The definition is written in the formalised metalanguage of L, but justified in the informal meta-metalanguage. It must use only higher-order logic, concepts expressible in the language L itself, and some syntactic notions. It must be extensionally correct: the objects satisfying it must be exactly the objects that we count intuitively as true sentences of L. The extensional correctness must be informally provable in the meta-metatheory of L. This is not the place to go into further details. The paper became well known through a German translation in 1935. It makes no reference to models, and model theorists don’t cite it.

In 1935 Tarski was persuaded to attend the International Congress of Philosophers in Paris. Worrying about what he could say to impress the philosophers, he formed the idea of presenting the truth definition as a vehicle for giving formal definitions of various notions from logical metatheory, among them the notion of logical consequence. The result was a pair of papers, [17] presenting the definition of logical consequence, and [18] discussing the general idea of defining semantic notions [5, pp. 95ff].

The paper [17] on logical consequence answered a methodological question, not a question of conceptual analysis. You can’t do conceptual analysis until you have a concept to analyse. But when Tarski wrote, there was no agreed concept of logical consequence to be analysed. (One should look first at what was available in the literature of his time. For example Hilbert and Ackermann [8, p. 1] have a proof-theoretic notion of Logische Folgerung, while Carnap [3, p. 10] speaks of one proposition being a Grund for another, without any clear definition. Tarski may also have factored in earlier ideas, like Bolzano’s Ableitbarkeit and various medieval notions of consequentia.) Tarski makes exactly this point in his opening paragraph, noting that ‘every precise definition of this concept will show arbitrary features to a greater or [lesser] degree’ [19, p. 409]. In fact the term ‘logical consequence’ itself seems to have become common in philosophical logic only as a result of Tarski’s paper.

To see what the methodological question was, we need to put the paper in context. Gödel had recently shown that there is no maximal proof calculus for pure logic of second or higher order. Ramsey [13] had discussed languages with infinite conjunctions, and both Bernays [1, pp. 86ff.] and Tarski himself [19, p. 288] had considered proof rules with infinitely many premises. So some very general questions about proof calculi were in the air, and some robust and well-motivated definitions were needed for handling them. Tarski seems to have clarified the central question in his own mind along the following lines:

He proposed to label these constraints as saying that the conclusion of the rule is a ‘logical consequence’ of its premises.

Now for Tarski in 1935 there were two kinds of formal language. In the first kind, which we can call ‘pure’ languages, all symbols are logical. In the second kind, which we can call ‘applied’, there are also nonlogical symbols, but these symbols are all required to be fully meaningful. For pure languages, Tarski adopted just the constraint that whenever the premises are true the conclusion must be true too. This constraint looks trivial, but in Paris in 1935 it served the purpose of advertising his recent formal definition of ‘true’.

For applied languages Tarski had to decide what to do about analytical relations between the meanings of the nonlogical constants. For example Hilbert in his Göttingen lectures around 1920 (which formed the basis of his book with Ackermann) had observed that ‘Tony Blair is a parent’ entails ‘Tony Blair has a child’ (my adaptation of Hilbert’s more traditional example). Would it be appropriate to allow an inference rule that takes one from the first sentence to the second? Tarski decided no. An inference rule should be invariant under systematic changes of the meanings of the nonlogical symbols; but if we swap the meanings of ‘has a child’ and ‘has bright red hair’, then the proposed inference rule would take a true premise to a false conclusion.

It’s noticeable that Tarski’s own text says almost nothing about relations between the meanings of the nonlogical constants (there is a brief parenthetical remark in the middle of P. 415 in [19]), but has at least a page on the importance of the difference between (i) changing a symbol to one with a different meaning and (ii) replacing the symbol by a variable that arbitrary objects can be assigned to. That tells me that Tarski in 1935 was really more interested in fine-tuning the notion of satisfaction than in accommodating the philosophers in Paris.

The paper does use the word ‘model’, though not in the modern sense. The name ‘model-theoretic definition of logical consequence’ is not Tarski’s, and I think it came into use only after the later developments that we turn to next.

1.2 Model Theory

During the 1930s and 1940s Tarski maintained a strict distinction between mathematics and metamathematics. Because of this, he was still in 1938 reluctant to accept that a set of formal axioms could serve to define the class of structures which satisfy them—as for example the class of rings consists of the structures that satisfy the axioms of ring theory. But mathematical developments put him under pressure to change his mind. By 1950 he was ready to embrace what we now know as model theory, and he devoted the early 1950s to setting up the basics of the theory.

In the course of this work, Tarski rejigged his old truth definition, so that instead of defining ‘\(\phi \) is a true sentence of the language L’ it defined ‘\(\phi \) is a sentence true in the structure M for the language L’, where now L is a formal language whose nonlogical symbols have no meaning and the structure M is used to assign meanings to these symbols. This new truth definition is known as the ‘model-theoretic truth definition’. You can find it in standard textbooks of model theory. But in practice model theorists mostly use just the separate recursive clauses of the definition, for example that \(\bar{a}\) satisfies \(\mathord {\forall }y \phi (\bar{x},y)\) in M if and only if for every element b of M, \(\bar{a}b\) satisfies \(\phi (\bar{x},y)\) in M. These clauses are all older than Tarski’s work. The definition as a whole does guarantee that the relation ‘\(\phi \) is true in the structure M’ is set-theoretically definable, though today most logicians would reckon that this is intuitively obvious. Occasionally it’s useful to know that the definition can be written as a set-theoretic formula of a particular form.

The model-theoretic truth definition uses an adaptation of the idea of satisfaction that Tarski introduced in his 1933 truth definition and exploited in the 1936 paper. If you apply that model-theoretic adaptation to the 1936 definition of logical consequence, you get

(3)

where now \(\phi \) is a sentence and T a set of sentences, in a language whose nonlogical symbols are meaningless. It happens that the righthand clause of (3) is a relation that appears very often in model theory, so it would be useful to have a name for it. On the basis of the facts above, Tarski in 1953 [20, p. 8] proposed reading the relation as ‘\(\phi \) is a logical consequence of T’. Model theorists have tended to follow Tarski’s lead and pronounce the relation as ‘T entails \(\phi \)’ or ‘\(\phi \) is a consequence of T’. The use of the name has nothing to do with any interest in the concept of logical consequence itself.

Tarski’s 1953 essay [20] seems to have had some unintended consequences among philosophers. A number of people conflated the 1936 definition with the 1953 one, and called both of them the ‘model-theoretic definition of logical consequence’. I think the conflation is unfortunate, because the question we discussed in 1.1.1 above, about analytical relations between meanings, is one of the most important questions addressed in the 1936 definition, but it is meaningless for the languages of first-order model theory. Later, during the 1980s, the ‘model-theoretic definition of logical consequence’ attracted the attention of some philosophers who reassessed it as a contribution to conceptual analysis.

Peter in his invitation to me (1) referred to a ‘defence of model theory, as far as the foundations of logic are concerned’. I think I’ll give this a miss. To me, model theory is a way of addressing certain kinds of question in mathematics, chiefly but not exclusively in geometry, algebra and number theory. The main link to foundations of logic is that some techniques of model theory made their way into axiomatic set theory around 1960 and continue to have an influence in large cardinal theory.

1.3 Model-Theoretic Semantics

So far, nothing that I’ve mentioned is directly to do with semantics, i.e. the study of meanings. Tarski called his truth definition the ‘semantic definition of truth’, most probably because of a formal similarity with what Kotarbiński had called ‘semantic definitions’. In his truth paper [19, p. 193f.] he listed some notions that he called ‘semantic’: denotation, definability, truth. The notion ‘meaning’ was not in his list, and this is certainly not an accident.

During the 1960s a number of papers appeared that were about extending model theory from non-modal formal languages to modal ones. Some people described this as giving ‘model-theoretic semantics’ for modal logics. I suppose that originally ‘giving a semantics’ meant giving a model theory that would allow one to talk in a concrete and precise way about truth and satisfaction of modal formulas. But a subtle shift started to take place. In a standard model for modal logic, each relation symbol has an ‘intension’, which is a function taking each possible world to a set that is the extension of the relation symbol in that world. You can think of extensions as references, and intensions as meanings—though a lot of people have criticised these analogies. So you can think of a model for the modal logic as assigning to each meaningful expression of the language an intension that represents the ‘meaning’ of that expression. Around 1970 Richard Montague adapted all these notions to the study of fragments of natural languages, building on earlier work of Rudolf Carnap. From that date onwards it became common to refer to Montague-style model theories of natural language as ‘model-theoretic semantics’. (Though Barbara Partee, a pioneer in this area, describes her field as ‘formal semantics’.) From the mid 1970s onwards, the people who did model-theoretic semantics were mostly linguists or philosophers of language. The earlier model-theoretic semantics had been done mostly by philosophical logicians, and almost never by model theorists.

Model-theoretic semantics is useless for lexicography—you learn nothing about the meaning of the Greek noun skindapsós by being told that its intension maps every possible world to the set of all the things in that world that fit the description skindapsós. But it comes into its own for describing how the meaning of a compound phrase depends on the meanings of its constituents. Earlier we illustrated how the clauses of Tarski’s truth definition tell us what things satisfy a compound formula, in terms of what things satisfy its immediate subformulas. Tarski had one clause for each logical operator: the logical operators \(\mathbin {\rightarrow }\), \(\lnot \), \(\mathord {\forall }\) etc., are all of them expressions whose meaning is explained by saying how the meaning of a compound formed by means of them depends on the meanings of the constituent expressions. In modal logic and its variants we add to those logical constants other expressions like ‘necessarily’, ‘believes’, ‘until’. Formal semanticists push the boat out and apply similar machinery to ‘himself’, ‘hardly ever’ and ‘so much as’ (for example).

Model-theoretic semantics and the model-theoretic definition of logical consequence were always completely separate. You might reckon that there is a link, because both of them are involved with giving meanings. But there are major differences. First, in studying logical consequence we are only concerned with the meaning of one expression; model-theoretic semantics aims to get a purchase on language as a whole. Second, Tarski always assumed that the expression ‘logical consequence of’ was not in the formal language L; it was an expression of the metatheory. Of course one can put it into the object language, but Tarski himself avoided doing this, because he had proved that languages containing enough of their own metatheory generate contradictions. So a person who wants to add ‘logical consequence of’ to the object language has the extra task of proving that the resulting language is still consistent. And third, the aim with logical consequence was to give a definition of it, under suitable constraints. Model-theoretic semantics doesn’t give definitions, it gives truth-conditions.

So it was curious to read the introduction to Peter Schroeder-Heister’s [14] and find him claiming that ‘classical model-theoretic semantics’ makes various assumptions about how logical consequence should be defined. I assumed at first that he was using ‘model-theoretic semantics’ as a name for the model-theoretic definition of logical consequence. But then almost at once he talks about model-theoretic treatment of the logical operators, and that really is in the realm of model-theoretic semantics. Well, it’s not good history but it’s an intriguing question all the same. Could there be a theory that helpfully combines definition of metatheoretic notions with the techniques of model-theoretic semantics? What problems would it run into? What constraints should it aim to observe? What kinds of new result could we expect from combining the two things? I think it’s clear that Peter himself doesn’t want to go down this road, but somebody else might. (Maybe somebody already has, in which case I give them my apologies and best wishes.)

2 Defining Meanings in General

We can separate out two strands in the aims of proof-theoretic semantics. One is to use proof theory to specify the meanings of logical constants. This can be generalised to specifying the meanings of other expressions too. (Peter tells me he would welcome faster progress in this direction, for example using more advanced proof-theoretic tools like those used to handle inductive definitions.) The other is to give a good description of logical consequence from the point of view of proof theory. I assume Peter’s invitation was to comment on both of these aims. In this section I tackle meanings in general, and in the next section I turn to logical consequence.

2.1 Defining Meanings: Specialise Then Generalise

In the introduction to his Stanford Encyclopedia entry on ‘Proof-Theoretic Semantics’ [15] Peter says:

That’s a very reasonable starting-point. I wasn’t clear whether Peter takes ‘our language’ to be English (or German), or a formal language used in logic, but I’ll assume the former. Paraphrasing Peter’s statement a little, the meaning of an expression E in a language L is what you need to know in order to use E in L. But we should exclude purely grammatical information about E, so a safer statement is

There is more to be said on this, but not here.

Straight away we hit a problem. Life is open-ended, and so is language. The same expression can be used in indefinitely many different situations, and a priori there is no reason to think we can write down the rules for using the expression in a manageable description that covers all cases. This certainly applies to the logical constants ‘and’, ‘every’ and so on, which occur throughout the language and not just in contexts of logical argument.

So in practice we do what linguists have to do constantly in their studies. We narrow down to a set of contexts that we can handle, and we give rules for using the expression in those contexts. Then we rely on general facts about life and language to determine how the expression would be used in other contexts. I will call the narrow set of contexts the primary applications, and I will call the arguments used for generalising from the primary applications to the whole language the transfer arguments.

The ‘Frege-Geach problem’ illustrates these notions. In 1965 Peter Geach wrote a paper [7] in which—among other things—he attacked the view that you can explain the meaning of the sentence

(4)

by saying that it ascribes a certain kind of action to ‘him’. Geach argues that this explanation won’t carry over to contexts where (4) is used but not asserted, for example when it follows the word ‘If’. In contexts where (4) is not asserted, it doesn’t ascribe anything. But, says Geach, the explanation needs to be carried over to these contexts, because we can apply modus ponens and argue

Moreover the two occurrences of the sentence, ‘by itself and in the “if” clause, must have the same sense if the modus ponens is not to be vitiated by equivocation’ [7, p. 462f].

I used to think that Geach’s argument was a very clever way of refuting all sorts of plausible theories. I still think it’s clever, but now it seems to me to prove almost nothing. When we explain how an expression is used in certain contexts, transfer arguments will always be needed to infer how it is used in other contexts. In fact looking again at Geach’s paper, I see that this agrees with his conclusion:

The key point that Geach contributes is that the validity of the modus ponens argument is a constraint on possible transfer arguments.

We must ask: Who has the responsibility for handling the transfer arguments?

To illustrate with ‘and’: a person who is explaining ‘the way it is used in our language’ will need to explain its use not just between propositions in deductions, but also such uses as

(5)

There are subtleties here: a formally correct and materially adequate definition is a formally correct definition that is also materially adequate, but a black and white cat is not a black cat that is also white. How did we know this?

You might argue that this property of ‘black and white’ is something for the linguists to worry about, and not a thing that proof theorists could be expected to have views on. But on the other hand linguists can’t make bricks without straw: if the proof theorists expect the linguists to explain how the proof-theoretic meaning of ‘and’ transfers to uses like those in (5), then they must be prepared for the linguists to complain that the proof-theoretic meaning just isn’t enough to generalise from. Somebody has to take responsibility for the join-up.

The point is very general. For example an explanation of the meaning of ‘He hit her’ in terms of truth conditions raises the question how we can infer what it means to say

Obviously if you specified the meaning of ‘hit’ as the set of ordered pairs (a, b) such that a hit b, then you are going to have serious problems answering this question. (I stole this example from the great 11th century semanticist Abd al-Qāhir al-Jurjānī. Today people working on the semantics of tree-adjoining grammars wrestle with the same problem.)

2.2 Representing the Meaning

When we describe the meaning of an expression, we always do it in some format: maybe a picture, or a diagram, or a formal definition in words, or a physical demonstration, or an abstract set, or ...  In other words, the information about the expression always has to be packaged up as an object—I will call the object the semantic value of the expression—in some form of representation. This places on us the burden on making sure that both we and the people we are speaking to can read the representation, i.e. that we can understand what information the semantic value is supposed to convey.

There is a great temptation for logicians just to throw symbols on the page and hope that they are self-explanatory. For example we might write, as a partial explanation of ‘and’:

(6)

But what does this diagram mean? Does it mean for example one of the following?

(a):

If we are entitled to assert \((\phi {\text {and}} \psi )\) then this fact entitles us to assert \(\phi \).

(b):

If we have already asserted \((\phi {\text {and}} \psi )\) then we are entitled to assert \(\phi \).

(c):

If we are committed to defending \((\phi {\text {and}} \psi )\) then we are committed to defending \(\phi \).

(d):

If \((\phi \mathbin {\wedge }\psi )\) is true then so is \(\phi \).

(e):

In any situation S, if \((\phi \mathbin {\wedge }\psi )\) is true in S then \(\phi \) is true in S.

Some of these statements are deducible from others by general principles. Let me straight away generalise the notion of transfer arguments to include the arguments that justify these deductions. These arguments generalise not from one context of use to another, but from one kind of statement about use to another kind of statement about use.

Note that if we use reading (e), then there is a very plausible argument to show that the natural deduction rules for \(\mathbin {\wedge }\) and the standard truth table for \(\mathbin {\wedge }\) give exactly the same information about \(\mathbin {\wedge }\), so that in this case the difference between a proof-theoretic semantics and a model-theoretic one becomes purely one of notation. But in any case a person who wants to compare model-theoretic semantics with proof-theoretic semantics for logical operators will need to answer the question above for (6), and similar ones for the other natural deduction diagrams and for truth tables. This applies to intuitionist logical operators just as much as to classical ones.

There seem to be more ways of reading a formal derivation than there are of reading a truth table. Derivations, particularly in Hilbert-style or natural deduction formalisms, look a bit like formalised natural language arguments. But usually they are missing the explanatory tags that we put all over the place in natural language arguments: ‘Then’, ‘But’, ‘Suppose’, ‘I grant that’, ‘I think I can show that’, ‘I claim that’ etc. etc.

To illustrate the possibilities, let me sketch how Ibn Sīnā thought we should read arguments in which an assumption is made and then discharged [9]. He observed that when we introduce an assumption \(\phi \) by saying ‘If \(\phi \)’, we don’t always repeat the ‘If \(\phi \)’ whenever we state a proposition that depends on the assumption. (That’s certainly so if \(\phi \) is introduced with ‘Let’ or ‘Suppose’. But Ibn Sīnā is right; one can find enough examples where it’s true with ‘If’ too.) So, he argued, we must intend that ‘If \(\phi \) then’ should be understood at the beginning of all relevant propositions down to the point where the assumption is discharged. So we should understand

(7)

In the ‘understood but not stated’ derivation on the right, the formula \((\phi \mathbin {\rightarrow }\phi )\) at the top is an axiom, and the discharging step that derives \((\phi \mathbin {\rightarrow }\chi )\) from \(\chi \) falls away. A general metarule asserts that for every step \(\Delta , \alpha \vdash \beta \) we have a step \(\Delta , (\phi \mathbin {\rightarrow }\alpha ) \vdash (\phi \mathbin {\rightarrow }\beta )\). (This analysis is extraordinarily close to Frege’s explanation of making and discharging assumptions, though it was given over 800 years before Frege. But as Peter noted at the meeting, Ibn Sīnā and Frege had different motivations. In fact Ibn Sīnā wanted to understand the real intentions of the person giving the proof, whereas Frege aimed through Begriffsschrift to display the true ‘logical weaving’ of informal proofs that begin ‘Let ...’ [6, pp. 379ff].)

Ibn Sīnā’s position is in effect a claim about what kind of contentful argument is expressed by the natural deduction rules. So it’s directly relevant to how we can read the proof rule of \(\mathbin {\rightarrow }\)-introduction as carrying information about the meaning of \(\mathbin {\rightarrow }\).

The discussion so far has used only natural deduction proof rules. It would be possible to give a semantics using \(\vdash \) as a primitive notion, so that for example we define \(\mathbin {\wedge }\) by

(8)

(There are well-known variants of this definition.) The difficulty with taking \(\vdash \) as primitive is that until we have a definition of \(\vdash \), there is going to be no purchase for transfer arguments. In particular we won’t be able even to raise the question whether (8) gives the same information as a truth table for \(\mathbin {\wedge }\), frankly because until \(\vdash \) is explained, we don’t know what information (8) is giving us.

One last point: some kinds of semantics refer to the semantic value of an expression as the ‘denotation’ of the expression. This is just a name, no more. It certainly doesn’t entail that the semantics treats expressions as proper names of their semantic values. To single out some kinds of semantics as ‘denotational’ is like singling out the semantics that are written in Turkish; the classification is pointless.

3 Defining Logical Consequence

In both his truth definition and his definition of logical consequence, Tarski set new standards of carefulness about the requirements he was imposing on the definitions: what concepts could be used in the definitions, and what assumptions could be used in the justifications of the definitions. You can attack his definitions either by showing that they failed to meet the requirements, or by arguing that the requirements were inappropriate for his purposes. Or of course you can propose some different requirements that suit a different agenda. This third option wouldn’t be an attack on Tarski; it would be an alternative venture.

Here is an example of an alternative venture. Suppose you want the definition of logical consequence to have the following property:

To make this realistic, maybe we should add ‘at least in simple or straightforward cases’. Also if you were a cognitive scientist, you might want to strengthen to ‘the criteria that we would in fact use for convincing ourselves ...’; then the definition would express a theory about how we think.

It’s not hard to show that Tarski’s definition doesn’t have this property. For Tarski the statement \(\Gamma (\phi ,\psi )\) takes the form

Because of the quantifier over all M, in practice the only way of showing that \(\Gamma (\phi ,\psi )\) holds will normally be to show the stronger statement

But this is just a more complicated variant of ‘\(\psi \) is a logical consequence of \(\phi \)’, so it can’t provide the criteria we asked for.

Prawitz presents this argument very clearly [11, p. 67f.]. But the basic point is older. It goes back at least to Ibn Sīnā, who used it to argue that you can’t use the notion ‘true in situation S’ as a device for making the validity of an inference intuitively clear. (This appears in his Qiyās iii.2, unfortunately still available only in Arabic.) Several people including me have suggested that the argument poses at least a theoretical difficulty for those mental model theorists who maintain that we do in fact reason by making the kind of move that Ibn Sīnā criticised. So I don’t think that proof-theoretic semanticists who present the argument should assume they are in any way swimming against the tide.

Looking around the literature in proof-theoretic semantics, I don’t in fact see anything that I would regard as a criticism of Tarski’s definition. Things that are phrased as attacks on the definition are usually pleas for a different agenda. Nothing compels us to stick to the agendas of eighty years ago.

A striking pair of papers by Peter Schroeder-Heister [14] and Kosta Došen [4] raise a number of questions about the nature of definitions, and about what can be defined in terms of what. I very much welcome the questions—the general theory of definition has had a very patchy treatment by logicians in the last century—and I agree with most of the positive points that Peter and Kosta make. But some of their claims about the views of other people seem to me mighty strange.

At the heart of their arguments against ‘model-theoretic semantics’ is the question what can be defined in terms of what. This was a question of constant interest to the traditional Aristotelian logicians, and a large part of what they said about it strikes me as codswallop. Ouch—on general principle one shouldn’t say that sort of thing about the logic of a distant culture. But what else can you say about people who insist that the only correct definition of ‘human’ is ‘mortal rational animal’, and give only circular arguments in support of this view?

There are still people who operate a broadly Aristotelian notion of the hierarchy of concepts. One notable example is the linguist Anna Wierzbicka [21, cf. p. 10]. She seems to operate by a kind of introspection of concepts. The main difficulty of introspection is that you can never be sure what is the source of the information that it serves up. I think in fact there are two main kinds of reason for regarding concept C as prior to concept D in the hierarchy of definitions. Both these reasons can in principle be lifted out of introspection and made objective, which is always an improvement.

The first kind of reason is that because of the way our minds work, we wouldn’t be able to understand D unless we already understood C. For example could you understand what it is to be vengeful if you didn’t already understand what it is to be angry? Could you understand what it is to be infectious if you didn’t understand what it is to be ill? Or closer to home, could you come to have a concept of satisfaction if you didn’t already have a concept of truth? In theory at least, questions of these kinds can be answered by seeing what you can teach to children, or whether there are natural languages in which there is a word for D but no word for C. There are surely important cognitive facts to be discovered here, but I for one would rather leave it to the experts.

The second kind of reason is not cognitive but semantic. An example is that you can define ‘x is a mother’ in terms of ‘x is the mother of y’ by quantifying out the y, but there is no logical operation that goes in the opposite direction. To handle examples like this, it’s almost essential to put in the variables, because the whole point is that ‘mother of’ has an extra argument that is missing in ‘mother’—it has an extra degree of freedom. In fact Tarski and his teacher Leśniewski seem to have been the first logicians who insisted on putting variables where they are needed, though Frege had already raised the point.

Kosta’s paper does draw attention to one place where variables are needed. He points out (in his §4) that a notation for derivations which only allows us to put a variable for the conclusion is much less useful than a notation that allows us to a variable for a hypothesis as well. This is clearly correct, and I can say so with an easy conscience because I have already (in (7) above) used a notation that does precisely have variables for the hypotheses. My notation is very standard, but in fact it’s not the one that Kosta himself recommends. In effect Kosta, working in a categorial framework, calls for a notation that sets out the variables in the concept

(9)

My notation doesn’t show the f, but if needed one could write an f in the middle of the triangle. Also Kosta’s notation can be written in a line; this is an advantage in text, but possibly a hindrance for writing out pictures of complex derivations. On the other hand my notation has the advantage that it allows one to write several hypotheses, whereas Kosta’s arrow notation allows just one source for the arrow; for my application in (7) above, that would have been a fatal flaw. As all this illustrates, there are some quite subtle relationships between notation and concept, and they are very sensitive to the purpose that the notation will be put to, and the mathematical context in which it will be used.

But elsewhere Kosta forgets the variables. For example he asks [4, §5]:

(10)

where should the variables go? I suggest that the concept of an inference needs three variables, essentially as in Kosta’s notation (9) for derivations:

(11)

The notion of consequence carries just two variables:

(12)

Kosta’s question (10) asks whether (11) is definable from (12), and he expects the answer No.

Clearly Kosta is right: (11) is not definable from (12) (and a fortiori not ‘reducible to’ (12)) for the glaring semantic reason that (11) carries an extra argument. This is not just an accident of Kosta’s formulation. It’s an essential part of the notion of z being inferable from y that people can perform an act called making an inference from y to z, but it is certainly not part of the notion of consequence that people can make a consequence. And I agree with Kosta that this is a point worth making. I also agree with him that for purposes of the foundations of logic, a psychological analysis of ‘making an inference’ is not the right way to go.

But then why does Kosta add this comment?

(He explains that ‘implication’ serves for ‘consequence’ here, so it is the same reduction as above.) Kosta seems here to be saying that the vast mass of twentieth century researchers in philosophy of logic and language all make a mistake not far short of adding 2 to 4 and getting 11. Sad to say, he is right that there are one or two professionals in this field who lack this elementary competence; I could document this but I won’t. But ‘practically all ...’: that seems to me an unreasonable accusation to make with no evidence offered.

Kosta also refers to ‘the second dogma of semantics’. As Kosta formulates it in his §3 (adjusting a similar statement in Peter’s [14]), this dogma states

If I understand this right, the notion of z being inferable from y is ‘hypothetical’ because one gets to z by using y as a ‘hypothesis’. The act of doing this is essentially the same as the act of making an inference from y to z, so we are hovering around the same semantic distinction as before. But I don’t think I recall ever hearing anybody argue that the notion of making an inference can be defined in terms of something being a Tarskian consequence of something else. Rather the opposite: Tarski gave his definition at least partly so that a usable notion of consequence was available to people who weren’t interested in the notion of making an inference. It’s a big world, there are lots of different things to be interested in. Preferring to work on B rather than A is not a kind of dogma.

Kosta adds that the second dogma ‘may be understood as a corollary’ of a dogma that categorical notions have ‘primacy’ over hypothetical notions. [4, §3] In the mainstream semantic and model-theoretic literature that I’ve seen, nobody talks about ‘prior’ notions or about one notion having ‘primacy’ over another. So the burden is on those who use these terms to explain what they mean by them, and what evidence they have for attributing views that involve these terms to semanticists. Otherwise it’s they that are the dogmatists.

Peter has asked whether people who use Tarski’s truth definition regard satisfaction as prior to truth. It’s a reasonable question, but I think that the answer is a straight No, except in a technical sense that is probably not much relevant to this paper. Tarski’s truth definition goes by recursion on the complexity of formulas. It’s a common mathematical experience that when we define or prove something by recursion, it can be nontrivial to formulate the notion that we carry up through the recursion. Often it will need to carry extra features that can be discarded at the end of the recursion. The notion of satisfaction was a technical requirement of just this sort, needed for the recursive definition. But if the question is about having informal concepts of truth and satisfaction, then my own view has always been that satisfaction has to be understood in terms of truth and not the other way round. I should add that this is a question I came to through trying to give an intuitive introduction to model theory for non-model-theorists. It’s not a question that model theorists ever have to deal with in their normal business.