1 Introduction

Portfolio optimization in continuous time goes back to Merton [17]. Merton assumes that the investor has two investment opportunities; one risk-free asset (bond) and one risky asset (stock) with dynamics given by

$$\begin{aligned} \mathrm{d}P_{0,0} (t)&= P_{0,0} (t) \, r_0 \, \mathrm{d}t, \quad \qquad \qquad \qquad \, P_{0,0} (0) = 1, \qquad \text {``bond''} \\ \mathrm{d}P_{0,1} (t)&= P_{0,1} (t) \left[ \mu _0 \, \mathrm{d}t + \sigma _0 \, \mathrm{d}W_0 (t) \right] , \qquad P_{0,1} (0) = p_{1}, \qquad \text {``stock''} \end{aligned}$$

with constant market coefficients \(\mu _0\), \(r_0\), \(\sigma _0 > 0\), and where \(W_0\) is a Brownian motion on a complete probability space \(( \varOmega , \fancyscript{F} , P )\). Finally, \(X_0^{\pi }\) denotes the wealth process of the investor given the portfolio strategy \(\pi \) (which denotes the fraction invested in the risky asset). More specifically, the wealth process satisfies

$$\begin{aligned} \mathrm{d}X^{\pi }_0 (t)&= X^{\pi }_0 \left( t \right) \left[ \left( r_0 + \pi (t) \left[ \mu _0 - r_0 \right] \right) \, \mathrm{d}t + \pi (t) \sigma _0 \, \mathrm{d}W_0 (t) \right] , \\ X^{\pi }_0 (0)&= x . \end{aligned}$$

Assuming that the utility function \(U (x)\) of the investor is given by \(U (x) = \ln (x)\), one can define the performance function for an arbitrary admissible portfolio strategy \(\pi (t)\) by

$$\begin{aligned} \fancyscript{J}_{0} \left( t , x , \pi \right)&:= \mathbb {E} \left[ \ln \left( X^{\pi ,t,x}_0 (T) \right) \right] = \ln \left( x \right) + \mathbb {E} \left[ \int \limits _t^T \left[ \varPsi _0 - \frac{ \sigma ^2_0 }{2} \left( \pi (s) - \pi ^{*}_0 \right) ^2 \right] \, \mathrm{d}s \right] .\quad \quad \end{aligned}$$
(1)

Here,

$$ \varPsi _0 := r_0 + \frac{1}{2} \left( \frac{\mu _0 - r_0}{\sigma _0} \right) ^2 = r_0 + \frac{\sigma _0^2}{2} \left( \pi ^{*}_0 \right) ^2 \quad \text {and} \quad \pi ^{*}_0 := \frac{\mu _0 - r_0}{\sigma _0^2} $$

will be called the utility growth potential or earning potential and the optimal portfolio strategy or Merton fraction, respectively. Using this, the portfolio optimization problem in the Merton case (that is without taking possible jumps into account) is given by

$$\begin{aligned} \sup \limits _{\pi (\cdot ) \in A_0(x)} \fancyscript{J}_{0} \left( t , x , \pi \right) =: \nu _0 (t,x) \quad \left[ = \ln (x) + \varPsi _0 ( T - t ) \right] , \end{aligned}$$
(2)

where \(\nu _0\) is known as the value function in the Merton case. From Eq. (1), it is clear that \(\pi ^{*}_0\) maximizes \(\fancyscript{J}_0\). Hence, it is the optimal portfolio strategy for Eq. (2).

Merton’s model has the disadvantage that it cannot model jumps in the price of the risky asset. Therefore, Aase [1] extended Merton’s model to allow for jumps in the risky asset. In the simplest case, the dynamics of the risky asset changes to

$$\begin{aligned} \mathrm{d} P_{J} (t)&= P_{J} (t) \left[ \mu _0 \, dt + \sigma _0 \, \mathrm{d}W_0 (t) - k \, \mathrm{d}N(t) \right] , \end{aligned}$$

where \(N\) is a Poisson process with intensity \(\lambda > 0\) on \(( \varOmega , \fancyscript{F} , P )\) and \(k > 0\) is the crash or jump size. In this setting, the performance function is given by

$$ \fancyscript{J}_{J} \left( t , x , \pi \right) = \ln \left( x \right) + \mathbb {E} \left[ \int \limits _t^T \left[ \varPsi _0 - \frac{ \sigma ^2_0 }{2} \left( \pi (s) - \pi ^{*}_0 \right) ^2 - \ln \left( 1 - \pi (s) k \right) \lambda \right] \, \mathrm{d}s \right] . $$

Using this, the optimal portfolio strategy can be computed to

$$ \pi ^{*}_J = \frac{1}{2} \left( \pi ^{*}_0 + \frac{1}{k} \right) - \sqrt{\frac{1}{4} \left( \pi ^{*}_0 - \frac{1}{k} \right) ^2 + \frac{\lambda }{\sigma _0^2}} \, . $$
Fig. 1
figure 1

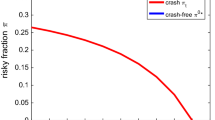
Examples of Merton’s optimal portfolio strategies. This figure is plotted with \(\pi ^{*}_0 = 1.25\), \(\sigma _0 = 0.25\), \(r = 0.05\), \(k = 0.25\), and \(T = 50\). This implies that \(\lambda _0 = \frac{\sigma _0^2 \pi ^{*}_0}{k} = 0.3125\), \(\varPsi _0 \approx 0.098828\), and \(\frac{1}{k^{*}} = 4\)

Full size image

Figure 1 shows the fraction invested in the risky asset in Merton’s (solid line) and Aase’s model for various \(\lambda \) (all the other lines). The dashed line below the solid line is the case where \(\frac{1}{\lambda } = 50\), that is the investor expects on average one crash within 50 years. By comparison, the lowest line (the dash–dotted line) is the case where \(\frac{1}{\lambda } = 2.5\), that is the investor expects on average one crash within 2.5 years. Note, however, that the fraction invested in the risky asset is negative in this case, meaning that the optimal strategy is that the investor goes short in the risky asset. This strategy is very risky because the probability that the investor will go bankrupt is strictly positive. This can also be observed in practice where several hedge funds went bankrupt which were betting on a crash in the way described above.

Therefore, let us consider an ansatz which overcomes this problem.

1.1 Alternative Ansatz of Korn and Wilmott

The ansatz made by Korn and Wilmott [9] is to distinguish between normal times and crash time. In normal times, the same set up as in Merton’s model is used. At the crash time, the price of the risky asset falls by a factor of \(k \in [ k_{*} , k^{*} ]\) (with \(0 \le k_{*} \le k^{*} < 1\)). This implies that the wealth process \(X_0^{\pi } (t)\) just before the crash time \(\tau \)– satisfies

$$\begin{aligned} X_0^{\pi } \left( \tau - \right)&= \underbrace{\left[ 1 - \pi (\tau ) \right] X_0^{\pi } \left( \tau - \right) }_{\text {bond investment}} + \underbrace{\pi (\tau ) X_0^{\pi } \left( \tau - \right) }_{\text {stock investment}} \, . \end{aligned}$$

At the crash time, the price of the risky asset drops by a factor of \(k\), implying

$$ \left[ 1 - \pi \left( \tau \right) \right] X_0^{\pi } \left( \tau - \right) + \pi ( \tau ) X_0^{\pi } \left( \tau - \right) \left[ 1 - k \right] = \left[ 1 - \pi (\tau ) k \right] X_0^{\pi } \left( \tau - \right) = X_0^{\pi } (\tau ) \, . $$

Therefore, one has a straightforward relationship of the wealth right before a crash with the wealth right after a crash.

The main disadvantage of this ansatz is that one needs to know the maximal possible number of crashes \(M\) that can happen at most—in the following, we assume for simplicity that \(M = 1\) if not stated otherwise—and one needs to know the worst crash size \(k^{*}\) that can happen. On the other hand, no probabilistic assumptions are made on the crash time or crash size. Therefore, Merton’s approach, to maximize the expected utility of terminal wealth, cannot be used in this context. Instead the aim is to find the best uniform worst-case bound, e.g. solve

$$\begin{aligned} \sup \limits _{\pi ( \cdot ) \in A (x)} \inf \limits _{\mathop {k \in K}\limits ^{0 \le \tau \le T}} \mathbb {E} \left[ \ln \left( X^{\pi } \left( T \right) \right) \right] , \end{aligned}$$
(3)

where the terminal wealth satisfies \(X^{\pi } \left( T \right) = \left( 1 - \pi ( \tau ) k \right) X_0^{\pi } \left( T \right) \) in the case of a crash of size \(k\) at stopping time \(\tau \). Moreover, \(K = \{ 0 \} \cup [ k_{*} , k^{*} ]\). This will be called the worst-case scenario portfolio problem.

Note that one requires that \(\pi (t) < \frac{1}{k^{*}}\) for all \(t \in [0,T]\) in order to avoid bankruptcy. The value function to the above problem is defined via

$$\begin{aligned} \nu _c (t,x) := \sup \limits _{\pi (\cdot ) \in A(t,x)} \inf \limits _{\mathop {k \in K}\limits ^{t \le \tau \le T,}} \mathbb {E} \left[ \ln \left( X^{\pi ,t,x} (T) \right) \right] . \end{aligned}$$
(4)

Observe that this optimization problem can be interpreted as a stochastic differential game (see Korn and Steffensen [12]), where the investor tries to maximize her expected utility of terminal wealth while the counterparty (the market or nature) tries to hit the investor as badly as possible by triggering a crash. The control of the investor is \(\pi \), the fraction of wealth invested into the risky asset, while the control of the counterparty is the crash time \(\tau \) and the crash size \(k\). Figure 2 depicts the optimization problem. For each control choice (that is portfolio strategy) of the investor (e.g., \(\pi _2\)), the investor calculates the expected utility of terminal wealth for all possible control choices (that is \((\tau ,k)\)) of the counterparty (which is the dotted line for the strategy \(\pi _2\)). Then the worst-case scenario is determined for each portfolio strategy (e.g., \(\left( \tau ^{ \left( \pi _2 \right) }, k^{ \left( \pi _2 \right) } \right) \) for the strategy \(\pi _2\)). Afterwards, the expected utility of terminal wealth for this worst-case scenario is calculated and denoted by \(\fancyscript{WC} \left( {\pi _2} \right) \). The last step is to find the strategy which maximizes the worst-case scenario function \(\fancyscript{WC} \left( \cdot \right) \). For the three examples given in Fig. 2, this would be \(\pi _3\). Notice that \(\pi _3\) is special in that all choices \((\tau ,k)\) lead to the same worst-case scenario, that is \(\fancyscript{WC} \left( {\pi _3} \right) \) is independent of the scenario \((\tau ,k)\).

Observe that Aase [1] would fix \(k\), model the crash time via a Poisson distribution, and maximize the expected utility of terminal wealth. Whereas, by comparison, the worst-case scenario optimization method uses a probability-free approach on crash time and size.

Fig. 2
figure 2

Schematic interpretation of the worst-case scenario optimization

Full size image

Apparently, it is quite cumbersome to determine the optimal portfolio strategy as described above. Instead consider the following approach. Define as \(\nu _1\) the value function as in Eq. (2), except that the subscript \(1\) indicates that this is the value function in the Merton case after a crash has happened (and where the market parameters might change—see Sect. 2 for details). To that end, a portfolio strategy \(\hat{\pi } \ge 0\) determined via the equation

$$\begin{aligned} \fancyscript{J}_0 \left( t,x,{\hat{\pi }} \right) = \nu _1 \left( t , x \left( 1 - \hat{\pi } (t) k^{*} \right) \right) \quad \text {for all}\quad t \in [0,T] \end{aligned}$$
(5)

will be called a crash indifference strategy. This is, because the investor gets the same expected utility of terminal wealth if either no crash happens (left-hand side) or a crash of the worst-case size \(k^{*}\) happens (right-hand side). It is straightforward to verify (see Korn and Menkens [10]) that there exists a unique crash indifference strategy \(\hat{\pi }\), which is given by the solution of the differential equation

$$\begin{aligned} \hat{\pi }' (t)&= \frac{ \sigma ^2_0 }{2} \left( \hat{\pi } (t) - \frac{1}{k^{*}} \right) \left( \hat{\pi } (t) - \pi ^{*}_0 \right) ^2 , \end{aligned}$$
(6)
$$\begin{aligned} \text {with} \quad \hat{\pi } (T)&= 0. \end{aligned}$$
(7)

This crash indifference strategy is bounded by \(0 \le \hat{\pi } \le \min \{ \pi ^{*}_0 , \frac{1}{k^{*}} \}\). It can be shown (see Korn and Wilmott [9] or Korn and Menkens [10]) that the optimal portfolio strategy for an investor, who wants to maximize her worst-case scenario portfolio problem, is given by

$$\begin{aligned} \bar{\pi } (t) := \min \left\{ \hat{\pi } (t) , \pi ^{*}_0 \right\} \qquad \text {for all } t \in [0,T] . \end{aligned}$$
(8)

\(\bar{\pi }\) will be named the optimal crash hedging strategy or optimal worst-case scenario strategy.

Fig. 3
figure 3

Examples of worst-case optimal portfolio strategies

Full size image

Figure 3 shows the optimal worst-case scenario strategies of Korn/Wilmott if at most one (solid line), two (dashed line), or three (dash–dotted line) crashes can happen. Assuming that the investor has an initial investment horizon of \(T = 50\) and expects to see at most three crashes, a optimal worst-case scenario investor would use the portfolio strategy \(\hat{\pi }_3 (t)\) until she observes a first crash, say at time \(\tau _1\). After having observed a crash, the investor would switch to the strategy \(\hat{\pi }_2 (t)\), since the investor expects to see at most two further crashes in the remaining investment horizon \(T-\tau _1\); and so on. Finally, if the investor expects to observe no further crash, she will switch to the Merton fraction \(\pi _0^{*}\).

The worst case scenario strategies are now compared to the optimal portfolio strategy in Aase’s model, where \(\lambda (t) = \frac{1}{T-t}\) (see dotted line in Fig. 3), that is the investor expects to see on average one crash over his remaining investment horizon \(T-t\). Clearly, setting \(\lambda \) in this way is somewhat unrealistic. Nevertheless, this extreme example is used to point out several disadvantages of the expected utility approach of Aase. First, considering a \(\lambda \) which changes over time and depends on the investment horizon of the investor, leads not only to a time-changing optimal strategy \(\pi _P (t)\), but also to a price dynamics of the risky asset which depends on the investment horizon of the investor. Hence, any two investors with different investment horizons would work with different price dynamics of the risky assets. Second, as the investor approaches the investment horizon, \(\lambda (t) \rightarrow \infty \) (that is a crash happens almost surely), thus, \(\pi _P (t) \rightarrow - \infty \), which would lead to big losses on short-term investment horizons if no crash happens. Of course, these losses would average out with the gains made if a crash happens remembering that the assumption is that—on average—every second scenario would observe at least one crash. This is the effect of averaging the crash out in an expected utility sense (compared to the worst-case approach of Korn/Wilmott).

Basically, it would be possible to cut off \(\pi _p (t)\) at zero, that is, one would not allow for short-selling. This would imply to cut off \(\lambda (t)\) at \(\frac{\mu _0 - r_0}{k}\) and there is no economic interpretation why this should be done (except that short-selling might not be allowed). Finally, note that it is also possible to set \(\lambda \) such that one expects to see at least one crash with probability \(q\) (e.g., \(q = 5\,\%\)), however this would not remedy the two disadvantages mentioned above.

Why is the worst-case scenario approach more suitable than the standard expected utility approach in the presence of jumps? The standard expected utility approach will average out the impact of the jumps over all possible scenarios. With other words, the corresponding optimal strategy will offer protection only on average over all possible scenarios, which will be good as long as either no jump or just a small jump happens. However, if a large jumps happens, the protection is negligible. By comparison, the worst-case scenario approach will offer full protection from a jump up to the worst-case jump size assumed.

The situation can be compared to the case of buying liability insurance. The standard utility approach would look at the average of all possible claim sizes (say e.g., 100,000 EUR)—and its optimal strategy would be to buy liability insurance with a cover of 100,000 EUR. However, the usual advice is to buy liability insurance with a cover which is as high as possible—this solution corresponds to the worst-case scenario approach. With other words, the aim is to insure the rare large jumps. This observation is supported by the fact that many insurances offer retention (which excludes small jumps from the insurance).

1.2 Literature Review

To the best of our knowledge, Hua and Wilmott [8] were the first to consider the worst-case scenario approach in a binomial model to price derivatives. Korn and Wilmott [9] were the first to apply this approach to portfolio optimization, and Korn and Menkens [10] developed a stochastic control framework for this approach, while Korn and Steffensen [12] considered this approach as a stochastic differential game. Korn and Menkens [10] and Menkens [16] looked at changing market coefficients after a crash. Seifried [22] evolved a martingale approach for the worst-case scenario. Moreover, the worst-case scenario approach has been applied to the optimal investment problem of an insurance company (see Korn [11]) and to optimize reinsurance for an insurance company (see Korn et al. [13]). Korn et al. [13] show also in their setting that the worst-case scenario approach has a negative diversification effect. Furthermore, both portfolio optimization under proportional transaction costs (see Belak et al. [4]) and the infinite time consumption problem (see Desmettre et al. [7]) have been studied in a worst-case scenario optimization setting. Mönnig [18] applies the worst-case scenario approach in a stochastic target setting to compute option prices. Finally, Belak et al. [2, 3] allow for a random number of crashes, while Menkens [15] analyzes the costs and benefits of using the worst-case scenario approach.

Notice that there is a different worst-case scenario optimization problem which is also known as Wald’s Maximin approach (see Wald [23, 24]). The following quotation is taken from Wald [23, p. 279]:

A problem of statistical inference may be interpreted as a zero sum two person game as follows: Player \(1\) is Nature and player \(2\) is the statistician. [...] The outcome \(K[\theta , w(E)]\) of the game is the risk \(r[\theta | w(E)]\) of the statistician. Clearly, the statistician wishes to minimize \(r[\theta | w(E)]\). Of course, we cannot say that Nature wants to maximize \(r[\theta | w(E)]\). However, if the statistician is in complete ignorance as to Nature’s choice, it is perhaps not unreasonable to base the theory of a proper choice of \(w(E)\) on the assumption that Nature wants to maximize \(r[\theta | w(E)]\).

This is a well-known concept in decision theory and is also known as robust optimization (see e.g., Bertsimas et al. [5] or Rustem and Howe [21] and the references therein). However, while the ansatz is the same, it is usually assumed that the parameters (in our case \(r_0\), \(\mu _0\), and \(\sigma _0\)) are unknown within certain boundaries. Therefore, this is a parameter uncertainty problem which is solved using a worst-case scenario approach—instead of using perturbation analysis. Observe that this usually involves optimization procedures done by a computer. Finally, note that the optimal strategies can be computed directly only in the special case that only \(\mu _0\) is uncertain (see Mataramvura and Øksendal [14, Øksendal and Sulem [19], or Pelsser [20] for a recent application in an insurance setting).

By comparison, the worst-case scenario approach considered in this paper is taking (possibly external) shocks/jumps/crashes into account—and not parameter uncertainty. While the original idea and the wording are similar or even the same, it is clear that the worst-case scenario approach of Korn and Wilmott [9] is different from the robust optimization approach in decision theory.

The remainder of this paper is organized as follows. Section 2 introduces the set up of the model which will be considered; and Sect. 3 solves the optimization problem if the probability of a potential crash is known. As a consequence, the \(q\)-quantile crash hedging strategy will be developed in Sect. 4. Section 5 gives examples of the \(q\)-quantile crash hedging strategy, while Sect. 6 shows that stochastic portfolio strategies are always inferior to their corresponding deterministic portfolio strategies. Finally, Sect. 7 concludes.

2 Setup of the Model

Let us work with the model introduced above and let us make the following refinements. First, it has been tacitly assumed that the investor is able to realize that the crash has happened. Thus, let us model its occurrence via a \(\fancyscript{F}\)—stopping time \(\tau \). To model the fact that the investor is able to realize that a jump of the stock price has happened it is supposed that the investor’s decisions are adapted to the \(P\)-augmentation \(\{ {\fancyscript{F}}_t \}\) of the filtration generated by the Brownian motion \(W(t)\). The difficulty of this approach is to determine the optimal strategy after a crash because the starting point is random, however Seifried [22] solved this problem.

Let us further suppose that the market conditions change after a possible crash. Let therefore \(k\) (with \(k \in [ k_{*} , k^{*} ]\)) be the arbitrary size of a crash at time \(\tau \). The price of the bond and the risky asset after a crash of size \(k\) happened at time \(\tau \) is assumed to be

$$\begin{aligned} \mathrm{d} P_{1,0} (t)&= P_{1,0} (t) \, r_1 \, \mathrm{d}t \, , \qquad \qquad \qquad P_{1,0} (\tau ) = P_{0,0} (\tau ) \, , \end{aligned}$$
(9)
$$\begin{aligned} \mathrm{d} P_{1,1} (t)&= P_{1,1} (t) \left[ \mu _1 \, \mathrm{d}t + \sigma _1 \, \mathrm{d}W (t) \right] \, , \qquad P_{1,1} (\tau ) = \left( 1 - k \right) P_{0,1} (\tau ) \, , \end{aligned}$$
(10)

with constant market coefficients \(r_1\), \(\mu _1\), and \(\sigma _1 > 0\) after a possible crash of size \(k\) at time \(\tau \). That is, this is the same market model as before the crash except that the market parameters are allowed to change after a crash has happened.

It is important to keep in mind that the investor does not know for certain that a crash will occur—the investor only thinks that it is possible. An investor who knows that a crash will happen within the time horizon \([0,T]\) has additional information and is therefore an insider. The set of possible crash heights of the insider is indeed \(K_I := [ k_{*} , k^{*} ]\), while the set of possible crash heights of the investor who thinks that a crash is possible is \(K := \{ 0 \} \cup [ k_{*} , k^{*} ]\). In this paper, only the portfolio problem of the investor, who thinks a crash is possible, is considered.

For simplicity, the initial market will also be called market \(0\), while the market after a crash will be called market \(1\). In order to set up the model, the following definitions are needed.

Definition 1

  1. (i)

    For \(i=0,1\), let \(A_i (s,x)\) be the set of admissible portfolio processes \(\pi (t)\) corresponding to an initial capital of \(x > 0\) at time \(s\), i.e., \(\{ {\fancyscript{F}}_t , s \le t \le T \}\)–progressively measurable processes such that

    1. (a)

      the wealth equation in market \(i\) in the usual crash-free setting

      $$\begin{aligned} \mathrm{d} X^{\pi ,s,x}_i (t)&= X^{\pi ,s,x}_i \left( t \right) \left[ \left( r_i + \pi (t) \left[ \mu _i - r_i \right] \right) \mathrm{d}t + \pi (t) \sigma _i \mathrm{d}W_i (t) \right] ,\quad \quad \end{aligned}$$
      (11)
      $$\begin{aligned} X^{\pi ,s,x}_i (s)&= x \end{aligned}$$
      (12)

      has a unique non-negative solution \(X^{\pi ,s,x}_i (t)\) and satisfies

      $$\begin{aligned} \int \limits _s^{T} \left[ \pi (t) X^{\pi ,s,x}_i (t)\right] ^2 \, \mathrm{d}t < \infty \quad P\text {--a.s.} \, , \end{aligned}$$
      (13)

      i.e. \(X^{\pi ,s,x}_i (t)\) is the wealth process in market \(i\) in the crash-free world, which uses the portfolio strategy \(\pi \) and starts at time \(s\) with initial wealth \(x\).

      Furthermore, \(X^{\pi }_i (t) := X^{\pi ,0,x}_i (t)\) will be used as an abbreviation.

    2. (b)

      \(\pi (t)\) has left-continuous paths with right limits.

  2. (ii)

    the corresponding wealth process \(X^{\pi } (t)\) in the crash model, defined as

    $$\begin{aligned} X^{\pi } (t) = \left\{ \begin{array}{ll} X^{\pi }_0 (t) &{}\quad \text {for}\, s \le t < \tau \\ \left[ 1 - \pi (\tau ) k \right] X^{\pi , \tau , X^{\pi }_0 (\tau )}_1 \left( t \right) &{}\quad \text {for}\, t \ge \tau \ge s \, , \end{array} \right. \end{aligned}$$
    (14)

    given the occurrence of a jump of height \(k\) at time \(\tau \), is strictly positive. Thereby, it is assumed that the crash time \(\tau \) is a \({\fancyscript{F}}\)–stopping time. The set of admissible portfolio strategies is obviously given by \(A_0 (s,x)\) as long as no crash happens. After a crash at time \(\tau \), the set is given by \(A_1 ( \tau ,x)\), which is defined scenario-wise, that is via \(A_1 ( \tau (\omega ) ,x)\) for all \(\omega \in \varOmega \). Hence,

    $$ A (s,x) := \left\{ \phi (t) \text { with } t \in [s,T] : \phi \big |_{[s, \tau ]} \in A_0 (s,x) \big |_{[s, \tau ]} \text { and } \phi \big |_{[\tau , T]} \in A_1 ( \tau , x) \right\} . $$
  3. (iii)

    \(A(x)\) is used as an abbreviation for \(A(0,x)\).

Finally, it is clear how to extend the definitions given above only for \(i = 0\) to \(i = 1\). Simply, replace the zeros by ones.

3 Optimal Portfolios Given the Probability of a Crash

In this section, let us suppose that the investor knows the probability of a crash occurring. Let \(p\), with \(p \in [0,1]\), be the probability that a crash can happen (but must not necessarily happen)Footnote 1. Note that the following argument holds also for time-dependent \(p\) (that is \(p (t)\)), however to simplify the notation, it is assumed that \(p\) is constant. In this situation, the optimization problem can be split up into two problems (crash can occur, no crash happens) which have to be solved simultaneously. To that end define for \(p \in [0,1]\)

$$ \mathbb {E}_{p} \left[ \ln \left( X^{\pi ,t,x} (T) \right) \right] := p \underbrace{\mathbb {E} \left[ \ln \left( X^{\pi ,t,x} (T) \right) \right] }_{\text {A crash can occur.}} + \left( 1 - p \right) \underbrace{\mathbb {E} \left[ \ln \left( X^{\pi ,t,x}_0 (T) \right) \right] }_{\text {No crash happens.}}. $$

Using this definition, the optimization problem can be written as

$$\begin{aligned}&\sup \limits _{\pi (\cdot ) \in A(t,x)} \inf \limits _{\mathop {k \in K}\limits ^{t \le \tau \le T, }} \mathbb {E}_{p} \left[ \ln \left( X^{\pi ,t,x} (T) \right) \right] \nonumber \\&\quad = \sup \limits _{\pi (\cdot ) \in A(t,x)} \left\{ p \left\{ \inf \limits _{\mathop {k \in K}\limits ^{ t \le \tau \le T,}} \mathbb {E} \left[ \ln \left( X^{\pi ,t,x} (T) \right) \right] \right\} + \left( 1 - p \right) \mathbb {E} \left[ \ln \left( X^{\pi ,t,x}_0 (T) \right) \right] \right\} \nonumber \\&\quad = \sup \limits _{\pi (\cdot ) \in A(t,x)} \left\{ p \cdot \left\{ \inf \limits _{\mathop {k \in K}\limits ^{ t \le \tau \le T, }} \nu _1 \left( \tau , X_0^{\pi ,t,x} (\tau ) \left( 1 - \pi (\tau ) k \right) \right) \right\} + \left( 1 - p \right) \fancyscript{J}_0 \left( t, x, \pi \right) \right\} .\nonumber \\ \end{aligned}$$
(15)

Observe that the two extremes, \(p \in \{ 0,1 \}\) are straightforward to solve:

  1. (A)

    \(p=1\):

    $$ \sup \limits _{\pi (\cdot ) \in A(t,x)} \inf \limits _{\mathop {k \in K}\limits ^{t \le \tau \le T, }} \mathbb {E}_{1} \left[ \ln \left( X^{\pi ,t,x} (T) \right) \right] = \sup \limits _{\pi (\cdot ) \in A(t,x)} \inf \limits _{\mathop {k \in K}\limits ^{t \le \tau \le T,}} \mathbb {E} \left[ \ln \left( X^{\pi ,t,x} (T) \right) \right] . $$

    Thus, this is the original worst-case scenario portfolio problem. The solution is already known.

  2. (B)

    \(p=0\):

    $$ \sup \limits _{\pi (\cdot ) \in A(t,x)} \inf \limits _{\mathop {k \in K}\limits ^{t \le \tau \le T, }} \mathbb {E}_{0} \left[ \ln \left( X^{\pi ,t,x} (T) \right) \right] = \sup \limits _{\pi (\cdot ) \in A_0(t,x)} \mathbb {E} \left[ \ln \left( X^{\pi ,t,x}_0 (T) \right) \right] , $$

    which is the classical optimal portfolio problem of Merton. The solution is well known and is given in our notation (compare with Eq. (2)) by \(\pi ^{*}_0\).

Let us now consider the case \(p \in (0,1)\). Denoting the optimal crash hedging strategy in this situation by \(\hat{\pi }_p\), Eq. (15) can be rewritten as

$$\begin{aligned} \fancyscript{J}_0 \left( t , x, \hat{\pi }_p \right)&= p \cdot \nu _1 \left( t , x \left( 1 - \hat{\pi }_p (t) k^{*} \right) \right) + \left( 1 - p \right) \fancyscript{J}_0 \left( t , x, \hat{\pi }_p \right) \\ \Longleftrightarrow \qquad \quad \fancyscript{J}_0 \left( t , x, \hat{\pi }_p \right)&= \nu _1 \left( t , x \left( 1 - \hat{\pi }_p (t) k^{*} \right) \right) , \end{aligned}$$

where the last equation is obtained from the first equation by solving the first equation for \(\fancyscript{J}_0\). Since the latter equation is the indifference Eq. (5) in this setting, which leads to the same ODE and boundary condition as in Korn and Wilmott [9], it follows that \(\hat{\pi }_p \equiv \hat{\pi }\) (see the paragraph between Eqs. (5) and (6) for details). This result shows that the crash hedging strategy remains the same even if the probability of a crash is known. Thus, this result justifies the wording worst-case scenario of the above-developed concept. This is due to the fact that the worst-case scenario should be independent of the probability of the worst case and which has been shown above. Let us summarize this result in a proposition.

Proposition 1

Given that the probability of a crash is positive, the worst-case scenario portfolio problem as it has been defined in Eq. (3) is independent of the probability of the worst-case occurring.

If the probability of a crash is zero, the worst-case scenario portfolio problem reduces to the classical crash-free portfolio problem.

4 The \(q\)-quantile Crash Hedging Strategy

Obviously, the concept of the worst case scenario has the disadvantage that additional information (namely the given probability of a crash and the probability distribution of the crash sizes) is not used. However, if the probability of a crash and the probability of the crash size is known, it is possible to construct the (lower) \(q\) -quantile crash hedging strategy.

Assume that \(p (t) \in [0,1]\) is the given probability of a crash at time \(t \in [0,T]\) and assume that \(f(k,t) \in [0,1]\) is the given density of the distribution function for a crash of size \(k \in \left[ k_{*} , k^{*} \right] \) at time \(t\). Moreover, suppose that a function \(q : [0,T] \longrightarrow [0,1]\) is given. With this, define

$$ k_q \left( t ; \pi \right) := \left\{ \begin{array}{ll} 0 &{}\quad \text {if}\, 1 - p (t) \ge q (t) \\ \inf \left\{ k_q : 1 - p (t) + p (t) \int \limits _{k_{*}}^{k_q} f(k,t) \, dk \ge q (t) \right\} &{}\quad \text {if}\, {1 - p (t)} < q (t)\,\text {and}\, {\pi \ge 0} \\ \sup \left\{ k_q : 1 - p (t) + p (t) \int \limits _{k_q}^{k^{*}} f(k,t) \, dk \ge q (t) \right\} &{}\quad \text {if}\, 1 - p (t) < q (t)\,\text {and}\, {\pi < 0} \end{array} \right\} $$

for any given portfolio strategy \(\pi \). This has the following interpretation. The probability that at most a crash of size \(k_q (t)\) at time \(t\) happens is \(q (t)\). Equivalently, the probability that a crash higher than \(k_q (t)\) will happen at time \(t\) is less than \(1 - q (t)\). Obviously, this is a value at risk approach which relaxes the worst-case scenario approach.

Notice that the worst case of a non-negative portfolio strategy is either a crash of size \(k^{*}\) or no crash. On the other hand, the worst case of a negative portfolio strategy is either a crash of size \(k_{*}\) or no crash. Correspondingly, the \(q\)-quantile calculates differently for negative portfolio strategies (see the third row) than for the non-negative portfolio strategies (see the second row). Furthermore, denote by

$$ K_q (t) := \left\{ \begin{array}{ll} \{ 0 \} &{}\quad \text {if}\, k_q (t) = 0 \\ \{ 0 \} \cup \left[ k_{*} , k_q (t) \right] &{}\quad \text {if}\, k_q (t) \not = 0 \text { and } \pi \ge 0 \\ \{ 0 \} \cup \left[ k_q ( \tau ) , k^{*} \right] &{}\quad \text {if}\, k_q (t) \not = 0 \text { and } \pi < 0 \end{array} \right\} \, . $$

Definition 2

  1. (i)

    The problem to solve

    $$\begin{aligned} \sup \limits _{\pi (\cdot ) \in A(x)} \inf \limits _{ \mathop {k \in K_q ( \tau )}\limits ^{0 \le \tau \le T,}} \mathbb {E} \left[ \ln \left( X^{\pi } (T) \right) \right] \, , \end{aligned}$$
    (16)

    where the terminal wealth \(X^{\pi } (T)\) in the case of a crash of size \(k\) at time \(\tau \) is given by

    $$\begin{aligned} X^{\pi } (T) = \left[ 1 - \pi (\tau ) k \right] X^{ \pi , \tau , X^{\pi }_0 ( \tau ) }_1 \left( T \right) \, , \end{aligned}$$
    (17)

    with \(X^{ \pi , \tau , X^{\pi }_0 ( \tau )}_1 \left( t \right) \) as above, is called the (lower) \(q\) -quantile scenario portfolio problem.

  2. (ii)

    The value function to the above problem is defined via

    $$\begin{aligned} w_q (t,x) := \sup \limits _{\pi (\cdot ) \in A(t,x)} \inf \limits _{\mathop {k \in K_q ( \tau )}\limits ^{t \le \tau \le T,}} \mathbb {E} \left[ \ln \left( X^{\pi ,t,x} (T) \right) \right] \, . \end{aligned}$$
    (18)
  3. (iii)

    A portfolio strategy \(\hat{\pi }_q\) determined via the equation

    $$ w_{q} \left( t , x \right) = \nu _1 \left( t , x \left( 1 - \hat{\pi }_q (t) k_q (t) \right) \right) \qquad \text {for all } t \in [0,T] \text { with } k_q (t) > 0 $$

    will be called a (lower) \(q\) -quantile crash hedging strategy.

  4. (iv)

    A portfolio strategy \(\tilde{\pi }_q\) is a partial (lower) \(q\) -quantile crash hedging strategy, if it is for any \(t \in [0,T]\) either a \(q\)-quantile crash hedging strategy or a solution to the \(q\)-quantile scenario portfolio problem.

It is straightforward to see that the \(1\)-quantile scenario portfolio problem is equivalent to the worst-case scenario portfolio problem given in Eq. (3). Moreover, the \(1\)-quantile crash hedging strategy is equivalent to the crash hedging strategy in Definition 3.1 in Menkens [16, p. 602].

Remark 1

  1. (i)

    Clearly, the definition given in Eq. (16) is different from the corresponding definition given in Sect. 3 and it leads only to the same solution in the two extreme cases of either \(p=1\) or \(p=0\).

  2. (ii)

    Notice that the \(q\)-quantile scenario portfolio problem is only a \(q\)-quantile concerning the crash. The randomness of the market movement represented in the model by a geometric Brownian motion has been averaged out, namely by taking the expectation—and not the \(q\)-quantile.

Define the support of \(k_q\) to be

$$ \mathrm supp\left( k_q \right) := \left\{ t \in [0,T] : k_q (t) > 0 \right\} . $$

Using this, it is possible to show the following.

Theorem 1

Let us suppose that \(k_q\) is continuously differentiable on \(\mathrm supp\left( k_q \right) \) with respect to \(t\).

  1. (i)

    Then there exists a unique (lower) \(q\)-quantile crash hedging strategy \(\hat{\pi }_q\), which is on \(\mathrm supp\left( k_q \right) \) given by the solution of the differential equation

    $$\begin{aligned} \hat{\pi }_q' (t)&= \left( \hat{\pi }_q (t) - \frac{1}{k_q (t)} \right) \left[ \frac{ \sigma ^2_0 }{2} \left( \hat{\pi }_q (t) - \pi ^{*}_0 \right) ^2 + \varPsi _1 - \varPsi _0 \right] - \hat{\pi }_q (t) k_q' (t) , \end{aligned}$$
    (19)
    $$\begin{aligned} \hat{\pi }_q (T)&= 0 . \end{aligned}$$
    (20)

    For \(t \in [0,T] \setminus \mathrm supp\left( k_q \right) \) set \(\hat{\pi }_q (t) : = \pi ^{*}_0 \).

    Moreover, if \(\varPsi _1 \ge r_0\), then the \(q\)-quantile crash hedging strategy is bounded by

    $$ 0 \le \hat{\pi }_q (t) < \frac{1}{k_q (t)} \le \frac{1}{k_{*}} \quad \text {for}\, t \in \mathrm supp\left( k_q \right) . $$

    Additionally, if \(\varPsi _1 \le \varPsi _0\) and \(\pi _0^{*} \ge 0\), the \(q\)-quantile crash hedging strategy has another upper bound with \(\hat{\pi }_q (t) < \pi ^{*}_0 - \sqrt{\frac{2}{\sigma _0^2} \left( \varPsi _0 - \varPsi _1 \right) }\).

    On the other side, if \(\varPsi _1 < r_0\) the \(q\)-quantile crash hedging strategy is bounded by

    $$ \pi ^{*}_0 - \sqrt{\frac{2}{\sigma _0^2} \left( \varPsi _0 - \varPsi _1 \right) } < \hat{\pi }_q (t) < 0 \quad \text {for}\, t \in [0,T). $$
  2. (ii)

    If \(\varPsi _1 < \varPsi _0\) and \(\pi _0^{*} < 0\), there exists a partial \(q\)-quantile crash hedging strategy \(\tilde{\pi }_q\) at time \(t\) (which is different from \(\hat{\pi }_q\)), if

    $$\begin{aligned} S_q (t) := T - \frac{\ln \left( 1 - \pi _0^{*} k_q (t) \right) }{ \varPsi _0 - \varPsi _1 } > 0 \quad \text {for}\,t \in \mathrm supp\left( k_q \right) . \end{aligned}$$
    (21)

    With this, \(\tilde{\pi }_q (t)\) is given by the unique solution of the differential equation

    $$\begin{aligned} \tilde{\pi }_q' (t)&= \left( \tilde{\pi }_q (t) - \frac{1}{k_q (t)} \right) \left[ \frac{ \sigma ^2_0 }{2} \left( \tilde{\pi }_q (t) - \pi ^{*}_0 \right) ^2 + \varPsi _1 - \varPsi _0 \right] - \tilde{\pi }_q (t) k_q' (t) , \\ \tilde{\pi }_q \left( S_q (t) \right)&= \pi _0^{*} . \end{aligned}$$

    For \(S_q (t) \le 0\) set \(\tilde{\pi }_q (t) := \pi _0^{*}\). This partial crash hedging strategy is bounded by

    $$ \pi ^{*}_0 - \sqrt{\frac{2}{\sigma _0^2} \left( \varPsi _0 - \varPsi _1 \right) } < \tilde{\pi }_q (t) \le \pi _0^{*} < 0 . $$

If \(k_q\) is independent of the time \(t\), the optimal portfolio strategy for an investor, who wants to maximize her \(q\)-quantile scenario portfolio problem, is given by

$$\begin{aligned} \bar{\pi }_q (t) := \min \left\{ \hat{\pi }_q (t) , \tilde{\pi }_q (t) , \pi ^{*}_0 \right\} \quad \text {for all}\,t \in [0,T] , \end{aligned}$$
(22)

where \(\tilde{\pi }_q\) will be taken into account, if it exists. \(\bar{\pi }_q\) will also be called the optimal  \(q\) -quantile crash hedging strategy.

Remark 2

Let us write \(\hat{\pi }_k (t)\) (instead of \(\hat{\pi }_q (t)\)) to emphasize the dependence on \(k\), whenever needed. It follows from Eqs. (19) and (20) that

$$\begin{aligned} \hat{\pi }_k' (T) = - \frac{1}{k} \left[ \varPsi _1 - r_0 \right] \quad \mathop {\longrightarrow }\limits ^{k \downarrow 0 ,k \not = 0} \left\{ \begin{array}{ll} \infty &{}\quad \text {if}\, \varPsi _1 < r_0 \\ 0 &{}\quad \text {if}\, \varPsi _1 = r_0 \\ - \infty &{}\quad \text {if}\, \varPsi _1 > r_0 \end{array} \right\} . \end{aligned}$$
(23)
  1. (a)

    First, observe that this implies that \(\hat{\pi }_q (t) \equiv 0\) if \(\varPsi _1 = r_0\), that is this is the only case where both the optimal \(q\)-quantile crash hedging strategy and the optimal crash hedging strategy are constant. That is, everything is invested in the risk-free asset if \(\varPsi _1 = r_0\).

  2. (b)

    Second, notice that \(\hat{\pi }_{k_1}' < \hat{\pi }_{k_2}'\) for \(k_1 < k_2\). Hence, \(\hat{\pi }_{k_1} \ge \hat{\pi }_{k_2}\) with strict inequality applying on \([0,T)\). Thus, in particular, \(\hat{\pi }_q (t) > \hat{\pi } (t)\) for \(t \in [0,T)\) for any \(q\) which satisfies \(q (t) < 1\) for \(t \in [0,T)\).

  3. (c)

    Third, for the remainder of this remark, let us consider only the case that \(\varPsi _1 \le \varPsi _0\) and \(\pi ^{*}_0 \ge 0\) (the other cases follow similarly). In this situation, one has that \(\hat{\pi }_k (t) \le \pi _0^{*}- \sqrt{\frac{2}{\sigma _0^2} \left( \varPsi _0 - \varPsi _1 \right) }\). Thus, it is clear that

    $$ \psi (t) := \left\{ \begin{array}{ll} 0 &{} \text {for } t = T \\ \pi _0^{*} - \sqrt{\frac{2}{\sigma _0^2} \left( \varPsi _0 - \varPsi _1 \right) } &{} \text {else} \end{array} \right\} $$

    is an upper bound for any \(\hat{\pi }_k\) with \(k > 0\). It follows that

    $$ \hat{\pi }_{k} (t) \longrightarrow \psi (t) \quad \text {pointwise for}\, k \downarrow 0\, \text {with}\, k \not = 0 \, , $$

    because of the convergence (23). Finally, keep in mind that the case \(k = 0\) yields \(\pi _0^{*}\) as the optimal portfolio with \(\pi _0^{*} \not \equiv \psi \). An example is given in Fig. 4.

Fig. 4
figure 4

Example of \(k \longrightarrow 0\) for \(\varPsi _1 = \varPsi _0\) and \(\pi _0^{*} \ge 0\)

Full size image

Proof

(of Theorem 1 ) If \(k_q (t)\) is constant in \(t\) this theorem follows from Theorem 4.1 in Korn and Wilmott [9, p.181], (for generalizations of this theorem see either Theorem 4.2 in Korn and Menkens [10, p.135] or Theorem 3.1 in Menkens [16, p.603]) by replacing \(k^{*}\) with \(k_q\). To verify the differential equation in the general case, keep in mind that by differentiating the—modified—Equation (A.5) in Korn and Wilmott [9, p.183] (or Eq. (3.1) in Menkens [16, p.602]) with respect to \(t\), \(k_q (t)\) has also to be differentiated with respect to \(t\). This leads to the differential equation (19).

5 Examples

5.1 Uniformly Distributed Crash Sizes

Suppose that the crash time has probability \(p (t) = p\) and that the crash size is uniformly distributed on \(\left[ k_{*} , k^{*} \right] \), that is

$$ f( k, t ) = \left\{ \begin{array}{ll} \frac{1}{k^{*} - k_{*}} &{}\quad \text {for}\, k \in \left[ k_{*} , k^{*} \right] \\ 0 &{}\quad \text {otherwise} \end{array} \right\} . $$

Using the defining equation for \(k_q\), that is

$$ 1 - p + p \int \limits _{k_{*}}^{k_q} \frac{1}{k^{*} - k_{*}} \, \mathrm{d}k = q $$

this leads to the following equation for \(k_q\)

$$ k_q = k_{*} + \frac{q + p - 1}{p} \left[ k^{*} - k_{*} \right] . $$

For \(q = 1\), we get the worst case back, that is \(k_1 = k^{*}\), as constructed.

5.2 Conditional Exponential Distributed Crash Sizes

Assume that the crash sizes are exponential distributed on the interval \(\left[ k_{*} , k^{*} \right] \). This means that

$$ f( k, t ) = \left\{ \begin{array}{ll} \frac{\lambda \mathrm{e}^{- \lambda k}}{\mathrm{e}^{-\lambda k_{*}} - \mathrm{e}^{- \lambda k^{*}}} &{}\quad \text {for}\, k \in \left[ k_{*} , k^{*} \right] \\ 0 &{}\quad \text {otherwise} \end{array} \right\} . $$

With this, \(k_q\) calculates to

$$ k_q = - \frac{1}{\lambda } \ln \left( \frac{1 - q - p}{p} \left[ \mathrm{e}^{- \lambda k_{*}} - \mathrm{e}^{- \lambda k^{*}} \right] + \mathrm{e}^{- \lambda k_{*}} \right) . $$

Again, \(k_q = k^{*}\) for \(q = 1\).

5.3 Conditional Exponential Distributed Crash Sizes with Exponential Distributed Crash Times

Suppose that not only the crash height has a conditional exponential distribution, but also the crash time has a conditional distribution, independent of the crash size, that is

$$\begin{aligned} p (t) = q + ( p - q ) \frac{1 - \mathrm{e}^{- \theta t}}{1 - \mathrm{e}^{- \theta T}}. \end{aligned}$$
(24)

This means that the probability of a crash happening is moving from \(q\) if \(t=0\) to \(p\) if \(t=T\) in an exponential decreasing way if \(q > p\). The defining equation of \(k_q\) writes in this case to

$$ 1 - q - ( p - q ) \frac{1 - \mathrm{e}^{- \theta t}}{1 - \mathrm{e}^{- \theta T}} + \left[ q + ( p - q ) \frac{1 - \mathrm{e}^{- \theta t}}{1 - \mathrm{e}^{- \theta T}} \right] \frac{\mathrm{e}^{- \lambda k_{*}} - \mathrm{e}^{- \lambda k_q (t)}}{\mathrm{e}^{- \lambda k_{*}} - \mathrm{e}^{- \lambda k^{*}}} = q. $$

This gives

$$\begin{aligned} k_q (t)&= - \frac{1}{\lambda } \ln \left( \mathrm{e}^{- \lambda k^{*}} + \frac{\left[ 1 - q \right] \left[ 1 - \mathrm{e}^{- \theta T} \right] \left[ \mathrm{e}^{- \lambda k_{*}} - \mathrm{e}^{- \lambda k^{*}} \right] }{ q \left[ 1 - \mathrm{e}^{- \theta T} \right] + (p-q) \left[ 1 - \mathrm{e}^{- \theta t} \right] } \right) . \end{aligned}$$

Clearly, this is an example where \(k_q\) depends on the time \(t\). Its derivative calculates to

$$\begin{aligned} \frac{\mathrm{d}k_q}{\mathrm{d}t} (t)&= - \frac{1}{\lambda } \frac{ \frac{- (p-q) \left[ 1 - q \right] \theta \mathrm{e}^{- \theta t} \left[ 1 - \mathrm{e}^{- \theta T} \right] }{\left[ q \left[ 1 - \mathrm{e}^{- \theta T} \right] + (p-q) \left[ 1 - \mathrm{e}^{- \theta t} \right] \right] ^2} \left[ \mathrm{e}^{- \lambda k_{*}} - \mathrm{e}^{- \lambda k^{*}} \right] }{\mathrm{e}^{- \lambda k^{*}} + \frac{\left[ 1 - q \right] \left[ 1 - \mathrm{e}^{- \theta T} \right] }{q \left[ 1 - \mathrm{e}^{- \theta T} \right] + (p-q) \left[ 1 - \mathrm{e}^{- \theta t} \right] } \left[ \mathrm{e}^{- \lambda k_{*}} - \mathrm{e}^{- \lambda k^{*}} \right] } \\&= \frac{1}{\lambda \left[ q \left[ 1 - \mathrm{e}^{- \theta T} \right] + (p-q) \left[ 1 - \mathrm{e}^{- \theta t} \right] \right] }\\&\times \frac{(p-q) \left[ 1 - q \right] \theta \mathrm{e}^{- \theta t} \left[ 1 - \mathrm{e}^{- \theta T} \right] \left[ \mathrm{e}^{- \lambda k_{*}} - \mathrm{e}^{- \lambda k^{*}} \right] }{(p-q) \left[ 1 - \mathrm{e}^{- \theta t} \right] \mathrm{e}^{- \lambda k^{*}} + \left[ 1 - \mathrm{e}^{- \theta T} \right] \left[ \mathrm{e}^{- \lambda k_{*}} \left[ 1 - q \right] - \mathrm{e}^{- \lambda k^{*}} \left[ 1 - 2 q \right] \right] }. \end{aligned}$$
Fig. 5
figure 5

The range of (optimal) \(q\)-quantile crash hedging strategies for \(\varPsi _1 = \varPsi _0\) and \(\pi _0^{*} \ge 0\). This graphic shows \(\hat{\pi }_{k^{*}}\) (solid line), \(\hat{\pi }_{k_{*}}\) (dotted line), the range of possible optimal \(q\)–quantile crash hedging strategies (grey area) if \(k_q\) is constant, and \(\pi ^{*}_0\) (solid straight line). The dash–dotted line is a uniform distributed example (see Sect. 5.1), the dashed line is an exponential distributed example (see Sect. 5.2), and the dotted line is a time–varying example (see Sect. 5.3).

Full size image

Figure 5 shows the potential range of the optimal \(q\)-quantile crash hedging strategy (the gray shaded area) if \(k_q (t) \not = 0\) is constant. Obviously, in the case of \(k_q (t) = 0\), one has that \(\hat{\pi }_q (t) = \pi _0^{*}\) (that is the optimal strategy is to invest according to the Merton fraction). Moreover, if \(k_q (t)\) is not constant, it can happen that the corresponding \(q\)-quantile crash hedging strategy moves outside the given range. However, this usually happens only if the derivative \(\frac{\mathrm{d}k_q}{\mathrm{d}t}\) is sufficiently large—which is not the case for most situations. The parameters used in these figures are \(k^{*} = 0.5\), \(k_{*} = 0.1\), \(\pi _0^{*} = 0.75\), and \(\sigma _0 = 0.25\). Additionally, the examples discussed above are plotted for the choices of \(p = 0.1\) and \(q = 0.95\). The dashed line is the example of a uniform distribution with \(p = 10\) % and \(q = 5\) %. The dash–dotted line is the example of an exponential distribution with the additional parameter \(\lambda = 10\) (where the other parameters are as above) and the dotted line is the example of a time varying crash probability given in Eq. (24) with the additional parameter \(\theta = 0.1\). Notice that the first two examples lead to similar strategies as in Korn and Wilmott [9], just that \(k^{*}\) is replaced by \(k_q\), which is constant in those two examples. The third example is clearly different from that. Starting with an investment horizon of \(T = 50\) years, the optimal strategy is to increase the fraction invested in the risky asset up to an investment horizon of about 30 years. This is due to the fact that the probability of a crash happening is \(95\) % at \(T=50\) and it is exponentially decreasing to \(10\) % as the investment horizon is reached.

6 Deterministic Portfolio Strategies

Definition 3

Let \(\pi \) be an admissible portfolio strategy.

$$ \pi _d (t) := \mathbb {E} \left[ \pi (t) \right] \quad \text {for all}\, t \in [0,T] $$

will be called the (to \(\pi \) ) corresponding deterministic portfolio strategy.

If \(\pi _d = \pi \), then \(\pi _d\) is admissible because \(\pi \) is admissible. If \(\pi _d (t) \not = \pi (t)\) for some \(t \in [0,T]\), then there exist \(\omega _1, \omega _2 \in \varOmega \), which depend on \(t\), such that

$$\begin{aligned} \pi \left( t , \omega _1 \right) \le \pi _d (t) \le \pi \left( t , \omega _2 \right) . \end{aligned}$$

Thus, \(\pi _d\) is bounded and therefore admissible.

Definition 4

Let us define

$$ k_{\pi } (t) := k^{*} \cdot 1 \!\mathrm{l}_{ \left\{ \pi (t) \ge 0 \right\} } + k_{*} \cdot 1 \!\mathrm{l}_{ \left\{ \pi (t) < 0 \right\} } . $$

Lemma 1

Let \(\pi \) be an admissible portfolio strategy. Then the corresponding deterministic portfolio strategy to \(\pi \) yields in the initial crash-free market at least the same expected utility of terminal wealth as \(\pi \). If, additionally \(\pi (t) < \frac{1}{k^{*}}\) holds for all \(t \in [0,T]\), then \(\pi _d\) yields in the initial market with a possible crash at least the same worst case expected utility of terminal wealth as \(\pi \).

Remark 3

This Lemma is important because often an optimization problem is solved only on the set of deterministic strategies (see e.g., Korn and Wilmott [9], Korn and Menkens [10], or Christiansen [6]) and not on the set of stochastic strategies (which include the deterministic ones). This is done because it is often simpler to solve the optimization problem on the set of deterministic strategies.

Proof

(of Lemma 1 ) Using the Theorem of Fubini, one has for any admissible portfolio strategy \(\pi \)

$$\begin{aligned} \fancyscript{J}_0 \left( t , x , \pi \right)&= \ln (x) + \mathbb {E} \left[ \int \limits _t^T \varPsi _0 - \frac{\sigma ^2_0}{2} \left( \pi (s) - \pi _0^{*} \right) ^2 \, \mathrm{d}s \right] \\&= \ln (x) + \int \limits _t^T \varPsi _0 - \frac{\sigma ^2_0}{2} \mathbb {E} \left[ \left( \pi (s) - \pi _0^{*} \right) ^2 \right] \, \mathrm{d}s \\&= \ln (x) + \int \limits _t^T \varPsi _0 - \frac{\sigma ^2_0}{2} \left( \mathbb {E} \left[ \pi (s) \right] - \pi _0^{*} \right) ^2 - \frac{\sigma ^2_0}{2} {\text {Var}}\left( \pi (s) \right) \, \mathrm{d}s \\&= \ln (x) + \int \limits _t^T \varPsi _0 - \frac{\sigma ^2_0}{2} \left( \pi _d (s) - \pi _0^{*} \right) ^2 - \frac{\sigma ^2_0}{2} {\text {Var}}\left( \pi (s) \right) \, \mathrm{d}s \\&= \fancyscript{J}_0 \left( t , x , \pi _d \right) - \frac{\sigma ^2_0}{2} \int \limits _t^T {\text {Var}}\left( \pi (s) \right) \, \mathrm{d}s \\&\le \fancyscript{J}_0 \left( t , x , \pi _d \right) . \end{aligned}$$

This is the case if no crash happens. In the case that a crash has happened, one gets with the definition

$$ A_{\pi } (t) := \ln \left( 1 - \mathbb {E} \left[ \pi (t) \right] k_{\pi _d} (t) \right) - \mathbb {E} \left[ \ln \left( 1 - \pi (t) k_{\pi } (t) \right) \right] $$

the following

$$\begin{aligned} \nu _1 \left( t , x \left( 1 - \pi (t) k_{\pi } (t) \right) \right)&= \ln (x) + \mathbb {E} \left[ \ln \left( 1 - \pi (t) k_{\pi } (t) \right) \right] + \varPsi _1 \left( T - t \right) \\&= \ln (x) + \ln \left( 1 - \pi _d (t) k_{\pi _d} (t) \right) + \varPsi _1 \left( T - t \right) - A_{\pi } (t) \\&= \nu _1 \left( t , x \left( 1 - \pi _d (t) k_{\pi _d} (t) \right) \right) - A_{\pi } (t) \\&\le \nu _1 \left( t , x \left( 1 - \pi _d (t) k_{\pi _d} (t) \right) \right) , \end{aligned}$$

where it has been used for the last inequality that \(A_{\pi } (t) \ge 0\). However, this is Jensen’s inequality which holds if \(1 - \pi (t) k_{\pi } (t) \ge 0\). The latter holds for \(\pi (t) < \frac{1}{k^{*}}\), which is the assumption. This proves the assertion.

Remark 4

The condition \(\pi (t) < \frac{1}{k^{*}}\) is natural if a crash of size \(k^{*}\) can happen, because it avoids that the investor can go bankrupt. Since \(k^{*} \le 1\), the condition means that the investor is not allowed to be too much leveraged.

7 Conclusion

It has been shown that the worst-case scenario approach of Korn and Wilmott [9] will not make use of additional probabilistic information of a crash happening. This is overcome by introducing a \(q\)-quantile approach which is a Value at Risk ansatz to the worst-case scenario method. Examples are given; in particular, one extreme example shows that it is possible with the \(q\)-quantile approach to obtain optimal portfolio strategies which are first increasing and then decreasing. Finally, it is shown that any stochastic portfolio strategy will give a lower expected utility of terminal wealth (or a lower worst-case scenario bound) than the corresponding deterministic portfolio strategy (defined by taking the expectation of the stochastic portfolio strategy)).