Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

10.1 Introduction

Tools for earthquake ground motion prediction (EGMP) are one of the key ingredients in seismic hazard analysis, both within probabilistic and deterministic frameworks, with the seminal objective to provide estimates of the expected ground motion at a site, given an earthquake of known magnitude, distance, faulting style, etc. A variety of procedures for EGMP has been proposed in the past four or five decades (Fig. 10.1), relying, on one side, on different information detail on the seismic source and propagation path, and, on the other side, providing different levels of output, either in terms of peak values of ground motion or of an entire time history. The level itself of complexity of the proposed procedures ranges from the empirical ground motion prediction equations, typically calibrated on the instrumental observations from real earthquakes, up to complex 3D numerical models, involving as a whole the system including source - propagation path – shallow soil layers. A comprehensive review of techniques for EGMP was recently published by Douglas and Aochi (2008).

Fig. 10.1
figure 1

Overview of approaches for earthquake ground motion prediction

Full size image

In the absence of suitable and performing numerical tools for physics-based modelling of source and path effects, research has been mainly directed in the past towards statistical processing of available records to provide empirical equations for EGMP. A recent compilation by Douglas (2011) has reported about 300 such equations to estimate peak ground acceleration (PGA) since 1964, and about 200 to estimate the response spectral ordinates. More recently, the ever increasing availability of high-quality records throughout the world, coupled with the improvement of the meta-files associated to the strong motion databases, has stimulated a further development of empirical tools for EGMP, both in the United States with the NGA West2 project (Boore et al. 2013) and in Europe with the calibration of updated pan-European ground motion prediction equations (Douglas et al. 2014).

Still, in spite of such a substantial effort, empirical ground motion prediction equations suffer of intrinsic limitations, such as: (1) the available records hardly cover the range of major potential interest for engineering applications (see Fig. 10.2), with relatively few records available in the near-field of large earthquakes; (2) they refer to generic site conditions, in the best cases represented in terms of VS,30; (3) they only provide peak values of ground motion, without the entire time history, which would be instead of major relevance in terms of input motion for engineering applications; (4) they are not suitable to be used for seismic scenario studies where the realistic representation of spatial variability of ground motion is an issue.

Fig. 10.2
figure 2

Magnitude and distance range covered by the strong motion database for calibration of pan-European ground motion prediction equations. Records are colour coded according to the network: red (Turkey); gray (Italy); blue (Greece); green (Iran); yellow (Iceland); black (other countries) (Adapted after Bindi et al. 2014)

Full size image

Physics-based numerical simulations of earthquake ground motion are often advocated as an alternative tool to cope with the previous limitations, since they provide, according to different methodologies, synthetic ground motion time histories compatible with a more or less detailed model of the seismic source process, of the propagation path, and of the local site response. Deterministic approaches rely on the rigorous numerical solution of the seismic wave propagation problem, based on detailed 3D models both of the seismic source and of the source-to-site propagation path. However, limited by the large computational requirements on one side, and, on the other side, by the insufficient information on the local seismic source features and on the local geology, the reliability range of such numerical solutions is most often limited to 1 or 2 Hz. For this reason, the frequency range of the numerical simulations is often enlarged to produce broadband waveforms, by considering hybrid approaches where high-frequency source and path effects are either modelled by stochastic or semi-stochastic processes (Seyhan et al. 2013) or random processes are introduced within a deterministic model to provide a realistic frequency-dependent spatial incoherency of ground motion.

The dream behind physics-based numerical simulations of earthquake ground motion is that they may become the engine to produce, effectively and with reasonable computing efforts, plausible realizations of future earthquakes. This is for example the idea behind the ShakeOut experiment in California, where the physics-based simulations of a hypothetical MW7.8 earthquake on the Southern San Andreas Fault (Porter et al. 2011) were the basis to construct a comprehensive earthquake risk scenario including costs evaluations and planning of emergency response activities.

The need for such advanced tools for EGMP was made clear by the consequences of the series of earthquakes from 2010 to 2012, started with Haiti in January 2010, followed by Chile in February 2010, by the Canterbury earthquake series in New Zealand in 2010–2011, by the gigantic Tohoku earthquake in Japan in March 2011, up to the Emilia, Italy, earthquakes of May 2012. All of them illustrating, in different terms and different scales, the increasing loss potential of seismic disasters. As a matter of fact, losses in the two-digit billion dollar range have become a reality, even outside the leading industrialized countries, and nowadays a much higher fraction of these losses is insured than in the past. Before the 2010 Chile earthquake, Santiago was last time affected by the 1985 Valparaiso M8 earthquake. Whereas the total economic loss in 2010 was about 25 times higher than 1985, the insured loss increased by a factor of 100. Furthermore, comparing the 1995 Kobe and the 2011 Tohoku earthquakes, the loss statistics shows a factor 3 increase for the economic loss, and a factor 13 for the insured loss.

Therefore, these recent disasters stimulated a re-thinking of several aspects of natural disaster risk management, which has not yet produced final conclusions, but shattered what may be called a false sense of security or complacency about how to assess and manage risk, including identification, evaluation, control and financing.

In the perspective of improving tools for seismic hazard identification, Munich RE funded a research activity with Politecnico di Milano, having the main objectives, on one side, of developing a certified computer code to run effectively numerical simulations of seismic wave propagation in large-scale models within high-performance computing architectures, and, on the other side, of applying this code to produce preliminary sets of physics-based earthquake ground shaking scenarios within large urban areas. This paper provides an overview of the progress within this research activity.

10.2 Numerical Approaches for Physics-Based Earthquake Ground Shaking Scenarios

Stimulated by the ever increasing power of large parallel computer architectures, numerical codes for seismic wave propagation have considerably evolved in the last decade and are presently becoming an appealing alternative to produce reliable physics-based earthquake ground motion scenarios in the presence of realistic 3D configurations of seismic source, complex basin structures and topographic features. Two major experiments of verification of such numerical codes were conducted in the second half of the last decade, namely within the ShakeOut (Bielak et al. 2010) and the Grenoble (Chaljub et al. 2010) benchmarks, while a further experiment is in progress (E2VP) based on the Euroseistest configuration (Chaljub et al. 2013).

Relatively few numerical codes exist for this purpose, mostly belonging to the classical finite difference (e.g., Graves 1996) and finite element (e.g., Bielak et al. 2005) schemes, while spectral element methods (e.g., Faccioli et al. 1997; Komatitsch and Vilotte 1998) have emerged subsequently as an alternative powerful technique, relying on a right balance between accuracy, ease of implementation and parallel efficiency. It is not surprising that three open source codes recently made available belong to the SE family. Namely, these are SPECFEM3D,Footnote 1 EFISPECFootnote 2 and SPEED,Footnote 3 the latter one being illustrated in the next section.

As a matter of fact, considering Table 10.1 which illustrates an overview of recent studies to produce physics-based earthquake ground shaking scenarios in large urban areas, most numerical methods included in this selection belong to the previous FD, FE or SE classes. Table 10.1 addresses as well further important issues of particular relevance:

Table 10.1 Selection of recent studies to produce physics-based earthquake ground shaking scenarios in large urban areas
Full size table

  • model sizes are very large, typically extending up to few hundreds of km size and few tens of km depth;

  • the maximum frequency propagated, f max , is only very seldom exceeding 1 Hz. However, even with such frequency limitation, the number of nodes of the numerical meshes exceeds as a rule 10 millions, implying a huge requirement in terms of computer time and memory requirement, so that these numerical simulations are typically carried out in parallel computer architectures;

  • as we move to recent years, there is an increasing trend in terms of number of simulations per case study, clearly showing that the computing power is presently opening this world to a much wider set of applications, including parametric analyses and production of large series of scenarios.

10.3 SPEED: SPectral Elements in Elastodynamics with Discontinuous Galerkin

10.3.1 Development of the Numerical Code

In the framework of the joint research activity between Munich RE and Politecnico di Milano, the SPEED code (SPectral Elements in Elastodynamics with Discontinuous Galerkin) was developed, as an open-source numerical code suitable to address the general problem of elastodynamics in arbitrarily complex media (Mazzieri et al. 2013). SPEED is designed for the simulation of large-scale seismic wave propagation problems including the coupled effects of a seismic fault rupture, the propagation path through Earth’s layers, localized geological irregularities such as alluvial basins and topographic irregularities. Some examples of applications with the additional presence of extended structures, such as railway viaducts, can be found in the SPEED web site.

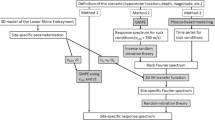
Treating numerical problems with such a wide range of spatial dimensions is allowed by a non-conforming mesh strategy implemented through a Discontinuous Galerkin (DG) approach (Antonietti et al. 2012). More specifically, the numerical algorithm can be summarized in the following steps (Fig. 10.3): consider an elastic heterogeneous 3D medium, (i) make a partition of the computational domain based on the involved materials and/or structures to be simulated, (ii) select a suitable spectral-element discretization in each non-overlapping sub-region, and (iii) enforce the continuity of the numerical solution at the internal interfaces by treating the jumps of the displacements through a suitable DG algorithm of the interior penalty type (De Basabe et al. 2008).

Fig. 10.3
figure 3

Non-conforming Spectral Element mesh (different element sizes and spectral degrees in each sub-domain) and its partition, with jumps along the interfaces treated according to a DG approach

Full size image

SPEED allows one to use non-conforming meshes (h-adaptivity) and different polynomial approximation degrees (N-adaptivity) in the numerical model. This makes mesh design more flexible (since grid elements do not have to match across interfaces) and permits to select the best-fitted discretization parameters in each subregion, while controlling the overall accuracy of the approximation. More specifically, the numerical mesh may consist of smaller elements and low-order polynomials where wave speeds are slowest, and of larger elements and high-order polynomial where wave speeds are fastest. Moreover, since the DG approach is applied only at a subdomain level, the complexity of the numerical model and the computational cost can be kept under control, avoiding the proliferation of unknowns, a drawback that is typical of classical DG discretizations.

Taking advantage of the built-in flexibility of the underlying discretization method and of the increasing computational power of parallel computer architecture, the code provides a versatile way to handle multi-scale earthquake engineering studies in a new “from-source-to-site” philosophy. This has been addressed in the recent years only by a few studies (Krishnan et al. 2006; Taborda et al. 2012; Isbiliroglu et al. 2013), due to the related intrinsic complexities of reproducing such phenomena in a single conforming model. A sketch of potential applications of SPEED is illustrated in Fig. 10.4.

Fig. 10.4
figure 4

Sketch of potential applications in elastodynamics of the SPEED code

Full size image

The code is naturally designed for multi-core computers or large clusters, but it can run as well on a single processor machine. It is written in Fortran90 with full portability in mind and conforms strictly the Fortran95 standards. It takes advantage of the hybrid parallel programming based upon the Message Passing Interface (MPI) library relying on the domain decomposition paradigm and the OpenMP library for multi-threading operations on shared memory. The mesh generation may be accomplished using a third party software, e.g. CUBIT (http://cubit.sandia.gov/) and load balancing is facilitated by graph partitioning based on the METIS library (glaros.dtc.umn.edu/) included in the package.

The code has been verified over different benchmarks, including that of Grenoble (Chaljub et al. 2010), and a further comparison with an independent solution is described in the following.

Physical discontinuities can be modeled either by the DG approach (creating physical interfaces) or by a not-honoring technique (where material properties are given node by node). The time-integration is performed either by the explicit second-order accurate leap-frog scheme or by the explicit fourth-order accurate Runge-Kutta method (Quarteroni et al. 2007).

Despite its short life-time, SPEED was awarded among the emerging applications with industrial relevance within the project PRACE-2IP (WP 9.3) and received substantial fundings for HPC resources (2012: ISCRA project MAgNITUd 500 k core hours, 2013: LISA project SISMAURB 2000 k core hours, PRACE project DN4RISC 40000 k core hours). Within the framework of PRACE-2IP, SPEED was optimized for use on the FERMI cluster at CINECA (Tier-0 machine), and optimal performances in term of efficiency, scalability and speed-up were obtained (see Dagna 2013).

10.3.2 Main Features

In its present version, SPEED allows the users to treat different seismic excitation modes, including: (i) kinematic seismic fault models (see below) (ii) plane wave load; (iii) Neumann surface load; (iv) volume force load. Dirichlet and/or Neumann boundary conditions can be set into the model; furthermore, first-order absorbing paraxial boundary conditions (Stacey 1988) have been implemented in order to prevent the propagation of spurious reflections from the external boundaries of the computational domain. The upgrade of the paraxial conditions to Perfectly Matched Layers (PML) is planned for the next release of the code.

Post-processing tools are available to produce ground shaking maps in a standard format that can be read by a variety of software, such as ArcGIS (www.esri.com), GID (gid.cimne.upc.es) and PARAVIEW (www.paraview.org).

10.3.2.1 Treatment of Kinematic Finite-Fault Models

SPEED adopts a kinematic description of the seismic source in terms of a distribution of double-couple point sources, whose mathematical representation is given by the seismic moment tensor density, i.e., \( {m}_{i j}\left(\underset{\bar{\mkern6mu}}{x}; t\right)=\frac{M_0\left(\underset{\bar{\mkern6mu}}{x}; t\right)}{V}\left({\nu}_i\cdot {n}_j+{\nu}_j\cdot {n}_i\right) \), where \( {M}_0\left(\underset{\bar{\mkern6mu}}{x}; t\right) \) is the time history of release at the source point x inside the elementary source volume V, n and ν denote the fault normal unit vector and the unit slip vector, respectively (Faccioli et al. 1997).

The code features a number of options for the kinematic modelling of an arbitrarily complex seismic source, by assigning realistic distributions of co-seismic slip along an extended fault plane through ad hoc pre-processing tools. These tools allow one to reproduce in a semi-automatic way realistic fault rupture models as compiled in the on-line Finite Source Rupture Models Database (Mai 2004) or computed by other methods using a specific format. Furthermore, it is also possible to define stochastically correlated random source parameters, in terms of slip pattern, rise time, rupture velocity and rupture velocity distribution along the fault plane, which may be crucial in deterministic simulations to excite high frequency components of ground motion (Smerzini and Villani 2012).

10.3.2.2 Attenuation Model

Modelling of visco-elastic media is handled by modifying the equation of motion according to the approach of Kosloff and Kosloff (1986). For this purpose, the inertial term \( \rho \frac{\partial^2 u}{\partial {t}^2} \) of the wave equation is replaced by \( \rho \frac{\partial^2 u}{\partial {t}^2}+2\zeta \frac{\partial u}{\partial t}+{\zeta}^2 u \), where u is the generic displacement component, ρ is mass density and ζ is an attenuation parameter. It can be shown that, with this substitution, all frequency components are equally attenuated with distance, resulting in a frequency proportional quality factor \( Q={Q}_0\frac{f}{f_0} \), where \( {Q}_0=\frac{\pi {f}_0}{\zeta} \) and f 0 is a reference value within the frequency range to be propagated.

This model is in agreement with numerous seismological observations supporting a frequency dependent law Q = Q 0 . f α, with α ~ 1 (e.g., Castro et al. 2004; Morozov 2008). Implementation of new rheological models is in progress, starting from the classical Rayleigh and Caughey damping.

10.3.2.3 Non-Linear Elastic Soil Behavior

A simple Non-Linear Elastic (NLE) soil model is implemented as a generalization to 3D load conditions of the classical modulus reduction (G−γ) and damping (D−γ) curves used within 1D linear-equivalent approaches (e.g. Kramer 1996), where G, D and γ are the shear modulus, damping ratio and 1D shear strain, respectively. Namely, to extend those curves to the 3D case, a scalar measure of shear strain amplitude is considered as follows:

$$ {\gamma}_{\max}\left(\underset{\bar{\mkern6mu}}{x}, t\right)= \max \left[\left|{\varepsilon}_I\left(\underset{\bar{\mkern6mu}}{x}, t\right)-{\varepsilon}_{I I}\left(\underset{\bar{\mkern6mu}}{x}, t\right)\right|,\left|{\varepsilon}_I\left(\underset{\bar{\mkern6mu}}{x}, t\right)-{\varepsilon}_{I I I}\left(\underset{\bar{\mkern6mu}}{x}, t\right)\right|,\left|{\varepsilon}_{I I}\left(\underset{\bar{\mkern6mu}}{x}, t\right)-{\varepsilon}_{I I I}\left(\underset{\bar{\mkern6mu}}{x}, t\right)\right|\right] $$
(10.1)

where ε I , ε II and ε III are the principal values of the strain tensor. Once the value of γ max is calculated at the generic position x and generic instant of time t, this value is introduced in the G−γ and D−γ curves and the corresponding parameters are updated for the following time step. Therefore, unlike the classical linear-equivalent approach, G and D values are updated step by step, so that the initial values of the dynamic soil properties are recovered at the end of the excitation. Application of this approach can be found in Stupazzini et al. (2009) for the case of Grenoble, France.

10.3.2.4 Hybrid Approach for the Generation of Broadband Synthetics

In spite of the increasing computer resources and tools, as shown in Table 10.1, 3D numerical simulations are still restricted to the low frequency range, up to about 1–2 Hz, mainly due to computational limitations as well as insufficient resolution of geologic and seismic source models. On the other hand, earthquake engineering applications need realistic ground motion time histories in the entire frequency range of interest for the analysis of structural response and damage assessment, say between 0 and 25 Hz.

A hybrid scheme is presently the best approach to generate broadband (BB) ground motions. In this work, Low Frequency (LF) waveforms from numerical simulations are combined by means of matching filters with the High Frequency (HF) synthetics computed by other independent approaches. Namely, the method of Sabetta and Pugliese (1996) was selected because of ease to treat in the post-processing phase the huge set of synthetics of the 3D numerical simulations. On the other side, it has the disadvantage of accounting neither of detailed kinematic fault rupture models, nor of specific 1D site amplification functions. Examples of other approaches for generation of synthetics, such as EXSIM (Motazedian and Atkinson 2005), are presented by Smerzini and Villani (2012) for the case of the 2009 L’Aquila earthquake.

The procedure adopted in this work to generate BB acceleration time histories at a given site can be summarized as follows (see Fig. 10.5): (i) compute N = 20 stochastic realizations by SP96 for each ground-motion component (EW and NS); (ii) for each stochastic realization, synchronize the LF and HF time histories in the time domain, so to have the same value for the time t 5% at which the normalized Arias intensity I a  = 5 % is reached both by the LF and HF synthetic; (iii) for each stochastic realization, combine HF and LF waveforms in the frequency domain by applying a match filter, defined as follows:

Fig. 10.5
figure 5

Generation of broadband ground motions (black) combining the LF waveforms from SPEED (red) with the HF synthetic accelerograms of Sabetta and Pugliese (1996), SP96 (blue), through suitable matching filters

Full size image
$$ BB(f)={w}_{LF}\cdot {A}_{LF}(f)+{w}_{HF}\cdot {A}_{HF}(f) $$
(10.2)

where A LF (f) and A HF (f) denote the Fourier transform of the LF and HF acceleration time histories, respectively; w LF and w HF are the corresponding weighting cosine-shape functions and BB(f) is the Fourier transform of the output BB signal.

10.4 Overview of Case Studies

Hybrid deterministic-stochastic ground shaking scenarios were generated in the following areas: (i) Santiago de Chile; (ii) Po Plain, NorthEastern Italy; (iii) Christchurch and (iv) Wellington, New Zealand. Besides a relevant interest from the economic loss exposure viewpoint, all of these sites were chosen because of availability of sufficiently detailed information both of the active faults surrounding the sites and of the shallow and deep geology structures, along with a significant amount of records, notably in the Christchurch and Po Plain cases.

The last rows of Table 10.1 summarize the main features of the adopted numerical models and the associated scenarios, so that a comparison with previous case studies can be made. All numerical meshes were built by the software CUBIT (cubit.sandia.gov/) and the numerical simulations were performed on parallel computer architectures, namely, the FERMI BlueGene/Q system, at CINECA (www.hpc.cineca.it/).

10.4.1 Santiago de Chile

Different earthquake rupture scenarios along the San Ramon fault, an active thrust structure crossing the eastern outskirts of the city of Santiago, were addressed. Recent works (e.g. Armijo et al. 2010) have shown that the San Ramon fault has a key role for the seismic hazard of the city.

The numerical model (see Fig. 10.6) was built by including: (i) surface topography; (ii) 3D model of the 80-km-long and 30-km-wide Santiago valley (Pilz et al. 2010); (iii) kinematic representation of potential ruptures breaking the San Ramon fault; (iv) linear visco-elastic soil behavior. 19 scenarios were considered by varying the magnitude (range from 5.5 to 7), slip pattern (7 different distributions) and hypocenters (8 different locations).

Fig. 10.6
figure 6

Computational domain for the Santiago region, Chile

Full size image

To appreciate the potential interest of these numerical simulations, Fig. 10.7 shows at top two representative scenarios in terms of PGV distribution in Santiago, and, at bottom, the simulated PGV variation with distance compared to the one predicted according to the empirical equation of Akkar and Bommer (2007). While, for the Mw6 scenario, there is an overall agreement of ground motion predicted by both approaches at stiff sites within the basin (EC8 class B), for the Mw 7 scenario the empirical equations are not fit to predict neither the very high near-fault PGV values, related to a fault slip mechanism affected by directivity, nor the high amplification levels at the edges of the basin in the vicinity of the fault (shaded areas in Fig. 10.7).

Fig. 10.7
figure 7

Top: Horizontal PGV (geometric mean) scenario maps for 2 out of 19 scenarios considered for Santiago de Chile. Bottom: comparison of simulated PGV values inside the basin with the empirical prediction based on the Akkar and Bommer (2007) equations. The superimposed ellipses on the right hand side denote areas where significant deviations from the GMPEs are found

Full size image

10.4.2 Po Plain, Italy

Stimulated by the major seismic sequence that struck the Emilia-Romagna region, Italy, from May to June 2012, a program for 3D numerical simulations of earthquake ground motion within the Po Plain was initiated. The model was constructed (Fig. 10.8) to include the seismogenic structures responsible of the MW 6.1 May 20 and MW 6.0 May 29 earthquakes (Ferrara and Mirandola faults, respectively). The irregular shape of the submerged bedrock topography in the Po Plain was also modelled, as derived by the isobaths of the basement of the Pliocene formations of the structural map of Italy (Bigi et al. 1992). Further details on the shear wave velocity model inside the Po Plain can be found in the sequel. A suite of 23 earthquake scenarios, characterized by magnitude ranging from 5.5 to 6.5, and different co-seismic slip distribution, focal mechanism, rupture velocity and rise time, was generated along both faults.

Fig. 10.8
figure 8

Po Plain, Italy: 3D numerical model including the seismic faults responsible of the MW 6.0 May 29 and MW 6.1 May 20 May earthquakes and the submerged topography. On the right, the assumed slip mechanisms to model the earthquakes

Full size image

Results of this case study will be explored in more detail in the next section, by comparison with the observed records.

10.4.3 The Canterbury Plains, New Zealand

A 3D numerical model of the Canterbury Plains, New Zealand, was constructed which includes the city of Christchurch, part of the Canterbury Plains and of the Banks Peninsula, extending over an area of about 45 × 45 × 20 km, and combines: (i) a horizontally layered deep crustal model as well as a reliable description of the alluvial-bedrock interface based on the available geological map and studies in the literature (Forsyth et al. 2008; Bradley 2012); (ii) the surface topography; (iii) a simplified velocity model of the Canterbury plain, filled with Quaternary deposits, constrained at shallow depths by extended MASW results within the Central Business District of ChristchurchFootnote 4; (iv) the kinematic fault models for the mainshocks of Feb 22 (MW 6.2), June 13 (MW 6.0) and Dec 23 2011 (MW 6.1), proposed by Beavan et al. (2012).

For sake of brevity, we refer the reader to the results published by Guidotti et al. (2011), based on a preliminary numerical model of the basin. We limit ourselves here to show in (Fig. 10.9) the PGV maps of the EW and NS components for the Feb 22, 2011 earthquake.

Fig. 10.9
figure 9

Christchurch, New Zealand: PGV map of the geometric mean of the horizontal components for the Feb 22, 2011 Mw6.2 earthquake. Coloured dots denote the corresponding observed values from earthquake records

Full size image

10.4.4 Wellington, New Zealand

Seismic hazard in the metropolitan area of Wellington is dominated by several major active fault systems, i.e., from West to East, the Ohariu, Wellington–Hutt and Wairarapa faults, as indicated by the superimposed red lines in Fig. 10.10, top-left panel. Although all these faults were incorporated in the numerical model, the scenarios are produced only for the Wellington–Hutt fault. This is a 75-km long strike-slip fault, characterized by a return period between 420 and 780 years for a magnitude between M 7.0 and 7.8 (Benites and Olsen 2005).

Fig. 10.10
figure 10

3D numerical model of the Wellington metropolitan area (bottom) with indications of the main active faults (top-left) and the Wellington Lower-Hutt basin (top-right) meshed by a non-conforming strategy

Full size image

Besides these faults, we incorporated in the numerical model (see Fig. 10.10, bottom panel) the most important geological features of the area, i.e., the 3D basin bedrock topography along with the 3D irregular soil layers deposited over the bedrock. This information is integrated based on the available geological and geophysical data (borehole, bathymetry, gravity, seismic), down to about 800 m depth (R. Benites, personal communication, 2013). To better describe such geological discontinuities, a non-conforming strategy was adopted to model the Wellington Valley, as depicted in Fig. 10.10, right-top panel. Note that the free-surface topography of the region is taken into account. Numerical simulations for this case study are presently in progress.

10.5 Insight of a Case Study: Earthquake Ground-Shaking Scenarios in the Po Plain

Among the previous case studies, we overview in this Section the numerical simulations of the seismic response of the Po Plain, with emphasis on the sites affected by the Emilia-Romagna earthquakes of May-June 2012, for which an exceptional set of strong motion records is available, especially for the MW 6.0 May 29 event. In addition to the simulation of this real earthquake, various fault rupture scenarios were produced, considering different hypothetical breaking mechanisms of the faults responsible of the May 20 and 29 earthquakes.

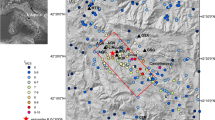
Leaving to other publications (e.g., Tizzani et al. 2013) an insight of the seismotectonic and geological environment, a critical step of this work is the validation of simulated results against strong motion records obtained during both earthquakes. While on May 20 the Mirandola (MRN) station alone was in operation, the number of near-source records from the May 29 event is much larger, mainly from temporary arrays (Fig. 10.11).

Fig. 10.11
figure 11

NS components of a selected set of velocity records of May 29 Emilia earthquake. Superimposed in the slip model assumed based on Atzori et al. (2012)

Full size image

The near-source records show similar features, with large velocity pulses in the fault normal direction reaching up to about 60 cm/s, while, at larger distance from the fault, peak values rapidly decrease and records tend to be dominated by surface waves generated by the complex subsoil structure of the Po Plain (Luzi et al. 2013). Peak values of horizontal acceleration reach about 0.3 g, while on May 29 the vertical acceleration at MRN reached a remarkable 0.9 g.

10.5.1 3D Numerical Simulations of the 29 May 2012 Earthquake

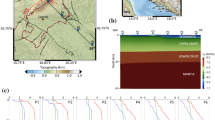
Numerical modelling of the 29 May earthquake was addressed, being this earthquake the best constrained in terms of strong motion recordings as well as of source inversion studies. For the shear velocity model (see Fig. 10.12a), a homogenous average soil profile was defined for the Po Plain sediments, while a horizontally layered model was assumed in the rock Miocene formations. These profiles were calibrated merging the information from the available V S profiles and published works (e.g. Margheriti et al. 2000; Martelli and Molinari 2008), along with the Down-Hole and Cross-Hole surveys (Project S2 2013). The resulting subsoil model has been found in reasonable agreement with the results recently published by Milana et al. (2013). The kinematic fault solution proposed by Atzori et al. (2012) has been adopted in the numerical simulations (see superimposed map in Fig. 10.11).

Fig. 10.12
figure 12

(a) VS profile adopted for the 3D numerical simulations (red: Po Plain sediments; black: Miocene bedrock formations). (b) G-γ and D-γ curves adopted for the first 150 m in a non-linear elastic approach. (c) Validation of SPEED numerical simulations with the Hisada (1994) code, assuming a 1D Vs soil profile, and the finite-fault of May 29 earthquake

Full size image

Both a linear visco-elastic and non-linear elastic soil behavior has been adopted for the numerical simulations, as discussed in the sequel. The G−γ and D−γ curves as derived by Fioravante and Giretti (2012) were used for the top 150 m layers.

Prior to the numerical simulations with the 3D model, we carried out a validation with the results of the Hisada (1994) code, by assuming a 1D Vs soil profile and the finite-fault of May 29 earthquake. The very good agreement of the two solutions (Fig. 10.12c) demonstrates the accuracy of SPEED.

Figure 10.13 shows some snapshots of the displacement wavefield (NS component) through a NS cross-section including the seismic fault, clearly showing the key role of the submerged topography to produce prominent surface wave trains affecting seismic ground response both at short and at large distance from the epicenter.

Fig. 10.13
figure 13

Top: Simplified sketch of a NS cross-section of the Po-plain across Mirandola and the seismic source of the May 29 earthquake. Bottom: snapshots of the NS displacement wavefield along this cross-section

Full size image

Figure 10.14 shows the comparison between synthetics and recordings in terms of three-component displacement waveforms at 12 representative strong motion stations, distributed about uniformly around the epicenter. Both recorded and simulated waveforms were band-passed filtered between 0.1 and 1.5 Hz, the latter being the frequency limit of the numerical model. The agreement between synthetics and recordings is satisfactory, especially for stations distant from the epicenter. On the other hand, at stations in the near-field region, such as MRN and SAN0, the numerical model tends to underestimate significantly the observed horizontal ground motion amplitudes, while a good agreement is found for the vertical component. This points to one of the most critical problems to be faced when physics-based simulations of real earthquakes are compared with observations, that is, near-fault records depend on details of the source slip mechanism and rupture propagation that are hardly predicted and are often beyond the frequency range on which earthquake source inversions are provided. While, the larger the epicentral distance is, the smaller is the relevance of such details.

Fig. 10.14
figure 14

Recorded (black) and simulated displacement waveforms (0.1–1.5 Hz). Results for both linear (blue dotted) and non-linear (red) visco-elastic soil behavior are shown. The location of stations is illustrated in Fig. 10.11

Full size image

The most significant effects of non-linear soil behavior are found at those stations where the thickness of soft sediments reaches considerable values of a few thousands of kilometers (see e.g. MDN station). Given the low frequency range propagated by the model (<1.5 Hz), the overall impact of soil nonlinearity is small especially for the stations in the near-fault region.

10.5.2 Ground Shaking Scenarios in the Po Plain

Starting from the 3D models developed for the May 20 and May 29 earthquakes, different hypothetical seismic rupture scenarios were assumed, all of them breaking either the Mirandola or the Ferrara faults, with magnitude ranging from 5.5 to 6.5. Realistic slip models along the faults were obtained either by source inversion of real earthquakes with similar fault mechanisms or they were computed using a self-similar k-square model (Herrero and Bernard 1994; Gallovič and Brokešová 2007). Twelve rupture scenarios are produced along the Ferrara fault (May 20) and eleven are activated along the Mirandola fault (May 29).

An overview of the ground shaking map in terms of spatial distribution of PGV (geometric mean of horizontal components), for eight selected scenarios, is shown in Fig. 10.15. For each scenario, the surface projection of the seismic fault is superimposed on the PGV map and the corresponding kinematic source model is displayed on the right hand side. It is interesting to note that the computed seismic response is strongly affected by the combination of directivity and radiation pattern effects, with near-fault PGV values that appear to be only slightly dependent on magnitude, in agreement with several theoretical and experimental studies (see e.g., McGarr and Fletcher 2007).

Fig. 10.15
figure 15

PGV (geometric mean of horizontal components) maps for selected ground shaking scenarios in the Po Plain

Full size image

Finally, we compare in Fig. 10.16 the PGV maps obtained through the hybrid BB approach outlined previously, by injecting high frequency components into the results of the physics-based numerical simulations, with those provided by ShakeMap tools (shakemap.rm.ingv.it) based on suitable interpolation procedures of available records. It can be noted that there is a qualitative agreement in terms of spatial distribution, but the near-fault peak values are significantly underestimated, by a factor of about 2. Namely, with the adopted kinematic fault solution and hypocenter location, it was not possible to reproduce the large recorded near-fault velocity peaks (see Fig. 10.14, stations MRN and SAN0).

Fig. 10.16
figure 16

PGV maps from BB (SPEED + SP96) numerical simulations (left) and from ShakeMap tool (right)

Full size image

10.6 A Web-Repository for Ground-Shaking Scenarios

One of the main outcomes of the cooperation of PoliMi with MunichRe was the development of a web-repository of the synthetic seismic scenarios produced in the urban areas considered, in a format suitable for risk assessment studies. The data structure of the web-repository is handled as a relational Access database, so that any standard/advanced query can be easily performed.

It is worth to remark here that the database is not constrained to SPEED results, rather it was envisioned as an open repository aiming at collecting the results of different complex scenarios, both from the simulation method and model description viewpoint.

Figure 10.17 illustrates the conceptual scheme adopted as a basis of the archive of synthetic seismic scenarios, with reference to the Po Plain case study: (1) the user first selects the target location; (2) then, the seismic fault is picked among those available for the location under study; (3) the target scenario is adopted, uniquely defined by magnitude, location and size of the broken fault, and by the additional parameters such as co-seismic slip distribution, nucleation point, rupture velocity, rise time and rake angle; (4) output ground shaking maps are downloaded. In a future version of the web site, BB time-histories at selected locations will also be downloadable.

Fig. 10.17
figure 17

Web-repository of earthquake ground shaking scenarios

Full size image

Output maps are stored in a standard format, on a regular grid of Latitude and Longitude in terms of the following strong motion parameters (geometric mean of horizontal components): Peak Ground Displacement (PGD), Peak Ground Velocity (PGV), Peak Ground Acceleration (PGA), response spectral Pseudo-Acceleration (PSA) at 0.3, 1.0, 3.0, and 5.0 s.

10.6.1 Conclusions

In the framework of a research contract between Politecnico di Milano, Italy, and Munich Re, Germany, we generated physics-based ground shaking scenarios from hypothetical earthquakes in large urban areas worldwide. These scenarios were obtained by the open-source high-performance computer code SPEED, based on a Discontinuous Galerkin spectral element formulation of the elastodynamics equations, allowing one to treat non-conforming meshes as well as non-uniform polynomial approximation degrees.

The case studies encompass Santiago de Chile, the Po Plain, Italy, Christchurch and Wellington, New Zealand. Taking advantage of the large set of records obtained in the near-fault region of the Po Plain, affected by the earthquake sequence of May-June 2012, results from the 3D numerical modelling of the MW 6 May 29 2012 earthquake were illustrated, under both assumptions of linear and non-linear visco-elastic materials. Comparisons with records were addressed, to highlight potential limitations of this numerical approach to obtain realistic ground shaking scenarios.

Although results for this case study were not fully satisfactory when compared to records, this simulation experiment pointed out some of the key points to be accounted for when physics-based earthquake ground motion simulations are carried out and compared with real records:

  • given the complexity of the numerical model, preliminary validation tests with independent numerical codes on simplified configurations (as shown in Fig. 10.12c) are recommended;

  • the accuracy of input data for finite-fault modelling is crucial, especially in the near-field region, where details on the asperity distribution along the fault, together with the relative position of the nucleation point with respect to the slip pattern, affect dramatically the ground motion computations;

  • if the input seismic source and geological models are sufficiently detailed to excite seismic ground motion within a sufficiently wide frequency range, physics-based numerical simulations are capable of providing realistic ground shaking scenarios and of capturing some features of ground motion variability (such as spatial coherency, dependence on the lateral variation of soil properties, basin edge effects, surface or submerged topographic irregularities), which are not taken into account by any other tool for EGMP.

As shown in Table 10.1, much progress has been done in the last 15 years in the production of realistic physics-based earthquake ground shaking scenarios in large urban areas. Several verification benchmarks of the numerical codes against independent solutions and/or cross-validation among codes have demonstrated that a satisfactory level of reliability of results has been reached. Furthermore, the computational progress allows one presently to run numerical meshes of hundreds of millions nodes in few hours, or tens of minutes, even without having access to very powerful computer architectures.

However, in order for such numerical approaches to be accepted confidently by the engineering community as alternative and reliable tools to empirical approaches for EGMP, physics-based numerical simulations of source-to-site earthquake ground motion prediction still need to convincingly provide answers to the following questions:

  • what is the level of detail required on the seismic source to excite ground motions in a large enough frequency range?

  • what is the level of detail required on the local geology to produce realistic ground motion scenarios useful for seismic risk evaluations?

  • how many numerical simulations are required to produce a sufficiently representative and reliable picture of the earthquake ground motion and of its spatial variability?

Answers to the previous questions will be by far more convincing if these methods will be proven to provide explanations of observed ground motions, especially in the near-source region, more satisfactory than conventional tools for EGMP.