Abstract
We show that (local) confluence of terminating logically constrained rewrite systems is undecidable, even when the underlying theory is decidable. Several confluence criteria for logically constrained rewrite systems are known. These were obtained by replaying existing proofs for plain term rewrite systems in a constrained setting, involving a non-trivial effort. We present a simple transformation from logically constrained rewrite systems to term rewrite systems such that critical pairs of the latter correspond to constrained critical pairs of the former. The usefulness of the transformation is illustrated by lifting the advanced confluence results based on (almost) development closed critical pairs as well as on parallel critical pairs to the constrained setting.
This research is funded by the Austrian Science Fund (FWF) project I5943.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Logically constrained rewrite systems (LCTRSs) [12] are a natural extension of plain term rewrite systems (TRSs) with native support for constraints that are handled by SMT solvers. The latter makes LCTRSs suitable for program analysis [3,4,5, 22]. In this paper we are concerned with confluence techniques for LCTRSs. Numerous techniques exist to (dis)prove confluence of TRSs. For LCTRSs much less is known. Kop and Nishida [12] established (weak) orthogonality as sufficient confluence criteria for LCTRSs. Joinability of critical pairs for terminating systems is implicit in [22]. Very recently, strong closedness for linear LCTRSs and (almost) parallel closedness for left-linear LCTRSs were established [17]. The proofs of these results were obtained by replaying existing proofs for TRSs in a constrained setting, involving a non-trivial effort. For more advanced confluence criteria, this is not feasible.
In particular, the conclusion in [12] that LCTRSs “are flexible: common analysis techniques for term rewriting extend to LCTRSs without much effort” is not accurate. On the contrary, in Sect. 3 we show that (local) confluence of terminating LCTRSs is undecidable, even for a decidable fragment of the theory of integers.
In Sect. 4 we present a simple transformation from LCTRSs to TRSs which allows us to relate results for the latter to the former. We use the transformation to extend two advanced confluence criteria based on (parallel) critical pairs from TRSs to LCTRSs: In Sect. 5 we prove that (almost) development closed left-linear LCTRSs are confluent by reusing the corresponding result for TRSs obtained by van Oostrom [15] and in Sect. 6 we lift the result of Toyama [20] based on parallel critical pairs from TRSs to LCTRSs. Both results are employed in state-of-the-art confluence provers for TRSs (ACP [2], CSI [14], Hakusan [19]) and have only recently been formally verified in the Isabelle proof assistant [7, 10, 11].
For the LCTRS extension of the result of Toyama [20] we observed a subtle problem in the definition of the equivalence relation on constrained terms, which goes back to [12] and has been used in subsequent work on LCTRSs [5, 17, 22]. We briefly discuss the issue at the end of the next section, after recalling basic notions for LCTRSs. For space reasons some of the more technical proofs are only available in an extended version of this paper [18]. The results in Sect. 4 and Sect. 5 were first announced in [13].
2 Preliminaries
We assume familiarity with the basic notions of term rewriting. In this section we recall a few key notions for LCTRSs. For more background information we refer to [12, 17, 22]. We assume a many-sorted signature \(\mathcal {F}= \mathcal {F}_{\textsf{te}}\cup \mathcal {F}_{\textsf{th}}\) with a term and theory part. For every sort \(\iota \) in \(\mathcal {F}_{\textsf{th}}\) we have a non-empty set \(\mathcal {V}\textsf{al}_\iota \subseteq \mathcal {F}_{\textsf{th}}\) of value symbols, such that all \(c \in \mathcal {V}\textsf{al}_\iota \) are constants of sort \(\iota \). We demand \(\mathcal {F}_{\textsf{te}}\cap \mathcal {F}_{\textsf{th}}\subseteq \mathcal {V}\textsf{al}\) where \(\mathcal {V}\textsf{al}= \bigcup _\iota \mathcal {V}\textsf{al}_\iota \). In the case of integers this results in an infinite signature with \(\mathbb {Z} \subseteq \mathcal {V}\textsf{al}\subseteq \mathcal {F}_{\textsf{th}}\). A term in \(\mathcal {T}(\mathcal {F}_{\textsf{th}},\mathcal {V})\) is called a logical term. Ground logical terms are mapped to values by an interpretation \(\mathcal {J}\): \([\![{f({t_1},\dots ,{t_{n}})}]\!] = f_\mathcal {J}([\![{t_1}]\!],\dots ,[\![{t_n}]\!])\). We assume a bijection between value symbols and elements in the domain of \(\mathcal {J}\), e.g., for integers: \([\![{\textsf{0}}]\!] = 0\), \([\![{\mathsf {-1}}]\!] = -1\), \([\![{\textsf{1}}]\!] = 1\) and so on. Logical terms of sort \(\textsf{bool}\) are called constraints. A constraint \(\varphi \) is valid if \([\![{\varphi \gamma }]\!] = \top \) for all substitutions \(\gamma \) such that \(\gamma (x) \in \mathcal {V}\textsf{al}\) for all \(x \in \mathcal {V}\textsf{ar}(\varphi )\). A constrained rewrite rule is a triple \(\ell \rightarrow r~[\varphi ]\) where \(\ell , r \in \mathcal {T}(\mathcal {F},\mathcal {V})\) are terms of the same sort such that \(\textsf{root}(\ell ) \in \mathcal {F}_{\textsf{te}}\setminus \mathcal {F}_{\textsf{th}}\) and \(\varphi \) is a constraint. We denote the set \(\mathcal {V}\textsf{ar}(\varphi ) \cup (\mathcal {V}\textsf{ar}(r) \setminus \mathcal {V}\textsf{ar}(\ell ))\) of logical variables in \(\ell \rightarrow r~[\varphi ]\) by \(\mathcal {L}\mathcal {V}\textsf{ar}(\ell \rightarrow r~[\varphi ])\). A constrained rewrite rule is left-linear (right-linear) if non-logical variables in the left-hand side (right-hand side) occur at most once. If a rule is left-linear and right-linear then it is called linear. An LCTRS is a set of constrained rewrite rules.
A substitution \(\sigma \) is said to respect a rule \(\ell \rightarrow r~[\varphi ]\), denoted by \(\sigma \vDash \ell \rightarrow r~[\varphi ]\), if \(\mathcal {D}\textsf{om}(\sigma ) \subseteq \mathcal {V}\textsf{ar}(\ell ) \cup \mathcal {V}\textsf{ar}(r) \cup \mathcal {V}\textsf{ar}(\varphi )\), \(\sigma (x) \in \mathcal {V}\textsf{al}\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\ell \rightarrow r~[\varphi ])\), and \([\![{\varphi \sigma }]\!] = \top \). Moreover, a constraint \(\varphi \) is respected by \(\sigma \), denoted by \(\sigma \vDash \varphi \), if \(\sigma (x) \in \mathcal {V}\textsf{al}\) for all \(x \in \mathcal {V}\textsf{ar}(\varphi )\) and \([\![{\varphi \sigma }]\!] = \top \). We call \(f({x_1},\dots ,{x_{n}}) \rightarrow y~[y = f({x_1},\dots ,{x_{n}})]\) with a fresh variable y and \(f \in \mathcal {F}_{\textsf{th}}\setminus \mathcal {V}\textsf{al}\) a calculation rule. Calculation rules are not part of the rules of an LCTRS \(\mathcal {R}\). The set of all calculation rules induced by the signature \(\mathcal {F}_{\textsf{th}}\) of an LCTRS \(\mathcal {R}\) is denoted by \(\mathcal {R}_\textsf{ca}\) and we abbreviate \(\mathcal {R}\cup \mathcal {R}_\textsf{ca}\) to \(\mathcal {R}_\textsf{rc}\). An LCTRS is called linear (left-linear, right-linear) if all its rules in \(\mathcal {R}\) are linear (left-linear, right-linear). A rewrite step
 satisfies \(s|_p = \ell \sigma \) and \(t = s[r\sigma ]_p\) for some position p, constrained rewrite rule \(\ell \rightarrow r~[\varphi ]\) in \(\mathcal {R}_\textsf{rc}\), and substitution \(\sigma \) such that \(\sigma \vDash \ell \rightarrow r~[\varphi ]\). We drop the subscript \(\mathcal {R}\) from
satisfies \(s|_p = \ell \sigma \) and \(t = s[r\sigma ]_p\) for some position p, constrained rewrite rule \(\ell \rightarrow r~[\varphi ]\) in \(\mathcal {R}_\textsf{rc}\), and substitution \(\sigma \) such that \(\sigma \vDash \ell \rightarrow r~[\varphi ]\). We drop the subscript \(\mathcal {R}\) from
 when no confusion arises. An LCTRS \(\mathcal {R}\) is confluent if there exists a term v with
when no confusion arises. An LCTRS \(\mathcal {R}\) is confluent if there exists a term v with
 whenever
whenever
 , for all terms s, t and u. For confluence analysis we need to rewrite constrained terms.
, for all terms s, t and u. For confluence analysis we need to rewrite constrained terms.
A constrained term is a pair \(s~[\varphi ]\) consisting of a term s and a constraint \(\varphi \). Two constrained terms \(s~[\varphi ]\) and \(t~[\psi ]\) are equivalent, denoted by \(s~[\varphi ] \sim t~[\psi ]\), if for every substitution \(\gamma \vDash \varphi \) with \(\mathcal {D}\textsf{om}(\gamma ) = \mathcal {V}\textsf{ar}(\varphi )\) there is some substitution \(\delta \vDash \psi \) with \(\mathcal {D}\textsf{om}(\delta ) = \mathcal {V}\textsf{ar}(\psi )\) such that \(s\gamma = t\delta \), and vice versa. Let \(s~[\varphi ]\) be a constrained term. If \(s|_p = \ell \sigma \) for some constrained rewrite rule \(\rho :\ell \rightarrow r~[\psi ] \in \mathcal {R}_\textsf{rc}\), position p, and substitution \(\sigma \) such that \(\sigma (x) \in \mathcal {V}\textsf{al}\cup \mathcal {V}\textsf{ar}(\varphi )\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\), \(\varphi \) is satisfiable and \(\varphi \Rightarrow \psi \sigma \) is valid then
 . The rewrite relation
. The rewrite relation
 on constrained terms is defined as
on constrained terms is defined as
 and
and
 indicates that the rewrite step in
indicates that the rewrite step in
 takes place at position p. Similarly, we write
takes place at position p. Similarly, we write
 if the position in the rewrite step is below position p. Note that in our definition of
if the position in the rewrite step is below position p. Note that in our definition of
 the constraint is not modified. This equals [5, Definition 2.15], but is different from [12, 17] where calculation steps \(s[f({v_1},\dots ,{v_{n}})]_p~[\varphi ] \rightarrow s[v]_p~[\varphi \wedge v = f({v_1},\dots ,{v_{n}})]\) modify the constraint. However, the relation
the constraint is not modified. This equals [5, Definition 2.15], but is different from [12, 17] where calculation steps \(s[f({v_1},\dots ,{v_{n}})]_p~[\varphi ] \rightarrow s[v]_p~[\varphi \wedge v = f({v_1},\dots ,{v_{n}})]\) modify the constraint. However, the relation
 can simulate the relation
can simulate the relation
 from [12, 17] as exemplified below.
from [12, 17] as exemplified below.
Example 1
Consider the constrained term \(x + \textsf{1}~[x > \textsf{3}]\). Calculation steps as defined in [12, 17] permit \(x + \textsf{1}~[x > \textsf{3}] \rightarrow z~[z = x + \textsf{1} \wedge x > \textsf{3}]\). In our setting, an initial equivalence step is required to introduce the fresh variable z and the corresponding assignment needed to perform a calculation: \(x + \textsf{1}~[x > \textsf{3}] \sim x + \textsf{1}~[z = x + \textsf{1} \wedge x > \textsf{3}] \rightarrow z~[z = x + \textsf{1} \wedge x > \textsf{3}]\).
Our treatment allows for a much simpler definition of parallel and multi-step rewriting since we do not have to merge different constraints.
2.1 Equivalence on Constrained Terms
The equivalence on constrained terms \(\sim \) used in this paper also differs from the equivalence relation used in [12, 17], which we will denote by \(\sim '\). In \(\sim '\) the domain of substitutions is not restricted, i.e., \(s~[\varphi ] \sim ' t~[\psi ]\) if and only if for all substitutions \(\gamma \vDash \varphi \) there exists a substitution \(\delta \) where \(\delta \vDash \psi \) and \(s\gamma = t\delta \). Intuitively, constrained terms are equivalent with respect to \(\sim '\) if their sets of “allowed” instances are equivalent, while for \(\sim \) we only instantiate variables appearing in the constraints and therefore representing some value. We have \({\sim } \subsetneq {\sim '}\). This can be seen as follows. First of all, any substitution \(\gamma \) with \(\gamma \vDash \varphi \) can be split into \(\gamma _1\) and \(\gamma _2\) such that \(\gamma = \gamma _1 \cup \gamma _2 = {} \gamma _1\gamma _2\) with \(\mathcal {D}\textsf{om}(\gamma _1) = \mathcal {V}\textsf{ar}(\varphi )\) and \(\gamma _1 \vDash \varphi \). From \(s~[\varphi ] \sim t~[\psi ]\) we obtain a substitution \(\delta _1\) where \(\mathcal {D}\textsf{om}(\delta _1) = \mathcal {V}\textsf{ar}(\psi )\), \(\delta _1 \vDash \psi \) and \(s\gamma _1 = t\delta _1\). Hence also \(s\gamma = s\gamma _1\gamma _2 = t\delta _1\gamma _2 = t\delta \) for \(\delta = \delta _1\gamma _2\), which implies \(s~[\varphi ] \sim ' t~[\psi ]\). However, \({\sim '} \subseteq {\sim }\) does not hold since \(x~[\textsf{true}] \sim ' y~[\textsf{true}]\) and \(x~[\textsf{true}] \not \sim y~[\textsf{true}]\).
The change is necessary, since we have to differentiate (non-logical) variables in constrained terms from one another, to keep track of them through rewrite sequences. Take the (LC)TRS \(\mathcal {R}\) consisting of the rule \(\textsf{f}(x,y) \rightarrow x\). When rewriting unconstrained terms we have
 and
and
 . When rewriting on constrained terms with respect to \(\sim '\), however, we have \(\textsf{f}(x,y)~[\textsf{true}] \sim ' \cdot \rightarrow \cdot \sim ' x~[\textsf{true}]\) and \(\textsf{f}(x,y)~[\textsf{true}] \sim ' \cdot \rightarrow \cdot \sim ' y~[\textsf{true}]\), losing any information connecting the resulting variable to the initial term. This is especially problematic in our analysis of parallel critical pairs in Sect. 6, where keeping track of variables through rewrite sequences is essential. Note that
. When rewriting on constrained terms with respect to \(\sim '\), however, we have \(\textsf{f}(x,y)~[\textsf{true}] \sim ' \cdot \rightarrow \cdot \sim ' x~[\textsf{true}]\) and \(\textsf{f}(x,y)~[\textsf{true}] \sim ' \cdot \rightarrow \cdot \sim ' y~[\textsf{true}]\), losing any information connecting the resulting variable to the initial term. This is especially problematic in our analysis of parallel critical pairs in Sect. 6, where keeping track of variables through rewrite sequences is essential. Note that
 but not
but not
 .
.
3 Undecidability
Confluence is a decidable property of finite terminating TRSs, a celebrated result of Knuth and Bendix [9] which forms the basis of completion. For LCTRSs matters are more complicated.
Theorem 1
Local confluence is undecidable for terminating LCTRSs.
Proof
We use a reduction from PCP [16]. Let \(P = \{(\alpha _1,\beta _1),\dots ,(\alpha _N,\beta _N)\}\) with \({\alpha _1},\dots ,{\alpha _{N}}, {\beta _1},\dots ,{\beta _{N}} \in \{0,1\}^+\) be an instance of PCP, where we assume that \(\alpha _i \ne \beta _i\) for at least one \(i \in \{1,\dots ,N\}\). This entails no loss of generality, since instances that violate this assumption are trivially solvable. We encode candidate strings over \(\{1,\dots ,N\}\) as natural numbers where the empty string \(\epsilon \) is represented by \([\epsilon ] = 0\), and a non-empty string \(i_0 i_1 \cdots i_k\) is represented by \([i_0 i_1 \cdots i_k] = N \cdot [i_1 \cdots i_k] + i_0\). So \([i_0 i_1 \cdots i_k] = i_0 + i_1 \cdot N + \cdots + i_k \cdot N^k\). For instance, assuming \(N = 3\), the number 102 encodes the candidate string \(\underline{3313}\) since \(102 = 3 \cdot 33 + \underline{3}\), \(33 = 3 \cdot 10 + \underline{3}\), \(10 = 3 \cdot 3 + \underline{1}\) and \(3 = 3 \cdot 0 + \underline{3}\). Conversely, the candidate string \(\underline{112}\) is mapped to \(22 = \underline{1} + \underline{1} \cdot 3^1 + \underline{2} \cdot 3^2\). It is not difficult to see that this results in a bijection between \(\mathbb {N}\) and candidate strings, for each \(N > 0\).
The LCTRS \(\mathcal {R}_P\) that we construct is defined over the theory \(\textsf{Ints}\), with theory symbols \(\mathcal {F}_{\textsf{th}}= \{>,+,\cdot ,=,\wedge \} \cup \mathcal {V}\textsf{al}\) and values \(\mathcal {V}\textsf{al}= \mathbb {B} \cup \mathbb {Z}\), with the additional sorts \(\textsf{PCP}\) and \(\textsf{String}\) and the following term signature:
The LCTRS \(\mathcal {R}_P\) consists of the following rules:

Here, for a string \(\gamma \in \{0,1\}^*\) and a term \(t : \textsf{String}\), \(\gamma (t) : \textsf{String}\) is defined as
Note that in the constraints n and m are variables, while N and i are values. Hence all constraints are in the decidable fragment of linear integer arithmetic and the rewrite relation \(\rightarrow _{\mathcal {R}_P}\) is computable.
We claim that \(\mathcal {R}_P\) is locally confluent if and only if P has no solution. The LCTRS \(\mathcal {R}_P\) admits the constrained critical pair
with \(n \ne m\). The rules with left-hand sides \(\textsf{alpha}(n)\) and \(\textsf{beta}(n)\) give rise to further constrained critical pairs but these are harmless since for all \(n, N > 0\) there are unique numbers i and m satisfying the constraint \([N \cdot m + i = n \wedge n > 0]\).
By construction of the rules for \(\textsf{test}\), \(\textsf{test}(\textsf{alpha}(n),\textsf{beta}(n)) \rightarrow ^* \top \) if n represents a solution of P and \(\textsf{test}(\textsf{alpha}(n),\textsf{beta}(n)) \rightarrow ^* \bot \) if n does not represent a solution of P. Since we assume that P is non-trivial, the latter happens for some \(n > 0\). Hence all instances of the constrained critical pairs can only be joined if \(\textsf{test}(\textsf{alpha}(n),\textsf{beta}(n)) \rightarrow ^* \bot \) for all \(n > 0\). Hence \(\mathcal {R}_P\) is locally confluent if and only if P has no solution.
The LCTRS \(\mathcal {R}_P\) is terminating by the recursive path order [12] with the precedence \(\textsf{start} > \textsf{test} > \textsf{alpha} > \textsf{beta} > \textsf{1} > \textsf{0} > \textsf{e} > \mathsf {\top } > \mathsf {\bot }\) and the well-founded order \(\sqsupset _{\textsf{Int}}\) on integers where \(x \sqsupset _{\textsf{Int}} y\) if and only if \(x > y\) and \(x \geqslant 0\). The key observation is that the constraint \([N \cdot m + i = n \wedge n > 0]\) in the recursive rules for \(\textsf{alpha}\) and \(\textsf{beta}\) ensure \(n > m\) since \(N > 0\) and \(i \geqslant 1\). \(\square \)
A key difference between TRSs and LCTRSs leading to this undecidability result can be seen in the first rule: \(\textsf{start} \rightarrow \textsf{test}(\textsf{alpha}(n),\textsf{beta}(n))\,[n > 0]\). Plain TRSs usually do not allow variables appearing only in the right-hand side of a rule, as is the case for n here, because then termination never holds. However, in LCTRSs such variables are useful, since they can be used to model computations on arbitrary values which are often used to represent user input in program analysis. For \(\mathcal {R}_P\) this leads to infinitely many possible steps starting from the term \(\textsf{start}\) and in turn to infinitely many critical pairs, breaking decidability.
4 Transformation
In this section we present a simple transformation from LCTRSs to possibly infinite TRSs, which exactly corresponds to the intuition behind LCTRSs. This allows us to lift results on TRSs more easily to LCTRSs than previously possible.
Definition 1
Given an LCTRS \(\mathcal {R}\), the TRS \(\overline{\mathcal {R}}\) consists of the following rules: \(\ell \tau \rightarrow r\tau \) for all \(\rho :\ell \rightarrow r~[\varphi ]\in \mathcal {R}_\textsf{rc}\) with \(\tau \vDash \rho \) and \(\mathcal {D}\textsf{om}(\tau ) = \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\).
Note that \(\overline{\mathcal {R}}\) typically consists of infinitely many rules.
Lemma 1
The rewrite relations of \(\mathcal {R}\) and \(\overline{\mathcal {R}}\) are the same. Moreover
 for all positions p.
for all positions p.
Proof
We first show
 . Assume
. Assume
 . We have \(s = s[\ell \sigma ]_p \rightarrow s[r\sigma ]_p = t\) for some \(\rho :\ell \rightarrow r~[\varphi ]\in \mathcal {R}_\textsf{rc}\) and \(\sigma \vDash \rho \). We split \(\sigma \) into two substitutions \(\tau = \{x \mapsto \sigma (x) \mid x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\}\) and \(\delta = \{x \mapsto \sigma (x) \mid x \in \mathcal {V}\textsf{ar}(\ell ) \setminus \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\}\). From \(\sigma \vDash \rho \) we infer \(\tau \vDash \rho \) and thus \(\tau (x) \in \mathcal {V}\textsf{al}\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\). Hence \(\sigma = \tau \cup \delta = \tau \delta \). We have \(\ell \tau \rightarrow r \tau \in \overline{\mathcal {R}}\). Hence
. We have \(s = s[\ell \sigma ]_p \rightarrow s[r\sigma ]_p = t\) for some \(\rho :\ell \rightarrow r~[\varphi ]\in \mathcal {R}_\textsf{rc}\) and \(\sigma \vDash \rho \). We split \(\sigma \) into two substitutions \(\tau = \{x \mapsto \sigma (x) \mid x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\}\) and \(\delta = \{x \mapsto \sigma (x) \mid x \in \mathcal {V}\textsf{ar}(\ell ) \setminus \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\}\). From \(\sigma \vDash \rho \) we infer \(\tau \vDash \rho \) and thus \(\tau (x) \in \mathcal {V}\textsf{al}\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\). Hence \(\sigma = \tau \cup \delta = \tau \delta \). We have \(\ell \tau \rightarrow r \tau \in \overline{\mathcal {R}}\). Hence
 as desired. To show the reverse inclusion
as desired. To show the reverse inclusion
 we assume
we assume
 . Otherwise
. Otherwise
 for some rule \(\rho :\ell \rightarrow r~[\varphi ]\in \mathcal {R}\) with \(\mu \vDash \rho \). Let \(\sigma = \mu \nu \). Since \(\mu (x) \in \mathcal {V}\textsf{al}\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\), we have \(x\sigma = x\mu \) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\). Hence \(\sigma \vDash \rho \) and thus
for some rule \(\rho :\ell \rightarrow r~[\varphi ]\in \mathcal {R}\) with \(\mu \vDash \rho \). Let \(\sigma = \mu \nu \). Since \(\mu (x) \in \mathcal {V}\textsf{al}\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\), we have \(x\sigma = x\mu \) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\). Hence \(\sigma \vDash \rho \) and thus
 . \(\square \)
. \(\square \)
Since
 and
and
 coincide, we drop the subscript in the sequel. We write \(\mathcal {E}\mathcal {V}\textsf{ar}(\ell \rightarrow r~[\varphi ])\) for the set \(\mathcal {V}\textsf{ar}(r) \setminus (\mathcal {V}\textsf{ar}(\ell ) \cup \mathcal {V}\textsf{ar}(\varphi ))\) of extra variables of a rule. In the computation of constrained critical pairs these variables of the overlapping rules would lose the property of being a logical variable without adding trivial constraints. Given a constrained rewrite rule \(\rho \), we write \(\mathcal{E}\mathcal{C}_\rho \) for \(\bigwedge \{x = x \mid x \in \mathcal {E}\mathcal {V}\textsf{ar}(\rho )\}\). The set of positions in a term s is denoted by \(\mathcal {P}\textsf{os}(s)\). We write \(\epsilon \) for the root position and \(\mathcal {P}\textsf{os}_\mathcal {F}(s)\) for the set of positions of function symbols in s.
coincide, we drop the subscript in the sequel. We write \(\mathcal {E}\mathcal {V}\textsf{ar}(\ell \rightarrow r~[\varphi ])\) for the set \(\mathcal {V}\textsf{ar}(r) \setminus (\mathcal {V}\textsf{ar}(\ell ) \cup \mathcal {V}\textsf{ar}(\varphi ))\) of extra variables of a rule. In the computation of constrained critical pairs these variables of the overlapping rules would lose the property of being a logical variable without adding trivial constraints. Given a constrained rewrite rule \(\rho \), we write \(\mathcal{E}\mathcal{C}_\rho \) for \(\bigwedge \{x = x \mid x \in \mathcal {E}\mathcal {V}\textsf{ar}(\rho )\}\). The set of positions in a term s is denoted by \(\mathcal {P}\textsf{os}(s)\). We write \(\epsilon \) for the root position and \(\mathcal {P}\textsf{os}_\mathcal {F}(s)\) for the set of positions of function symbols in s.
Definition 2
An overlap of an LCTRS \(\mathcal {R}\) is a triple \(\langle \rho _1, p, \rho _2 \rangle \) with rules \(\rho _1:\ell _1 \rightarrow r_1~[\varphi _1]\) and \(\rho _2:\ell _2 \rightarrow r_2~[\varphi _2]\), satisfying the following conditions: (1) \(\rho _1\) and \(\rho _2\) are variable-disjoint variants of rewrite rules in \(\mathcal {R}_\textsf{rc}\), (2) \(p \in \mathcal {P}\textsf{os}_\mathcal {F}(\ell _2)\), (3) \(\ell _1\) and \(\ell _2|_p\) unify with mgu \(\sigma \) such that \(\sigma (x) \in \mathcal {V}\textsf{al}\cup \mathcal {V}\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho _1) \cup \mathcal {L}\mathcal {V}\textsf{ar}(\rho _2)\), (4) \(\varphi _1\sigma \wedge \varphi _2\sigma \) is satisfiable, and (5) if \(p = \epsilon \) then \(\rho _1\) and \(\rho _2\) are not variants, or \(\mathcal {V}\textsf{ar}(r_1) \nsubseteq \mathcal {V}\textsf{ar}(\ell _1)\). In this case we call \(\ell _2\sigma [r_1\sigma ]_p \approx r_2\sigma ~ [\varphi _1\sigma \wedge \varphi _2\sigma \wedge \psi \sigma ]\) a constrained critical pair obtained from the overlap \(\langle \rho _1, p, \rho _2 \rangle \). Here \(\psi = \mathcal{E}\mathcal{C}_{\rho _1} \wedge \mathcal{E}\mathcal{C}_{\rho _2}\). The peak
 with \(\varPhi = (\varphi _1 \wedge \varphi _2 \wedge \psi )\sigma \), from which the constrained critical pair originates, is called a constrained critical peak. The set of all constrained critical pairs of \(\mathcal {R}\) is denoted by \(\textsf{CCP}(\mathcal {R})\). A constrained critical pair \(s \approx t~[\varphi ]\) is trivial if \(s\sigma = t\sigma \) for every substitution \(\sigma \) with \(\sigma \vDash \varphi \).
with \(\varPhi = (\varphi _1 \wedge \varphi _2 \wedge \psi )\sigma \), from which the constrained critical pair originates, is called a constrained critical peak. The set of all constrained critical pairs of \(\mathcal {R}\) is denoted by \(\textsf{CCP}(\mathcal {R})\). A constrained critical pair \(s \approx t~[\varphi ]\) is trivial if \(s\sigma = t\sigma \) for every substitution \(\sigma \) with \(\sigma \vDash \varphi \).
A key ingredient of our approach is to relate critical pairs of the transformed TRS to constrained critical pairs of the original LCTRS.
Theorem 2
For every critical pair \(s \approx t\) of \(\overline{\mathcal {R}}\) there exists a constrained critical pair \(s' \approx t'~[\varphi ']\) of \(\mathcal {R}\) and a substitution \(\gamma \) such that \(s = s'\gamma \), \(t = t'\gamma \) and \(\gamma \vDash \varphi '\).
Proof
Let \(s \approx t\) be a critical pair of \(\overline{\mathcal {R}}\), originating from the critical peak \(\ell _2\mu \sigma [r_1\nu \sigma ]_p \leftarrow \ell _2\mu \sigma = \ell _2\mu \sigma [\ell _1\nu \sigma ]_p \rightarrow r_2\mu \sigma \) with variants \(\rho _1:\ell _1 \rightarrow r_1~[\varphi _1]\) and \(\rho _2:\ell _2 \rightarrow r_2~[\varphi _2]\) of rules in \(\mathcal {R}_\textsf{rc}\) without shared variables. Let \(\psi _i = \mathcal{E}\mathcal{C}_{\rho _i}\) for \(i \in \{1,2\}\). Furthermore we have \(\mathcal {D}\textsf{om}(\nu ) = \mathcal {L}\mathcal {V}\textsf{ar}(\rho _1)\), \(\mathcal {D}\textsf{om}(\mu ) = \mathcal {L}\mathcal {V}\textsf{ar}(\rho _2)\), \(\nu \vDash \varphi _1 \wedge \psi _1\), \(\mu \vDash \varphi _2 \wedge \psi _2\), \(p \in \mathcal {P}\textsf{os}_\mathcal {F}(\ell _2\mu )\), and \(\sigma \) is an mgu of \(\ell _2\mu |_p\) and \(\ell _1\nu \). Moreover, if \(p = \epsilon \) then \(\ell _1\nu \rightarrow r_1\nu \) and \(\ell _2\mu \rightarrow r_2\mu \) are not variants. Define \(\tau = \nu \uplus \mu \). We have \(\mathcal {D}\textsf{om}(\tau ) = \mathcal {L}\mathcal {V}\textsf{ar}(\rho _1) \cup \mathcal {L}\mathcal {V}\textsf{ar}(\rho _2)\). Let \(\varphi = \varphi _1 \wedge \varphi _2 \wedge \psi _1 \wedge \psi _2\). Clearly, \(\ell _1\tau = \ell _1\nu \), \(r_1\tau = r_1\nu \), \(\ell _2\tau = \ell _2\mu \), \(r_2\tau = r_2\mu \) and \(\tau \vDash \varphi \). Hence the given peak can be written as \(\ell _2\tau \sigma [r_1\tau \sigma ]_p \leftarrow \ell _2\tau \sigma = \ell _2\tau \sigma [\ell _1\tau \sigma ]_p \rightarrow r_2\tau \sigma \) and \(\tau \vDash \varphi \). Since \(\ell _2|_p\tau \sigma = \ell _1\tau \sigma \) there exists an mgu \(\delta \) of \(\ell _2|_p\) and \(\ell _1\), and a substitution \(\gamma \) such that \(\delta \gamma = \tau \sigma \). Let \(s' = \ell _2\delta [r_1\delta ]_p\) and \(t' = r_2\delta \). We claim that \(\langle \rho _1, p, \rho _2 \rangle \) is an overlap of \(\mathcal {R}\), resulting in the constrained critical pair \(s' \approx t'~[\varphi \delta ]\). Condition (1) of Definition 2 is trivially satisfied. For condition (2) we need to show \(p \in \mathcal {P}\textsf{os}_\mathcal {F}(\ell _2)\). This follows from \(p \in \mathcal {P}\textsf{os}_\mathcal {F}(\ell _2\mu )\), \(\mu (x) \in \mathcal {V}\textsf{al}\) for every \(x \in \mathcal {D}\textsf{om}(\mu )\), and \(\textsf{root}(\ell _2\mu |_p) = \textsf{root}(\ell _1\nu ) \in \mathcal {F}\setminus \mathcal {V}\textsf{al}\). For condition (3) it remains to show that \(\delta (x) \in \mathcal {V}\textsf{al}\cup \mathcal {V}\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho _1) \cup \mathcal {L}\mathcal {V}\textsf{ar}(\rho _2)\). Suppose to the contrary that \(\textsf{root}(\delta (x)) \in \mathcal {F}\setminus \mathcal {V}\textsf{al}\) for some \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho _1) \mathop {\cup }\mathcal {L}\mathcal {V}\textsf{ar}(\rho _2)\). Then \(\textsf{root}(\delta (x)) = \textsf{root}(\gamma (\delta (x))) = \textsf{root}(\sigma (\tau (x))) \in \mathcal {F} \setminus \mathcal {V}\textsf{al}\), which contradicts \(\tau \vDash \varphi \). Condition (4) follows from the identity \(\delta \gamma = \tau \sigma \) together with \(\tau \vDash \varphi \) which imply \(\delta \gamma \vDash \varphi \) and thus \(\varphi \delta \) is satisfiable. Hence also \(\varphi _1\delta \wedge \varphi _2\delta \) is satisfiable. It remains to show condition (5), so let \(p = \epsilon \) and further assume that \(\rho _1\) and \(\rho _2\) are variants. So there exists a variable renaming \(\pi \) such that \(\rho _1\pi = \rho _2\). In particular, \(\ell _1\pi = \ell _2\) and \(r_1\pi = r_2\). Let \(x \in \mathcal {V}\textsf{ar}(\ell _1)\). If \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho _1) = \mathcal {D}\textsf{om}(\nu )\) then \(\tau (x) = \nu (x) \in \mathcal {V}\textsf{al}\). Moreover, \(\pi (x) \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho _2) = \mathcal {D}\textsf{om}(\mu )\) and thus \(\tau (\pi (x)) = \mu (\pi (x)) \in \mathcal {V}\textsf{al}\). Since \(\ell _1\tau \) and \(\ell _2\tau \) are unifiable, \(\pi (\tau (x)) = \tau (x) = \tau (\pi (x))\). If \(x \notin \mathcal {L}\mathcal {V}\textsf{ar}(\rho _1)\) then \(\tau (x) = x\), \(\pi (x) \notin \mathcal {L}\mathcal {V}\textsf{ar}(\rho _2)\) and similarly \(\tau (\pi (x)) = \pi (x) = \pi (\tau (x))\). All in all, \(\ell _1\tau \pi = \ell _1\pi \tau = \ell _2\tau \). Now, if \(\mathcal {V}\textsf{ar}(r_1) \subseteq \mathcal {V}\textsf{ar}(\ell _1)\) then we obtain \(r_1\tau \pi = r_1\pi \tau = r_2\tau \), contradicting the fact that \(\ell _1\nu \rightarrow r_1\nu \) and \(\ell _2\mu \rightarrow r_2\mu \) are not variants. We conclude that \(s' \approx t'~[\varphi \delta ]\) is a constrained critical pair of \(\mathcal {R}\). So we can take \(\varphi ' = \varphi \delta \). Clearly, \(s = s'\gamma \) and \(t = t'\gamma \). Moreover, \(\gamma \vDash \varphi '\) since \(\varphi '\gamma = \varphi \tau \sigma = \varphi \tau \) and \(\tau \vDash \varphi \). \(\square \)
The converse does not hold in general.
Example 2
Consider the LCTRS \(\mathcal {R}\) consisting of the single rule \(\textsf{a} \rightarrow x~[x = 0]\) where the variable x ranges over the integers. Since x appears on the right-hand side but not the left, we obtain a constrained critical pair \(x \approx x'~[x = 0 \wedge x' = 0]\). Since the constraint uniquely determines the values of x and \(x'\), the TRS \(\overline{\mathcal {R}}\) consists of the single rule \(\textsf{a} \rightarrow 0\). Obviously \(\overline{\mathcal {R}}\) has no critical pairs.
The above example also shows that orthogonality of \(\overline{\mathcal {R}}\) does not imply orthogonality of \(\mathcal {R}\). However, the counterexample relies somewhat on a technicality in condition (5) of Definition 2. It only occurs when the two rules \(\ell _1 \rightarrow r_1~[\varphi _1]\) and \(\ell _2 \rightarrow r_2~[\varphi _2]\) involved in the critical pair overlap at the root and have instances \(\ell _1\tau _1 \rightarrow r_1\tau _1\) and \(\ell _2\tau _2 \rightarrow r_2\tau _2\) in \(\overline{\mathcal {R}}\) which are variants of each other. By dealing with such cases separately we can prove the following theorem.
Theorem 3
For every constrained critical pair \(s \approx t~[\varphi ]\) of \(\mathcal {R}\) and every substitution \(\sigma \) with \(\sigma \vDash \varphi \), (1) \(s\sigma = t\sigma \) or (2) there exist a critical pair \(u \approx v\) of \(\overline{\mathcal {R}}\) and a substitution \(\delta \) such that \(s\sigma = u\delta \) and \(t\sigma = v\delta \).
Proof
Let \(s \approx t~[\varphi ]\) be a constrained critical pair of \(\mathcal {R}\) originating from the critical peak \(s = \ell _2 \theta [r_1\theta ]_p \leftarrow \ell _2\theta [\ell _1\theta ]_p \rightarrow r_2\theta = t\) with variants \(\rho _1:\ell _1 \rightarrow r_1~[\varphi _1]\) and \(\rho _2:\ell _2 \rightarrow r_2~[\varphi _2]\) of rules in \(\mathcal {R}_\textsf{rc}\), and an mgu \(\theta \) of \(\ell _2|_p\) and \(\ell _1\) where \(p \in \mathcal {P}\textsf{os}_\mathcal {F}(\ell _2)\). Moreover \(\theta (x) \in \mathcal {V}\textsf{al}\cup \mathcal {V}\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho _1) \cup \mathcal {L}\mathcal {V}\textsf{ar}(\rho _2)\), and \(\varphi = \varphi _1\theta \wedge \varphi _2\theta \wedge \psi \theta \) with \(\psi = \mathcal{E}\mathcal{C}_{\rho _1} \wedge \mathcal{E}\mathcal{C}_{\rho _2}\). Let \(\sigma \) be a substitution with \(\sigma \vDash \varphi \). Hence \(\theta \sigma \vDash \varphi _1 \wedge \varphi _2 \wedge \psi \) and further \(\sigma (\theta (x)) \in \mathcal {V}\textsf{al}\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho _1) \cup \mathcal {L}\mathcal {V}\textsf{ar}(\rho _2)\). We split \(\theta \sigma \) into substitutions \(\tau _1\), \(\tau _2\) and \(\pi \) as follows: \(\tau _i(x) = x\theta \sigma \) if \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho _i)\) and \(\tau _i(x) = x\) otherwise, for \(i \in \{1,2\}\), and \(\pi (x) = x\theta \sigma \) if \(x \in \mathcal {D}\textsf{om}(\theta \sigma ) \setminus (\mathcal {L}\mathcal {V}\textsf{ar}(\rho _1) \cup \mathcal {L}\mathcal {V}\textsf{ar}(\rho _2))\) and \(\pi (x) = x\) otherwise. From \(\theta \sigma \vDash \varphi _1 \wedge \varphi _2 \wedge \psi \) and \(\mathcal {V}\textsf{ar}(\varphi _i) \subseteq \mathcal {L}\mathcal {V}\textsf{ar}(\rho _i)\) we infer \(\tau _i \vDash \varphi _i\) for \(i \in \{1,2\}\). Since \(\mathcal {D}\textsf{om}(\tau _i) = \mathcal {L}\mathcal {V}\textsf{ar}(\rho _i)\), \(\ell _i\tau _i \rightarrow r_i\tau _i \in \overline{\mathcal {R}}\) for \(i \in \{1,2\}\). Furthermore, \(\tau _i\pi = \tau _i \cup \pi \) for \(i \in \{1,2\}\). Hence \(\ell _2|_p\tau _2\pi = \ell _2|_p\theta \sigma = \ell _1\theta \sigma = \ell _1\tau _1\pi \), implying that \(\ell _2|_p\tau _2\) and \(\ell _1\tau _1\) are unifiable. Let \(\gamma \) be an mgu of these two terms. There exists a substitution \(\delta \) such that \(\gamma \delta = \pi \). Clearly \(p \in \mathcal {P}\textsf{os}_\mathcal {F}(\ell _2\tau _2)\). If \(p \ne \epsilon \) or \(\ell _1\tau _1 \rightarrow r_1\tau _1\) and \(\ell _2\tau _2 \rightarrow r_2\tau _2\) are not variants, then \(u \approx v\) with \(u = \ell _2\tau _2\gamma [r_1\tau _1\gamma ]_p\) and \(v = r_2\tau _2\gamma \) is a critical pair of \(\overline{\mathcal {R}}\). Moreover \(t\sigma = r_2\theta \sigma = r_2\tau _2\pi = r_2\tau _2\gamma \delta = v\delta \), and similarly \(s\sigma = u\delta \). Thus option (2) is satisfied. If \(p = \epsilon \) and \(\ell _1\tau _1 \rightarrow r_1\tau _1\) and \(\ell _2\tau _2 \rightarrow r_2\tau _2\) are variants then \(s\sigma = r_1\tau _1\gamma \delta = r_2\tau _2\gamma \delta = t\sigma \), fulfilling (1). \(\square \)
A TRS (LCTRS) is weakly orthogonal if it is left-linear and all its (constrained) critical pairs are trivial. Since \(\overline{\mathcal {R}}\) is left-linear if and only if \(\mathcal {R}\) is left-linear, a direct consequence of Theorem 3 is that weak orthogonality of \(\overline{\mathcal {R}}\) implies weak orthogonality of \(\mathcal {R}\).
Our transformation is not only useful for confluence analysis.
Example 3
For the LCTRS \(\mathcal {R}_P\) in the proof of Theorem 1 the TRS \(\overline{\mathcal {R}}_P\) consists of all unconstrained rules of \(\mathcal {R}_P\) together with \(f({v_1},\dots ,{v_{n}}) \rightarrow [\![{f({v_1},\dots ,{v_{n}})}]\!]\) for all \(f \in \mathcal {F}_{\textsf{th}}\setminus \mathcal {V}\textsf{al}\) and \({v_1},\dots ,{v_{n}} \in \mathcal {V}\textsf{al}\), \(\textsf{start} \rightarrow \textsf{test}(\textsf{alpha}(n),\textsf{beta}(n))\) for all \(n > 0\), \(\textsf{alpha}(n) \rightarrow \alpha _i(\textsf{alpha}(m))\) and \(\textsf{beta}(n) \rightarrow \beta _i(\textsf{beta}(m))\) for all \(i \in \{1,\dots ,N\}\), \(n > 0\) and \(m \geqslant 0\) such that \(N \cdot m + i = n\). Termination of the infinite TRS \(\overline{\mathcal {R}}_P\) is easily shown by LPO or dependency pairs.
5 Development Closed Critical Pairs
Using Theorem 2 we can easily transfer confluence criteria for TRSs to LCTRSs. Rather than reproving the confluence results reported in [12, 17, 22], in this section we illustrate this by extending the result of van Oostrom [15] concerning (almost) development closed critical pairs from TRSs to LCTRSs. This result subsumes most critical-pair based confluence criteria, as can be seen in Fig. 2 in the concluding section.
Definition 3
Let \(\mathcal {R}\) be an LCTRS. The multi-step relation
 on terms is defined inductively as follows: (1)
on terms is defined inductively as follows: (1)
 for all variables x, (2)
for all variables x, (2)
 if
if
 with \(1 \leqslant i \leqslant n\), (3)
with \(1 \leqslant i \leqslant n\), (3)
 if \(\ell \rightarrow r~[\varphi ] \in \mathcal {R}_\textsf{rc}\), \(\sigma \vDash \ell \rightarrow r~[\varphi ]\) and
if \(\ell \rightarrow r~[\varphi ] \in \mathcal {R}_\textsf{rc}\), \(\sigma \vDash \ell \rightarrow r~[\varphi ]\) and
 , where
, where
 denotes
denotes
 for all variables \(x \in \mathcal {D}\textsf{om}(\sigma )\).
for all variables \(x \in \mathcal {D}\textsf{om}(\sigma )\).
Definition 4
A critical pair \(s \approx t\) is development closed if
 . It is almost development closed if it is not an overlay and development closed, or it is an overlay and
. It is almost development closed if it is not an overlay and development closed, or it is an overlay and
 . A TRS is called (almost) development closed if all its critical pairs are (almost) development closed.
. A TRS is called (almost) development closed if all its critical pairs are (almost) development closed.
The following result from [15] has recently been formalized in Isabelle [10, 11].
Theorem 4
Left-linear almost development closed TRSs are confluent. \(\square \)
We define multi-step rewriting on constrained terms.
Definition 5
Let \(\mathcal {R}\) be an LCTRS. The multi-step relation
 on constrained terms is defined inductively as follows:
on constrained terms is defined inductively as follows:
-
1.
 for all variables x,
for all variables x, -
2.
 if
if
 for \(1 \leqslant i \leqslant n\),
for \(1 \leqslant i \leqslant n\), -
3.
 if \(\rho :\ell \rightarrow r~[\psi ] \in \mathcal {R}_\textsf{rc}\), \(\sigma (x) \in \mathcal {V}\textsf{al}\cup \mathcal {V}\textsf{ar}(\varphi )\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\), \(\varphi \) is satisfiable, \(\varphi \Rightarrow \psi \sigma \) is valid, and
if \(\rho :\ell \rightarrow r~[\psi ] \in \mathcal {R}_\textsf{rc}\), \(\sigma (x) \in \mathcal {V}\textsf{al}\cup \mathcal {V}\textsf{ar}(\varphi )\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\), \(\varphi \) is satisfiable, \(\varphi \Rightarrow \psi \sigma \) is valid, and
 .
.
Here
 denotes
denotes
 for all variables \(x \in \mathcal {D}\textsf{om}(\sigma )\). The relation
for all variables \(x \in \mathcal {D}\textsf{om}(\sigma )\). The relation
 on constrained terms is defined as
on constrained terms is defined as
 .
.
Example 4
Consider the following LCTRS \(\mathcal {R}\) over the theory Ints with the rules:
Rewriting the term \(\textsf{max}(\textsf{1} + \textsf{2}, \textsf{3} + \textsf{2})\) to its normal form \(\textsf{5}\) requires three single steps. These steps can be combined into a single multi-step
 .
.
The constrained term \(\textsf{max}(\textsf{1} + x,\textsf{3} + y)~[x > \textsf{3} \wedge y = \textsf{1}]\) rewrites in a single multi-step to its normal form \(z~[z = \textsf{1} + x \wedge x > \textsf{3}]\). This involves the following parts of Definition 5. Let \(\varphi \) be \(x > \textsf{3} \wedge y = \textsf{1} \wedge z = \textsf{1} + x \wedge z' = \textsf{3} + y\). Case (3) gives
 and
and
 . Using this we obtain
. Using this we obtain
 by case (2). A final application of case (3) yields
by case (2). A final application of case (3) yields
 . Together with the equivalences
. Together with the equivalences
we obtain
 .
.
Definition 4 is extended to LCTRSs as follows.
Definition 6
A constrained critical pair \(s \approx t~[\varphi ]\) is development closed if
 for some trivial \(u \approx v~[\psi ]\). A constrained critical pair is almost development closed if it is not an overlay and development closed, or it is an overlay and
for some trivial \(u \approx v~[\psi ]\). A constrained critical pair is almost development closed if it is not an overlay and development closed, or it is an overlay and
 for some trivial \(u \approx v~[\psi ]\). An LCTRS is called (almost) development closed if all its constrained critical pairs are (almost) development closed.
for some trivial \(u \approx v~[\psi ]\). An LCTRS is called (almost) development closed if all its constrained critical pairs are (almost) development closed.
Similar to [17, 22], the symbol \(\approx \) is treated as a fresh binary function symbol, resulting in constrained equations whose positions are addressed in the usual way. Therefore positions below 1 in \(s \approx t~[\varphi ]\) refer to subterms of s.
Figure 1 conveys the idea how the main result (Theorem 5) in this section is obtained. For every critical pair in the transformed TRS \(\overline{\mathcal {R}}\) there exists a corresponding constrained critical pair in the original LCTRS \(\mathcal {R}\) (Theorem 2). Almost development closure of the constrained critical pair implies almost development closure of the critical pair (Lemma 4). Since the rewrite relations of \(\mathcal {R}\) and \(\overline{\mathcal {R}}\) coincide (Lemma 1), we obtain the confluence of almost development closed left-linear LCTRSs from the corresponding result in [15].
Proof idea for Theorem 5.
We now present a few technical results that relate rewrite sequences and multi-steps on (constrained) terms. These prepare for the use of Theorem 2 to obtain the confluence of (almost) development closed LCTRSs. The proofs of the following two lemmata can be found in [18].
Lemma 2
Suppose
 with \(\gamma \vDash \varphi \) and position p. If \(p = 1q\) for a position q then \(s\gamma \rightarrow _{\geqslant q}^{*} u\delta \) and \(t\gamma = v\delta \) for some substitution \(\delta \) with \(\delta \vDash \psi \). If \(p = 2q\) for a position q then
with \(\gamma \vDash \varphi \) and position p. If \(p = 1q\) for a position q then \(s\gamma \rightarrow _{\geqslant q}^{*} u\delta \) and \(t\gamma = v\delta \) for some substitution \(\delta \) with \(\delta \vDash \psi \). If \(p = 2q\) for a position q then
 for some substitution \(\delta \) with \(\delta \vDash \psi \). \(\square \)
for some substitution \(\delta \) with \(\delta \vDash \psi \). \(\square \)
Lemma 3
If
 then for all substitutions \(\sigma \vDash \varphi \) there exists \(\delta \vDash \psi \) such that
then for all substitutions \(\sigma \vDash \varphi \) there exists \(\delta \vDash \psi \) such that
 and \(t\sigma = v\delta \). \(\square \)
and \(t\sigma = v\delta \). \(\square \)
Lemma 4
If a constrained critical pair \(s \approx t~[\varphi ]\) is almost development closed then for all substitutions \(\sigma \) with \(\sigma \vDash \varphi \) we have
 .
.
Proof
Let \(s \approx t~[\varphi ]\) be an almost development closed constrained critical pair, and \(\sigma \vDash \varphi \) some substitution. From Definition 6 we obtain

where \(u\tau = v\tau \) for all \(\tau \vDash \psi \) for some constrained term \(u' \approx v'~[\psi ']\). We apply Lemma 3 to the first step in (1). This yields a substitution \(\delta \) where
 , \(t\sigma = v'\delta \) and \(\delta \vDash \psi '\). For the second part of (1) we use Lemma 2 and obtain \(v'\delta \rightarrow ^{*} v \gamma \), \(u'\delta = u\gamma \) for some \(\gamma \vDash \psi \). Moreover we have \(u\gamma = v\gamma \). Hence
, \(t\sigma = v'\delta \) and \(\delta \vDash \psi '\). For the second part of (1) we use Lemma 2 and obtain \(v'\delta \rightarrow ^{*} v \gamma \), \(u'\delta = u\gamma \) for some \(\gamma \vDash \psi \). Moreover we have \(u\gamma = v\gamma \). Hence
 . \(\square \)
. \(\square \)
Theorem 5
If an LCTRS \(\mathcal {R}\) is almost development closed then so is \(\overline{\mathcal {R}}\).
Proof
Take any critical pair \(s \approx t\) from \(\overline{\mathcal {R}}\). From Theorem 2 we know that there exists a constrained critical pair \(s' \approx t'~[\varphi ]\) in \(\mathcal {R}\) where \(s'\sigma = s\) and \(t'\sigma = t\) for some \(\sigma \vDash \varphi \). Since the constrained critical pair must be almost development closed, Lemma 4 yields
 if it is an overlay and
if it is an overlay and
 otherwise. This proves that \(\overline{\mathcal {R}}\) is almost development closed. \(\square \)
otherwise. This proves that \(\overline{\mathcal {R}}\) is almost development closed. \(\square \)
Interestingly, the converse does not hold, as seen in the following example.
Example 5
Consider the LCTRS \(\mathcal {R}\) over the theory Ints with the rules
The TRS \(\overline{\mathcal {R}}\) consists of the rules
and has two (modulo symmetry) critical pairs \(\textsf{g}(\textsf{1}) \approx \textsf{h}(\textsf{1})\) and \(\textsf{g}(\textsf{2}) \approx \textsf{h}(\textsf{2})\). Since
 , \(\overline{\mathcal {R}}\) is almost development closed. The constrained critical pair \(\textsf{g}(x) \approx \textsf{h}(x)~[\textsf{1} \leqslant x \leqslant \textsf{2}]\) is not almost development closed, since it is a normal form with respect to the rewrite relation on constrained terms.
, \(\overline{\mathcal {R}}\) is almost development closed. The constrained critical pair \(\textsf{g}(x) \approx \textsf{h}(x)~[\textsf{1} \leqslant x \leqslant \textsf{2}]\) is not almost development closed, since it is a normal form with respect to the rewrite relation on constrained terms.
This also makes intuitive sense, since a rewrite step
 implies that the same step can be taken on all instances \(s\sigma \approx t\sigma \) where \(\sigma \vDash \varphi \). However it may be the case, like in the above example, that different instances of the constrained critical pair require different steps to obtain a closing sequence, which cannot directly be modeled using rewriting on constrained terms.
implies that the same step can be taken on all instances \(s\sigma \approx t\sigma \) where \(\sigma \vDash \varphi \). However it may be the case, like in the above example, that different instances of the constrained critical pair require different steps to obtain a closing sequence, which cannot directly be modeled using rewriting on constrained terms.
Since left-linearity of \(\overline{\mathcal {R}}\) is preserved, the following corollary is obtained from Theorems 4 and 5. In fact \(\mathcal {R}\) only has to be linear in the variables \(x \notin \mathcal {L}\mathcal {V}\textsf{ar}\), since that is sufficient for \(\overline{\mathcal {R}}\) to be linear.
Corollary 1
Left-linear almost development closed LCTRSs are confluent. \(\square \)
Example 6
The LCTRS \(\mathcal {R}\) over the theory \(\textsf{Ints}\) with the rules
admits the two constrained critical pairs (with simplified constraints)
Both are almost development closed:

Here \(\varphi \) is the constraint \(x = y \wedge y = \textsf{2}\). Hence \(\mathcal {R}\) is almost development closed. Since \(\mathcal {R}\) is left-linear, confluence follows by Corollary 1.
6 Parallel Critical Pairs
In this section we extend the confluence result by Toyama [20] based on parallel critical pairs to LCTRSs. Recently there is a renewed interest in this result; Shintani and Hirokawa proved in [19] that it subsumes Toyama’s later confluence result in [21]. The latter was already lifted to LCTRSs in [17] and is also subsumed by Corollary 1. The result of Toyama [20] is a proper extension of the confluence criterion on parallel critical pairs by Gramlich [6]. In the sequel we mainly follow the notions from [19].
Definition 7
Let \(\mathcal {R}\) be an LCTRS. The parallel rewrite relation
 on terms is defined inductively as follows:
on terms is defined inductively as follows:
-
1.
 for all variables x,
for all variables x, -
2.
 if
if
 for \(1 \leqslant i \leqslant n\),
for \(1 \leqslant i \leqslant n\), -
3.
 if \(\ell \rightarrow r~[\varphi ] \in \mathcal {R}_\textsf{rc}\) and \(\sigma \vDash \ell \rightarrow r~[\varphi ]\)
if \(\ell \rightarrow r~[\varphi ] \in \mathcal {R}_\textsf{rc}\) and \(\sigma \vDash \ell \rightarrow r~[\varphi ]\)
We extend
 to constrained terms inductively as follows:
to constrained terms inductively as follows:
-
1.
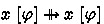 for all variables x,
for all variables x, -
2.
 if
if
 for \(1 \leqslant i \leqslant n\),
for \(1 \leqslant i \leqslant n\), -
3.
 if \(\rho :\ell \rightarrow r~[\psi ] \in \mathcal {R}_\textsf{rc}\), \(\sigma (x) \in \mathcal {V}\textsf{al}\cup \mathcal {V}\textsf{ar}(\varphi )\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\), \(\varphi \) is satisfiable and \(\varphi \Rightarrow \psi \sigma \) is valid.
if \(\rho :\ell \rightarrow r~[\psi ] \in \mathcal {R}_\textsf{rc}\), \(\sigma (x) \in \mathcal {V}\textsf{al}\cup \mathcal {V}\textsf{ar}(\varphi )\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\), \(\varphi \) is satisfiable and \(\varphi \Rightarrow \psi \sigma \) is valid.
The parallel rewrite relation
 on constrained terms is defined as
on constrained terms is defined as
 .
.
Let s be a term and \(P \subseteq \mathcal {P}\textsf{os}(s)\) be a set of parallel positions. Given terms \(t_p\) for \(p \in P\), we denote by \(s[t_p]_{p \in P}\) the simultaneous replacement of the terms at position \(p \in P\) in s by \(t_p\). We recall the definition of parallel critical pairs for TRSs.
Definition 8
Let \(\mathcal {R}\) be a TRS, \(\rho :\ell \rightarrow r\) a rule in \(\mathcal {R}\), and \(P \subseteq \mathcal {P}\textsf{os}_\mathcal {F}(\ell )\) a non-empty set of parallel positions. For every \(p \in P\) let \(\rho _p:\ell _p \rightarrow r_p\) be a variant of a rule in \(\mathcal {R}\). The peak
 forms a parallel critical pair \(\ell \sigma [r_p\sigma ]_{p \in P} \approx r\sigma \) if the following conditions are satisfied:
forms a parallel critical pair \(\ell \sigma [r_p\sigma ]_{p \in P} \approx r\sigma \) if the following conditions are satisfied:
-
1.
\(\mathcal {V}\textsf{ar}(\rho _1) \cap \mathcal {V}\textsf{ar}(\rho _2) = \varnothing \) for different rules \(\rho _1\) and \(\rho _2\) in \(\{\rho \} \cup \{\rho _p \mid p \in P\}\),
-
2.
\(\sigma \) is an mgu of \(\{\ell _p \approx \ell |_p \mid p \in P\}\),
-
3.
if \(P = \{\epsilon \}\) then \(\rho _\epsilon \) is not a variant of \(\rho \).
The set of all constrained parallel critical pairs of \(\mathcal {R}\) is denoted by \(\textsf{PCP}(\mathcal {R})\).
We lift this notion to the constrained setting and define it for LCTRSs.
Definition 9
Let \(\mathcal {R}\) be an LCTRS, \(\rho :\ell \rightarrow r~[\varphi ]\) a rule in \(\mathcal {R}_\textsf{rc}\), and \(P \subseteq \mathcal {P}\textsf{os}_\mathcal {F}(\ell )\) a non-empty set of parallel positions. For every \(p \in P\) let \(\rho _p:\ell _p \rightarrow r_p~[\varphi _p]\) be a variant of a rule in \(\mathcal {R}_\textsf{rc}\). Let \(\psi = \mathcal{E}\mathcal{C}_{\rho } \wedge \bigwedge _{p \in P} \mathcal{E}\mathcal{C}_{\rho _p}\) and \(\varPhi = \varphi \sigma \wedge \psi \sigma \wedge \bigwedge _{p \in P} \varphi _p\sigma \). The peak
 forms a constrained parallel critical pair \(\ell \sigma [r_p\sigma ]_{p \in P} \approx r\sigma ~[\varPhi ]\) if the following conditions are satisfied:
forms a constrained parallel critical pair \(\ell \sigma [r_p\sigma ]_{p \in P} \approx r\sigma ~[\varPhi ]\) if the following conditions are satisfied:
-
1.
\(\mathcal {V}\textsf{ar}(\rho _1) \cap \mathcal {V}\textsf{ar}(\rho _2) = \varnothing \) for different rules \(\rho _1\) and \(\rho _2\) in \(\{\rho \} \cup \{\rho _p \mid p \in P\}\),
-
2.
\(\sigma \) is an mgu of \(\{\ell _p = \ell |_p \mid p \in P\}\) such that \(\sigma (x) \in \mathcal {V}\textsf{al}\cup \mathcal {V}\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho ) \cup \bigcup _{p \in P} \mathcal {L}\mathcal {V}\textsf{ar}(\rho _p)\),
-
3.
\(\varphi \sigma \wedge \bigwedge _{p \in P} \varphi _p\sigma \) is satisfiable,
-
4.
if \(P = \{\epsilon \}\) then \(\rho _\epsilon \) is not a variant of \(\rho \) or \(\mathcal {V}\textsf{ar}(r) \nsubseteq \mathcal {V}\textsf{ar}(\ell )\).
A constrained peak forming a constrained parallel critical pair is called a constrained parallel critical peak. The set of all constrained parallel critical pairs of \(\mathcal {R}\) is denoted by \(\textsf{CPCP}(\mathcal {R})\).
For a term t and a set of parallel positions P in t, we write \(\mathcal {V}\textsf{ar}(t,P)\) to denote \(\bigcup _{p \in P} \mathcal {V}\textsf{ar}(t|_p)\). For a set of parallel positions P we denote by
 that each rewrite step obtained in case (3) of Definition 7 is performed at a position \(p \in P\) and no two steps share a position. Moreover, for a set of parallel positions P and a position q we denote by
that each rewrite step obtained in case (3) of Definition 7 is performed at a position \(p \in P\) and no two steps share a position. Moreover, for a set of parallel positions P and a position q we denote by
 that \(p \geqslant q\) for all \(p \in P\).
that \(p \geqslant q\) for all \(p \in P\).
Definition 10
A critical pair \(s \approx t\) is 1-parallel closed if
 . A TRS is 1-parallel closed if all its critical pairs are 1-parallel closed. A parallel critical pair \(\ell \sigma [r_p\sigma ]_{p \in P} \approx r\sigma \) originating from the peak
. A TRS is 1-parallel closed if all its critical pairs are 1-parallel closed. A parallel critical pair \(\ell \sigma [r_p\sigma ]_{p \in P} \approx r\sigma \) originating from the peak
 is 2-parallel closed if there exists a term v and a set of parallel positions Q such that
is 2-parallel closed if there exists a term v and a set of parallel positions Q such that
 with \(\mathcal {V}\textsf{ar}(v,Q) \subseteq \mathcal {V}\textsf{ar}(\ell \sigma ,P)\). A TRS is 2-parallel closed if all its parallel critical pairs are 2-parallel closed. A TRS is parallel closed if it is 1-parallel closed and 2-parallel closed.
with \(\mathcal {V}\textsf{ar}(v,Q) \subseteq \mathcal {V}\textsf{ar}(\ell \sigma ,P)\). A TRS is 2-parallel closed if all its parallel critical pairs are 2-parallel closed. A TRS is parallel closed if it is 1-parallel closed and 2-parallel closed.
The following result from [20] has recently been formalized in Isabelle [7].
Theorem 6
Left-linear parallel closed TRSs are confluent. \(\square \)
In the remainder of this section we extend this result to LCTRSs. To this end we introduce the notion \(\mathcal {T}\mathcal {V}\textsf{ar}(t,\varphi ) = \mathcal {V}\textsf{ar}(t) \setminus \mathcal {V}\textsf{ar}(\varphi )\) denoting the set of non-logical variables in term t with respect to the logical constraint \(\varphi \). We restrict this to non-logical variables in subterms below a set of parallel positions P in t: \(\mathcal {T}\mathcal {V}\textsf{ar}(t,\varphi ,P) = \bigcup _{p \in P} \mathcal {T}\mathcal {V}\textsf{ar}(t|_p,\varphi )\).
Definition 11
A constrained critical pair \(s \approx t~[\varphi ]\) is 1-parallel closed if
 for some trivial \(u \approx v~[\psi ]\). An LCTRS is 1-parallel closed if all its constrained critical pairs are 1-parallel closed. A constrained parallel critical pair \(\ell \sigma [r_p\sigma ]_{p \in P} \approx r\sigma ~[\varphi ]\) is 2-parallel closed if there exists a set of parallel positions Q such that
for some trivial \(u \approx v~[\psi ]\). An LCTRS is 1-parallel closed if all its constrained critical pairs are 1-parallel closed. A constrained parallel critical pair \(\ell \sigma [r_p\sigma ]_{p \in P} \approx r\sigma ~[\varphi ]\) is 2-parallel closed if there exists a set of parallel positions Q such that

for some trivial \(u \approx v~[\psi ]\) and \(\mathcal {T}\mathcal {V}\textsf{ar}(v,\psi ,Q) \subseteq \mathcal {T}\mathcal {V}\textsf{ar}(\ell \sigma ,\varphi ,P)\). An LCTRS is 2-parallel closed if all its constrained parallel critical pairs are 2-parallel closed. An LCTRS is parallel closed if it is 1-parallel closed and 2-parallel closed.
Recall from Sect. 2 that our definition of \(\sim \) differs from the equivalence relation \(\sim '\) defined in [12, 17]. The change is necessary for the variable condition of 2-parallel closedness to make sense, as illustrated in the following example.
Example 7
Consider the (LC)TRS consisting of the rules
The peak
 gives rise to the (constrained) parallel critical pair \(\textsf{f}(\textsf{a},y) \approx \textsf{f}(\textsf{b},y)~[\textsf{true}]\). Using \(\sim '\) we have
gives rise to the (constrained) parallel critical pair \(\textsf{f}(\textsf{a},y) \approx \textsf{f}(\textsf{b},y)~[\textsf{true}]\). Using \(\sim '\) we have

and the variable condition \(\mathcal {T}\mathcal {V}\textsf{ar}(x,\textsf{true},\{\epsilon \}) \subseteq \mathcal {T}\mathcal {V}\textsf{ar}(\textsf{f}(\textsf{g}(x),y),\textsf{true},\{1\})\) holds. Since the system has no logical constraints it can also be analyzed in the TRS setting. Following Definition 10 we would have to check the variable condition \(\mathcal {V}\textsf{ar}(y,\{\epsilon \}) \subseteq \mathcal {V}\textsf{ar}(\textsf{f}(\textsf{g}(x),y),\{1\})\), which does not hold. Using \(\sim \) resolves this difference, since \(y \approx y~[\textsf{true}] \not \sim x \approx x~[\textsf{true}]\). So the conditions in Definition 11 reduce to the ones in Definition 10 for TRSs.
In Theorem 2 in Sect. 4 we related critical pairs of the transformed TRS to constrained critical pairs of the originating LCTRS. The following theorem does the same for parallel critical pairs.
Theorem 7
For every parallel critical pair \(s \approx t\) of \(\overline{\mathcal {R}}\) there exists a constrained parallel critical pair \(s' \approx t'~[\varphi ']\) of \(\mathcal {R}\) and a substitution \(\gamma \) such that \(s = s'\gamma \), \(t = t'\gamma \) and \(\gamma \vDash \varphi '\).
Proof
Let \(s \approx t\) be a parallel critical pair of \(\overline{\mathcal {R}}\), originating from the parallel critical peak
 with variants \(\rho :\ell \rightarrow r~[\varphi ]\) and \(\rho _p:\ell _p \rightarrow r_p~[\varphi _p]\) for \(p \in P\) of rules in \(\mathcal {R}_\textsf{rc}\) without shared variables, \(\psi = \mathcal{E}\mathcal{C}_\rho \) and \(\psi _p = \mathcal{E}\mathcal{C}_{\rho _p}\) for \(p \in P\). Furthermore, \(\mathcal {D}\textsf{om}(\nu _p) = \mathcal {L}\mathcal {V}\textsf{ar}(\rho _p)\) for \(p \in P\), \(\mathcal {D}\textsf{om}(\mu ) = \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\), \(\nu _p \vDash \varphi _p \wedge \psi _p\) for \(p \in P\), \(\mu \vDash \varphi \wedge \psi \), \(p \in \mathcal {P}\textsf{os}_\mathcal {F}(\ell \mu )\), and \(\sigma \) is an mgu of \(\{\ell \mu |_p \approx \ell _p\nu _p \mid p \in P\}\). Moreover, if \(P = \{\epsilon \}\) then \(\ell _\epsilon \nu _\epsilon \rightarrow r_\epsilon \nu _\epsilon ~[\varphi _\epsilon \nu _\epsilon ]\) and \(\ell \mu \rightarrow r\mu ~[\varphi \mu ]\) are not variants. Define the substitution \(\tau \) as \(\bigcup \,\{\nu _p \mid p \in P\} \uplus \mu \). Clearly, \(\ell _p\tau = \ell _p\nu _p\) and \(r_p\tau = r_p\nu _p\) for \(p \in P\), \(\ell \tau = \ell \mu \), \(r\tau = r\mu \), \(\tau \vDash \varphi \wedge \psi \) and \(\tau \vDash \varphi _p \wedge \psi _p\) for all \(p \in P\). Hence the given peak can be written as
with variants \(\rho :\ell \rightarrow r~[\varphi ]\) and \(\rho _p:\ell _p \rightarrow r_p~[\varphi _p]\) for \(p \in P\) of rules in \(\mathcal {R}_\textsf{rc}\) without shared variables, \(\psi = \mathcal{E}\mathcal{C}_\rho \) and \(\psi _p = \mathcal{E}\mathcal{C}_{\rho _p}\) for \(p \in P\). Furthermore, \(\mathcal {D}\textsf{om}(\nu _p) = \mathcal {L}\mathcal {V}\textsf{ar}(\rho _p)\) for \(p \in P\), \(\mathcal {D}\textsf{om}(\mu ) = \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\), \(\nu _p \vDash \varphi _p \wedge \psi _p\) for \(p \in P\), \(\mu \vDash \varphi \wedge \psi \), \(p \in \mathcal {P}\textsf{os}_\mathcal {F}(\ell \mu )\), and \(\sigma \) is an mgu of \(\{\ell \mu |_p \approx \ell _p\nu _p \mid p \in P\}\). Moreover, if \(P = \{\epsilon \}\) then \(\ell _\epsilon \nu _\epsilon \rightarrow r_\epsilon \nu _\epsilon ~[\varphi _\epsilon \nu _\epsilon ]\) and \(\ell \mu \rightarrow r\mu ~[\varphi \mu ]\) are not variants. Define the substitution \(\tau \) as \(\bigcup \,\{\nu _p \mid p \in P\} \uplus \mu \). Clearly, \(\ell _p\tau = \ell _p\nu _p\) and \(r_p\tau = r_p\nu _p\) for \(p \in P\), \(\ell \tau = \ell \mu \), \(r\tau = r\mu \), \(\tau \vDash \varphi \wedge \psi \) and \(\tau \vDash \varphi _p \wedge \psi _p\) for all \(p \in P\). Hence the given peak can be written as
 with \(\tau \vDash \varphi ''\) where
with \(\tau \vDash \varphi ''\) where
Since \(\ell |_p\tau \sigma = \ell _p\tau \sigma \) for all \(p \in P\) there exists an mgu \(\delta \) of \(\{\ell |_p = \ell _p \mid p \in P\}\) and a substitution \(\gamma \) such that \(\delta \gamma = \tau \sigma \). Let \(s' = \ell \delta [r_p\delta ]_{p \in P}\) and \(t' = r\delta \). We claim that this results in the constrained parallel critical pair \(s' \approx t'~[\varphi ''\delta ]\). Condition (1) of Definition 9 is trivially satisfied. We obtain \(P \subseteq \mathcal {P}\textsf{os}_\mathcal {F}(\ell )\) because \(P \subseteq \mathcal {P}\textsf{os}_\mathcal {F}(\ell \mu )\), \(\mu (x) \in \mathcal {V}\textsf{al}\) for every \(x \in \mathcal {D}\textsf{om}(\mu )\), and \(\textsf{root}(\ell \mu |_p) = \textsf{root}(\ell _p\nu ) \in \mathcal {F}\setminus \mathcal {V}\textsf{al}\) for all \(p \in P\). For condition (2) it remains to show that \(\delta (x) \in \mathcal {V}\textsf{al}\cup \mathcal {V}\) for all \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho ) \cup \bigcup _{p \in P} \mathcal {L}\mathcal {V}\textsf{ar}(\rho _p)\). Suppose to the contrary that \(\textsf{root}(\delta (x)) \in \mathcal {F}\setminus \mathcal {V}\textsf{al}\) for some \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho ) \mathop {\cup }\bigcup _{p \in P} \mathcal {L}\mathcal {V}\textsf{ar}(\rho _p)\). Then \(\textsf{root}(\delta (x)) = \textsf{root}(\gamma (\delta (x))) = \textsf{root}(\sigma (\tau (x))) \in \mathcal {F}\setminus \mathcal {V}\textsf{al}\), which contradicts \(\tau \vDash \varphi ''\). Condition (3) follows from the identity \(\delta \gamma = \tau \sigma \) together with \(\tau \vDash \varphi ''\) which imply \(\delta \gamma \vDash \varphi ''\) and thus \(\varphi ''\delta \) is satisfiable. Hence also \(\varphi \delta \wedge \bigwedge _{p \in P} \varphi _p\delta \) is satisfiable. It remains to show condition (4), so let \(P = \{\epsilon \}\) and further assume that \(\rho _\epsilon \) and \(\rho \) are variants. So there exists a variable renaming \(\pi \) such that \(\rho _\epsilon \pi = \rho \). In particular, \(\ell _\epsilon \pi = \ell \) and \(r_\epsilon \pi = r\). We show \(\tau (\pi (x)) = \pi (\tau (x))\) for all \(x \in \mathcal {V}\textsf{ar}(\ell _\epsilon )\). Let \(x \in \mathcal {V}\textsf{ar}(\ell _\epsilon )\). If \(x \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho _\epsilon ) = \mathcal {D}\textsf{om}(\nu )\) then \(\tau (x) = \nu (x) \in \mathcal {V}\textsf{al}\). Moreover, \(\pi (x) \in \mathcal {L}\mathcal {V}\textsf{ar}(\rho ) = \mathcal {D}\textsf{om}(\mu )\) and thus \(\tau (\pi (x)) = \mu (\pi (x)) \in \mathcal {V}\textsf{al}\). Since \(\ell _\epsilon \tau \) and \(\ell \tau \) are unifiable, \(\pi (\tau (x)) = \tau (x) = \tau (\pi (x))\). If \(x \notin \mathcal {L}\mathcal {V}\textsf{ar}(\rho _\epsilon )\) then \(\tau (x) = x\), \(\pi (x) \notin \mathcal {L}\mathcal {V}\textsf{ar}(\rho )\) and similarly \(\tau (\pi (x)) = \pi (x) = \pi (\tau (x))\). All in all, \(\ell _\epsilon \tau \pi = \ell _\epsilon \pi \tau = \ell \tau \). Now, if \(\mathcal {V}\textsf{ar}(r_\epsilon ) \subseteq \mathcal {V}\textsf{ar}(\ell _\epsilon )\) then we obtain \(r_\epsilon \tau \pi = r_\epsilon \pi \tau = r\tau \), contradicting the fact that \(\ell _\epsilon \nu \rightarrow r_\epsilon \nu \) and \(\ell \mu \rightarrow r\mu \) are not variants. We conclude that \(s' \approx t'~[\varphi ''\delta ]\) is a constrained parallel critical pair of \(\mathcal {R}\). So we can take \(\varphi ' = \varphi ''\delta \). Clearly, \(s = s'\gamma \) and \(t = t'\gamma \). Moreover, \(\gamma \vDash \varphi '\) since \(\varphi '\gamma = \varphi ''\tau \sigma = \varphi ''\tau \) and \(\tau \vDash \varphi ''\). \(\square \)
The proofs of the following lemmata are given in [18].
Lemma 5
If
 then for all substitutions \(\sigma \vDash \varphi \) there exists a substitution \(\delta \) such that \(\delta \vDash \psi \),
then for all substitutions \(\sigma \vDash \varphi \) there exists a substitution \(\delta \) such that \(\delta \vDash \psi \),
 and \(t\sigma = v\delta \). \(\square \)
and \(t\sigma = v\delta \). \(\square \)
Lemma 6
If a constrained critical pair \(s \approx t~[\varphi ]\) is 1-parallel closed then
 for all substitutions \(\sigma \) with \(\sigma \vDash \varphi \). \(\square \)
for all substitutions \(\sigma \) with \(\sigma \vDash \varphi \). \(\square \)
Lemma 7
If a constrained parallel critical pair \(s = \ell \sigma '[r_p\sigma ']_{p \in P} \approx r\sigma ' = t~[\varphi ]\) is 2-parallel closed then there exist a term v and a set Q of parallel positions such that
 and \(\mathcal {V}\textsf{ar}(v,Q) \subseteq \mathcal {V}\textsf{ar}(\ell \sigma '\sigma ,P)\) for all substitutions \(\sigma \) with \(\sigma \vDash \varphi \). \(\square \)
and \(\mathcal {V}\textsf{ar}(v,Q) \subseteq \mathcal {V}\textsf{ar}(\ell \sigma '\sigma ,P)\) for all substitutions \(\sigma \) with \(\sigma \vDash \varphi \). \(\square \)
Theorem 8
If an LCTRS \(\mathcal {R}\) is parallel closed then \(\overline{\mathcal {R}}\) is parallel closed.
Proof
Let \(\mathcal {R}\) be a parallel closed LCTRS. First consider an arbitrary critical pair \(s \approx t \in \textsf{CP}(\overline{\mathcal {R}})\). From Theorem 2 we know that there exist a constrained critical pair \(s' \approx t'~[\varphi ] \in \textsf{CCP}(\mathcal {R})\) and a substitution \(\sigma \) such that \(s'\sigma = s\), \(t'\sigma = t\) and \(\sigma \vDash \varphi \). Since the constrained critical pair is 1-parallel closed, Lemma 6 yields
 . Hence \(\overline{\mathcal {R}}\) is 1-parallel closed.
. Hence \(\overline{\mathcal {R}}\) is 1-parallel closed.
Next consider an arbitrary parallel critical pair \(s \approx t \in \textsf{PCP}(\overline{\mathcal {R}})\). Theorem 7 yields a constrained parallel critical pair \(s' = \ell \sigma '[r_p\sigma ']_{p \in P} \approx r\sigma ' = t'~[\varphi ]\) in \(\textsf{CPCP}(\mathcal {R})\) and a substitution \(\sigma \) such that \(s'\sigma = s\), \(t'\sigma = t\) and \(\sigma \vDash \varphi \). Since the constrained parallel critical pair is 2-parallel closed, by Lemma 7 there exist a term v and a set of parallel positions Q such that
 and \(\mathcal {V}\textsf{ar}(v,Q) \subseteq \mathcal {V}\textsf{ar}(\ell \sigma '\sigma ,P)\). Hence \(\overline{\mathcal {R}}\) is 2-parallel closed. \(\square \)
and \(\mathcal {V}\textsf{ar}(v,Q) \subseteq \mathcal {V}\textsf{ar}(\ell \sigma '\sigma ,P)\). Hence \(\overline{\mathcal {R}}\) is 2-parallel closed. \(\square \)
Since left-linearity of \(\mathcal {R}\) is preserved in \(\overline{\mathcal {R}}\) and left-linear, parallel closed TRSs are confluent by Theorem 6, we obtain the following corollary via Theorems 7 and 8. Again, \(\mathcal {R}\) only has to be left-linear in the variables \(x \notin \mathcal {L}\mathcal {V}\textsf{ar}\), since that is sufficient for \(\overline{\mathcal {R}}\) to be left-linear.
Corollary 2
Every left-linear parallel closed LCTRS is confluent. \(\square \)
We illustrate the corollary on a concrete example.
Example 8
Consider the LCTRS \(\mathcal {R}\) over the theory Ints with the rules
The constrained (parallel) critical pair \(\textsf{f}(\textsf{g}(\textsf{1} + \textsf{1},\textsf{3} + \textsf{1})) \approx \textsf{g}(\textsf{4},\textsf{4})~[\textsf{true}]\) originating from the peak
 is 2-parallel closed:
is 2-parallel closed:

Note that the condition \(\mathcal {T}\mathcal {V}\textsf{ar}(\textsf{f}(\textsf{g}(\textsf{2},\textsf{4})),\textsf{true},\{2\}) \subseteq \mathcal {T}\mathcal {V}\textsf{ar}(\textsf{f}(\textsf{a}),\textsf{true},\{1\})\) is trivially satisfied. One easily checks that the corresponding constrained critical pair is 1-parallel closed. Since the only other remaining constrained critical pair is trivial, we conclude confluence by Corollary 2.
7 Conclusion
We presented a left-linearity preserving transformation from LCTRSs to TRSs such that (parallel) critical pairs in the latter correspond to constrained (parallel) critical pairs in the former. As a consequence, confluence results for TRSs based on restricted joinability conditions easily carry over to LCTRSs. This was illustrated by generalizing the advanced confluence results of van Oostrom [15] and Toyama [20] from TRSs to LCTRSs. We also proved that (local) confluence of terminating LCTRSs over a decidable theory is undecidable in general.
Figure 2 relates the confluence criteria in this paper to the earlier ones from [12, 17]. The acronyms stand for weak orthogonality (WO, [12, Theorem 4]), strong closedness (SC, [17, Theorem 2]), almost parallel closedness (APC, [17, Theorem 4]), almost development closedness (ADC, Corollary 1), and parallel closedness of (parallel) critical pairs (PCP, Corollary 2). All areas are inhabited and the numbers refer to examples in this paper.
The confluence results of [12, 17] have been implemented in crest.Footnote 1 The tool is currently under heavy development, not only to incorporate the results in this paper but also termination and completion techniques. Confluence of LCTRSs is a new category in the upcoming edition of the Confluence CompetitionFootnote 2 and we expect to present experimental results obtained with crest at the conference.
For TRSs numerous other confluence techniques, not based on restricted joinability conditions of critical pairs, as well as sufficient conditions for non-confluence are known [1, 8, 19, 23]. We plan to investigate which techniques generalize to LCTRSs with our transformation. The transformation also makes the formal verification of confluence criteria for LCTRSs in a proof assistant a more realistic goal.
References
Aoto, T.: Disproving confluence of term rewriting systems by interpretation and ordering. In: Fontaine, P., Ringeissen, C., Schmidt, R.A. (eds.) FroCoS 2013. LNCS (LNAI), vol. 8152, pp. 311–326. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40885-4_22
Aoto, T., Yoshida, J., Toyama, Y.: Proving confluence of term rewriting systems automatically. In: Treinen, R. (ed.) RTA 2009. LNCS, vol. 5595, pp. 93–102. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02348-4_7
Ciobâcă, S., Lucanu, D., Buruiană, A.S.: Operationally-based program equivalence proofs using LCTRSs. J. Log. Algebr. Methods Program. 135, 100894 (2023). https://doi.org/10.1016/j.jlamp.2023.100894
Ciobâcă, Ş, Lucanu, D.: A coinductive approach to proving reachability properties in logically constrained term rewriting systems. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS (LNAI), vol. 10900, pp. 295–311. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_20
Fuhs, C., Kop, C., Nishida, N.: Verifying procedural programs via constrained rewriting induction. ACM Trans. Comput. Log. 18(2), 14:1–14:50 (2017). https://doi.org/10.1145/3060143
Gramlich, B.: Confluence without termination via parallel critical pairs. In: Kirchner, H. (ed.) CAAP 1996. LNCS, vol. 1059, pp. 211–225. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-61064-2_39
Hirokawa, N., Kim, D., Shintani, K., Thiemann, R.: Certification of confluence- and commutation-proofs via parallel critical pairs. In: Timany, A., Traytel, D., Pientka, B., Blazy, S. (eds.) Proceedings of 13th ACM SIGPLAN International Conference on Certified Programs and Proofs, pp. 147–161. ACM (2024). https://doi.org/10.1145/3636501.3636949
Hirokawa, N., Nagele, J., van Oostrom, V., Oyamaguchi, M.: Confluence by critical pair analysis revisited. In: Fontaine, P. (ed.) CADE 2019. LNCS (LNAI), vol. 11716, pp. 319–336. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-29436-6_19
Knuth, D.E., Bendix, P.B.: Simple word problems in universal algebras. In: Leech, J. (ed.) Computational Problems in Abstract Algebra, pp. 263–297. Pergamon Press, Oxford (1970). https://doi.org/10.1016/B978-0-08-012975-4.50028-X
Kohl, C., Middeldorp, A.: A formalization of the development closedness criterion for left-linear term rewrite systems. In: Krebbers, R., Traytel, D., Pientka, B., Zdancewic, S. (eds.) Proceedings of 12th ACM SIGPLAN International Conference on Certified Programs and Proofs, pp. 197–210 (2023). https://doi.org/10.1145/3573105.3575667
Kohl, C., Middeldorp, A.: Formalizing almost development closed critical pairs. In: Naumowicz, A., Thiemann, R. (eds.) Proceedings of 14th International Conference on Interactive Theorem Proving. Leibniz International Proceedings in Informatics, vol. 268, pp. 38:1–38:8 (2023). https://doi.org/10.4230/LIPIcs.ITP.2023.38
Kop, C., Nishida, N.: Term rewriting with logical constraints. In: Fontaine, P., Ringeissen, C., Schmidt, R.A. (eds.) FroCoS 2013. LNCS (LNAI), vol. 8152, pp. 343–358. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40885-4_24
Mitterwallner, F., Schöpf, J., Middeldorp, A.: Reducing confluence of LCTRSs to confluence of TRSs. In: Proceedings of 12th International Workshop on Confluence, pp. 3–8 (2023)
Nagele, J., Felgenhauer, B., Middeldorp, A.: CSI: new evidence – a progress report. In: de Moura, L. (ed.) CADE 2017. LNCS (LNAI), vol. 10395, pp. 385–397. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63046-5_24
van Oostrom, V.: Developing developments. Theor. Comput. Sci. 175(1), 159–181 (1997). https://doi.org/10.1016/S0304-3975(96)00173-9
Post, E.L.: A variant of a recursively unsolvable problem. Bull. Am. Math. Soc. 52, 264–268 (1946). https://doi.org/10.1090/S0002-9904-1946-08555-9
Schöpf, J., Middeldorp, A.: Confluence criteria for logically constrained rewrite systems. In: Pientka, B., Tinelli, C. (eds.) CADE 2023. LNCS, vol. 14132, pp. 474–490. Springer, Cham (2023). https://doi.org/10.1007/978-3-031-38499-8_27
Schöpf, J., Mitterwallner, F., Middeldorp, A.: Confluence of logically constrained rewrite systems revisited. CoRR abs/2402.13552 (2024). https://doi.org/10.48550/ARXIV.2402.13552
Shintani, K., Hirokawa, N.: Compositional confluence criteria. In: Felty, A.P. (ed.) Proceedings of 7th International Conference on Formal Structures for Computation and Deduction. Leibniz International Proceedings in Informatics, vol. 228, pp. 28:1–28:19 (2022). https://doi.org/10.4230/LIPICS.FSCD.2022.28
Toyama, Y.: On the Church–Rosser property of term rewriting systems. NTT ECL Technical report 17672, NTT ECL (1981). (in Japanese)
Toyama, Y.: Commutativity of term rewriting systems. In: Programming of Future Generation Computers II, pp. 393–407. North-Holland (1988)
Winkler, S., Middeldorp, A.: Completion for logically constrained rewriting. In: Kirchner, H. (ed.) Proceedings of 3rd International Conference on Formal Structures for Computation and Deduction. Leibniz International Proceedings in Informatics, vol. 108, pp. 30:1–30:18 (2018). https://doi.org/10.4230/LIPIcs.FSCD.2018.30
Zankl, H., Felgenhauer, B., Middeldorp, A.: Labelings for decreasing diagrams. J. Autom. Reason. 54(2), 101–133 (2015). https://doi.org/10.1007/s10817-014-9316-y
Acknowledgments
The detailed feedback of the reviewers improved the presentation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Ethics declarations
Disclosure of Interests
The authors have no competing interests to declare that are relevant to the content of this article.
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Schöpf, J., Mitterwallner, F., Middeldorp, A. (2024). Confluence of Logically Constrained Rewrite Systems Revisited. In: Benzmüller, C., Heule, M.J., Schmidt, R.A. (eds) Automated Reasoning. IJCAR 2024. Lecture Notes in Computer Science(), vol 14740. Springer, Cham. https://doi.org/10.1007/978-3-031-63501-4_16
Download citation
DOI: https://doi.org/10.1007/978-3-031-63501-4_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-63500-7
Online ISBN: 978-3-031-63501-4
eBook Packages: Computer ScienceComputer Science (R0)


 for all variables x,
for all variables x, if
if
 for
for  if
if  .
.
 for all variables x,
for all variables x, if
if
 for
for  if
if 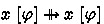 for all variables x,
for all variables x, if
if
 for
for  if
if 