Abstract
In recent breakthrough results, novel use of grabled circuits yielded constructions for several primitives like Identity-Based Encryption (IBE) and 2-round secure multi-party computation, based on standard assumptions in public-key cryptography. While the techniques in these different results have many common elements, these works did not offer a modular abstraction that could be used across them.
Our main contribution is to introduce a novel notion of obfuscation, called Reach-Restricted Reactive-Program Obfuscation (R3PO) that captures the essence of these constructions, and exposes additional capabilities. We provide a powerful composition theorem whose proof fully encapsulates the use of garbled circuits in these works.
As an illustration of the potential of R3PO, and as an important contribution of independent interest, we present a variant of Multi-Authority Attribute-Based Encryption (MA-ABE) that can be based on (single-authority) CP-ABE in a blackbox manner, using only standard cryptographic assumptions (e.g., DDH) in addition. This is in stark contrast to the existing constructions for MA-ABE, which rely on the random oracle model and supports only limited policy classes.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Consider the following approach to Identity-Based Encryption (IBE):
-
The master key pair is a verification/signing key pair for a signature scheme.
-
The decryption key for an identity is simply a signature on the identity.
-
The ciphertext is an obfuscation of the following program: it checks if its input is a valid signature on a target identity, and if so, it outputs the message.
With the right notion of obfuscation, as we shall see, this construction indeed translates to a secure IBE scheme! Further, such an obfuscation can be instantiated using standard cryptographic assumptions like DDH, based on the tools in [19, 20].
The motivation of this work comes from the breakthrough results of [6, 16, 20, 27]. These results were surprising not only because of the end results, but also because the central tools involved – garbled circuits, oblivious transfer, smooth projective hash functions, etc. – were all well known for a long time. The power behind these results lay in a machinery that carefully meshed these tools together.
However, this line of works has lacked reusable high-level abstractions, even as the low-level techniques were clearly similar across multiple works. Even the few abstractions of this machinery that appeared subsequently, e.g., in the form of hash-garbling [23], were not comprehensive enough to capture the multifarious applications of the machinery itself.
The main contribution of this work is to develop a versatile abstraction of the common machinery underlying the above works, and take it beyond the current set of applications. Our abstraction involves a strong form of obfuscation, which can be realized for programs that are appropriately sampled. The obfuscation formulation gives an intuitive description of potential solutions, and facilitates realizing it via a novel composition theorem. This not only aids in understanding the current constructions better, but also shows the way to new applications. As an illustration, and as an important contribution of independent interest, we present a variant of Multi-Authority Attribute-Based Encryption (MA-ABE) that can be based on (single-authority) ABE in a blackbox manner, using only standard cryptographic assumptions (e.g., DDH) in addition. This is in stark contrast to the constructions available for the original formulation of MA-ABE, which rely on specific assumptions, are for special restricted policy classes and/or are in the random oracle model [15, 17, 40, 46].
1.1 Our Contributions
Our contributions are in two parts – (1) developing a powerful new framework to capture several important results from the recent literature, and (2) using it to construct a multi-authority version of ABE.
The R3PO Framework. Our primary contribution is to develop the notion of Reach-Restricted Reactive Program Obfuscation (R3PO) that modularly encapsulates and extends the powerful techniques behind the surprising results of [6, 16, 20, 24, 27]. Our definition of R3PO allows an intuitive description of prior constructions like IBE [20] (with an easy extension to Identity-Based Functional Encryption [54]), 2-Round MPC [6, 27], and RBE [24], all of them using obfuscation of natural reactive programs.
-
We present a library of useful R3PO schemes. The library includes obfuscations for non-reactive programs that check a commitment opening, verify a signature, and verify the (partial) opening of a hashed value.
-
We present a composition theorem that can be used to obtain an R3PO scheme for a reactive program from R3PO schemes for smaller (non-reactive) programs (like those in the library above) into which it decomposes.
-
For each of the applications we consider (as well as some of the programs in the library), we define an appropriate reactive program, construct an R3PO for it and use it to complete our construction. The requisite R3PO maybe directly available from the library, or is constructed using the composition theorem.
The grabled circuit technique is entirely encapsulated within the proof of the composition theorem above. This is in contrast with prior work that used these techniques, where the proof would use a sequence of indistinguishability arguments interleaving garbled circuit simulation with other arguments specific to the construction. Indeed, one of the main technical challenges we overcome is to allow disentangling the garbled circuits from the other cryptographic elements, in these security proofs, using a strong simulation based definition of R3PO and our novel notion of decomposition.
Private Multi-Authority ABE. Another important contribution of this work is a new version of Multi-Authority Attribute-Based Encryption (called Private Multi-Authority ABE or \({\text {p-MA-ABE}}\)), and a construction for it, conceived in terms of an R3PO.
The motivation for \({\text {p-MA-ABE}}\) stems from the natural use-case for MA-ABE (or even ABE) where a user has privacy requirements against an attribute authority (e.g., they may want to obtain attributes corresponding to a city and a state that they consider their primary home, but without revealing the name of those locations to the authority). Correspondingly, the authority would be willing to issue attributes that satisfy a (possibly private) attribute-granting policy (e.g., issue the attributes for any one state and any one city within that state). The privacy requirement is that the authority (or authorities) shall not learn anything about the attributes of a user, and the user shall not learn anything about the attribute-granting policy, beyond whether the policy is met by the attribute set.
Now, a non-private MA-ABE (or ABE) scheme can be easily converted into a private version, via secure 2-party computation of a function to which the user’s input is their attribute request, and the authority’s input is its master secret key and its attribute-granting policy. Since such a 2PC protocol can be implemented in two rounds (e.g., a simple protocol based on Yao’s Garbled Circuit works, as we consider the authorities to be honest-but-curious), this only requires the user to send a single message to the server – which we call an attribute request – before the server responds.
\({\text {p-MA-ABE}}\) captures this trade-off: allow the user to initiate the contact with the authority,Footnote 1 and in return obtain a strong privacy guarantee. Though the above transformation shows that standard MA-ABE can be easily turned into \({\text {p-MA-ABE}}\), the former is known to be realizable only for very limited functions and in the random oracle model. In contrast, our results show that \({\text {p-MA-ABE}}\) is as widely realizable as ABE itself!
We give a construction for \({\text {p-MA-ABE}}\) from any (single-authority, ciphertext-policy) ABE scheme in a blackbox manner, using R3PO for (non-reactive) programs for signature checking and commitment opening, that is provably secure in the standard model. The scheme supports general access policies as supported by the underlying ABE scheme, and is policy-hiding if the ABE is policy-hiding.
1.2 Related Work
We mention a few related works below, and discuss how R3PO relate to other notions in Sect. 2.7.
Obfuscation. A large variety of notions of obfuscation have been studied in the literature leading to several important breakthroughs along the way (e.g., [2, 4, 5, 7, 22, 31, 35,36,37, 41, 49, 51]). Like R3PO, many of these require security only when the program being obfuscated is generated appropriately [4, 7, 33, 51].
Composition. Composition has been considered in the context of cryptographic protocols, leading up to UC security and its variants [3, 11,12,13, 18, 21, 32, 45, 47, 52], as well as alternate approaches like Constructive Cryptography [44]. Composition for obfuscation has received far less attention, although it was explicitly considered in an early work [43].
Garbled Circuits. Garbled circuits were conceived by Yao [53]. The techniques of chaining multiple garbled circuits appeared in garbled RAM schemes [25, 26, 28, 42], and later several results like Laconic OT [16], IBE from DDH [19, 20], 2-round MPC [6, 27], and several extensions of these works have all relied on these techniques.
Multi-Authority Attribute Based Encryption (MA-ABE). The notion of Ciphertext Policy-Attribute Based Encryption (CP-ABE) was introduced in [48] and formally defined in [30]. There is a rich sequence of works realizing ABE, based on lattice based (LWE) [9, 29] and pairing based assumptions [30, 34, 39]. But for MA-ABE, first proposed in [15], realizations so far have been limited. In the standard GID model, [40] formalized the notion of decentralized MA-ABE (where in, no trusted setup algorithm other than a common reference string is allowed), and gave a scheme for it under appropriate bilinear maps assumptions in the random oracle model (supporting general policy structures). A sequence of works culminated in [17], where they gave a scheme under the Learning With Errors (LWE) assumption in the random oracle model for policies corresponding to DNF formulae. Concurrently, [46] modified the definition to consider sender security (policy hiding) as well as receiver security (attribute hiding), and gave a construction for it under the k-linear assumption in the random oracle model for a special subset of policies. More recently, [50] gave a (current state-of-the-art) construction for MA-ABE in the plain model for subset policies (including DNF formulae) from the new evasive LWE assumption. Their construction however requires a global setup.
[38] proposed a variant of MA-ABE called the OT model. It is a relaxed model where there is no global identity fixed for the users. However, as pointed out in [17], this allows multiple users to pool their attributes, defeating one of the main goals of ABE. Our model has a global identity that an authority would incorporate into the key issued for a party, and as captured in the security definition, the user can combine only attributes that are issued for the same global id. Another drawback of [38] was that it used a global setup; we do not. Our setup is local to each authority (as in the global id model). Our model much more closely resembles the standard global id model, but with an additional key request step in the syntax. On the other hand, our results are much stronger than those available in the standard model (which are in the random oracle model and/or for limited function classes). We also offer further flexibility by not requiring each attribute to be attached to a unique authority.
We also note that MA-ABE can be modeled as an appropriate functionality in the framework of public-key Multi-Party Functional Encryption (MPFE) [1]. Their work gives a construction for public-key MPFE for general functionalities. However, this does not yield the result in our work due to the following limitations. Their construction uses an interactive setup, forcing the authorities to be aware of and interact with each other, while we require the MA-ABE authorities to only use “local” setup. Further, their construction is based on Multi-Input Functional Encryption for general functionalities (which is a strong assumption that implies iO). In contrast, we rely only on ABE and standard assumptions. Indeed, the main motivation behind R3PO and the entire line of work leading to it, is to be able to base various cryptographic schemes on simpler assumptions, and to avoid the need for assumptions like iO.
2 Technical Overview
2.1 Motivating Examples
We start with a few motivating constructions, along the lines of the IBE construction mentioned at the beginning of this paper, which we seek to base on our new notion of obfuscation. In the general case, we would be obfuscating a reactive program (or more specifically, a Moore machine), which at each step, accepts an input, updates its state, and produces an output based on the new state.
Identity-Based Functional Encryption. IBFE is an extension of IBE where each identity \(\textsf{id}\) is associated with a unique function \(f_\textsf{id} \) (not known to the encryptor), so that when an encryption of a message m addressed to \(\textsf{id}\) is decrypted using the key for \(f_\textsf{id} \), one receives \(f_\textsf{id} (m)\). An IBFE scheme can be obtained by simply modifying the IBE scheme above so that the obfuscated program takes a signature on \((\textsf{id}, f)\) (where \(\textsf{id}\) is already fixed in the program, but f is not), and transitions to a state encoding f, where it outputs f(m).
IBFE has been explored in a prior work [54], but their definition is incomparable to our notion above. On the one hand, their definition does not allow the adversary to obtain any function keys – under any IDs – for a function f such that \(f(m_0)\) and \(f(m_1)\) are not equal; on the other hand, it is not made very clear if the adversary is restricted to obtaining a single function key for the challenge id, as is the case in our definition. Finally, they offer a construction for the primitive only for a very restricted class of functions, while our construction supports general functionalities.
2-Round MPC. Following the constructions in [6, 27], an underlying (multi-round) MPC protocol can be reinterpreted as evaluating a blinded circuit, in which each boolean gate is owned by a party, and the protocol amounts to evaluating the wires of this circuit publicly. The wire values are public, but each gate is private to its owner.
The 2-round MPC constructed from the blinded circuit is as follows. In the first round, each party broadcasts a commitment to the 4 bits (separately) of the truth table of each of its gates. In the second round, each party broadcasts the obfuscation of the following reactive program:
-
The program maintains a public state consisting of all the wire values of the circuit, evaluated thus far.
-
If the next gate is owned by another party, the program accepts as input the output wire value of the gate, along with an opening of the corresponding commitment in the gate. If the opening verifies, it updates its state to correspond to having evaluated this wire. It produces no output for this transition.
-
If the next gate is owned by this party, then it takes no input, transitions to a state that includes the output wire value of this gate, and outputs the opening of the corresponding commitment.
Finally, given these obfuscated reactive programs, the parties evaluate the blinded circuit gate by gate, at each step first running the program from the owner of the gate, and then feeding its inputs to all the other programs.
Laconic OT. This is a version of OT in which the receiver has a vector D of choice-bits, which it commits to by sending a short string y to the sender. Later, on input \((i,x_0,x_1)\), the sender should send a string to the receiver from which the latter should learn only \(x_{D_i}\).
We consider the following implementation of Laconic OT: Using a hash that supports “selective opening” of a bit in the hashed string, with a collision resistance guarantee that prevents opening any bit in two different ways, the receiver hashes D to obtain y. On input \((i,x_0,x_1)\), the sender obfuscates the following (small) program and sends it over to the receiver: The program accepts as input an opening of y at position i to a bit b, and if the opening is valid, then it outputs \(x_b\).
Each of the above simplistic constructions relied on an intuitive notion of “obfuscation.” In the sequel, we develop a formal notion of obfuscation which will let us make the above descriptions precise, while retaining their simplicity. Importantly, our new obfuscation notion is indeed realizable in all the above cases, using the same standard cryptographic assumptions as in the prior works which introduced these constructions.
2.2 Defining R3PO
At a high-level, we consider obfuscation of reactive programs. A reactive program (a finite-state machine, or more precisely, a Moore machine) takes inputs over multiple rounds, updating its state and producing an output based on the state at each round. It is specified by a start state, a transition function \(\pi \) and a message function \(\mu \), so that, on reaching a state \(\sigma \), the program outputs \(\mu (\sigma )\).
Before discussing the definitions, it will be useful to have a couple of running examples in mind. In these examples, \(\mu \) is arbitrary (and secret), and a public \(\pi \) is as specified below.
-
Commitment. \(\pi _c\) incorporates a commitment string c. On input d at the start state, if d decommits c to m, then \(\pi _c\) transitions to a state \(\sigma _m\) encoding m.
-
Signature. A signature verification key \(\textsf{vk}\) is encoded in the start state \(\sigma _\textsf{vk} \) of \(\pi \) (denoted as \(\pi [\sigma _\textsf{vk} ]\)), from where, given a valid signature on a message m as input, it transitions to a state \(\sigma _m\) encoding m.
These are both instances of “one-step programs” which have transitions only out of the start state. (We shall later explain the slightly different choices for how the values c and \(\textsf{vk}\) are incorporated into \(\pi \) in the two cases.) In these examples, \(\pi \) is not hidden, and the goal of obfuscating such a program would be to hide \(\mu \). More generally, \(\pi \) and \(\mu \) can both have secrets in them (when defining reactive programs formally, we will denote them as \({\pi ^{(\alpha )}}\) and \({\mu ^{(\beta )}}\), where \(\alpha \) and \(\beta \) are the secrets).
Reach Extraction and Simulation. Our simulation-based notion of obfuscation requires that a “reach-extractor” should exist for the program being obfuscated. A reach extractor would predict all the states of a reactive program that are reachable using inputs that can be efficiently computed by any adversary. Then, the obfuscation of the program should be simulated using only the outputs produced by the program at those states. We elaborate on reach-exaction and the rest of the simulation below.
Reach Extractability. Which states in a program \(\pi \) are efficiently reachable is a consequence of the process that generates the program (analogous to how an “evasive program” being evasive is a consequence of sampling it from a distribution). This process involves a generator G and an adversary Q. A reach extractor for an adversary Q is a program that passively (possibly in a non-blackbox manner) observes Q as it interacts with G, and then predicts (a superset of) the set of states that the adversary will be able to reach in the program output by G. This prediction is made explicitly in the form of inputs to a (possibly different) reactive program \(\mathsf {{\Pi }}\) that will reach all the states reachable by the adversary, and perhaps more. Here we allow the extractor to specify \(\mathsf {{\Pi }}\), which belongs to a transition function family \(\mathring{\mathcal {P}}\) that may be different from the transition program family \(\mathcal {P}\) that is obfuscated. We refer to this as the “reach bounding” guarantee of the reach extractor.
We illustrate a reach extractor for the two running examples.
-
Commitment: G accepts a commitment string c from Q, and then outputs \(\pi _c\). A reach extractor can extract a value m from the commitment, either when Q is semi-honest, or when a setup is used that the extractor can control. Now, m is not a decommitment as expected by \(\pi _c\). Instead, we allow the extractor to specify a different program \(\mathsf {{\Pi }} _m\) which accepts m itself as the input and transitions to \(\sigma _m\).
This extractor is reach bounding, because, due to the binding property of the commitment scheme, the only state Q could reach in \(\pi _c\) is also \(\sigma _m\).
-
Signature: In this case, G internally samples a pair \((\textsf{sk},\textsf{vk})\) of signing and verification keys. It sends \(\textsf{vk}\) to Q, and further may answer signature requests by Q. An extractor can collect all the signatures Q receives from G and output them as a reach-bounding set of inputs for \(\mathsf {{\Pi }} =\pi [\sigma _\textsf{vk} ]\). Note that here the program family to be used by the extractor \(\mathring{\mathcal {P}}\) is the same as the one being obfuscated \(\mathcal {P}\) (and it has only one program in it but with various start states). The reach bounding property follows from unforgeability of the signature scheme.
Simulation. An obfuscator for a generator R3PO security definition requires that a 2-stage simulation exists for any adversary Q, as follows:
-
Stage 1: After Q finishes interacting with G, a reach extractor observing Q specifies a set of reachable states (in the form of a program \(\mathsf {{\Pi }}\) and inputs to it).
-
Stage 2: Given the output of the original message function \(\mu \) on those states, a simulated obfuscation is produced. This should be indistinguishable from the obfuscation of the reactive program produced by G, even given auxiliary information output by both G and Q.
Note that this is a stronger notion of simulation than even VBB obfuscation, which only requires the simulation of one predicate at a time, rather than a simulation of the entire obfuscated program. Indeed, requiring such a simulator would typically entail that the program is learnable and hence trivial to obfuscate. What keeps our definition from becoming trivial is the fact that the extracted inputs are a function of the program generation process, and are not available to the obfuscator.
Reach Restriction. The final component in our definition of R3PO is in the form of an additional requirement on the reach extractor in Stage 1 above. This requirement stems from the “one-time” nature of Yao’s Garbled Circuits, a key ingredient in the constructions that we wish to capture. Intuitively, these constructions require that an adversary can evaluate any garbled circuit on only one set of inputs. We incorporate a corresponding reach restriction requirement into our definition of reach extractability of a reactive program (Definition 3), which leads to the name reach-restricted reactive programs (R3P).Footnote 2
To define reach restriction, we require the state space of the reactive programs to be a priori partitioned into a polynomial number of parts, \(\varSigma = \varSigma _1 \cup \cdots \cup \varSigma _N\). Then, informally, the reach restriction property of a reactive program is that no efficient adversary would be able to find inputs that take \(\pi \) to two different states that belong to the same part. Formally, the reach restriction property is imposed on the reachable states produced by the reach-extractor.
We return to our running examples.
-
Commitment: We let \(\varSigma _1\) consist only of the start state and \(\varSigma _2\) consist of all states of the form \(\sigma _m\). Since the extractor outputs only one message m, the reach restriction property already holds.
-
Signature: We let \(\varSigma _1\) consist of all the potential start states \(\sigma _\textsf{vk} \) and \(\varSigma _2\) consist of all states of the form \(\sigma _m\) (the two kind of states are encoded so that \(\varSigma _1 \cap \varSigma _2 = \emptyset \)). To be reach restricting, we will require that the generator G gives out at most one signature. Further, we would want to enforce that breaking reach restriction in \(\mathsf {{\Pi }}\) must correspond to forging signatures with respect to the key sampled by G. This is enforced by keeping \(\textsf{vk}\) in the start state of \(\pi [\textsf{vk} ]\) (rather than in the transition function itself), which in turn forces \(\mathsf {{\Pi }}\) to use the same start state and hence the same verification key.
2.3 R3PO Composition Theorem
As noted earlier, a major motivation of this work is to encapsulate a range of powerful techniques using garbled circuits in a reusable form. This result takes the form of a composition theorem, which allows obfuscating a reactive program via an obfuscation of its various components.
The high-level idea is to view a reactive program \(\pi \in \mathcal {P} \), over a state space \(\varSigma =\varSigma _1 \cup \cdots \cup \varSigma _N\) as consisting of separate programs \(\widehat{\pi } _1,\ldots ,\widehat{\pi } _N\), such that \(\widehat{\pi } _i\) is identical to \(\pi \) on states \(\sigma \in \varSigma _i\), and in other states it ignores all inputs (i.e., remains at the same state). Let \(\mathcal {P} _i\) denote the class of such programs \(\widehat{\pi } _i\). W.l.o.g. (due to reach-restriction), we require \(\pi \) to not have any transitions between states in the same part, and hence each \(\widehat{\pi } _i\) is a “one-step” (or non-reactive) program that halts after its first transition out of the start state. However, attempting to formalize this leads to a couple of conundrums.
Conundrum 1: Dynamically Determined Programs. As a naïve starting point, one could try building an obfuscator for \(\mathcal {P}\) from obfuscators for \(\mathcal {P} _i\). However, this runs into an immediate problem: When executing a program in \(\mathcal {P}\), the state reached in \(\varSigma _i\) is dynamically determined by the inputs used, whereas when obfuscating a program in \(\mathcal {P} _i\), its start state needs to be fixed. The resolution of this conundrum, which goes back to [16, 19, 20, 25, 26, 28, 42], is to provide a garbled circuit that can dynamically compute the obfuscation of \(\widehat{\pi } _i[\sigma _i]\) with the correct start state \(\sigma _i\); the input to this garbled circuit would be the labels encoding \(\sigma _i\), which in turn would be released by the obfuscation of a previous program \(\pi _j[\sigma _j]\) on an input x such that \(\pi _j(\sigma _j,x)=\sigma _i\).
However, the price we pay for using garbled circuits is that only one set of labels can be made available to the adversary for each garbled circuit, in turn resulting in the reach-restriction requirement.
Conundrum 2: Intertwined Generators. Recall that to formalize reach restriction, our definition needed to take into account the generators. Now, when we try to map the different parts of a single reactive program as being generated by multiple generators, the generators can become deeply intertwined, sharing secret keys and state variables. Further, the program generated by one generator needs to have a start state that is determined by the outputs produced by programs in other parts. So it may not always be possible to view a (reach-restricted) reactive program produced by a generator as the composition of single-step reactive programs produced by separate generators.
The resolution to this conundrum is to require some additional relation between the generator for the reactive program and the generators for the one-step programs. This leads us to the notion of decomposition.
Decomposition. Unlike in the case of MPC protocols, wherein the subprotocols are explicitly executed by a composite protocols, a reactive program generator need not have “sub-generators” running within it. Indeed, this presents a challenge to composition that is fundamentally different from composition in MPC.
Our novel solution is to define decomposition in terms of a bisimulation requirement. Roughly, for G to decompose into a smaller generator H (and additional computation), we require that G can be viewed as H via a simulator, and vice versa. More precisely, we require that there be two simulators J and Z such that  (denoting that J internally runs G as a black box) and
(denoting that J internally runs G as a black box) and  are indistinguishable from each other from the point of view of any adversary Q (or more precisely, for
are indistinguishable from each other from the point of view of any adversary Q (or more precisely, for  , where the wrapper W is also part of the simulation). This by itself can be trivially arranged by letting \(J=H\) and \(Z=G\). We need to further capture the requirement that the program \(\widehat{\pi }\) produced by H corresponds to a single step in the program \(\pi \) produced by G. More precisely, the state space of the generator H corresponds to a part \(\varSigma _i\) of the state space of G, and we require that the start state of \(\widehat{\pi } \) is the same as the only state in \(\varSigma _i\) that is reachable in \(\pi \).
, where the wrapper W is also part of the simulation). This by itself can be trivially arranged by letting \(J=H\) and \(Z=G\). We need to further capture the requirement that the program \(\widehat{\pi }\) produced by H corresponds to a single step in the program \(\pi \) produced by G. More precisely, the state space of the generator H corresponds to a part \(\varSigma _i\) of the state space of G, and we require that the start state of \(\widehat{\pi } \) is the same as the only state in \(\varSigma _i\) that is reachable in \(\pi \).
Now, by requiring this, we require J to know the reachable state in \(\pi \) produced by G. While this is possible in some cases (e.g., when the reachable state is determined by a signed message sent by G), in certain other cases it is not possible (e.g., when it is determined by a message hidden in a commitment). To accommodate these different situations, we allow J to obtain this information from the wrapper W, which is in turn allowed to obtain this from a reach-extractor for G (or more precisely, from a “partial” reach extractor which only extracts the reach within \(\varSigma _i\)).
Finally, for use in our composition theorem, we shall require a uniformly sampled message function to be associated with the reactive program produced by J. (While the definition of decomposition allows arbitrary message function class here, the composition theorem is for decomposition that uses a particular message function class.)
We refer the reader to Sect. 4.1 for a more detailed discussion and a precise definition of decomposition.
Composition. Having defined decomposition, we turn to stating and proving the composition theorem. Informally, it states that if a generator G decomposes into generators \((H_1,\ldots ,H_N)\) (for a partition of its state space \((\varSigma _1,\ldots ,\varSigma _N)\)), and if each \(H_i\) has an R3PO scheme \(\mathcal {O} _i\), then there is one for G as well. The construction uses garbled circuits, following the outline at the beginning of this section. The final obfuscation consists of one garbled circuit \({\textsc {GC}}_{i}\) for each part \(\varSigma _i\), such that on reaching \(\sigma \in \varSigma _i\), an evaluator would have the labels that encode \(\sigma \) as input for \({\textsc {GC}}_{i}\), and \({\textsc {GC}}_{i}\) would then output \(\mu (\sigma )\) as well as an obfuscation \(\mathcal {O} _i(\widehat{\pi } _i[\sigma ],\widehat{\mu } _i)\) (using a hard-coded random tape). Feeding an input x to this obfuscated program will release the labels for the state \(\widehat{\pi } _i(\sigma ,x)=\pi (\sigma ,x)\).
To prove that this construction yields an R3PO for G, we use a sequence of hybrids that would replace one garbled circuit at a time with a simulated one, which in turn outputs not the actual obfuscation \(\mathcal {O} _i(\widehat{\pi } _i[\sigma ],\widehat{\mu } _i)\), but a simulated one. At each step, we will be able to apply the decomposition guarantee (using an inductively maintained partial reach extractor) to go from G to  to
to  , wherein we use the R3PO guarantee to replace the actual obfuscation used to simulate \({\textsc {GC}}_{i}\) with a simulated one (while also extending the partial extractor); then we move back from
, wherein we use the R3PO guarantee to replace the actual obfuscation used to simulate \({\textsc {GC}}_{i}\) with a simulated one (while also extending the partial extractor); then we move back from  to
to  and then G.
and then G.
2.4 R3PO Library
We present R3PO schemes for a few basic program classes which can be combined together in a variety of constructions.
-
Commitment-Opening. This is similar to the running example presented above. In the full version, we realize the R3PO for a couple of flavors of this (UC secure commitment, and “weakly secure” commitment that is suitable for semi-honest committers), based on the standard assumption of 2-round OT.
-
Signature-Checking. We provide an R3PO for signature-checking programs as in the running example. To facilitate full security in applications like IBE and IBFE, we support puncturable signature schemes.Footnote 3 We instantiate a puncturable signature scheme and give an R3PO scheme for this program family assuming an OTSE scheme in the full version.
-
Hash-Opening. This is similar to the commitment opening reactive program, but with a compressing hash instead of a binding commitment. The R3PO for this program class can be constructed from Laconic OT [16]. Alternately, we can use our composition theorem to bootstrap from an R3PO for the same class instantiated with a factor-2 compressing laconic OT (see Sect. 2.5 below).
-
\(\epsilon \)-Transition While specifying reactive programs using the above building blocks, often it is useful to transition from state reached via one building block to a state that is suitable as the start state of another building block. \(\epsilon \)-transitions provide the essential syntactic sugar to enable this. R3PO for an \(\epsilon \)-transition is implemented using a garbled circuit.
2.5 Applications: The Different Ways of Using R3PO
Our R3PO library and our composition theorem form a versatile toolkit for instantiating new and old constructions. There are a few different ways in which they can be put to use.
Off-the-Shelf Without Composition. In certain cases, the components in our library are already powerful enough off-the-shelf to yield a construction for a desired application. An illustrative example is that an R3PO for (puncturable) signature-checking can be used to construct an IBFE scheme (and, as a special case, IBE), as sketched in Sect. 2.1 and elaborated in the full version. The security proof is fairly direct, by using a generator for the R3PO that models the security experiment of IBFE.
Using Composition. We illustrate a typical “workflow” for using the R3PO composition theorem in a higher-level application. We use the example of Laconic OT [16], which is one of the early constructions that form the inspiration for this work. For the sake of readability we use slightly imprecise terminology.
-
We start by identifying a reactive program family, such that an R3PO for it directly yields our application.In the case of laconic OT, this reactive program traverses a pre-determined path along a Merkle tree, with states holding the hash value at each node, and making a transition if the input “explains” the hash at that node. The Merkle tree uses an underlying hash scheme which compresses by a factor of 2.
-
We consider the one-step restrictions of this reactive program as another reactive program family, and carry out the following two steps:
-
We show that the original reactive programs can be decomposed into its one-step restrictions. This involves matching the definition of decomposition with straightforward constructions.
-
We give an R3PO scheme for these one-step restrictions. This can be directly based on the construction in [16] for factor-2-compression laconic OT (not involving garbled circuit chaining).
-
-
Then we simply invoke our composition theorem to obtain an R3PO for the original program family.
-
We package the original reactive program as another one-step program, so that it can be included in our R3PO library for various applications (see the full version). Laconic OT is a direct consequence of an R3PO for this one-step program.
Another example of this workflow is in the construction of the R3PO for signature-checking that was mentioned above as part of our library (where the smaller non-reactive programs used correspond to one-time signature checking).
R3PO as a Component. In the above examples, once an R3PO is constructed, the final application is fairly immediately realized. However, it is also possible to use R3PO as a component in a larger construction, wherein the step from R3PO to the final security proof may be non-trivial. The proof may involve multiple hybrids, with R3PO security used to replace a real obfuscation in one hybrid with the simulated obfuscation in the next. One such example is the 2-round MPC protocol of [6, 27], which we rederive in the full version using R3PO for commitment opening. In this construction, as sketched in Sect. 2.1, several programs obfuscated using R3PO are involved. The security of R3PO can be used to move to an “ideal” execution of the MPC protocol (or more precisely, build a simulator for the 2-round MPC using the simulators of R3PO and the simulator for the underlying MPC protocol).
Our main application of \({\text {p-MA-ABE}}\) (discussed below) also falls into this category, where the security of the final construction depends on several components, one of which is an R3PO scheme. This construction also illustrates the possibility of combining multiple library components (commitment-opening and signature-checking) in the same reactive program.
2.6 Private Multi-Authority ABE
In this section, we give a brief overview of the new variant of MA-ABE that we introduce, called Private Multi-Authority ABE (\({\text {p-MA-ABE}}\)), and the main ideas behind our construction for it. Our construction is intuitive in terms of an obfuscation of a reactive program, and can indeed be realized using R3PO. The flexibility of the new framework allows a relatively easy construction, using existing ABE schemes, and with a robust security definition. The full description can be found in Sect. 5.
Defining p-MA-ABE: The setting of \({\text {p-MA-ABE}}\) (as well as MA-ABE) involves a set of mutually distrusting authorities (say \(A_1, \ldots , A_\textsf{N} \)), a sender and a receiver. The algorithms in an \({\text {p-MA-ABE}}\) scheme are as follows:
-
Setup: At the start of the execution, each authority \(A_i\) does a local (decentralized) setup to generate its public and secret keys \((\textsf{mpk} _i, \textsf{msk} _i)\) and shares the public key \(\textsf{mpk} _i\) with the other users in the system.
-
Key-Request: a receiver can construct a set of key-requests \(\textsf{req} =(\textsf{req} _1,\ldots ,\textsf{req} _\textsf{N})\) for a global identifier \(\textsf{gid} \) and attribute set \(\bar{\textsf{x}} \) from the public keys. It can then submit a key-request query (of the form \((\textsf{gid}, \textsf{req} _i)\)) to an authority \(A_i\) and get back a key-component \(\textsf{sk} _{\textsf{gid},\textsf{req} _i}\) from \(A_i\) (\(\textsf{req}\) will hide \(\bar{\textsf{x}}\)).
-
Key-Gen: an authority \(A_i\) receives as input a key-request \(\textsf{req} _i\) for a global identifier \(\textsf{gid}\), and outputs a key-component \(\textsf{sk} _{\textsf{gid},\textsf{req} _i}\) that incorporates an attribute-granting policy \(\varTheta ^\textsf{gid} _i\) (which, for simplicity, we do not consider a secret).
-
Encryption: a sender can encrypt a message m with a ciphertext policy \(\phi \), using the public keys of the authorities to produce a ciphertext \(\textsf{ct} _{m,\phi }\).
-
Decryption: a receiver can decrypt a ciphertext \(\textsf{ct} _{m,\phi }\) using key components of the form \((\textsf{sk} _{\textsf{gid},\textsf{req} _1},\cdots ,\textsf{sk} _{\textsf{gid},\textsf{req} _\textsf{N}})\) where all the requests \(\textsf{req} _i\) were generated using \(\textsf{gid}\) and \(\bar{\textsf{x}}\) such that \(\varTheta ^\textsf{gid} _i(\bar{\textsf{x}})=1\) for all i, and \(\phi (\bar{\textsf{x}})=1\).
Compared to the original definition of MA-ABE, there are two main differences in \({\text {p-MA-ABE}}\): Firstly, since the attributes are to be kept private even from the authorities, there is a key-request step, wherein the user generates the key-request messages to all the authorities based on its desired set of attributes. Secondly, we allow each authority to use an arbitrary attribute-granting policy, which depends on the entire attribute vector.Footnote 4
We define security w.r.t. a corruption model where the adversary is allowed to maliciously corrupt the receivers and semi-honestly corrupt any subset of authorities. If a receiver is honest, we require that the key-request \(\textsf{req} \) reveals nothing about \(\bar{\textsf{x}}\) to the authorities, even if all of them collude. When the receiver is corrupt, we guarantee that, for any choice of \((\phi ,m_0,m_1)\), the adversary cannot distinguish between the encryptions of \(m_0\) and \(m_1\) w.r.t. a policy \(\phi \), unless for a pair \((\textsf{gid},\bar{\textsf{x}})\) such that \(\varTheta ^\textsf{gid} _i(\bar{\textsf{x}})=1\) for all honest authorities \(A_i\), \(\phi (\bar{\textsf{x}})=1\) and the adversary sent a valid key request for \((\textsf{gid},\bar{\textsf{x}})\) (i.e., a request that can be produced by the Key-Request algorithm on those inputs) to at least one honest authority (and it could have sent it to the others as well).
A p-MA-ABE Scheme: Our scheme is easily described in terms of obfuscating a reactive program. The key-request \(\textsf{req} _i\) is a commitment to \(\bar{\textsf{x}}\) (using a common random string in the public-key of \(A_i\)). The key issued by each authority is the obfuscation of a reactive program; the reactive programs by the different authorities “talk” to each other and confirm that they all agree on granting the same attribute \(\bar{\textsf{x}}\) to \(\textsf{gid}\), and if so, issue standard CP-ABE keys for \(\bar{\textsf{x}}\). More precisely, the reactive program \(({\pi ^{(\alpha )}},{\mu ^{(\beta )}})\) works as follows (with \(A_i\)’s CP-ABE master secret-key constituting the secret \(\beta \); \(\alpha \) can be empty, or alternately, can be used to store \(\varTheta ^\textsf{gid} _i\) privately):
-
at the start state accepts a decommitment for \(\textsf{req} _i\) and transitions to a state with \(\bar{\textsf{x}}\). There, if \(\varTheta ^\textsf{gid} _i(\bar{\textsf{x}})=1\), then it outputs a signature on \((\textsf{gid},\bar{\textsf{x}})\), using \(A_i\)’s signature key.
-
Then, it moves through \(\textsf{N}-1\) states accepting signatures on \((\textsf{gid},\bar{\textsf{x}})\) from all the other servers.
-
On reaching the last of these states, it outputs a CP-ABE key for the attribute \(\bar{\textsf{x}}\), under a (standard) CP-ABE scheme for which \(A_i\) is the authority.
If \(\varTheta ^\textsf{gid} _i(\bar{\textsf{x}})=1\) for all i, then the receiver can obtain the CP-ABE keys for \(\bar{\textsf{x}}\) under all the authorities. Now, to encrypt a message under a policy \(\phi \), one simply secret-shares m into \(\textsf{N}\) shares, and encrypts each share under the CP-ABE public key of the corresponding authority.
Note that if even one (honest) authority’s key component is missing, no honest authority’s CP-ABE key can be obtained. This is crucial because the CP-ABE keys do not involve \(\textsf{gid}\) and cannot prevent the use of keys obtained using multiple \(\textsf{gid}\) s.
Using the composition theorem, we show that there is an R3PO for a suitably defined generator that models the \({\text {p-MA-ABE}}\) security game. (As it turns out, we need to do this for two different generators to handle two different hybrids; the first hybrid does not rely on the unforgeability of the signatures, and lets the adversary specify all the signing keys. We show that the same obfuscator \(\mathcal {O} \) is an R3PO scheme for both the generators.)
2.7 Comparison of R3PO with Existing Primitives
It is instructive to compare R3PO with various existing primitives and techniques.
Hash Garbling. This abstraction from [23] gives a similar interface to R3PO for a specific class of program generators, namely, “Hash Opening.” More precisely, hash garbling involves a hash-opening check as well as a circuit evaluation, which corresponds to a reactive program that carries out a hash-opening transition followed by an epsilon transition (that evaluates the circuit).
{Batch, Hash, Chameleon, OneTime Signature}-Encryption. These flavors of encryption that were introduced in prior work [8, 19, 20] correspond to R3PO schemes for one-step programs that are included in our library (Hash Opening and Signature Checking). While these original definitions differ in their details, R3PO provides a simulation-based definition that can be uniformly used in all their applications.
Witness Encryption over Commitments (cWE). cWE, recently defined in [10], is quite similar to an R3PO for “Commitment Opening” followed by an epsilon transition. It was instantiated from Oblivious Transfer (OT) and garbled circuits, just as the R3PO scheme obtained directly from our library and the composition theorem is.
Garbled Circuit Chaining. The technique of garbled circuit chaining has appeared in a long line of works [6, 20, 24, 27, 42]. We note that R3PO allows different one-step programs (for example combining commitment and signature in \({\text {p-MA-ABE}}\)), while all prior works used garbled circuit chaining with links that correspond to a single cryptographic element. Also, as already mentioned, the prior works do not separate out the chaining from the cryptographic elements that are chained together.
Obfuscation Notions. Our notion of R3PO is different in many ways from the other notions of obfuscation. Many notions of obfuscation are either unrealizable in general or inhabit “obfustopia,” requiring a combination of relatively strong assumptions, and are not practical in terms of efficiency [2, 4, 5, 7, 7, 14, 35]. But there are a few exceptions for specialized applications, like obfuscation of reencryption based on bilinear pairings [33] or compute-and-compare obfuscation based on LWE [51]. R3PO could be considered to be in the latter group, but with a much richer class of applications compared to the others.
The original notions of obfuscation require worst-case security, but there are several others, including obfuscation of evasive circuit families [4], strong iO [7], reencryption obfuscation [33], compute-and-compare obfuscation [51], etc. which require only distributional security, when the program being obfuscated is sampled from distributions with particular properties. Again, R3PO falls into the latter class here, with the sampling process being interactive.
3 The R3PO Framework
3.1 Reactive Programs and Generators
Below we define a reactive program as a stateful machine that takes inputs, transitions its state and produces outputs as a function of its state. Formally, such a program consists of a deterministic transition function \(\pi \) and a deterministic message function \(\mu \), both of which can be parameterized by (secret) values \(\alpha \), \(\beta \) (hardwired into circuits \({\pi ^{(\cdot )}}\), \({\mu ^{(\cdot )}}\) respectively).
Definition 1
(Reactive Program over ( \(\mathcal {X} \) , \(\varSigma \) , \(\mathcal {A} \) , \(\mathcal {B} \) , \(\textsf{M}\) ). A reactive program \(({\pi ^{(\alpha )}}, {\mu ^{(\beta )}})\), with input alphabet \(\mathcal {X} \), a state-space \(\varSigma \), a start-state \(\textsf{start} \in \varSigma \) and secret spaces \(\mathcal {A} \), \(\mathcal {B} \) is specified by a deterministic transition program \({\pi ^{(\alpha )}}:\varSigma \times \mathcal {X} \rightarrow \varSigma \) parameterized by a secret \(\alpha \in \mathcal {A} \) and a deterministicFootnote 5 message function \({\mu ^{(\beta )}}: \varSigma \rightarrow \textsf{M} \) parameterized by a secret \(\beta \in \mathcal {B} \), that on input sequence \((x_1,\ldots ,x_\ell ) \in \mathcal {X} \), reaches a state \(\sigma _\ell \), where \(\sigma _i={\pi ^{(\alpha )}} (\sigma _{i-1},x_i)\) for \(i=1,\ldots ,\ell \) and \(\sigma _0=\textsf{start} \), and outputs a message \({\mu ^{(\beta )}} (\sigma _\ell )\). We also define \({\textsc {reach}}_{{\pi ^{(\alpha )}}}(x_1,\ldots ,x_\ell ) =\{\sigma _0,\cdots ,\sigma _\ell \}\) and \({\overline{\pi } ^{(\alpha )}} (x_1,\ldots ,x_\ell )=\sigma _\ell \). \(\lhd \)
Reactive programs have an associated implicit security parameter \(\kappa \); specifically, we require that the states in \(\varSigma \) and secrets in \(\mathcal {A} \), \(\mathcal {B} \) are represented as binary strings of length polynomial in the security parameter \(\kappa \), and the functions \({\pi ^{(\alpha )}}\) and \({\mu ^{(\beta )}}\) are polynomial in \(\kappa \). Throughout the rest of the paper, we shall omit \(\kappa \) and implicitly refer to “polynomial in \(\kappa \) ” as simply being polynomial.
Partition Function and Program Class. A transition function class \(\mathcal {P}\) refers to a set of transition functions along with an associated partition function \(\mathcal {I} \) that maps states to integers, i.e., \(\mathcal {I} : \varSigma \rightarrow [N]\) for some positive integer N. We say that \(\mathcal {I} \) partitions the state space \(\varSigma \) into \(\varSigma _1,\cdots ,\varSigma _N\) where,
Unless otherwise stated, the start state of a reactive program is assumed to be in \(\varSigma _1\). We say that a transition function \({\pi ^{(\alpha )}}\) is tree-ordered with respect to \(\mathcal {I} \), if the directed graph over [N] (each partition as a vertex) with an edge-set
is a tree, and all its edges (i, j) satisfy \(i<j\). That is, for any partition j, there is at most a single partition \(i < j\) from which states in partition j can be transitioned to. Further, we say that a transition function class \(\mathcal {P}\) is tree-ordered if every \({\pi ^{(\alpha )}} \in \mathcal {P} \) is tree-ordered w.r.t. the partition associated with \(\mathcal {P}\).
A program class \((\mathcal {P}, \mathcal {M} )\) is a set of reactive programs \(({\pi ^{(\alpha )}}, {\mu ^{(\beta )}}) \) with \({\pi ^{(\alpha )}} \in \mathcal {P} \) and \({\mu ^{(\beta )}} \in \mathcal {M} \).
Reactive Program Generator. We now describe the process which generates a reactive program to be obfuscated. A PPT program G (which we call the generator) interacts with a PPT program Q (which we call the adversary) over many rounds; at the end G outputs a reactive program \(({\pi ^{(\alpha )}}, {\mu ^{(\beta )}})\). Both G and Q are also allowed to produce auxiliary outputs.
Definition 2
(( \(\mathcal {P}\) , \(\mathcal {M} \) )-Generator \(G\) ). A \((\mathcal {P},\mathcal {M} )\)-generator \(G\) for a transition function class \(\mathcal {P}\) and message function class \(\mathcal {M} \) is a PPT interactive program that interacts with an arbitrary PPT program Q. We write
to indicate that at the end of the interaction, \(G\) outputs \(\Big ( ({\pi ^{(\alpha )}},{\mu ^{(\beta )}}),a _G \Big )\) and Q outputs \(a _Q \) (where \({\pi ^{(\alpha )}} \in \mathcal {P} \), \({\mu ^{(\beta )}} \in \mathcal {M} \)). A generator class is simply a set of generators. \(\lhd \)
An adversary class \(\mathcal {Q}\) is simply a set of adversaries Q. Some useful adversary classes depending on the application are: set of all PPT machines (for active corruption) and set of “semi-honest” PPT machines which follow a given protocol. We also consider adversary classes with setup. For any T that is a program in a setup class \(\mathcal {T}\), we use \(Q^T\) to denote an adversary Q that gets oracle access to an honest execution of T.
3.2 Reach Extractor
To define a reach extractor, we introduce some notation. We write \(Q\hat{|} \mathcal {E} \) to denote a composite machine in which \(\mathcal {E} \) semi-honestly runs Q internally in a straight-line manner (where \(\mathcal {E} \) can read the internal state of Q), letting Q directly communicate externally (with a generator). \(\mathcal {E} \) produces the final auxiliary output. For an adversary class with a setup, given an adversary \(Q^T\) in the composite machine \(Q^T\hat{|} \mathcal {E} \), \(\mathcal {E}\) is allowed to replace T with any program from \(\mathcal {T}\). For example, to capture common reference strings as a setup, \(\mathcal {T}\) would correspond to \(\{ \textsf{Setup}, \textsf{Setup} _{\textrm{Sim}} \}\), where \(\textsf{Setup}\) is the standard setup algorithm and \(\textsf{Setup} _{\textrm{Sim}}\) produces a simulated CRS.
\(\mathcal {E}\) is a valid reach-extractor if the following hold: in the \({\textsc {ideal}}\) interaction, \(\mathcal {E}\) observes the adversary Q and produces an extra output \((\mathsf {{\Pi }},X ^*)\) such that the states reached in \(\mathsf {{\Pi }}\) using \(X ^*\) (that is, \({\textsc {reach}}_{\mathsf {{\Pi }}}(X ^*) \)) is an upper bound on what D can reach in \({\pi ^{(\alpha )}}\); further the output is such that it reaches at-most a single state in each partition.Footnote 6
Definition 3
(Reach-Extractor for Q w.r.t. \((\mathcal {G},\mathring{\mathcal {P}})\)). A reach-extractor for an adversary \(Q \in \mathcal {Q} \) w.r.t. a (\(\mathcal {P}\),\(\mathcal {M} \))-generator class \(\mathcal {G}\) and a transition function class \(\mathring{\mathcal {P}}\), is a PPT program \(\mathcal {E}\) such that, for all \(G \in \mathcal {G} \) and PPT D, the output X produced by the following two experiments are indistinguishable:

and further the following hold:
-
In \({\textsc {ideal}} (G, Q\hat{|} \mathcal {E} , D)\), \(\mathsf {{\Pi }} \in \mathring{\mathcal {P}} \).
-
Suppose \(\mathcal {I} \) partitions \(\varSigma \) into N parts \(\varSigma _1,\cdots ,\varSigma _N\). Then
-
Reach-Bound: For all \(i \in [N]\), \(\Pr [({\textsc {reach}}_{{\pi ^{(\alpha )}}}(X) \cap \varSigma _i) \nsubseteq ({\textsc {reach}}_{\mathsf {{\Pi }}}(X ^*) \cap \varSigma _i)]\) is negligible.
-
Reach-Restriction: For all \(i \in [N]\), \(|{\textsc {reach}}_{\mathsf {{\Pi }}}(X ^*) \cap \varSigma _i | \le 1\). \(\lhd \)
-
Real and Ideal Program Classes. Note that, in the above definition, \(\mathcal {E}\) in the ideal world is allowed to extract an idealized reactive program \(\mathsf {{\Pi }} \in \mathring{\mathcal {P}} \) to describe the set of states reachable by the adversary Q. While in many of our examples, \(\mathring{\mathcal {P}}\) is the same as \(\mathcal {P}\), the class of “real world” reactive programs being obfuscated, this is not mandatory. This flexibility in the ideal world can help with enabling reach extraction while remaining useful in a higher level application. Please refer to the full version for more details.
3.3 Reach-Restricted Reactive Program Obfuscation
Recall that, our goal in obfuscating a reactive program is to hide the parameters \(\alpha \), \(\beta \), except for the states an adversary can reach. Let \(\mathcal {E} \) be a reach-extractor for Q w.r.t. \(\mathcal {G}\) s.t. \(\mathcal {E} \) outputs \(\mathsf {{\Pi }} \), \(X ^*\) and \({\textsc {reach}}_{\mathsf {{\Pi }}}(X ^*) \) bounds the reach of the adversary in \({\pi ^{(\alpha )}}\). Then, we define a secure obfuscation as requiring a simulator \(\textsf{Sim}\) which, given only the circuits \({\pi ^{(\cdot )}}\), \({\mu ^{(\cdot )}}\) and the reachable states \((\overline{x}, {\mu ^{(\beta )}} (\mathsf {{\Pi }} (\overline{x})))\) for input sequences \(\overline{x} \in X ^*\), can output an obfuscation indistinguishable from a real obfuscation.
Definition 4
(R3PO scheme \(\mathcal {O} \) for ( \(\mathcal {G}\),\(\mathcal {Q}\),\(\mathring{\mathcal {P}}\) )). A PPT program \(\mathcal {O} \) is an Reach-Restricted Reactive Program Obfuscation (R3PO) scheme for a \((\mathcal {P},\mathcal {M} )\)-Generator class \(\mathcal {G}\) and transition function class \(\mathring{\mathcal {P}}\), if the following hold:Footnote 7
-
Correctness: For all \({\pi ^{(\alpha )}} \in \mathcal {P} \), \({\mu ^{(\beta )}} \in \mathcal {M} \), \(\rho \leftarrow \mathcal {O} ({\pi ^{(\alpha )}}, {\mu ^{(\beta )}})\), and \(\overline{x} \in \mathcal {X} ^*\), it holds that \(\rho (\overline{x})={\mu ^{(\beta )}} ({\overline{\pi } ^{(\alpha )}} (\overline{x}))\).
-
Security: There exists a PPT program \(\textsf{Sim}\) s.t. \(\forall Q \in \mathcal {Q} \), there exists a reach-extractor \(\mathcal {E} \) w.r.t. (\(\mathcal {G}\), \(\mathring{\mathcal {P}}\)), so that \(\forall \; G \in \mathcal {G} \), the outputs of the following two experiments are indistinguishable:
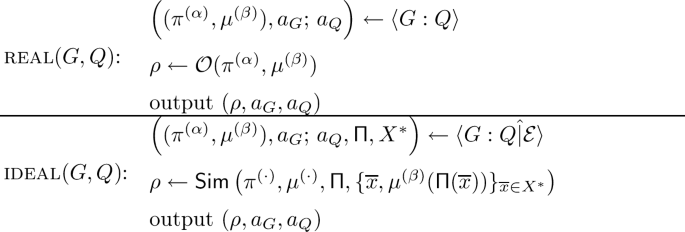
\(\lhd \)
4 A Composition Theorem for R3PO
We now describe our composition theorem that enables building an R3PO for a generator class from R3PO s for generator classes that produces smaller “one-step” (or non-reactive) programs. First we formalize the notion of decomposition.
4.1 Decomposition
The goal of decomposition is to view the transition function \(\pi \) of a reactive program produced by a generator G, as consisting of several one-step transitions \(\pi _i\) of reactive programs produced by generators \(H_i\). Below, we define the notion of a \(\sigma \)-restriction of \(\pi \) at a state \(\sigma \).
One-Step Restriction of a Transition Function. Given a reactive program’s transition function \({\pi ^{(\alpha )}}\) and one of its states \(\sigma \), we define a one-step \(\sigma \) -restriction of \({\pi ^{(\alpha )}}\) as a transition function \(\widehat{\pi }^{(\alpha )} _\sigma \) with start state \(\sigma \), where
(i.e., in \(\widehat{\pi }^{(\alpha )} _\sigma \), the only transitions allowed are from its start state \(\sigma \)).
Note that the state space \(\varSigma \) of \(\pi \) can be exponentially large in \(\kappa \), and correspondingly \(\pi \) consists of that many one-step transition functions. When decomposing \(\pi \), we will group them into polynomially many classes of transition functions, using the partition \(\mathcal {I} \) of the state space, \(\varSigma =\varSigma _1 \cup \cdots \cup \varSigma _N\) associated with \(\pi \). This imposes the following structure on the class of transition functions \(\mathcal {P}\) to which \(\pi \) belongs.
The transition function class \(\mathcal {P} _1 \times \cdots \times \mathcal {P} _N\). For any set of N classes \(\mathcal {P} _1, \cdots , \mathcal {P} _N\) over the (same) state space \(\varSigma \) and partition function \(\mathcal {I} : \varSigma \rightarrow [N]\), we define \(\mathcal {P} _1 \times \cdots \times \mathcal {P} _N\) to consist of transition functions \({\pi ^{(\alpha )}}\) such that for each state \(\sigma \in \varSigma _i\), the one-step \(\sigma \)-restriction of \({\pi ^{(\alpha )}}\) is in \(\mathcal {P} _i\). That is, for all \(\sigma \in \varSigma \) and inputs x, \({\pi ^{(\alpha )}} (\sigma , x) = \widehat{\pi }^{(\alpha )} _{\sigma }(\sigma , x)\) where \(\widehat{\pi }^{(\alpha )} _{\sigma } \in \mathcal {P} _{\mathcal {I} (\sigma )}\).
Though \(\pi \) can have exponentially many states, we would like to view it as composed of N transition functions, \(\widehat{\pi } _{\sigma _i} \in \mathcal {P} _i\), where \(\sigma _i\in \varSigma _i\). Thanks to the reach-restriction requirement on the reactive programs that we are interested in, for each i, there would indeed be only one state \(\sigma _i\in \varSigma _i\) that we need to consider. However, recall that \(\pi \) is dynamically generated by a generator G interacting with an adversary Q, and the reachable states in \(\pi \) are determined by this interaction. So the decomposition should be framed at the level of the interactive generators, rather than individual transition functions.
This leads us to a bi-simulation based definition of decomposition that views the generator G as incorporating another generator H (which produces one-step programs), and gives a two-way equivalence between them. To formalize this notion of bi-simulation, we introduce the following notation of composite machines.
Composite Machines. It will be convenient to define a few different ways in which a program (a generator or an adversary) can be wrapped by another program. As described below, a generator will be wrapped by a blackbox simulator, J or Z.Footnote 8 We also introduce a non-blackbox wrapper W which will be used to adapt an adversary Q (that expects to interact with G) so that it can interact with both G and H.
-
For a generator H, we write
 to denote a composite machine in which Z runs H internally in a blackbox straight-line manner. The reactive program output by the composite generator is produced H, and the auxiliary output produced by it contains outputs from both H and Z. H may communicate with Z, and further the composite machine can communicate externally as described shortly. The running time of
to denote a composite machine in which Z runs H internally in a blackbox straight-line manner. The reactive program output by the composite generator is produced H, and the auxiliary output produced by it contains outputs from both H and Z. H may communicate with Z, and further the composite machine can communicate externally as described shortly. The running time of  is bounded by that of H plus an additive \(\textsf{poly} (\kappa )\) overhead that depends on Z.
is bounded by that of H plus an additive \(\textsf{poly} (\kappa )\) overhead that depends on Z. -
For a generator G, we write
 to denote a slightly different composite machine, which is similar to
to denote a slightly different composite machine, which is similar to  (G is run internally by J in a blackbox straight-line manner, and the auxiliary information is produced by both) but the reactive program it produces is output by J. The external communication pattern is also different as described below.
(G is run internally by J in a blackbox straight-line manner, and the auxiliary information is produced by both) but the reactive program it produces is output by J. The external communication pattern is also different as described below. -
For an adversary Q, we write
 to denote a composite machine in which W internally runs Q in a straight-line manner with additive overhead, but W can read the internal state of Q. The auxiliary output of this composite machine is the entire view of W (which includes the auxiliary information \(a _Q\) produced by Q). The communication pattern is described below.
to denote a composite machine in which W internally runs Q in a straight-line manner with additive overhead, but W can read the internal state of Q. The auxiliary output of this composite machine is the entire view of W (which includes the auxiliary information \(a _Q\) produced by Q). The communication pattern is described below. -
Each of
 and
and  has three external communication channels – one used by the internal machine (shown boxed) and the other two by the wrapper machine. In all machines the “middle” channel is used by the wrapper (J, Z and W, respectively); the “top” channel is used by G, Z and Q (resp.); the “bottom” channel is used by J, H and W (resp.). Note that when
has three external communication channels – one used by the internal machine (shown boxed) and the other two by the wrapper machine. In all machines the “middle” channel is used by the wrapper (J, Z and W, respectively); the “top” channel is used by G, Z and Q (resp.); the “bottom” channel is used by J, H and W (resp.). Note that when  is connected to
is connected to  , Q directly interacts with G, whereas when
, Q directly interacts with G, whereas when  is connected to
is connected to  , Q interacts with Z.
, Q interacts with Z.
For the ease of writing expressions, we shall denote  by
by  , and
, and  by
by  . We will denote
. We will denote  by
by  ; in fact, we will be interested in
; in fact, we will be interested in  (where \(Q\hat{|} \mathcal {E} \) itself is a composite machine involving a reach-extractor which interacts with Q as defined in Definition 3); we shall denote it by
(where \(Q\hat{|} \mathcal {E} \) itself is a composite machine involving a reach-extractor which interacts with Q as defined in Definition 3); we shall denote it by  .
.
Partial Reach-Extractor: For a valid decomposition, it will be important to have a bi-simulation that maps \(\pi \) to a one-step restriction \(\pi _\sigma \) such that \(\sigma \) is the unique reachable state in a subset of states \(\varSigma _i\). To enforce this, we shall rely on an extractor for the adversary Q w.r.t. the generator G that produces \(\pi \). However, the purpose of decomposition and composition is to be able to obtain an extractor for Q w.r.t. G along with a simulator, as in the definition of R3PO (Definition 4). To break this apparent circularity, we use the notion of a partial reach extractor: An \((i-1)\)-partial reach extractor will be sufficient for defining decomposition “at part \(\varSigma _i\),” and it can be extended to an i-partial reach extractor, using the R3PO guarantee for the one-step generator.
Formally, a t-partial reach-extractor is defined identically to Definition 3, but with the relaxation that the reach-bound condition needs to hold only for \(i \le t\), instead of \(i\le N\). (The reach-restriction condition is still required to hold for all \(i \in N\).) Thus, an N-partial reach extractor is a “full” reach-extractor.
Now we are ready to state the definition of decomposition. While informally we shall refer to decomposing a reactive program (or even a transition function) to one-step programs, formally, the decomposition is of a generator class to a sequence of generator classes, specified along with corresponding adversary classes and relaxed program classes.
Definition 5
(Decomposition of ( \(\mathcal {G}\) , \(\mathcal {Q}\) ) to \(\boldsymbol{\mathcal {L}}\) ). Let \(\mathcal {G}\) be a \((\mathcal {P},\mathcal {M} )\)-generator class where \(\mathcal {P} = \mathcal {P} _1 \times \cdots \times \mathcal {P} _N\) is tree-ordered. Let \(\mathcal {L} = (\mathcal {H}, \mathcal {Q}, \mathring{\mathcal {P}})\), where  for a fixed \((\mathcal {P} _i,\mathcal {M} _{i})\)-generator H, \(\mathcal {Q}\) is an adversary class, and \(\mathring{\mathcal {P}}\) is a transition function class.
for a fixed \((\mathcal {P} _i,\mathcal {M} _{i})\)-generator H, \(\mathcal {Q}\) is an adversary class, and \(\mathring{\mathcal {P}}\) is a transition function class.
Then, a generator \(G\in \mathcal {G} \) is said to be decomposable at part i to \(\mathcal {L} \) if, there exist PPT J, Z, W so that \(\forall Q \in \mathcal {Q} \), and all \((i-1)\)-partial reach-extractors \(\mathcal {E}\) for Q w.r.t. \((\mathcal {G},\mathring{\mathcal {P}})\), it holds that \(Q\hat{|} \mathcal {E} |W \in \mathcal {Q} \) and:
-
Indistinguishability:
 .
. -
In
 , let the output of G be \((({\pi ^{(\alpha )}}, {\mu ^{(\beta )}}), a _G )\), and of \(\mathcal {E}\) be \((a _Q, \mathsf {{\Pi }}, X ^*)\); then J outputs \(((\widehat{\pi }^{(\alpha )} _{\sigma },{\widehat{\mu }^{({\widehat{\beta }})}} _{\sigma }),a _J)\) s.t.
, let the output of G be \((({\pi ^{(\alpha )}}, {\mu ^{(\beta )}}), a _G )\), and of \(\mathcal {E}\) be \((a _Q, \mathsf {{\Pi }}, X ^*)\); then J outputs \(((\widehat{\pi }^{(\alpha )} _{\sigma },{\widehat{\mu }^{({\widehat{\beta }})}} _{\sigma }),a _J)\) s.t.-
Correct One-Step Restriction: \({\textsc {reach}}_{\mathsf {{\Pi }}}(X ^*) \cap \varSigma _i \subseteq \{ \sigma \}\).
-
Correct Message Function: \({\widehat{\mu }^{({\widehat{\beta }})}} _\sigma \leftarrow \mathcal {M} _{i}\) is uniformly sampled at the end of the execution.
-
\((\mathcal {G},\mathcal {Q})\) is said to be decomposable into \(\boldsymbol{\mathcal {L}} = ( \mathcal {L} _1, \ldots , \mathcal {L} _N )\) if \(\forall G \in \mathcal {G}, \; i \in [N]\), it holds that \(\mathcal {L} _i=(\mathcal {H} _i,\mathcal {Q} _i,\mathring{\mathcal {P}} _i)\) where \(\mathcal {Q} _i \supseteq \mathcal {Q} \), and G is decomposable at part i to \(\mathcal {L} _i\). \(\lhd \)
Above, we require two simulations to produce indistinguishable outputs (which includes their communication, as  outputs its entire view as part of output), with J mimicking H, and Z mimicking G. The “correct one-step restriction” condition forces J (and hence H) to output a one-step restriction whose start state is the state that is reachable, as reported by a (partial) reach-extractor for G.
outputs its entire view as part of output), with J mimicking H, and Z mimicking G. The “correct one-step restriction” condition forces J (and hence H) to output a one-step restriction whose start state is the state that is reachable, as reported by a (partial) reach-extractor for G.
4.2 Composition Theorem
Obfuscator \(\mathcal {O} \) used to prove Theorem 1.
Above, decomposition related the transition functions in \(\mathcal {P} =\mathcal {P} _1\times \cdots \times \mathcal {P} _N\) to those in each \(\mathcal {P} _i\). Before stating our composition theorem, we need to specify the message function space \(\widehat{\mu } _i\) of these one-step programs as well.
As described in Sect. 2.3, \(\widehat{\mu } _i\) should release garbled circuit labels for the state at which it is evaluated. For our purposes, it will be helpful to consider a labeling function (denoted below as \({\widehat{\beta }} \)) which takes the part index i as an input, along with a bit position j and bit value b. Then \(\widehat{\mu } _i\) will be of the form \(\textsf{encode} ^{\mathcal {I} , t}_{\widehat{\beta }} \) defined below, which only retains the part of \({\widehat{\beta }} \) for parts \(i>t\).
Definition 6
(Message function space \(\widehat{\mathcal {M} }\) ). Let \(\varSigma =\{0,1\}^n\), with a partition function \(\mathcal {I} : \varSigma \rightarrow [N]\), and \({\widehat{\beta }} :[N]\times [n]\times \{0,1\}\rightarrow \{0,1\}^\kappa \). A state labeling function \(\textsf{encode} ^{\mathcal {I} ,t}_{{\widehat{\beta }} }:\varSigma \rightarrow \{0,1\}^{n\kappa }\) is defined as
where \(\sigma = (a_1,...,a_n)\). Then, we define \(\widehat{\mathcal {M} } = \bigcup _{\mathcal {I} : \varSigma \rightarrow [N], t \in [N]} \widehat{\mathcal {M} } _{\mathcal {I} ,t}\), where
\(\lhd \)
We are now ready to state our composition theorem.
Theorem 1
Suppose \(\mathcal {G}\) is a \((\mathcal {P}, \mathcal {M} )\)-generator class that is decomposable into \(\boldsymbol{\mathcal {L}} = \{ \mathcal {H} _i, \mathcal {Q} _i, \mathring{\mathcal {P}} _i \}_{i \in [N]}\), such that, for each \(i\in [N]\), \(\mathcal {H} _i\) is a \((\mathcal {P} _i,\widehat{\mathcal {M} } _{\mathcal {I} ,i})\)-generator class and there exists an R3PO scheme \(\mathcal {O} _i\) for \((\mathcal {H} _i, \mathcal {Q} _i,\mathring{\mathcal {P}} _{i})\). Then there exists an R3PO scheme \(\mathcal {O} \) for \((\mathcal {G},\mathcal {Q},\mathring{\mathcal {P}})\) where \(\mathring{\mathcal {P}} = \mathring{\mathcal {P}} _1 \times \cdots \times \mathring{\mathcal {P}} _N\).
The obfuscator \(\mathcal {O} \) used to prove Theorem 1 is shown in Fig. 1. Please refer to the full version for the proof that it is an R3PO scheme.
5 Private Multi-Authority ABE
In this section, we define Private Multi-Authority ABE and show how to instantiate it from any CP-ABE scheme, using R3PO schemes for commitment-opening and signatures together. Section 2.6 gives an overview of the notion and the construction described below.
5.1 Definition for Private Multi-Authority ABE
Let the authorities in the system be \(\mathbb {A} _1, \ldots , \mathbb {A} _\textsf{N} \), s.t. each authority \(\mathbb {A} _i\) publishes its public key \(\textsf{mpk} _i\) after a local non-interactive setup. Each authority \(\mathbb {A} _i\) also has an attribute-granting policy \(\varTheta ^\textsf{gid} _i\) w.r.t. each \(\textsf{gid}\). A sender encrypts a message m with a ciphertext-policy \(\phi \) under the public keys of all the authorities, s.t. a receiver with global identifier \(\textsf{gid}\) and attribute vector \(\bar{\textsf{x}}\) can decrypt it only if it has attribute key for \(\bar{\textsf{x}}\) and each authorities’ attribute-granting policies accepts (that is, \(\forall i \in [N], \varTheta ^\textsf{gid} _i(\bar{\textsf{x}}) = 1\)) and the ciphertext-policy accepts (that is, \(\phi (\bar{\textsf{x}}) = 1\)). To get the attribute key for attribute vector \(\bar{\textsf{x}}\), the receiver sends a key-request \(\textsf{req} _i\) to each authority \(\mathbb {A} _i\), gets back a key-component \(\textsf{sk} _{\textsf{req} _i}\), and combines all the key-components to construct the key \(\textsf{sk} _{\bar{\textsf{x}}}\).
We define security w.r.t. a corruption model where the adversary is allowed to maliciously corrupt the receiver and semi-honestly corrupt any subset of the authorities. If the receiver is honest, we require that any key-request \(\textsf{req}\) reveals nothing about \(\bar{\textsf{x}}\) to the adversary (even if it semi-honestly corrupts all the authorities). If the receiver is corrupt, we require that the adversary is unable to distinguish between encryptions of any \(m_0\) and \(m_1\) w.r.t. a policy \(\phi \), if it did not send a key-request for any \(\bar{\textsf{x}}\) that satisfies \(\phi \) to the honest authorities.
Definition 7
(Private Multi-Authority ABE (p-MA-ABE)). A \({\text {p-MA-ABE}}\) scheme for N authorities, message space \(\textsf{M}\), class \(\mathcal {C}\) of ciphertext-policies and class \(\boldsymbol{\varTheta }\) of attribute-granting policies, both over n-bit attributes, and global identifiers space \(\textsf{GID}\) consists of PPT algorithms as follows:
-
\(\textsf{SetupAuth} (1^\kappa ) \rightarrow (\textsf{mpk},\textsf{msk})\): On input the security parameter \(\kappa \), outputs the master keys for an individual authority.
-
\(\textsf{Encrypt} \left( \{\textsf{mpk} _i\}_{i \in [\textsf{N} ]}, \phi , m\right) \rightarrow \textsf{ct} \): On input the master public keys of all authorities, a policy \(\phi : \{0,1\}^{n} \rightarrow \{0,1\}\) in \(\mathcal {C}\) and a message \(m \in \textsf{M} \), outputs a ciphertext \(\textsf{ct} \).
-
\(\textsf{KeyRequest} \left( \{\textsf{mpk} _i\}_{i \in [\textsf{N} ]}, \textsf{gid}, \bar{\textsf{x}} \right) \rightarrow (\textsf{st}, \{\textsf{req} _i\}_{i \in [\textsf{N} ]})\): On input the master public keys of all authorities, a global identity \(\textsf{gid} \in \textsf{GID} \) and an attribute vector \(\bar{\textsf{x}} \in \{0,1\}^{n}\), outputs a recipient state \(\textsf{st} \) and requests \(\{ \textsf{req} _1,\ldots , \textsf{req} _\textsf{N} \}\).
-
\(\textsf{KeyGen} \left( i, \textsf{msk} _i, \varTheta ^\textsf{gid} _i, \textsf{req} _i, \{\textsf{mpk} _j\}_{j \in [\textsf{N} ]}\right) \rightarrow \textsf{sk} _{\textsf{req} _i}\): On input an authority index \(i \in [\textsf{N} ]\), master secret key \(\textsf{msk} _i\), an attribute-granting policy \(\varTheta ^\textsf{gid} _i\), a request \(\textsf{req} _i\) and the master public keys of all authorities, outputs a key component \(\textsf{sk} _{\textsf{req} _i}\) or \(\bot \).
-
\(\textsf{KeyCombine} \left( \textsf{st}, \{\textsf{sk} _{\textsf{req} _i}\}_{i \in [\textsf{N} ]}\right) \rightarrow \textsf{sk} _{\bar{\textsf{x}}}\): On input a recipient state \(\textsf{st} \) and a set of key components \(\{\textsf{sk} _{\textsf{req} _i}\}_{i \in [\textsf{N} ]}\), outputs a secret key \(\textsf{sk} _{\bar{\textsf{x}}}\).
-
\(\textsf{Decrypt} \left( \textsf{sk} _{\bar{\textsf{x}}}, \textsf{ct} \right) \rightarrow m\): On input a secret key \(\textsf{sk} _{\bar{\textsf{x}}}\) and a ciphertext \(\textsf{ct} \), outputs a message m or \(\bot \).
The following correctness and security properties are required:
-
1.
Correctness: \(\forall \) security parameter \(\kappa \), number of authorities \(\textsf{N} \in \mathbb {N}\), identities \(\textsf{gid} \in \textsf{GID} \), messages \(m \in \textsf{M} \), ciphertext policies \(\phi \in \mathcal {C} \), attribute granting policies \(\{ \varTheta ^\textsf{gid} _i \in \boldsymbol{\varTheta } \}_{i\in [\textsf{N} ]}\), and attribute vectors \(\bar{\textsf{x}} \) s.t \(\phi (\bar{\textsf{x}}) = 1\) and \(\varTheta ^\textsf{gid} _i(\bar{\textsf{x}}) = 1\) for all \(i \in [\textsf{N} ]\), it holds that if:
$$\begin{aligned} \forall i \in [\textsf{N} ], \quad &\,& (\textsf{mpk} _i,\textsf{msk} _i) &\leftarrow \textsf{SetupAuth} (1^\kappa ) \\ \quad &\,& (\textsf{st}, \{ \textsf{req} _i\}_{i \in [\textsf{N} ]}) &\leftarrow \textsf{KeyRequest} (\{\textsf{mpk} _i\}_{i \in [\textsf{N} ]}, \textsf{gid}, \bar{\textsf{x}}) \\ \forall i \in [\textsf{N} ], \quad &\,& \textsf{sk} _{\textsf{req} _i} &\leftarrow \textsf{KeyGen} \left( i, \textsf{msk} _i, \varTheta ^\textsf{gid} _i, \textsf{req} _i, \{\textsf{mpk} _i\}_{i \in [\textsf{N} ]}\right) \\ \quad &\,& \textsf{sk} _{\bar{\textsf{x}}} &\leftarrow \textsf{KeyCombine} \left( \textsf{st}, \{\textsf{sk} _{\textsf{req} _i}\}_{i \in [\textsf{N} ]}\right) \end{aligned}$$then \(\Pr \big [ \textsf{Decrypt} \left( \textsf{sk} _{\bar{\textsf{x}}}, \textsf{Encrypt} (\{\textsf{mpk} _i\}_{i \in [\textsf{N} ]}, \phi , m)\right) = m \big ] = 1\).
-
2.
Security of encryption: For any PPT adversary \(\mathcal {A} = (\mathcal {A} _0, \mathcal {A} _1,\mathcal {A} _2, \mathcal {A} _3)\) with semi-honest corruption of any subset of authorities and malicious corruption of the receiver, there exists a negligible function \(\textsf{negl} (.)\) such that the following holds in the experiment \({\textsc {IND}}_{{\text {mesg}}}^{{\text {p-MA-ABE}}} \) shown in Fig. 2:
$$\begin{aligned} \Pr [{\textsc {IND}}_{{\text {mesg}}}^{{\text {p-MA-ABE}}} (\mathcal {A}) = 0] \le \frac{1}{2} + \textsf{negl} (\lambda ). \end{aligned}$$ -
3.
Receiver Privacy against Semi-honest Adversary: For any PPT adversary \(\mathcal {A} = (\mathcal {A} _0,\mathcal {A} _1)\) that corrupts each authority in a semi-honest way, there exists a negligible function \(\textsf{negl} (.)\) such that the following holds in the experiment \({\textsc {IND}}_{{\text {attr}}}^{{\text {p-MA-ABE}}} \) shown in Fig. 2:
$$\begin{aligned} \Pr [{\textsc {IND}}_{{\text {attr}}}^{{\text {p-MA-ABE}}} (\mathcal {A}) = 0] \le \frac{1}{2} + \textsf{negl} (\lambda ). &\end{aligned}$$
\(\lhd \)
5.2 Construction for Private Multi-Authority ABE
In this section, we give a scheme for \({\text {p-MA-ABE}}\) from the following primitives:
-
a CP-ABE scheme
-
a non-interactive UC secure commitment scheme
-
a puncturable signature scheme
-
an R3PO scheme \(\mathcal {O} _{\text {p-MA-ABE}} \) w.r.t. \((\mathcal {G} _{{\text {p-MA-ABE}}}^{1}, \mathcal {Q} _{\text {p-MA-ABE}})\) and \((\mathcal {G} _{{\text {p-MA-ABE}}}^{2}, \mathcal {Q} _{\text {p-MA-ABE}})\), which we describe in the full version.
Let the number of authorities be \(\textsf{N} \), space of access policies \(\mathcal {C}\) correspond exactly to the policies supported by the underlying single-authority CP-ABE scheme.
Completeness Requirement of Commitment Scheme: We will additionally require that, given a commitment setup \(\mathsf {\textsf{Com}.crs}\), for any c, d s.t. \(\mathsf {\textsf{Com}.Open} (\mathsf {\textsf{Com}.crs}, c,d) = m\), it holds that (m, c, d) lies in the support of the commit algorithm, that is: there exists r s.t. \((c, d) \leftarrow \mathsf {\textsf{Com}.Commit} (\mathsf {\textsf{Com}.crs}, m; r)\). Any commitment scheme can be enhanced to have this property, by modifying it as follows.
We now prove that the protocol in Fig. 3 is in fact a secure \({\text {p-MA-ABE}}\) scheme.
Lemma 1
If there exists a CP-ABE scheme, a non-interactive UC secure commitment scheme, a puncturable signature scheme, and an R3PO scheme \(\mathcal {O} _{\text {p-MA-ABE}} \) w.r.t. \((\mathcal {G} _{{\text {p-MA-ABE}}}^{1}, \mathcal {Q} _{\text {p-MA-ABE}})\)Footnote 9, then there exists a secure \({\text {p-MA-ABE}}\) scheme.
Please refer to the full version for the full details of the proof.
Notes
- 1.
We remark that in a practical situation, this extra round comes at virtually no cost, since anyway a user would first need to establish a secure channel and authenticate itself with the authority before receiving its credentials.
- 2.
Formally, we do not define R3P, but only an R3P Generator, as a program generator (Definition 2) that has a reach extractor.
- 3.
In our constructions of IBE and IBFE, the ciphertext corresponds to an obfuscated program. For full security, the adversary must be allowed to make key queries even after receiving the ciphertext. But, no interaction is allowed between the program generator and the adversary after the program has been generated. Hence, we consider a generator which gives out an appropriately punctured signing key before the interaction finishes.
- 4.
In particular, it captures the standard formulation of MA-ABE, where each authority \(A_i\) “owns” a set of attributes and its key-issuing decision is based on the values of the attributes it owns.
- 5.
As described in the full version, restricting our obfuscations to deterministic message functions is without loss of generality, even if we are interested in randomized message functions.
- 6.
As discussed just before Sect. 2.3, the reach-restriction condition is to enable our composition theorem (which depends on the use of garbled circuits).
- 7.
We assume that the programs \({\pi ^{(\alpha )}}, {\mu ^{(\beta )}}, \mathcal {I} , \mathcal {O} \) are all specified as circuits. Further, \({\pi ^{(\alpha )}} \) and \({\mu ^{(\beta )}} \) are given as circuits for \({\pi ^{(\cdot )}}\) and \({\mu ^{(\cdot )}}\) (resp.), which take \(\alpha \) and \(\beta \) (resp.) as an input.
- 8.
Looking ahead, the role of J below is to simulate the presence of a one-step generator H when the actual execution involves the generator G, and the role of Z is to simulate the presence of G when the actual execution involves H.
- 9.
Which is also an R3PO w.r.t. \((\mathcal {G} _{{\text {p-MA-ABE}}}^{2}, \mathcal {Q} _{\text {p-MA-ABE}})\).
References
Agrawal, S., Goyal, R., Tomida, J.: Multi-party functional encryption. In: Nissim, K., Waters, B. (eds.) TCC 2021. LNCS, vol. 13043, pp. 224–255. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-90453-1_8
Ananth, P., Boneh, D., Garg, S., Sahai, A., Zhandry, M.: Differing-inputs obfuscation and applications. Cryptology ePrint Archive, Report 2013/689 (2013)
Backes, M., Pfitzmann, B., Waidner, M.: A general composition theorem for secure reactive systems. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 336–354. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_19
Barak, B., Bitansky, N., Canetti, R., Kalai, Y.T., Paneth, O., Sahai, A.: Obfuscation for evasive functions. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 26–51. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_2
Barak, B., et al.: On the (Im)possibility of obfuscating programs. J. ACM 59(2) (2012). ISSN: 0004-5411
Benhamouda, F., Lin, H.: k-round multiparty computation from k-round oblivious transfer via garbled interactive circuits. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 500–532. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_17
Bitansky, N., Canetti, R., Kalai, Y.T., Paneth, O.: On virtual grey box obfuscation for general circuits. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 108–125. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_7
Brakerski, Z., Lombardi, A., Segev, G., Vaikuntanathan, V.: Anonymous IBE, leakage resilience and circular security from new assumptions. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10820, pp. 535–564. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_20
Brakerski, Z., Vaikuntanathan, V.: Lattice-based FHE as secure as PKE. In: ITCS 2014, pp. 1–12 (2014)
Campanelli, M., David, B., Khoshakhlagh, H., Konring, A., Nielsen, J.B.: Encryption to the future: a paradigm for sending secret messages to future (anonymous) committees. Cryptology ePrint Archive, Paper 2021/1423 (2021)
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: Proceedings 42nd IEEE Symposium on Foundations of Computer Science, pp. 136–145 (2001)
Canetti, R.: Security and composition of multiparty cryptographic protocols. J. Cryptol. 13(1), 143–202 (2000)
Canetti, R., Cohen, A., Lindell, Y.: A simpler variant of universally composable security for standard multiparty computation. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 3–22. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_1
Canetti, R., Lin, H., Tessaro, S., Vaikuntanathan, V.: Obfuscation of probabilistic circuits and applications. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 468–497. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_19
Chase, M.: Multi-authority attribute based encryption. In: Theory of Cryptography, pp. 515–534 (2007)
Cho, C., Döttling, N., Garg, S., Gupta, D., Miao, P., Polychroniadou, A.: Laconic oblivious transfer and its applications. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10402, pp. 33–65. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_2
Datta, P., Komargodski, I., Waters, B.: Decentralized multi-authority ABE for DNFs from LWE. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021. LNCS, vol. 12696, pp. 177–209. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77870-5_7
Dolev, D., Dwork, C., Naor, M.: Non-malleable cryptography. SIAM J. Comput. 30, 391–437 (2001)
Döttling, N., Garg, S.: From selective IBE to Full IBE and selective HIBE. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 372–408. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_13
Döttling, N., Garg, S.: Identity-based encryption from the Diffie-Hellman assumption. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 537–569. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_18
Dwork, C., Naor, M., Sahai, A.: Concurrent zero-knowledge. J. ACM 51(6), 851–898 (2004)
Galbraith, S.D., Zobernig, L.: Obfuscating finite automata. In: Dunkelman, O., Jacobson, Jr., M.J., O’Flynn, C. (eds.) SAC 2020. LNCS, vol. 12804, pp. 90–114. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-81652-0_4
Garg, S., Hajiabadi, M., Mahmoody, M., Rahimi, A.: Registration-based encryption: removing private-key generator from IBE. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11239, pp. 689–718. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_25
Garg, S., Hajiabadi, M., Mahmoody, M., Rahimi, A., Sekar, S.: Registration-based encryption from standard assumptions. In: Lin, D., Sako, K. (eds.) PKC 2019. LNCS, vol. 11443, pp. 63–93. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17259-6_3
Garg, S., Lu, S., Ostrovsky, R.: Black-Box Garbled RAM. Cryptology ePrint Archive, Report 2015/307 (2015)
Garg, S., Lu, S., Ostrovsky, R., Scafuro, A.: Garbled RAM from one-way functions. In: STOC 2015, pp. 449–458 (2015)
Garg, S., Srinivasan, A.: Two-round multiparty secure computation from minimal assumptions. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 468–499. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_16
Gentry, C., Halevi, S., Lu, S., Ostrovsky, R., Raykova, M., Wichs, D.: Garbled RAM revisited. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 405–422. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_23
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. J. ACM 62(6), 1–33 (2015)
Goyal, V., Pandey, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: Proceedings of the 13th ACM Conference on Computer and Communications Security, CCS 2006, pp. 89–98 (2006)
Hada, S., Tanaka, T.: On the existence of 3-round zero-knowledge protocols. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 408–423. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055744
Dennis Hofheinz and Victor Shoup: GNUC: a new universal composability framework. J. Cryptol. 28(3), 423–508 (2015)
Hohenberger, S., Rothblum, G.N., Shelat, A., Vaikuntanathan, V.: Securely obfuscating re-encryption. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 233–252. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_13
Hohenberger, S., Waters, B.: Attribute-based encryption with fast decryption. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 162–179. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36362-7_11
Ishai, Y., Pandey, O., Sahai, A.: Public-Coin Differing-Inputs Obfuscation and Its Applications. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 668–697. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_26
Jain, A., Lin, H., Sahai, A.: Indistinguishability obfuscation from well-founded assumptions. In: STOC 2021, pp. 60–73 (2021)
Jutla, C.S., Roy, A.: Shorter Quasi-adaptive NIZK proofs for linear subspaces. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 1–20. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42033-7_1
Kim, S.: Multi-authority attribute-based encryption from LWE in the OT model. Cryptology ePrint Archive, Report 2019/280 (2019)
Lewko, A., Okamoto, T., Sahai, A., Takashima, K., Waters, B.: Fully secure functional encryption: attribute-based encryption and (hierarchical) inner product encryption. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 62–91. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_4
Lewko, A., Waters, B.: Decentralizing attribute-based encryption. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 568–588. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_31
Lin, H., Pass, R., Seth, K., Telang, S.: Indistinguishability obfuscation with non-trivial efficiency. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9615, pp. 447–462. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49387-8_17
Lu, S., Ostrovsky, R.: How to garble RAM programs? In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 719–734. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_42
Lynn, B., Prabhakaran, M., Sahai, A.: Positive results and techniques for obfuscation. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 20–39. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_2
Maurer, U.: Constructive cryptography – a new paradigm for security definitions and proofs. In: Mödersheim, S., Palamidessi, C. (eds.) TOSCA 2011. LNCS, vol. 6993, pp. 33–56. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-27375-9_3
Micciancio, D., Tessaro, S.: An equational approach to secure multi-party computation. In: ITCS 2013, pp. 355–372 (2013)
Michalevsky, Y., Joye, M.: Decentralized policy-hiding ABE with receiver privacy. In: Lopez, J., Zhou, J., Soriano, M. (eds.) ESORICS 2018, Part II. LNCS, vol. 11099, pp. 548–567. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-98989-1_27
Prabhakaran, M., Sahai, A.: New notions of security: achieving universal composability without trusted setup. In: STOC 2004, pp. 242–251 (2004)
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_27
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: STOC 2014, pp. 475–484 (2014)
Waters, B., Wee, H., Wu, D.J.: Multi-authority ABE from lattices without random oracles. Cryptology ePrint Archive, Paper 2022/1194 (2022). https://eprint.iacr.org/2022/1194
Wichs, D., Zirdelis, G.: Obfuscating compute-and-compare programs under LWE. In: FOCS, pp. 600–611 (2017)
Wikström, D.: Simplified universal composability framework. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 566–595. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_24
Yao, A.C.-C.: How to generate and exchange secrets. In: 27th Annual Symposium on Foundations of Computer Science (SFCS 1986), pp. 162–167 (1986)
Yun, K., Wang, X., Xue, R.: Identity-based functional encryption for quadratic functions from lattices. In: Naccache, D., et al. (eds.) ICICS 2018. LNCS, vol. 11149, pp. 409–425. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-01950-1_24
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2024 International Association for Cryptologic Research
About this paper
Cite this paper
Bhushan, K., Obbattu, S.L.B., Prabhakaran, M., Raghunath, R. (2024). R3PO: Reach-Restricted Reactive Program Obfuscation and Its Applications. In: Tang, Q., Teague, V. (eds) Public-Key Cryptography – PKC 2024. PKC 2024. Lecture Notes in Computer Science, vol 14603. Springer, Cham. https://doi.org/10.1007/978-3-031-57725-3_3
Download citation
DOI: https://doi.org/10.1007/978-3-031-57725-3_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-57724-6
Online ISBN: 978-3-031-57725-3
eBook Packages: Computer ScienceComputer Science (R0)


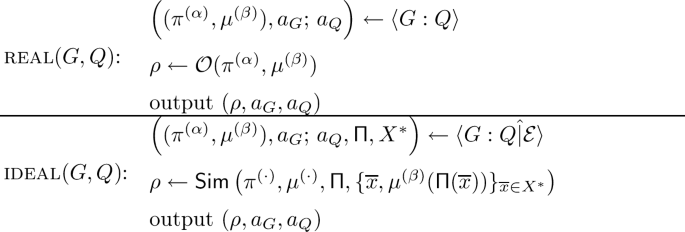
 to denote a composite machine in which Z runs H internally in a blackbox straight-line manner. The reactive program output by the composite generator is produced H, and the auxiliary output produced by it contains outputs from both H and Z. H may communicate with Z, and further the composite machine can communicate externally as described shortly. The running time of
to denote a composite machine in which Z runs H internally in a blackbox straight-line manner. The reactive program output by the composite generator is produced H, and the auxiliary output produced by it contains outputs from both H and Z. H may communicate with Z, and further the composite machine can communicate externally as described shortly. The running time of  is bounded by that of H plus an additive
is bounded by that of H plus an additive  to denote a slightly different composite machine, which is similar to
to denote a slightly different composite machine, which is similar to  (G is run internally by J in a blackbox straight-line manner, and the auxiliary information is produced by both) but the reactive program it produces is output by J. The external communication pattern is also different as described below.
(G is run internally by J in a blackbox straight-line manner, and the auxiliary information is produced by both) but the reactive program it produces is output by J. The external communication pattern is also different as described below. to denote a composite machine in which W internally runs Q in a straight-line manner with additive overhead, but W can read the internal state of Q. The auxiliary output of this composite machine is the entire view of W (which includes the auxiliary information
to denote a composite machine in which W internally runs Q in a straight-line manner with additive overhead, but W can read the internal state of Q. The auxiliary output of this composite machine is the entire view of W (which includes the auxiliary information  and
and  has three external communication channels – one used by the internal machine (shown boxed) and the other two by the wrapper machine. In all machines the “middle” channel is used by the wrapper (J, Z and W, respectively); the “top” channel is used by G, Z and Q (resp.); the “bottom” channel is used by J, H and W (resp.). Note that when
has three external communication channels – one used by the internal machine (shown boxed) and the other two by the wrapper machine. In all machines the “middle” channel is used by the wrapper (J, Z and W, respectively); the “top” channel is used by G, Z and Q (resp.); the “bottom” channel is used by J, H and W (resp.). Note that when  is connected to
is connected to  , Q directly interacts with G, whereas when
, Q directly interacts with G, whereas when  is connected to
is connected to  , Q interacts with Z.
, Q interacts with Z. .
. , let the output of G be
, let the output of G be 


