Abstract
This chapter constitutes the core of the part of the book devoted to spontaneously broken internal symmetries. It develops two methods for construction of effective actions for Nambu–Goldstone bosons. The first method is based on identification of various contributions to the effective Lagrangian with tensor fields on the coset space of broken symmetry. The requirement of invariance of the action is imposed and solved directly using the tools of differential geometry. However, to understand and utilize the final result requires just elementary linear algebra and group theory. The second approach to construction of effective actions introduces a set of background gauge fields, coupled to the Noether currents of the symmetry. This makes it possible to classify invariant actions using elementary field theory, without heavy use of differential geometry. A comparison of the two approaches sheds light on the conditions under which a global symmetry can be gauged. The last section of the chapter revisits the spectrum of Nambu–Goldstone bosons. It is shown, among others, that type-A and type-B Nambu–Goldstone bosons have a distinct geometric interpretation, associated with a presymplectic structure on the coset space.
You have full access to this open access chapter, Download chapter PDF
We are now finally in the position to construct a low-energy effective field theory (EFT) for systems with a spontaneously broken internal symmetry. We do not need any specific model to describe the dynamics of spontaneous symmetry breaking (SSB). All we need is information about the internal symmetry group G and its unbroken subgroup H. These determine the basic degrees of freedom of the EFT: the Nambu–Goldstone (NG) fields. With the known symmetry and field content, one must then include in the effective Lagrangian all operators allowed by the symmetry (Chap. 12 of [1]). This ensures that the predictions of the EFT match, to the desired accuracy, those of any microscopic theory with the same pattern of SSB.
The NG fields can be thought of as (local) coordinates on the coset space \(G/H\). In the previous chapter, I showed that the action of the symmetry on these fields can be assumed to take the “standard form,” cf. Sect. 7.3. The task to construct the most general action invariant under such nonlinear realization of symmetry is nontrivial. In Sects. 8.1 and 8.2, I will offer two different approaches to this problem. The first of these is more general but requires substantial background in differential geometry. The second approach is based on certain simplifying assumptions but has the benefit of only requiring elementary field theory. In the concluding Sect. 8.3, I use the EFT to derive the equation of motion (EoM) for the NG fields. With the help of the latter, I then reanalyze the spectrum of NG bosons.
1 Structure of the Effective Lagrangian
To keep the discussion simple, I will assume unbroken symmetry under continuous spacetime translations and continuous spatial rotations. This is just a matter of practical convenience; the same methodology can be applied, for instance, to systems whose spatial rotation symmetry spans a (possibly finite) subgroup of \(\mathrm {SO}(d)\). I will also assume that the spatial dimension is \(d\geq 2\). On the practical side, this is needed for any continuous rotations to exist. On a more fundamental note, the possibility of SSB in one spatial dimension is severely restricted; see Sect. 15.2.
The action of the low-energy EFT must inherit the symmetries of the underlying microscopic theory. As a rule, the symmetry admits an infinite number of operators in the effective Lagrangian, which require an infinite number of a priori unknown coupling constants. In order that the EFT has any predictive power, we need an organizing principle to tell us which of the allowed operators are “relevant.” Recall that the EFT is expected to be valid at low energies such that the only active degrees of freedom are the NG bosons. The individual operators in the Lagrangian can then be sorted by the number of derivatives they contain. The more derivatives, the smaller effects the operator is expected to produce. Such ordering of operators in the effective Lagrangian is called derivative expansion.
Since spatial and temporal derivatives are not related by any of the assumed symmetries, we must count them separately. The low-energy effective Lagrangian can then be organized as a double series,
where \(s,t\) denote respectively the numbers of spatial and temporal derivatives. Following loosely [2], I will focus in this section on contributions with at most two derivatives, \(s+t\leq 2\). These are needed to pin down the kinetic term for all the NG fields, and thus carry information about the spectrum of NG bosons. At the same time, they encode the dominant interactions of NG bosons at low energies. Operators with a higher number of derivatives are classified more easily using the approach developed in Sect. 8.2.
Within the diagrammatic expansion of quantum field theory, a given observable may receive contributions from graphs with different numbers of loops. The relative importance of various contributions depends on the operators that enter the interaction vertices and the number of loops. I will work out a precise power-counting scheme in Chap. 9, where concrete examples of EFTs are discussed at length. For the time being, I will content myself with the rule of thumb that loops lead to parametric suppression just like derivatives in the interaction vertices. This justifies the approach adopted throughout the whole book, whereby NG bosons are treated in the classical (tree-level) approximation.
The analysis of the structure of the effective Lagrangian (8.1) is considerably simplified using the language of differential geometry. Following the presentation below will therefore require some familiarity with the contents of Appendix A. A reader uninterested in the details will find a summary of the leading part of the effective Lagrangian (that is operators with \(s+t\leq 2\)) in Sect. 8.1.4.
1.1 Reminder of the Standard Nonlinear Realization
I will start with a brief reminder of the standard nonlinear realization of symmetry. The intention is to have the basic elements of the formalism at one place for easy reference. Further details can, if needed, be found in Chap. 7.
Every point on the coset space \(G/H\) is labeled with a representative \(U(\pi )\in G\) of the corresponding coset, where \(\pi ^a\) are local coordinates on \(G/H\) (NG fields). The action of the group G on the coset space can then be defined via left multiplication,

where \(h(\pi ,g)\in H\). The choice of the representative \(U(\pi )\) is not unique, but can be made so that \(U(0)=e\) and that any \(g\in H\) acts on \(U(\pi )\) by conjugation,  . In other words, \(h(\pi ,g)=g\) for any \(g\in H\) independently of \(\pi ^a\).
. In other words, \(h(\pi ,g)=g\) for any \(g\in H\) independently of \(\pi ^a\).
The generators of G are denoted as \(Q_{A,B,\dotsc }\). A subset of these, \(Q_{\alpha ,\beta ,\dotsc }\), spans the Lie algebra \(\mathfrak {h}\) of the unbroken subgroup H. The remaining, broken generators of G are denoted by \(Q_{a,b,\dotsc }\).Footnote 1 The structure of the Lie algebra \(\mathfrak {g}\) is fixed by the structure constants  through
through  . Under the action of a group element infinitesimally close to unity,
. Under the action of a group element infinitesimally close to unity,  , (8.2) reduces to
, (8.2) reduces to
The functions \(\xi ^a_A(\pi )\) define a set of vector fields on \(G/H\), \(\boldsymbol \xi _A(\pi )\equiv \xi ^a_A(\pi )\partial {}/\partial {\pi ^a}\), whose Lie bracket reproduces the structure of \(\mathfrak {g}\),
An object of fundamental importance is the \(\mathfrak {g}\)-valued Maurer–Cartan (MC) form,
This can be split into a part belonging to the subspaces \(\mathfrak {h}\) and \(\mathfrak {g}/\mathfrak {h}\),
The components \(\omega ^A\) of the MC form and the vector fields \(\boldsymbol \xi _A\) are mutually dual in a well-defined sense. Their precise relationship is expressed by the identities
where the matrix function \(\nu ^B_A(\pi )\) is defined by the conjugation
Under G, the unbroken and broken parts of the MC form transform as

In the language of differential geometry, infinitesimal symmetry transformations of tensor fields on \(G/H\) are given by the Lie derivative along the vector fields \(\boldsymbol \xi _A\). Combining (8.3) and (8.9) thus corresponds to
Finally, the exterior derivative of the MC 1-form is expressed by the MC equation \(\mathrm{d} \omega ^A=(1/2)f^A_{BC}\omega ^B\wedge \omega ^C\). In terms of the \(\omega _\parallel \) and \(\omega _\perp \) components of the MC form, this breaks down into
1.2 Lagrangians with Two Spatial or Two Temporal Derivatives
Invariance of the effective action under a symmetry group G requires that the Lagrangian (density) be quasi-invariant, that is invariant up to a surface term. Internal symmetry transformations, covered in this part of the book, do not involve any derivatives of NG fields. This implies that all the different parts  of the effective Lagrangian (8.1) must be quasi-invariant separately. The piece without any derivatives,
of the effective Lagrangian (8.1) must be quasi-invariant separately. The piece without any derivatives,  , must be strictly G-invariant; its variation under G cannot be a derivative of any local operator.Footnote 2 However, requiring
, must be strictly G-invariant; its variation under G cannot be a derivative of any local operator.Footnote 2 However, requiring  leaves a constant, \(\pi ^a\)-independent
leaves a constant, \(\pi ^a\)-independent  as the only option. The derivative expansion of the effective Lagrangian thus starts with operators with at least one derivative. Having a sole spatial derivative is forbidden by rotational invariance, hence
as the only option. The derivative expansion of the effective Lagrangian thus starts with operators with at least one derivative. Having a sole spatial derivative is forbidden by rotational invariance, hence  for any \(t\geq 0\). The only options for \((s,t)\) with \(s+t\leq 2\) that are left are therefore \((0,1)\), \((0,2)\) and \((2,0)\). The Lagrangian
for any \(t\geq 0\). The only options for \((s,t)\) with \(s+t\leq 2\) that are left are therefore \((0,1)\), \((0,2)\) and \((2,0)\). The Lagrangian  with one temporal derivative will be analyzed in Sect. 8.1.3. Here I will focus on
with one temporal derivative will be analyzed in Sect. 8.1.3. Here I will focus on  and
and  , which turn out to be much easier to understand and thus constitute a good starting point.
, which turn out to be much easier to understand and thus constitute a good starting point.
Invariance under spacetime translations and spatial rotations restricts the two-derivative Lagrangians to the generic form
where \(b_{ab}(\pi )\), \(g_{ab}(\pi )\) and \(\bar g_{ab}(\pi )\) are some functions on \(G/H\). Note that the \(b_{ab}\) term can only exist in \(d=2\) spatial dimensions. Also, I have discarded from the outset operators containing a second derivative of \(\pi ^a\), since those can be brought to the form (8.12) by partial integration.
The \(g_{ab}\) and \(\bar g_{ab}\) terms must be strictly G-invariant. Indeed, should an infinitesimal transformation of, say, the \(g_{ab}\) term produce a surface term, it would have to be of the form \(\boldsymbol \nabla \cdot [f_a(\pi )\boldsymbol \nabla \pi ^a]\). But that would inevitably contain a second derivative of \(\pi ^a\) that was not present in the original Lagrangian. This argument does not apply to the \(b_{ab}\) term, which is antisymmetric in spatial derivatives. However, in that case, possible quasi-invariance can be disregarded on physical grounds. Namely, the \(b_{ab}\) term contributes to the canonical Hamiltonian density, and its mere quasi-invariance would imply that the energy density of the EFT is ill-defined. All in all, both  and
and  must be strictly invariant under the symmetry group G.
must be strictly invariant under the symmetry group G.
Let us see what strict G-invariance tells us about the function \(g_{ab}(\pi )\). The latter gives rise to a symmetric rank-2 tensor field on \(G/H\),
We know that the broken components of the MC form, \(\omega ^a(\pi )\), furnish a basis of the cotangent space (coframe) to \(G/H\); see Sect. 7.4 for a detailed justification. In this basis, the tensor \(g(\pi )\) can be expanded as
where the components \(\kappa _{ab}(\pi )\) are some as yet unknown functions on \(G/H\). Using (8.10), we readily calculate the Lie derivative along \(\boldsymbol \xi _A\),
The requirement of strict G-invariance then leads to the following condition on \(\kappa _{ab}\),
It is now convenient to resort to the exponential parameterization,
in which \(\xi ^a_A(\pi )=\delta ^a_A+\mathcal {O}(\pi )\) and \(k^\alpha _A(\pi )=\delta ^\alpha _A+\mathcal {O}(\pi )\), cf. (7.41). By choosing the index A in (8.16) in turn as an unbroken and broken index, we thus get the following initial conditions at the origin of \(G/H\),
For a fixed broken index A, (8.16) can be viewed as an ordinary differential equation that uniquely determines \(\kappa _{ab}(\pi )\) along the integral curve of \(\boldsymbol \xi _A\), passing through the origin of \(G/H\). We conclude that \(\kappa _{ab}\) must be constant, subject to the constraint
This is equivalent to requiring that \(\kappa _{ab}\) is a constant invariant tensor under the adjoint action of the unbroken subgroup H.
The same reasoning applies without change to any G-invariant operator constructed solely out of the broken part of the MC form, \(\omega _\perp \). As a consequence, the most general form consistent with G-invariance that the functions \(b_{ab}(\pi )\), \(g_{ab}(\pi )\) and \(\bar g_{ab}(\pi )\) can take is
The constant matrices \(\lambda _{ab}\), \(\kappa _{ab}\) and \(\bar {\kappa }_{ab}\) are all invariant tensors under the adjoint action of H. In the exponential parameterization (8.17), \(\omega ^a_b(\pi )=\delta ^a_b+\mathcal {O}(\pi )\) and thus \(\lambda _{ab}=b_{ab}(0)\), \(\kappa _{ab}=g_{ab}(0)\) and \(\bar {\kappa }_{ab}=\bar g_{ab}(0)\).
For the kinetic term of the NG fields to have the correct signature, the symmetric matrices \(\kappa _{ab}\) and \(\bar {\kappa }_{ab}\) should be positive-definite. Hence, both \(g(\pi )\) and its cousin \(\bar g(\pi )\) constitute a G-invariant Riemannian metric on \(G/H\). These two metrics are in principle independent from each other. However, in case G is compact and semisimple and all the broken generators \(Q_a\) span a single irreducible multiplet of H, Schur’s lemma requires that \(\kappa _{ab},\bar {\kappa }_{ab}\) be proportional to each other. The metrics \(g(\pi )\) and \(\bar g(\pi )\) then coincide up to an overall factor.
Example 8.1
Suppose that the symmetry group G is completely broken. Then the matrices \(\kappa _{ab}\), \(\bar \kappa _{ab}\), \(\lambda _{ab}\) remain unconstrained by symmetry, the only physical requirement being the positive-definiteness of \(\kappa _{ab}\) and \(\bar {\kappa }_{ab}\). This, however, does not mean that when constructing an EFT for NG bosons on \(G/\{e\}\simeq G\), we have to work with arbitrary matrices of couplings of rank \(\dim G\). The number of independent parameters can be reduced by a judicious choice of coordinates \(\pi ^a\) on G. In the theory of small oscillations of mechanical systems [3], it is known that two quadratic forms, at least one of which is positive-definite, can be simultaneously diagonalized. Thus, we can always assume that, say, \(\kappa _{ab}=\delta _{ab}\) and moreover that \(\bar {\kappa }_{ab}\) is diagonal and positive-definite. We just have to keep in mind that this simplicity is a consequence of a particular choice of coordinates, not of symmetry. This may restrict the otherwise arbitrary choice of parameterization of the coset space.
1.3 Lagrangians with One Temporal Derivative
The part of the effective Lagrangian with one time derivative reads, generically,
The functions \(c_a(\pi )\) define locally a 1-form on \(G/H\), \(c(\pi )\equiv c_a(\pi )\mathrm{d} \pi ^a\). The requirement of quasi-invariance of  under the action of G is then equivalent to
under the action of G is then equivalent to
where \(\bar c_A(\pi )\) is a set of local functions (0-forms) on \(G/H\). Using the fact that the Lie derivative commutes with the exterior derivative, one deduces that \(\mathcal {L}_{\boldsymbol \xi _A}(\mathrm{d} c)=\mathrm{d} (\mathcal {L}_{\boldsymbol \xi _A}c)=\mathrm{d} (\mathrm{d} \bar c_A)=0\). Hence \(\mathrm{d} c(\pi )\) is a strictly G-invariant closed 2-form on \(G/H\). Strict G-invariance requires that
where \(\sigma _{ab}\) is a constant antisymmetric matrix, invariant under the adjoint action of H. This follows by the same argument I used above to derive (8.20).
Not every H-invariant matrix \(\sigma _{ab}\) will do, however, since the 2-form \(\mathrm{d} c(\pi )\) must also be closed. Upon using (8.11), closedness of \(\mathrm{d} c(\pi )\) is seen to be equivalent to
The former of these conditions just reasserts the H-invariance of \(\sigma _{ab}\). The latter constitutes a new constraint that we must now deal with. I will not be able to give a fully general explicit solution to the algebraic conditions on \(\sigma _{ab}\), and thus a general solution for  . We can get very far even without an explicit solution, though. First, note that (8.24) is a set of linear equations for \(\sigma _{ab}\). In a concrete case where the structure constants are known, the space of solutions to (8.24) can therefore be found using elementary linear algebra. Second, we can do even better and link possible solutions for \(\sigma _{ab}\) to the structure of the Lie groups G, H and their Lie algebras \(\mathfrak {g}\), \(\mathfrak {h}\).
. We can get very far even without an explicit solution, though. First, note that (8.24) is a set of linear equations for \(\sigma _{ab}\). In a concrete case where the structure constants are known, the space of solutions to (8.24) can therefore be found using elementary linear algebra. Second, we can do even better and link possible solutions for \(\sigma _{ab}\) to the structure of the Lie groups G, H and their Lie algebras \(\mathfrak {g}\), \(\mathfrak {h}\).
In the parameterization (8.17), \(\mathrm{d} c(\pi )=(1/2)[\sigma _{ab}+\mathcal {O}(\pi )]\mathrm{d} \pi ^a\wedge \mathrm{d} \pi ^b\). Thus, the corresponding Lagrangian can be power-expanded in the NG fields as
Following the argument of Sect. 6.3.2, the matrix \(\sigma _{ab}\) can be related to the set of vacuum expectation values (VEVs) of commutators of broken generators,
There is a possibility that the representation of the symmetry group G on the Hilbert space of our system features a central extension. Let us write the extended commutation relation of symmetry generators as \([Q_A,Q_B]=\mathrm{i} f^C_{AB}Q_C+\mathrm{i} Vz_{AB}\), where \(z_{AB}\) are the densities of the central charges. Then we find that
We conclude that possible solutions for \(\sigma _{ab}\) directly reflect the Lie algebra of symmetry generators, including possible central extensions. One class of solutions to (8.24) that always exists is
The latter constraint expresses, once again, the invariance of the constant tensor \(\sigma _A\) under the adjoint action of H. This solution corresponds to vanishing (VEVs of) central charges, and \(\sigma _A\) can then be interpreted as the density of \(Q_A\) in the ground state. The H-invariance of \(\sigma _A\) descends directly from the H-invariance of the ground state. For this class of solutions, (8.23) is readily integrated using the MC equation (8.11), leading to
up to addition of a closed 1-form (surface term). The variation of  under infinitesimal transformations from G can now be computed with the help of (8.10),
under infinitesimal transformations from G can now be computed with the help of (8.10),
where in the last step I used that \(\sigma _Bf^B_{\alpha C}=0\) by (8.28). The operators proportional to \(\sigma _a\) are strictly G-invariant. Mere quasi-invariance of the Lagrangian thus requires nonzero \(\sigma _\alpha \), that is nonzero VEV of an unbroken charge in the ground state.
Example 8.2
In ferromagnets, \(G/H\simeq \mathrm {SU}(2)/\mathrm {U}(1)\simeq S^2\). Up to an overall factor, there is a unique closed and G-invariant 2-form on \(S^2\), provided by the volume (area) form. In terms of the unit-vector parameterization of the sphere, this is proportional to \(\varepsilon _{ijk}n^i\mathrm{d} n^j\wedge \mathrm{d} n^k\), cf. Example A.7. The solution (8.28) descends from the nonzero magnetization in the ferromagnetic ground state, corresponding to a nonzero VEV of the generator of the unbroken \(\mathrm {U}(1)\) subgroup. I will give an explicit form of the Lagrangian \(\mathcal {L}_{\mathrm {eff}}^{(0,1)}\) for ferromagnets in Sect. 9.2.
In case the symmetry group G is semisimple, its Lie algebra \(\mathfrak {g}\) cannot have any nontrivial central charges (Sect. 2.7 of [1]). Equation (8.29) is then the only possible solution for the 1-form \(c(\pi )\) and the corresponding Lagrangian  . For G that are not semisimple, solutions with nonzero \(z_{ab}\) may exist.
. For G that are not semisimple, solutions with nonzero \(z_{ab}\) may exist.
Example 8.3
Consider the coset space \(G/H\simeq \mathrm {U}(1)\times \mathrm {U}(1)/\{e\}\simeq T^2\). In this case, the symmetry group is Abelian so the conditions (8.24) are trivially satisfied. Up to an overall factor, there is a unique rank-2 antisymmetric tensor, \(\sigma _{ab}=\varepsilon _{ab}\). According to (8.27), this necessarily arises from a central extension of the Lie algebra \(\mathfrak {g}\) of G. In the exponential parameterization (8.17), \(\omega ^a(\pi )=\mathrm{d} \pi ^a\), which leads to \(c(\pi )=(1/2)\varepsilon _{ab}\pi ^a\mathrm{d} \pi ^b\). This is merely quasi-invariant under the action of G as expected. Note that the NG fields \(\pi ^a\) are angular variables on the torus \(T^2\) that are only locally defined, and so is therefore the 1-form \(c(\pi )\). What is well-defined globally on the whole coset space is only the G-invariant 2-form \(\mathrm{d} c(\pi )\).
To conclude the analysis of the Lagrangian  , let us see under what conditions we can expect it to actually shift by a surface term upon a G-transformation. Should
, let us see under what conditions we can expect it to actually shift by a surface term upon a G-transformation. Should  be strictly G-invariant, it would necessarily assume the form
be strictly G-invariant, it would necessarily assume the form
with a constant H-invariant \(\sigma _a\), that is \(f^b_{\alpha a}\sigma _b=0\). This follows by imposing directly the constraint \(\mathcal {L}_{\boldsymbol \xi _A}(\sigma _a\omega ^a)=0\). The corresponding closed 2-form is then
that is, \(\sigma _{ab}=-f^c_{ab}\sigma _c\). Quasi-invariant Lagrangians  are therefore in a one-to-one correspondence with antisymmetric matrices \(\sigma _{ab}\) satisfying (8.24) that cannot be written as \(\sigma _{ab}=-f^c_{ab}\sigma _c\) with some H-invariant tensor \(\sigma _a\). Such antisymmetric matrices span the so-called second Lie algebra cohomology of \(\mathfrak {g}\) relative to the subalgebra \(\mathfrak {h}\). See Sect. 3 of [4] for a mild introduction and further references.
are therefore in a one-to-one correspondence with antisymmetric matrices \(\sigma _{ab}\) satisfying (8.24) that cannot be written as \(\sigma _{ab}=-f^c_{ab}\sigma _c\) with some H-invariant tensor \(\sigma _a\). Such antisymmetric matrices span the so-called second Lie algebra cohomology of \(\mathfrak {g}\) relative to the subalgebra \(\mathfrak {h}\). See Sect. 3 of [4] for a mild introduction and further references.
Example 8.4
In case the symmetry under G is completely spontaneously broken, only the second of the conditions in (8.24) survives. In this case, nontrivial solutions for \(\sigma _{ab}\), that is those that cannot be written as \(\sigma _{ab}=-f^c_{ab}\sigma _c\) with some \(\sigma _c\), are in a one-to-one correspondence with the central charges \(z_{ab}\). Both of these are classified by the second Lie algebra cohomology of \(\mathfrak {g}\).
1.4 Overview of the Lowest-Order Effective Lagrangian
Let me summarize what we have found so far. The basic assumptions I made are that an internal symmetry group G is spontaneously broken to its subgroup H, but the symmetry under continuous spacetime translations and spatial rotations remains intact. Then in \(d\geq 2\) spatial dimensions, the parts of the effective Lagrangian with up to two derivatives of NG fields take the generic form
Here \(\kappa _{ab}\) and \(\bar {\kappa }_{ab}\) are constant symmetric H-invariant matrices,
Likewise, \(\lambda _{ab}\) is a constant antisymmetric matrix invariant under H,
The \(\lambda _{ab}\) term can only exist in \(d=2\) spatial dimensions. In the special case of a Lorentz-invariant system, both  and the \(\lambda _{ab}\) term in
and the \(\lambda _{ab}\) term in  are forbidden. Moreover, \(\kappa _{ab}=\bar {\kappa }_{ab}\) under the convention that the speed of light is set to unity. The entire effective Lagrangian with up to two derivatives then shrinks to a single term,
are forbidden. Moreover, \(\kappa _{ab}=\bar {\kappa }_{ab}\) under the convention that the speed of light is set to unity. The entire effective Lagrangian with up to two derivatives then shrinks to a single term,
Both  and
and  are strictly G-invariant. On the other hand,
are strictly G-invariant. On the other hand,  may be only quasi-invariant. The functions \(c_a(\pi )\) on \(G/H\) are constrained by the requirement that the 2-form \(\mathrm{d} c\equiv \mathrm{d} (c_a\mathrm{d} \pi ^a)=(\partial {c_b}/\partial {\pi ^a})\mathrm{d} \pi ^a\wedge \mathrm{d} \pi ^b\) is closed and G-invariant. This implies
may be only quasi-invariant. The functions \(c_a(\pi )\) on \(G/H\) are constrained by the requirement that the 2-form \(\mathrm{d} c\equiv \mathrm{d} (c_a\mathrm{d} \pi ^a)=(\partial {c_b}/\partial {\pi ^a})\mathrm{d} \pi ^a\wedge \mathrm{d} \pi ^b\) is closed and G-invariant. This implies
where \(\sigma _{ab}\) is a constant antisymmetric matrix subject to the conditions
Those Lagrangians  that are strictly G-invariant assume the form
that are strictly G-invariant assume the form
In this case, \(c_a(\pi )=-\sigma _b\omega ^b_a(\pi )\) and \(\sigma _{ab}=-f^c_{ab}\sigma _c\). In general, the 1-form \(c(\pi )\) is determined by (8.37), hence by \(\sigma _{ab}\), up to addition of a closed 1-form, \(c(\pi )\to c(\pi )+\mathrm{d} \tilde c(\pi )\). Such a shift only changes the Lagrangian by a total time derivative,
and so does not affect the dynamics of the low-energy EFT.
Let me conclude the overview with some remarks on the topological aspects of the effective Lagrangian. First of all, the broken part of the MC form \(\omega _\perp \) is globally well-defined on the coset space \(G/H\). This is because it furnishes a coframe, dual to the frame built out of the vector fields that realize the action of G on \(G/H\). All the parts of the effective Lagrangian (8.33) that are strictly invariant under G are constructed out of products of \(\omega ^a(\pi )\) with constant tensor coefficients. As a consequence, all these parts are themselves globally well-defined on \(G/H\), even though their explicit form may depend on the local coordinates \(\pi ^a\). In particular the \(\kappa _{ab},\bar {\kappa }_{ab}\) terms correspond to G-invariant Riemannian metrics on \(G/H\).
The global existence of  , on the other hand, is not guaranteed by our construction. Problems may arise only if
, on the other hand, is not guaranteed by our construction. Problems may arise only if  is merely quasi-invariant, otherwise the same argument as that for
is merely quasi-invariant, otherwise the same argument as that for  and
and  applies. Quasi-invariant Lagrangians
applies. Quasi-invariant Lagrangians  are classified by the second Lie algebra cohomology of \(\mathfrak {g}\) relative to the subalgebra \(\mathfrak {h}\). Should the group G be compact and connected and the subgroup H closed and connected, this relative Lie algebra cohomology is isomorphic to the second de Rham cohomology of \(G/H\) (Theorem 7.4 in [5]). Cohomologically nontrivial \(\sigma _{ab}\) then ensures that the 2-form \(\mathrm{d} c\) is closed but not exact. As a consequence, the 1-form \(c(\pi )\) cannot be extended from the local coordinate patch to the entire coset space.
are classified by the second Lie algebra cohomology of \(\mathfrak {g}\) relative to the subalgebra \(\mathfrak {h}\). Should the group G be compact and connected and the subgroup H closed and connected, this relative Lie algebra cohomology is isomorphic to the second de Rham cohomology of \(G/H\) (Theorem 7.4 in [5]). Cohomologically nontrivial \(\sigma _{ab}\) then ensures that the 2-form \(\mathrm{d} c\) is closed but not exact. As a consequence, the 1-form \(c(\pi )\) cannot be extended from the local coordinate patch to the entire coset space.
Example 8.5
Let us contrast the coset spaces \(G/H\simeq G/\{e\}\) with respectively \(G\simeq \mathrm {U}(1)\times \mathrm {U}(1)\) and \(G\simeq \mathbb {R}\times \mathbb {R}\). These have identical Lie algebras \(\mathfrak {g},\mathfrak {h}\) that possess a single generator of the second (relative) Lie algebra cohomology, \(\sigma _{ab}=\varepsilon _{ab}\). The single-derivative Lagrangian  is quasi-invariant under G in both cases.
is quasi-invariant under G in both cases.
Now in the first case, \(G/H\simeq \mathrm {U}(1)\times \mathrm {U}(1)\simeq T^2\). The 2-form \(\mathrm{d} c(\pi )\) is proportional to the volume form on the torus, and constitutes the single generator of the second de Rham cohomology of \(T^2\). This agrees with the fact that G is compact and connected and thus the two cohomology groups are necessarily isomorphic. The Lagrangian  is obviously not globally well-defined on \(T^2\) because the fields \(\pi ^a\) are not.
is obviously not globally well-defined on \(T^2\) because the fields \(\pi ^a\) are not.
In the second case, on the other hand, \(G/H\simeq \mathbb {R}^2\). In the Euclidean plane, the Poincaré lemma holds and the second de Rham cohomology is trivial. Accordingly,  is globally well-defined, since \(\pi ^a\) are now nothing but the two Cartesian coordinates in the plane.
is globally well-defined, since \(\pi ^a\) are now nothing but the two Cartesian coordinates in the plane.
A pedant might object that a Lagrangian that is not well-defined everywhere on the coset space renders the whole EFT ill-defined. However, in classical field theory, one is largely interested just in the EoM. The latter only involves the functions \(c_a(\pi )\) through the combinations \(\partial {c_b}/\partial {\pi ^a}-\partial {c_a}/\partial {\pi ^b}\), that is, only depends on \(\mathrm{d} c(\pi )\). Unlike the Lagrangian, the classical EoM is therefore globally well-defined on \(G/H\).
The situation is quite different in quantum theory where we need to be able to perform a functional integral over all field configurations on the coset space. Luckily, we do not really need the Lagrangian \(\mathcal {L}_{\mathrm {eff}}[\pi ]\), or even the action \(S_{\mathrm {eff}}\), to be well-defined. What should be unambiguous is just the phase factor \(\exp (\mathrm{i} S_{\mathrm {eff}})\). To ensure this, one needs to cover the coset space with a set of coordinate patches and define the action by piecewise integration. A detailed analysis is well-beyond the scope of this book. A curious reader will find more details and further references in [6], which puts forward a modern classification of topological terms in the action using a homology-based approach. Here I will just state without proof that consistency and G-invariance require that the so-called Manton condition be satisfied: the 1-forms \({\upiota }_{\boldsymbol \xi _A}(\mathrm{d} c)\) must be exact for all the vector fields \(\boldsymbol \xi _A\) realizing the action of G on \(G/H\). This is a stronger condition than G-invariance of \(\mathrm{d} c\) that I used above, which implies merely that \({\upiota }_{\boldsymbol \xi _A}(\mathrm{d} c)\) is closed. The Manton condition is automatically satisfied by our  whenever the first de Rham cohomology of \(G/H\) is trivial. This is the case for instance when G is compact and simply connected and H is connected; cf. Example A.28.
whenever the first de Rham cohomology of \(G/H\) is trivial. This is the case for instance when G is compact and simply connected and H is connected; cf. Example A.28.
2 Effective Lagrangians from Background Gauge Invariance
I this section I will switch gears and outline another approach to the construction of effective Lagrangians for SSB. This is based on a technical assumption that rules out some of the more exotic theories covered by the method of Sect. 8.1, notably systems with a central extension of the symmetry algebra. The reward for making this sacrifice is a drastic simplification of the classification of possible contributions to the effective action. All we shall need will be elementary field theory with no recourse to differential geometry. The method presented here was pioneered by Leutwyler [7, 8], and I will largely follow the pedagogical account of [9].
The generating functional formalism constitutes an arsenal of important tools in both classical and quantum field theory. In this framework, one couples a given theory to a set of classical external (or background) fields and subsequently integrates, if only formally, over the dynamical degrees of freedom. The physical properties of the theory are encoded in the ensuing generating functional of the background fields. See Chap. 16 of [10] for an introduction to the formalism.
In principle, one has the freedom to choose the background at will. However, in presence of a continuous internal symmetry group G, it is convenient to introduce a set of background gauge fields \(A^A_\mu \), one for each generator \(Q_A\) of G. These can be clustered into a matrix-valued gauge field  . The important technical assumption I am making here is that the symmetry under G is gaugeable. That is, it is possible to add the gauge fields so that the generating functional \(W\{A\}\) of the systemFootnote 3 is invariant under the gauge transformation
. The important technical assumption I am making here is that the symmetry under G is gaugeable. That is, it is possible to add the gauge fields so that the generating functional \(W\{A\}\) of the systemFootnote 3 is invariant under the gauge transformation

Example 8.6
Consider a theory of a set of (not necessarily scalar) fields \(\phi ^i\), whose Lagrangian density \(\mathcal {L}[\phi ]\) is strictly invariant under a linear representation of the symmetry group G,  . Such a Lagrangian can always be made invariant under the simultaneous local transformation of \(\phi ^i\) and (8.41). All one has to do is to replace derivatives of \(\phi ^i\) with gauge-covariant derivatives,
. Such a Lagrangian can always be made invariant under the simultaneous local transformation of \(\phi ^i\) and (8.41). All one has to do is to replace derivatives of \(\phi ^i\) with gauge-covariant derivatives,

In order to assert gauge invariance of the generating functional \(W\{A\}\), one still needs to check that the functional integral measure does not change upon the local transformation of \(\phi ^i\). That would indicate an anomaly. In general, the assumption of gauge invariance of \(W\{A\}\) essentially amounts to the absence of anomalies or other obstructions to gauging.
A linear realization of symmetry is typical for microscopic field theory models. There, one can usually check explicitly that the assumption of gauge invariance of the generating functional is satisfied. The low-energy EFT for the NG bosons should then, when coupled to the same external fields, reproduce the same generating functional. In other words, we expect that the effective action  can be replaced with a “gauged” action
can be replaced with a “gauged” action  such that
such that
Leutwyler [7] showed that gauge invariance of \(W\{A\}\) is sufficient to ensure that the effective action \(S_{\mathrm {eff}}\{\pi ,A\}\) is invariant under the simultaneous local transformations (8.2) and (8.41) of the NG and gauge fields. The locality of (8.2) is implemented by allowing g therein to depend arbitrarily on spacetime coordinates as in (8.41).
It is common to gloss over this detail and simply assume right away that the effective action is G-invariant. I did the same in Sect. 8.1. It is therefore worth stressing that this is a consequence of the properties of the generating functional, established at the microscopic level. The proof is technical and I refer the reader to [7] for details.
We have replaced the problem of classifying possible G-invariant actions \(S_{\mathrm {eff}}\{\pi \}\) with that of constructing locally G-invariant actions \(S_{\mathrm {eff}}\{\pi ,A\}\). How does that make our task easier? In short, a lot. I will now show in a series of simple steps how the problem of finding all possible gauged actions \(S_{\mathrm {eff}}\{\pi ,A\}\) can be reduced to an exercise in group theory. If desired, one can then always discard the background gauge fields and thus recover (most of) the results of Sect. 8.1. But the gauged action in fact carries more information, as it tells us how the EFT responds to certain external perturbations.
2.1 Methodology of Construction of Effective Actions
In the first step, we exploit the gauge invariance to eliminate explicit dependence of the action on the NG fields. Namely, by setting \(g=U(\pi )^{-1}\), we get
By combining (8.2) and (8.41), we find that under the local action of G, the composite field \(T_{U(\pi )^{-1}}A_\mu \) transforms as

This is a special case of a local transformation of \(T_{U(\pi )^{-1}}A_\mu \) from H. Thus, gauged actions \(S_{\mathrm {eff}}\{\pi ,A\}\) locally invariant under G are in a one-to-one correspondence with locally H-invariant functionals of \(T_{U(\pi )^{-1}}A_\mu \).
Let us have a closer look at this composite field. By (8.41),
Up to an overall sign, this is just a gauged version of the MC form (8.5). We can make the analogy explicit by turning the gauge field into a 1-form, \(A\equiv A_\mu \mathrm{d} x^\mu \), and defining the gauged MC form viaFootnote 4
This \(\mathfrak {g}\)-valued 1-form can again be split into unbroken and broken parts, \(\Omega =\Omega _\parallel +\Omega _\perp \). These inherit the transformation rules (8.9) under the local action of G,

The second step is to realize that we can temporarily forget about the origin of \(\Omega _\parallel ,\Omega _\perp \) in terms of the NG fields \(\pi ^a\) and gauge fields \(A^A_\mu \). For the purposes of constructing the effective action, all we need is that \(-\Omega _\parallel \) transforms as a gauge field of H, whereas \(\Omega _\perp \) transforms linearly under the adjoint action of H. Once a locally H-invariant action \(S_{\mathrm {eff}}\{\Omega _\parallel ,\Omega _\perp \}\) has been found, we can reconstruct the dependence on \(\pi ^a,A^A_\mu \) using (8.47). Now define two new vector fields by taking a variation of the action with respect to \(\Omega _\parallel \) and \(\Omega _\perp \),
In spite of the different transformation properties of \(\Omega _\parallel \) and \(\Omega _\perp \), both \(J^\mu _\alpha \) and \(\Sigma ^\mu _a\) transform linearly under the adjoint action of H. This is just an auxiliary statement, and I therefore refer the reader to Appendix C of [9] for a detailed proof. The main message is that to construct such covariantly transforming objects is straightforward, and once we have done so, we can reconstruct the action.
To that end, introduce real scaling parameters \(u,v\). It follows from (8.49) that
Setting without loss of generality \(S_{\mathrm {eff}}\{0,0\}=0\), the full action is then obtained by integration along the path in the \(u\,v\) space, shown in Fig. 8.1,
Equivalently, the effective Lagrangian \(\mathcal {L}_{\mathrm {eff}}[\Omega _\parallel ,\Omega _\perp ]\) can be split into two pieces, \(\mathcal {L}_{\mathrm {eff}}[\Omega _\parallel ,\Omega _\perp ]=\mathcal {L}_{\mathrm {CS}}[\Omega _\parallel ]+\mathcal {L}_{\mathrm {inv}}[\Omega _\parallel ,\Omega _\perp ]\), such that
As a consequence of the linear transformation properties of \(\Omega ^a_\mu \) and \(\Sigma ^\mu _a\), the part \(\mathcal {L}_{\mathrm {inv}}[\Omega _\parallel ,\Omega _\perp ]\) is strictly invariant under the local action of G. Possibly quasi-invariant contributions to the effective Lagrangian reside in the part \(\mathcal {L}_{\mathrm {CS}}[\Omega _\parallel ]\), which only depends on the \(\mathfrak {h}\)-valued gauge field \(-\Omega _\parallel \). I will refer to this part as Chern–Simons (CS) due to its resemblance of the CS theory with gauge group H.
Integration path in the space of parameters \(u,v\) (shown by the oriented solid line), used to reconstruct the effective action from its partial derivatives (8.50)
The strategy to reconstruct the effective Lagrangian is now as follows. The gauge-invariant part of the Lagrangian, \(\mathcal {L}_{\mathrm {inv}}[\Omega _\parallel ,\Omega _\perp ]\), can be built directly out of \(\Omega ^a_\mu \), the field-strength of \(-\Omega ^\alpha _\mu \),  , and their covariant derivatives. This is common lore but if desired, a detailed proof can be found in Appendix D of [9]. In the same way, one can construct possible gauge-covariant “currents” \(J^\mu _\alpha \), except that now the available building blocks are only \(G^\alpha _{\mu \nu }\) and its covariant derivatives. In both cases, products of the covariant building blocks must be contracted with tensor coefficients that ensure invariance under the residual linearly realized symmetries (spatial rotations and the unbroken subgroup H). Finally, the CS part of the Lagrangian is obtained from the current \(J^\mu _\alpha \) by integration over u as indicated in (8.52). Here the quasi-invariance under H must be checked explicitly and may impose further constraints on the tensor couplings.
, and their covariant derivatives. This is common lore but if desired, a detailed proof can be found in Appendix D of [9]. In the same way, one can construct possible gauge-covariant “currents” \(J^\mu _\alpha \), except that now the available building blocks are only \(G^\alpha _{\mu \nu }\) and its covariant derivatives. In both cases, products of the covariant building blocks must be contracted with tensor coefficients that ensure invariance under the residual linearly realized symmetries (spatial rotations and the unbroken subgroup H). Finally, the CS part of the Lagrangian is obtained from the current \(J^\mu _\alpha \) by integration over u as indicated in (8.52). Here the quasi-invariance under H must be checked explicitly and may impose further constraints on the tensor couplings.
Up to any desired order in the derivative expansion, only a finite number of covariant operators can contribute to \(\mathcal {L}_{\mathrm {inv}}[\Omega _\parallel ,\Omega _\perp ]\) or \(J^\mu _\alpha [\Omega _\parallel ]\), and they can be enumerated by inspection. See [9] for a full list up to order four in derivatives. The problem of constructing all gauge-invariant actions then boils down to solving the group-theoretic linear constraints on the tensor couplings of the individual operators. The full dependence on the fields \(\pi ^a,A^A_\mu \) is already completely fixed by the structure of the operators. The practical use of this algorithmic procedure is best illustrated on the sample analysis of effective Lagrangians with up to two derivatives, worked out below.
2.2 Lagrangians Up to Order Two in Derivative Expansion
For the derivative expansion to be consistent, the Lorentz index on \(A^A_\mu \) has to count equally to the derivative \(\partial {}/\partial {x^\mu }\). Each of \(\Omega ^\alpha _\mu ,\Omega ^a_\mu \) is then of order one in (spatial or temporal) derivatives. Up to order two, the invariant Lagrangian \(\mathcal {L}_{\mathrm {inv}}[\Omega _\parallel ,\Omega _\perp ]\) may contain the following contributions,
where \(D_\mu \Omega ^a_\nu \equiv \partial _\mu \Omega ^a_\nu +\mathrm{i} [\Omega _{\parallel \mu },\Omega _{\perp \nu }]^a\). However, a G-invariant Lagrangian density built out of \(D_\mu \Omega ^a_\nu \) alone would be a pure surface term. Similarly, a term of the type  would boil down to
would boil down to  , the rest of
, the rest of  being a surface term. But the combination
being a surface term. But the combination  would necessarily vanish due to the H-invariance condition imposed on the coefficient \(c_\alpha \). Altogether, upon adding the appropriate tensor couplings, the most general gauge-invariant and rotationally invariant Lagrangian up to second order in derivatives is
would necessarily vanish due to the H-invariance condition imposed on the coefficient \(c_\alpha \). Altogether, upon adding the appropriate tensor couplings, the most general gauge-invariant and rotationally invariant Lagrangian up to second order in derivatives is
From (8.48), the coefficients \(\sigma _a,\kappa _{ab},\bar {\kappa }_{ab},\lambda _{ab}\) must be invariant under the adjoint action of H, that is satisfy the constraints
In order to pin down \(\mathcal {L}_{\mathrm {CS}}[\Omega _\parallel ]\) up to second order in derivatives, we need \(J^\mu _\alpha [\Omega _\parallel ]\) up to order one. But the basic building block available, \(G^\alpha _{\mu \nu }\), already has order two. The only possibility left therefore is a constant current, restricted by rotation invariance to \(J^\mu _\alpha [\Omega _\parallel ]=-\delta ^\mu _0\sigma _\alpha \). By (8.52), this leads in turn to
as the sole possibility. Quasi-invariance under H imposes a constraint on \(\sigma _\alpha \),
Note how effortlessly we recovered the effective Lagrangian, obtained in Sect. 8.1 and summarized in (8.33). The only difference is that out of all the possible solutions for the \(c_a(\pi )\) functions, those found here correspond to vanishing VEV of the central charges \(z_{ab}\) in (8.27). This class of solutions is selected by the requirement that the symmetry under G is gaugeable.
However, our newly deduced effective Lagrangian consisting of (8.54) and (8.56) does not just reproduce the previously found results. It also tells us how the NG fields couple to the background gauge fields \(A^A_\mu \). To see how the Lagrangian depends on the latter, we combine the definition (8.47) with (8.7) and (8.8) to write
This makes perfect sense: the vector fields \(\boldsymbol \xi _A\) define infinitesimal group motions on the coset space. As a consequence,
is the correct definition of a derivative of the NG field, covariant under local G-transformations. Altogether, the effective Lagrangian up to second order in derivatives can then be written as
Example 8.7
A chemical potential describing a statistical many-body state of a system can be introduced into its Lagrangian as a constant temporal gauge field (see Chap. 2 of [11]). Replacing  in (8.60) therefore allows us to analyze the effect on the EFT of a set of chemical potentials \(\mu ^A\). In particular, one can thus determine the ground state triggered by the chemical potentials as well as the spectrum of NG modes above it. A detailed discussion can be found in [12], where this setup was used to pin down the spectrum of massive NG bosons, introduced in Sect. 6.4.3.
in (8.60) therefore allows us to analyze the effect on the EFT of a set of chemical potentials \(\mu ^A\). In particular, one can thus determine the ground state triggered by the chemical potentials as well as the spectrum of NG modes above it. A detailed discussion can be found in [12], where this setup was used to pin down the spectrum of massive NG bosons, introduced in Sect. 6.4.3.
In spin systems, the chemical potentials \(\mu ^A\) for the generators of \(G\simeq \mathrm {SU}(2)\) can be interpreted as the components of an external magnetic field \(\boldsymbol B\). This is because the magnetic field couples to the conserved charge of \(\mathrm {SU}(2)\): spin. With the help of Example 7.14, one can easily check that the second term in  in (8.60) is proportional to \(\boldsymbol {B}\cdot \boldsymbol {n}\). This is the Zeeman interaction of spins with the magnetic field. Its normalization is fixed by \(\sigma _A\), hence by the magnetization of the ground state.
in (8.60) is proportional to \(\boldsymbol {B}\cdot \boldsymbol {n}\). This is the Zeeman interaction of spins with the magnetic field. Its normalization is fixed by \(\sigma _A\), hence by the magnetization of the ground state.
2.3 Effects of Explicit Symmetry Breaking
So far in this chapter, I have assumed the symmetry of the EFT to be perfect. There are however good reasons to consider the effects of (presumably small) perturbations breaking the symmetry explicitly. First, I already used this idea in Sect. 5.2 to isolate a unique ground state in presence of SSB. Second, symmetries of real physical systems are almost always just approximate, even if to a high precision.
I will not attempt a general analysis of explicit symmetry breaking in the EFT, but rather focus on a special case that is commonplace and admits a very simple treatment. Suppose that the microscopic Lagrangian of the system contains a contribution \(m_\varrho \mathcal {O}^\varrho \) where \(m_\varrho \) are real constant parameters and \(\mathcal {O}^\varrho \) a set of local operators. Suppose these operators transform under some (real) linear representation \(\mathcal {R}\) of G,

Such a perturbation violates the invariance of the action under G unless \(m_\varrho =0\) for all the components \(\mathcal {O}^\varrho \) that belong to a nontrivial irreducible representation of G.
In order to understand how the effects of the perturbation propagate to the low-energy EFT, it is convenient to promote the parameters \(m_\varrho \) to background fields. The generating functional \(W\{A,m\}\) then remains exactly invariant under the simultaneous local transformation

This translates to the invariance of the gauged effective action \(S_{\mathrm {eff}}\{\pi ,A,m\}\) under a simultaneous transformation of \(\pi ^a,A^A_\mu ,m_\varrho \), generalizing (8.44) to
The action therefore depends on \(\pi ^a\), \(A^A_\mu \) and \(m_\varrho \) only through two composite fields, \(T_{U(\pi )^{-1}}A_\mu \) and  . The field \(\Xi _\varrho (\pi ,m)\) transforms under G through a linear representation of H,
. The field \(\Xi _\varrho (\pi ,m)\) transforms under G through a linear representation of H,

By extension of the argument in Sect. 8.2.1, we can localize \(\Xi _\varrho \) in the strictly invariant part of the Lagrangian. The complete Lagrangian then takes the form
Exactly which operators containing \(\Xi _\varrho \) should be included at a given order of the derivative expansion depends on how we decide to count \(\Xi _\varrho \). It does not contain any derivatives of NG fields but, being proportional to the perturbations \(m_\varrho \), it makes sense to treat it as small. Depending on the concrete system, only a finite number of operators including \(\Xi _\varrho \) is then needed at any fixed order of the derivative expansion. The leading perturbation of the effective Lagrangian is linear in \(\Xi _\varrho \),
The effective coupling \(\eta ^\varrho \) must be H-invariant, which amounts to  for any generator \(Q_\alpha \) of H. A more complete list of operators containing \(\Xi _\varrho \) and contributing to the effective Lagrangian can be found in [9].
for any generator \(Q_\alpha \) of H. A more complete list of operators containing \(\Xi _\varrho \) and contributing to the effective Lagrangian can be found in [9].
Example 8.8
The choice of background fields and their transformation properties is up to us. To illustrate this freedom, note that it is possible to treat the gauge fields \(A^A_\mu \) themselves as linear perturbations. In this case, the operators \(\mathcal {O}^\varrho \) are the Noether currents \(J^\mu _A\) of the symmetry group G. These transform according to the dual of the adjoint representation of G,

where \(\mathcal {R}\) is the adjoint representation itself. The gauge fields \(A^A_\mu \) are now introduced to the microscopic Lagrangian through the linear coupling  . Equation (8.62) assigns them the transformation rule
. Equation (8.62) assigns them the transformation rule  , which amounts to discarding the derivative piece of the background gauge transformation (8.41). Following (8.63) then leads to the composite field
, which amounts to discarding the derivative piece of the background gauge transformation (8.41). Following (8.63) then leads to the composite field

The leading contribution of such a perturbation to the effective Lagrangian is then \(\eta _A\nu ^A_B(\pi )A^B_0\). The coupling \(\eta _A\) must be H-invariant, that is  .
.
We have successfully recovered the structure of the second term in  in (8.60). Note that treating \(A^A_\mu \) as a linear perturbation leaves the effective coupling \(\eta _A\) unfixed. One could in principle apply the same reasoning case by case to other operators in the effective Lagrangian containing \(A^A_\mu \). However, imposing full background gauge invariance is obviously much more efficient, as it fixes the dependence of the EFT on the gauge fields entirely without any free parameters.
in (8.60). Note that treating \(A^A_\mu \) as a linear perturbation leaves the effective coupling \(\eta _A\) unfixed. One could in principle apply the same reasoning case by case to other operators in the effective Lagrangian containing \(A^A_\mu \). However, imposing full background gauge invariance is obviously much more efficient, as it fixes the dependence of the EFT on the gauge fields entirely without any free parameters.
2.4 Coupling to Matter Fields
Throughout the whole book, I mostly assume that the NG bosons are the only low-energy degrees of freedom present in the given system. This is justified in case any other, non-NG modes in the spectrum possess a gap. The validity of the low-energy EFT for NG bosons is then limited to energies well below this gap. However, there are physical systems where strictly gapless non-NG degrees of freedom naturally occur. One generic possibility is that the spectrum includes a Fermi sea of particles such as electrons, protons, neutrons, or quarks. Any local low-energy EFT must then necessarily include such additional gapless degrees of freedom. It is therefore worthwhile to digress and see how such modes fit into the EFT framework developed in this chapter.
The question how non-NG fields (also called matter fields) transform under the nonlinearly realized symmetry was already resolved in Chap. 7. Namely, any set of (not necessarily scalar) matter fields \(\chi ^\varrho \) can without loss of generality be assumed to transform under some linear representation D of the unbroken subgroup H. The action of the whole group G is then given by

alongside (8.2) which defines the matrix \(h(\pi ,g)\in H\).
We are now looking for the most general effective action \(S_{\mathrm {eff}}\{\pi ,A,m,\chi \}\) consistent with the background gauge invariance under G. Our basic trick has been to eliminate explicit dependence on the NG fields by performing a gauge transformation with \(g=U(\pi )^{-1}\). For this transformation, \(h(\pi ,U(\pi )^{-1})=e\), hence the matter fields \(\chi ^\varrho \) remain unaffected. The effective action can therefore be built out of the composite fields \(T_{U(\pi )^{-1}}A_\mu \) and \(\Xi _\varrho (\pi ,m)\), and \(\chi ^\varrho \). The rest is just group theory. Since the matter fields may also enter the Lagrangian with derivatives, it is useful to have at hand their covariant derivative,

The transformation rule (8.69) is not necessarily the only possible choice for the action of G on matter fields. Suppose that the (presumably reducible) representation D of H can be extended to a linear representation of the whole group G on the same set of fields \(\chi ^\varrho \). The redefinition  then gives variables that transform linearly under the whole G,
then gives variables that transform linearly under the whole G,  . Such fields, while superficially natural, however conceal the physical structure of the spectrum. The degenerate energy levels are still organized in multiplets of the unbroken subgroup H. States from different multiplets of H, even if formally belonging to the same multiplet of G, will have different dispersion relations, and different interactions. In the extreme case, it may not even be possible to form complete multiplets of G. The arguably more complicated nonlinear transformation rule (8.69) is then the only option. An explicit example will illustrate this best.
. Such fields, while superficially natural, however conceal the physical structure of the spectrum. The degenerate energy levels are still organized in multiplets of the unbroken subgroup H. States from different multiplets of H, even if formally belonging to the same multiplet of G, will have different dispersion relations, and different interactions. In the extreme case, it may not even be possible to form complete multiplets of G. The arguably more complicated nonlinear transformation rule (8.69) is then the only option. An explicit example will illustrate this best.
Example 8.9
Most natural ferromagnets are metals, which betrays the presence of gapless, conducting electrons. While their appearance in spin doublets would seem natural, this is no longer mandatory once the \(G\simeq \mathrm {SU}(2)\) spin symmetry is spontaneously broken down to \(H\simeq \mathrm {U}(1)\). Let us denote the two possible polarizations of the electron as up (\(\uparrow \)) and down (\(\downarrow \)). Each of these carries a one-dimensional complex representation of H. The action of the full spin group G is then defined in accord with (8.69),

In the effective Lagrangian, Schrödinger-type terms for the up and down electrons can be added independently from each other,
Here \(m_\sigma \) and \(\mu _\sigma \) are the effective mass and chemical potential of \(\chi _\sigma \), and the ellipsis denotes other possible operators, compatible with all the assumed symmetries. The covariant derivatives induce coupling between the electrons and the magnon (spin wave) degrees of freedom. There is nothing that prevents us from setting one of \(c_\uparrow \), \(c_\downarrow \) to zero: we do not need both spin polarizations to preserve the invariance under \(\mathrm {SU}(2)\). Physically, this amounts to the possibility of magnons interacting with a fully polarized Fermi sea of electrons or other spin-\(1/2\) fermions such as neutrons.
Another important application of the formalism for coupling matter fields to NG bosons is the description of interactions between baryons and pseudoscalar mesons. The latter are pseudo-NG bosons a of spontaneously broken symmetry of quantum chromodynamics. Baryons play the role of matter fields that are much heavier than the NG modes, but may nevertheless be added to the low-energy EFT if desired. An interested reader will find more details in Chap. 4 of [13].
3 Equation of Motion
For many applications, it is useful to have at hand the EoM for the NG bosons. This is of obvious value in classical physics, it is however also very useful in quantum field theory. First, the linearized EoM can be used to identify the spectrum of excitations above the ground state and their perturbative propagators. Second, within a derivative expansion of the EFT, knowing the leading-order EoM helps to eliminate redundancies in the effective Lagrangian at higher orders.
Let us return to the general effective Lagrangian (8.33) without background gauge fields, this time augmented with the perturbation (8.66). Deriving the EoM from the effective action amounts in principle to a mere variation with respect to the NG field \(\pi ^a\). However, the complicated dependence of the Lagrangian on \(\pi ^a\) makes this a rather odious task. I will therefore make a rare exception and leave out all details, simply displaying the final result. A reader wishing to verify it should be prepared to a repeated use of the MC equation (8.11) and of the algebraic constraints on all the effective couplings.
I will use the shorthand notation \(\omega ^A_\mu (\pi )\equiv \omega ^A_a(\pi )\partial _\mu \pi ^a\). Also, I will need the covariant derivative of the broken part of the MC form,
With these preparations, the EoM descending from the lowest-order effective Lagrangian (8.33) can be written as

This does not appear particularly elegant, but it is not that bad. In concrete applications, one or more of the terms in (8.74) are often missing. The last term obviously vanishes in the limit of exact symmetry. The term proportional to \(\varepsilon ^{rs}\) is absent in \(d\neq 2\) spatial dimensions. Moreover, all the terms containing a structure constant with three broken indices, \(f^c_{ab}\) or similar, drop for symmetric coset spaces (see Sect. 7.3.2). One last special case, in which the form of (8.74) drastically simplifies, deserves spelling out explicitly.
Example 8.10
Consider the class of EFTs for Lorentz-invariant systems. This amounts to setting \(\bar {\kappa }_{ab}=\kappa _{ab}\) as well as to dropping the single-time-derivative term and the purely spatial two-dimensional term proportional to \(\varepsilon ^{rs}\),

Under the additional assumption that the coset space \(G/H\) is symmetric, which is the case for many relevant physical systems, the EoM takes the extremely compact form  . This is essentially a nonlinear generalization of the Klein–Gordon equation to symmetric coset spaces.
. This is essentially a nonlinear generalization of the Klein–Gordon equation to symmetric coset spaces.
A couple of remarks on the main result (8.74) are due. First, the last term proportional to \(m_\varrho \) looks like it might contribute a nonzero constant in the limit \(\pi ^a\to 0\). That would indicate an instability of the origin of the coset space under the symmetry-breaking perturbation. This is hardly surprising; in presence of the perturbation, we can no longer expect all the points of the coset space to correspond to physically equivalent vacua. In order to ensure that \(\pi ^a=0\) is at least a stationary point of the potential induced by the perturbation, one has to demand that such a constant term in (8.74) is absent. That amounts to the condition

Second, the contribution of the two-dimensional term proportional to \(\varepsilon ^{rs}\) vanishes if \(f^d_{ab}\lambda _{cd}+f^d_{bc}\lambda _{ad}+f^d_{ca}\lambda _{bd}=0\). This implies by means of (8.24) that the 2-form  is closed, hence contributes a mere surface term to
is closed, hence contributes a mere surface term to  . This makes sense, since surface terms do not affect the EoM.
. This makes sense, since surface terms do not affect the EoM.
What if we want to know how the EoM depends on the external gauge fields \(A^A_\mu \)? It might appear we could obtain a gauge-invariant EoM by replacing everywhere in (8.74) \(\omega ^a_\mu \) and \(\omega ^\alpha _\mu \) with their gauged counterparts \(\Omega ^a_\mu ,\Omega ^\alpha _\mu \). Yet, there are subtleties hidden in this naive guess. First, we know from Sects. 8.1 and 8.2 that there are admissible values of \(\sigma _{ab}\) for which the symmetry under G cannot be gauged. The catch is that not every modification of (8.74) renders it a well-defined variational equation. That is, it may not be possible to construct a Lagrangian bottom-up from the gauged EoM. It is not difficult to show that consistency of the gauged EoM and background gauge invariance of the corresponding action require that \(\sigma _{ab}\) satisfies the constraints (8.28).
Second, it is not obvious that even when the symmetry under G can be gauged, the minimal replacement of \(\omega ^a_\mu \) and \(\omega ^\alpha _\mu \) with \(\Omega ^a_\mu \) and \(\Omega ^\alpha _\mu \) gives the correct gauged EoM. Repeating the derivation of the EoM but this time starting with the gauged Lagrangian (8.60), one finds instead of (8.74) the following,

Here \(F_{\mu \nu }\equiv \partial _\mu A_\nu -\partial _\nu A_\mu -\mathrm{i} [A_\mu ,A_\nu ]\) is the field-strength tensor of \(A_\mu \). The slight modification of the first term agrees with the fact that the symmetry under G can only be gauged if \(\sigma _{ab}=-f^C_{ab}\sigma _C\). Most importantly, however, there is an extra term that could not have been guessed by the naive gauging of (8.74). This has interesting consequences. Even when the 2-form  is closed, thus contributing a mere surface term, gauging it leads to a nontrivial modification of the Lagrangian as well as the EoM.
is closed, thus contributing a mere surface term, gauging it leads to a nontrivial modification of the Lagrangian as well as the EoM.
3.1 Spectrum of Nambu–Goldstone Bosons Revisited
It is common to analyze the excitation spectrum by expanding the Lagrangian to second order in fluctuations around the ground state. Here I will take an alternative route to illustrate the utility of the EoM. Namely, I will linearize (8.74), that is expand it to first order in the NG fields \(\pi ^a\). For the sake of simplicity, I will discard all external fields including the perturbations \(m_\varrho \). By invoking the exponential parameterization (8.17) in which \(\omega ^a_b(0)=\delta ^a_b\), we get at once
The \(\approx \) symbol reminds us of the linearization done. This has plane-wave solutions
where the amplitude \(\hat \pi ^a\), energy E and momentum \(\boldsymbol p\) satisfy
We would now like to understand how the dispersion relations of the various NG modes are related to the matrices \(\kappa _{ab}\), \(\bar {\kappa }_{ab}\) and \(\sigma _{ab}\). From Sect. 6.3.2, we expect to find type-A and type-B NG bosons. I even declared therein that the dispersion of type-A NG modes is linear in momentum, whereas that of type-B NG modes is quadratic. We are now in the position to justify this claim. First, one can always change the basis of the variables \(\hat \pi ^a\) so that \(\kappa _{ab}=\delta _{ab}\). Moreover, \(\sigma _{ab}\) can be brought by an additional orthogonal transformation to a block-diagonal form,

The upper-left block \(\Sigma \) corresponds to the type-B sector; these are the fields that enter the bilinear part of  . The lower-right block will analogously correspond to the type-A sector. The numbers of the different types of modes agree with our previous counting rule (6.24).
. The lower-right block will analogously correspond to the type-A sector. The numbers of the different types of modes agree with our previous counting rule (6.24).
One last simplification we can make is to diagonalize the lower-right part of \(\bar {\kappa }_{ab}\) by yet another orthogonal transformation without spoiling the already reduced forms of \(\kappa _{ab}\) and \(\sigma _{ab}\). Thus, \(\bar {\kappa }_{ab}\) can be assumed to take the generic form

where A is symmetric and \(\Delta \) is positive-definite and diagonal. Altogether, the spectrum of NG bosons is obtained by imposing the condition that the determinant of the matrix of coefficients in (8.80) vanishes,

The exact solution \(E(\boldsymbol p)\) for the dispersion relation of the various modes will be very complicated. However, the asymptotic behavior of the dispersion in the limit of low momentum is easy to extract from (8.83). Namely, in this limit, the contribution of the off-diagonal blocks can be neglected, as can be the \(E^2A\) term in the upper-left block. The asymptotic dispersions in the type-A and type-B sectors therefore descend from the already diagonalized matrix equations
The presence of both first and second time derivatives in the type-B sector indicates that (8.83) has solutions \(E(\boldsymbol p)\) with nonzero limit as \(\boldsymbol p\to \mathbf 0\). Taken at face value, the linearized EoM (8.78) thus predicts the existence of gapped modes, accompanying type-B NG states. The required balance of operators with one and two time derivatives may however violate the derivative expansion of the EFT. In general, the presence of such gapped partners of type-B NG bosons cannot be asserted from the symmetry-breaking pattern alone.
3.2 More on the Geometry of the Coset Space
We had a first look at homogeneous spaces from the point of view of differential geometry in Sect. 7.4. I showed that any coset space \(G/H\) possesses a collection of G-invariant (pseudo-)Riemannian metrics. In this chapter, we found a use for them: two such metrics, \(g(\pi )\) and \(\bar g(\pi )\), enter the part of the effective Lagrangian for NG bosons with two derivatives. In Sect. 7.4, I also introduced a class of affine connections on coset spaces. I have not made use of the ensuing curvature and torsion so far. However, we will see in Chap. 10 that these appear naturally in scattering amplitudes of NG bosons.
What I want to briefly discuss now is yet another geometric structure on homogeneous spaces that is intimately connected to the spectrum of NG bosons. The reader might, if needed, want to recall the contents of Sect. 4.3.1 before proceeding. The exposition below follows [2], to which the reader is referred for a much more thorough discussion of geometric and topological aspects of type-B NG bosons.
Suppose that the spectrum of NG bosons were purely type-B as in ferromagnets. The matrix \(\sigma _{ab}\) must then be nonsingular. The same applies to the 2-form \(\mathrm{d} c(\pi )\) that defines the part of the effective Lagrangian with one time derivative,  . Being simultaneously closed, this 2-form therefore establishes a symplectic structure on the coset space. The 1-form \(c(\pi )\) is the corresponding symplectic potential. The NG fields that block-diagonalize the bilinear part of
. Being simultaneously closed, this 2-form therefore establishes a symplectic structure on the coset space. The 1-form \(c(\pi )\) is the corresponding symplectic potential. The NG fields that block-diagonalize the bilinear part of  as in (6.23) constitute a set of (local) Darboux coordinates. The existence of a symplectic structure on \(G/H\) underlines that it should be treated as the phase space of the EFT. The EoM is of first order in time derivatives. The number of independent modes in the spectrum equals \((1/2)\dim G/H\).
as in (6.23) constitute a set of (local) Darboux coordinates. The existence of a symplectic structure on \(G/H\) underlines that it should be treated as the phase space of the EFT. The EoM is of first order in time derivatives. The number of independent modes in the spectrum equals \((1/2)\dim G/H\).
What if the spectrum includes both type-A and type-B NG bosons? Then the 2-form \(\mathrm{d} c(\pi )\) becomes singular, yet it still defines a new structure on \(G/H\), called presymplectic. Intuitively, the coset space becomes partially a phase space and partially a configuration space. The paired NG fields giving rise to type-B NG bosons are “phase space coordinates.” These are augmented with additional “configuration space coordinates,” corresponding to the type-A NG fields. The dynamics of the former and the latter is respectively of first and second order in time.
Let us try to be a bit more precise while remaining physically intuitive. Suppose that the commutator matrix (8.26) were the sole order parameter our system possesses. This would break the symmetry group G to some subgroup K. Suppose also that G is compact and that its Lie algebra \(\mathfrak {g}\) does not have any nontrivial central charges (for instance because G is semisimple). According to the discussion in Sect. 6.3.2, our order parameter then corresponds to the VEVs of a set of conserved charges that belong to a Cartan subalgebra of \(\mathfrak {g}\). These charges together generate an Abelian subgroup \(T\subset G\), usually called a torus. In group theory terminology, the subgroup \(K=\{g\in G\,|\,gh=hg\ \forall h\in T\}\) is the centralizer of the torus T in G.
The NG modes owing their existence to the order parameter \(\sigma _{ab}\) should be described by an EFT that lives on the coset space \(G/K\). A coset space \(G/K\) where K is the centralizer of a torus in G is called a flag manifold; see Chap. 7 of [14] for an introduction. Flag manifolds are known to carry a natural symplectic structure, corresponding to (8.23) with our order parameter \(\sigma _{ab}\). In physics terms, the spectrum of the EFT on \(G/K\) contains by construction only type-B NG modes. Their number is \((1/2)\dim G/K\).
Example 8.11
Consider \(G\simeq \mathrm {U}(n)\) and the torus T generated by the diagonal matrices

where \(\lambda _{1,2}\in \mathbb {R}\). The centralizer of this torus in G consists of all block-diagonal unitary matrices, \(K\simeq \mathrm {U}(m)\times \mathrm {U}(n-m)\). The flag manifold \(\mathrm {U}(n)/[\mathrm {U}(m)\times \mathrm {U}(n-m)]\) is called the (complex) Grassmannian. The special case of \(m=1\) is the complex projective space, \(\mathbb {C} P^n\simeq \mathrm {U}(n+1)/[\mathrm {U}(n)\times \mathrm {U}(1)]\).
How do we add the type-A NG bosons then? In presence of additional order parameters, the symmetry will be broken further down from K to H. This will lead to additional \(\dim K/H\) modes, which we can identify with the type-A NG bosons. All this of course does not mean that we will have two different EFTs, one living on \(K/H\) for the type-A NG bosons, and the other living on \(G/K\) for the type-B NG bosons. The two coset spaces are geometrically integrated into \(G/H\) through a fiber bundle structure,Footnote 5 . Ignoring the type-A NG degrees of freedom amounts to the projection \(\pi :G/H\to G/K\) from the total space\(G/H\) to the base space\(G/K\). The type-A NG fields span the fiber\(K/H\) above each point of the base space. The presymplectic structure on \(G/H\) is obtained by pulling back the symplectic 2-form on the base space \(G/K\) via the projection map \(\pi \).
. Ignoring the type-A NG degrees of freedom amounts to the projection \(\pi :G/H\to G/K\) from the total space\(G/H\) to the base space\(G/K\). The type-A NG fields span the fiber\(K/H\) above each point of the base space. The presymplectic structure on \(G/H\) is obtained by pulling back the symplectic 2-form on the base space \(G/K\) via the projection map \(\pi \).
Example 8.12
Consider a theory with a \(G\simeq \mathrm {U}(n)\) symmetry. Suppose that the symmetry is broken down to \(H\simeq \mathrm {U}(n-1)\) by the expectation value of a complex scalar field \(\Phi \) that transforms in the fundamental representation of G. Since the action of G preserves the norm of \(\Phi \), the coset space \(\mathrm {U}(n)/\mathrm {U}(n-1)\) is obviously equivalent to \(S^{2n-1}\). For convenience, we can choose the order parameter as \(\langle {\Phi }\rangle =(1,0,\dotsc ,0)^T\). The Lie algebra \(\mathfrak {g}\) of G includes two linearly independent singlets of H, \(Q_1\equiv \mathbb {1}\) and \(Q_2\equiv \operatorname {\mathrm {diag}}(-n+1,1,\dotsc ,1)\). Their linear combination, \(Q_\parallel \equiv [Q_2+(n-1)Q_1]/n= \operatorname {\mathrm {diag}}(0,1,\dotsc ,1)\), generates the sole \(\mathrm {U}(1)\) factor of H. The generator \(Q_1\) is a singlet of the whole group G and its VEV therefore does not break the symmetry. On the other hand, the VEV of \(Q_2\) constitutes a candidate order parameter responsible for type-B NG bosons in the spectrum. See the closely related Example 6.6.
If \(\langle {Q_2}\rangle =0\), or \(\langle {Q_\parallel }\rangle =(n-1)/n\langle {Q_1}\rangle \), we have no order parameter, hence \(K\simeq G\). In this case, the coset space \(G/H\) is pure type-A; there are \(2n-1\) type-A NG modes. If, however, \(\langle {Q_2}\rangle \neq 0\), there are \(n-1\) type-B NG modes that parameterize the coset space \(G/K\simeq \mathrm {U}(n)/[\mathrm {U}(1)\times \mathrm {U}(n-1)]\simeq \mathbb {C} P^{n-1}\). Above each point of this base space, there is a fiber \(K/H\simeq \mathrm {U}(1)\), carrying one type-A NG degree of freedom.
Notes
- 1.
The basis \(Q_{a,b,\dotsc }\) is to be chosen so that it spans a subspace \(\mathfrak {g}/\mathfrak {h}\) of the Lie algebra \(\mathfrak {g}\) of G carrying a representation of H, hence \(\mathfrak {g}\simeq \mathfrak {h}\oplus \mathfrak {g}/\mathfrak {h}\).
- 2.
It is in principle possible that the variation of
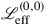 under G is a field-independent constant. This can however only happen if
under G is a field-independent constant. This can however only happen if 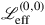 is a tadpole operator, linear in \(\pi ^a\). Such operators must be discarded for the EFT to be perturbatively well-defined.
is a tadpole operator, linear in \(\pi ^a\). Such operators must be discarded for the EFT to be perturbatively well-defined. - 3.
- 4.
This is a slight abuse of notation. The gauge field A is a 1-form on the spacetime. In order for \(\Omega (\pi ,A)\) to be a well-defined 1-form on the spacetime as well, the MC form \(\omega (\pi )\) has to be pulled back by the map \(\pi ^a:x\to \pi ^a(x)\).
- 5.
Since this is the only place in the book where the concept of a fiber bundle appears, I have decided not to include a detailed explanation in Appendix A. I hope that even a reader without the necessary mathematical background can extract some useful information from the discussion.
References
S. Weinberg, The Quantum Theory of Fields, vol. I (Cambridge University Press, Cambridge, 1995). https://doi.org/10.1017/CBO9781139644167
H. Watanabe, H. Murayama, Phys. Rev. X4, 031057 (2014). https://doi.org/10.1103/PhysRevX.4.031057
H. Goldstein, C.P. Poole, J.L. Safko, Classical Mechanics (Pearson Education Limited, Harlow, 2013)
G. Goon, K. Hinterbichler, A. Joyce, M. Trodden, J. High Energy Phys. 06, 004 (2012). https://doi.org/10.1007/JHEP06(2012)004
J.A. de Azcárraga, J.M. Izquierdo, J.C. Pérez Bueno, Rev. R. Acad. Cien. Exactas Fis. Nat. Ser. A Mat. 95, 225 (2001)
J. Davighi, B. Gripaios, J. High Energy Phys. 09, 155 (2018). https://doi.org/10.1007/JHEP09(2018)155
H. Leutwyler, Ann. Phys. 235, 165 (1994). https://doi.org/10.1006/aphy.1994.1094
H. Leutwyler, Phys. Rev. D49, 3033 (1994). https://doi.org/10.1103/PhysRevD.49.3033
J.O. Andersen, T. Brauner, C.P. Hofmann, A. Vuorinen, J. High Energy Phys. 08, 088 (2014). https://doi.org/10.1007/JHEP08(2014)088
S. Weinberg, The Quantum Theory of Fields, vol. II (Cambridge University Press, Cambridge, 1996). https://doi.org/10.1017/CBO9781139644174
J.I. Kapusta, C. Gale, Finite-Temperature Field Theory: Principles and Applications (Cambridge University Press, Cambridge, 2006). https://doi.org/10.1017/CBO9780511535130
H. Watanabe, T. Brauner, H. Murayama, Phys. Rev. Lett. 111, 021601 (2013). https://doi.org/10.1103/PhysRevLett.111.021601
S. Scherer, M.R. Schindler, A Primer for Chiral Perturbation Theory. Lecture Notes in Physics, vol. 830 (Springer, Berlin, 2012). https://doi.org/10.1007/978-3-642-19254-8
A. Arvanitoyeorgos, An Introduction to Lie Groups and the Geometry of Homogeneous Spaces. Student Mathematical Library, vol. 22 (American Mathematical Society, Providence, 2003)
Author information
Authors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution-NonCommercial 4.0 International License (http://creativecommons.org/licenses/by-nc/4.0/), which permits any noncommercial use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this chapter
Cite this chapter
Brauner, T. (2024). Low-Energy Effective Field Theory. In: Effective Field Theory for Spontaneously Broken Symmetry. Lecture Notes in Physics, vol 1023. Springer, Cham. https://doi.org/10.1007/978-3-031-48378-3_8
Download citation
DOI: https://doi.org/10.1007/978-3-031-48378-3_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-48377-6
Online ISBN: 978-3-031-48378-3
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)



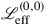 under G is a field-independent constant. This can however only happen if
under G is a field-independent constant. This can however only happen if 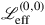 is a tadpole operator, linear in
is a tadpole operator, linear in