Abstract
The first obstacle to the application of the effective field theory program to spacetime symmetries is the identification of independent fluctuations of the order parameter. The redundancy among fluctuations induced by different broken symmetry generators often arises from the equivalence of the corresponding local symmetry transformations. This is explored in the present chapter. First, it is shown that symmetries that are locally equivalent give rise to closely related Noether currents. This explains how the Ward identities for the correlation functions of Noether currents can be saturated with a lower number of Nambu–Goldstone bosons than naively expected. The redundancy of different coordinate-dependent symmetries is then addressed from the point of view of background gauge invariance. The last part of the chapter returns to scattering of Nambu–Goldstone bosons. It shows how the presence of redundant symmetries may lead to the enhancement of scattering amplitudes in the soft limit.
You have full access to this open access chapter, Download chapter PDF
Our discussion of effective field theory (EFT) for Nambu–Goldstone (NG) bosons has so far been limited to internal symmetries. The application of the EFT program to symmetries that depend on or affect spacetime coordinates is associated with numerous subtleties. The first of these lies in the identification of the degrees of freedom of the low-energy EFT. We saw already in Chap. 6 that the fluctuations of the order parameter induced by independent broken symmetry generators may be related to each other. Very often, this is a consequence of a redundancy between the localized actions of different symmetry transformations. This chapter explores such local equivalence of coordinate-dependent symmetries as a preparation for the more detailed discussion of broken spacetime symmetries in the following chapters.
The first two sections follow the pedagogical exposition in [1]. In Sect. 11.1, I show that local equivalence of symmetries leads to a linear relation between the corresponding Noether currents. This lifts the intuitive classical picture of redundancy among NG modes, outlined in Chap. 6, to the language of quantum field theory. In Sect. 11.2, I then reinterpret the local equivalence of symmetries in terms of their simultaneous gauging. The whole Sect. 11.3 is reserved for several physically relevant examples, illustrating the general theory of locally equivalent symmetries. Finally, in Sect. 11.4, I return to scattering of NG bosons of internal symmetries. I show how the relations between Noether currents derived in this chapter help explain the enhancement of the soft limit of scattering amplitudes in the Dirac–Born–Infeld (DBI) and Galileon theories.
1 Relations Between Noether Currents
Consider a theory of a set of (not necessarily scalar) fields \(\psi ^i\), and suppose that its action is invariant under two different classes of continuous symmetries. As we know from Chap. 4, the associated Noether currents can be extracted by evaluating the variation of the action under the corresponding localized transformations. The evolutionary form of these transformations can be written generally as
As before, the square bracket notation indicates local functions of the fields and their derivatives, possibly also depending explicitly on the spacetime coordinates. Furthermore, \(\epsilon ^A_1(x)\) and \(\epsilon ^{\mathfrak {A}}_2(x)\) are the localized parameters of the transformations. The presence of derivatives of the parameters in (11.1) hints that I allow for a generic localization of the transformations; the ellipses represent terms with higher derivatives of  and
and  . The original symmetries are recovered by reducing the coordinate-dependent parameters to constants,
. The original symmetries are recovered by reducing the coordinate-dependent parameters to constants,  and
and  . I will call the two symmetries locally equivalent if there is a set of smooth functions
. I will call the two symmetries locally equivalent if there is a set of smooth functions  such that setting
such that setting
makes the two transformations in (11.1) identical, \(\updelta _1\psi ^i(x)=\updelta _2\psi ^i(x)\).
Locally equivalent symmetry transformations should give the same variation of the action as expressed in terms of the corresponding Noether currents,
However, the latter expression does not automatically vanish for constant \(\epsilon ^{\mathfrak {A}}_2\) as it should. In order to ensure this, we have to impose the integrability condition
where  is some local vector function of the fields and their derivatives. Combining (11.4) with (11.3) and integrating by parts in the latter then leads to the Noether current equivalence relation
is some local vector function of the fields and their derivatives. Combining (11.4) with (11.3) and integrating by parts in the latter then leads to the Noether current equivalence relation
This is the main result of the chapter that deserves a few comments. First, an alternative approach to local equivalence is to start with constant  , that is the actual symmetry with generators \(Q_{2\mathfrak {A}}\). One then demands the existence of smooth functions
, that is the actual symmetry with generators \(Q_{2\mathfrak {A}}\). One then demands the existence of smooth functions  such that this symmetry is reproduced by a localized transformation of the type \(\updelta _1\psi ^i\) with parameter
such that this symmetry is reproduced by a localized transformation of the type \(\updelta _1\psi ^i\) with parameter  . This is the origin of the integrability condition (11.4). If needed, the localized transformation \(\updelta _2\psi ^i\) can then be defined as \(\updelta _1\psi ^i\) with the parameter \(\epsilon ^A_1(x)\) as given in (11.2). It is therefore reasonable to think of \(\updelta _1\psi ^i\) as a parent symmetry and of \(\updelta _2\psi ^i\) as its descendant.
. This is the origin of the integrability condition (11.4). If needed, the localized transformation \(\updelta _2\psi ^i\) can then be defined as \(\updelta _1\psi ^i\) with the parameter \(\epsilon ^A_1(x)\) as given in (11.2). It is therefore reasonable to think of \(\updelta _1\psi ^i\) as a parent symmetry and of \(\updelta _2\psi ^i\) as its descendant.
Second, I have not imposed the equation of motion. Thus, both the equivalence relation (11.5) and the integrability condition (11.4) must hold off-shell. By taking a divergence of (11.5) and using (11.4), we obtain another off-shell relation,
This makes the Ward identities for the correlation functions of  a consequence of those for
a consequence of those for  . By the same token, the two sets of currents couple to the same one-particle NG states. This explains in a quantum-field-theoretic language the redundancy of NG modes generated by locally equivalent symmetries.
. By the same token, the two sets of currents couple to the same one-particle NG states. This explains in a quantum-field-theoretic language the redundancy of NG modes generated by locally equivalent symmetries.
Third, should  be constant, the integrability condition (11.4) is fulfilled for
be constant, the integrability condition (11.4) is fulfilled for  . The equivalence relation (11.5) is then strictly linear in the currents. The corresponding generators \(Q_{1A}\) and \(Q_{2\mathfrak {A}}\) are also linearly related,
. The equivalence relation (11.5) is then strictly linear in the currents. The corresponding generators \(Q_{1A}\) and \(Q_{2\mathfrak {A}}\) are also linearly related,  . This special case therefore amounts to a mere change of basis of symmetry generators, or a choice of a subset thereof, and is of little interest. A nontrivial current equivalence relation only arises from a set of non-constant functions
. This special case therefore amounts to a mere change of basis of symmetry generators, or a choice of a subset thereof, and is of little interest. A nontrivial current equivalence relation only arises from a set of non-constant functions  . Without loss of generality, one can drop the constant part of
. Without loss of generality, one can drop the constant part of  and assume that
and assume that  . This assumption is satisfied for all the examples worked out below. It also guarantees a posteriori that the relation (11.2) cannot be inverted. In other words, the distinction between a parent symmetry and its descendant is well-defined and cannot be reversed.
. This assumption is satisfied for all the examples worked out below. It also guarantees a posteriori that the relation (11.2) cannot be inverted. In other words, the distinction between a parent symmetry and its descendant is well-defined and cannot be reversed.
Finally, recall that the Noether current is determined by the symmetry transformation only up to addition of a vector field whose divergence vanishes off-shell. Suppose that we modify the parent Noether current by  such that \(\partial _\mu \updelta J^\mu _{1A}=0\). Then the integrability condition (11.4) can still be satisfied if we shift
such that \(\partial _\mu \updelta J^\mu _{1A}=0\). Then the integrability condition (11.4) can still be satisfied if we shift  appropriately,
appropriately,  . It follows that the ambiguity of the parent current does not affect the descendant current \(J^\mu _{2\mathfrak {A}}\) as given by (11.5). The descendant current of course suffers from its own ambiguity under
. It follows that the ambiguity of the parent current does not affect the descendant current \(J^\mu _{2\mathfrak {A}}\) as given by (11.5). The descendant current of course suffers from its own ambiguity under  such that
such that  off-shell. The ambiguities of the two currents are therefore independent of each other and do not constrain the validity of the equivalence relation (11.5).
off-shell. The ambiguities of the two currents are therefore independent of each other and do not constrain the validity of the equivalence relation (11.5).
2 Noether Currents from Background Gauging
The derivation of the Noether current of a given symmetry, based on (4.7), treats the localized symmetry transformation as a mere technical trick. There is however an alternative approach to Noether’s theorem that takes the local transformation seriously and promotes it to an actual symmetry of the action. This offers additional insight into the structure of Noether currents, the price to pay being a technical assumption that has to be verified case by case.
This key assumption is that it is possible to make the action of the theory exactly invariant under the localized symmetry transformation by adding a set of background gauge fields  . More concretely, we want to promote the original action \(S\{\psi \}\) to a functional \(\tilde S\{\psi ,A\}\) such that \({{\tilde S\{\psi ,A\}}\big \rvert _{\mathrm {vac}}=S\{\psi \}}\), where the subscript “vac” indicates removing the background. I allow for a generic local transformation of \(\psi ^i\) with parameters \(\epsilon ^A(x)\), following (11.1),
. More concretely, we want to promote the original action \(S\{\psi \}\) to a functional \(\tilde S\{\psi ,A\}\) such that \({{\tilde S\{\psi ,A\}}\big \rvert _{\mathrm {vac}}=S\{\psi \}}\), where the subscript “vac” indicates removing the background. I allow for a generic local transformation of \(\psi ^i\) with parameters \(\epsilon ^A(x)\), following (11.1),
As for the local transformation of the gauge field, we can assume a similar generic expansion in derivatives of the parameters \(\epsilon ^A(x)\),
the ellipsis again stands for terms with higher derivatives of  . It is important that
. It is important that  does not depend on the dynamical fields \(\psi ^i\) so that
does not depend on the dynamical fields \(\psi ^i\) so that  can be treated as a fixed external background.
can be treated as a fixed external background.
The variation of action under a simultaneous transformation of \(\psi ^i\) and  consists of contributions from varying the former and the latter, \(\updelta \tilde S\equiv \updelta _\psi \tilde S+\updelta _A\tilde S\), where
consists of contributions from varying the former and the latter, \(\updelta \tilde S\equiv \updelta _\psi \tilde S+\updelta _A\tilde S\), where
Next we remove the background. In this limit, \(\updelta _\psi \tilde S\) turns by construction into  . In order that \(\updelta \tilde S\) vanishes at least when \(\epsilon ^A\) is constant, there must be a local function
. In order that \(\updelta \tilde S\) vanishes at least when \(\epsilon ^A\) is constant, there must be a local function  such that
such that
With this consistency condition satisfied, the vanishing of \(\updelta \tilde S\) for any \(\epsilon ^A(x)\) leads to the identification
Equations (11.10) and (11.11) already constitute a fairly general tool for derivation of Noether currents. Yet, the approach based on background gauge invariance can be further extended to higher-rank tensor background fields. Instead of cluttering the formalism with additional indices, I will content myself with a couple of illustrative examples, worked out in Sects. 11.3.2 and 11.3.3.
The notation used in (11.10) and (11.11) is tailored to what I called the parent symmetry. What if the system possesses an additional, descendant set of symmetries? By (11.2), the localized transformations of the descendant type form a subset of all localized transformations of the parent type. All we therefore have to do is to gauge the parent symmetry by adding its background gauge fields  . That we can in fact do so is the sole technical assumption we have to make. The descendant symmetry is then automatically gauged as well without the need for any additional gauge fields. This once again underlines the redundancy of the descendant symmetry. In particular, the background gauging makes it possible to recover the equivalence relation (11.5) for Noether currents; see [1] for a detailed proof.
. That we can in fact do so is the sole technical assumption we have to make. The descendant symmetry is then automatically gauged as well without the need for any additional gauge fields. This once again underlines the redundancy of the descendant symmetry. In particular, the background gauging makes it possible to recover the equivalence relation (11.5) for Noether currents; see [1] for a detailed proof.
3 Examples
I will now illustrate the general theory developed above with several examples. These are chosen mostly for their relevance to EFTs discussed elsewhere in the book. I will therefore not shy away from showing certain amount of details.
3.1 Galileon Symmetry
Consider a class of theories of a single real relativistic scalar field \(\phi \), invariant under the Galileon symmetry
This can be localized by replacing the constant parameters with arbitrary functions, \(\epsilon _1\to \epsilon _1(x)\) and \(\epsilon ^\mu _2\to \epsilon ^\mu _2(x)\). The shift by \(\epsilon _1\) is the parent symmetry. The descendant symmetry with parameter \(\epsilon ^\mu _2\) can be recovered locally by setting \(\epsilon _1(x)=\epsilon ^\mu _2(x)x_\mu \). This is the local equivalence condition (11.2) where \(f_\mu (x)=x_\mu \). The integrability condition (11.4) and the current equivalence relation (11.5) then translate to
Interestingly, the set of functions \(N^\mu _\nu [\phi ,x]\) is in this case the primary object, which by means of (11.13) determines both currents.
Let us see how this works explicitly. Take the class of Lagrangians of the type
Here  is an arbitrary function of second derivatives of \(\phi \), which is manifestly invariant under (11.12). Furthermore,
is an arbitrary function of second derivatives of \(\phi \), which is manifestly invariant under (11.12). Furthermore,  with \(n=0,\dotsc ,D\) is the set of quasi-invariant Galileon Lagrangians, cf. Sect. 10.3.2,
with \(n=0,\dotsc ,D\) is the set of quasi-invariant Galileon Lagrangians, cf. Sect. 10.3.2,

It is easy to extract the current \(J^\mu _1\) by evaluating the variation of the action under the shift \(\phi (x)\to \phi (x)+\epsilon _1(x)\). With the shorthand notation for the symmetric tensor

the current takes the compact form
This matches the integrability condition in (11.13) since \(X^{\mu \nu }\) obviously has vanishing divergence and so \(X^{\mu \nu }\partial _\nu \phi =\partial _\nu (X^{\mu \nu }\phi )\). It follows that

and the current \(J^\mu _{2\nu }\) is then given by the second relation in (11.13). This result can be easily verified by evaluating the variation of the action under \(\phi (x)\to \phi (x)+\epsilon ^\mu _2(x)x_\mu \).
Example 11.1
The simplest example of a theory from the class (11.14) is the theory of a free massless scalar, \(\mathcal {L}=(1/2)(\partial _\mu \phi )^2\). This amounts to \(c_1=(-1)^D/[2(D-1)!]\) and discarding all the other operators contributing to (11.14). By (11.16), this leads to \(X^{\mu \nu }=2c_1g^{\mu \nu }(-1)^D(D-1)!=g^{\mu \nu }\). We then find in turn
To illustrate the background gauging formalism, we need to gauge the parent symmetry. This is most easily done by first integrating the quasi-invariant Galileon terms by parts so that each factor of \(\phi \) carries at least one derivative. All one then has to do is to replace every \(\partial _\mu \phi \) with \(D_\mu \phi \equiv \partial _\mu \phi -A_\mu \). This gives the gauged action

This is manifestly invariant under the simultaneous gauge transformation \(\updelta \phi (x)=\epsilon _1(x)\) and \(\updelta A_\mu (x)=\partial _\mu \epsilon _1(x)\). The latter corresponds to (11.8) with \(\tilde F_{1\mu }=0\) and \(\tilde K^\nu _{1\mu }=\delta ^\nu _\mu \); no terms with higher derivatives of \(\epsilon _1(x)\) are present. The consistency condition (11.10) is trivially satisfied with \(R^\mu =0\), and (11.11) then gives
It takes little effort to convince oneself that this exactly reproduces (11.17).
To extract the descendant current \(J^\mu _{2\nu }\) from the same gauged action, we set \(\epsilon _1(x)=\epsilon ^\mu _2(x)x_\mu \), which changes the transformation rule for \(A_\mu \) to
This matches (11.8) with  and
and  , and (11.10) then becomes
, and (11.10) then becomes
With the help of the first relation in (11.13) this is seen to be solved by  . The master Eq. (11.11) then gives
. The master Eq. (11.11) then gives  in agreement with the current equivalence relation, that is the second identity in (11.13).
in agreement with the current equivalence relation, that is the second identity in (11.13).
3.2 Spacetime Translations and Rotations
In relativistic theories with only scalar fields, spacetime translations and rotations can be implemented through their action on Minkowski coordinates,
The vector \(\epsilon ^\mu _1\) parameterizes infinitesimal translations and the antisymmetric tensor \(\epsilon ^{\mu \nu }_2\) infinitesimal spacetime rotations. The evolutionary form (11.1) of the transformations induced on the fields \(\psi ^i\) is obtained by setting, respectively,Footnote 1
Translations and rotations are locally equivalent via (11.2); the latter can be recovered from the former by setting
The translations are the parent symmetry and the rotations its descendant. The Noether current corresponding to the parent symmetry is the canonical energy–momentum (EM) tensor , defined by
, defined by

The left-hand side of the integrability condition (11.4) then becomes

It is known that in purely scalar theories, the canonical EM tensor is symmetric; I will justify this below using the background gauging approach. The integrability condition is then satisfied by \(N^\mu _{\alpha \beta }=0\). The equivalence relation (11.5) in turn gives the Noether current for spacetime rotations, that is the angular momentum tensor,

This is just the familiar relation between momentum and angular momentum.
The equivalence relation (11.29) does not apply to theories of fields with nonzero spin without further qualification. Namely, in such theories, spacetime translations and rotations are not automatically locally equivalent. The reason for this is that the components of fields with spin undergo a transformation under spacetime rotations, which cannot be reproduced by the naive local translation, \(\updelta _1\psi ^i(x)=-\epsilon _1^\mu (x)\partial _\mu \psi ^i(x)\), for any choice of \(\epsilon ^\mu _1(x)\). The problem can be circumvented by a judicious choice of the localized transformation under translations. Instead of developing a general theory, let me illustrate the idea on a simple example.
Example 11.2
Recall Example 4.3 where I introduced the following theory of a real scalar field \(\phi \) and a vector field \(A_\mu \),
We found that the canonical EM tensor of this theory is not symmetric. However, we could solve the problem by considering a modified local translation,

This is motivated by the fact that under a general local coordinate transformation, \(A_\mu \) should transform as a covariant vector. Noether’s theorem then gives the improved, off-shell-symmetric EM tensor
The prescription (11.31) restores local equivalence of spacetime translations and rotations in spite of the presence of the vector field. Namely, inserting  with constant
with constant  in (11.31) gives
in (11.31) gives

This is exactly how \(A_\mu \) should transform under a spacetime rotation. We can then localize both translations and rotations by using (11.31) augmented with (11.26). Since \(\tilde T^{\mu \nu }\) is symmetric, the integrability condition is now satisfied and we reproduce the angular momentum tensor by replacing (11.29) with

Let us now address the relation between spacetime translations and rotations within the background gauging formalism. We start by gauging the parent symmetry: spacetime translations. This amounts to promoting the flat Minkowski spacetime to a possibly curved spacetime manifold. Here it proves useful to invoke the differential-geometric language developed in Appendix A, to which I refer the reader for the basic terminology. Thus, the geometry of the spacetime manifold can be characterized by a local coframe (basis of differential 1-forms),  .Footnote 2 Under an infinitesimal coordinate transformation, \(x^\mu \to x^\mu +\epsilon ^\mu _1(x)\), the coordinate components of the coframe change as
.Footnote 2 Under an infinitesimal coordinate transformation, \(x^\mu \to x^\mu +\epsilon ^\mu _1(x)\), the coordinate components of the coframe change as

This matches (11.8) provided we identify  and
and  . A gauge-invariant action \(\tilde S\{\psi ,e^*\}\) is obtained from \(S\{\psi \}\) by replacing derivatives of \(\psi ^i\) therein with covariant derivatives, and the flat Minkowski metric
. A gauge-invariant action \(\tilde S\{\psi ,e^*\}\) is obtained from \(S\{\psi \}\) by replacing derivatives of \(\psi ^i\) therein with covariant derivatives, and the flat Minkowski metric  with the spacetime metric,
with the spacetime metric,  . An appropriate volume element is built using the determinant of the coframe
. An appropriate volume element is built using the determinant of the coframe  as a matrix.
as a matrix.
Eventually, we want to remove the background and go back to the flat Minkowski spacetime. I assume that the latter is described by global coordinates \(x^\mu \) in which the components  are constant. Then the consistency condition (11.10) is solved by \(R^\mu _\nu =0\), and (11.11) reduces to
are constant. Then the consistency condition (11.10) is solved by \(R^\mu _\nu =0\), and (11.11) reduces to

Suppose now that the theory at hand can be coupled to the background geometry in a way that the action \(\tilde S\{\psi ,e^*\}\) depends on  only through the spacetime metric, \(g_{\mu \nu }\). This is an example of a higher-rank tensor background hinted at above. Then the variation of the action (11.9) is replaced with
only through the spacetime metric, \(g_{\mu \nu }\). This is an example of a higher-rank tensor background hinted at above. Then the variation of the action (11.9) is replaced with
On a flat Minkowski background, this automatically vanishes for constant \(\epsilon ^\mu _1\) thanks to  . The EM tensor is then identified as
. The EM tensor is then identified as
This is the Hilbert EM tensor. Should our theory be Lorentz-invariant and only contain scalar fields, it can always be coupled to the spacetime background using the metric \(g_{\mu \nu }\). At the same time, the scalar fields retain the transformation rule \(\updelta _1\psi ^i(x)=-\epsilon ^\mu _1(x)\partial _\mu \psi ^i(x)\). This guarantees that the canonical and Hilbert EM tensors coincide, and shows that the canonical EM tensor is necessarily symmetric.
Theories of fields with spin can be coupled to background geometry in different manners, depending on how the spin index of the fields is treated. Let me illustrate this in the case of a vector field \(A_\mu \). One already mentioned possibility is to treat this as a covariant vector that transforms under a general coordinate transformation via the second relation in (11.31). It is then possible to construct a generally covariant action \(\tilde S\{A,g\}\) that only depends on the background through the metric. The resulting EM tensor (11.38) is symmetric.
On the other hand, we may project the field on the local frame  and treat
and treat  as a set of spacetime scalars. This corresponds to keeping the naive transformation under local translations,
as a set of spacetime scalars. This corresponds to keeping the naive transformation under local translations,  . In this case, the gauged action \(\tilde S\{A,e^*\}\) may depend explicitly on the local frame. We then have to use (11.36) instead of (11.38). This gives the canonical EM tensor which is not necessarily symmetric.
. In this case, the gauged action \(\tilde S\{A,e^*\}\) may depend explicitly on the local frame. We then have to use (11.36) instead of (11.38). This gives the canonical EM tensor which is not necessarily symmetric.
The general moral is that different choices of gauging the symmetry may lead to different expressions for the Noether current. This is tantamount to different choices of the localized symmetry transformation (11.7). The resulting alternative Noether currents however only differ by terms that vanish on-shell, modulo the inevitable ambiguity with respect to contributions whose divergence vanishes off-shell.
With the EM tensor at hand, we can extract the Noether current for any descendant symmetry that can be locally reproduced by spacetime translations (see e.g. Sect. 14.3 of [2]). Consider a one-parameter group of symmetries, generated by a vector field \(\boldsymbol \xi (x)\). The corresponding local transformation with parameter \(\epsilon _2(x)\) can be written as \(x^\mu \to x^\mu +\epsilon ^\mu _1(x)\) with \(\epsilon ^\mu _1(x)=\epsilon _2(x)\xi ^\mu (x)\). This turns (11.35) to

whence we extract  and
and  . The consistency condition (11.10) then boils down to
. The consistency condition (11.10) then boils down to

In the last step, I assumed that \(T^{\mu \nu }\) is symmetric, which we now know to be guaranteed in case the action \(\tilde S\{\psi ,e^*\}\) only depends on the coframe through the metric. But should \(\boldsymbol \xi (x)\) actually generate a symmetry of the flat Minkowski spacetime, \(\partial _\mu \xi _\nu +\partial _\nu \xi _\mu \) must vanish by the Killing equation (A.92). Then (11.10) is satisfied with \(R^\mu =0\) and (11.11) gives immediately
This confirms, among others, a general relation between the Hilbert EM tensor and the angular momentum tensor, anticipated in (11.34).
3.3 Galilei Invariance
The previous two examples were relativistic in spirit. Let us therefore have a look at one more example that is intrinsically nonrelativistic. Consider a theory of a complex Schrödinger field \(\psi (\boldsymbol x,t)\) whose excitations are nonrelativistic particles with mass m. Suppose that the theory is invariant under spatial translations and under the internal \(\mathrm {U}(1)\) group of phase transformations of the field. These symmetries act respectively on the spatial coordinates, \(\boldsymbol x'=\boldsymbol x+\boldsymbol \epsilon \), and the field, \(\psi '=\mathrm{e} ^{\mathrm{i} \alpha }\psi \), and so correspond to
Finally, it is well-known from elementary quantum mechanics that the Schrödinger equation for a free particle is invariant under Galilei boosts,
Here \(\boldsymbol v\) is the boost velocity which plays the role of the transformation parameter. Let us assume that the invariance under (11.43) is inherited by our possibly interacting nonrelativistic field theory.
The evolutionary form of an infinitesimal Galilei boost is
This can be locally recovered as a combination of a spatial translation and a phase transformation if we set
In this case, therefore, the combination of spatial translations and internal \(\mathrm {U}(1)\) is the parent symmetry, whereas the Galilei boosts are its descendants. The rest follows a familiar pattern. The integrability condition (11.4) requires that there is a local function \(N^{\mu r}[\psi ,\boldsymbol x,t]\) of the field and its derivatives such that
where \(J^\mu \) is the current of the internal \(\mathrm {U}(1)\) symmetry. The general equivalence relation (11.5) then gives the current \(B^{\mu r}\) corresponding to Galilei boosts,
Should \(N^{\mu r}\) happen to be zero, the integrability condition (11.46) would boil down to \(T^{0r}=-mJ^r\). Except for the sign convention in the definition of the two currents, this is the usual nonrelativistic relation between momentum and velocity. Moreover, (11.47) would imply \(B^{0r}=mx^rJ^0+tT^{0r}=m(x^rJ^0-tJ^r)\). This generalizes to field theory the well-known fact that the conserved charge for a Galilei boost of a particle of mass m is \(m\boldsymbol x-\boldsymbol pt\), where \(\boldsymbol p\) is the particle momentum. Whether or not, or under what conditions, \(N^{\mu r}\) actually is zero needs to be inspected case by case.
The story of Galilei invariance becomes very interesting, and nontrivial, once we consider background gauging. What we need is to gauge simultaneously spatial translations, Galilei boosts and the internal \(\mathrm {U}(1)\) phase transformations. Since the Galilei boosts are descendant, we want to primarily gauge spatial translations and the internal \(\mathrm {U}(1)\). The actions of these cannot be trivially separated as one could do in a Lorentz-invariant field theory. Namely, the gauged translations must affect the phase of the Schrödinger field in a way that reproduces (11.43).
It turns out that the minimal setup that does the job includes a background spatial metric \(g_{rs}(x)\) and a gauge field \(A_\mu (x)\) for the \(\mathrm {U}(1)\) symmetry [3]. Under a combination of an infinitesimal local translation, \(\boldsymbol x'=\boldsymbol x+\boldsymbol \epsilon (\boldsymbol x,t)\), and a \(\mathrm {U}(1)\) transformation with parameter \(\alpha (\boldsymbol x,t)\), the background fields vary by
The first two lines take the expected form. The only nontrivial ingredient really is the last term on the third line of (11.48), which depends on the mass parameter m. This reflects the fact that the realization of spatial translations and Galilei boosts on a Schrödinger field is centrally extended, with m playing the role of the central charge. The associated nonrelativistic spacetime geometry is known as Newton–Cartan. See [4, 5] for more details on nonrelativistic field theory in Newton–Cartan spacetimes, and [6] for broader background on nonrelativistic geometry.
The localized transformation of the Schrödinger field itself is given by (11.42). By combining this with (11.48), we then generate at once the Noether currents of all the symmetries in terms of a gauged action \(\tilde S\{\psi ,g,A\}\). First, the current of the \(\mathrm {U}(1)\) symmetry is given by a trivial modification of (11.21),
where “vac” now indicates setting \(g_{rs}\) to the flat Euclidean metric \(\delta _{rs}\) and \(A_\mu \) to zero. Next comes the EM tensor. By (11.27), the only components that the invariance under (time-dependent) spatial coordinate transformations gives us access to are

Note that (11.49) and (11.50) together imply a relation between momentum density and the particle number current, \(T^{0r}=-mJ^r\). This corresponds to (11.46) with vanishing \(N^{\mu r}\). It might come as a surprise that the background gauge invariance yields a stronger constraint on the Noether currents than the original, physical symmetry. After all, background gauge invariance per se is merely a handy tool to encode the consequences of the symmetry. However, recall that the realization of Galilei transformations on the Schrödinger field is centrally extended. This is an obstruction that makes gauging of the symmetry nontrivial. It is ultimately the assumption that the gauging is possible that is responsible for the vanishing of \(N^{\mu r}\). This does not add any new physics, but rather constrains the class of theories to which the background gauging procedure can be applied.
Next, the current \(B^{\mu r}\) for Galilei boosts can be identified by using (11.9) together with  . Upon inserting (11.45) in (11.48), we find that the consistency condition (11.10) is satisfied with \(R^\mu _r=0\). This leads via (11.11) to
. Upon inserting (11.45) in (11.48), we find that the consistency condition (11.10) is satisfied with \(R^\mu _r=0\). This leads via (11.11) to
These can be combined using (11.49) and (11.50) into \(B^{\mu r}=mx^rJ^\mu +tT^{\mu r}\), which is just (11.47) without the \(N^{\mu r}\) term. This is consistent with our conclusion above that \(N^{\mu r}=0\) as a consequence of the assumption that the gauged action \(\tilde S\{\psi ,g,A\}\) is invariant under (11.48).
3.4 Changing the Background: Magnetic Translations
Our discussion in this chapter started with declaring the existence of certain symmetry and its subsequent localization. However, it is also possible to adopt the opposite approach. Suppose we know a priori the type of background gauge fields and the local transformations that make the action \(\tilde S\{\psi ,A\}\) invariant. It is then possible to identify the original symmetry as the subset of the gauge transformations that preserve a trivial background.
Example 11.3
Recall the Galileon symmetry of Sect. 11.3.1. Out of all the gauge transformations  , only those with constant \(\epsilon \) preserve the background, in this case regardless of the specific choice of \(A_\mu (x)\). Constant \(\epsilon \) corresponds exactly to the shift symmetry, acting on the Galileon scalar field \(\phi \).
, only those with constant \(\epsilon \) preserve the background, in this case regardless of the specific choice of \(A_\mu (x)\). Constant \(\epsilon \) corresponds exactly to the shift symmetry, acting on the Galileon scalar field \(\phi \).
Example 11.4
In case of relativistic theories of fields with integer spin, we can consider as the background a generic spacetime metric \(g_{\mu \nu }(x)\). The set of local general coordinate transformations that preserve such a background corresponds to (the continuous part of) its isometry group (see Appendix A.6.2 for the necessary mathematical background). In case of the flat Minkowski spacetime, this is just the Poincaré group, as follows from a trivial modification of Example A.15. Note that choosing the background geometry is not equivalent to fixing the coframe  as (11.36) might naively suggest. The reason is that the coframe is not uniquely determined for a given spacetime manifold. This underlines the necessity to carefully identify the geometric data, tailored to the given spacetime symmetry and uniquely representing the spacetime background.
as (11.36) might naively suggest. The reason is that the coframe is not uniquely determined for a given spacetime manifold. This underlines the necessity to carefully identify the geometric data, tailored to the given spacetime symmetry and uniquely representing the spacetime background.
Once we have the gauged action \(\tilde S\{\psi ,A\}\), we may use it to study physics on nontrivial backgrounds. Indeed, the vanishing of the variation of \(\tilde S\{\psi ,A\}\) under a localized symmetry transformation is an exact statement valid for any choice of  . Imposing the equation of motion on the dynamical fields \(\psi ^i\) amounts to setting
. Imposing the equation of motion on the dynamical fields \(\psi ^i\) amounts to setting  , which turns (11.9) into a generalized “conservation law,”
, which turns (11.9) into a generalized “conservation law,”
For this to represent an actual divergence-type conservation law, the chosen background must possess some symmetry. This may however be different from the symmetry that we originally gauged by introducing the fields \(A^A_\mu \) in the first place. I will illustrate this on an interesting example starting from Galilei invariance in \(d=3\) spatial dimensions.
The flat nonrelativistic spacetime corresponds to \(g_{rs}=\delta _{rs}\) and \(A_\mu =0\). The only infinitesimal transformations of type (11.48) that preserve this background are a linear combination of Euclidean translations and rotations, Galilei boosts, and the internal \(\mathrm {U}(1)\) transformations. This is not obvious but is straightforward to check.
Let us now change the background by introducing a uniform magnetic field \(\boldsymbol B\). Such a uniform background field should preserve some notion of translation invariance. This however cannot be the naive Euclidean translations due to the coordinate-dependence of the vector potential \(\boldsymbol A(\boldsymbol x)\) of the magnetic field. The details turn out to depend on the choice of gauge; I will adopt the symmetric gauge, \(\boldsymbol A(\boldsymbol x)=(\boldsymbol B\times \boldsymbol x)/2\). The translation invariance can now be rescued if it is accompanied by a local \(\mathrm {U}(1)\) transformation. In terms of the Schrödinger field \(\psi (\boldsymbol x,t)\), this so-called magnetic translation symmetry takes the form
One remarkable consequence of this twisted translation symmetry is that the components of its generator \(P_r\) no longer commute with each other. It is easy to check that they satisfy the commutation relation \([P_r,P_s]=-\mathrm{i} \varepsilon _{rsu}B^uQ\), where Q is the generator of the \(\mathrm {U}(1)\) symmetry.
The magnetic translation symmetry (11.53) can be localized by promoting \(\boldsymbol \epsilon \) to a function of spacetime coordinates and setting
where \(\boldsymbol A(x)\) is now the spatial part of the variable \(A_\mu (x)\). At the infinitesimal level, this is equivalent to (11.42) with \(\alpha (x)=-\boldsymbol \epsilon (x)\cdot \boldsymbol A(x)\). Following the same reasoning as in Sect. 11.3.3, we then get modified relations for the EM tensor,
which generalize (11.50) to a uniform magnetic background. Here “vac” refers to the background vector potential,  . The components of \(J^\mu [\psi ,x]\) are still given by (11.49).
. The components of \(J^\mu [\psi ,x]\) are still given by (11.49).
The magnetic translations illustrate in a very nontrivial manner many of the concepts introduced in Chap. 4 and this chapter. On the magnetic background, the Lagrangian of the Schrödinger field depends explicitly on the spacetime coordinates, yet possesses a nontrivial notion of translation symmetry. The Lie algebra of infinitesimal translations is centrally extended. The translation symmetry can be gauged simultaneously with the internal \(\mathrm {U}(1)\) symmetry by introducing a spatial metric and allowing the background fields to transform according to (11.48). This allows one to identify a nontrivial relation between the EM tensor and the Noether current of the \(\mathrm {U}(1)\) symmetry, shown in (11.55).
4 Application to Scattering of Nambu–Goldstone Bosons
I will now return to the promise I made in Sect. 10.3.Footnote 3 Therein, I suggested that the enhanced soft limit of scattering amplitudes of NG bosons in the DBI and Galileon theories arises from the presence of extended symmetry. We now have all we need to be able to understand why. The material of this section loosely follows [7].
4.1 Galileon Theory
Let us start with the simpler Galileon theory and recall the discussion of the Galileon symmetry in Sect. 11.3.1. In any translationally-invariant theory endowed with the Galileon symmetry, the parent current \(J^\mu _1[\phi ]\) will not depend explicitly on the coordinates. By the integrability condition in (11.13), the same holds for the local function \(N^\mu _\nu [\phi ]\). Following the philosophy of Sect. 10.1, we now consider an arbitrary scattering process \(\alpha \to \beta \). Using the translation property \(J^\mu _1[\phi ](x)=\mathrm{e} ^{\mathrm{i} P\cdot x}J^\mu _1[\phi ](0)\mathrm{e} ^{-\mathrm{i} P\cdot x}\) and analogously  , we deduce
, we deduce

where \(p^\mu \equiv p^\mu _\alpha -p^\mu _\beta \).
The general rules of polology dictate that when \(p^\mu \) approaches the mass shell of a massless particle, the matrix element  develops a pole. This corresponds to the emission of a NG boson with momentum \(\boldsymbol p\) and allows one to extract the on-shell scattering amplitude
develops a pole. This corresponds to the emission of a NG boson with momentum \(\boldsymbol p\) and allows one to extract the on-shell scattering amplitude  ; cf. (10.1). The same reasoning can however also be applied to the operator \(N^\mu _\nu [\phi ]\), leading to
; cf. (10.1). The same reasoning can however also be applied to the operator \(N^\mu _\nu [\phi ]\), leading to

where  is by definition free of poles. By combining this with (11.56), we find a relation between
is by definition free of poles. By combining this with (11.56), we find a relation between  and the function
and the function  in (10.1),
in (10.1),
From (10.2) we then finally get an explicit expression for the on-shell amplitude,
where F is determined by  , and \(p^\mu _{\mathrm {on}}\equiv (\left \lvert {\boldsymbol p}\right \rvert ,\boldsymbol p)\).
, and \(p^\mu _{\mathrm {on}}\equiv (\left \lvert {\boldsymbol p}\right \rvert ,\boldsymbol p)\).
The general relation (10.2) allows one to assert the existence of Adler zero, provided the function  remains regular in the soft limit \(p^\mu \to 0\). A sufficient condition to ensure this is, as we know from Chap. 10, the absence of bilinear operators in the current \(J^\mu _1[\phi ]\). This automatically translates into the absence of bilinear operators in \(N^\mu _\nu [\phi ]\). We then conclude from (11.59) without further assumptions that in the soft limit, the scattering amplitudes in the Galileon theory vanish at least with the second power of momentum. In other words, the soft limit of scattering amplitudes in the Galileon theory is enhanced with the soft scaling parameter \(\sigma =2\).
remains regular in the soft limit \(p^\mu \to 0\). A sufficient condition to ensure this is, as we know from Chap. 10, the absence of bilinear operators in the current \(J^\mu _1[\phi ]\). This automatically translates into the absence of bilinear operators in \(N^\mu _\nu [\phi ]\). We then conclude from (11.59) without further assumptions that in the soft limit, the scattering amplitudes in the Galileon theory vanish at least with the second power of momentum. In other words, the soft limit of scattering amplitudes in the Galileon theory is enhanced with the soft scaling parameter \(\sigma =2\).
4.2 Theories with Generalized Shift Symmetry
Having warmed up on the Galileon theory, we can now generalize the above argument to a much broader class of theories. For simplicity of notation, I will restrict the discussion to Lorentz-invariant theories of a single NG field \(\phi \) that are invariant under the constant shift \(\phi \to \phi +\epsilon \) [7]. Further generalization to theories invariant under spacetime translations but mere spatial rotations can be found in [8]. A generalization to theories of multiple flavors of NG bosons presumably exists but, as far as I know, has not been worked out in the literature.
Suppose that in addition to the constant shift symmetry, our theory is also invariant under a generalized shift of the type
Here \(f(x)\) is assumed to be a polynomial function of the spacetime coordinates of degree \(\deg f\equiv n\geq 1\). The local operator \(\Phi [\phi ,x]\) may depend explicitly on the coordinates as well, but is required to be polynomial in \(x^\mu \) of degree lower than n. Examples of symmetries of this type include both the symmetry of the DBI theory (10.51) and the special Galileon symmetry (10.56).
Let us now localize (11.60) and treat it as a generalized coordinate-dependent shift of the field, that is \(\updelta \phi (x)=\tilde \epsilon [\phi ,x](x)\) with \(\tilde \epsilon [\phi ,x](x)\equiv \epsilon (x)\{f(x)+\Phi [\phi ,x](x)\}\). The corresponding variation of the action is
where  is the parent current due to the constant shift symmetry. An integrability condition required so that (11.60) really is a symmetry of the action reads
is the parent current due to the constant shift symmetry. An integrability condition required so that (11.60) really is a symmetry of the action reads
Unlike the parent current  , the local function \(N^\mu [\phi ,x]\) may depend explicitly on the coordinates. For (11.62) to hold, however, the polynomial degree of \(N^\mu [\phi ,x]\) in \(x^\mu \) can be at most that of \(\partial _\mu f(x)\), that is \(n-1\).
, the local function \(N^\mu [\phi ,x]\) may depend explicitly on the coordinates. For (11.62) to hold, however, the polynomial degree of \(N^\mu [\phi ,x]\) in \(x^\mu \) can be at most that of \(\partial _\mu f(x)\), that is \(n-1\).
The next step is to rewrite (11.62) in the form
The new local function \(M^\mu [\phi ,x]\) of the field and its derivatives is again of polynomial degree at most \(n-1\) in the spacetime coordinates. It satisfies the translation property \(M^\mu [\phi ,x](x)=\mathrm{e} ^{\mathrm{i} P\cdot x}M^\mu [\phi ,x](0)\mathrm{e} ^{-\mathrm{i} P\cdot x}\), with the fields on the right-hand side evaluated at the origin but the explicit coordinate dependence left intact. Applying the polology rules to this operator then gives, in analogy to (11.57),
The coordinate dependence of the remainder function  comes entirely from that of \(M^\mu [\phi ,x](0)\). Therefore,
comes entirely from that of \(M^\mu [\phi ,x](0)\). Therefore,  is a polynomial function of the coordinates with degree at most \(n-1\).
is a polynomial function of the coordinates with degree at most \(n-1\).
The crucial observation is that due to current conservation, the on-shell matrix element of  between any initial and final states, \(\left \lvert {\alpha }\right \rangle \) and \(\left \lvert {\beta }\right \rangle \), vanishes. By combining (11.63) and (11.64), we then get a constraint on the remainder functions, generalizing (11.58),
between any initial and final states, \(\left \lvert {\alpha }\right \rangle \) and \(\left \lvert {\beta }\right \rangle \), vanishes. By combining (11.63) and (11.64), we then get a constraint on the remainder functions, generalizing (11.58),
To understand the implications of this identity, we expand  and
and  in a formal power series in \(p^\mu \). Let us denote their coefficients of order k in \(p^\mu \) respectively as \(a_k\) and \(b_k(x)\), and write (11.65) symbolically as
in a formal power series in \(p^\mu \). Let us denote their coefficients of order k in \(p^\mu \) respectively as \(a_k\) and \(b_k(x)\), and write (11.65) symbolically as
This must hold as an equality between polynomial functions of the coordinates. We now use repeatedly the fact that \(\deg b_k(x)\leq n-1\) for all k. Setting \(k=0\), we infer that \(a_0=0\) and simultaneously \(\partial \cdot b_0(x)=0\), which implies that \(b_0(x)\) is constant, \(\deg b_0(x)=0\). In case \(n\geq 2\), we can next take (11.66) with \(k=1\). This can only hold if \(a_1=0\) and simultaneously \(\partial \cdot b_1(x)\simeq -b_0(x)\), that is, \(\deg b_1(x)\leq 1\). By induction, we find that for any \(k\leq n-1\), \(a_k=0\) and simultaneously \(\deg b_k(x)\leq k\).
The main conclusion is that for a generalized shift symmetry of the type (11.60) where \(\deg f(x)=n\), the series expansion of  starts at order n in energy–momentum. By (10.2), the soft limit of scattering amplitudes of the theory is then enhanced with the soft degree \(\sigma =n+1\). This confirms in particular that \(\sigma =2\) for the DBI theory and \(\sigma =3\) for the special Galileon theory.
starts at order n in energy–momentum. By (10.2), the soft limit of scattering amplitudes of the theory is then enhanced with the soft degree \(\sigma =n+1\). This confirms in particular that \(\sigma =2\) for the DBI theory and \(\sigma =3\) for the special Galileon theory.
Notes
- 1.
The factor \(1/2\) in \(\updelta _2\psi ^i\) is conventional and compensates for the fact that the components
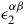 and
and 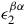 with fixed \(\alpha \neq \beta \) parameterize the same transformation. The derivation of the angular momentum tensor
with fixed \(\alpha \neq \beta \) parameterize the same transformation. The derivation of the angular momentum tensor 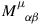 below assumes that the same factor \(1/2\) is used in its definition via (4.7).
below assumes that the same factor \(1/2\) is used in its definition via (4.7). - 2.
Following the notation introduced in Sect. 10.2.3, I use underlined indices to indicate components within a local (co)frame. Ordinary Lorentz indices refer to a set of local spacetime coordinates, \(x^\mu \).
- 3.
A reader interested primarily in the development of the general theory for spontaneously broken spacetime symmetry may proceed directly to the next chapter.
References
T. Brauner, Phys. Scr. 95, 035004 (2020). https://doi.org/10.1088/1402-4896/ab50a5
C.P. Burgess, Introduction to Effective Field Theory (Cambridge University Press, Cambridge, 2021). https://doi.org/10.1017/9781139048040
D.T. Son, M. Wingate, Ann. Phys. 321, 197 (2006). https://doi.org/10.1016/j.aop.2005.11.001
M. Geracie, D.T. Son, C. Wu, S.F. Wu, Phys. Rev. D91, 045030 (2015). https://doi.org/10.1103/PhysRevD.91.045030
K. Jensen, SciPost Phys. 5, 011 (2018). https://doi.org/10.21468/SciPostPhys.5.1.011
E. Bergshoeff, J. Figueroa-O’Farrill, J. Gomis, SciPost Phys. Lect. Notes 69, (2023). https://doi.org/10.21468/SciPostPhysLectNotes.69
C. Cheung, K. Kampf, J. Novotný, C.H. Shen, J. Trnka, J. High Energy Phys. 02, 020 (2017). https://doi.org/10.1007/JHEP02(2017)020
M.A. Mojahed, T. Brauner, J. High Energy Phys. 03, 086 (2022). https://doi.org/10.1007/JHEP03(2022)086
Author information
Authors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution-NonCommercial 4.0 International License (http://creativecommons.org/licenses/by-nc/4.0/), which permits any noncommercial use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this chapter
Cite this chapter
Brauner, T. (2024). Locally Equivalent Symmetries. In: Effective Field Theory for Spontaneously Broken Symmetry. Lecture Notes in Physics, vol 1023. Springer, Cham. https://doi.org/10.1007/978-3-031-48378-3_11
Download citation
DOI: https://doi.org/10.1007/978-3-031-48378-3_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-48377-6
Online ISBN: 978-3-031-48378-3
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


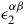 and
and 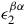 with fixed
with fixed 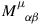 below assumes that the same factor
below assumes that the same factor