Abstract
Which modifications does the account of PTS developed in the second chapter need to undergo for it to be applicable to languages containing paradoxical expressions? We argue that one of the basic tenets of Prawitz-Dummett PTS—namely, the definition of the correctness of an inference as validity preservation—must be given up. As a result, the proposed account of PTS is enriched by introducing a notion of sense alongside the one of denotation. Paradoxical derivations are shown to act as the proof-theoretic analog of singular terms endowed with sense but lacking a denotation. The question of which class of derivations should be regarded as having a denotation is reconsidered, and we show the consequences of the choice of different criteria of identity of proofs for the analysis of languages containing paradoxical expressions.
You have full access to this open access chapter, Download chapter PDF
1 Paradoxes as Non-denoting Derivations
The Prawitz-Tennant analysis of paradoxes is a way to characterize paradoxes by their proof-theoretic behavior, looking at the derivation of absurdity generated. Although this is not per se a solution to the paradoxes and Tennant stresses is should not be meant as such (see e.g. [108], p. 268) it can be naturally turned into a solution. This is implicitly suggested by both Prawitz and Tennant who write:
In other words, the set-theoretical paradoxes are ruled out by the requirement that derivations shall be normal. (Prawitz [64], p. 95)
and
The general loss of normalisability, confined as it is according to our conjecture above to just the paradoxical part of the semantically closed language, is a small price to pay for the protection it gives against paradox itself. Logic plays its role as an instrument of knowledge only insofar as it keeps proofs in sharp focus, through the lens of normality. Normalisability, in the context of semantically closed languages, is not to be pressed as a general pre-condition for the very possibility of talking sense; rather, normality of proof is to be pressed as a general pre-condition for the very possibility of telling the truth. (Tennant [108], p.284)
Neither Prawitz nor Tennant did develop these remarks any further.1 However, the idea that requiring derivations to be normalisable can rule out paradoxes seems to fit, and induce a refinement of, the conception of derivations as linguistic representations of proofs that we developed in Chap. 2.
The relationship of derivations to proofs has been there developed by closely following an analogy with the relationship between numerical terms and numbers. The analogy can be further extended by taking into account an additional element. In the case of numerical expressions, nothing prohibits the possibility of considering languages which allow the formation of non-denoting expressions, such as ‘5 : 0’, or expressions obtained using a definite description operator, such as ‘the greatest even number’. Clearly, there is no way of rewriting expressions such as these onto a numeral. Given that numerals represent numbers in the most direct way, in a language for arithmetic allowing for the formation of non-denoting expressions, that a numerical expression denotes a number means that it can be rewritten into a numeral.
As numeral are the most direct expressions denoting numbers, in Sect. 2.8 we argued that in harmonious calculi closed normal derivations can be regarded as the most direct way of denoting proofs (although we stressed that there are different options as to what exactly ‘normal’ should be taken to mean). By analogy with the arithmetical case, that a derivation denotes a proof can be taken to mean that it can be rewritten into a normal derivation.
As we stressed in Sect. 2.8, the claim that normal derivations in harmonious calculi can be regarded as the most direct way of denoting proofs is backed by Fact 3 (see Sect. 1.7), i.e. by the fact that in harmonious calculi every closed normal derivation ends with an introduction rule. (As we stressed in Sect. 2.7, Fact 3 holds not only for \(\beta \)-normal—and hence also for \(\beta \eta \)-normal—derivations, but for \(\beta _w\)-normal derivations as well).
This suggests to take as a necessary (though not necessarily sufficient) condition for a closed derivation \(\mathscr {D}\) of an arbitrary calculus (i.e. one that need not be harmonious) to “really” denote a proof, to be that \(\mathscr {D}\) reduces to a canonical derivation.
Paradoxical derivations fail to normalize, thus they act as the proof-theoretic analogue of non-denoting singular terms: a paradoxical derivation such as the derivation \(\textbf{R}\) of Russell’s paradox (see Sect. 4.1 above) fails to denote a proof, that is it lacks a denotation. This squares very well with the above remarks by Prawitz and Tennant. In Prawitz’s calculus for naive set theory \(\texttt{NI}^{\mathbin {\supset }\bot \in }\), or in its simplified relative \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\), although there are derivations of \(\bot \), there is no closed canonical derivation of it. The reason is simply that there are no introduction rules for \(\bot \) and thus all derivations of \(\bot \) in Prawitz’s calculus for naive set theory cannot be canonical nor reducible to a canonical derivation.
Hence, any such derivation will fail to denote a proof. This squares with the BHK interpretation as well, which tells us that \(\bot \) is the proposition of which there is no proof!
2 Non-denoting Derivations and (In)validity
In Chap. 2, we presented PTS in a two-fold manner, either as being based on the idea that derivations denote proofs, or as based on the specification of a validity predicate. The intuitive connection between the two ways of presenting PTS is that a derivation is called ‘valid’ iff it denotes a proof.
In truth-conditional semantics, truth has to be a distinguishing feature of some but not all propositions if the semantics is to be of any interest at all. Analogously, validity-based presentations of PTS stress that validity should be a distinguishing feature of some but not all derivations, if PTS is to be of any interest at all.
To show that validity applies only to some, but not all derivations, Prawitz and Dummett consider derivations built up not just from the inference rules of a specific calculus, but rather from “arbitrary” inference rules (see Sect. 2.9 for details). Among these rules, one also finds rules which are intuitively not correct, such as the following:

By admitting non-correct inference rules, they can then distinguish between valid and invalid derivations, the latter being those in which non-correct inference rules have been applied. Note however, that Prawitz and Dummett do not define the validity of a derivation as its being constituted by applications of correct inference rules. Rather, it is the correctness of an inference that is defined in terms of the validity of the derivations in which it is applied (see Sects. 2.10 and 2.11).
In the present chapter we will argue that paradoxical languages offer another setting in which validity can be shown to apply only to some, but not all derivations available. In the previous section, building on remarks by Prawitz and Tennant we argued that paradoxical derivations do not denote proofs. As the validity predicate is meant to apply to a derivation iff this denotes a proof, paradoxical derivations in systems such as those discussed in the previous chapter are therefore the natural candidate for non-valid derivations.
As we will show in the next section, the notion of validity as defined by Prawitz cannot however be meaningfully applied to derivations of a calculus such as \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\). The main task of the present chapter will be that of proposing an alternative definition of validity suitable to be applied to the derivations of such a calculus. Rather than using validity of derivations to define correcntess of rules (as done by Dummett and Prawitz), the notion of validity to be proposed will rely on the notion of correctness of rules, which will therefore need to be defined first.
Since the analysis of paradoxes presented in the previous chapter goes back to Prawitz [64] himself, it might be somewhat surprising that his definition of validity cannot be applied to derivations in \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\). It should however be remarked that Prawitz never came back to discuss his treatment of paradoxes in any of his later writings. Similarly, considerations on the set-theoretic and semantic paradoxes play only a marginal role in Dummett’s writings. Thus, when framing the notion of validity, they were not in the least interested in having a notion that could be applied to paradoxical derivations.
3 The Need of Revising Prawitz’s Validity
In this section, as well as later on in the chapter, we will repeatedly refer to the derivations \(\lnot \mathscr {R}\) and \(\mathscr {R}\) of \(\lnot \rho \) and \(\rho \) as well as to the two derivations \(\textbf{R}\) and \(\mathbf {R'}\) of \(\bot \) from the previous chapter (the reader can find them in Sect. 4.1).
On Prawitz’s definition of validity (see Definition 2.2 in Sect. 2.9), we immediately see that the closed derivation \(\textbf{R}\) of \(\bot \) in \(\texttt{NI}^{\mathbin {\supset }\bot \in }\) or \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\) fails to qualify as valid, since it cannot be reduced to a canonical derivation, not just relative to the set of reduction procedures \(\mathcal {J}\) consisting of \(\mathord {\supset }\beta \) and \(\mathord {\in }\beta \), or \(\rho \beta \), but on any extension of \(\mathcal {J}\), as there is no canonical derivation of \(\bot \) at all.
Troubles with Prawtiz’s definition arises however when we consider the derivations \(\lnot \mathscr {R}\) and \(\mathscr {R}\) of \(\lnot \rho \) and \(\rho \). Although \(\lnot \mathscr {R}\) and \(\mathscr {R}\) are both closed and canonical (and actually \(\beta \)-normal as well) if we try to evaluate their validity using the clauses of Prawitz’s definition, we obtain contradictory results.
Consider the immediate subderivation of \(\lnot \mathscr {R}\):

Using Prawitz’s definition, we can easily show that the derivation (\(*\)) is valid relative to \(\mathcal {J}\) and any arbitrary atomic system \(\mathcal {S}\). Being an open derivation, it is valid relative to \(\mathcal {J}\) and \(\mathcal {S}\) iff for every closed derivation \(\mathscr {D}\) of \(\rho \) that is valid relative to \(\mathcal {J}'\supseteq \mathcal {J}\) and \(\mathcal {S}\), the corresponding closed instance of (\(*\)):

is valid relative to \(\mathcal {J}'\) and \(\mathcal {S}\) as well. The validity of \(\mathscr {D}\) relative to \(\mathcal {J}'\) and \(\mathcal {S}\) means that \(\mathscr {D}\) \(\mathcal {J}'\)-reduces to a valid canonical derivation, and hence that (\(**\)) \(\mathcal {J}'\)-reduces to a derivation of the following form:

(where \(\mathscr {D}'\) is valid relative to \(\mathcal {J}'\) and \(\mathcal {S}\)). Now observe that (\(***\)) \(\beta \)-reduces to:

which is warranted to be valid by the validity of \(\mathscr {D}'\).
We have therefore shown that (\(*\))—i.e. the immediate subderivation of \(\lnot \mathscr {R}\)—is valid relative to \(\mathcal {J}\) and \(\mathcal {S}\). Hence so are \(\lnot \mathscr {R}\) and, in turn, \(\mathscr {R}\) as well (since these are closed canonical derivations with valid immediate subderivations).
Unfortunately, we can at this point easily establish the contradictory of these claims, namely that these derivations are also not valid. Consider again \(**\) and look at what happens when we take the derivation \(\mathscr {D}\) to be \(\mathscr {R}\). We thereby obtain a particular closed instance of (\(*\)), namely the derivation \(\mathbf {R'}\) (see Sect. 4.2). As we know, \(\mathbf {R'}\) does not reduce to canonical form, thus (\(*\)) (and hence \(\lnot \mathscr {R}\) and \(\mathscr {R}\) as well) are not valid.
The contradiction we arrived at has a clearly identifiable cause, namely the application of Prawitz’ definition of validity to derivations of \(\texttt{NI}^{\mathbin {\supset }\bot \in }\) and \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\). Prawitz’ definition is by induction on the joint complexity of the conclusion and the undischarged assumptions of derivations. Thus, the induction underlying the definition is well-founded only when the introduction rules satisfy the following complexity condition: the consequence of any application of an introduction rule must be of higher logical complexity than its immediate premises and assumptions discharged by the rule application. This condition is not satisfied by either \(\in \)I or \(\rho \)I. Hence, when applied to derivations of \(\texttt{NI}^{\mathbin {\supset }\bot \in }\) or \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\) the definition has to be understood as a partial inductive definition in the sense of Hallnäs [29].2
This situation prompts to revise the definition of validity of Prawitz in order to be able to consistently apply it to the derivations of calculi such as \(\texttt{NI}^{\mathbin {\supset }\bot \in }\) and \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\). We will in particular explore the prospects of defining a notion of validity on which
-
as in Prawitz’ definition, a necessary condition for a closed derivation to be valid is its reducing to a canonical derivation (and this is enough to rule out \(\textbf{R}\) as invalid);
-
both \(\lnot \mathscr {R}\) and \(\mathscr {R}\) qualify as valid.
This is not the only possible choice. One could for instance try to figure out a notion of validity on which not only \(\textbf{R}\), but also both \(\lnot \mathscr {R}\) and \(\mathscr {R}\) qualify as invalid. Such a notion of validity may be more congenial to the advocates of solutions to the problem of paradoxes based on the rejection of the structural rule of contraction (see Sect. 4.4). Yet a further option would be of course that of denying the acceptability of the introduction rule for \(\rho \) due to its violating the complexity condition, and thereby rejecting the idea of revising Prawitz’ definition altogether. We take our choice to be the closest in spirit to the remarks of Tennant and Prawitz quoted at the beginning of this chapter. The derivations \(\lnot \mathscr {R}\) and \(\mathscr {R}\) are normal and the remarks of Tennant and Prawitz seem to suggest that this is a sufficient condition to qualify as valid in a calculus like \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\).
The goal of this investigation is not that of arguing in favor of a formal system, such as that of naive set theory, in which normalization fails, but rather of bringing to light the assumptions that are needed to make sense of the core idea of proof-theoretic semantics (i.e. that a derivation is valid iff it denotes a proof) in the context of paradoxical languages. Whether such assumptions should be accepted or rejected, will be mainly left to the reader, but we will try to make clear what does the acceptance or rejection of these assumptions commit one to.
To regard both \(\lnot \mathscr {R}\) and \(\mathscr {R}\) as valid is tantamount to commit oneself to accepting that both \(\lnot \rho \) and \(\rho \) have a proof, and thus to endorse a form of paraconsistency. As we will show, this gives rise to two distinct issues: the first concerns the way in which the BHK explanation should be extended, so as to provide an explanation of what a proof of \(\rho \) is; the second concerns the way in which the BHK clause for implication has to be understood in a paradoxical language.
Before giving an exact formulation of the alternative definition of validity and coping with these two issues, we will discuss a further problem arising by the adoption of a notion of validity on which both \(\lnot \mathscr {R}\) and \(\mathscr {R}\) but not \(\textbf{R}\) qualify as valid: namely, that of a proper understanding of the correctness of rules.
4 The Local Correctness of an Inference
If we intend to revise the notion of validity along the lines envisaged, we immediately realize that we also need to revise the notion of correctness of an inference rule. Given the prospected revision of the notion of validity, the correctness of an inference rule cannot be any more defined as the fact that, given proofs of its premises, the rule yields a proof of its consequence: that would be too strong a requirement in the presence of paradoxes.
If we look again at \(\textbf{R}\), we can observe that it is obtained by applying \(\supset \)E to two closed derivations that we want to regard as valid. As we want to deny the validity of \(\textbf{R}\), we have that, on the revised notion of validity, by applying \(\supset \)E to two valid derivations one would obtain an invalid one. Thus this would be a case in which \(\supset \)E would not preserve validity.3
Hence, would we keep Prawitz’ definition of correctness (see Definition 2.3 in Sect. 2.10)—according to which an inference is correct iff it yields closed valid derivations when applied to closed valid derivations—we would be forced to say that \(\supset \)E is not correct.
This we take as a reason to revise the notion of correctness as well. We do not want the adoption of the (currently only envisaged) notion of validity to force us to deny the correctness of \(\supset \)E: the proper diagnose for the fact that \(\supset \)E fails to preserve (the revised notion of) validity is not that \(\supset \)E is not correct but rather the presence of \(\rho \). How can this intuition be spelled out?
As observed in Sect. 2.11, the availability of reduction procedures usually suffices to warrant the correctness of the elimination rules with which they are associated. It should now be clear that, when the language contains paradoxical expressions such as \(\rho \), this is no more the case. To repeat, while in standard cases the existence of reduction procedures associated with the rule is enough to show that the rule preserves validity, this not so in general.
The problem with Prawitz and Dummett’s definitions of validity and correctness is that they are too much tied to the standard cases. A way out of the problem is just to deny that preservation of validity is the right way of characterizing the correctness of rules. Although in standard cases correct rules do transmit validity, it is way too demanding to expect a correct rule to preserve validity in all cases.
The fact that the availability of reduction procedures for an inference rule suffices to warrant validity preservation tells us something important about the standard cases. However, from the fact that in general this does not happen, it should not follow that the availability of reduction procedures for an inference is not sufficient for the rule to be correct. Rather, it should only signal that we are not in a standard case.
The application of a reduction procedure “cuts away” two consecutive applications of an introduction rule and of an elimination rule. Plausibly, a necessary condition for “standardness” (i.e. for the availability of reduction procedures to be sufficient for the correctness of the rule in Prawitz’s sense) is that all reduction procedures under consideration have the following property: The formulas which are conclusion of the application of the introduction and the major premise of the application of the elimination rule cut away by the application of the reduction procedures must be of a higher logical complexity than the formulas surrounding it. Clearly, \(\rho \beta \) violates such a condition.4
As detailed in Sect. 2.10, given Prawitz and Dummett’s definitions of validity and correctness, the correctness of different kinds of rules is shown in substantially different ways. The correctness of introduction rules is almost “automatic”, and this reflects their “self-justifying” nature, i.e. the fact that they “define” the meaning of the logical constant involved (see in particular Note 22 to Chap. 2). Elimination rules, as well as other non-introductory inference rules, are shown to be correct by appealing to reduction procedures. There we stressed however that in the case of rules which are neither introduction nor elimination rules, reduction procedures boil down to derivations of the rules from the introduction and elimination rules. It is therefore natural to distinguish between the correctness of introduction rules (by definition), of elimination rules (which means that they are in harmony with the introduction rules) and of other rules (which means that they are derivable from introduction and elimination rules.
Rather than obtaining this articulation of correctness as a byproduct of the definition of correctness in terms of validity (as in Prawitz-Dummett PTS), we propose to use it as a direct definition of a notion of correctness (to distinguish it from Prawitz’ definition, we refer to this notion as ‘correctness\(^*\)’):
Definition 5.1
(Correctness \(^*\) of an inference rule) An inference rule schema is correct\(^*\) iff
-
It is an introduction rule;
-
it is an elimination rule for \(\dagger \) that belongs to the collection of elimination rules obtained by inversion from the collection of introduction rules for \(\dagger \).
-
it is derivable from the introduction and elimination rules governing the expressions that occur in the rule.5
The adoption of Definition 5.1 instead of Prawitz’s Definition 2.3 results in a better analysis of the situation. Even adopting a notion of validity on which both \(\lnot \mathscr {R}\) and \(\mathscr {R}\) count as valid and \(\textbf{R}\) as invalid, \(\mathbin {\supset }\)E still qualifies as correct\(^*\) since it is in harmony with \(\mathbin {\supset }\)I.
It is true that \(\mathbin {\supset }\)E does not preserve validity in all cases. But this is due to the presence of the paradoxical \(\rho \) (indeed, in standard cases \(\mathbin {\supset }\)E does preserve validity).
5 Local Correctness Versus Global Validity
It may be retorted that the revision the definition of correctness according to Definition 5.1 has the drawback of forcing the rejection of the principle (V), according to which an argument is valid if it is constituted by correct rules (see Sect. 2.11). All rules in \(\textbf{R}\) are correct\(^*\) but we want to deny that the argument as a whole is valid.
As we saw, although Prawitz rejected (V) as a definition of validity, he stressed that the principle still holds under his definitions of validity and correctness. On the contrary, by replacing Prawitz’s Definition 2.3 with Definition 5.1 we are forced to give up principle (V).
Is this really an unwanted consequence? I do not think so.
The revised definition of the correctness of an inference makes the two notions of ‘being valid’ and ‘being constituted by applications of correct\(^*\) inference rules’ diverge. As we saw, the semantic content of an argument being valid is its having a denotation. In the following, I will argue that, the notion of ‘being constituted by applications of correct\(^*\) inference rules’ has also a genuine semantic content which, furthermore, should be kept distinct from that of having a denotation: Namely, having sense.
According to Dummett [11], what Frege called the sense of an expression is best understood as a procedure, i.e. a set of instructions, to determine its denotation. Without entering the details of the idea, it should be clear enough that in general, it may be the case that although one is in possession of a set of instructions to identify something, any attempt to carry out the instructions fails. We may refer to such a situation as one in which the set of instructions is inapplicable. The inapplicability may depend on there not being a something satisfying the conditions codified in the set of instructions. Or on factual contingencies (such as time and space limitations). But one may also conceive cases of, say, structural inapplicability of the instructions. That is, cases in which the instructions are shaped in such a way that one cannot successfully bring to the end the procedure they codify.
The core intuition underlying the notion of validity is that proofs are denoted by valid arguments. As we argued in Sect. 2.8, in harmonious calculi normal derivation can be seen as the most direct way of representing proofs. Although it is an abuse of language (since derivations and proofs belong to two distinct realms) it is tempting to “identify” proofs with normal derivations and thus, to view reduction to normal form as the process of interpreting derivations, i.e. as the process of ascribing them their denotation.
Dummett’s model of sense perfectly applies to this picture: the set of instructions telling how a derivation is to be reduced to normal form is the set of instructions telling how to identify the denotation of the derivation, i.e. it is the sense of the derivation. In the case of \(\textbf{R}\), we have a derivation that does not reduce to canonical form, it does not denote a proof, i.e. it lacks a denotation. However, as there is a reduction procedure associated with each of its elimination rules, we can say that also in this case there is a procedure to determine its denotation. Thus, there is a sense associated with the derivation. However, although each step of the procedure in which the sense of \(\textbf{R}\) consists can be carried out, it is not possible to bring the procedure to the end, due to its entering the oscillating loop.
The result of replacing Definition 2.3 with Definition 5.1 is thus that of making room, alongside the idea that derivations have a denotation, for the idea that they also have a sense, where having sense means that they are constituted by applications of inference rules which are correct\(^*\).
Taking ‘having sense’ as the semantic content of ‘being constituted by applications of correct\(^*\) inferences rules’ and ‘having a denotation’ as the semantic content of ‘being valid’, we can express the failure of principle (V) as a feature of PTS: Namely that of allowing the existence of derivations endowed with sense which lack a denotation.
The alternative picture resulting from the adoption of Definition 5.1 returns an enlightening picture of paradoxes. Paradoxical derivations are not nonsense. On the contrary, what is paradoxical in them is exactly that they make perfectly sense. But putting this sense in action reveals their awkward features. For a derivation to be paradoxical, it must have sense. Its being paradoxical means that it does not denote a proof of its conclusion.
6 \(\rho \) Versus \(\texttt{tonk}\)
To really appreciate that the proposed distinction between sense and denotation is not an ad hoc solution to the problem of paradoxes, I believe it is worth comparing \(\textbf{R}\) with another kind of arguments for \(\bot \), namely those that can be constructed in \(\texttt{NI}^{\mathbin {\supset }\bot \texttt{tonk}}\), the extension of \(\texttt{NI}^{\mathbin {\supset }\bot }\) with \(\texttt{tonk}\)’s rules. The following closed derivation of \(\bot \) is obtained by replacing the atomic proposition p with \(\bot \) in the derivation \(\textbf{T}\) discussed in Sect. 1.7:

The common features of \(\textbf{R}\) and \(\textbf{T}'\) are the following:
-
they have \(\bot \) as conclusion;
-
they are both non-canonical, since they end with an elimination rule;
-
they are both irreducible to canonical form.
Being both not reducible to canonical form, they both qualify as invalid, that is, they both fail to denote a proof.
Nonetheless, there is a crucial difference between \(\textbf{R}\) and \(\textbf{T}'\). On the one hand, \(\textbf{R}\) cannot be reduced to canonical form because it is not normal and if one tries to apply the reduction procedures associated with its elimination rules one enters an oscillating loop. On the other hand, \(\textbf{T}'\) does not reduce to canonical form because no reduction is (nor can be) associated with tonk’s rules, that is, because it is already a normal argument.
As the derivation \(\textbf{T}\) discussed in Sect. 1.7, \(\textbf{T}'\) is normal, since there is no reduction procedure that can be applied to it. This of course does not depend on the set of reduction procedures one is considering because, under any plausible notion of reduction procedures, there cannot be a reduction procedure associated with patterns constituted by an application of \(\texttt{tonk}\,\)I followed immediately by an application of \(\texttt{tonk}\,\)E.
As observed, two are the features of \(\texttt{NI}\) which suggested the development of a semantics on proof-theoretic basis. The first one is that every derivation \(\beta \)-normalizes; the second is the canonicity of closed \(\beta \)-normal derivations. The additions of \(\rho \) and \(\text {\texttt {tonk}}\) to a well-behaving calculus (such as \(\texttt{NI}^{\mathbin {\supset }\bot }\)) pose two different kinds of problems. On the one hand, the addition of \(\rho \) blocks normalization, but does not threat the canonicity of closed \(\beta \)-normal derivations : Although not every argument normalizes (as exemplified by \(\textbf{R}\)), closed normal derivations always end with an introduction rule. On the other hand, in spite of the addition of \(\text {\texttt {tonk}}\) normalization still holds (\(\textbf{T}'\) is normal since there is no reduction which can be applied to it); but the normality of \(\textbf{T}'\) ruins the semantic significance of closed normal derivation, since it is no more the case that every closed normal derivation ends with an introduction.
Observe that although \(\textbf{R}\) is invalid, it is composed of applications of correct\(^*\) inference rules. This is not the case for \(\textbf{T}'\): as there is no reduction procedure associated with tonk’s elimination rule, the rule is neither correct nor correct\(^*\). In semantic terms, not only \(\textbf{T}'\) (like \(\textbf{R}\)) lacks a denotation, but also a procedure to determine it, since we do not have any reduction procedure telling us how to transform it into canonical form. In other words, \(\textbf{T}'\) not only lacks a denotation but also sense. An argument such as \(\textbf{T}'\) thus fails to count as paradoxical. It is just nonsensical.
7 Paradox and Partial Functions
Considerations that are fully analogous to those that prompted the revision of the definition of correctness apply to the validity of open derivations.
On the revised (but so far only envisaged) notion of validity, on which both \(\lnot \mathscr {R}\) and \(\mathscr {R}\) are to count as valid, we have that there are at least one proof of \(\lnot \rho \) and one of \(\rho \). According to BHK a proof of \(A\mathbin {\supset }B\) is a function from proofs of A to proofs of B. As \(\lnot \rho \) is shorthand for \(\rho \mathbin {\supset }\bot \), a proof of \(\lnot \rho \) is a function from proofs of \(\rho \) to proofs of \(\bot \).
The provability of both \(\lnot \rho \) and \(\rho \) together with the unprovability of \(\bot \) forces the view that, in presence of paradoxical phenomena, the functions proving an implication must be understood as being sometimes partial. In particular, the proof of \(\lnot \rho \) denoted by \(\lnot \mathscr {R}\) is a function from proofs of \(\rho \) to proofs of \(\bot \), but when we apply this function to the proof of \(\rho \) denoted by \(\mathscr {R}\), we do not obtain a proof of \(\bot \).
The derivation \(\lnot \mathscr {R}\) denotes a proof of \(\lnot \rho \) that is a function as course-of-value obtained by abstraction from the function as unsaturated entity denoted by the derivation (\(*\)). Both the function as course-of-value and the function as unsaturated entity are however partial, in that they should yield proofs of \(\bot \) when applied to proofs of \(\rho \).
This situation brings to the fore the fact that, in the context of a paradoxical language, we cannot expect the validity of an open derivation to consist in the validity of its closed instances (i.e. that when its undischarged assumptions are replaced by closed valid derivations one obtains a closed valid derivation for the conclusion). In particular, the result of replacing the derivation \(\mathscr {R}\) for the undischarged assumptions of (\(*\)) yields the invalid derivation \(\mathbf {R'}\). In these contexts, a weaker notion of validity for open arguments should be adopted, a notion of validity which is not based on the idea of validity-transmission.
A radical way of weakening the notion of validity for open derivations consists in simply requiring for an open derivation to qualify as valid that it is constituted by inference rules that are correct\(^*\). We therefore obtain the following (to distinguish it from Prawitz’ definition, we refer to this notion as ‘validity\(^*\)’).
Definition 5.2
(Validity \(^*\)) A derivation \(\mathscr {D}\) is valid\(^*\) with respect to a set of reduction procedures \(\mathcal {J}\) iff:
-
It is closed and it \(\mathcal {J}\)-reduces to a canonical derivation whose immediate subderivations are valid\(^*\) with respect to \(\mathcal {J}\);
-
or it is open and it is constituted by correct\(^*\) inference rules.
The revised definition achieves its goals, in that \(\textbf{R}\) qualifies as non-valid\(^*\) (since it is closed but is not reducible to canonical form) whereas both \(\lnot \mathscr {R}\) and \(\mathscr {R}\) qualify as valid\(^*\) (they are closed canonical derivations, and their immediate subderivation are valid, being constituted by correct\(^*\) inference rules. The derivation \(\textbf{T}'\) fails to be valid (since, like \(\textbf{R}\) it is closed but not reducible to canonical form), and so is the following derivation:

This derivation is normal (i.e. cannot be reduced any further) and canonical, but its immediate subderivation is not valid, as it is constituted by an application of \(\texttt{tonk}\, \)E, an inference rule which is not correct\(^*\).
It is easy to check that, in calculi whose rules are in harmony, for a closed derivation to be valid\(^*\) means to be reducible to a \(\beta _w\)-normal derivation, and conversely, derivations that are reducible to \(\beta _w\)-normal form qualify as valid\(^*\). This is the aspect in which the definition of validity\(^*\) remains faithful to Prawitz’ original definition (see Sect. 2.9).
The differences are however substantial. As detailed in Sect. 2.10, in the case of the Prawitz-Dummett approach it is the notion of correctness of an inference that depends on that of validity. On the contrary, it is our notion of validity\(^*\) to depend on that of correctness\(^*\).
As we observed, Prawitz’s definition of validity proceeds by induction on the joint complexity of the conclusion and the undischarged assumptions. Thus, for the induction to be well-founded, introduction rules should satisfy the complexity condition: in the introduction rules the consequence of the rule must be of higher logical complexity than all immediate premises and all dischargeable assumptions. The different clause for open derivations makes the definition of validity\(^*\) well-founded even in cases in which Prawitz’s definition is not. The reason is that in order to check whether a closed canonical derivation is valid\(^*\) one has to check the validity\(^*\) of its immediate subderivations (like in the case of Prawitz’s validity). The difference is however that the validity\(^*\) of open subderivation consists in their being constituted by correct\(^*\) inference rules (and not, as in Prawitz’s definition in transmitting closed validity from the assumptions to the conclusion). Hence, in order for the definition to be well-founded, it is enough that the introduction rules satisfy a weaker complexity condition: the consequence of any application of an introduction rule must be of higher logical complexity of those immediate premises which are the conclusion of closed subderivations.
The introduction rule for \(\rho \) does not satisfy even this weaker condition, in that it does not discharge any assumption and the complexity of the premise is higher than that of the consequence, thus inducing the need of checking the validity\(^*\) of a closed derivation of \(\lnot \rho \) in evaluating the validity\(^*\) of a closed canonical derivation of \(\rho \), hence giving no warrant that the process of checking the validity of a given derivation in \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\) terminates. However, the well-foundedness of validity\(^*\) can be warranted by considering the following revised version of the paradoxical \(\rho \), which we call \(\rho ^*\) (cf. also [76]):

The reduction for \(\rho ^*\) is the following:

Using \(\rho ^*\) we can construct a valid closed normal derivation of \(\rho ^*\) as follows:

and by combining two copies of it using the elimination rule for \(\rho ^*\) one obtains the following closed non-normalizing derivation of \(\bot \):

As desirable, this derivation is not valid\(^*\) because it is closed and it does not reduce to canonical form (as the reduction of its only maximal formula occurrence using \(\rho ^*\beta \) gives back the derivation itself).6 As it will be shown in the final sections of the chapter, the proposed modification of Prawitz’ definition may still be found demanding in some respects. Before discussing these issues, however, we wish to address a further issue, namely the sense in which the rules for \(\rho \) can be said to endow it with meaning.
8 Meaning Explanations for Paradoxes
How can one state the proof-conditions for \(\rho \) or \(\rho ^*\)? Following the pattern of explanation common to the standard logical constants, to answer this question we stipulate an operation on proofs such that the result of applying it to a proof of \(\lnot \rho \) is a proof of \(\rho \), this operation reflecting the kind of negative self-reference encoded in the instance of \(\in \)I which entitles one to pass over from \(\lnot \rho \) to \(\rho \). The introduction rule for \(\rho \) stipulates that a proof of \(\rho \) is what one obtains by applying this operation to a proof of \(\lnot \rho \). The elimination rule for \(\rho \) does no more than stating that this is the only means of constructing proofs of \(\rho \) (cf. Sect. 3.6).
Though weak, these principles are strong enough to establish interesting facts, such as for instance the existence of both a proof of \(\rho \) and of its negation. At the same time, these principles are not arbitrary, as shown by the fact that they do not allow to establish the existence of proofs of \(\bot \).
Similarly, a BHK-clause-like explanation of the proof-conditions of \(\rho ^*\) would be the following: a proof of \(\rho ^*\) is the result of applying a self-referential abstraction-like operation to a function (as unsaturated entity) from proofs of \(\rho ^*\) to proofs of \(\bot \). The result of this operation are objects whose nature is similar to that of the functions as courses-of-value that constitute proofs of propositions of the form \(A\supset B\), with the crucial difference that proofs of \(\rho ^*\) take proofs of \(\rho ^*\) as arguments and yields proofs of \(\bot \) as values.
As in the case of the proof of \(\lnot \rho \) denoted by \(\lnot \mathscr {R}\), these functions must be sometimes be understood as partial. Moreover, it is easy to see that, in a calculus equipped with the rules for \(\rho ^*\), the proofs of implications must be understood as functions (as course-of-value) which sometimes fail to be total as well. For example, this is the case for the proof denoted by the following valid\(^*\) derivation:

which does not yield a proof of \(\bot \) when applied to the proof of \(\rho ^*\) denoted by \(\mathscr {R}^*\) above, but only a derivation which fails to denote (being closed and not being reducible to canonical form).
In both cases, however, it is clear that compositionality is violated, since their introduction rules fail to explain the meaning of \(\rho \) and \(\rho ^*\) in terms of that of propositions of lower complexity. This could be taken as constituting too big a departure from standard meaning explanation to qualify as acceptable.
It is however worth stressing, that Dummett himself conceives the compositionality of meaning as compatible with local forms of circular meaning-dependencies, presenting the names of colors as a typical example of words whose meaning is interdependent and cannot but be learned together. The case of an expression such as \(\rho ^*\) is the limit case of a circular meaning-dependency in which to understand an expression one needs a previous understanding of that very expression. If the idea of self-dependence is too disturbing, it is easy to see that the formulation of paradoxes does not rely on it in an essential way. If one considers instead of \(\rho ^*\) the pair of expressions \(\sigma \) and \(\tau \) governed by the following rules:


one can easily reconstruct Jourdain’s paradox and the considerations developed in the present chapter equally apply to a calculus equipped with both \(\sigma \) and \(\tau \) (see [108], p. 281).
It is true that there is a fundamental difference between colors and paradoxes, namely that in the case of paradoxes we have chains of dependencies which make an expression depend “negatively” on itself. It is however far from obvious why compositionality should be compatible with positive but not with negative forms of dependency. It therefore seems that the burden of proof lays on the side of who wants to deny the viability of a PTS account of paradoxical expressions, rather than on the side of who wants to defend it.
9 Conservativity
As a matter of fact, the adoption of validity\(^*\) for derivations in \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\) implies the existence of at least one proof of \(A\mathbin {\supset }B\) for any A and B, denoted by a derivation of the following form:

Being closed and canonical, any derivation of this form is valid\(^*\) iff its immediate subderivation is valid\(^*\), which in fact is the case since we defined an open derivation to be valid\(^*\) iff it is constituted by correct rules, and \(\mathbin {\supset }\)E, \(\bot \)E as well as all rules applied in \(\boldsymbol{R}\) are correct since they are either introduction rules or harmonious elimination rules.
It is true that one may argue that this is unproblematic, by claiming that all such function are undefined for every argument . However, the need of introducing partial function in the explanation of the meaning of implication seems to be essentially tied to paradoxical expressions. Thus if A and B do not contain \(\rho \) as a subformula, one may expect that if there is a proof of \(A\mathbin {\supset }B\), the proof should be a function defined for all its arguments.
In other words, one may wish to adopt a notion of validity such that if there is a valid derivation of a \(\rho \)-free proposition A in \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\), there must be a valid derivation of A already in \(\texttt{NI}^{\mathbin {\supset }\bot }\). This requirement is strongly reminiscent of Belnap’s conservativity with a crucial different. While Belnap’s requirement of conservativity is formulated using derivability (i.e. existence of derivations), we formulated the requirement for “valid derivability” (i.e. existence of valid derivations).
As we have seen in the previous chapter, although the rules for \(\rho \) are in harmony, they extend in a non-conservative way derivability in \(\texttt{NI}^{\mathbin {\supset }\bot }\). In the extension \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\) of \(\texttt{NI}^{\mathbin {\supset }\bot }\), the proposition \(\bot \) (which belongs to the language of the restricted calculus) is derivable, although it is not derivable in the original calculus.
A conservativity result of the kind envisaged can however be established for \(\beta \gamma \)-normal derivations of \(\texttt{NI}^{\mathbin {\supset }\bot }\): as we will now show, if neither A nor \(\Gamma \) contain \(\rho \) as subformula, then there is a \(\beta \gamma \)-normal derivation of A from \(\Gamma \) in \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\) if and only if there one in \(\texttt{NI}^{\mathbin {\supset }\bot }\). This will be taken as a reason to consider a further notion of validity by strengthening the notion of valid\(^*\) derivation to the effect that a derivation is valid iff it \(\beta \gamma \)-reduces to a \(\beta \gamma \)-normal derivation.
As we have seen, \(\beta \)-reduction—and a fortiori \(\beta \gamma \)-reduction—is not normalizing in \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\) with the derivation \(\textbf{R}\) providing a typical counterexample. In spite of this, \(\beta \gamma \)-normal derivations in \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\) also have the peculiar structure of \(\beta \gamma \)-normal derivations in \(\texttt{NI}^{\mathbin {\supset }\bot }\) (see Sect. 3.5). Prawitz [64] already observed that in \(\texttt{NI}^{\mathbin {\supset }\in }\), the tracks in \(\beta \)-normal derivations are still divided into an introduction and elimination part. This holds for \(\beta \gamma \)-normal derivation in \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\) as well. The reason is essentially the same as in \(\texttt{NI}^{\mathbin {\supset }\bot }\): In order for the consequence of an application of an introduction (or of \(\bot \)E) to act as the major premise of an application of an elimination, the derivation must be non-normal.
However, given the standard definition of subformula.
Definition 5.3
(subformula)
-
For all A, A is a subformula of A;
-
all subformulas of A and B are subformulas of \(A\mathbin {\supset }B\),
the neat subformula relationships between the formula occurrences constituting a track of a \(\beta \gamma \)-normal derivation are lost in \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\). To wit, both in \(\lnot \mathscr {R}\) and \(\mathscr {R}\) we need to pass through \(\lnot \rho \) in order to establish \(\bot \) from \(\rho \). Thus, \(\beta \gamma \)-normal derivations in \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\) do not enjoy the subformula property.
The reason for this is that the premise of \(\rho \)I is the formula \(\lnot \rho \) which is more complex than its consequence \(\rho \). If we take the rules of a connective to codify semantic information, this situation is unsurprising. The rule \(\mathbin {\supset }\)I gives the meaning of an implication in terms of its subformulas, and thus the semantic complexity of an implicational formula corresponds to its syntactic complexity. In the case of \(\rho \), the rule \(\rho \)I gives the meaning of \(\rho \) in terms of the more complex formula \(\lnot \rho \). Whereas the syntactic complexity of formulas in the \(\{\mathbin {\supset },\bot ,\rho \}\)-language fragment is well-founded, one could say that their semantic complexity is not.
This informal remark can be spelled out by defining the following notion, which in lack of a better name we call ‘pre-formula’. Intuitively, it reflects the semantic complexity of a formula, in the sense that the pre-formulas of a formula A are those formula one has to understand in order to understand A.
Definition 5.4
(Pre-formula)
-
For all A, A is a pre-formula of A;
-
all pre-formulas of A and B are pre-formulas of \(A\mathbin {\supset }B\);
-
all pre-formulas of \(\lnot \rho \) are pre-formulas of \(\rho \).
The seemingly inductive process by which pre-formulas are defined is clearly non-well-founded. However, this is not a reason to reject it as a definition.7 Indeed, the notion of pre-formula turns out to be very useful in describing the structure of tracks in \(\beta \gamma \)-normal derivations in \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\): The neat subformula relationship holding between the members of a track in \(\beta \gamma \)-normal derivations in \(\texttt{NI}^{\mathbin {\supset }\bot }\) are replaced by pre-formula relationships between members of a track in \(\beta \gamma \)-normal derivations in \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\).
By replacing ‘subformula’ with ‘pre-formula’, one can establish a fact analogous to to Fact 4 (see Sect. 3.5) for \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\), from which one obtains the following:
Fact 5
(Pre-formula property) All formulas in a \(\beta \gamma \)-normal derivation in \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\) are either pre-formulas of the conclusion or of some undischarged assumption.
Proof
By induction on the order of tracks (see proof of Fact 2 in Sect. 1.5). \(\blacksquare \)
We thus have that.
Fact 6
If \(\Gamma \) and A are \(\rho \)-free, then there is a \(\beta \gamma \)-normal derivation of A from \(\Gamma \) in \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\) iff there is one in \(\texttt{NI}^{\mathbin {\supset }\bot }\).
Proof
This follows immediately from Fact 5 together with the fact that if \(\rho \) does not occur in a formula than it is not a pre-formula of it (which can be established by induction on the degree of formulas). \(\blacksquare \)
That is, \(\beta \gamma \)-normal derivability in \(\texttt{NI}^{\mathbin {\supset }\bot \rho }\) is a conservative extension of \(\beta \gamma \)-normal derivability in \(\texttt{NI}^{\mathbin {\supset }\bot }\). More briefly, we will refer to this fact by saying that the rules for \(\rho \) are conservative over \(\beta \gamma \)-normal derivability in \(\texttt{NI}^{\mathbin {\supset }\bot }\).8
Fact 6 suggests to strengthen the condition for the validity of open derivations by requiring not only that they are constituted by correct\(^*\) inference rules, but also that they reduce to \(\beta \gamma \)-normal form. Accordingly, for closed derivations in a calculus consisting of correct\(^*\) inference rules, in order to qualify as valid it would not be enough for them to reduce to \(\beta _w\)-normal derivations (which is what being valid\(^*\) boils down to) but to reduce to a \(\beta \gamma \)-normal derivation. This would yield a further alternative to Prawitz’s validity, which we may call validity\(^{**}\):
Definition 5.5
(Validity \(^{**}\)) A derivation is valid\(^{**}\) iff it is constituted by correct inference rules and it reduces to a \(\beta \gamma \)-normal derivation.
Though valid\(^*\), the derivations of the form (5.9.1) are not valid\(^{**}\) (as they fail to reduce to a \(\beta \gamma \)-normal derivation). The adoption of validity\(^{**}\) as the notion to characterize the closed derivations having a denotation would allow one to avoid to accept that any proposition of the form \(A\mathbin {\supset }B\) has a proof.
A general concern undermines however the notion of validity\(^{**}\), namely it requires to apply reductions not only to closed, but also to open derivations.
The validity\(^*\) of open derivations is not defined in term of the validity\(^*\) of its closed instances, and in this sense it represents a major deviation from the traditional notion of Prawitz. However, validity\(^*\) remains faithful to the idea that reduction is of semantic significance only for closed derivations, and not for open derivations. This very fact, on the other hand, would be denied by the adoption of validity\(^{**}\), since validity\(^{**}\) is defined in terms of reduction for open derivations as well.
Compared to validity\(^*\), the advantage of adopting validity\(^{**}\) is the fact that the addition of the rules for a paradoxical expression like \(\rho \) does not enrich the set of proofs in the \(\rho \)-free language. On the other hand the addition of the rules for a paradoxical expression result in novel valid\(^*\) closed derivations of propositions belonging to the \(\rho \)-free language. Whether this is a drawback for validity\(^*\) is debatable, since in general it is not the case that the addition of a new expression (governed by harmonious rules) yields a conservative extension of the language to which it is added (a counterexample, mentioned by Prawitz [71], is provided by the rules for second-order quantifiers, which extend in a non-conservative way first-order arithmetic).
To conclude, we ended up with two possible accounts of validity which can be applied to a paradoxical language. One is validity\(^*\), that is more faithful to the basic philosophical tenet that reduction is of semantic significance only for closed derivations, but has the drawback of making room for unwanted proofs of large classes of propositions (in particular for each pair of propositions A and B there is at least one function from proofs of A to proofs of B).
The other is validity\(^{**}\) which is more restrictive in that, although its adoption leads in some cases to the existence of both a proof of a proposition and of its negation (e.g. \(\rho ^*\) and \(\lnot \rho ^*\)), it tames the proliferation of undesired proofs of propositions belonging to the paradox-free fragment. However, this requires a major departures from the Prawitz-Dummett conception of validity: namely it requires to ascribe semantic significance to the notion of reduction for open derivations, which requires the adoption of an extensional conception of functions from proof to proof.
Notes to This Chapter
-
1.
In recent years Tennant has further developed his analysis of paradoxes by proof-theoretic means (see Note 4 to Chap. 4). However, he did not explored the connection between the proof-theoretic analysis of paradoxes and the idea that proofs are the denotations of formal derivations.
-
2.
In other words, Prawitz’ definition of validity as applied to \(\texttt{NI}^{\mathbin {\supset }\bot \in }\) is a meta-linguistic analog of the paradoxical definition of R discussed in Sect. 4.2.
-
3.
In the type-theoretic setting (see Note 6 to Chap. 4), this means that \(\texttt{app}(x,y)\) does not denote a total function from proofs of \(A\supset B\) and A to proofs of B, since when we replace for x and y the terms corresponding to the derivations \(\lnot \mathscr {R}\) and \(\mathscr {R}\) we obtain the non-denoting term corresponding to \(\textbf{R}\). In the untyped \(\lambda \)-calculus, this corresponds to the fact that application does not preserve normalizability in the untyped setting.
-
4.
In sequent calculus, this condition is essentially that reductions for a principal cut on a formula A (or, in one-sided calculi, on two formulas A and \(A^{\bot }\) having the same complexity) yield one or more cuts on formulas of strictly lower complexity than A (and \(A^\bot \)). We also remark that, in the light of the considerations made in Sect. 4.4, it is clear that this condition is plausible only in presence of contraction. In its absence, it is unnecessary restrictive.
-
5.
The idea that the correctness of an inference rule can be shown by deriving it from other, previously accepted, rules, is referred to by Dummett [12] as ‘the proof-theoretic justification of first-grade’. A justification of this kind requires obviously that some other rules have been previously justified as correct. The notion of correctness* embodies this idea, in that introduction rules are correct* by fiat; elimination rules are correct* iff they are in harmony with the introduction rules; and all other rules are justified using introduction and elimination rules. Dummett [12] follows a different path: he rather argues that there must be more powerful means of justification which he calls justifications of second and of third degree respectively. A justification of third degree amounts to showing that whenever a rule is applied to valid closed canonical derivations for the premises it yields a valid closed canonical derivation of the conclusion. This essentially coincide with showing that the rule is correct in Prawitz’s sense, as discussed in Sect. 2.10 (with some caveats due to the different way in which Dummett and Prawitz define canonical derivations, see Note 23 to Chap. 1 and Notes 6 and 14 to Chap. 2).
-
6.
In a type-theoretic setting, the introduction and elimination rules could be presented as follows:

and the reduction for \(\rho ^*\) could be internalized with the following equality rule:

The derivation \(\mathscr {R}^*\) would be encoded by the term
 and the derivation \(\mathbf {R^*}\) by the term
and the derivation \(\mathbf {R^*}\) by the term
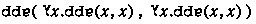 which resembles even more closely than the term associated with \(\mathscr {R}\) the untyped loopy combinator \((\lambda x.xx)(\lambda x.xx)\) (see Note 6 to Chap. 4 above).
which resembles even more closely than the term associated with \(\mathscr {R}\) the untyped loopy combinator \((\lambda x.xx)(\lambda x.xx)\) (see Note 6 to Chap. 4 above). -
7.
To see that there is nothing wrong with the notion of pre-formula one could first define the notion of immediate pre-formula as follows: (i) the immediate pre-formulas of \(A\mathbin {\supset }B\) are A and B; (ii) the immediate pre-formula of \(\rho \) is \(\lnot \rho \). The notion of pre-formula could then be introduced as the reflexive and transitive closure of the one of immediate pre-formula.
-
8.
As briefly recalled in Sect. 4.4, the notion of cut-free derivation roughly corresponds to the notion of normal derivation. The conservativity result for natural deduction parallels an analogous conservativity result in sequent calculus [78]. In that setting, one can take \(\rho \) to be governed by the following left and right rules:

Let LK \(_{\rho }\) be the extension of the (cut-free) implicative fragment of the sequent calculus for classical logic LK, whose rules are:

together with identity, exchange, weakening and contraction (for the present scopes, one could equivalently consider an intuitionistic or minimal variant of the calculus). The following hold:
Fact 7
For \(\Gamma \) and \(\Delta \) \(\rho \)-free: \(\Gamma \Rightarrow \Delta \) is deducible in LK iff it is deducible in LK \(_\rho \).
Proof
Given the rules for LK \(_\rho \) if there is no occurrence of \(\rho \) in the consequence of a rule-application then there is none in the premises of the rule-application. Thus if the end-sequent of a derivation is \(\rho \)-free, the whole derivation is. \(\blacksquare \)
There is however a remarkable difference between the natural deduction and sequent calculus approach. In sequent calculus, the same reasoning allows to establish a result analogous to Fact 7 for \(\texttt {LK}_{\mathbin {\texttt{tonk}}}\), the extension of \(\texttt {LK}\) with the following rules for \(\texttt{tonk}\):

On the other hand, the rules for \(\texttt{tonk}\) are not conservative over \(\beta \gamma \)-normal derivations in \(\texttt{NI}^{\mathbin {\supset }\bot }\): the derivation \(\textbf{T}'\) established \(\bot \) in \(\texttt{NI}^{\mathbin {\supset }\bot \texttt{tonk}}\) by means of a \(\beta \gamma \)-normal derivation. The difference is due to the fact that in natural deduction the addition of \(\texttt{tonk}\) and \(\rho \) have different effects: the addition of \(\texttt{tonk}\) does not invalidate normalization, but invalidates the canonicity of closed normal derivations; on the other hand, the addition of \(\rho \) invalidates normalization but not the canonicity of closed normal derivations. To recover the full analogy with the natural deduction setting one can consider \(\texttt {LK}^*\), \(\texttt {LK}_\rho ^*\) and \(\texttt {LK}_{\mathbin {\texttt{tonk}}}^*\), the calculi extending (respectively) \(\texttt {LK}\), \(\texttt {LK}_\rho \) and \(\texttt {LK}_{\mathbin {\texttt{tonk}}}\) with the cut rule. Whereas for the rules for \(\mathbin {\supset }\) and \(\rho \) opportune reductions can be defined to push applications of the cut rule towards the axioms, this cannot be done in the case of the rules for \(\mathbin {\texttt{tonk}}\). Consequently, although cut is neither eliminable in LK \(_{\mathbin {\texttt{tonk}}}^*\) nor in LK \(_\rho ^*\), this would be for different reasons: in LK \(_{\mathbin {\texttt{tonk}}}^*\) one would have derivations containing applications of the cut rule which cannot be further reduced; in LK \(_\rho ^*\) one would have derivations containing applications of the cut rule to which reductions can be applied, but that cannot be brought into cut-free form due to a loop arising in the process of reduction. By introducing the notion of normal derivation as one to which no reduction can be further applied, it would be possible to show that whereas the rules for \(\rho \) are conservative over normal derivations in LK \(^*\), the rules for \(\mathbin {\texttt{tonk}}\) are not.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this chapter
Cite this chapter
Tranchini, L. (2024). Validity, Sense and Denotation in the Face of Paradoxes. In: Harmony and Paradox. Trends in Logic, vol 62. Springer, Cham. https://doi.org/10.1007/978-3-031-46921-3_5
Download citation
DOI: https://doi.org/10.1007/978-3-031-46921-3_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-46920-6
Online ISBN: 978-3-031-46921-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)




 and the derivation
and the derivation 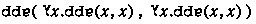 which resembles even more closely than the term associated with
which resembles even more closely than the term associated with 
