Keywords

1 Models in Modern Society

Models are one of the most important tools in the natural sciences. This became very clear during the coronavirus disease 2019 (COVID-19) pandemic in 2020. Mathematical models were used to predict the course of the pandemic. Government action was considered and integrated into the forecasts. This is an example of the use of models and modelling as a central aspect of scientific inquiry. Modelling tasks are characterised by their interdisciplinarity. This becomes clear especially through problems in everyday life. Due to their interdisciplinary character, these can usually only be solved with the help of several different fields.

Therefore, a setting from the field of biochemistry is particularly suitable for teaching biological concepts and working methods, as it already represents a recognised interdisciplinary field. In addition, it provides the basis for central subject areas of biology, such as cell biology (e.g. lipid bilayers), animal and plant physiology (e.g. glycolysis and photosynthesis) or genetics (e.g. how RNA polymerase works). This shows that both chemical and biological subject concepts are necessary for this subject. Therefore, it must be considered fundamental to the teaching of modern STEM-classes to include interdisciplinary tasks. Müller et al. (2018) concluded mathematical knowledge as a predictor of success in science. Mathematics is seen as a catalyst for achieving competence in the natural sciences. This implicates the importance of mathematical knowledge for understanding models. However, at this point it must be emphasised that scientific knowledge is also necessary to derive a valid mathematical model from a scientific model. Nevertheless, mathematics is one source of students’ difficulties in learning natural sciences (Müller et al., 2018).

2 Theoretical Background

2.1 (Mathematical) Models

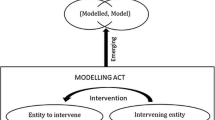
Mahr (2008) distinguished between the model and the modelled object. The model focuses on the original idea; the modelled object is mostly what is understood as the model. This heterogeneity of models (in combination with models’ illustration feature ‘models being representations’) allows the derivation of additional domain-specific functions of models. An example is the elimination of misconceptions through conceptual change (Krüger, 2007; Posner et al., 1982). Furthermore, the simplifications that are made possible by models improve the communication of technically correct information (Krell et al., 2019).

Therefore Mahr (2008) distinguished between two perspectives: model usage and model creation. The ‘creation’ perspective focusses on the induction of views, experiences, measurements, characteristics, findings, or rules through selection and generalisation (Grünkorn et al., 2014; Upmeier zu Belzen & Krüger, 2010). The opposite is true from the perspective of ‘usage’. The deduction of a modelled object to facilitate multiple applications of the model is foregrounded (Mahr, 2008). Mathematical models are understood as models based on mathematical relations, functions or methods.

Reiss and Hammer (2012) described mathematisation as an ‘essential element of working in physics,’ thus spanning the important arc from mathematics to the natural sciences. The corresponding mathematical modelling has been described by Eck et al. (2017) as the translation of concrete problems in applied sciences into well-defined mathematical tasks. They described two essential aspects of mathematical models: A concrete application problem as a basis, as well as the simplification of the application problem during the modelling process.

2.2 Modelling Competence

The ability to construct, apply and evaluate models is understood as modelling competence (Grünkorn et al., 2014; Upmeier zu Belzen & Krüger, 2010; Blum & Leiss 2007). They distinguished specialist knowledge from modelling competence, which is assigned primarily to knowledge acquisition. They identified two dimensions of modelling competence: ‘knowledge about models’ and modelling’ (Upmeier zu Belzen & Krüger, 2010, p. 50). Upmeier zu Belzen and Krüger (2010) defined the aspects of the ‘knowledge about models’ dimension as the ability to understand models as reconstructions from the creation perspective and to consider the possibility for alternative reconstructions. Whereas modelling describes the process of gaining knowledge, this process includes different steps. Therefore, they identified three aspects of the modelling dimension: The dimension ‘purpose of models’ refers to the understanding of models as useful reconstructions; the dimensions ‘testing’ and ‘revision’ refer to the ability to test or to apply models to phenomena and to modify them if necessary (Grünkorn et al., 2014; Upmeier zu Belzen & Krüger, 2010). They identified three levels for each sub-competence. The levels differ in the description of the relationship between the model and reality, and the role of concepts in dealing with models. At the first level, models are classified by their level of representation. At the second and third levels, the classification is based on the usage and creation perspectives (Mahr, 2008). The levels are not hierarchical (Mahr, 2008).

For the special case of mathematical modelling, Borromeo Ferri et al. (2013) developed even more precise components, which are based on the modelling competences identified by Maaß (2004) and Kaiser (2007). These result from the different steps within the mathematical modelling process that are necessary to successfully complete a process. The components are understanding, simplifying, mathematising, interpreting, validating, and communicating. The components are deduced sequentially, thereby facilitating the development of modelling cycles.

2.3 Modelling Cycles

Modelling cycles allow chronological splitting of the whole modelling process and provide insight into the modelling process (Grünkorn et al., 2014; Upmeier zu Belzen & Krüger, 2010).

Mathematical Modelling Cycle (Blum & Leiss, 2005)

Blum and Leiss (2005) (Fig. 3.1, blue), Borromeo Ferri (2006), and Blum and Borromeo Ferri (2009) developed the mathematical modelling cycle.

Fig. 3.1
A diagram. It has 4 circles, one small, and 3 large, elongated ones from left to right. 1 and 2 have an outer ring. 2, 3, and 4 overlap. Labels include real situation and rest of the world in 1, chemistry, chemical problem, and results in 2, and mathematical model problem and results in 3.

Mathematical modelling cycle and mathematical modelling cycle for chemical contexts. (Blum & Leiss, 2005; Schmidt & Di Fuccia, 2012)

Full size image

The first category is ‘real situation’. It describes a macroscopic problem, task or phenomenon. Followed by creating a mental representation, the situation model, on the base of the real situation (Blum & Borromeo Ferri, 2009; Blum & Leiss, 2005). It corresponds to the constructed multiple mental representations of the presented situation, as described by Kintsch and van Dijk (1983) for texts and Schnotz (2001) for pictures and diagrams. The following real model is created through the addition of knowledge from memory to the situation model (Borromeo Ferri, 2006). The developed real model is formalised into a mathematical model through additional mathematical knowledge (Kimpel, 2018). The resulting description of the mathematical model allows the use of mathematical methods to determine a mathematical result (Borromeo Ferri, 2006). The translation or interpretation of the mathematical results into real results occurs before the final step, ‘validation’ (Borromeo Ferri, 2006). Validation is performed to determine the plausibility of the real results.

Chemical Modelling Cycle (Schmidt & Di Fuccia, 2012)

Schmidt and Di Fuccia (2012) applied the modelling cycle to chemistry (Fig. 3.1, green). They inserted an additional area ‘chemistry’ between mathematics and reality (referred to as ‘the rest of the world’). Accordingly, ‘the rest of the world’ area represents only the macroscopic area of a subject. Furthermore, the mathematical results need to be checked not only for mathematical, but also for chemical plausibility. This translation from macroscopic phenomena to mathematical symbols indicates that chemical phenomena can be described through models at different aspects according to Johnstone (1991). Thus, phenomena can be described or explained through symbolic and sub-microscopic models and representations (Kimpel, 2018).

2.4 Multiple External Representations

Each representation has strengths, such as organising diagrams (Larkin & Simon, 1987). Multiple representations, like simultaneous presentations of familiar and unfamiliar representations, can help to prevent misinterpretation (Ainsworth, 1999).

Schnotz and Bannert (2003) identified two channels for the cognitive analysis of descriptive representations (e.g. text) and depictional representations (e.g. diagrams). Descriptive representations are processed in two steps sub-semantically and semantically in learners’ working memory. Through sub-semantic processing, words, word groups and complete sentences are identified and analysed (Schnotz, 2001, 2002). A mental representation of the text surface is then formed. The text surface, organised in cognitive schemata, can be activated during semantic processing and enables the creation of a coherent propositional representation (Schnotz, 2001, 2002). The second channel focusses on the processing of depictional representations. Information is also processed first sub-semantically, through the perception of the image as a whole, as well as its graphic design elements (Schnotz, 2001). The mental model of the illustration is constructed from this visual image through semantic processing (Schnotz, 2001). This informed the structural model developed by Lachmayer et al. (2007) to describe the processing of diagrams. There are close interactions between mental models and propositional representations (Schnotz & Bannert, 2003). This includes mutual transference via the cognitive processes of model inspection or model construction, whereby new information can be generated in the process (Schnotz, 2001). This suggests that descriptive representations are processed internally to become propositional representations, as well as mental models, and vice versa (Schnotz & Bannert, 2003). According to Gilbert and Treagust (2009), the interaction between mental models and propositional representations connects two main types of representations: model type and symbolic type. The ability to switch between different representations is important for understanding science (‘scientific literacy’) (Norris & Phillips, 2003). The mediation of the relationships among representations is achieved through the translation process in which the content-related connections become apparent and understanding increases (Ainsworth, 1999).

3 Research Question

According to the PISA study, pupils have difficulties in representing situations mathematically (e.g. in recognising mathematical structures, regularities, relationships and patterns). In addition, there are also difficulties in evaluating mathematical solutions and placing them in the context of the modelling tasks (Edo, Putri & Hartono, 2013). Jankvist & Niss (2020) came to a similar conclusion. They were also able to identify mathematisation as one of the crucial difficulties in developing solutions. In addition, the structuring of the tasks (here called ‘pre-mathematisation’) was a problem for the students. These findings on student difficulties on modelling and the positive effects of multiple external representations on learning (Ainsworth, 1999) led to the following questions and hypotheses:

  • Question 1: Do external representations have an effect on (mathematical) modelling competence in biochemistry?

  • Leads to Hypothesis 1: External Representations have a positive effect on (mathematical) modelling competence in biochemistry.

  • Question 2: Does mathematical expertise have an effect on (mathematical) modelling competence in biochemistry?

  • Leads to Hypothesis 2: Mathematical expertise has a positive effect on (mathematical) modelling.

  • Question 3: Are external representations helpful for learners with less prior knowledge about the modelling process?

  • Leads to Hypothesis 3: External representations have a positive effect on modelling processes of learners with less prior knowledge.

4 Methods

4.1 Sample

Twelve individuals (M = 24.3 years old, SD = 2.06) participated in the study. Eleven were Technical University of Munich students of science and one was a high school graduate. In order to obtain the broadest possible distribution of prior knowledge, participants without a university place were also included. For the study, students who were studying both mathematics and chemistry (n = 6) were defined as mathematics experts. The other participants (n = 6) are referred to as mathematics novices (Table 3.1). Their study subjects are natural science, such as biology, chemistry or health science, but not mathematics. The students were randomly assigned to the experimental conditions.

Table 3.1 Research design
Full size table

4.2 Experimental and Learning Environment Design

A two-factorial experimental design was used. The first independent variable, learning environment design, was systematically modified regarding the used representations (IV1, triple-staged; see IV1.a [text and symbol], IV1.b [text, symbol and diagram], and IV1.c [text, symbol and image]). The participants’ mathematical expertise was checked as a second factor (double-staged; see IV2.a [mathematic experts] and IV2.b [mathematic novices]; Table 3.1). The participants worked on a task related to enzyme kinetics using pen and paper. The learning environment included examples for the participants to elaborate on. Using methanol poisoning as the task topic, the students had to determine the amount of ethanol needed to treat poisoning. The task was divided into six subtasks based on the steps in Schmidt and Di Fuccia’s (2012) chemical modelling cycle (see also Sect. 3.2.4).

4.3 Survey Method

The relevant participant characteristics were obtained from a questionnaire. The participants had to use the ‘thinking aloud’ method (Sandmann, 2014) while working on the learning environment. Their verbal utterances were recorded and transcribed in accordance with the guidelines by Kuckartz (2008). Qualitative content analysis was performed in accordance with Mayring (2010) on the basis of the elaboration profiles generated by the participants.

Frick’s (2019) category system was used (Table 3.2). This was originally used to gather students’ mental models while solving mathematical modelling tasks. The category system was deductively extended in accordance with the modelling competences (category 3: modelling competence) identified by Upmeier zu Belzen and Krüger (2010) and Grünkorn et al. (2014). First- and second-level subcategories were also created. These were developed on the basis of the model by Upmeier zu Belzen and Krüger (2010). Accordingly, there were two subcategories based on the dimensions ‘knowledge about models’ (3.1) and ‘modelling’ (3.2). For those two, concrete subcategories were developed based on the levels described in the model (e.g., ‘statements about the relationship between the model object and the initial object’ (3.1.2)). A total of three such categories were developed for 3.1 and eight for 3.2. The ‘monitoring’ category concluded with statements of understanding, misunderstanding, astonishment, doubt, and joy.

Table 3.2 Main categories
Full size table

4.4 Evaluation

For the qualitative analysis, the independent variables, experts and novices, as well as TS, TDS and TBS, grouped the participants. The dependent variable, i.e. the participants’ ‘elaboration profiles’, was evaluated by qualitative content analysis based on Mayring (2010). The profiles were analysed with MAXQDA 12 (version 12; VERBI). For this purpose, the statements from the elaboration protocols were assigned to the corresponding categories of the category system. The frequencies for the individual and cumulative subcategories were considered. For every category, contingency tables were generated. They were the base for chi-square tests of independence for selected categories.

5 Results

5.1 Categories

In order to examine model competence, category 3 was divided into two subcategories: ‘knowledge about models’ and ‘modelling’ (see Sects. 3.2.3 and 3.4.3). The individual sub-competences within a dimension were used together with the levels to differentiate within the category. To examine modelling competence, a distinction was made between knowledge about models and modelling (Upmeier zu Belzen & Krüger, 2010). Therefore category 3.1 ‘knowledge about models’ focusses on comparisons of reality and the model at an abstract level (3.1.1) and a concrete level (3.1.2). The simplification of a real situation (category 3.2.1) was identified as the ‘purpose of models’ sub-competence. The use of models to describe phenomena and to evaluate results was characterised by two categories (3.2.2 & 3.2.3). The comparison of the model to reality and the validation of the model were understood as model testing (category 3.2.5). The ability to make revisions on the basis of the test results was a sub-competence (3.2.6).

5.2 Elaboration Profiles and Modelling Strategies

To explore elaboration, the elaboration profiles (superficial + deep) developed by Lind et al. (2005) were applied to the relevant categories. Superficial elaboration includes (re-)reading a text, unsuccessful attempts at remembering, retrieving information in the text and the creation of inferences to develop a text base (Lind et al., 2005). Deep elaboration is characterised by the creation of inferences that facilitate the development of a situation model and the retrieval of knowledge from raw content.

Analogous modelling strategies were constructed on the basis of the levels identified by Upmeier zu Belzen and Krüger (2010). Level 1 was defined as recognition and application of models, and Levels 2 and 3 were defined as modelling (Table 3.3).

Table 3.3 Assignment rules for modelling strategies
Full size table

5.3 Qualitative Analysis

5.3.1 Comparison of the Effect Different Representations

Some of the frequencies for the individual categories related to the usable external representations were noteworthy, e.g., ‘2.1.4 description of solutions’ (Category which includes all descriptions of solutions). The absolute values for ‘additional representations’ were twice as large as those for the control condition [hTBS(2.1.4) = 48, hTDS(2.1.4) = 44, hTS(2.1.4) = 27]. The explication of the mathematical reasoning (Categories 2.5) improved with additional external representations (cumulative frequencies in Category 2.5: hTS[2.5] = 67, hTBS[2.5] = 101, hTDS[2.5] = 113).

Regarding elaboration (Categories 1.1.1 (‘Successful recall of knowledge from the information text’), 1.3 (‘Explicit use of external sources of knowledge’), 2.1 (‘Inferences that serve to build a text base’), 1.1.3 (‘Successful recall of knowledge from memory’), and 2.5 (‘Inferences that serve to build an integrated situation model’), all the participants engaged more often in superficial elaboration [Es(TS) = 131, Es(TBS) = 193, Es(TDS) = 173] rather than deep elaboration [Ed(TS) = 70, Ed(TBS) = 105, Ed(TDS) = 118]. There were differences between the groups (Fig. 3.2). The TBS group often engaged in superficial elaboration; the TDS group in deeper elaboration.

Fig. 3.2
2 multi-line graphs plot the number of codings for 2 categories. 1. Plots a declining trend for T S, T D S, and T B S in superficial and deep elaboration profiles. 2. Plots a rising trend for T D S, T S, and T B S in recognition and application of models and modelling in modelling strategies.

Frequencies (Total number of expressions made by students in these categories) for superficial and deep elaboration profiles (left) and modelling strategies (right) by representation

Full size image

The frequencies for ‘recognition and application of models’ were nearly the same in all three test groups [Mn(TS) = 14, Mn(TBS) = 13, Mn(TDS) = 15]. However, there were differences in the frequencies for modelling [Me(TS) = 38, Me(TBS) = 35, Me(TDS) = 47]. The participants with access to additional diagrams created models more often.

5.3.2 Expertise

Experts paraphrased mathematically (Category 2.1.4) twice as high as the novices [hE(2.1.4) = 41, hN(2.1.4) = 18]. There was also a difference in the quality of the paraphrasing. Novices paraphrased mainly concrete numerical values (‘If I see this correctly, we have an alpha of 1 plus 559.9, i.e. 560 approximately or 561 betters’ (TS & N [novice])). Experts tended to paraphrase qualitatively (‘The Michaelis–Menten equation is … for very high concentrations, the Km in the denominator is [negligible], and it can be considered void in the limit value [of the Michaelis–Menten equation]’ (TDS & E)). Novices orientated themselves through quantitative data: ‘To reach the value 1, c(inhibitor) would have to be 1 × 10 to the power of −5’. In contrast, the expert group used mathematical paraphrases much more frequently (‘So [in] Michaelis–Menten kinetics, the current velocity v is equal to Vmax times c of the substrate divided by the specific Km value plus c of the substrate’ (TBS & E)).

Expertise seemed to have a positive effect on the ability to integrate representations (hE(2.3) = 18, hN(2.3) = 4). The examination of the elaboration profiles and modelling strategies (Fig. 3.3) revealed different tendencies, regarding the participants’ expertise.

Fig. 3.3
2 2-line graphs plot number of codings for 2 categories. 1. Plots a declining trend for experts and novices in superficial and deep elaboration profiles. 2. Plots a rising trend for experts and novices in recognition and application of models and modelling in modelling strategies.

Frequencies (Total number of expressions made by students in these categories) for superficial and deep elaboration profiles (left) and modelling strategies (right) by expertise

Full size image

Both groups more likely engaged in superficial elaboration [Es(Novices) = 166, Ed(Novices) = 77; Es(Experts) = 331, Ed(Experts) = 216]. It was evident that the expert group more likely engaged in elaboration. The same picture emerged for the modelling strategies. Again, the values for the novices were much lower. [MN(Novices) = 1, MN(Experts) = 41, ME(Novices) = 24, ME(Experts) = 79]. Therefore, experts used modelling strategies much more frequently than the novices.

5.3.3 Chi-Square Test

A chi-square test of independence was performed on the numbers of verbal utterances of all categories to identify correlation between variables. A selection of categories that showed statistical correlation within the expertise groups are listed in Table 3.4.

Table 3.4 Test of independence
Full size table

The results revealed a statistically highly significant correlation between representation and the participants’ expertise in the description of solutions (2.1.4) and the calculation of the sought-after variables (2.5.5). For ‘mathematical reasoning’ (2.5.4), there was also a highly significant correlation between the participants’ expertise and the use of additional external representations.

The elaboration profiles yielded different results. There was no statistically significant correlation for superficial elaboration (Es). Analysis of deep elaboration (Ed) indicated a highly significant correlation between expertise and external representations. The correlation between mathematical expertise and additional external representation was highly significant regarding modelling strategy MN (Recognition and Application of models).

6 Discussion

6.1 Method

It should be noted that there are limitations regarding the generalisability of the results. These results were produced in a biochemical context and are meaningful only in that context. Another limitation is the small sample, which emphasises its qualitative character. To make quantitative conclusions, the sample would need to be larger and more representative (Kroß & Lind, 2001). This would make the results of frequency analyses and inferential statistics more meaningful.

6.2 Results

Hypothesis 1

The results indicate that additional external representations can have a positive influence on modelling competence, but learning with diagrams requires greater cognitive effort because of the abstract structural similarity. Learners might lack the additional cognitive capability for text–diagram integration (Schnotz, 2001, 2002). Looking at the sample as a whole, a positive effect is nevertheless evident. The situation is different when the test groups (Experts vs. Novices) are considered individually (See hypothesis 3).

The hypothesis regarding mathematical conclusions was confirmed. The learning environment with images contained the highest number of codes. This implies that the participants with additional images modelled more than the group without additional representations. Since the learning environment differs only through the representations it contains, the additional modelling work can be explained by the representations. Category 3.1.1 (Assessment of the degree of similarity and abstraction of the model) revealed an advantage for the variant without additional representation. A possible explanation is that the images contained implicit estimates or simplifications that did not require prior elaboration. The number of codes with deep elaboration and different representations was at least half that of the number of codes with superficial elaboration. This indicates differences in the effectiveness of images and diagrams. Images seem to invite superficial elaboration because of their concrete similarity to the represented object, and diagrams require more cognitive power and stimulate deep elaboration (Lowe, 1993; Schnotz, 2002).

In summary, pictorial representations were found to have a positive effect on modelling competence in biochemistry. This is primarily based on the increased frequency of modelling (category Me), as well as the superficial and deep elaborations in all categories relevant to modelling.

Hypothesis 2

The positive influence of mathematical expertise on mathematical modelling competence was also confirmed. On the one hand, this can be explained by the frequency of the statements in the modelling categories (Fig. 3.3 right). On the other hand, it can also be explained from the significant chi-square test carried out for the category MN.

The experts argued mainly on a mathematical level. The novices avoided mathematical abstraction. Experts included mathematical concepts in task definitions and contributed additional mathematical knowledge.

Experts were more actively involved in the creation of situation models than novices. It was evident that mathematical conclusions required appropriate mathematical expertise to achieve text–image integration that fosters learning. In contrast, novices experienced difficulty in applying external representations to mathematical conclusions. This corresponds to the intrinsic cognitive load component of the cognitive load theory (Sweller et al., 1998). The examination of the knowledge about models indicated that the experts made statements more frequently (Experts 39 times; Novices 2 times). The recognition and description of the model in relation to the phenomenon under study are an important step in model construction (Grünkorn et al., 2014; Upmeier zu Belzen & Krüger, 2010). The experts in all the test groups described the relationship between the real object and the model. This indicated a deeper understanding of the mathematical model. There were also differences in validation strategies. The experts tended to estimate their results on the basis of their prior knowledge (Category 1 ‘Adding knowledge from memory’, experts 147 times; novices 70 times). The novices tended to make their assessments intuitively. This is consistent with validation strategies formulated by Borromeo Ferri (2006).

The results of the chi-square test indicated that in modelling, representation and expertise seemed to be mutually influential. Experts used external representations twice as often as novices. This suggests that external representations help experts to generate estimates and simplifications.

Hypothesis 3

The general positive effect of additional external representation from hypothesis 1 could only be observed for the expert. The hypothesised positive effect of representations on novices was not confirmed. The findings indicate that external representations can be fully used only with appropriate expertise. Experts used additional representations more frequently and effectively. Kozma and Russell (1997) found that experts in chemistry were more likely to use multimedia representations than novices. This contrasts with Schnotz (2001), who found that learners with little prior content-specific knowledge achieved greater success in multimedia learning environments (Schnotz, 2001). The reason was that the variety in the presentation of information stimulated the construction of multiple mental representations. Therefore, Category 3.1.1 indicated that external representations were helpful, especially for experts, in the generation of estimates and simplifications.

7 Conclusions

The results suggest that external representations and mathematical expertise have a positive influence on mathematical modelling competence with the limitation that it is mainly experts who benefit from additional representations. Because this mixed-methods approach was used in combination with a small sample, these results serve only as a source of inspiration for future studies. Studies with larger samples that allow for quantification would be the logical next step. Participants could be classified as mathematics, biology or chemistry experts and novices. Other subject areas, such as epidemiology or physical chemistry, could be studied to determine the role of prior discipline-specific knowledge.

The application of the results to competence-oriented academic tasks would reveal the positive effects of multimedia representations. It should also be noted that the use of additional representations for performing mathematical modelling tasks had a positive effect, especially for high-performing students; however, this was not the case for underachieving students.

It is therefore important to determine appropriate designs to promote the success of low-achieving learners in understanding intensive modelling strategies. The use of dynamic representations might better emphasise the model character. This could provide additional support to students as they learn about modelling. A further possibility for instructional design would be to explain and demonstrate the mathematical modelling cycle over time to clearly define the modelling process.

The equally low rate on modelling Me for the experts and novices indicated that the defined modelling strategy, especially model criticism and modification, was seldom used in the school environment. There, learners seem to get a wrong picture of models as something absolute. However, modelling, the relevant working method, is hardly ever taught. Perhaps different teaching methods can eliminate the misconception of the ‘absolute model’ through conceptual change (Posner et al., 1982). This could be achieved by active engagement in model criticism.