Abstract
Byzantine fault-tolerant distributed systems are designed to provide resiliency despite arbitrary faults, i.e., even in the presence of agents who do not follow the common protocol and/or despite compromised communication. It is, therefore, common to focus on the perspective of correct agents, to the point that the epistemic state of byzantine agents is completely ignored. Since this view relies on the assumption that faulty agents may behave arbitrarily adversarially, it is overly conservative in many cases. In blockchain settings, for example, dishonest players are usually not malicious, but rather selfish, and thus just follow some “hidden” protocol that is different from the protocol of the honest players. Similarly, in high-availability large-scale distributed systems, software updates cannot be globally instantaneous, but are rather performed node-by-node. Consequently, updated and non-updated nodes may simultaneously be involved in a protocol for solving a distributed task like consensus or transaction commit. Clearly, the usual assumption of common knowledge of the protocol is inappropriate in such a setting. On the other hand, joint protocol execution and, sometimes, even basic communication becomes problematic without this assumption: How are agents supposed to interpret each other’s messages without knowing their mutual communication protocols? We propose a novel epistemic modality creed for epistemic reasoning in heterogeneous distributed systems with agents that are uncertain of the actual communication protocol used by their peers. We show that the resulting logic is quite closely related to modal logic \(\textsf{S5}\), the standard logic of epistemic reasoning in distributed systems. We demonstrate the utility of our approach by several examples .
G. Cignarale and R. Kuznets—Supported by the Austrian Science Fund (FWF) projects ByzDEL (P33600).
H.R. Galeana—Supported by the Doctoral College Resilient Embedded Systems, which is run jointly by the TU Wien’s Faculty of Informatics and the UAS Technikum Wien.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
A distributed system is a system with multiple processes, or agents, located on different machines that communicate and coordinate actions, via message passing or shared memory, in order to accomplish some task [8, 21]. This common task is achieved by means of agent protocols instructing agents how to exchange information and act. Designing distributed systems is difficult due to the inherent uncertainty agents have about the global state of the system, caused, e.g., by different computation speeds and message delays.
Knowledge [15] is a powerful conceptual way of reasoning about this uncertainty [13, 14]. Indeed, knowledge is at the core of the agents’ ability to act according to the protocol: According to the Knowledge of Preconditions principle [22], a protocol instruction to act based on a precondition \(\varphi \) can only be followed if the agent knows \(\varphi \) to hold. While trivial for preconditions based on the local state of the acting agent itself, this observation comes to the fore for global preconditions, also involving other agents, as is common for coordination problems such as consensus.
One of the standard ways of modeling agents’ knowledge is via the possible world semantics that takes into account all the possible global states the agents can be in and which of these possible worlds a particular agent can distinguish based on its local information. In this view, agent i knows a proposition \(\varphi \), written \(K_i \varphi \), in a global state s iff this proposition holds in all global states \(s'\) that are indistinguishable from s for i. The primary means of obtaining new knowledge — and the only way of increasing knowledge about the local states of other agents — in a distributed system is by means of communication.
Fault-tolerant systems add another layer of complexity, in particular, when processes may not only stop operating or drop messages but can be (or become) byzantine [19], i.e., may behave arbitrarily erroneously, in particular, can communicate in erratic, arbitrary, or deceptive manner. Malicious faulty agents may have a “hidden agenda”, in which case, instead of following the original commonly known protocol, a faulty agent (or a group of faulty agents) can execute actions (possibly in consort with each other) that jeopardize the original goals of the system.
Although these hidden agendas are typically not transparent for correct agents, some assumptions must be made to restrict the types and numbers of protocol-defying actions and messages. Without such restrictions, provably correct solutions for a distributed task do not exist. These assumptions must usually be commonly known by all agents, like the basic communication mechanism, the protocol of all correct agents, the data encoding used in its messages, etc. In [7], the whole corpus of these common assumptions is referred to as a priori knowledge.Footnote 1 For the possible world semantics, this translates into the assumption of common knowledge of the model [3], which enables the agents to compute epistemic states of other agents, a task necessary for a typical coordination problem like consensus [6].
Since correct agents generally cannot distinguish a simple malfunction from malintent, erroneous messages, i.e., messages sent in contravention of the commonly known joint protocol, are usually left uninterpreted. For instance, in the epistemic modeling and analysis framework [11, 16,17,18] for byzantine agents, message \(\varphi \) received from agent i is interpreted by means of the hope modality
where \(B_i \varphi \) represents belief of agent i and is understood in the spirit of belief as defeasible knowledge [24], where
This hope modality \(H_i \varphi \) is equivalent to a disjunction
suggesting that a message \(\varphi \) from i is interpreted as the uncertainty between agent i being faulty or the epistemic state of i confirming \(\varphi \) in case i is a correct agent. Note that in the former case, the message carries no meaning whatsoever. Indeed, the axiomatization of hope in [10] takes \(H_i \bot \) to be the definition of faulty agents because only a faulty agent can send contradictory messages. Given that in normal modal logic \(H_i\bot \rightarrow H_i \varphi \) holds for any \(\varphi \), the consequence is that a faulty agent can send any message independent of its epistemic state. In other words, no conclusions about the epistemic state of a faulty agent can be drawn from its messages, as reflected in the hope modality.
However, not all systems exhibit such a stark dichotomy between commonly known and fully transparent us (correct processes) and the mysterious and uninterpretable them (faulty processes). Rational agents in blockchain settings [12], for instance, do not necessarily have the same goal as the rest of the system. Nevertheless, neither their actions nor their communication are arbitrary, not to speak of adversarial. Consequently, game theoretic modeling, based on a model of their beliefs and goals, can be applied for the analysis of such systems [2].
In this paper, we extend this finer-grained view to the epistemic modeling of distributed systems and consider heterogeneous distributed systems, where different processes may run different protocols and where the assumption that all protocols are commonly known is dropped. In such systems, we assume that processes are partitioned into types (or roles, or classes) of agents, so that within one type the protocols are commonly known to the agents of that type. While such a strong assumption is not made for agents of different types, we do not assume them to have zero knowledge of each other’s protocol either. In particular, we assume that each class is equipped with an interpretation function that encodes the amount of knowledge agents have regarding the preconditions for communication agents of a different type have.
Since having no preconditions for sending a message is an allowed instance, this setting generalizes the byzantine setting described earlier, where there are two types — correct and faulty agents — and only messages of correct agents have a non-trivial interpretation. These interpretation functions are formalized by means of the new creed modality \(\mathbb {C}_{p}^{A \setminus B} \varphi \) introduced in this paper, which generalizes the hope modality for the byzantine case and represents the information an agent of type A can infer upon receiving message \(\varphi \) from agent p of type B.
We illustrate the communication scenarios where this creed modality may be useful by means of some examples:
Example 1
(“The Murders in the Rue Morgue”). This famous story by Edgar Allan Poe describes a murder mystery. Several witnesses heard the murderer (agent m) but nobody saw m. The problem in interpreting their testimony is that they seem to contradict each other: for instance, a French witness f thinks m spoke Italian and is certain m was not French, whereas a Dutch witness d thought m was French, etc. Importantly, none of the witnesses could understand what was being said (f does not speak Italian, while d does not speak French, etc.). The standard byzantine framework considers the possibility of a faulty agent sending different messages to different agents to confuse them, but provides no means to describe one uncorrupted message being treated so differently by correct agents. Standard epistemic methods either accept all incoming information as being of equal value or make a priori preferential judgements. However, in the story, Monsieur C. Auguste Dupin correctly surmises that m spoke neither of the languages. Dupin neither dismisses witness accounts completely as lies nor accepts them completely. Instead he chooses some of the witness statements over others without prejudging them.
Example 2
(Knights and Knaves puzzles). There is a series of logical puzzles, popularized by Smullyan [26], about an island, all inhabitants of which are either knights who always tell the truth or knaves who always lie. One of the simplest ones [26, Puzzle 28] is as follows:
There are only two people, p and q, each of whom is either a knight or a knave. p makes the following statement: “At least one of us is a knave.” What are p and q?
Our goal is to incorporate the uncertainty about the mode of communication (knaves lie/knights tell the truth) into the logic. Fault-tolerant systems do not provide a satisfactory model since there information from faulty agents is either accepted (in case of benign faults) or ignored as completely unreliable (in case of byzantine faults). Instead, enough information is collected from correct agents (and they must constitute an overwhelming majority for most problems to be solvable). By contrast, knights and knaves puzzles are typically solvable even if all agents involved are knaves. The answer to the puzzle above, for instance, is that p is a knight and q is a knave. We would like to derive this answer fully within the logic.
Example 3
(Software Updates). In a highly available large scale distributed system like an ATM network, it is impossible to simultaneously update the software executed by the processes. Rather, processes are usually updated more or less sequentially during normal operation of the system, at unpredictable times. As a consequence, the joint protocol executed in the system while a software update is in progress might mix both old and new protocol instances. Existing solutions like [1, 25], which aim at updating complex protocols/software, typically provide “consistent update” environments that prevent such mixing.
Thanks to our creed modality, however, mixed joint protocols could be allowed, by explicitly considering those in the development of the new protocol instance: Indeed, when implementing a bug fix or feature update, the developer obviously knows the previous implementation. A message received at some process p from some process q in the new implementation just needs to be interpreted differently, depending on whether q runs an old or a new protocol instance. Note that backward compatibility typically rules out incorporating a version number into the messages of the (new) protocol here, in which case p would be uncertain about the actual status of q, despite having received a message from it.
For light-weight low-level protocols, this approach might indeed constitute an attractive alternative to complex consistent update mechanisms.
After introducing our framework, we explain in Sect. 6 how these examples could be formalized.
Related Work. Our logical framework generalizes the hope modality [10] introduced to reason about byzantine agents in distributed systems. We extend the standard formulation by considering the byzantine case as a special agent-type. Agent-types in the field of epistemic logic are formulated in [5], where names are used as abstract roles for groups of agents, depending on their characteristics. From the dynamic epistemic logic [9] perspective, a public announcement logic with agent types is presented in [20], providing a dynamic framework to reason about uncertainty of agent-types that is used to formalize the knights and knaves puzzle. Due to the different motivations, while treating a closely related problems set, [5] and [20] make different and at times incomparable choices regarding the postulates underlying the systems. For instance, a precondition for an announcement for an agent in [20] need not entail the agent knowing this precondition, which contradicts the fundamental Knowledge of Preconditions principle for distributed systems [22]. On the other hand, all agents in [20] possess the same knowledge about each of the existing agent types, in particular, all agents share one common interpretation of messages from a particular type, an assumption in line with the rather centralized nature of updates in dynamic epistemic logic but less sensible for distributed systems.
Paper Organization. In Sect. 2, we introduce the basic preliminary definitions and lemmas for describing heterogeneous distributed system where agents are grouped into types, each characterized by a different protocol. In Sect. 3, we provide an epistemic logic for representing heterogeneous distributed settings by introducing the creed modality and prove soundness and completeness in Sect. 4. We derive the properties of creed in Sect. 5. Having done that, in Sect. 6 we show how to apply this framework to the motivating examples. Finally, some conclusions are provided in Sect. 7.
2 Heterogeneous Distributed Systems
In this paper, we focus on heterogeneous distributed systems where agents are of different types characterized by different protocols. All agents are assumed to be at most benign faulty,Footnote 2 in the sense that they do not take actions not specified by their protocol, cannot communicate wrong information, and have perfect recall. At any time, however, agents may change their type, i.e., change their protocol.
These different protocols partition the set of processes into different types, which are identified with the names of the protocols. The set of all existing types is commonly known to all the agents. All agents of the same type, which typically work towards the same goal, use the same protocol that is commonly known to all agents of this type. What is not generally known to an agent is the distribution of agents into types and the actual protocol of a type different from its own. In other words, agent a generally does neither know the type nor the protocol of agent b.
Communication in the system is governed by the protocols. Whereas all protocols must use the same basic communication mechanism and a common layering structure [23], i.e., (possibly non-synchronous) communication rounds, agents of different types generally communicate according to different protocol rules, data formats, encodings, etc. Communication actions are triggered by preconditions that depend on the protocol of the agent’s type. Consequently, the interpretation of each message depends on:
-
the knowledge of the receiver about the type(s) the sender may belong to;
-
the knowledge of the receiver about the communication protocol of this (these) type(s).
More formally, we consider a finite set of processes \(\varPi = \{ p_1, \ldots , p_n\}\) that communicate with each other by using a joint communication mechanism, such as, e.g., shared memory objects or point-to-point messages. Each process executes some protocol with a name (= type) taken from a commonly known set of names \(\mathcal {A}\). However, no assumption is made about the types and the actual protocols of distinct agents i and j being identical or mutually known. All protocols are organized in a common, possibly non-synchronous communication round structure. We also require that the system has a common notion of time, represented by a directed set T. Common choices for T are the set of natural number \(\mathbb {N}\), or even the set of real numbers \(\mathbb {R}\). It should be noted that in Definitions 4–5, we assume that concepts such as configuration and protocol match the standard notions in distributed computing literature [4, 21].
Definition 4
(Heterogeneous distributed system). We say that a tuple \(\langle \varPi , \mathcal {A}, \mathcal {P}, \mathcal {C}, T \rangle \) is a heterogeneous distributed system iff
-
\(\varPi = \{ p_1, \ldots , p_n\}\) is a finite set of processes;
-
\(\mathcal {A}= \{ A_1, \ldots , A_k\}\) is a partition of \(\varPi \) into agent types;
-
\(\mathcal {P} = \{\mathcal {P}_1, \ldots , \mathcal {P}_k\} \) is a collection of protocols that correspond to \(\mathcal {A}\), one protocol per agent type;
-
\(\mathcal {C}\) is a communication medium; and
-
T is a directed set representing global times.
The joint protocol of \(\langle \varPi , \mathcal {A}, \mathcal {P}, \mathcal {C}, T \rangle \) is the protocol formed by the protocols of all the agents.
In this setting, given multiple possibly non-cooperating teams of agents, we need to re-define the notion of tasks and solvability. In particular, we generally cannot impose restrictions on the output of processes in other partitions.
Definition 5
(Partial task). We say that a tuple \(\langle S, \mathcal {I}, \mathcal {O}, \varDelta \rangle \) is a partial task relative to \(S \subseteq \varPi \) iff \(\mathcal {I}\) is a set of input configurations for \(\varPi \); \(\mathcal {O}\) is a set of output configurations for S; and \(\varDelta \) is a validity correspondence that maps valid initial configurations of the system to a subset of valid output configurations for S.
Definition 6
(Solvability). Let \(\langle \varPi , \mathcal {A}, \mathcal {P}, \mathcal {C}, T \rangle \) be a heterogeneous distributed system. We say that agents of type \(A_i \in \mathcal {A}\) can solve a partial task \(\mathcal {T} = \langle S, \mathcal {I}, \mathcal {O}, \varDelta \rangle \) iff for any input configuration \(\sigma \in \mathcal {I}\), the execution of the joint protocol of \(\langle \varPi , \mathcal {A}, \mathcal {P}, \mathcal {C}, T \rangle \) leads to an output configuration \(\rho \vert _{S} \in \varDelta (\sigma )\).
Note that traditional distributed systems with benign failures fall into the particular case where \(\mathcal {A} = \{\varPi \}\) and there is one unique protocol executed by all processes. Similarly, distributed systems with send-restricted byzantine faults (no false perceptions of received messages, but arbitrary message sending) could be modeled as an instance with two types \(\mathcal {A}^B = \{\textsf{Correct}, \textsf{Faulty}\}\), where all agents of type \(\textsf{Correct}\) follow the intended protocol, whereas agents of type \(\textsf{Faulty}\) can arbitrarily deviate from it.
3 Epistemic Logic for Heterogeneous Distributed Systems
We consider a heterogeneous distributed system \(\langle \varPi , \mathcal {A}, \mathcal {P}, \mathcal {C}, T \rangle \) according to Definition 4, where processes are partitioned into different types according to their protocol. Agents of the same type share a common protocol, which also includes information on how to interpret messages from agents of various types. Recall that we assume that each process knows its own protocol/type, and, therefore, the protocol of all other agents of the same type, but not necessarily which agents are of this type. In particular, an agent may be unsure whether another agent belongs to its own type or not.
Agents interpret received messages by means of an interpretation function:
Definition 7
(Interpretation function). Let \(\mathbb {F}\) be the set of well-defined formulas used by agents to communicate. An interpretation function for type \(A \in \mathcal {A}\) with respect to type \(E\in \mathcal {A}\) messages is any function \(f_{AE}: \mathbb {F} \rightarrow \mathbb {F}\).
Intuitively, \(f_{AE}(\varphi )\) corresponds to the knowledge that type A agents (or simply A agents) have about the preconditions for E agents to send message \(\varphi \). We assume that function \(f_{AE}\), for every type E, is a priori known by every A agent, as part of its protocol.
Example 8
Interpretation function \(f_{AE}(\varphi ) :=\top \) for all \(\varphi \in \mathbb {F}\) corresponds to the case when A agents have no knowledge about the communication protocol of E agents. For instance, byzantine agents who can send any message at any time (send-unrestricted byzantine agents) can be captured by choosing \(f_{\textsf{Correct},\textsf{Faulty}}(\varphi ) = \top \) for partition \(\mathcal {A}^E = \{\textsf{Correct}, \textsf{Faulty}\}\). The minimal requirement that all correct agents tell the truth translates into \(f_{\textsf{Correct},\textsf{Correct}}(\varphi ) = \varphi \).
Since we want to be able to express partition membership into our language and formulas, we need to define partition membership atoms.
Definition 9
(Propositional variables and partition atoms). We consider, for each process \(p_i \in \varPi \), a finite set \( Prop _i\) of propositional variables. In addition, for each agent type \(A \in \mathcal {A}\), we consider the set \(\varPi _A :=\{A_p \mid p \in \varPi \}\) of partition atoms. The set of all atomic propositions is defined as
Since \(\mathcal {A}\) is a partition, every agent belongs to one and only one type. For convenience, we denote the type of agent p by \(\bar{p}\). Furthermore, we will assume that each agent knows its own type, i.e., \(K_p (\bar{p}_p)\).
Now that we have established the basics of our heterogeneous distributed systems, we can proceed to define the language.
Definition 10
(Language of EHL). The language \(\mathcal {L}\) of the epistemic heterogeneous logic extends the standard (multi-modal) epistemic language by a new family of modalities called creed and is given by the grammar:
where \(r \in Prop \) is an atomic proposition (i.e., propositional variable or partition atom), \(p \in \varPi \) is an agent, and \(A,E \in \mathcal {A}\) are agent types. Other boolean connectives, as well as boolean constants \(\top \) and \(\bot \), are defined in the usual way. We use the following derived modalities: \(\hat{K}_p \varphi :=\lnot K_p \lnot \varphi \) and creed defined as
for any agent \(p \in \varPi \) and agent types \(A,E \in \mathcal {A}\).
Creed \(\mathbb {C}_{p}^{A \setminus E}\varphi \) represents the amount of information an A agent can extract from a message \(\varphi \) received from agent p under the assumption that p belongs to type E of the partition. It is based on the a priori knowledge A agents possess of the preconditions for an E agent to send message \(\varphi \), as encoded in the interpretation function \(f_{AE}\) from Definition 7, which is external to the language. This precondition already takes into account the Knowledge of Preconditions principle [22], by assuming that the sender must know that the preconditions hold. We use the standard Kripke model semantics with additional restrictions for partition atoms:
Definition 11
(Semantics). Let \(\langle \varPi , \mathcal {A}, \mathcal {P}, \mathcal {C}, T \rangle \) be a heterogeneous distributed system and \(\{f_{AE} \mid A, E \in \mathcal {A}\}\) be the collection of interpretation functions for it. An (epistemic) Kripke frame \(F = (W,\sim )\) is a pair of a non-empty set W of worlds (or states) and a function \(\sim :\varPi \rightarrow \mathcal {P}(W \times W)\) that assigns to each agent \(p \in \varPi \) an equivalence relation \(\sim _p \subseteq W \times W\) on W. A Kripke model \(M = (W,\sim ,V)\) is a triple where \((W,\sim )\) is an epistemic Kripke frame and \(V :W \rightarrow \mathcal {P}( Prop )\) is a valuation function for atomic propositions. The truth relation \(\models \) between Kripke models and formulas is defined as follows: \(M, s \models r\) iff \(r \in V(s)\) for any \(r \in Prop \); cases for the boolean connectives are standard; \(M,s \models K_p \varphi \) iff \(M,t \models \varphi \) for all \(t \in W\) such that \(s\sim _pt\). As usual, validity in a model, denoted \(M \models \varphi \), means \(M, s \models \varphi \) for all \(s \in W\).
A Kripke model \(M=(W,\sim , V)\) is called an \(\textsf{EHL}\) model iff the following two conditions hold:
-
1.
For any state \(s\in W\) and any agent \(p \in \varPi \),
$$\begin{aligned} \bigl |V(s) \cap \{A_p \mid A \in \mathcal {A}\}\bigr | = 1, \end{aligned}$$(3)i.e., exactly one of partition atoms \(A_p\) involving agent p is true at state s.
-
2.
For any agent p, any agent type A, and pair of states s and t,
$$\begin{aligned} s \sim _p t \qquad \Longrightarrow \qquad \Bigl ( A_p \in V(s) \quad \Leftrightarrow \quad A_p \in V(t)\Bigr ), \end{aligned}$$(4)i.e., p can distinguish worlds where it is of different types.
General validity, denoted \(\models \varphi \), means \(M \models \varphi \) for all EHL models.
Example 12
For the interpretation functions from Example 8 for send-unrestricted byzantine agents, \( \mathbb {C}_{p}^{\textsf{Correct} \setminus \textsf{Faulty}} \varphi = \textsf{Faulty}_p \rightarrow K_p \top \). For epistemic models, it is logically equivalent to \(\top \), meaning that no information can be gleaned from a message under the assumption that it is sent by a fully byzantine agent without perception flaws. At the same time, for truth-telling correct agents
which closely matches the hope modality
from [10]. Indeed, since we assume agents to know their own type, it is the case that \(\textsf{Correct}_p \rightarrow K_p \textsf{Correct}_p\) holds, making \(H_p \varphi \) equivalent to \( \mathbb {C}_{p}^{\textsf{Correct} \setminus \textsf{Correct}}\varphi \).
Example 13
Apart from helping to understand messages, an interpretation function can be used to gain knowledge about the type of the sender. For instance, if A agents know enough about the way E agents communicate to conclude that a particular message \(\varphi \) can never be sent by an E agent, which corresponds to \(f_{AE}(\varphi ) = \bot \), then \(\mathbb {C}_{q}^{A \setminus E} \varphi = E_q \rightarrow K_q \bot \). For epistemic models, such \(\mathbb {C}_{q}^{A \setminus E} \varphi \) is logically equivalent to \(\lnot E_q\). In other words, having received \(\varphi \) from agent q, an A agent p learns at least \(K_p \lnot E_q\).
Remark 14
(Information from message passing). Let \(p,q \in \varPi \) be agents and \( \mathcal {A}\) be a partition of \(\varPi \). The knowledge gained by agent p upon receiving a message \(\varphi \) from agent q can be described by \(K_p \mathbb {C}_{q}^{p} \varphi \), where
In other words, knowing its own type, p considers all possible types for the sender q and for each type considers the respective interpretation of the message; the conjunction combined with the implications within creed make sure that the appropriate type is chosen. Note that the presence of send-unrestricted agents from Example 12 adds a conjunct to (5) that is equivalent to \(\top \). Hence, send-unrestricted agents can be safely ignored in determining the message meaning. By the same token, some conjuncts in (5) can rule out a particular type for agent q as in Example 13. Finally, if p has already ruled out some type E, then \(K_p\lnot E_q\) logically implies \(K_p(E_q \rightarrow K_q f_{AE}(\varphi ))\) independent of the interpretation function. In this case, the E-conjunct of (5) becomes redundant.
Example 15
In the system from Example 8 with send-unrestricted byzantine agents, upon receiving message \(\varphi \) from agent q, agent p can ignore the possibility of the sender being \(\textsf{Faulty}\) and conclude \( \textsf{Correct}_q \rightarrow K_q \varphi \), i.e., hope \(H_q \varphi \) for the case of factive beliefs, in full accordance with [10]. Note also that p may infer \(K_q \varphi \) from this message if p is sure that q is correct.
Now that we have established the basic definitions and semantics for the logic, we will now provide an axiomatization that we prove sound and complete in the next section.
Definition 16
(Logic EHL). Let \(\langle \varPi , \mathcal {A}, \mathcal {P}, \mathcal {C}, T \rangle \) be a heterogeneous distributed system and \(\{f_{AE} \mid A, E \in \mathcal {A}\}\) be the collection of interpretation functions for it. Logic EHL is obtained by adding to the standard axiomatization of modal logic of knowledge \(\textsf{S5}\) the partition axioms \(\textsf{P1}\)–\(\textsf{P3}\). The resulting axiom system is as follows: for all \(p \in \varPi \), all \(A\in \mathcal {A}\), and all \(E \in \mathcal {A}\) such that \(E \ne A\),
- \(\textsf{Taut}\):
-
All propositional tautologies in the language of EHL;
- \(\textsf{k}\):
-
\(K_p (\varphi \rightarrow \psi ) \rightarrow (K_p \varphi \rightarrow K_p \psi )\); \(\textsf{4}\) \(K_p \varphi \rightarrow K_p K_p \varphi \);
- \(\textsf{t}\):
-
\(K_p \varphi \rightarrow \varphi \);\(\textsf{5}\) \(\lnot K_p \varphi \rightarrow K_p \lnot K_p \varphi \);
- \((\textsf{MP})\):
-
rule inferring \(\psi \) from \(\varphi \rightarrow \psi \) and \(\varphi \); \((\textsf{Nec})\) rule inferring \(K_p \varphi \) from \(\varphi \);
Partition axiom \(\textsf{P1}\) states that each agent belongs to at least one of the types. Partition axiom \(\textsf{P2}\) postulates that each agent belongs to at most one of the types. Together they imply that agent types partition the set of agent. Partition axiom \(\textsf{P3}\) expresses that every process knows its own type.
4 Soundness and Completeness of EHL
Since \(\textsf{EHL}\) is an extension of \(\textsf{S5}\) with partition axioms governing the behavior of partition atoms while \(\textsf{EHL}\) models are instances of epistemic models, the soundness and completeness for \(\textsf{EHL}\) follows the standard proof for \(\textsf{S5}\) (see, e.g., [9]), where additionally it is necessary to establish that the partition axioms are sound and that the canonical model satisfies the additional restrictions.
Theorem 17
(Soundness). Logic EHL is sound with respect to EHL models, i.e., \(\textsf{EHL} \vdash \varphi \) implies \(\models \varphi \).
Proof
We only establish the validity of partition axioms. Axioms P1 and P2 hold due to condition (3). Similarly, P3 holds because of (4). \(\square \)
Completeness is proved by the standard canonical model construction, which requires several definitions. We omit the proofs of the following lemmas if completely standard and only treat new cases otherwise.
Definition 18
(Maximal consistent sets). A set \(\varGamma \subseteq \mathbb {F}\) of formulas is called consistent iff \(\textsf{EHL} \nvdash \lnot \bigwedge \varGamma _0\) for any finite subset \(\varGamma _0 \subseteq \varGamma \). A set \(\varGamma \) is called maximal consistent iff \(\varGamma \) is consistent but no proper superset \(\varDelta \supsetneq \varGamma \) is consistent.
Lemma 19
(Lindenbaum Lemma). Any consistent set \(\varGamma \) can be extended to a maximal consistent set \(\varDelta \supseteq \varGamma \).
Definition 20
(Canonical model). We define the canonical model \(M^C =( S^C, \sim ^C, V^C)\) is defined as follows:
-
\(S^C\) is the collection of all maximal consistent sets;
-
\(\varGamma \sim _p \varDelta \) iff \( \{K_p \varphi \mid K_p \varphi \in \varGamma \} = \{K_p \varphi \mid K_p \varphi \in \varDelta \}; \)
-
\(V^C(\varGamma ) :=\{ r \in Prop \mid r \in \varGamma \}\).
Lemma 21
(Truth Lemma). For any \(\varphi \in \mathbb {F}\) and any \(\varGamma \in S^C\),
Lemma 22
(Correctness). The canonical model is an EHL model.
Proof
That \(S^C \ne \varnothing \) and \(\sim _p\) is an equivalence relation for each \(p \in \varPi \) is proved the same way as for S5. It remains to show that (3) and (4) hold.
- (3):
-
Consider any maximal consistent set \(\varGamma \in S^C\) and any agent \(p \in \varPi \). By the standard properties of maximal consistent sets, all theorems of EHL belong to each maximal consistent set, in particular, \(\left( \bigvee _{A \in \mathcal {A}} A_p\right) \in \varGamma \) because of axiom P1. A disjunction belongs to a maximal consistent set iff one of the disjuncts does. Hence, there exists at least one type A such that \(A_p \in \varGamma \). At the same time, for any other type E, we have \((A_p \rightarrow \lnot E_p) \in \varGamma \) because of axiom P2. Hence, \(E_p \notin \varGamma \) because maximal consistent sets are consistent and closed with respect to (MP). It follows that there is exactly one partition atom of the form \(A_p\) in \(\varGamma \). Hence, by the definition of \(V^C\),
$$ \left| V^C(\varGamma ) \cap \{A_p \mid A \in \mathcal {A}\} \right| = 1. $$ - (4):
-
Consider two maximal consistent sets \(\varGamma \sim _p \varDelta \). Let \(A_p \in \varGamma \). By P3, also \(K_p A_p \in \varGamma \). Hence, \(K_p A_p \in \varDelta \) by the definition of \(\sim _p\). Finally, \(A_p \in \varDelta \) by axiom t. We proved that \(A_p \in \varGamma \) implies \(A_p \in \varDelta \). The inverse implication is analogous. \(\square \)
Theorem 23
(Completeness). Logic EHL is complete with respect to EHL models, i.e., \(\textsf{EHL} \vdash \varphi \) whenever \(\models \varphi \).
Proof
We prove the contrapositive. Assume \(\textsf{EHL} \nvdash \varphi \). That means that \(\{\lnot \varphi \}\) is consistent. By Lindenbaum Lemma 19, there exists a maximal consistent set \(\varGamma \supseteq \{\lnot \varphi \}\). Hence, this \(\varGamma \in S^C\) for the canonical model \(M^C\) defined in Definition 20, which is an EHL model by Lemma 22. By the Truth Lemma 21, it follows that \(M^C, \varGamma \models \lnot \varphi \). Since \(M^C, \varGamma \not \models \varphi \) for some EHL model, \(\varphi \) is not valid, i.e., \(\not \models \varphi \). \(\square \)
5 Properties of Creed
In this section, we derive several useful properties of creed modalities.
The explicit assumption P3 that each agent knows which type it belongs to implies a complete knowledge of own type, i.e., each agent a knows whether it belongs to any type A:
Theorem 24
\(\textsf{EHL} \vdash \lnot A_p \rightarrow K_p\lnot A_p\) for all \(p \in \varPi \), \(A \in \mathcal {A}\), i.e., agents know which type they do not belong to.
Proof
By P1, agent p must belong to one of the types. Hence, if not type A, it must be one of the remaining types, i.e., \(\lnot A_p \rightarrow \bigvee _{E \ne A} E_p\). Therefore, we have \(\lnot A_p \rightarrow \bigvee _{E \ne A} K_pE_p\) due to P3. Given that \(E_p \rightarrow \lnot A_p\) for each \(E \ne A\) by P2, also \(K_p E_p \rightarrow K_p \lnot A_p\) for each \(E \ne A\) by standard modal reasoning. Hence, \(\lnot A_p \rightarrow K_p \lnot A_p\). \(\square \)
Corollary 25
\(\textsf{EHL} \vdash K_p A_p \vee K_p\lnot A_p\) for all \(p \in \varPi \), \(A \in \mathcal {A}\)
Proof
It follows directly from P3 and Theorem 24 by propositional reasoning.
The creed modality amounts to \(\textsf{K45}\)-belief:
Theorem 26
Creed satisfies the normality, positive and negative introspection axioms if applied to statements already translated by an interpretation function. Formally, let
 stand for any formula \(\xi \) such that \(f_{AE}(\xi ) = \varphi \). Then the following formulas are derivable in EHL:
stand for any formula \(\xi \) such that \(f_{AE}(\xi ) = \varphi \). Then the following formulas are derivable in EHL:
- \(\textsf{k}_{\mathbb {C}}\):
-

- \(\textsf{4}_{\mathbb {C}}\):
-

- \(\textsf{5}_{\mathbb {C}}\):
-

Proof
We start by deriving \(\textsf{k}_{\mathbb {C}}\):
-
1.
 definition of creed
definition of creed -
2.
\( K_p(\varphi \rightarrow \psi ) \rightarrow (K_p \varphi \rightarrow K_p \psi )\) axiom \(\textsf{k}\)
-
3.
 prop. reasoning from 1.,2.
prop. reasoning from 1.,2. -
4.
 definition of creed
definition of creed -
5.
 prop. reasoning from 3.,4.
prop. reasoning from 3.,4. -
6.
 definition of creed
definition of creed -
7.
 rewriting of 5. using 6.
rewriting of 5. using 6.
The following is a derivation of \(\textsf{4}_{\mathbb {C}}\):
-
1.
 definition of creed
definition of creed -
2.
\(K_p \varphi \rightarrow K_pK_p \varphi \) axiom \(\textsf{4}\)
-
3.
 prop. reasoning from 1.,2.
prop. reasoning from 1.,2. -
4.
\( K_p \varphi \rightarrow (E_p \rightarrow K_p \varphi )\) prop. tautology
-
5.
\( K_p K_p \varphi \rightarrow K_p(E_p \rightarrow K_p \varphi )\) normal modal reasoning from 4.
-
6.
 prop. reasoning from 3.,5. using 1.
prop. reasoning from 3.,5. using 1. -
7.
 definition of creed
definition of creed -
8.
 rewriting of 6. using 7.
rewriting of 6. using 7.
The following is a derivation of \(\textsf{5}_{\mathbb {C}}\):
-
1.
 prop. reasoning from the definition of creed
prop. reasoning from the definition of creed -
2.
\( E_p \rightarrow K_pE_p\) axiom P3
-
3.
\( \lnot K_p \varphi \rightarrow K_p \lnot K_p \varphi \) axiom 5
-
4.
 normal modal reasoning from 1.–3.
normal modal reasoning from 1.–3. -
5.
 normal modal reasoning from 1.,4.
normal modal reasoning from 1.,4. -
6.
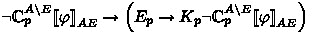 prop. reasoning from 5.
prop. reasoning from 5. -
7.
 rewriting of 6. \(\square \)
rewriting of 6. \(\square \)
In addition, this creed belief is factive whenever the speaker type is correctly identified (cf. a similar conditional factivity for hope in [10]):
Theorem 27
 .
.
Proof
-
1.
 definition of creed
definition of creed -
2.
\(\vdash K_p \varphi \rightarrow \varphi \) axiom \(\textsf{t}\)
-
3.
 prop. reasoning from 1.,2. \(\square \)
prop. reasoning from 1.,2. \(\square \)
On the other hand, misidentifying the speaker’s type may easily destroy factivity. Let \(p \notin E\). Given that
 , we have \(E_p \rightarrow K_p \varphi \) true simply because \(E_p\) is false. Accordingly, there is no reason why \(\varphi \) must hold.
, we have \(E_p \rightarrow K_p \varphi \) true simply because \(E_p\) is false. Accordingly, there is no reason why \(\varphi \) must hold.
This provides a formal model of how a true statement can lead to false beliefs due to misinterpretation. Moreover, as Theorem 26 shows, such false beliefs cannot be detected by introspection.
6 Applications
6.1 Formalizing “The Murders in the Rue Morgue”
Example 1 describes a situation where honest witnesses provide contradictory information that is, nevertheless, successfully filtered by Dupin. We show how his reasoning can be formalized and explained using the creed modality. Dupin reads all witness accounts from a paper. We assume no misinterpretation of what the witnesses said. In addition, the paper mentions the exact type of each witness (French not speaking Italian, Dutch not speaking French, etc.), which again is assumed to be factive. Hence, we use only one creed modality with the identity interpretation function per witness account read by Dupin. In other words, Dupin reasons about the available information without the need to interpret it. The crucial question is: Why does Dupin ignore some but not all of the information provided by each witness? The answer becomes clear if we view each witness account as one or several creed modalities regarding what this witness heard from m. Ignoring slight variations in details, all witness statements can be divided into two types: (a) m did not speak the language I speak; (b) m spoke a language I do not speak. Dupin accepts statements (a) but ignores statements (b). Even when statement (b) of a witness contradicts statement (a) of another witness, Dupin accepts statements (a) from both witnesses. Here is how these statements of, say, the French witness \(f \in F\) regarding the utterance \(\varphi \) of m can be represented via the creed modality:
Indeed, for (a), since the interpreting function from French to French is meaningful (in the simplest case, is the identity function), the fact that f could not understand what m was saying in this case means that \(f_{FF}(\varphi ) = \bot \). On the other hand, for (b), since f does not know Italian, he has \(f_{FI}(\psi )=\top \) for all \(\psi \). As discussed in Example 13, (a) yields \(\lnot F_m\). Similarly, (b) yields \(\top \) as per Example 12. This rightfully leads Dupin to the conclusion \(\lnot F_m\), i.e., \(m \notin F\). In other words, statements (b) are ignored because they are trivial, not because they are false. One might say that, for f, a stronger precondition of m saying something in Italian is \(m \in I\). But using \(I_m \rightarrow K_m I_m\) in place of (b) would yield axiom \(\textsf{P3}\), still a logically trivial statement.
In the story, m was an orangutan (Ourang-Outang in Poe’s spelling), thus, fulfilling \(m \notin A\) for any language A discussed.
6.2 Solution to Knights and Knaves
Clearly the partition of the island from Example 2 involves two types: I for knIghts and A for knAves. Let s be the reasoner and L be his type. The puzzle postulates that \( f_{LI}(\varphi ) = \varphi \) and \(f_{LA}(\varphi ) = \lnot \varphi \) for any formula \(\varphi \). Accordingly, the full information agent s receives from agent p’s statement that \(\varphi \) is
In the puzzle in question, p states that at least one of p and q is a knave, \(A_p \vee A_q\) in formulas. Hence, agent s learns
Here is how to derive in EHL that p is a knight and q is a knave, i.e., \(I_p \wedge A_q\):
-
1.
\(A_p \rightarrow K_p \lnot (A_p \vee A_q)\) prop. reasoning from (7)
-
2.
\(K_p \lnot (A_p \vee A_q) \rightarrow \lnot A_p \) t and prop. reasoning
-
3.
\(\lnot A_p\) prop. reasoning since \(A_p \rightarrow \lnot A_p\) follows from 1. and 2.
-
4.
\(\lnot A_p \rightarrow I_p\) P1 and prop. reasoning
-
5.
\(I_p\) (MP) from 3. and 4.
-
6.
\(I_p \rightarrow K_p (A_p \vee A_q)\) prop. reasoning from (7)
-
7.
\(I_p \rightarrow A_p \vee A_q\) t and prop. reasoning from 6.
-
8.
\(I_p \rightarrow A_q\) prop. reasoning from 7. since \(I_p \rightarrow \lnot A_p\) by P2
-
9.
\(I_p \wedge A_q\) prop. reasoning from 5. and 8.
Hence, \(\textsf{EHL} \vdash \mathbb {C}_{p}^{s} (A_p \vee A_q) \rightarrow I_p \wedge A_q\).
6.3 Modelling of Software Updates
Consider an heterogeneous distributed system with two agent-types, U for the updated agents running the most recent software and O for the agents running the old protocol, which is designed with the possibility of future updates in mind. Since the new protocols are designed by taking into account the existence of processes running the old protocol, the interpretation functions can be built asymmetrically. Each type interprets information from its own type directly: \(f_{UU} (\varphi ) = \varphi \) and \(f_{OO} (\varphi ) = \varphi \). U agents can interpret messages from O agents using backward compatibility \(f_{UO} (\varphi ) = g\bigl (f_{OO}(\varphi )\bigr )\), where g translates into the updated system language.
The opposite is not always possible as O agents have no knowledge of the new protocols. Accordingly, messages \(\varphi \) compatible with the old protocol will be processed as before, i.e., using \(f_{OO}(\varphi )\). But if \(\varphi \) is unknown to the old protocol, i.e., \(f_{OO} (\varphi ) = \bot \), the creed under the assumption that sender \(s \in O\) would yield \(\mathbb {C}_{s}^{O \setminus O} \varphi \leftrightarrow \lnot O_s\). In this case, receiver r can conclude that the sender process s does not conform to the old protocol. Since this error flagging disappears when r is also updated, however, it may very well be the case that this does not violate the fault resilience properties of the old protocol, in particular, when not too many processes are updated simultaneously. In this case, r could be guaranteed to always compute a correct result.
6.4 Comparison to Related Work
The interpretation functions in the knights and knaves puzzles depend on the speaker only, which made it possible to formalize them in [20] by means of public announcements. In the other two examples (Rue Morgue and software update), there is an additional difficulty: even knowing the sender’s type, agents interpret messages differently based on the varying levels of knowledge about the sender’s protocol. This important degree of freedom of our method compared to [20] is especially central to the software update example.
7 Conclusion and Future Work
This paper provides a sound and complete axiomatization for a logic for heterogeneous distributed systems that generalizes the logic of fault-tolerant distributed systems and enables us to explicitly model the interpretation of messages sent by agents that execute different protocols (identified by types). It revolves around a (derived) new modality called creed, a generalization of the hope modality for byzantine agents, that satisfies positive and negative introspection post message-interpretation and enjoys factivity when the sender’s type is correctly identified. We demonstrated the explanatory power of our approach by applying it to three representative examples from areas ranging from detective reasoning to logic puzzles to distributed systems. The current formalization assumes that agents knowledge is factive even if this factivity does not affect how they communicated. Relaxing this assumption and working with agents whose beliefs may be compromised, e.g., due to sensor errors or memory failures, is a natural next step. Another natural extension is to allow for on-the-fly updates to the interpretation functions based on received information.
Notes
- 1.
The focus of [7] is on a priori assumptions that can be erroneous and may require later updates, hence, the term a priori beliefs there. In this paper, we generally assume these assumptions to be factive, hence, we use a priori knowledge instead.
- 2.
Adding byzantine faults to the picture will be left for future research.
References
Ajmani, S., Liskov, B., Shrira, L.: Modular software upgrades for distributed systems. In: Thomas, D. (ed.) ECOOP 2006. LNCS, vol. 4067, pp. 452–476. Springer, Heidelberg (2006). https://doi.org/10.1007/11785477_26
Amoussou-Guenou, Y., Biais, B., Potop-Butucaru, M., Tucci-Piergiovanni, S.: Rational vs byzantine players in consensus-based blockchains. In: AAMAS 2020: Proceedings of the 19th International Conference on Autonomous Agents and MultiAgent Systems, pp. 43–51. IFAAMAS (2020). https://dl.acm.org/doi/abs/10.5555/3398761.3398772
Artemov, S.: Observable models. In: Artemov, S., Nerode, A. (eds.) LFCS 2020. LNCS, vol. 11972, pp. 12–26. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-36755-8_2
Attiya, H., Welch, J.: Distributed Computing: Fundamentals, Simulations and Advanced Topics, 2nd edn. Wiley, Hoboken (2004)
Bílková, M., Christoff, Z., Roy, O.: Revisiting epistemic logic with names. In: Proceedings Eighteenth Conference on Theoretical Aspects of Rationality and Knowledge: Beijing, China, June 25–27, 2021. Electronic Proceedings in Theoretical Computer Science, vol. 335, pp. 39–54. Open Publishing Association (2021). https://doi.org/10.4204/eptcs.335.4
Castañeda, A., Gonczarowski, Y.A., Moses, Y.: Unbeatable consensus. Distrib. Comput. 35(2), 123–143 (2022). https://doi.org/10.1007/s00446-021-00417-3
Cignarale, G., Schmid, U., Tahko, T., Kuznets, R.: The role of a priori belief in the design and analysis of fault-tolerant distributed systems. Mind. Mach. 33(2), 293–319 (2023). https://doi.org/10.1007/s11023-023-09631-3
Coulouris, G., Dollimore, J., Kindberg, T., Blair, G.: Distributed Systems: Concepts and Design, 5th edn. Addison-Wesley, Boston (2011)
van Ditmarsch, H., van der Hoek, W., Kooi, B.: Dynamic Epistemic Logic, Synthese Library, vol. 337. Springer, Dordrecht (2007). https://doi.org/10.1007/978-1-4020-5839-4
Fruzsa, K., Kuznets, R., van Ditmarsch, H.: A new hope. In: Fernández-Duque, D., Palmigiano, A., Pinchinat, S. (eds.) Advances in Modal Logic, vol. 14, pp. 349–370. College Publications (2022)
Fruzsa, K., Kuznets, R., Schmid, U.: Fire! In: Proceedings Eighteenth Conference on Theoretical Aspects of Rationality and Knowledge: Beijing, China, June 25–27, 2021. Electronic Proceedings in Theoretical Computer Science, vol. 335, pp. 139–153. Open Publishing Association (2021). https://doi.org/10.4204/EPTCS.335.13
Groce, A., Katz, J., Thiruvengadam, A., Zikas, V.: Byzantine agreement with a rational adversary. In: Czumaj, A., Mehlhorn, K., Pitts, A., Wattenhofer, R. (eds.) ICALP 2012. LNCS, vol. 7392, pp. 561–572. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31585-5_50
Halpern, J.Y.: Using reasoning about knowledge to analyze distributed systems. Ann. Rev. Comput. Sci. 2, 37–68 (1987). https://doi.org/10.1146/annurev.cs.02.060187.000345
Halpern, J.Y., Moses, Y.: Knowledge and common knowledge in a distributed environment. J. ACM 37(3), 549–587 (1990). https://doi.org/10.1145/79147.79161
Hintikka, J.: Knowledge and Belief: An Introduction to the Logic of the Two Notions. Cornell University Press, New York (1962)
Kuznets, R., Prosperi, L., Schmid, U., Fruzsa, K.: Causality and epistemic reasoning in byzantine multi-agent systems. In: Moss, L.S. (ed.) Proceedings Seventeenth Conference on Theoretical Aspects of Rationality and Knowledge: Toulouse, France, 17–19 July 2019. Electronic Proceedings in Theoretical Computer Science, vol. 297, pp. 293–312. Open Publishing Association (2019). https://doi.org/10.4204/EPTCS.297.19
Kuznets, R., Prosperi, L., Schmid, U., Fruzsa, K.: Epistemic reasoning with byzantine-faulty agents. In: Herzig, A., Popescu, A. (eds.) FroCoS 2019. LNCS (LNAI), vol. 11715, pp. 259–276. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-29007-8_15
Kuznets, R., Prosperi, L., Schmid, U., Fruzsa, K., Gréaux, L.: Knowledge in byzantine message-passing systems I: framework and the causal cone. Technical report. TUW-260549, TU Wien (2019). https://publik.tuwien.ac.at/files/publik_260549.pdf
Lamport, L., Shostak, R., Pease, M.: The Byzantine Generals Problem. ACM Trans. Program. Lang. Syst. 4(3), 382–401 (1982). https://doi.org/10.1145/357172.357176
Liu, F., Wang, Y.: Reasoning about agent types and the hardest logic puzzle ever. Mind. Mach. 23(1), 123–161 (2013). https://doi.org/10.1007/s11023-012-9287-x
Lynch, N.A.: Distributed Algorithms. Morgan Kaufmann, Burlington (1996)
Moses, Y.: Relating knowledge and coordinated action: the knowledge of preconditions principle. In: Ramanujam, R. (ed.) Proceedings Fifteenth Conference on Theoretical Aspects of Rationality and Knowledge: Carnegie Mellon University, Pittsburgh, USA, June 4–6, 2015. Electronic Proceedings in Theoretical Computer Science, vol. 215, pp. 231–245. Open Publishing Association (2015). https://doi.org/10.4204/EPTCS.215.17
Moses, Y., Rajsbaum, S.: A layered analysis of consensus. SIAM J. Comput. 31(4), 989–1021 (2002). https://doi.org/10.1137/S0097539799364006
Moses, Y., Shoham, Y.: Belief as defeasible knowledge. Artif. Intell. 64(2), 299–321 (1993). https://doi.org/10.1016/0004-3702(93)90107-M
Saur, K., Collard, J., Foster, N., Guha, A., Vanbever, L., Hicks, M.: Safe and flexible controller upgrades for SDNs. In: Symposium on Software Defined Networking (SDN) Research (SOSR 2016): March 14–15, 2016, in Santa Clara, CA. ACM (2016). https://doi.org/10.1145/2890955.2890966
Smullyan, R.M.: What is the Name of this Book? The Riddle of Dracula and Other Logical Puzzles. Prentice-Hall, Hoboken (1978)
Acknowledgments
The authors would like to thank Stephan Felber, Krisztina Fruzsa, Rojo Randrianomentsoa, and Thomas Schlögl as well as the participants of Dagstuhl Seminar 23272 “Epistemic and Topological Reasoning in Distributed Systems” for discussions and suggestions. We also thank the anonymous reviewers for their useful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Cignarale, G., Kuznets, R., Rincon Galeana, H., Schmid, U. (2023). Logic of Communication Interpretation: How to Not Get Lost in Translation. In: Sattler, U., Suda, M. (eds) Frontiers of Combining Systems. FroCoS 2023. Lecture Notes in Computer Science(), vol 14279. Springer, Cham. https://doi.org/10.1007/978-3-031-43369-6_7
Download citation
DOI: https://doi.org/10.1007/978-3-031-43369-6_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-43368-9
Online ISBN: 978-3-031-43369-6
eBook Packages: Computer ScienceComputer Science (R0)





 definition of creed
definition of creed prop. reasoning from 1.,2.
prop. reasoning from 1.,2. definition of creed
definition of creed prop. reasoning from 3.,4.
prop. reasoning from 3.,4. definition of creed
definition of creed rewriting of 5. using 6.
rewriting of 5. using 6. definition of creed
definition of creed prop. reasoning from 1.,2.
prop. reasoning from 1.,2. prop. reasoning from 3.,5. using 1.
prop. reasoning from 3.,5. using 1. definition of creed
definition of creed rewriting of 6. using 7.
rewriting of 6. using 7. prop. reasoning from the definition of creed
prop. reasoning from the definition of creed normal modal reasoning from 1.–3.
normal modal reasoning from 1.–3. normal modal reasoning from 1.,4.
normal modal reasoning from 1.,4.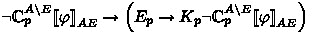 prop. reasoning from 5.
prop. reasoning from 5. rewriting of 6.
rewriting of 6.  definition of creed
definition of creed prop. reasoning from 1.,2.
prop. reasoning from 1.,2.