Abstract
We explore the relationship between weighted path orders and (monotonic) semantic path orders. Our findings reveal that weighted path orders can be considered instances of a variant of semantic path orders that comprise order pairs. This observation leads to a generalization of weighted path orders that does not impose simplicity on their underlying algebras. As a result, the generalized version is capable of proving termination of term rewrite systems beyond the realm of simple termination. In order to assess practicality we provide experimental data comparing generalized weighted path orders with the original ones as well as other well-known classes of reduction orders.
T. Saito—supported by JST SPRING, Grant Number JPMJSP2102. N. Hirokawa—supported by JSPS KAKENHI Grant Number JP22K11900.
You have full access to this open access chapter, Download conference paper PDF
Keywords
1 Introduction
Reduction orders are a fundamental tool in termination analysis of term rewrite systems, and they also underlie completion-based automated theorem proving. Weighted path orders (WPOs) [27] are known as a versatile class of reduction orders; WPOs can simulate (generalized) Knuth–Bendix orders [7, 13, 16] and lexicographic path orders [12], depending on the choice of parameters, namely simple monotone algebras and precedences. In fact, weighted path orders are so powerful that they characterize simple termination of term rewrite systems [20, Definition 6.3.7], that is, a term rewrite system is simply terminating if and only if it admits a compatible WPO. Besides automated termination analysis [14, 26], WPOs are used in reachability analysis [25], and automated theorem proving [11, 18].
Another well-known class of reduction orders is the class of monotonic semantic path orders (MSPOs) [4, 5], which are a monotonic version of semantic path orders (SPOs) [12]. MSPOs take triples of orders (called reduction triples) as parameters, and provide a complete characterization of terminating term rewrite systems: A term rewrite system is terminating if and only if it admits a compatible MSPO. However, the relationship between WPOs and MSPOs has not been known [24].
In this paper, we give a solution to the open problem, demonstrating an effective construction of an MSPO from the algebra and the precedence of a given WPO. The key of the proof lies in finding a suitable new variant of MSPOs, which is described as follows: First, the variant uses lexicographic comparison [4, Definition 4.5.1], as the original WPOs [27, Definition 5] are based on this comparison strategy. Second, the variant employs reduction triples [4, Definition 4.1.19] because an example shows that a variant based on (quasi-)reduction pairs [5, Definition 4] leads to an invalid construction.
The obtained simulation result leads to a generalization of WPOs that does not impose simplicity on their underlying algebras. The generalization can show termination of term rewrite systems that are not simply terminating. This is a sharp contrast to the termination proving power of WPOs. In addition, upgrading WPOs to GWPOs can be done with little implementation effort, so we anticipate that tools which employ WPOs as reduction orders (e.g. [11, 14, 18, 23, 25, 26]) may benefit from power of GWPOs.
The remaining part of the paper is organized as follows. After recalling notions and notations for term rewriting and WPOs in Sect. 2, we introduce a slightly modified version of semantic path orders that employs order pairs in Sect. 3. In Sect. 4 we show that weighted path orders are instances of semantic path orders. Using this fact, we introduce a generalization of WPOs in Sect. 5. In Sect. 6 experimental data for (generalized) weighted path orders are reported. As in the case of MSPOs [5, Section 5.2], GWPOs are capable of simulating a basic version of the dependency pair method [1]. This is discussed in Sect. 7. The paper is concluded by stating related work in Sect. 8.
2 Preliminaries
Throughout the paper, we assume familiarity with term rewriting [3, 20]. First we briefly recall basic notions for term rewriting and reduction orders, and then introduce weighted path orders.
2.1 Term Rewriting
Let \(\mathcal {F}\) be a signature and \(\mathcal {V}\) a countable set of variables with \(\mathcal {F}\cap \mathcal {V}= \varnothing \). The set of all terms built from \(\mathcal {F}\) and \(\mathcal {V}\) is referred to as \(\mathcal {T}(\mathcal {F},\mathcal {V})\), or just as \(\mathcal {T}\) when \(\mathcal {F}\) and \(\mathcal {V}\) are clear from the context. When we need to indicate the arity n of a function symbol f, we write \(f^{(n)}\) for f. Quasi-orders on the signature are called (quasi-)precedences. A quasi-precedence \(\succsim \) is called well-founded if its strict part \(\succ \) is well-founded. The size |t| of a term t is the number of function symbols and variables occurring in t. Let \(\Box \) be a constant with \(\Box \notin \mathcal {F}\). Contexts are terms over \(\mathcal {F}\cup \{ \Box \}\) that contain exactly one \(\Box \). The term resulting from replacing \(\Box \) in a context C by a term t is denoted by C[t]. We write
 if there is a context C with \(s = C[t]\). The strict part of
if there is a context C with \(s = C[t]\). The strict part of
 is denoted by \(\rhd \). A substitution is a mapping \(\sigma \) from variables to terms such that \(\{ x \in \mathcal {V}\mid \sigma (x) \ne x \}\) is finite. The application \(t\sigma \) of a substitution \(\sigma \) to a term t is inductively defined as follows: \(t\sigma = \sigma (t)\) if t is a variable, and \(t\sigma = f(t_1\sigma ,\ldots ,t_n\sigma )\) if \(t = f({t_1},\dots ,{t_{n}})\).
is denoted by \(\rhd \). A substitution is a mapping \(\sigma \) from variables to terms such that \(\{ x \in \mathcal {V}\mid \sigma (x) \ne x \}\) is finite. The application \(t\sigma \) of a substitution \(\sigma \) to a term t is inductively defined as follows: \(t\sigma = \sigma (t)\) if t is a variable, and \(t\sigma = f(t_1\sigma ,\ldots ,t_n\sigma )\) if \(t = f({t_1},\dots ,{t_{n}})\).
A pair \((\ell ,r)\) of terms is said to be a rewrite rule if \(\ell \) is not a variable and every variable in r occurs in \(\ell \). Rewrite rules \((\ell ,r)\) are written by \(\ell \rightarrow r\). A set of rewrite rules is called a term rewrite system (TRS). Let \(\mathcal {R}\) be a TRS. We write \(\mathcal {D}_\mathcal {R}\) for the set of defined symbols \(\{ f \mid f({\ell _1},\dots ,{\ell _{n}}) \rightarrow r \in \mathcal {R}\}\). The relation \(\rightarrow _\mathcal {R}\) is defined on terms as follows: \(s \rightarrow _\mathcal {R}t\) if there exist a rewrite rule \(\ell \rightarrow r \in \mathcal {R}\), a context C, and a substitution \(\sigma \) such that \(s = C[\ell \sigma ]\) and \(t = C[r\sigma ]\) hold. The TRS \(\mathcal {R}\) is said to be terminating if there is no infinite sequence \(t_1 \rightarrow _\mathcal {R}t_2 \rightarrow _\mathcal {R}\cdots \). A relation \(\leadsto \) on terms is closed under contexts if \(C[s] \leadsto C[t]\) holds whenever \(s \leadsto t\) and C is a context, and it is called closed under substitutions or just stable if \(s\sigma \leadsto t\sigma \) holds whenever \(s \leadsto t\) and \(\sigma \) is a substitution. We say \(\leadsto \) has the subterm property if \(s \leadsto t\) for all terms s, t satisfying \(s \rhd t\). Relations closed under contexts and substitutions are called rewrite relations.
Termination is often shown by using orders. We say that a rewrite relation is a rewrite preorder or reduction order if it is a preorder or a well-founded order, respectively. A TRS \(\mathcal {R}\) is compatible with a strict order > if \(\mathcal {R}\subseteq {>}\).
Proposition 1
A TRS \(\mathcal {R}\) is terminating if \(\mathcal {R}\) is compatible with some reduction order >.
An ordered \(\mathcal {F}\)-algebra is a triple \((A, \{f_\mathcal {A}\}_{f \in \mathcal {F}}, {>})\), where A is a set called a carrier, \(f_\mathcal {A}\) is an n-ary function on A (called an interpretation function) associated with each \(f^{(n)} \in \mathcal {F}\), and > is a strict order on A. Let \(\mathcal {A}= (A, \{f_\mathcal {A}\}_{f \in \mathcal {F}}, {>})\) be an ordered algebra. A mapping from \(\mathcal {V}\) to A is called an assignment for \(\mathcal {A}\). The interpretation \([\alpha ]_\mathcal {A}(t)\) of a term t under an assignment \(\alpha \) is inductively defined as follows: \([\alpha ]_\mathcal {A}(t) = \alpha (t)\) if t is a variable, and \([\alpha ]_\mathcal {A}(t) = f_\mathcal {A}([\alpha ]_\mathcal {A}(t_1),\ldots ,[\alpha ]_\mathcal {A}(t_n))\) if \(t = f({t_1},\dots ,{t_{n}})\). We write \(s >_\mathcal {A}t\) if \([\alpha ]_\mathcal {A}(s) > [\alpha ]_\mathcal {A}(t)\) for all assignments \(\alpha \). The relation \(>_\mathcal {A}\) is a strict order. Similarly we write \(s \geqslant _\mathcal {A}t\) if \([\alpha ]_\mathcal {A}(s) \geqslant [\alpha ]_\mathcal {A}(t)\) holds for all assignments \(\alpha \), where \(\geqslant \) stands for the reflexive closure of >. The relation \(\geqslant _\mathcal {A}\) is a quasi-order, and satisfies \(\geqslant _\mathcal {A}\cdot>_\mathcal {A}\cdot \geqslant _\mathcal {A}{\subseteq } >_\mathcal {A}\). We say that the ordered algebra \(\mathcal {A}\) is
-
simple if \(f_\mathcal {A}(a_1, \ldots , a_i, \ldots , a_n) \geqslant a_i\) for all \(f^{(n)} \in \mathcal {F}\), \(1 \leqslant i \leqslant n\), and \({a_1},\dots ,{a_{n}} \in A\);
-
weakly monotone if \( f_\mathcal {A}(a_1,\ldots ,a_i,\ldots ,a_n) \geqslant f_\mathcal {A}(a_1,\ldots ,b,\ldots ,a_n) \) for all \(f^{(n)} \in \mathcal {F}\), argument positions \(1 \leqslant i \leqslant n\), and \({a_1},\dots ,{a_{n}}, b \in A\) with \(a_i > b\);
-
simple monotone if it is simple and weakly monotone; and
-
well-founded if > is well-founded.
If > is well-founded, so is \(>_\mathcal {A}\). If \(\mathcal {A}\) is a weakly monotone algebra, \(\geqslant _\mathcal {A}\) is a rewrite preorder. If in addition \(\mathcal {A}\) is simple, \(\geqslant _\mathcal {A}\) has the subterm property \({\rhd } \subseteq {\geqslant _\mathcal {A}}\).
2.2 Weighted Path Orders
Weighted path orders (WPOs) are reduction orders introduced by Yamada et al. [27]. The definition of WPOs is based on the pair of an ordered algebra \(\mathcal {A}\) and a precedences \(\succsim \). A WPO compares terms s, t as a generalized KBO does: First the terms are compared by \(s >_\mathcal {A}t\). If only weak inequality \(s \geqslant _\mathcal {A}t\) holds then their root symbols, say f and g, are compared by the precedence \(\succsim \). If again only weak inequality \(f \succsim g\) holds, arguments are compared lexicographically.
Lexicographic comparison is formalized as follows. Let > be a strict order on a set A and let \(A^*\) denote the set of all strings (tuples) over A. The lexicographic extension \(>^\textsf{lex}\) of > is defined on \(A^*\) as follows: \((a_1, \ldots , a_n) >^{\textsf{lex}} (b_1, \ldots , b_m)\) if there is a natural number \(k < n\) such that
-
\(a_j = b_j\) for all \(1 \leqslant j \leqslant k\), and
-
either \(k = m\), or \(k < m\) and \(a_{k+1} > b_{k+1}\).
It is known that \(>^{\textsf{lex}}\) is a strict order on \(A^*\).
Definition 1
([27]). Let \(\mathcal {A}\) be an ordered \(\mathcal {F}\)-algebra and \(\succsim \) a precedence. The weighted path order \(>_\textsf{wpo}\) is defined on terms over \(\mathcal {F}\) as follows: \(s >_\textsf{wpo}t\) if
-
1.
\(s >_\mathcal {A}t\), or
-
2.
\(s \geqslant _\mathcal {A}t\), \(s = f({s_1},\dots ,{s_{m}})\), and one of the following conditions holds.
-
a.
\(s_i \geqslant _\textsf{wpo}t\) for some \(1 \leqslant i \leqslant m\).
-
b.
\(t = g({t_1},\dots ,{t_{n}})\) and \(s >_\textsf{wpo}t_j\) for all \(1 \leqslant j \leqslant n\), and moreover
-
(i)
\(f \succ g\), or
-
(ii)
\(f \succsim g\) and \(({s_1},\dots ,{s_{m}}) >_\textsf{wpo}^\textsf{lex}({t_1},\dots ,{t_{n}})\).
-
(i)
-
a.
Here \(\geqslant _\textsf{wpo}\) denotes the reflexive closure of \(>_\textsf{wpo}\).
Theorem 1
([27]). Suppose that the signature is finite. For every simple monotone well-founded algebra and well-founded precedence the induced relation \(>_\textsf{wpo}\) is a reduction order with the subterm property.
Example 1
Consider the following TRS \(\mathcal {R}\) taken from [27, Example 9]:
Let \(\mathcal {A}\) be the simple monotone algebra on \(\mathbb {N}\) with \(\textsf{f}_\mathcal {A}(x) = \textsf{h}_\mathcal {A}(x) = x\) and \(\textsf{g}_\mathcal {A}(x) = x + 1\). Take a precedence \(\succsim \) with \(\textsf{f} \succ \textsf{g} \succ \textsf{h}\). The relation \(\textsf{f}(\textsf{g}(x)) >_\textsf{wpo}\textsf{g}(\textsf{f}(\textsf{f}(x)))\) is verified by the following derivation:

Here WPO 1 and WPO 2b(i) indicate the corresponding conditions in Definition 1. Similarly, one can verify \(\textsf{f}(\textsf{h}(x)) >_\textsf{wpo}\textsf{h}(\textsf{h}(\textsf{f}(x)))\). Therefore, \(\mathcal {R}\subseteq {>_\textsf{wpo}}\) follows. Hence, we conclude that \(\mathcal {R}\) is terminating.
The following example shows that the simplicity condition cannot be dropped from Theorem 1.
Example 2
Any WPO \(>_\textsf{wpo}\) induced by the weakly monotone but non-simple algebra \(\mathcal {A}\) on \(\mathbb {N}\) with \(\textsf{a}_\mathcal {A}= 1\) and \(\textsf{f}_\mathcal {A}(x) = 0\) lacks well-foundedness as it admits the cyclic sequence \(\textsf{f}(\textsf{a})>_\textsf{wpo}\textsf{f}(\textsf{f}(\textsf{a})) >_\textsf{wpo}\textsf{f}(\textsf{a})\).
3 Semantic Path Orders Based on Order Pairs
Borralleras [4, Definition 4.1.19] introduced a variant of SPO that employs a pair of a quasi-order and a strict order. This variant compares arguments of terms by a multiset order. In order to simulate WPOs which compare arguments in a lexicographic manner, we introduce another variant of SPO.
We say that the pair \(({\gtrsim },{>})\) of a quasi-order \(\gtrsim \) and a strict order > is an order pair if \(\gtrsim \cdot > \cdot \gtrsim {\subseteq }>\). The inclusion is referred to as compatibility. We say that an order pair
 on terms is stable if both
on terms is stable if both
 and \(\sqsupset \) are stable.
and \(\sqsupset \) are stable.
Definition 2
Let
 be a stable order pair on \(\mathcal {T}\setminus \mathcal {V}\).Footnote 1 The semantic path order \(>_\textsf{spo}\) (SPO) is defined on terms as follows: \(s >_\textsf{spo}t\) if \(s = f({s_1},\dots ,{s_{m}})\) and one of the following conditions hold:
be a stable order pair on \(\mathcal {T}\setminus \mathcal {V}\).Footnote 1 The semantic path order \(>_\textsf{spo}\) (SPO) is defined on terms as follows: \(s >_\textsf{spo}t\) if \(s = f({s_1},\dots ,{s_{m}})\) and one of the following conditions hold:
-
1.
\(s_i \geqslant _\textsf{spo}t\) for some \(1 \leqslant i \leqslant m\).
-
2.
\(t = g({t_1},\dots ,{t_{n}})\) and \(s >_\textsf{spo}t_j\) for all \(1 \leqslant j \leqslant n\), and moreover
-
a.
\(s \sqsupset t\), or
-
b.
 and \(({s_1},\dots ,{s_{m}}) >_\textsf{spo}^{\textsf{lex}} ({t_1},\dots ,{t_{n}})\).
and \(({s_1},\dots ,{s_{m}}) >_\textsf{spo}^{\textsf{lex}} ({t_1},\dots ,{t_{n}})\).
-
a.
Here \(\geqslant _\textsf{spo}\) denotes the reflexive closure of \(>_\textsf{spo}\).
Remark 1
The standard definitions of SPOs ( [12] and [4, Definition 4.1.19]) use the multiset extension of \(>_\textsf{spo}\) in SPO 2b instead of the lexicographic extension. The lexicographic version of SPOs, introduced by Borralleras [4, Definition 4.5.1], can be obtained by setting \(\sqsupset \) to the strict part of
 in Definition 2.
in Definition 2.
Example 3
Lexicographic path orders (LPOs) are special instances of SPOs. Let \(\succsim \) be a precedence. Define
 by \(f \succsim g\), and let \(\sqsupset \) be the strict part of
by \(f \succsim g\), and let \(\sqsupset \) be the strict part of
 . The semantic path order induced by
. The semantic path order induced by
 is the lexicographic path order induced by \(\succsim \).
is the lexicographic path order induced by \(\succsim \).
Let
 be a stable order pair on \(\mathcal {T}\setminus \mathcal {V}\) and let \(>_\textsf{spo}\) be the semantic path order induced by
be a stable order pair on \(\mathcal {T}\setminus \mathcal {V}\) and let \(>_\textsf{spo}\) be the semantic path order induced by
 . The transitivity, reflexivity, and stability of \(>_\textsf{spo}\) are straightforward. A small remark is that the compatibility
. The transitivity, reflexivity, and stability of \(>_\textsf{spo}\) are straightforward. A small remark is that the compatibility
 is used in the proof of the transitivity.
is used in the proof of the transitivity.
Lemma 1
The SPO \(>_\textsf{spo}\) is a stable strict order. \(\square \)
When the signature is infinite, the lexicographic version of SPOs is not well-founded in general even if \(\sqsupset \) is well-founded. This forms a contrast to the multiset versions of SPOs mentioned in Remark 1.
Example 4
Consider the signature consisting of \(\textsf{a}^{(0)}\), \(\textsf{b}^{(0)}\), and \(\textsf{f}_i^{(i)}\) for all numbers \(i \in \mathbb {N}\). Let \(\succsim \) be a well-founded precedence satisfying \(\textsf{a} \succ \textsf{b}\) and \(\textsf{f}_i \succsim \textsf{f}_j\) for all \(i, j \in \mathbb {N}\). The pair
 defined as in Example 3 is an order pair with \(\sqsupset \) well-founded, but the SPO \(>_\textsf{spo}\) induced from
defined as in Example 3 is an order pair with \(\sqsupset \) well-founded, but the SPO \(>_\textsf{spo}\) induced from
 admits the infinite chain:
admits the infinite chain:
See [22, Section 3] and [19, Section 3] for related discussions.
Well-foundedness of \(>_\textsf{spo}\) is restored by assuming existence of an upper bound of arities. We refer to this property as boundedness of the signature. Needless to say, a signature is bounded whenever it is finite.
Hereafter we assume that \(\sqsupset \) is well-founded and \(\mathcal {F}\) is bounded. For showing that \(>_\textsf{spo}\) is well-founded, we adopt Buchholz’s method [6]. One can find a similar proof in [27, Lemma 8]. We write \(\textsf{SN}(>_\textsf{spo})\) for the set of all terms t such that there is no infinite descending sequence \(t>_\textsf{spo}t_1>_\textsf{spo}t_2 >_\textsf{spo}\cdots \) starting from t.Footnote 2 The following properties are immediate:
-
The restriction of \(>_\textsf{spo}\) to \(\textsf{SN}(>_\textsf{spo})\) is a well-founded order on \(\textsf{SN}(>_\textsf{spo})\).
-
\(t \in \textsf{SN}(>_\textsf{spo})\) if \(u \in \textsf{SN}(>_\textsf{spo})\) for all terms u with \(t >_\textsf{spo}u\).
Buchholz’s method proves well-foundedness by well-founded induction. To express our well-founded order for induction, we recall the notion of the lexicographic product of order pairs. Let \(({\gtrsim _1},{>_1}), \ldots ,({\gtrsim _n},{>_n})\) be n order pairs on sets \(A_1, \ldots , A_n\), respectively. The lexicographic product \( ({\gtrsim _1},{>_1}) \otimes \cdots \otimes ({\gtrsim _n},{>_n}) \) is the strict order > defined on \(A_1 \times \cdots \times A_n\) as follows: \(({a_1},\dots ,{a_{n}}) > ({b_1},\dots ,{b_{n}})\) if there exists an index \(k \in \{ 1, \ldots , n \}\) such that \(a_k >_k b_k\) and \(a_j \gtrsim _j b_j\) for all \(1 \leqslant j < k\). Note that the lexicographic product > is well-founded if every \(>_i\) is well-founded.
Given a set A, we write \(A^{\leqslant k}\) for the union of \(A^{i}\) for all \(i \leqslant k\). If a strict order > on A is well-founded, then the restriction of \(>^\textsf{lex}\) to \(A^{\leqslant k}\) is also well-founded, see [19, Section 3]. Thus, the lexicographic product \(\gg \) given by

is a well-founded order on \((\mathcal {T}\setminus \mathcal {V}) \times \mathcal {T}^{\leqslant M} \times \mathcal {T}\). Here M stands for the maximum arity in the signature \(\mathcal {F}\), and \(\geqslant _\textsf{spo}^\textsf{lex}\) for the reflexive closure of \(>_\textsf{spo}^\textsf{lex}\).
Lemma 2
The term u belongs to \(\textsf{SN}(>_\textsf{spo})\) whenever \(t = f({t_1},\dots ,{t_{n}}) >_\textsf{spo}u\) and \({t_1},\dots ,{t_{n}} \in \textsf{SN}(>_\textsf{spo})\).
Proof
We show the claim by well-founded induction on \((t, ({t_1},\dots ,{t_{n}}), u)\) with respect to \(\gg \). Here we proceed by analyzing the derivation of \(t >_\textsf{spo}u\). If \(t >_\textsf{spo}u\) is derived from SPO 1 then \(t_i \geqslant _\textsf{spo}u\) for some \(i \in \{ 1, \ldots , n \}\). In this case \(u \in \textsf{SN}(>_\textsf{spo})\) trivially follows from \(t_i \in \textsf{SN}(>_\textsf{spo})\). If \(t >_\textsf{spo}u\) is derived from SPO 2a or SPO 2b, then u is of the form \(g({u_1},\dots ,{u_{m}})\) and \(t >_\textsf{spo}u_j\) for all \(j \in \{ 1, \ldots , m \}\). From \(u \rhd u_j\) we have \((t, ({t_1},\dots ,{t_{n}}), u) \gg (t, ({t_1},\dots ,{t_{n}}), u_j)\). So from the induction hypothesis \(u_i \in \textsf{SN}(>_\textsf{spo})\) for each j. For showing our goal \(u \in \textsf{SN}(>_\textsf{spo})\) fix an arbitrary term v with \(u >_\textsf{spo}v\). We further distinguish the case of SPO 2a and that of SPO 2b.
-
a.
If \(t >_\textsf{spo}u\) is derived from SPO 2a then \(t \sqsupset u\). Thus, \((t, ({t_1},\dots ,{t_{n}}), u) \gg (u, ({u_1},\dots ,{u_{m}}), v)\), and the induction hypothesis yields \(v \in \textsf{SN}(>_\textsf{spo})\).
-
b.
If \(t >_\textsf{spo}u\) is derived from SPO 2b then we additionally have
 and \(({t_1},\dots ,{t_{n}}) >_\textsf{spo}^{\textsf{lex}} ({u_1},\dots ,{u_{m}})\). Thus, \(({t}, {({t_1},\dots ,{t_{n}})}, {u}) \gg ({u}, {({u_1},\dots ,{u_{m}})}, {v})\) holds. So from the induction hypothesis we obtain \(v \in \textsf{SN}(>_\textsf{spo})\).
and \(({t_1},\dots ,{t_{n}}) >_\textsf{spo}^{\textsf{lex}} ({u_1},\dots ,{u_{m}})\). Thus, \(({t}, {({t_1},\dots ,{t_{n}})}, {u}) \gg ({u}, {({u_1},\dots ,{u_{m}})}, {v})\) holds. So from the induction hypothesis we obtain \(v \in \textsf{SN}(>_\textsf{spo})\).
In either case \(v \in \textsf{SN}(>_\textsf{spo})\). So we conclude \(u \in \textsf{SN}(>_\textsf{spo})\). \(\square \)
Lemma 3
The relation \(>_\textsf{spo}\) is well-founded.
Proof
We show that \(t \in \textsf{SN}(>_\textsf{spo})\) by induction on |t|. If t is a variable trivially \(t \in \textsf{SN}(>_\textsf{spo})\). Otherwise, Lemma 2 applies. \(\square \)
Theorem 2
Every semantic path order is a stable well-founded order, provided that the signature is bounded. \(\square \)
In general, semantic path orders are not closed under contexts. For a remedy, Borralleras et al. [5] propose the use of another preorder with the harmony property. This results in monotonic semantic path orders.
Definition 3
([4, Definition 4.1.20]). A triple
 is a reduction triple if \(\gtrsim \) is a rewrite preorder on terms,
is a reduction triple if \(\gtrsim \) is a rewrite preorder on terms,
 is a stable order pair on \(\mathcal {T}\setminus \mathcal {V}\) with \(\sqsupset \) well-founded, and \(\gtrsim \) and
is a stable order pair on \(\mathcal {T}\setminus \mathcal {V}\) with \(\sqsupset \) well-founded, and \(\gtrsim \) and
 have the harmony property, meaning that for every \(f^{(n)} \in \mathcal {F}\) the implication
have the harmony property, meaning that for every \(f^{(n)} \in \mathcal {F}\) the implication

holds for all terms \({s_1},\dots ,{s_{n}},t\) and argument positions \(1 \leqslant i \leqslant n\).
Definition 4
Let
 be a reduction triple, and let \(>_\textsf{spo}\) be the semantic path order induced from
be a reduction triple, and let \(>_\textsf{spo}\) be the semantic path order induced from
 . The monotonic semantic path order \(s >_\textsf{mspo}t\) (MSPO) is defined as \(s \gtrsim t\) and \(s >_\textsf{spo}t\).
. The monotonic semantic path order \(s >_\textsf{mspo}t\) (MSPO) is defined as \(s \gtrsim t\) and \(s >_\textsf{spo}t\).
Theorem 3
Every monotonic semantic path order is a reduction order, provided that the signature is bounded.
Proof
The proof due to Borralleras et al. [5, Theorem 2] goes through. \(\square \)
4 Simulating WPOs by SPOs
We show that WPOs are instances of SPOs by constructing a suitable order pair
 from a weakly monotone well-founded algebra \(\mathcal {A}\) and a well-founded precedence \(\succsim \). For terms \(s = f({s_1},\dots ,{s_{m}}), t = g({t_1},\dots ,{t_{n}})\) we write
from a weakly monotone well-founded algebra \(\mathcal {A}\) and a well-founded precedence \(\succsim \). For terms \(s = f({s_1},\dots ,{s_{m}}), t = g({t_1},\dots ,{t_{n}})\) we write
 if \(s >_\mathcal {A}t\), or both \(s \geqslant _\mathcal {A}t\) and \(f \succsim g\). Similarly, we define \(s \sqsupset t\) if \(s >_\mathcal {A}t\), or both \(s \geqslant _\mathcal {A}t\) and \(f \succ g\). It is worth noting that the proof of [27, Lemma 8] also combines the interpretation order and precedence in a lexicographic manner.
if \(s >_\mathcal {A}t\), or both \(s \geqslant _\mathcal {A}t\) and \(f \succsim g\). Similarly, we define \(s \sqsupset t\) if \(s >_\mathcal {A}t\), or both \(s \geqslant _\mathcal {A}t\) and \(f \succ g\). It is worth noting that the proof of [27, Lemma 8] also combines the interpretation order and precedence in a lexicographic manner.
Lemma 4
The pair
 is a stable order pair with \(\sqsupset \) well-founded. \(\square \)
is a stable order pair with \(\sqsupset \) well-founded. \(\square \)
In the remaining part of the section we consider the WPO \(>_\textsf{wpo}\) induced by \(\mathcal {A}\) and \(\succsim \), and the SPO \(>_\textsf{spo}\) induced by the corresponding order pair
 . Note that \(\sqsupset \) is not a strict part of
. Note that \(\sqsupset \) is not a strict part of
 in general, as \(>_\mathcal {A}\) is not necessarily the strict part of \(\geqslant _\mathcal {A}\). This is why we decoupled \(\sqsupset \) from
in general, as \(>_\mathcal {A}\) is not necessarily the strict part of \(\geqslant _\mathcal {A}\). This is why we decoupled \(\sqsupset \) from
 in Definition 2; see also Remark 1.
in Definition 2; see also Remark 1.
Example 5
Let the signature \(\mathcal {F}= \{ \textsf{f}^{(1)} \}\). Consider the trivial precedence \(\textsf{f} \succsim \textsf{f}\) and the algebra \(\mathcal {A}\) over the carrier \(\mathbb {N}\) with the interpretation \(\textsf{f}_\mathcal {A}(x) = 2 x\). On the one hand we have
 from \(\textsf{f}(\textsf{f}(x)) \geqslant _\mathcal {A}\textsf{f}(x)\) but not
from \(\textsf{f}(\textsf{f}(x)) \geqslant _\mathcal {A}\textsf{f}(x)\) but not
 as \(\textsf{f}(x) \ngeqslant _\mathcal {A}\textsf{f}(\textsf{f}(x))\). On the other hand \(\textsf{f}(\textsf{f}(x)) \sqsupset \textsf{f}(x)\) does not hold.
as \(\textsf{f}(x) \ngeqslant _\mathcal {A}\textsf{f}(\textsf{f}(x))\). On the other hand \(\textsf{f}(\textsf{f}(x)) \sqsupset \textsf{f}(x)\) does not hold.
We illustrate how the derivation of \(>_\textsf{wpo}\) in Example 1 is simulated by the semantic path order.
Example 6 (continued from Example 1)
From \(\textsf{f}(\textsf{g}(x)) \geqslant _\mathcal {A}\textsf{g}(\textsf{f}(\textsf{f}(x)))\) and \(\textsf{f} \succ \textsf{g}\) the inequality \(\textsf{f}(\textsf{g}(x)) \sqsupset \textsf{g}(\textsf{f}(\textsf{f}(x)))\) is obtained. Moreover, we have \(\textsf{f}(\textsf{g}(x)) >_\mathcal {A}\textsf{f}(\textsf{f}(x))\). Since \(\geqslant _\mathcal {A}\) has the subterm property, the subterm \(\textsf{f}(x)\) of \(\textsf{f}(\textsf{f}(x))\) also satisfies \(\textsf{f}(\textsf{g}(x)) >_\mathcal {A}\textsf{f}(x)\). Thus we obtain \(\textsf{f}(\textsf{g}(x)) \sqsupset \textsf{f}(\textsf{f}(x)), \textsf{f}(x)\). Therefore, \(\textsf{f}(\textsf{g}(x)) >_\textsf{spo}\textsf{g}(\textsf{f}(\textsf{f}(x)))\) is verified as follows:

Similarly, \(\textsf{f}(\textsf{h}(x)) >_\textsf{spo}\textsf{h}(\textsf{h}(\textsf{f}(x)))\) can be verified. Hence, the inclusion \(\mathcal {R}\subseteq {>_\textsf{spo}}\) holds. Observe that the use of WPO 1 in Example 1 is replaced by successive application of SPO 1 and SPO 2a.
As shown in the example, the subterm property of \(\geqslant _\mathcal {A}\) is a key for filling in the gap between \(>_\textsf{spo}\) and \(>_\textsf{wpo}\).
Lemma 5
Suppose that \(\mathcal {A}\) is simple. If \(s >_\textsf{wpo}t\) then \(s >_\textsf{spo}t\).
Proof
We prove the claim by induction on \(|s| + |t|\). Let \(s = f({s_1},\dots ,{s_{m}}) >_\textsf{wpo}t\). Depending on the derivation of \(s >_\textsf{wpo}t\), we distinguish five cases.
-
Suppose that t is a variable and \(s >_\textsf{wpo}t\) is derived from \(s >_\mathcal {A}t\). One can verify that t occurs in s. Because s is not a variable, \(s \rhd t\) follows. By the subterm property of \(>_\textsf{spo}\) we obtain \(s >_\textsf{spo}t\).
-
Suppose that \(t = g({t_1},\dots ,{t_{n}})\) and \(s >_\textsf{wpo}t\) is derived from \(s >_\mathcal {A}t\). From \(s >_\mathcal {A}t\) we obtain \(s \sqsupset t\). Since \(\mathcal {A}\) is simple, for every \(1 \leqslant j \leqslant n\) we have \(s >_\mathcal {A}t \geqslant _\mathcal {A}t_j\), which leads to \(s >_\mathcal {A}t_j\). Hence, \(s >_\textsf{spo}t\) is derived as follows:

-
Suppose that \(s >_\textsf{wpo}t\) is derived as follows:

By the induction hypothesis we have \(s_i \geqslant _\textsf{spo}t\) for some i, and thus \(s >_\textsf{spo}t\).
-
Suppose that \(s >_\textsf{wpo}t\) is derived as follows:
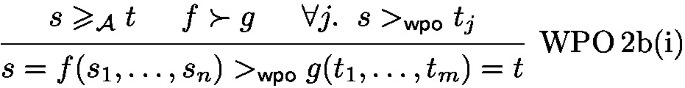
From \(s \geqslant _\mathcal {A}t\) and \(f \succ g\) we obtain \(s \sqsupset t\). Thus, we have:

-
Suppose that \(s >_\textsf{wpo}t\) is derived as follows:

From \(s \geqslant _\mathcal {A}t\) we obtain
 . Thus, we have:
. Thus, we have: 
In any case we have \(s >_\textsf{spo}t\). \(\square \)
Next we prove the converse direction of Lemma 5. The next lemma is a basic property of WPOs.
Lemma 6
If \(s >_\textsf{wpo}t\) then \(s \geqslant _\mathcal {A}t\). \(\square \)
Lemma 7
Suppose that \(\mathcal {A}\) is simple. If \(s >_\textsf{spo}t\) then \(s >_\textsf{wpo}t\).
Proof
We prove the claim by induction on \(|s| + |t|\). We distinguish three cases, depending on the derivation of \(s >_\textsf{spo}t\).
-
Suppose that \(s >_\textsf{spo}t\) is derived as follows:

The induction hypothesis yields \(s_i \geqslant _\textsf{wpo}t\) for some i. By Lemma 6 and the subterm property of \(\geqslant _\mathcal {A}\) we have \(s \geqslant _\mathcal {A}t\). Thus, we obtain the following derivation of \(s >_\textsf{wpo}t\):

-
Suppose that \(s >_\textsf{spo}t\) is derived as follows:

According to the definition of \(s \sqsupset t\), we further distinguish two subcases. If \(s >_\mathcal {A}t\) then \(s >_\textsf{wpo}t\) is immediate. Otherwise, \(s \geqslant _\mathcal {A}t\) and \(f \succ g\) hold. In this case we derive \(s >_\textsf{wpo}t\) as follows:

-
Suppose that \(s >_\textsf{spo}t\) is derived as follows:
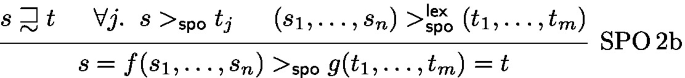
Because of
 , we have \(s >_\mathcal {A}t\) or both \(s \geqslant _\mathcal {A}t\) and \(f \succsim g\). In the former case \(s >_\textsf{wpo}t\) is immediate. In the latter case \(s >_\textsf{wpo}t\) is derived by WPO 2b(ii) as follows:
, we have \(s >_\mathcal {A}t\) or both \(s \geqslant _\mathcal {A}t\) and \(f \succsim g\). In the former case \(s >_\textsf{wpo}t\) is immediate. In the latter case \(s >_\textsf{wpo}t\) is derived by WPO 2b(ii) as follows: 
In any case we have \(s >_\textsf{wpo}t\). \(\square \)
As a consequence, \(>_\textsf{wpo}\) and \(>_\textsf{spo}\) coincide, provided that \(\mathcal {A}\) is simple. This result can be extended to monotonic semantic path orders.
Lemma 8
The triple
 is a reduction triple. \(\square \)
is a reduction triple. \(\square \)
Let \(>_\textsf{mspo}\) denote the monotonic semantic path order induced from \(\geqslant _\mathcal {A}\) and \(>_\textsf{spo}\). Since \(s >_\textsf{wpo}t\) implies \(s \geqslant _\mathcal {A}t\) (Lemma 6), \(s >_\textsf{mspo}t\) is equivalent to \(s >_\textsf{spo}t\). By using this equivalence together with Lemmata 5 and 7, we obtain the following result.
Theorem 4
The three orders \(>_\textsf{wpo}\), \(>_\textsf{spo}\), and \(>_\textsf{mspo}\) coincide, provided that \(\mathcal {A}\) is simple. \(\square \)
5 Generalized Weighted Path Orders
According to Theorem 4, weighted path orders can be defined as monotonic semantic path orders. Moreover, Lemma 8 reveals that even for non-simple algebras the construction of reduction triples is valid. This observation suggests a generalization of weighted path orders, which does not impose simplicity on algebras. Besides, we exploit the fact that stable order pairs need not be closed under contexts, marking root symbols of function applications; see [1] and [5, Definition 5].
Let \(\mathcal {F}\) be a signature. For each \(f \in \mathcal {F}\) we associate a marked function symbol \(f^\sharp \notin \mathcal {F}\) of the same arity. The set \(\{ f^{\sharp } \mid f \in \mathcal {F}\}\) is denoted by \(\mathcal {F}^\sharp \). For each term \(t = f({t_1},\dots ,{t_{n}}) \in \mathcal {T}(\mathcal {F},\mathcal {V})\) we denote \(f^\sharp ({t_1},\dots ,{t_{n}})\) by \(t^\sharp \). Let \(\mathcal {A}\) be a weakly monotone well-founded \((\mathcal {F}\cup \mathcal {F}^\sharp )\)-algebra and \(\succsim \) a well-founded precedence on \(\mathcal {F}\). The pair
 of relations on \(\mathcal {T}(\mathcal {F}, \mathcal {V}) \setminus \mathcal {V}\) is defined as follows: Let \(s = f({s_1},\dots ,{s_{n}})\) and \(t = g({t_1},\dots ,{t_{m}})\). We write
of relations on \(\mathcal {T}(\mathcal {F}, \mathcal {V}) \setminus \mathcal {V}\) is defined as follows: Let \(s = f({s_1},\dots ,{s_{n}})\) and \(t = g({t_1},\dots ,{t_{m}})\). We write
 if \(s^\sharp >_{\mathcal {A}} t^\sharp \), or \(s^\sharp \geqslant _{\mathcal {A}} t^\sharp \) and \(f \succsim g\). Similarly, we write \(s \sqsupset ^\sharp t\) if \(s^\sharp >_{\mathcal {A}} t^\sharp \), or \(s^\sharp \geqslant _{\mathcal {A}} t^\sharp \) and \(f \succ g\). The relation \(\gtrsim \) is defined as the restriction of \(\geqslant _\mathcal {A}\) to \(\mathcal {T}(\mathcal {F}, \mathcal {V})\).
if \(s^\sharp >_{\mathcal {A}} t^\sharp \), or \(s^\sharp \geqslant _{\mathcal {A}} t^\sharp \) and \(f \succsim g\). Similarly, we write \(s \sqsupset ^\sharp t\) if \(s^\sharp >_{\mathcal {A}} t^\sharp \), or \(s^\sharp \geqslant _{\mathcal {A}} t^\sharp \) and \(f \succ g\). The relation \(\gtrsim \) is defined as the restriction of \(\geqslant _\mathcal {A}\) to \(\mathcal {T}(\mathcal {F}, \mathcal {V})\).
Proposition 2
The triple
 is a reduction triple on \(\mathcal {T}(\mathcal {F}, \mathcal {V})\). \(\square \)
is a reduction triple on \(\mathcal {T}(\mathcal {F}, \mathcal {V})\). \(\square \)
Definition 5
The generalized weighted path order (GWPO) \(>_\textsf{gwpo}\) induced from \(\mathcal {A}\) and \(\succsim \) is the monotonic semantic path order induced from
 .
.
Corollary 1
Every generalized weighted path order is a reduction order, provided that the signature is bounded. \(\square \)
For convenience, we reformulate the definition of \(>_\textsf{gwpo}\) in the style of Definition 1.
Definition 6
The relation \(>_\mathsf {wpo'}\) is defined on terms as follows: \(s >_\mathsf {wpo'}t\) if \(s = f({s_1},\dots ,{s_{m}})\) and one of the following conditions hold.
-
1.
\(s_i \geqslant _\mathsf {wpo'}t\) for some \(1 \leqslant i \leqslant m\).
-
2.
\(t = g({t_1},\dots ,{t_{n}})\), \(s^\sharp \geqslant _{\mathcal {A}} t^\sharp \), and \(s >_\mathsf {wpo'}t_j\) for all \(1 \leqslant j \leqslant n\), and moreover
-
a.
\(s^\sharp >_{\mathcal {A}} t^\sharp \),
-
b.
\(f \succ g\), or
-
c.
\(f \succsim g\) and \(({s_1},\dots ,{s_{m}}) >_\mathsf {wpo'}^\textsf{lex}({t_1},\dots ,{t_{n}})\).
-
a.
Proposition 3
The SPO \(>_\textsf{spo}\) induced from
 coincides with \(>_\mathsf {wpo'}\). For all terms s and t the relation \(s >_\textsf{gwpo}t\) is equivalent to \(s \geqslant _\mathcal {A}t\) and \(s >_\mathsf {wpo'}t\). \(\square \)
coincides with \(>_\mathsf {wpo'}\). For all terms s and t the relation \(s >_\textsf{gwpo}t\) is equivalent to \(s \geqslant _\mathcal {A}t\) and \(s >_\mathsf {wpo'}t\). \(\square \)
Corollary 2
The relations \(>_\textsf{gwpo}\) and \(>_\textsf{wpo}\) coincide, provided that \(\mathcal {A}\) is simple and \(f_\mathcal {A}({x_1},\dots ,{x_{n}}) = f^\sharp _\mathcal {A}({x_1},\dots ,{x_{n}})\) for all \(f^{(n)} \in \mathcal {F}\). \(\square \)
Since polynomial interpretation orders [15] and Knuth–Bendix orders [13] as well as LPOs are simulated by WPOs [27], they are also subsumed by GWPOs. We demonstrate termination proofs by GWPOs with a few examples. All examples are not handled by WPOs.
Example 7
Consider the TRS \(\mathcal {R}\) for round-up division:
Let \(\mathcal {A}\) be the weakly monotone algebra on \(\mathbb {N}\) with the interpretations
and let \(\succsim \) be an arbitrary precedence. The GWPO induced from \(\mathcal {A}\) and \(\succsim \) orients all rules in \(\mathcal {R}\). In particular, \(x - \textsf{s}(y) >_\mathsf {wpo'}\textsf{p}(x) - y\) is derived from the inequalities \(x -^\sharp \textsf{s}(y) >_\mathcal {A}\textsf{p}(x) -^\sharp y\) and \(x -^\sharp \textsf{s}(y) >_\mathcal {A}\textsf{p}^\sharp (x)\).
Example 8
Consider the TRS \(\mathcal {R}\) taken from [2, Example 4.28], which computes the bit length of a natural number:

Let \(\mathcal {A}\) be the weakly monotone algebra on \(\mathbb {N}\) with:
The GWPO \(>_\textsf{gwpo}\) induced by \(\mathcal {A}\) and a precedence \(\succsim \) with \(\textsf{half}, \textsf{bits} \succ \textsf{s}\) satisfies \(\mathcal {R}\subseteq {>_\textsf{gwpo}}\) as \(\ell \geqslant _\mathcal {A}r\) and \(\ell >_\mathsf {wpo'}r\) for all rules \(\ell \rightarrow r \in \mathcal {R}\). In particular, \(\textsf{bits}(\textsf{s}(x)) >_\mathsf {wpo'}\textsf{s}(\textsf{bits}(\textsf{half}(\textsf{s}(x))))\) is derived as follows. The inequality \(\textsf{bits}(\textsf{s}(x)) >_\mathsf {wpo'}\textsf{bits}(\textsf{half}(\textsf{s}(x)))\) is derived from repeated application of WPO\('\) 2a:

Thus, \(\textsf{bits}(\textsf{s}(x)) >_\mathsf {wpo'}\textsf{s}(\textsf{bits}(\textsf{half}(\textsf{s}(x))))\) follows from WPO\('\) 2b with \(\textsf{bits} \succ \textsf{s}\) and \(\textsf{bits}^\sharp (\textsf{s}(x)) \geqslant _\mathcal {A}\textsf{s}^\sharp (\textsf{bits}(\textsf{half}(\textsf{s}(x))))\).
6 Experimental Results
In order to evaluate GWPOs in termination analysis we implemented a prototype termination tool based on Proposition 1 and Corollary 1. Following the automation techniques of WPO [27], we search a suitable weakly monotone well-founded algebra from two classes of algebras over \(\mathbb {N}\): One is linear interpretation and the other is max/plus interpretation. Since simplicity of algebras is not required for GWPOs, we may use more general forms of interpretations.
Linear Interpretations. Algebras \(\mathcal {A}\) of this class use linear polynomials over \(\mathbb {N}\) like Example 7. For each \(f^{(n)} \in \mathcal {F}\cup \mathcal {F}^\sharp \) its interpretation is of the form \(f_\mathcal {A}(x_1, \ldots , x_n) = c_0 + c_1 x_1 + \cdots + c_n x_n\) where \(c_0 \in \mathbb {N}\) and \(c_1, \ldots , c_n \in \{ 0, 1 \}\). Simple monotone algebras for WPOsFootnote 3 are obtained by setting \(c_1 = \cdots = c_n = 1, f_\mathcal {A}= f^\sharp _\mathcal {A}\) for all \(f^{(n)} \in \mathcal {F}\), and those for Knuth–Bendix orders (KBOs) are obtained by further restriction for admissibility, see [27]. Comparison of linear polynomials is reduced to that of coefficients by using the following trivial fact:
Proposition 4
Let \(f({x_1},\dots ,{x_{n}}) = c_0 + c_1 x_1 + \cdots + c_n x_n\) and \(g({x_1},\dots ,{x_{n}}) = d_0 + d_1 x_1 + \cdots + d_n x_n\) be linear polynomials over \(\mathbb {N}\). The next statements hold.
-
\(f \geqslant g\) if and only if \(c_0 \geqslant d_0\) and \(c_i \geqslant d_i\) for all \(1 \leqslant i \leqslant n\).
-
\(f > g\) if and only if \(c_0 > d_0\) and \(c_i \geqslant d_i\) for all \(1 \leqslant i \leqslant n\).
Here \(f \geqslant g\) (\(f > g\)) means that \(f({a_1},\dots ,{a_{n}}) \geqslant g({a_1},\dots ,{a_{n}})\) (\(f({a_1},\dots ,{a_{n}}) > g({a_1},\dots ,{a_{n}})\)) for all \({a_1},\dots ,{a_{n}} \in \mathbb {N}\).
Max/plus Interpretations. Algebras \(\mathcal {A}\) of this class use a combination of \(+\) and \(\max \) like Example 8. For each \(f^{(n)} \in \mathcal {F}\cup \mathcal {F}^\sharp \) its interpretation is of the form \(f_\mathcal {A}(x_1, \ldots , x_n) = \max \{c_0, c_1 + c'_1 x_1, \cdots , c_n + c'_n x_n\}\) where \(c_0 \in \mathbb {N}, c_1, \ldots , c_n \in \mathbb {Z}\) and \(c'_1, \ldots , c'_n \in \{ 0, 1 \}\). Simple monotone algebras for WPOs are obtained by imposing \(c_1, \ldots , c_n \in \mathbb {N}, c'_1 = \cdots = c'_n = 1, f_\mathcal {A}= f^\sharp _\mathcal {A}\) for all \(f^{(n)} \in \mathcal {F}\), and algebras for lexicographic path orders (LPOs) are obtained by additionally setting \(c_0 = c_1 = \cdots = c_n = 0\) for all \(f^{(n)} \in \mathcal {F}\) as in [27]. The restriction \(c_1, \ldots , c_n \in \mathbb {N}\) is necessary for WPOs because allowing \(c_1, \ldots , c_n < 0\) results in non-simple interpretations such as \(\max \{0, x -1\}\). Under this form of algebras, an interpretation of a term is flattened to the form of \(\max \{g_1, \ldots , g_m\}\) where \(g_1, \ldots , g_m\) are linear polynomials over \(\mathbb {N}\). So comparison of max/plus interpretation is reduced to that of coefficients, using the following trivial fact and Proposition 4 in turn:
Proposition 5
Let G and H be non-empty sets of linear polynomials over \(\mathbb {N}\). The next statements hold.
-
\(\max G \geqslant \max H\) if and only if for every \(h \in H\) there exists a linear polynomial \(g \in G\) with \(g \geqslant h\).
-
\(\max G > \max H\) if and only if for every \(h \in H\) there exists a linear polynomial \(g \in G\) with \(g > h\).
Since precedence constraints can be regarded as inequalities on natural numbers [28], searching a suitable combination of a precedence and an interpretation is done by solving linear arithmetic constraints (with if-then-else expressions).
The problem set for experiments consists of 1511 term rewrite systems from version 11.3 of the Termination Problem Database (TPDB) [21]. The reference implementation uses the SMT solver Z3 [17] as an external tool for solving linear constraints. The experiments were run on a PC with Intel Core i7-1065G7 CPU (1.30 GHz) and 16 GB memory.
Now let us discuss the experimental results.Footnote 4 Table 1 shows that, as a whole, use of non-simple algebras substantially improves termination analysis, at the small cost of extra running time. In particular, in the case of linear interpretation, GWPOs significantly outperform WPOs. As a matter of fact, linear WPOs are unable to orient variable duplicating rules \(\ell \rightarrow r\) such as \(\textsf{f}(x) \rightarrow \textsf{g}(x, x)\) since \(\ell \geqslant _\mathcal {A}r\) cannot be satisfied, but this does not apply to GWPOs based on linear interpretations with \(\{ 0, 1 \}\)-coefficients. In the case of max/plus interpretations there are two TRSs (with over 100 rules) that are proved to be terminating by WPOs, but not by GWPOs due to the time limit. This indicates that using non-simple algebras for max/plus interpretation can result in increase of search space. This is not the case for linear interpretations.
7 Simulating Dependency Pairs by GWPOs
The powerfulness of GWPOs revealed in Sect. 6 can partly be explained by the fact that GWPO is capable of simulating a basic result of the dependency pair method [1]. To show the fact, we recall the dependency pair method. The set \(\textsf{DP}(\mathcal {R})\) of dependency pairs of a TRS \(\mathcal {R}\) is defined as follows:

An order pair \(({\geqslant }, {\sqsupset })\) on terms is a reduction pair if \(\geqslant \) is a rewrite preorder and \(\sqsupset \) is a well-founded stable order. The following theorem states a basic result of the dependency pair method.
Theorem 5
([1]). A TRS \(\mathcal {R}\) is terminating if \(\mathcal {R}\subseteq {\geqslant }\) and \(\textsf{DP}(\mathcal {R}) \subseteq {\sqsupset }\) for some reduction pair \(({\geqslant }, {\sqsupset })\).
We illustrate Theorem 5, using the fact that every weakly monotone algebra \(\mathcal {A}\) on \(\mathbb {N}\) induces the reduction pair \(({\geqslant _\mathcal {A}}, {>_\mathcal {A}})\).
Example 9
Consider the TRS \( \mathcal {R}= \{ \textsf{f}(\textsf{f}(x)) \rightarrow \textsf{f}(\textsf{g}(\textsf{f}(x))), \textsf{f}(x) \rightarrow \textsf{g}(x) \} \). We show the termination of \(\mathcal {R}\) using Theorem 5. The set \(\textsf{DP}(\mathcal {R})\) consists of the two dependency pairs:
By taking the \(\{\textsf{f},\textsf{g}, \textsf{f}^\sharp ,\textsf{g}^\sharp \}\)-algebra \(\mathcal {A}\) with the interpretations
the inclusions \(\mathcal {R}\subseteq {\geqslant _\mathcal {A}}\) and \(\textsf{DP}(\mathcal {R}) \subseteq {>_\mathcal {A}}\) hold. Hence, \(\mathcal {R}\) is terminating.
We show that every termination proof by Theorem 5 with a weakly monotone algebra on \(\mathbb {N}\) can be simulated by a GWPO. This class of algebras include linear polynomial interpretations and max/plus interpretations described in Sect. 6. Let \(\mathcal {R}\) be a TRS and \(\mathcal {A}\) a weakly monotone \((\mathcal {F}\cup \mathcal {F}^\sharp )\)-algebra on \(\mathbb {N}\) satisfying \(\mathcal {R}\subseteq {\geqslant _\mathcal {A}}\) and \(\textsf{DP}(\mathcal {R}) \subseteq {>_\mathcal {A}}\). Define the \((\mathcal {F}\cup \mathcal {F}^\sharp )\)-algebra \(\mathcal {B}\) on \(\mathbb {N}\) by
for each \(f^{(n)} \in \mathcal {F}\). Let \(>_\textsf{gwpo}\) and \(>_\mathsf {wpo'}\) denote the orders induced from \(\mathcal {B}\) and an arbitrary but fixed precedence. First, let us see that \(\mathcal {R}\subseteq {>_\textsf{gwpo}}\) holds for the last example.
Example 10 (continued from Example 9)
The corresponding algebra \(\mathcal {B}\) is:
We have \(\mathcal {R}\subseteq {\geqslant _\mathcal {B}}\) by construction. The inequality \(\textsf{f}(\textsf{f}(x)) >_\mathsf {wpo'}\textsf{f}(\textsf{g}(\textsf{f}(x)))\) is derived by successive application of WPO\('\) 2a as follows:

The inequality \(\textsf{f}(x) >_\mathsf {wpo'}\textsf{g}(x)\) follows from \(\textsf{f}^\sharp (x) >_\mathcal {B}\textsf{g}^\sharp (x)\). Hence \(\mathcal {R}\subseteq {>_\textsf{gwpo}}\). Note that neither \(\textsf{f}^\sharp (\textsf{f}(x)) >_\mathcal {A}\textsf{g}^\sharp (\textsf{f}(x))\) nor \(\textsf{f}^\sharp (x) >_\mathcal {A}\textsf{g}^\sharp (x)\) holds.
Now we verify that \(\mathcal {R}\subseteq {>_\textsf{gwpo}}\) holds in general. By construction \(\mathcal {R}\subseteq {\geqslant _\mathcal {B}}\) is immediate from \(\mathcal {R}\subseteq {\geqslant _\mathcal {A}}\). So it remains to show \(\mathcal {R}\subseteq {>_\mathsf {wpo'}}\). We prove the following stronger property.
Lemma 9
Let \(\ell \rightarrow r \in \mathcal {R}\). For every subterm t of r the relation \(\ell >_\mathsf {wpo'}t\) holds.
Proof
We use structural induction on t. If t is a variable, then x must be a subterm of \(\ell \), and thus \(\ell >_\mathsf {wpo'}t\). Otherwise, t is in the form of \(g({t_1},\dots ,{t_{n}})\). The induction hypothesis yields \(\ell >_\mathsf {wpo'}t_j\) for all \(1 \leqslant j \leqslant n\). We claim \(\ell ^\sharp >_\mathcal {B}t^\sharp \), from which the desired inequality \(\ell >_\mathsf {wpo'}t\) follows by WPO\('\) 2a. To show the claim, consider an arbitrary assignment \(\alpha \) for \(\mathcal {B}\). Depending on g, we distinguish two cases.
-
If \(g \notin \mathcal {D}_\mathcal {R}\) then \( [\alpha ]_\mathcal {B}(\ell ^\sharp ) = [\alpha ]_\mathcal {A}(\ell ^\sharp ) + 1 > 0 = [\alpha ]_\mathcal {B}(t^\sharp ) \).
-
If \(g \in \mathcal {D}_\mathcal {R}\) then \(\ell ^\sharp \rightarrow t^\sharp \in \textsf{DP}(\mathcal {R})\). The assumption \(\textsf{DP}(\mathcal {R}) \subseteq {>_\mathcal {A}}\) yields the inequality \(\ell ^\sharp >_\mathcal {A}t^\sharp \). Thus, \( [\alpha ]_\mathcal {B}(\ell ^\sharp ) = [\alpha ]_\mathcal {A}(\ell ^\sharp ) + 1 > [\alpha ]_\mathcal {A}(t^\sharp ) + 1 = [\alpha ]_\mathcal {B}(t^\sharp ) \).
In either case \([\alpha ]_\mathcal {B}(\ell ^\sharp ) > [\alpha ]_\mathcal {B}(t^\sharp )\) is obtained. Hence, \(\ell ^\sharp >_\mathcal {B}t^\sharp \) holds. \(\square \)
Theorem 6
The inclusion \(\mathcal {R}\subseteq {>_\textsf{gwpo}}\) holds. \(\square \)
8 Conclusion
We have shown that weighted path orders can be simulated by a suitable variant of SPOs based on order pairs, and introduced a generalization of WPOs whose termination proving power goes beyond the realm of simple termination. To conclude the paper, we discuss related work and future work.
Simulating KBOs by SPOs. A key observation for simulating WPOs by SPOs is that weight comparison can be simulated by successive application of SPO 1 and SPO 2a as observed in Example 6. Another observation is that the SPOs are already reduction orders without a help of harmonious rewrite preorders. These two observations owe to Geser’s work [9, Theorem 5], where it is shown that extended KBOs [7, Sect. 5] can be simulated by SPOs. Unifying our result and Geser’s result is future work.
General Path Orders. In this paper the lexicographic versions of path orders were investigated. However, it is very likely that the same result can be obtained even if we adopt multiset comparison or status functions. General path orders (GPOs) [8, 10] are a unifying framework for such extensions, parameterizing the way to compare arguments. It is worth investigating simulation results between GPOs and WPOs by extending the parameters of GPOs so as to take order pairs.
Reduction Pairs Based on WPOs. In order to build reduction pairs from WPOs Yamada et al. [27, Sect. 4] extended the definition of WPOs by the notion of partial status function \(\pi \). The extension allows us to specify argument positions \(\pi (f) = [{i_1},\dots ,{i_{m}}]\) compared in WPO 2b and WPO 2b(ii) for each function symbol \(f^{(n)} \in \mathcal {F}\cup \mathcal {F}^\sharp \). We anticipate that partial status functions can also be integrated into GWPOs and the thus-obtained version characterizes the reduction pair version of WPOs.
Notes
- 1.
The restriction to \(\mathcal {T}\setminus \mathcal {V}\) is not essential but meant to be a minimum requirement. Observe that Definition 2 uses the order pair only when s and t are not variables.
- 2.
SN stands for strong normalization, which is another name of termination.
- 3.
Our WPOs based on linear interpretations correspond to \(\text {WPO}(\mathcal {S}um)\) by Yamada et al. [27] but without status functions.
- 4.
The implementation and the detailed experimental data are available at: https://www.jaist.ac.jp/project/maxcomp/23frocos/
References
Arts, T., Giesl, J.: Termination of term rewriting using dependency pairs. Theoret. Comput. Sci. 236, 133–178 (2000). https://doi.org/10.1016/S0304-3975(99)00207-8
Arts, T., Giesl, J.: A collection of examples for termination of term rewriting using dependency pairs. Tech. rep, RWTH Aachen (2001)
Baader, F., Nipkow, T.: Term rewriting and all that. Cambridge Univ. Press (1998). https://doi.org/10.1017/CBO9781139172752
Borralleras, C.: Ordering-Based Methods for Proving Termination Automatically. Ph.D. thesis, Universitat Politècnica de Catalunya (2003)
Borralleras, C., Ferreira, M., Rubio, A.: Complete monotonic semantic path orderings. In: Proc. 17th International Conference on Automated Deduction. LNCS (LNAI), vol. 1831, pp. 346–364 (2000). https://doi.org/10.1007/10721959_27
Buchholz, W.: Proof-theoretic analysis of termination proofs. Ann. Pure Appl. Logic 75, 57–65 (1995). https://doi.org/10.1016/0168-0072(94)00056-9
Dershowitz, N.: Orderings for term-rewriting systems. Theoret. Comput. Sci. 17, 279–301 (1982). https://doi.org/10.1016/0304-3975(82)90026-3
Dershowitz, N., Hoot, C.: Natural termination. Theoret. Comput. Sci. 142, 179–207 (1995). https://doi.org/10.1016/0304-3975(94)00275-4
Geser, A.: On a monotonic semantic path ordering. Tech. Rep. 92–13, Ulmer Informatik-Berichte, Universität Ulm, Germany (1992)
Geser, A.: An improved general path order. Appl. Algebra Eng. Commun. Comput. 7, 469–511 (1996). https://doi.org/10.1007/BF01293264
Jakubův, J., Kaliszyk, C.: Relaxed weighted path order in theorem proving. Math. Comput. Sci. 14(3), 657–670 (2020). https://doi.org/10.1007/s11786-020-00474-0
Kamin, S., Lévy, J.: Two generalizations of the recursive path ordering. Tech. rep., University of Illinois (1980), unpublished manuscript
Knuth, D., Bendix, P.: Simple word problems in universal algebras. In: Leech, J. (ed.) Computational Problems in Abstract Algebra, pp. 263–297. Pergamon Press (1970)
Korp, M., Sternagel, C., Zankl, H., Middeldorp, A.: Tyrolean Termination Tool 2. In: Proc. 20th International Conference on Rewriting Techniques and Applications. LNCS, vol. 5595, pp. 295–304 (2009). https://doi.org/10.1007/978-3-642-02348-4_21
Lankford, D.: On proving term rewriting systems are noetherian. Louisiana Technical University, Tech. rep. (1979)
Middeldorp, A., Zantema, H.: Simple termination of rewrite systems. Theoret. Comput. Sci. 175, 127–158 (1997). https://doi.org/10.1016/S0304-3975(96)00172-7
de Moura, L.M., Bjørner, N.S.: Z3: an efficient SMT solver. In: Proc. 14th International Conference on Tools and Algorithms for the Construction and Analysis of Systems. LNCS, vol. 4963, pp. 337–340 (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Saito, T., Hirokawa, N.: Toma 0.2: An equational theorem prover. In: Proceedings of 11th Workshop on Confluence. p. 59 (2022), the tool is available at https://www.jaist.ac.jp/project/maxcomp/
Sternagel, C., Thiemann, R.: Formalizing Knuth–Bendix orders and Knuth–Bendix completion. In: Proc. 13th International Conference on Rewriting Techniques and Applications. LIPIcs, vol. 21, pp. 287–302 (2013). https://doi.org/10.4230/LIPIcs.RTA.2013287
Terese: Term Rewriting Systems. Cambridge University Press (2003)
Termination Community: The Termination Problem Database (TPDB). https://github.com/TermCOMP/TPDB. Accessed 12 May 2023
Toyama, Y.: Termination of S-expression rewriting systems: Lexicographic path ordering for higher-order terms. In: Proc. 15th International Conference on Rewriting Techniques and Applications. LNCS, vol. 3091, pp. 40–54 (2004). https://doi.org/10.1007/978-3-540-25979-4_3
Winkler, S., Moser, G.: MædMax: A Maximal Ordered Completion Tool. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) Proc. 9th International Joint Conference on Automated Reasoning. LNCS (LNAI), vol. 10900, pp. 472–480. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_31
Yamada, A.: Towards a unified method for termination. In: Proc. 16th Workshop on Termination, pp. 248–267 (2018), the presentation slides are available at http://wst2018.webs.upv.es/
Yamada, A.: Term orderings for non-reachability of (conditional) rewriting. In: Proc. 11th International Joint Conference on Automated Reasoning. LNCS, vol. 13385, pp. 248–267 (2022). https://doi.org/10.1007/978-3-031-10769-6_15
Yamada, A., Kusakari, K., Sakabe, T.: Nagoya Termination Tool. In: Proc. Joint 25th International Conference on Rewriting Techniques and Applications and 12th International Conference on Typed Lambda Calculi and Applications. vol. 8560, pp. 466–475 (2014). https://doi.org/10.1007/978-3-319-08918-8_32
Yamada, A., Kusakari, K., Sakabe, T.: A unified ordering for termination proving. Sci. Comput. Program. 111, 110–134 (2015). https://doi.org/10.1016/j.scico.2014.07.009
Zankl, H., Hirokawa, N., Middeldorp, A.: KBO orientability. J. Autom. Reason. 43, 173–201 (2009)
Acknowledgements
We are grateful to Vincent van Oostrom for his valuable questions and comments on our preliminary work. We also thank Alfons Geser for his support on literature. The suggestions by the anonymous referees greatly helped to improve the presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Saito, T., Hirokawa, N. (2023). Weighted Path Orders Are Semantic Path Orders. In: Sattler, U., Suda, M. (eds) Frontiers of Combining Systems. FroCoS 2023. Lecture Notes in Computer Science(), vol 14279. Springer, Cham. https://doi.org/10.1007/978-3-031-43369-6_4
Download citation
DOI: https://doi.org/10.1007/978-3-031-43369-6_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-43368-9
Online ISBN: 978-3-031-43369-6
eBook Packages: Computer ScienceComputer Science (R0)


 and
and  and
and 

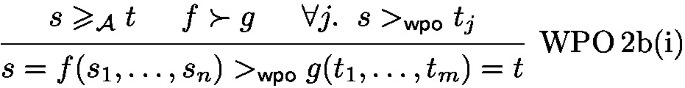


 . Thus, we have:
. Thus, we have: 




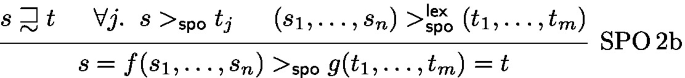
 , we have
, we have 