Abstract
Sledgehammer, a component of the interactive proof assistant Isabelle/HOL, aims to increase proof automation by automatically discharging proof goals with the help of external provers. Among these provers are a group of satisfiability modulo theories (SMT) solvers with support for the SMT-LIB input language. Despite existing formalizations of IEEE floating-point arithmetic in both Isabelle/HOL and SMT-LIB, Sledgehammer employs an abstract translation of floating-point types and constants, depriving the SMT solvers of the opportunity to make use of their dedicated decision procedures for floating-point arithmetic.
We show that, by extending Sledgehammer’s translation from the language of Isabelle/HOL into SMT-LIB with an interpretation of floating-point types and constants, floating-point reasoning in SMT solvers can be made available to Isabelle/HOL. Our main contribution is a description and implementation of such an extension. An evaluation of the extended translation shows a significant increase of Sledgehammer’s success rate on proof goals involving floating-point arithmetic.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Interactive theorem proving is one of the more flexible and powerful formal verification techniques available. However, finding a proof outline with intermediate proof steps just simple enough for a proof assistant to be able to discharge automatically may require a considerable amount of time and effort, even from a seasoned user. As an example, the seL4 micro-kernel, the product of about two person-years and 9000 lines of code, took a total of about 20 person-years and 200,000 lines of proof development to formally verify [29]. For this reason, increasing proof automation in interactive proof assistants is crucial to further broaden their applicability.
As a way of tackling this issue, many interactive proof assistants have the ability to transfer the proof burden of some of the intermediate steps onto automated reasoning systems with automatic proof methods better suited for the task. This approach has proven to be quite successful in bringing the number of required user interactions down for many types of problems, thus increasing productivity.
Among these proof assistants, we find Isabelle/HOL [34] and its powerful proof-delegation tool Sledgehammer [36], which acts as an interface between Isabelle/HOL and a number of external provers. In addition to traditional (resolution-based) first-order automated theorem provers (ATPs) such as E [40], SPASS [45] and Vampire [38] and the higher-order ATP Zipperposition [9], these external provers include satisfiability modulo theories (SMT) solvers such as CVC4 [7], veriT [15] and Z3 [31]. SMT solvers are highly specialized for reasoning within certain logical theories (e.g., integers, real numbers, and bit vectors), and often implement decision procedures more efficient than those found in the automatic proof methods of Isabelle/HOL.
Whether an external prover succeeds in solving a delegated proof obligation depends, among other factors, on how the proof obligation is encoded in the language of the prover. SMT solvers support the SMT-LIB input language [6], which offers both uninterpreted (free) type and function symbols that are declared by the user, as well as theory-specific interpreted types and operations that have a fixed semantics. Dedicated inference rules and decision procedures for specific theories that are available in SMT solvers are typically employed only when the types and operations that appear in the delegated proof obligation are interpreted. An abstract translation that leaves types and operations uninterpreted will deprive external solvers of the opportunity to make use of their dedicated decision procedures for specific background theories, and will instead have to rely on a sufficient set of facts being passed to the solver along with the proof obligation.
One of the more recent additions to the growing set of theories supported by major SMT solvers is that of floating-point arithmetic [16]. A formalization of IEEE floating-point arithmetic in Isabelle/HOL has been available in the Archive of Formal Proofs for nearly a decade [46]. However, Sledgehammer has not yet caught up to this development; its SMT component does not implement an interpretation of floating-point types and operations. Our aim is to provide such an interpretation, with the purpose of increasing the success rate for floating-point proof obligations delegated to SMT solvers, and thereby to increase the degree of automation in the interactive proof process.
As an example, let us consider the commutativity of floating-point addition. SMT solvers that support floating-point arithmetic typically have no trouble proving that \(\texttt {x + y = y + x}\) when they can assume that \(\texttt {x}\) and \(\texttt {y}\) denote floating-point numbers, and that \(\texttt {+}\) denotes IEEE floating-point addition (i.e., when \(\texttt {+}\) is translated as fp.add). However, if this formula is translated in an uninterpreted fashion, the problem becomes much harder: it now requires to show commutativity of a user-declared function over a user-declared type. Whether the SMT solver will succeed in this case depends on many factors, including which additional facts (definitions and lemmas) are passed along from the interactive proof assistant together with the proof obligation itself.
Contributions. We define a formal model of floating-point arithmetic in Isabelle/HOL that implements the SMT-LIB floating-point theory (Sect. 3).
We then extend the SMT solver integration in Isabelle/HOL by adding support for floating-point arithmetic, i.e., by treating floating-point types and operations as interpreted in the translation from the language of Isabelle/HOL to the SMT-LIB input format. In addition to describing this extension in detail (Sect. 4), we provide an implementation (in the Archive of Formal Proofs [46]) that supports Sledgehammer. To the best of our knowledge, this makes Isabelle/HOL the first interactive proof assistant to employ an interpreted translation for floating-point arithmetic in its integration of automated theorem provers.
An evaluation (Sect. 5), performed on a representative set of floating-point proof obligations from interactive proof, confirms the expectation that our translation extension significantly increases Sledgehammer’s success rate on proof goals involving floating-point arithmetic, albeit at the cost of lower success rates for proof reconstruction—at this stage, our integration typically requires the external SMT solvers to be trusted as oracles.
2 Background
In this section, we cover additional background information regarding Sledgehammer and floating-point arithmetic.
2.1 The Sledgehammer Proof Process
When trying to prove a conjecture in Isabelle, a user may, via a simple call to Sledgehammer, pass along the proof obligation to several external provers, which will then work on the problem in parallel. The statement to be proven is used by a relevance filter [30] to select additional facts (axioms and previously proven statements) that may help in finding a proof. All of these statements are then translated and compiled into a file in the input format of the external prover (in the case of SMT solvers, an SMT-LIB input file), as illustrated in Fig. 1.
After working on the problem, the external prover (if it does not time out) returns to Isabelle with its findings. At this point, if a prover reported the conjecture to be true, the user can either choose to view the prover as an oracle and accept the conjecture as a theorem (the dashed path in Fig. 1), or make Isabelle try to automatically reconstruct the proof internally, based on the additional facts sent with the conjecture and any proof details the prover may provide. Theorems that are only proved externally are marked with an oracle tag, meant to convey a certain amount of skepticism—reconstructed proofs are generally preferred, as they remove the consideration of possible bugs in the external prover, or in the translation between formats.
In Sledgehammer’s translation module, types and constants are generally declared with a unique (freshly generated) identifier that has no inherent meaning to the external prover. A few Isabelle theories (e.g., those for integer arithmetic, real arithmetic, and bit vectors) define types and constants that are treated as interpreted by the translation into SMT-LIB [11], in which case they are mapped directly to their counterpart in the target logic—thereby allowing the SMT solvers to use their built-in decision procedures designed specifically to reason within the theories in question.
2.2 IEEE 754 Binary Floating-Point Arithmetic
The most common way to approximate the real numbers to a suitable finite set of numbers in modern hardware is via floating-points. Simulating real arithmetic using floating-points is not a straightforward task; the definitions of arithmetic operations are not always obvious, and should ideally not vary between implementations. To this end, the IEEE developed the technical standard IEEE 754 [26], aiming to provide clear specifications and recommendations on all aspects of floating-point arithmetic. To meet the needs of different applications, the standard specifies several floating-point formats, each defining a unique set of numbers.
A binary floating-point format is characterized by its exponent width \(w \in \mathbb {N}\), and its precision \(p \in \mathbb {N}\). A binary floating-point number, x, may then be represented in this format by a triple (s, e, f) of bit vectors of length 1, w, and \(p-1\), respectively, such that (for finite x)
where \({\text {bias}}(w) = 2^{w-1}-1\). The standard also specifies two signed infinities, \(+\infty \) and \(-\infty \), denoting values that are too great in magnitude for the format. These are represented by the triples \((0, 1\ldots 1, 0\ldots 0)\) and \((1, 1\ldots 1, 0\ldots 0)\), respectively. Together, the sign s, the (biased) exponent e, and the fraction f constitute a unique representation of any finite or infinite floating-point number; in particular, the two numbers \(+0\), represented by \((0, 0\ldots 0, 0\ldots 0)\), and \(-0\), represented by \((1, 0\ldots 0, 0\ldots 0)\), are considered distinct. To represent the result of invalid operations, such as 0/0, the standard defines a special Not-a-Number (NaN) value, represented via any triple \((s, 1\ldots 1, f)\) such that \(f \ne 0\ldots 0\).Footnote 1
Additionally, IEEE 754 specifies various arithmetic operations on floating-point numbers. Conceptually, floating-point arithmetic is carried out by converting floating-point numbers to more precise values, performing the corresponding arithmetic operation, and converting the result back to the original floating-point format, in an emulation of a rounded infinitely precise calculation. In an environment like Isabelle/HOL, where theories of real arithmetic are available, the task of carrying out calculations with infinite precision falls upon these, whereas the floating-point operations handle the rounding and special cases (e.g., an argument being NaN or infinite). IEEE 754 specifies precisely how this handling should be performed.
3 An Implementation of SMT-LIB Floating-Point Arithmetic in Isabelle/HOL
Formalizations of floating-point arithmetic are readily available for many proof assistants. For Isabelle/HOL, a formalization originally developed by Lei Yu is available from the Archive of Formal Proofs [46]. This defines a (polymorphic) type of floating-point numbers, whose instances correspond to IEEE floating-point formats with specific width and precision, and various arithmetic operations over this type.
However, although both are based on the IEEE standard, there are important semantic differences between this model and the SMT-LIB floating-point theory [16]. These differences would have rendered a direct interpretation of Lei Yu’s model in the SMT-LIB floating-point theory unsound.
First, the SMT-LIB theory offers five rounding modes. The mode roundNearestTiesToAway (which is optional according to IEEE 754) was not available in the Isabelle/HOL model. Therefore, the enumerated type of rounding modes in Isabelle/HOL did not correspond to the RoundingMode sort in SMT-LIB. We have resolved this difference by adding support for roundNearestTiesToAway to Lei Yu’s model. Although rounding is pervasive in IEEE—it is performed by most arithmetic operations—it is factored out into only two functions in the Isabelle/HOL model (round and intround), so that this was a relatively minor, local change.
Second, the formalization by Lei Yu emphasizes the bit representation of floating-point values (corresponding to specification level 4 in IEEE 754), while the SMT-LIB floating-point theory takes a more abstract view (corresponding to specification level 2 in IEEE 754). Specifically, in Lei Yu’s formalization, each floating-point format contains multiple NaN values (with different bit representations), while the corresponding floating-point format in SMT-LIB only contains a single (abstract) NaN value. To resolve this fundamental difference, we have constructed a new model of floating-point arithmetic in Isabelle/HOL. Our starting point is a quotient construction over the type (’e,’f) float of floating-point numbers offered by Lei Yu’s model. We first define an equivalence relation is_nan_equivalent on this type that relates all NaN values:

We then define a new type (’e,’f) floatSingleNaN that contains the equivalence classes of (’e,’f) float with respect to the relation is_nan_equivalent:

The resulting type (’e,’f) floatSingleNaN contains a single (abstract) NaN value. The (type) arguments ’e and ’f indicate the bit width of the exponent and fraction, respectively. A similar construction, but limited to the double-precision (64-bit) format, was used in [8] to facilitate OCaml code generation for floating-point numbers. Flocq [14], a Coq library of floating-point arithmetic, defines a type with similar semantics inductively, rather than using a quotient construction.
Most floating-point operations can then be lifted [25] in a straightforward manner from (’e,’f) float to (’e,’f) floatSingleNaN. We have additionally defined various operations that are supported in SMT-LIB but that were not available in Lei Yu’s model, such as conversion functions between floating-point numbers and bit vectors. Our model now covers all operations that are available in the SMT-LIB floating-point theory.
Some (rather subtle) semantic differences between our model and the SMT-LIB floating-point theory remain. In SMT-LIB, the result of certain operations, such as converting NaN or infinities to a real number, is unspecified. Isabelle/HOL does not support partial specifications; therefore, the result of these operations is definedFootnote 2 in our model. Technically, the Isabelle/HOL model is an implementation of the SMT-LIB specification. This does not affect the soundness of interpreting the model in SMT-LIB: any theorem provable under SMT-LIB semantics also holds for the Isabelle/HOL model.
An error in the remainder function \(\texttt {float\_rem}\) as defined in Isabelle/HOL was discovered during implementation and has been patched: the remainder of a finite floating-point value x and \(\pm \infty \) shall be x [26, §5.3.1].
4 Interpreting Isabelle/HOL Floating-Point Arithmetic in SMT-LIB
This section describes an interpreted translation of floating-point types and operations from Isabelle/HOL to SMT-LIB. Our translation extends a preexisting general translation [11] targeting SMT solvers that is part of Sledgehammer, which treats floating-point arithmetic as uninterpreted. It supports the formal model of IEEE floating-point arithmetic in Isabelle/HOL that was described in the previous section. We aim to be comprehensive but restrict attention to those floating-point concepts that are defined in both Isabelle/HOL and SMT-LIB.
4.1 SMT-LIB Logic
The first task of our translation module is to select an SMT-LIB logic within which the SMT solver is to reason when deciding the satisfiability of the formula. For performance reasons, it is generally a good idea to select a logic that is as specific as allowed by the contents and structure of the formula. However, FP, the logic for floating-point arithmetic, is too restrictive for many of Isabelle’s proof obligations, which may freely combine floating-point operations with other types and constants. When translated, these will require support for symbols that are either free (uninterpreted) or defined in other SMT-LIB theories.
Sledgehammer’s SMT integration relies on callback functions to analyze the proof obligation and determine the problem’s logic. However, only one of these functions may select a logic. In the absence of a framework allowing for a more modular approach (e.g., incrementally generalizing the logic as little as necessary, based on the types and constants that appear in the proof obligation), we need to select a logic that covers all operations that appear in the proof obligation. To achieve this, whenever a supported floating-point type is detected in the formula to be translated, our callback function returns the (pseudo-)logic \(\texttt {ALL}\). Available since version 2.5 of the SMT-LIB standard, this provides a convenient way to select the most general logic that the respective SMT solver supports.
4.2 Types
Both Isabelle/HOL and SMT-LIB define binary floating-point formats of arbitrary width of the exponent and fraction fields. In Isabelle/HOL, (m,n) floatSingleNaN is the type of floating-point numbers with an exponent field of width \(\texttt {m}\) and a fraction field of width \(\texttt {n}\) (and thus with precision \(\texttt {n+1}\)). In SMT-LIB, the hidden bit of the significand (the bit preceding the fraction) is included in the format specification, making \(\texttt {(\_ FloatingPoint m n+1)}\) the corresponding sort. The SMT-LIB sorts are only defined for formats with \(\texttt {m} > 1\) and \(\texttt {n} > 0\), whereas \(\texttt {m}\) and \(\texttt {n}\) are merely required to be positive in Isabelle/HOL. Thus, any type \(\texttt {(1,n) floatSingleNaN}\) lacks a corresponding sort in SMT-LIB, and is left uninterpreted by the translation.
In Isabelle/HOL, all floating-point formats (m,n) floatSingleNaN are instances of a polymorphic type (’e,’f) floatSingleNaN. Here, ’e and ’f are type variables that may be instantiated with concrete (type) arguments, or left uninstantiated to express generic properties that hold for all floating-point formats. Due to the current lack of support for polymorphism in SMT-LIB, (m,n) floatSingleNaN is interpreted only when m and n are (type) arguments encoding fixed numeric values; polymorphic types are left uninterpreted.
In addition to the types for floating-point formats, Isabelle/HOL defines an enumerated type roundmode for the rounding modes used by the arithmetic operations. SMT-LIB provides a corresponding type; roundmode is interpreted as RoundingMode in SMT-LIB.
4.3 Constants
For the sake of brevity, we focus here on some of the more interesting aspects of the translation of constants. (In HOL, constants are not limited to arity 0, but may have a function type.) An exhaustive enumeration of the mapping is provided in Table 1.
Polymorphism. The issue regarding polymorphism, described in the previous section, affects the translation of constants as well. A constant can only be interpreted if its type is not polymorphic. Since Isabelle’s automatic type inference assigns constants the most general type possible with respect to the context, variables and constants with a floating-point type will in many cases need to be attached with explicit type constraints in order to trigger the interpretation.
Direct Correspondence. For many floating-point related constants in Isabelle, there is a direct semantic-preserving mapping to a function in SMT-LIB. Among these we find, e.g., the rounding modes and comparison operations together with many arithmetic operations and classification predicates. The translation of these does not involve much more than simply replacing their name with the corresponding identifier in SMT-LIB.
Format Parameter Extraction. A few SMT-LIB functions targeted by our translation are technically elements of an infinite family of functions generated by an index over all floating-point formats. This holds, e.g., for the conversion operation from reals to floating-points, and for the (nullary) functions denoting the special floating-point values \(\pm 0\), \(\pm \infty \) and NaN. Their behavior depends on the result sort, which is not necessarily derivable from context and must be indicated explicitly in SMT-LIB. In these cases, we extract the type arguments of the (result) type of the constant to be translated, and add them explicitly as arguments to the corresponding function symbol in SMT-LIB. For instance, the Isabelle/HOL function round of type \(\texttt {roundmode} \Rightarrow \texttt {real} \Rightarrow \texttt {('e,'f) floatSingleNaN}\), which converts a real number into a floating-point number (rounding as necessary), is interpreted as (_ to_fp m n+1) whenever its result type is of the form (m,n) floatSingleNaN, where \(\texttt {m}\) and \(\texttt {n}\) encode fixed numeric values.
Term Translation. Isabelle/HOL supports the definition of advanced concepts on top of the types and constants that are provided by the model of floating-point arithmetic. Our translation does not interpret such derived concepts directly. Instead, these can be handled by unfolding their definitions in Isabelle when desired, or by relying on Sledgehammer’s relevance filter, which can make their definitions and other relevant facts available to external provers automatically.
5 Evaluation
To investigate the difference in the performance of Sledgehammer brought on by the interpreted translation, and to get a clear overview of the comparative performance of the SMT solvers, we conducted an experimental evaluation on a set of proof obligations that involve floating-point operations. Freely available Isabelle formalizations of floating-point properties are scarce; only a few properties are included with the formal IEEE model in the Archive of Formal Proofs. We complemented these with our own formalizations of floating-point properties taken from the IEEE 754 standard and the Handbook of Floating-point Arithmetic [32], resulting in a set of 124 formulas. The formulas in the evaluation set exhibit difficulties ranging from nearly trivial to levels on par with Sterbenz’s lemma [42].
All formulas in the evaluation set are polymorphic over a single floating-point type (’e,’f) floatSingleNaN. This type was instantiated to different fixed-size floating-point formats: half (16-bit), single (32-bit), double (64-bit), and quadruple (128-bit) precision formats, as specified by IEEE 754. The interpreted translation was evaluated on each of these fixed-size formats. For comparison, the abstract (uninterpreted) translation that was previously employed by Sledgehammer was additionally evaluated on the original (polymorphic) evaluation set. This gives rise to nine different models—technically, Isabelle theories with different type annotations—for measuring Sledgehammer’s performance on the evaluation set, defined for \(x \in \{ \texttt {(5,10)}, \texttt {(8,23)}, \texttt {(11,52)}, \texttt {(15,112)} \}\) as:
-
 : interpretation is enabled and all floating-points are of type
: interpretation is enabled and all floating-points are of type
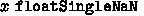 .
. -
 : interpretation is disabled and all floating-points are of type
: interpretation is disabled and all floating-points are of type
 .
. -
 : interpretation is disabled and all floating-points are of polymorphic
: interpretation is disabled and all floating-points are of polymorphic
 type \(\texttt {('e,'f) floatSingleNaN}\).
type \(\texttt {('e,'f) floatSingleNaN}\).
We used the Mirabelle [17] tool with default settings—including a 30 s time limit per formula—to apply Sledgehammer to each proof obligation. The default external provers invoked by Sledgehammer in Isabelle2022 are the ATPs E (version 2.6-1), SPASS (version 3.8ds-2), Vampire (version 4.6) and Zipperposition (version 2.1-1), along with the SMT solvers CVC4 (version 1.8), veriT (version 2021.06.2-rmx), and Z3 (version 4.4.0_4.4.1). Since the floating-point solver in this version of Z3 suffers from a soundness bug, we evaluated Z3 version 4.12.2 instead. We did not evaluate newer versions of the other solvers, such as cvc5 [3], as they are not yet integrated with Isabelle.
Out of the three SMT solvers, only CVC4 and Z3 support the floating-point theory of SMT-LIB. For each of the nine models, we evaluated four different prover configurations: CVC4 only, Z3 only, CVC4+Z3, and Sledgehammer’s default prover configuration, which includes all of the ATPs and SMT solvers listed above. For the \(\mathcal {I}_x\) models, where interpretation is enabled, the default prover configuration uses both interpreted and uninterpreted translations (depending on the prover). For CVC4, we enabled its experimental floating-point solver (option --fp-exp) to obtain support for floating-point formats beyond single and double precision.
Sledgehammer’s relevance filter had access to a large collection of theorems from the Isabelle/HOL library, including the definitions of all types and operations, and (for later formulas in the evaluation set) to all formulas that were evaluated earlier. This mimics realistic use in interactive proof, where users can rely on proven statements and employ them as lemmas in subsequent proofs. To avoid later runs being affected by earlier runs, the status of the machine learning selection of facts (stored in the Isabelle configuration file mash_state) was reset before each Mirabelle run.
The experiments were conducted under Debian GNU/Linux 6.1.0-10-amd64, running on an i9-9980HK CPU at 2.4 GHz with 16 processor threads and 32 GB of main memory.
5.1 Results
Table 2 shows Sledgehammer’s success rates for the four different prover configurations when run on the evaluation set in the models described above. For convenience, the four fixed formats are abbreviated by their total bit length (16, 32, 64, and 128, respectively) in the model name. Sledgehammer succeeds when at least one of the external provers reports that it found a proof within the time limit of 30 s.
In this case, Sledgehammer attempts to reconstruct the external proof in Isabelle using a collection of automated proof methods (as discussed in Sect. 2.1). The success rates for this process, again as a percentage of the total number (124) of proof obligations, are shown in Table 3.
For each floating-point format (and also for the polymorphic model), the largest success rate across prover configurations, with or without interpretation enabled, is indicated in boldface.
5.2 Discussion
Based on the results of our evaluation, we put forward the following observations:
-
1.
An interpreted translation increases Sledgehammer’s success rate for all prover configurations and fixed-size floating point formats. With an uninterpreted translation, success rates vary between 35% and 58%. This increases to between 77% and 95% with an interpreted translation. Across the board, the interpreted translation performs significantly better than the uninterpreted translation.
-
2.
The increase in Sledgehammer’s success rate is most pronounced for the half (16-bit) and double (64-bit) precision formats. The uninterpreted translation performs worse for these two formats (with success rates of 35% to 41%) than for single and quadruple precision. In contrast, the interpreted translation consistently yields high success rates (of 89% to 95% in the best solver configuration) regardless of the format’s precision.
-
3.
Sledgehammer’s success rate on the polymorphic model is generally comparable to, and in some cases better than, its success rate for fixed-size formats with an uninterpreted translation. When the external provers cannot take advantage of their decision procedures for fixed-size floating-point arithmetic, reasoning about fixed-size properties is no easier for them than reasoning about polymorphic properties. (Indeed, depending on the additional facts chosen by Sledgehammer’s relevance filter, it may well be harder.) This changes when interpretation is enabled.
-
4.
CVC4 outperforms Z3 on most models. This is true both with and without interpretation enabled. The only exception is the polymorphic model, where Z3 performs slightly better than CVC4. Using all available provers typically results in (only) slightly higher success rates than using CVC4 alone, but can also lead to slightly lower success rates (mainly because of non-determinism in Sledgehammer’s behavior).
-
5.
With interpretation disabled, proof reconstruction success rates are often close to Sledgehammer’s success rates. In other words, proof reconstruction in the uninterpreted models succeeds on the vast majority of proofs found by external provers. This is a testament to the power of Isabelle’s built-in proof methods (in particular, metis), which provide strong automation for first-order reasoning.
-
6.
Interpretation leads to (much) lower proof reconstruction rates for all prover configurations and fixed-size floating point formats. Although interpretation allows external provers to find more proofs, these proofs are rarely successfully reconstructed in Isabelle. This is to be expected: Isabelle currently does not offer built-in automated proof procedures for floating-point reasoning that could be used to reconstruct such proofs.
Many formulas from the evaluation set were previously proven with 10–20 lines of interactively developed Isabelle proof script, and can now (after interpretation) be proven completely automatically by CVC4 or Z3. The interpreted translation can save significant amounts of human labor in formal proof developments that involve floating-point arithmetic. However, due to the lower proof reconstruction rate, interpretation of floating-point arithmetic is currently primarily of interest to users who are willing to accept CVC4 and Z3 as oracles (cf. Sect. 2.1).
6 Related Work
The practice of employing automatic provers as back-ends in interactive theorem provers is not unique to Isabelle. Generic proof-delegation tools similar to Sledgehammer have also been developed for other proof assistants, e.g., Miz\(\mathbb{A}\mathbb{R}\) [43] for Mizar [2], and HOL(y)Hammer [27] for HOL Light [22] and HOL4 [41]. There are also proof-delegation tools aimed specifically toward SMT solvers, e.g., Smtlink [37] for ACL2 [28] and SMTCoq [1] for Coq [10].
Single integrations of SMT solvers have perhaps been more common than these larger-scale tools. The interactive theorem prover PVS [35] is tightly connected with the SMT solver Yices [18] (and its predecessor ICS), which has been available as a decision procedure for a long time. An oracle integration of Yices in Isabelle by Erkök and Matthews [20] makes use of its dedicated decision procedures, but refrains from translating into SMT-LIB, and instead targets the native input format of Yices due to its expressiveness. Weber [44] proposes a similar oracle integration of Yices into HOL4, but extends it with support for additional SMT solvers via the SMT-LIB format. This integration has since been supplemented with proof reconstruction and become part of HOL(y)Hammer [13].
The work presented here is based on the original integration of SMT solvers in Isabelle’s Sledgehammer by Blanchette et al. [11]. It is dependent on various aspects of their translation into SMT-LIB, including the interpretation of bit-vector types and constants. In this sense, it also bears resemblance to how SMTCoq was recently extended with dedicated support for the theory of bit vectors [19].
Formalizations of IEEE 754 floating-point arithmetic are readily available in interactive proof assistants, e.g., in HOL Light [23], ACL2 [39], and Coq [14], and have been used extensively to verify floating-point related properties. However, to the best of our knowledge, no integration of SMT solvers in interactive proof assistants takes advantage of the dedicated decision procedures for floating-point arithmetic available in the former.
Superficially, the work perhaps most similar to ours is a Why3 [12] formalization of floating-point arithmetic and its mapping to the SMT-LIB floating-point theory [21]. Why3, however, is not a prover itself, but a stand-alone proof-delegation tool relying completely on external provers. Thus greater automation in interactive proof assistants is not a shared objective.
7 Conclusions
In the years since its introduction in Isabelle, Sledgehammer has seen a number of improvements. In varying degree, they have each gradually brought us closer to the ultimate goal of powerful proof automation in interactive proof assistants. By defining a formal model of floating-point arithmetic in Isabelle/HOL that implements SMT-LIB semantics, and by enhancing the translation from Isabelle to SMT-LIB with an interpretation of floating-point types and constants, we have taken another step in this direction. Sledgehammer enjoys a significant increase in success rates (before proof reconstruction) for proof obligations that involve floating-point arithmetic.
Many proof obligations that were previously out of reach for any automated prover can now be solved automatically. For users who are willing to trust the external SMT solvers, enhancing Sledgehammer’s translation with a floating-point interpretation increases proof automation and reduces the manual effort required to construct proofs in this important application domain.
Our translation does not require formulas to be fully interpretable in the SMT-LIB floating-point theory. The SMT solvers are instructed to reason in a more general logic, where interpreted and uninterpreted sorts and functions can be combined freely.
There are two notable limitations, which we propose to address through future work. First, the interpretation of floating-point arithmetic is restricted to fixed-size formats. In many situations, this is not a severe limitation—fixed-size reasoning is sufficient, for instance, when one wants to verify a specific hardware architecture, or a software implementation that uses a specific floating-point type such as binary64. However, floating-point properties that hold for all formats are most naturally stated polymorphically in Isabelle/HOL. Such properties cannot be interpreted in the floating-point theory of SMT-LIB, which (in its current version 2.6) lacks support for polymorphism: although it offers a type \(\texttt {(\_ FloatingPoint m n)}\) for any sufficiently large \(\texttt {m}\) and \(\texttt {n}\), it does not offer a polymorphic type \(\texttt {(\_ FloatingPoint}\ m\ n\texttt {)}\) where m and n are variables that may be instantiated.
Supporting polymorphism in SMT solvers is no small feat. Fortunately, there is ongoing work to obtain a tighter integration of automatic provers, including SMT solvers, with proof assistants. One of the means by which to achieve this is via support for higher-order logic in these provers [5]. Most likely, SMT-LIB 3—the next major update to SMT-LIB—will facilitate these changes by supporting polymorphism [4]. When such support becomes available in SMT solvers that support floating-point arithmetic, an interpreted translation can be employed also for polymorphic floating-point properties. There has already been work on supporting parametric bit-vector formulas in SMT solvers by encoding them as formulas over non-linear integer arithmetic, uninterpreted functions, and universal quantifiers (the UFNIA logic in SMT-LIB) [33]. This approach could in principle be extended to floating-point numbers.
Second, interpretation of floating-point arithmetic allows SMT solvers to find more proofs, but reduces proof reconstruction rates in Isabelle. There is a mismatch between the reasoning capabilities of SMT solvers that support floating-point arithmetic and Isabelle’s built-in automated proof procedures, which are used to reconstruct proofs. The latter currently do not offer dedicated support for floating-point reasoning, but need to rely on explicit lemmas to reason about concepts for which the SMT solver, when interpretation is enabled, can employ specialized decision procedures. Users may opt to bypass proof reconstruction and use external SMT solvers as oracles; however, this reduces trust in the resulting theorems, as errors in the SMT solver, in the translation from Isabelle/HOL to SMT-LIB, or in the Isabelle/HOL model of floating-point arithmetic could lead to unsound results. The approach preferred by the interactive theorem proving community is that of a skeptic [24]—external proofs should be reconstructed internally. If successful, this approach combines the speed of the SMT solver with the reliability of the proof assistant.
Efficient reconstruction of proofs has previously been achieved for other SMT-LIB logics [11], and is likely possible also for floating-point reasoning, through improving on the proof information provided by SMT solvers and translating theory-specific inferences. An automated proof procedure for floating-point arithmetic implemented on top of Isabelle’s inference kernel would both facilitate the reconstruction of external proofs and increase the built-in automation for floating-point reasoning available in Isabelle/HOL. The implementation of such a proof procedure will require substantial work, but the evaluation results in this paper—in particular, the difference between Tables 2 and 3—clearly indicate that the effort would not be wasted.
Notes
- 1.
The IEEE 754 standard defines a quiet and a signalling NaN. This distinction is not present in the SMT-LIB floating-point theory, which is based on a higher level of abstraction.
- 2.
For instance, in terms of a special constant called undefined.
References
Armand, M., Faure, G., Grégoire, B., Keller, C., Théry, L., Werner, B.: A modular integration of SAT/SMT solvers to coq through proof witnesses. In: Jouannaud, J.-P., Shao, Z. (eds.) CPP 2011. LNCS, vol. 7086, pp. 135–150. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25379-9_12
Bancerek, G., et al.: Mizar: state-of-the-art and beyond. In: Kerber, M., Carette, J., Kaliszyk, C., Rabe, F., Sorge, V. (eds.) CICM 2015. LNCS (LNAI), vol. 9150, pp. 261–279. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-20615-8_17
Barbosa, H., et al.: cvc5: a versatile and industrial-strength SMT solver. In: TACAS 2022. LNCS, vol. 13243, pp. 415–442. Springer, Cham (2022). https://doi.org/10.1007/978-3-030-99524-9_24
Barbosa, H., Blanchette, J.C., Cruanes, S., Ouraoui, D.E., Fontaine, P.: Language and proofs for higher-order SMT (work in progress). In: Dubois, C., Paleo, B.W. (eds.) Fifth Workshop on Proof eXchange for Theorem Proving - PxTP 2017. Electronic Proceedings in Theoretical Computer Science, vol. 262, pp. 15–22 (2017). https://doi.org/10.4204/EPTCS.262.3
Barbosa, H., Reynolds, A., El Ouraoui, D., Tinelli, C., Barrett, C.: Extending SMT solvers to higher-order logic. In: Fontaine, P. (ed.) CADE 2019. LNCS (LNAI), vol. 11716, pp. 35–54. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-29436-6_3
Barrett, C., Fontaine, P., Tinelli, C.: The SMT-LIB standard: version 2.6. Technical report, Department of Computer Science, The University of Iowa (2017). https://www.smt-lib.org/
Barrett, C., et al.: CVC4. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 171–177. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_14
Basin, D., et al.: A formally verified, optimized monitor for metric first-order dynamic logic. In: Peltier, N., Sofronie-Stokkermans, V. (eds.) IJCAR 2020. LNCS (LNAI), vol. 12166, pp. 432–453. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-51074-9_25
Bentkamp, A., Blanchette, J., Tourret, S., Vukmirovic, P.: Superposition for higher-order logic. J. Autom. Reason. 67(1), 10 (2023). https://doi.org/10.1007/s10817-022-09649-9
Bertot, Y., Castéran, P.: Interactive Theorem Proving and Program Development - Coq’Art: The Calculus of Inductive Constructions. Texts in Theoretical Computer Science. An EATCS Series. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-662-07964-5
Blanchette, J.C., Böhme, S., Paulson, L.C.: Extending sledgehammer with SMT solvers. J. Autom. Reason. 51(1), 109–128 (2013). https://doi.org/10.1007/s10817-013-9278-5
Bobot, F., Filliâtre, J.C., Marché, C., Paskevich, A.: Why3: shepherd your herd of provers. In: Boogie 2011: First International Workshop on Intermediate Verification Languages, pp. 53–64 (2011)
Böhme, S., Weber, T.: Fast LCF-style proof reconstruction for Z3. In: Kaufmann, M., Paulson, L.C. (eds.) ITP 2010. LNCS, vol. 6172, pp. 179–194. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14052-5_14
Boldo, S., Melquiond, G.: Some formal tools for computer arithmetic: Flocq and Gappa. In: 28th IEEE Symposium on Computer Arithmetic, ARITH 2021, Lyngby, Denmark, 14–16 June 2021, pp. 111–114. IEEE (2021). https://doi.org/10.1109/ARITH51176.2021.00031
Bouton, T., Caminha B. de Oliveira, D., Déharbe, D., Fontaine, P.: veriT: an open, trustable and efficient SMT-solver. In: Schmidt, R.A. (ed.) CADE 2009. LNCS (LNAI), vol. 5663, pp. 151–156. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02959-2_12
Brain, M., Tinelli, C., Rümmer, P., Wahl, T.: An automatable formal semantics for IEEE-754 floating-point arithmetic. In: 22nd IEEE Symposium on Computer Arithmetic - ARITH 2015, pp. 160–167. IEEE (2015). https://doi.org/10.1109/ARITH.2015.26
Desharnais, M., Vukmirovic, P., Blanchette, J., Wenzel, M.: Seventeen provers under the hammer. In: Andronick, J., de Moura, L. (eds.) 13th International Conference on Interactive Theorem Proving, ITP 2022, 7–10 August 2022, Haifa, Israel. LIPIcs, vol. 237, pp. 8:1–8:18. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2022). https://doi.org/10.4230/LIPIcs.ITP.2022.8
Dutertre, B.: Yices 2.2. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 737–744. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08867-9_49
Ekici, B., Katz, G., Keller, C., Mebsout, A., Reynolds, A.J., Tinelli, C.: Extending SMTCoq, a certified checker for SMT (extended abstract). In: Blanchette, J.C., Kaliszyk, C. (eds.) First International Workshop on Hammers for Type Theories - HaTT@IJCAR 2016. Electronic Proceedings in Theoretical Computer Science, vol. 210, pp. 21–29 (2016). https://doi.org/10.4204/EPTCS.210.5
Erkök, L., Matthews, J.: Using Yices as an automated solver in Isabelle/HOL. In: Rushby, J., Shankar, N. (eds.) AFM 2008: Third Workshop on Automated Formal Methods, pp. 3–13 (2008)
Fumex, C., Marché, C., Moy, Y.: Automated verification of floating-point computations in Ada programs. Research Report RR-9060, Inria Saclay Ile de France (2017). https://hal.inria.fr/hal-01511183
Harrison, J.: HOL light: a tutorial introduction. In: Srivas, M., Camilleri, A. (eds.) FMCAD 1996. LNCS, vol. 1166, pp. 265–269. Springer, Heidelberg (1996). https://doi.org/10.1007/BFb0031814
Harrison, J.: Floating-point verification using theorem proving. In: Bernardo, M., Cimatti, A. (eds.) SFM 2006. LNCS, vol. 3965, pp. 211–242. Springer, Heidelberg (2006). https://doi.org/10.1007/11757283_8
Harrison, J., Théry, L.: A skeptic’s approach to combining HOL and Maple. J. Autom. Reason. 21(3), 279–294 (1998). https://doi.org/10.1023/A:1006023127567
Huffman, B., Kunčar, O.: Lifting and transfer: a modular design for quotients in Isabelle/HOL. In: Gonthier, G., Norrish, M. (eds.) CPP 2013. LNCS, vol. 8307, pp. 131–146. Springer, Cham (2013). https://doi.org/10.1007/978-3-319-03545-1_9
IEEE standard for floating-point arithmetic. IEEE STD 754-2019 (Revision of IEEE 754-2008), pp. 1–84 (2019). https://doi.org/10.1109/IEEESTD.2019.8766229
Kaliszyk, C., Urban, J.: HOL(y)Hammer: online ATP service for HOL Light. Math. Comput. Sci. 9(1), 5–22 (2014). https://doi.org/10.1007/s11786-014-0182-0
Kaufmann, M., Moore, J.S.: An industrial strength theorem prover for a logic based on Common Lisp. IEEE Trans. Software Eng. 23(4), 203–213 (1997). https://doi.org/10.1109/32.588534
Klein, G., et al.: seL4: formal verification of an operating-system kernel. Commun. ACM 53(6), 107–115 (2010). https://doi.org/10.1145/1743546.1743574
Meng, J., Paulson, L.C.: Lightweight relevance filtering for machine-generated resolution problems. J. Appl. Log. 7(1), 41–57 (2009). https://doi.org/10.1016/j.jal.2007.07.004
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Muller, J.M., et al.: Handbook of Floating-Point Arithmetic. Birkhäuser (2010). https://doi.org/10.1007/978-0-8176-4705-6
Niemetz, A., Preiner, M., Reynolds, A., Zohar, Y., Barrett, C., Tinelli, C.: Towards satisfiability modulo parametric bit-vectors. J. Autom. Reason. 65(7), 1001–1025 (2021). https://doi.org/10.1007/s10817-021-09598-9. http://www.cs.stanford.edu/ barrett/pubs/NPR+21c.pdf
Nipkow, T., Wenzel, M., Paulson, L.C. (eds.): Isabelle/HOL. LNCS, vol. 2283. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45949-9
Owre, S., Rushby, J.M., Shankar, N.: PVS: a prototype verification system. In: Kapur, D. (ed.) CADE 1992. LNCS, vol. 607, pp. 748–752. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-55602-8_217
Paulson, L.C., Blanchette, J.C.: Three years of experience with Sledgehammer, a practical link between automatic and interactive theorem provers. In: Sutcliffe, G., Schulz, S., Ternovska, E. (eds.) The 8th International Workshop on the Implementation of Logics - IWIL 2010. EPiC Series in Computing, vol. 2, pp. 1–11. EasyChair (2010). https://easychair.org/publications/paper/wV
Peng, Y., Greenstreet, M.R.: Extending ACL2 with SMT solvers. In: Kaufmann, M., Rager, D.L. (eds.) Thirteenth International Workshop on the ACL2 Theorem Prover and Its Applications - ACL2 2015. Electronic Proceedings in Theoretical Computer Science, vol. 192, pp. 61–77 (2015). https://doi.org/10.4204/EPTCS.192.6
Riazanov, A., Voronkov, A.: The design and implementation of VAMPIRE. AI Commun. 15(2–3), 91–110 (2002). http://content.iospress.com/articles/ai-communications/aic259
Russinoff, D.M.: A mechanically checked proof of IEEE compliance of the floating point multiplication, division and square root algorithms of the AMD-K7 processor. LMS J. Comput. Math. 1, 148–200 (1998). https://doi.org/10.1112/S1461157000000176
Schulz, S., Cruanes, S., Vukmirović, P.: Faster, higher, stronger: E 2.3. In: Fontaine, P. (ed.) CADE 2019. LNCS (LNAI), vol. 11716, pp. 495–507. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-29436-6_29
Slind, K., Norrish, M.: A brief overview of HOL4. In: Mohamed, O.A., Muñoz, C., Tahar, S. (eds.) TPHOLs 2008. LNCS, vol. 5170, pp. 28–32. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-71067-7_6
Sterbenz, P.H.: Floating-Point Computation. Prentice-Hall, Hoboken (1974)
Urban, J., Rudnicki, P., Sutcliffe, G.: ATP and presentation service for Mizar formalizations. J. Autom. Reason. 50(2), 229–241 (2013). https://doi.org/10.1007/s10817-012-9269-y
Weber, T.: SMT solvers: new oracles for the HOL theorem prover. Int. J. Softw. Tools Technol. Transfer 13(5), 419–429 (2011)
Weidenbach, C.: Combining superposition, sorts and splitting. In: Robinson, J.A., Voronkov, A. (eds.) Handbook of Automated Reasoning (in 2 volumes), pp. 1965–2013. Elsevier and MIT Press (2001). https://doi.org/10.1016/b978-044450813-3/50029-1
Yu, L.: A formal model of IEEE floating point arithmetic. Archive of Formal Proofs (2013). http://isa-afp.org/entries/IEEE_Floating_Point.html. Formal proof development
Acknowledgments
This work was partially supported by the Wallenberg AI, Autonomous Systems and Software Program (WASP) funded by the Knut and Alice Wallenberg Foundation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Torstensson, O., Weber, T. (2023). Hammering Floating-Point Arithmetic. In: Sattler, U., Suda, M. (eds) Frontiers of Combining Systems. FroCoS 2023. Lecture Notes in Computer Science(), vol 14279. Springer, Cham. https://doi.org/10.1007/978-3-031-43369-6_12
Download citation
DOI: https://doi.org/10.1007/978-3-031-43369-6_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-43368-9
Online ISBN: 978-3-031-43369-6
eBook Packages: Computer ScienceComputer Science (R0)



 : interpretation is enabled and all floating-points are of type
: interpretation is enabled and all floating-points are of type
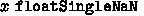 .
. : interpretation is disabled and all floating-points are of type
: interpretation is disabled and all floating-points are of type
 .
. : interpretation is disabled and all floating-points are of polymorphic
: interpretation is disabled and all floating-points are of polymorphic
 type
type