Keywords

1 Introduction

1.1 Welding Problem

Welding is one of the most critical manufacturing processes in the world of metallurgy; it is present in the industry due to its versatility when joining parts of complex structures, providing economic and technological advantages. With the development of computational techniques, the welding and metallurgy industry has opted for the mathematical modeling of the physical processes that characterize the phenomenon and allow us to understand the thermomechanical behavior of the physical variables involved in the manufacturing process [1].

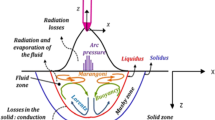
In this work, the scheme of Fig. 1 will be considered to analyze the welding process. A heat source travels through a solid and communicates a heat power that increases its temperature. When the melting temperature of the material \(T_F\) is reached, the solid begins to melt, passing some areas to a liquid part. In the fusion zone, the temperature is kept constant, and the heat is used in the phase change, appearing a mixing zone (called ‘mushy region’), where the liquid and solid phases coexist. When all the solid has melted locally, the resulting liquid can continue to increase its temperature when it receives heat (or, conversely, the liquid solidifies if it gives up heat to other parts of the solid or the environment). When the molten zone increases its temperature \(T > T_F\), and in the presence of the gravitational field, it generates convection currents due to the buoyancy induced by gravity.

Fig. 1.
figure 1

Diagram of the welding process considered in this work.

Full size image

Joint modeling of the three zones appearing in the domain (solid phase, liquid phase, and mixing zone) will be carried out to study this phenomenon. To do this, the energy conservation equation written in terms of enthalpy is proposed, together with mass and momentum conservation equations to determine the velocity of the fluid when it appears. It is noted that most of the models presented in the literature formulate the energy equation solely in terms of temperature. An approach that is erroneous if one wants to realistically describe the melting zone in pure materials that are kept at a constant temperature while the phase change occurs.

Numerous numerical methods are used to numerically solve problems of a metallurgical nature, such as the Galerkin method for free elements [2], the Petrov-Galerkin method [3], the finite volume method [4] and the finite element method [5]. In this work, a Lagrange-Galerkin scheme in a finite element framework [6,7,8,9] has been used to solve the mathematical model.

2 Mathematical Modeling

2.1 Equations of Conservation of Mass and Momentum

In the first place, the equations of conservation of mass and momentum are presented to calculate the velocity field of the liquid phase. To simplify the model, it will be considered that the density of the solid and the liquid is the same, a constant value that does not depend on the temperature or the stress state of the solid.

For the momentum equation, we assume that the liquid behaves as a Newtonian fluid with constant viscosity and the density variation due to temperature changes are only retained in the buoyancy term according to the Boussinesq model in the molten zone. On the other hand, to model the flow of fluid through porous media, the Darcy model [10] has also been considered.

2.2 Equation of Energy Conservation

For the description of welding problems, the enthalpy \(h,\) is revealed as the most appropriate state variable to describe the mixed zone, where the solid and liquid phases coexist. Leaving all the equations as the dimensionless form in the following way:

$$ \left\{ {\begin{array}{*{20}c} {\nabla^{*} \cdot {\bf{v}}^* = 0, } \\ {\,} \\ {\frac{{\partial {\bf{v}}^{*} }}{{\partial {\text{t}}^{*} }} + \left( {{\bf{v}}^* \cdot \nabla^* } \right){\bf{v}}^* = - \nabla^* p^{*} + \frac{1}{{{\text{Re}}}}\Delta^{*} {\bf{v}}^{*} + \frac{{{\text{Gr}}}}{{{\text{Re}}^2 }}\left( {{\uptheta } - 1} \right){\bf{e}}_{{\varvec{x}}_2 } - \frac{1}{{{\text{ReDa}}}}\frac{{\left( {1 - {\text{Y}}_{\text{L}} } \right)^2 }}{{{\text{Y}}_{\text{L}}^3 }}{\bf{v}}^* ,} \\ {\,} \\ {\frac{{\partial h^{*} }}{{\partial {\text{t}}^{*} }} + \nabla^* \cdot \left( {{\bf{v}}^* h^* } \right) = \frac{1}{{{\text{Pe}}}}\nabla^* (\lambda \nabla^* \theta ) + {\text{Q}}^{*} } \\ \end{array} } \right. $$
(1)

where, the dimensionless variables are: v* is the velocity field, \(p^{*}\) is the pressure, \({\uptheta }\) is the temperature, \({\text{Y}}_{\text{L}}\) is the liquid fraction, \(h^{*}\) is the enthalpy, \({\text{Q}}^{*}\) is the heat source. On the other hand, we consider the following dimensionless numbers as: \({\text{Re}}\) is the Reynolds Number, \({\text{Gr}}\) is the Grashof Number, \({\text{Da}}\) is the Darcy Number, \({\text{Pe}}\) is the Peclet Number.

3 Numerical Method

For the numerical resolution of the proposed mathematical model, the conservative formulation of the Lagrange-Galerkin scheme will be used. After this, the temporal and spatial discretization will proceed, which will lead us to the matrix problem to be solved. The unknown variables of the problem will be v*, \(p^{*}\) and \(h^{*}\); moreover \({\uptheta }\), \({\text{Y}}_{\text{L}}\) and \(du^{*} = \lambda d{\uptheta }\) will be auxiliar variables which can be expressed as a function of \(h^{*}\). For a temporal discretization BDF2 scheme will be used. For this purpose, we develop a Newton-type algorithm to solve the energy conservation equation, given its non-linear nature as can be seen in Fig. 2.

Fig. 2.
figure 2

A Newton-type algorithm for solving equation of energy conservation.

Full size image

4 Results

In Figs. 3 and 4 we can see a graphical representation of the solution of our problem in several instants of time. The isolines that mark the border between the solid and liquid area are represented in the lower part of the figures, together with blue current lines that indicate where there is fluid movement. In the upper panel, a section is represented by the line \(x_2 = - 0.5\) of the domain, to observe the profiles of the thermodynamic variables of the problem and of the vertical component of the velocity field \(v_{x_2 }\).

Specifically, Fig. 3, represents the solution in the first moments of time \({\text{t}} \le 1.0\) in which the heat source acts. It can be seen that from \({\text{t}} \approx 0.25\) the heat supplied has managed to warm the solid up to the melting temperature \({\uptheta } = 1.0\), and the phase mixing zone begins to appear, called the ‘mushy region’. The source in its movement continues to provide heat and at \({\text{t}} \approx 0.5\) the first zone of pure liquid is observed at temperatures higher than those of fusion. It is from that moment, when the buoyancy terms are no longer zero and the movement of the fluid begins. For longer times, a coexistence of the 3 regions is observed (solid zone, liquid zone, and mixing zone). In the front zone (where the heat source is reaching) the fusion of the solid takes place and presents relatively smooth gradients in the variable enthalpy \(h\). However, in the rear part (where the heat source is away from) the resolidification of the liquid formed takes place, and very marked fronts are formed in the variable enthalpy h around the lines that mark the mixing zone and that causes the area where the phases coexist to shrink.

Once the source is turned off, the phenomenon of cooling and homogenization of the temperature will begin, an effect that can be observed in detail in Fig. 4. In a few instants of time, the area where the phase mixture exists begins to drastically reduce, as a result of resolidification of the material. This disappearance of the mixing zone can be seen very well on the sides and in the upper zone where the movement of the fluid is slower. However, in the lower zone is where the mixing zone is maintained until the last moments of time. On the other hand, as time progresses, the complete disappearance of the mixing zone is observed, leaving only the solid phase and the liquid phase, separated by a zone of discontinuity, which gradually reduces in size due to the heat that is being lost.

But the heat only flows at the edges of the interface, because inside, where the liquid is at a temperature \({\uptheta } = 1.0\), there is no heat conduction.

Fig. 3.
figure 3

Solutions obtained in the first moments of time \({\text{t}} \le 1.0\), in which the external heat source Q is acting.

Full size image
Fig. 4.
figure 4

Solutions obtained in the final moments of time \({\text{t}} > 1.0\), in which the external heat source Q off.

Full size image

5 Conclusions

This paper presents a numerical method based on the Lagrange-Galerkin methodology to solve a welding problem. The mathematical model is formulated to correctly define the solid, liquid zone and the mixed or soft zone, which appear in the problem.

The energy equation is written conservatively in the enthalpy variable and Newton’s algorithm is used to obtain the value of enthalpy \(h\). The advantage of using the enthalpy state variable \(h\) is that the rest of the thermodynamic variables can be written in a monotonic and single-valued way as a function of it. The good properties of Newton’s algorithm have been verified in terms of convergence speed, the fact that it does not require additional parameters, and the cheap computational cost to perform the matrix assembly in each iteration.

To describe the velocity field v, the laws of conservation of mass and momentum are used, which are valid in all three areas of the material. It is considered an incompressible fluid, except in the buoyancy terms given by the Boussinesq model. The phase mixing zone is considered a porous medium where Darcy’s law is considered. To numerically solve the Stokes problem that is formed, the Uzawa-type conjugate gradient algorithm is used.

Finally, the finite element method with anisotropic mesh adaptation techniques was used to carry out the numerical simulations. This substantially improves the calculation times and the precision obtained.