Keywords

1 Introduction

The study of wake dynamics, which originated from the interaction between a body and a fluid stream, has been an important field of research. On the one hand, this type of research is developed with the interest of studying the effect on structural engineering components that can be affected by dynamics loads originated by the interaction with a fluid: heat exchange lines, marine structures, chimneys, bridges, energy recovery system, among other [1, 2]. On the other hand, in many of these applications, vortex shedding emits acoustic noise and flow-induced vibrations [3]. In this context, researches on the modification of wakes to attenuate and/or control vortex emission have been relevant for developing passive and active devices considered in engineering systems [4,5,6].

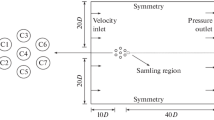
On the other hand, cylinders introduced in a fluid stream are used as a “test bed” to explore the wake instability in open flows [7]. For a stationary system composed of a cylinder, the Reynolds number is an important indicator for the formation of a non-stationary wake. This condition is obtained when a critical Reynolds number is reached [8], initiating the well-known Bérnard von Kármán (BvK) street. Under the critical Reynolds, the wake is stationary, forming a symmetric pair of vortices attached to the body’s surface called a recirculation bubble. The bubble growth is linear as the Reynolds number increases [9]. The interaction of wakes developed by a binary cylinder system could activate or deactivate the shedding of vortices in the vicinity of critical Reynolds; in this sense, the present work seeks to study the interaction around considering a two-dimensional flow regime (see Fig. 1).

2 Methodology

Fig. 1.
figure 1

a) Schematic of a binary system using cylinders in different positions (D: diameter of the main cylinder, d: diameter of the secondary cylinder, L: distance between centers, alpha: position angle, Uo velocity of the linear movement of the carriage). b) Schematic of the system coupling 1) linear bearing; 2) rail; 3) connection platform with bearings; 4) mounting structure for the camera, electrode, and cylinders; 5) CCD sensor; 6) cylinders; 7) electrode. c) Illumination for PIV. The MATLAB PIVLab algorithm is used [10]

Full size image

2.1 Water Tank

The binary system is introduced into the tank and coupled to a carriage with linear motion. Since the Reynolds number involved is low (of the order of the critical Reynolds), the BvK instability develops through the relative movement between the binary system and the water initially at rest.

On the other hand, hydrogen bubbles are used to visualize the vortex structures downstream of the cylinder system [11]. A 50 µm diameter platinum wire is used as the cathode, while imaging is performed by a Sony IMX477 camera (CCD sensor) which is activated by a Raspberry. For the PIV analysis, tracer particles are incorporated in the water pond (Sphericel 110P8) of 11.7 μm diameter. The sampling frequency of the camera was adjusted to 30 fps to comply with the Nyquist principle [12].

2.2 Wind Tunnel

The velocity profiles measured with PIV were compared with measurements in a closed-loop subsonic wind tunnel with two test sections for high and low velocity [13]. The measuring instrument is a hot wire anemometer located downstream of the system. The digital signal is prepared through a low-pass filter (Hz), an offset adjustment, and an amplifier of the filtered signal.

3 Results

3.1 Single Cylinder

Fig. 2.
figure 2

Measurement and visualization system in a tank with water: D = 6.4 mm, Re = 67. a) Visualization of the Bérnard von Kármán Instability using hydrogen bubbles. b) Measure the transverse component of velocity dimensionless with the free stream velocity.

Full size image

The Bernard von Kárman instability is visualized in Fig. 2-a) through the hydrogen bubble technique, showing the advection of vortices downstream of the cylinder (relative motion). In Fig. 2-b), the transverse velocity field dimensionless with the free stream velocity, obtained through PIV. Two segmented lines (x/D = 4.2 and x/D = 8.8) are drawn to measure the profile of velocities averaged downstream of the cylinder position.

3.2 Binary System Wakes Measured in Water

α = 90° In Fig. 3-a), the wakes and the activation of the instability of the secondary cylinder by the wake of the main cylinder can be seen. On the other hand, Fig. 3-b) presents the transverse component of the velocity field whose alternation of the main cylinder wake is coupled with the instability activation of the secondary cylinder wake. The averaged velocity profile is presented in Fig. 4, and the asymmetric shape of the profile can be visualized from an asymmetric configuration of the binary system.

α = 75° The results of the visualization and velocity field are presented in Fig. 5. It is observed that both wakes develop with vortex emission downstream of the system. Qualitatively, it is observed that the development of the wakes is closer to each other because the “y” component of the distance between cylinder centers decreases due to the inclination of the secondary cylinder. This condition impacts the increase in the size of the vortices generated downstream of the secondary cylinder compared to the position of the secondary cylinder.

Fig. 3.
figure 3

A binary system under a configuration of α = 90°. D = 6.4 mm, d = 3.9 mm, L = 20 mm, ReD = 67, Red = 42. a) Visualization with HB. b) Field of the transverse component of velocities using PIV technique.

Full size image
Fig. 4.
figure 4

α = 90°. Average velocity profile and time evolution of the transverse component of the velocity.

Full size image
Fig. 5.
figure 5

α = 75°, D = 6.4 mm, d = 3.9 mm, L = 20 mm, ReD = 67, Red = 42. a) visualization with HB. B) Field of the transverse component of velocities using PIV technique.

Full size image

Figure 6 shows the averaged velocity profile for the asymmetric configuration of α = 75°. It can be seen that for positions closer to the binary system (decrease of “x”), the shape of the profile takes a symmetric condition, whose average velocity perturbation of the main cylinder is of the same order as the average perturbation of the secondary cylinder. A decrease in the intensity of the transverse velocity component is observed compared to the values presented for the condition of α = 90°. However, a longer transient region reappears than the previous configuration but is lower than that of the single cylinder.

Fig. 6.
figure 6

α = 75°. Average velocity profile and time evolution of the transverse component of the velocity

Full size image

3.3 Binary System Wakes Measured in Wind Tunnel

The Fig. 7 shows the profile of averaged velocities measured through hot wire anemometry in a wind tunnel, the shape of average velocities can be seen for α = 75°, finding a great symmetry analogous to that measured in the tank with water. This effect is interesting because the system that generates the disturbance in the flow is entirely asymmetric (position and size), so there is a strong interaction between the two wakes. The vortex emission frequency is altered under the condition of α = 75°. Only one fundamental frequency of the velocity magnitude measured with the anemometer is presented, whose value corresponds to f2c_75 = 15.8 Hz.

Fig. 7.
figure 7

Average velocity profile measured in a wind tunnel and PSD from x/D = 8.8.

Full size image

4 Conclusions

Using a secondary cylinder as a passive controller modifies the onset of the system instability, varying the frequency of vortex shedding due to the perturbative interaction between the wakes.

According to the visualizations and velocity field measurements presented, it is inferred that under specific configurations, both cylinders emit vortices, so the emission of the main cylinder excites the wake of the secondary cylinder.

The feedback interactions of both wakes generate a symmetric averaged velocity profile under a completely asymmetric geometrical condition (different diameters and forward position of the secondary cylinder).

For future work, other positions and sizes of the second cylinder will be studied, mainly for the description of the asymmetric region, applying other measurement techniques such as Laser Doppler anemometry to measure the effect of the interaction between wakes.