Keywords

1 Introduction

Tribology is the science that studies the interaction between surfaces. One of its main fields of study is the minimization of friction and wear, and one of the most common solutions to reduce these phenomena is lubrication. The lubricant can be considered a third body that is placed between two surfaces to prevent contact between them and facilitate their relative movement [1].

One of the most common applications of lubrication lies in hydrodynamic bearings. These consist of a static element named hub with a cylindrical hollow in which a shaft is housed. For their study, starting from the basic equations of fluid mechanics and accepting certain fundamental hypotheses, we reach the most common starting point, the Reynolds equation. This, for the case of incompressible fluid in bearings is:

$$ \frac{\partial }{\partial \theta }\left( {\frac{h^3 }{{R^2 \eta }}\frac{\partial p}{{\partial \theta }}} \right) + \frac{\partial }{\partial z}\left( {\frac{h^3 }{\eta }\frac{\partial p}{{\partial z}}} \right) = 6\omega \frac{\partial h}{{\partial \theta }}, $$
(1)

where \(\theta\) is the angular coordinate, z is the axial coordinate, η is the dynamic viscosity, ω is the rotational speed and h is the film thickness, for which an analytical expression is known,

$$ h = C + e\cdot \cos \left( \theta \right) = C\left( {1 + \epsilon \cdot \cos \left( \theta \right)} \right), $$
(2)

where C is the difference of radii between hub and shaft, e is the distance between centers, called eccentricity, and ϵ is the eccentricity coefficient.

From (1) it is possible to approximate analytical solutions for the pressure distribution when either L ≫ D or L ≪ D is satisfied, L being the axial length of the bearing and D its diameter. However, in bearings one usually has L ≈ D, so it becomes necessary to solve numerically the two-dimensional Reynolds equation. To reach realistic solutions, cavitation of the fluid must be considered in the model.

The model used in this work, known as the Elrod-Adams model, is complemented by the Floberg condition on the boundary between the cavitation and non-cavitation regions [2]. The boundary between these regions is not known at the beginning of the problem and must be found, meaning this is a free boundary problem. The approach involves introducing an additional variable, denoted by γ, which is the mass fraction of liquid lubricant.

The value of γ is equal to one in the non-cavitation zone (p > pv), and 0 ≤ γ < 1 is satisfied in the cavitation region (p = pv). The relation between the pressure p and γ is given through the so-called maximal monotonic operator, H, which is multivalued and introduces into the problem a nonlinear relation, γ ∈ H(p).

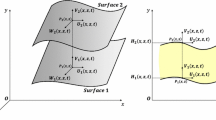
Let Ω be the domain [0,2π] × [0,L/R] resulting from the nondimensionalization of the variables θ and z. This can be seen in Fig. 1. The dimensionless pressure function, \(\overline{p}\) must satisfy the Reynolds equation in the region where there is no cavitation. In the cavitation zone, denoted by \(\Omega_C\), this equation does not model the fluid behaviour.

Fig. 1.
figure 1

Source: own elaboration

Non-dimensional domain of the problem.

Full size image

These ideas lead to the Elrod-Adams mathematical model. In papers such as [2, 3] and [4] the existence and uniqueness of solution of the Elrod-Adams model is proved. It is also obtained that the associated weak problem is:

Find \(\left( {\overline{p}, \gamma } \right) \in K \times L^\infty \left( {\Omega } \right)\) so that:

$$ \left\{ {\begin{array}{*{20}c} { \smallint \limits_{\Omega } \overline{h}^3 \nabla \overline{p}\cdot \nabla \varphi + \smallint \limits_{\Omega } \frac{{\partial \left( {\overline{h}\gamma } \right)}}{\partial x_1 }\cdot \varphi = 0,\;\forall \varphi \in K_0 } \\ {\gamma \in H\left( {\overline{p}} \right)} \\ {p\left( {x = 0,y} \right) = p\left( {x = 2\pi ,y} \right); p\left( {x,y = 0} \right) = 0; p\left( {x,y = \frac{L}{R}} \right) = \Delta p} \\ \end{array} } \right. $$
(3)

2 Methodology

In order to solve this problem numerically, a strategy based on the ideas of [2] and [3] will be used, which makes use of the method of characteristics and the Bermudez-Moreno algorithm [5].

2.1 Method of Characteristics

First, the problem is transformed into an evolution one, so that the solution sought is the stationary state of the problem. An artificial time dependence t is introduced in all the functions of the problem and denoted by “ ~ ”. Using an artificial velocity field \(\vec{V}\left( {x_1 ,x_2 } \right) = \left( {1,0} \right)\), the derivative in the problem is expressed as a material derivative.

We denote by \(X^k \left( x \right)\) the position at instant t-k of a particle that reaches at instant t the position x when convected by the velocity field. The material derivative operator in this case can be discretized with time step k and, following the ideas of [2], one can formulate the weak problem as a fixed-point iteration problem.

Given \(\tilde{\gamma }^n\), find \(\tilde{p}^{n + 1}\) y \(\tilde{\gamma }^{n + 1}\) such that:

$$ \left\{ {\begin{array}{*{20}c} {k \smallint \limits_{\Omega } \tilde{h}^3 \nabla \tilde{p}^{n + 1} \cdot \nabla \varphi + \smallint \limits_{\Omega } \tilde{h}\tilde{\gamma }^{n + 1} \varphi = \smallint \limits_{\Omega } \left( {\left( {\tilde{h}\tilde{\gamma }^n } \right) \circ X^k } \right)\varphi \forall \varphi \in K_0 } \\ {\tilde{\gamma }^{{\text{n}} + 1} \in H\left( {{\tilde{\text{p}}}^{n + 1} } \right)} \\ \end{array} } \right. $$
(4)

If this iteration converges it will converge to the solution of the weak problem, \(\left( {\tilde{p}, \tilde{\gamma }} \right)\).

2.2 Bermúdez-Moreno Algorithm

This algorithm introduces the variable \(\beta^{n + 1} = \gamma^{n + 1} - \omega p^{n + 1}\) in the problem and applies certain transformations to convert the problem into one with univalued operators. The goal is to apply the Yosida regularization, \(H_\lambda^\omega\) [5] and use the property that if one employs suitable ω and λ, then

$$ \beta \in \left( {H - \omega I} \right)\left( {\text{p}} \right) \Leftrightarrow {\upbeta } = H_\lambda^\omega \left( {p + \lambda \beta } \right) $$
(5)

The advantage of \(H_\lambda^\omega\) is that it is univalued. This means that it is possible to find \(\beta^{n + 1}\) as the solution of the fixed-point problem \(\beta^{n + 1} = H_\lambda^\omega \left( {p^{n + 1} + \lambda \beta^{n + 1} } \right)\). Thus, we must introduce a second fixed-point iteration, in j, where the problem to be solved is:

Given \(\beta_j^{n + 1}\), find \(\tilde{p}_j^{n + 1}\) y \(\beta_{j + 1}^{n + 1}\) such that:

$$ \left\{ {\begin{array}{*{20}c} {k\mathop \smallint \limits_{\Omega }^{\,} \tilde{h}^3 \nabla \tilde{p}_j^{n + 1} \cdot \nabla \varphi + \omega \mathop \smallint \limits_{\Omega }^{\,} \tilde{h}\tilde{p}_j^{n + 1} \varphi = \smallint \limits_{\Omega } \left( {\left( {\tilde{h}\tilde{\gamma }^n } \right) \circ X^k } \right)\varphi - \mathop \smallint \limits_{\Omega }^{\,} \tilde{h}\beta_j^{n + 1} \varphi \forall \varphi \in K_0 } \\ {\beta_j^{n + 1} = H_\lambda^\omega \left( {\tilde{p}_j^{n + 1} + \lambda \beta_j^{n + 1} } \right)} \\ \end{array} } \right. $$
(6)

We now have a double fixed-point iteration. Within each iteration in n, in order to obtain the solutions \( (\tilde{p}^{n + 1} ,\;\tilde{\gamma }^{n + 1} ),\) the convergence of the Bermudez-Moreno iterations must be reached in j, which provides new values \(\tilde{p}^{n + 1}\) and \(\beta^{n + 1}\) which will be used to update the value of \(\tilde{\gamma }^{n + 1}\).

Upon reaching convergence of the iterations in n, the values of \(\tilde{p}\) and \(\tilde{\gamma }\) obtained are the solution of the weak problem (4). This convergence is guaranteed by [6] provided that the chosen method parameters satisfy λ·ω = 0.5. A spatial discretization based on the finite element method (FEM) is employed to solve this problem.

2.3 Mass Conservation

The equations of the lubrication problem guarantee that the fluid mass in the domain must be conserved upon convergence of the iterative method. The use of the FEM guarantees the mass conservation if the integrals that appear in the weak formulation are calculated exactly. However, when applying the FEM, the presence of \(X^k\) in the terms implies that some integrals are not computed exactly when using the conventional approach, which results in an error in mass conservation.

One option to keep the mass error small is to use a large number of quadrature points to find a good approximation [7], and another option to achieve an accurate machine error calculation in these terms, is to use mesh intersection methods such as the supermesh technique [8]. In this work, both approaches have been employed to compare their results. The construction of the supermesh is performed with a local approach according to the algorithm explained in [8].

3 Results

3.1 Model Validation

The numerical model should provide solutions similar to the analytical ones in the cases where these are valid. In addition, the parameter values obtained with the numerical model in the area where L ≈ D, must present a coherent and smooth evolution in relation to those predicted by the analytical solutions in their area of application.

To verify this behaviour, a study of the evolution of the Sommerfeld number as a function of L/D is carried out. The results in Fig. 2 show the expected evolution.

Fig. 2.
figure 2

Source: own elaboration.

Evolution of Sommerfeld number as a function of bearing axial length. Comparison with analytical solutions.

Full size image

3.2 Convergence Study

It is known that the convergence speed of the Bermudez-Moreno algorithm depends largely on the choice of the parameter ω [5]. A study, particularized to the lubrication problem, of the optimal value of ω, i.e., the one that provides the minimum number of iterations until convergence, has been carried out, checking the influence on this optimal value of the rest of the input parameters of the model.

The total number of iterations of the Bermudez-Moreno algorithm, at index j, is analysed for 80 iterations in n, after verifying that for this number of iterations in n the process can be considered to have reached convergence. The influence of physical and numerical parameters of the model on the value of the optimal ω is analysed.

The results show a dependence of the optimal ω as a function of other parameters of the model. Some input variables, such as the mesh size, keep the optimum at a practically constant value, but others make the optimum value of ω vary significantly.

3.3 Mass Conservation Study

In the problem, the lubricant mass in the domain must remain constant at the steady state, i.e., when \(n \to \infty\). Mass errors appear only for numerical reasons. A study of the mass error is carried out varying the iterative method tolerance and the integration technique for integrals where \(X^k\) is present.

The graphs in Fig. 3 show the results. As expected, the accuracy improves as the stopping tolerance of the iterative method is reduced. It is also found that the use of the supermesh technique can achieve results up to 5 orders of magnitude more accurate when combined with a small tolerance. This study also shows that in certain cases the supermesh achieves lower computational cost than the conventional approach.

Fig. 3.
figure 3

Source: own elaboration.

Flow errors for different stopping tolerances using conventional \(L^2\) projection and Supermesh technique for the calculation of terms composed with \(X^k\).

Full size image

4 Conclusions

This work starts with the Elrod-Adams model for hydrodynamic bearings. The model leads to a free boundary problem as the limits of the zones with and without cavitation are not known. To deal with it, the variable γ is introduced.

In the associated weak problem, a nonlinear relationship between the unknowns of the problem appears through a multivalued operator. To solve the problem, the method of characteristics and the iterative algorithm of Bermudez-Moreno [5] are introduced, obtaining a double fixed-point iteration that is solved using the finite element method for spatial discretization.

The proposed algorithm has been implemented in the C programming language to perform the simulations. In addition, the functions of the supermesh technique have been incorporated in order to calculate exactly certain integrals that appear when applying the method of the characteristics.

A study was executed comparing the numerical solutions with the analytical solutions in the cases where these are accepted, which allowed the model to be validated.

Finally, we have conducted a study of the performance of the algorithm and of the mass error. In this aspect, although the use of the supermesh technique considerably improves the mass conservation accuracy, the truncation error inherent to the Bermudez-Moreno method makes it difficult to achieve a mass error at the machine error level, as it is the case when applying this technique to pure convection problems [8].