Abstract
This paper introduces a uniform substitution calculus for \({\textsf {d{}L}} {}_{\text {CHP}}\), the dynamic logic of communicating hybrid programs. Uniform substitution enables parsimonious prover kernels by using axioms instead of axiom schemata. Instantiations can be recovered from a single proof rule responsible for soundness-critical instantiation checks rather than being spread across axiom schemata in side conditions. Even though communication and parallelism reasoning are notorious for necessitating subtle soundness-critical side conditions, uniform substitution when generalized to \({\textsf {d{}L}} {}_{\text {CHP}}\) manages to limit and isolate their conceptual overhead. Since uniform substitution has proven to simplify the implementation of hybrid systems provers substantially, uniform substitution for \({\textsf {d{}L}} {}_{\text {CHP}}\) paves the way for a parsimonious implementation of theorem provers for hybrid systems with communication and parallelism.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Hybrid systems and parallel systems are notoriously subtle to analyze. Combining both not only culminates these subtleties but is further complicated because parallel hybrid systems are interlocked by synchronization in a shared global time. The dynamic logic of communicating hybrid programs \({\textsf {d{}L}} {}_{\text {CHP}}\) [6] tames the complexity of parallel hybrid systems providing a compositional proof calculus that disentangles reasoning into purely discrete, continuous, and communication pieces. However, the calculus is subject to schematic side conditions whose implementation is generally error-prone causing large soundness-critical code bases [30]. In particular, compositional reasoning about parallelism as in the idealized proof rule in Fig. 1 holds the challenge to exhaustively characterize all side conditions required to make all instances of this proof rule sound. Proof systems for discrete parallelism [1, 19, 27, 35, 44, 46] already have complicated side conditions, but complexity only increases with continuous interactions in shared global time.
In order to compositionally support compositional reasoning for parallel hybrid systems, this paper generalizes Church’s uniform substitution [8] and develops a uniform substitution calculus [30,31,32] for \({\textsf {d{}L}} {}_{\text {CHP}}\). Uniform substitution modularizes the calculus itself enabling its parsimonious implementation. Although applicable to discrete parallelism, the \({\textsf {d{}L}} {}_{\text {CHP}}\) development resolves the inherent challenge that parallel hybrid systems always synchronize in time.
Uniform substitution adopts a finite list of concrete formulas as axioms instead of an infinite set of formulas via axiom schemata with side conditions. This enables theorem provers without the extensive algorithmic checks otherwise required for each schema to sort out unsound instances. Thanks to the proof rule
 for uniform substitution, only sound instances derive from the axioms such that the parallel composition rule in \({\textsf {d{}L}} {}_{\text {CHP}}\) could be adopted almost literally as above, but with all the soundness-critical checking encapsulated solely in rule
for uniform substitution, only sound instances derive from the axioms such that the parallel composition rule in \({\textsf {d{}L}} {}_{\text {CHP}}\) could be adopted almost literally as above, but with all the soundness-critical checking encapsulated solely in rule
 . Thanks to
. Thanks to
 ’s checking, parallel systems reasoning even reduces to a single parallel injection axiom \([ \alpha ] \psi \rightarrow [ \alpha \parallel \beta ] \psi \) that merely describes the preservation of property \(\psi \) of one parallel component \(\alpha \) in the parallel system \(\alpha \parallel \beta \). Proofs about \(\alpha \parallel \beta \) reduce to a sequence of property embeddings with this axiom from local abstractions of the subcomponents, which combine soundly due to
’s checking, parallel systems reasoning even reduces to a single parallel injection axiom \([ \alpha ] \psi \rightarrow [ \alpha \parallel \beta ] \psi \) that merely describes the preservation of property \(\psi \) of one parallel component \(\alpha \) in the parallel system \(\alpha \parallel \beta \). Proofs about \(\alpha \parallel \beta \) reduce to a sequence of property embeddings with this axiom from local abstractions of the subcomponents, which combine soundly due to
 .
.
Soundness checks in uniform substitution are ultimately determined by the binding structures as identified in the static semantics. The development of uniform substitution for \({\textsf {d{}L}} {}_{\text {CHP}}\) is, therefore, grounded in the following key observation: Communication and parallelism both cause additional binding structure that needs attention in the substitution process performed by rule
 :
:
-
(B I)
Expressions depend on communication along (co)finite channel sets (besides finitely many free variables), which, by the core substitution principle [8], must not be introduced free into contexts where they are written.
-
(B II)
Subprograms in a parallel context need to be restricted in the variables and channels written as compositional proof rules for parallelism require local abstractions of subprograms not depending on the internals of the context [35].
Grounded in the need for abstraction (B II), \([ \alpha ] \psi \rightarrow [ \alpha \parallel \beta ] \psi \) can only be adopted as a sound axiom schema if \(\alpha \) and \(\beta \) do not share state, and if program \(\beta \) does not interfere with the contract \(\psi \), i.e., (i) \(\psi \) has no free variables bound by \(\beta \) (with exceptions), and (ii) \(\psi \) does not depend on communication channels written by \(\beta \) (except for channels joint with \(\alpha \)). This extensive side condition would need nontrivial soundness-critical implementations of \({\textsf {d{}L}} {}_{\text {CHP}}\) axiom schemata. Still, uniform substitution can be lifted with only small changes locally checking for clashes with written channels, and prohibited variables or channels.
The modularity of uniform substitution is the key to the parsimonious implementation [23] of the theorem prover KeYmaera X [11] for differential dynamic logic dL and differential game logic dGL [29], thus paving the way for a straightforward theorem prover implementation of \({\textsf {d{}L}} {}_{\text {CHP}}\). Since \({\textsf {d{}L}} {}_{\text {CHP}}\) conservatively generalizes dL [6], its uniform substitution calculus inherits the complete [33] axiomatic treatment of differential equation invariants [30]. All proofs are in [7].
2 Dynamic Logic of Communicating Hybrid Programs
This section briefly recaps \({\textsf {d{}L}} {}_{\text {CHP}}\) [6], the dynamic logic of communicating hybrid programs (CHPs). It combines hybrid programs [28] with CSP-style communication and parallelism [15]. By assumption-commitment (ac) reasoning [22, 46, 47], \({\textsf {d{}L}} {}_{\text {CHP}}\) allows compositional verification of parallelism in dL. For uniform substitution, function and predicate symbols, and program constants are added.
2.1 Syntax
The set of variables \(V= V_\mathbb {R}\cup V_\mathbb {N}\cup V_\mathcal {T}\) has real (\(V_\mathbb {R}\)), integer (\(V_\mathbb {N}\)), and trace (\(V_\mathcal {T}\)) variables. For each \(x \in V_\mathbb {R}\), the differential symbol \(x'\) is in \(V_\mathbb {R}\), too. The designated variable \(\mu \in V_\mathbb {R}\) represents the shared global time. The set of channel names is \(\varOmega \). By convention \(x, y \in V_\mathbb {R}\), \(n\in V_\mathbb {N}\), \(h\in V_\mathcal {T}\), \(\text {ch}{} \in \varOmega \), and \(z\in V\). Channel set \(Y\subseteq \varOmega \) is (co)finite. Vectorial expressions are denoted \(\bar{e}\). Moreover, \(f^{\mathbb {M}}\), \(g^{\mathbb {M}}\) are \(\mathbb {M}\)-valued function symbols and \(p, q, r\) are predicate symbols, where argument sorts are annotated by \(\_ : \mathbb {M}_1, \ldots , \mathbb {M}_k\). Finally, \(a, b\) are program constants.
Definition 1
(Terms). Terms consist of real \((\text {Trm}_{\mathbb {R}})\), integer \((\text {Trm}_{\mathbb {N}})\), channel \((\text {Trm}_{\varOmega })\), and trace \((\text {Trm}_{\mathcal {T}})\) terms, and are defined by the grammar below, where \(\theta , \theta _1, \theta _2 \in \mathbb {Q}[V_\mathbb {R}] \subset \text {Trm}_{\mathbb {R}}\) are polynomials in \(V_\mathbb {R}\):

Real terms are polynomials in \(V_\mathbb {R}\) enriched with function symbols \(f^\mathbb {R}(Y, \bar{e})\) (including constants \(c \in \mathbb {Q}\)) only depending on communication along channels \(Y\) and terms \(\bar{e}\), differential terms \((\theta )'\), and \(\texttt{val}({te})\) and \(\texttt{time}({te})\), which access the value and the timestamp of the last communication in \({te}\), respectively. By convention, \(\theta \in \mathbb {Q}[V_\mathbb {R}]\) denotes a pure polynomial in \(V_\mathbb {R}\) without \((\cdot )'\), \(\texttt{val}(\cdot )\), and \(\texttt{time}(\cdot )\) as they occur in programs. For simplicity, we do not define \(\mathbb {Q}[V_\mathbb {R}] \subset \text {Trm}_{\mathbb {R}}\) as a fifth term sort but use the convention that function symbols \(g^{\mathbb {R}}\) can only be replaced with \(\mathbb {Q}[V_\mathbb {R}]\)-terms. Integer terms are variables \(n\), function symbols \(f^{\mathbb {N}}(Y, \bar{e})\) (including constants 0, 1), addition, and length \(| {te} |\) of trace term \({te}\).Footnote 1 The function symbol \(f^{\varOmega }(Y, \bar{e})\) includes constants \(\text {ch}{} \in \varOmega \), and \(\texttt{chan}({te})\) is channel access. Trace terms record the communication history of programs. They encompass variables \(h\), function symbols \(f^{\mathcal {T}}(Y, \bar{e})\) (including the empty trace \(\epsilon \)), communication items \(\langle \text {ch}{}, \theta _1, \theta _2 \rangle \) with value \(\theta _1\) and timestamp \(\theta _2\), projection \({te}\mathbin {\downarrow }Y\) onto channels \(Y\), and access \({te} {[} {ie} {]}\) of the \({ie}\)-th item in \({te}\). Where useful, \(\texttt{op}(\bar{e})\) denotes built-in function symbols of fixed interpretation, e.g., \(\boldsymbol{\cdot }+ \boldsymbol{\cdot }\).
\(\textsf {d{}L}_{\text {CHP}}\)’s context-sensitive program and formula syntax presumes notions of free and bound variables (Sect. 2.3) defined on the context-free syntax:
Definition 2
(Programs). Communicating hybrid programs are defined by the following grammar, where \(\theta \in \mathbb {Q}[V_\mathbb {R}]\) is a polynomial in \(V_\mathbb {R}\) and \(\chi \in \text {FOL}_{\mathbb {R}}\) is a formula of first-order real-arithmetic. In \(\alpha \parallel \beta \), the subprograms must not share state but can share time and history, i.e., \(\mathop {\mathsf {B\! V}}(\alpha ) \cap \mathop {\mathsf {B\! V}}(\beta ) \subseteq \{\mu ,\mu '\} \cup V_\mathcal {T}\).Footnote 2

The program constant
 restricts the written channels to \(Y\subseteq \varOmega \) and the bound variables to \(\bar{z}\subseteq V_\mathbb {R}\cup V_\mathcal {T}\), where \(Y\) and \(\bar{z}\) are (co)finite. Instead of
restricts the written channels to \(Y\subseteq \varOmega \) and the bound variables to \(\bar{z}\subseteq V_\mathbb {R}\cup V_\mathcal {T}\), where \(Y\) and \(\bar{z}\) are (co)finite. Instead of
 , write \(a\) if \(Y\) and \(\bar{z}\) can be arbitrary. Assignment \(x \mathrel {{:}{=}}\theta \) updates x to \(\theta \), nondeterministic assignment \(x \mathrel {{:}{=}}*\) assigns an arbitrary real value to x, and the test
, write \(a\) if \(Y\) and \(\bar{z}\) can be arbitrary. Assignment \(x \mathrel {{:}{=}}\theta \) updates x to \(\theta \), nondeterministic assignment \(x \mathrel {{:}{=}}*\) assigns an arbitrary real value to x, and the test
 does nothing if \(\chi \) holds and aborts the computation otherwise. The continuous evolution
does nothing if \(\chi \) holds and aborts the computation otherwise. The continuous evolution
 follows the ODE \(x' = \theta \) for any duration as long as formula \(\chi \) is not violated. The global time \(\mu \) evolves with every continuous evolution according to ODE \(\mu ' = 1\). Sequential composition \(\alpha ;\beta \) executes \(\beta \) after \(\alpha \), choice \(\alpha \cup \beta \) executes \(\alpha \) or \(\beta \) nondeterministically, \(\alpha ^*\) repeats \(\alpha \) zero or more times,
follows the ODE \(x' = \theta \) for any duration as long as formula \(\chi \) is not violated. The global time \(\mu \) evolves with every continuous evolution according to ODE \(\mu ' = 1\). Sequential composition \(\alpha ;\beta \) executes \(\beta \) after \(\alpha \), choice \(\alpha \cup \beta \) executes \(\alpha \) or \(\beta \) nondeterministically, \(\alpha ^*\) repeats \(\alpha \) zero or more times,
 sends \(\theta \) along channel \(\text {ch}{}\), and
sends \(\theta \) along channel \(\text {ch}{}\), and
 receives a value into variable x along channel \(\text {ch}{}\). The trace variable \(h\) records communication. Finally, \(\alpha \parallel \beta \) executes \(\alpha \) and \(\beta \) in parallel synchronized in global time \(\mu \).
receives a value into variable x along channel \(\text {ch}{}\). The trace variable \(h\) records communication. Finally, \(\alpha \parallel \beta \) executes \(\alpha \) and \(\beta \) in parallel synchronized in global time \(\mu \).
Example 3
The program \(\texttt {ct}^*\parallel \texttt {ve}^*\) models a simplified cruise control [24]. The vehicle \(\texttt {ve}\) repeatedly receives a target velocity \(v^\text {tr}_{\texttt {ve}}\) from the controller \(\texttt {ct}\) along channel \(\text {tar}\). The target \(v^\text {tr}_{\texttt {ct}}\) sent by \(\texttt {ct}\) is in range \([0,V]\). Hence, \(\texttt {ve}\)’s velocity \(v_{\texttt {ve}}\) stays in range \([0, V]\) within the \(\epsilon > 0\) time units till the next communication if \(v_{\texttt {ve}} \in [0,V]\) held initially. The evolution
 allows passage of time in \(\texttt {ct}\).
allows passage of time in \(\texttt {ct}\).

Definition 4
(Formulas). Formulas are defined by the grammar below for relations \(\sim \), terms \(e_1, e_2 \in \text {Trm}\) of equal sort, and \(z\in V\). Moreover, the ac-formulas are unaffected by state change in \(\alpha \), i.e., \((\mathop {\mathsf {F\! V}}(\textsf{A}) \cup \mathop {\mathsf {F\! V}}(\textsf{C})) \cap \mathop {\mathsf {B\! V}}(\alpha ) \subseteq V_\mathcal {T}\).
The formulas combine first-order dynamic logic with ac-reasoning. Predicate symbols \(p(Y, \bar{e})\) depend on channels \(Y\) and terms \(\bar{e}\). The ac-box \([ \alpha ] _{\{\textsf{A}, \textsf{C}\}}\psi \) expresses that \(\textsf{C}\) holds after each communication event and \(\psi \) in the final state, for all runs of \(\alpha \) whose incoming communication satisfies \(\textsf{A}\). Other connectives \(\vee \), \(\rightarrow \), \(\leftrightarrow \) and quantifiers \(\exists z \, \varphi \equiv \lnot \forall z \, \lnot \varphi \) can be derived. The relations \(\sim \) include \(=\) for all term sorts, \(\ge \) on real and integer terms, and prefixing \(\preceq \) on trace terms.
By convention, the predicate symbol \(q_{\mathbb {R}}\) can only be replaced with formulas of first-order real arithmetic. It serves as placeholder for tests \(\chi \) in CHPs.
Example 5
The cruise control from Example 3 is safe if its velocity stays in range \([0, V]\). This can be expressed with the formula \({\varphi }\rightarrow [ \texttt {ct}^*\parallel \texttt {ve}^*] {\psi _\text {safe}}\), where \({\psi _\text {safe}}\equiv 0 \le v_{\texttt {ve}} \le V\) and \({\varphi }\equiv {\psi _\text {safe}}\wedge \epsilon> 0 \wedge V> 0\).
2.2 Semantics
A trace \(\tau = (\tau _1, ..., \tau _k)\) is a finite chronological sequence of communication events \(\tau _i = \langle \text {ch}{}_i, d_i, s_i \rangle \), where \(\text {ch}{}_i \in \varOmega \), and \(d_i \in \mathbb {R}\) is the communicated value, and \(s_i \in \mathbb {R}\) is a timestamp such that \(s_i \le s_j\) for \(1 \le i < j \le k\). A recorded trace \(\tau = (\tau _1, ..., \tau _k)\) additionally carries a trace variable \(h_i \in V_\mathcal {T}\) with each event, i.e., \(\tau _i = \langle h_i, \text {ch}{}_i, d_i, s_i \rangle \). For variable \(z\in V_\mathbb {M}\) and \(\mathbb {M}\in \{\mathbb {R}, \mathbb {N}, \mathcal {T}\}\), let \(type(z) = \mathbb {M}\). A state \(v\) maps each \(z\in V\) to a value \(v(z) \in type(z)\). The sets of traces, recorded traces, and states are denoted \(\mathcal {T}\), \(\mathcal {T}_\text {rec}\), and \(\mathcal {S}\), respectively.
For \(d\in type(z)\), the state \(v _{z}^{d}\) is the modification of \(v\) at \(z\) to \(d\). For \(\tau \in \mathcal {T}_\text {rec}\), the trace \(\tau (h) \in \mathcal {T}\) is obtained from the subsequence of \(\tau \) carrying \(h\in V_\mathcal {T}\) by removing the carried variable. State-trace concatenation \(v \cdot \tau \in \mathcal {S}\) for \(\tau \in \mathcal {T}_\text {rec}\), appends \(\tau (h)\) to \(v\) at \(h\) for all \(h\in V_\mathcal {T}\). The projection \(\tau \mathbin {\downarrow }Y\) of (recorded) trace \(\tau \) is the subsequence of all communication events in \(\tau \) whose channel is in \(Y\subseteq \varOmega \). The state projection \(v \mathbin {\downarrow }Y\in \mathcal {S}\) modifies \(v\) at \(h\) to \(v(h) \mathbin {\downarrow }Y\) for all \(h\in V_\mathcal {T}\).
An interpretation \(I\) assigns a function
 to each function symbol \(f^{\mathbb {M}}\) that is smooth in all real-valued arguments if \(\mathbb {M}= \mathbb {R}\), and a relation
to each function symbol \(f^{\mathbb {M}}\) that is smooth in all real-valued arguments if \(\mathbb {M}= \mathbb {R}\), and a relation
 to each k-ary predicate symbol \(p\).
to each k-ary predicate symbol \(p\).
Definition 6
(Term Semantics). The valuation \(Iv [\![e ]\!] \in \mathbb {R}\cup \mathbb {N}\cup \varOmega \cup \mathcal {T}\) of term \(e\) in interpretation \(I\) and state \(v\) is defined as follows:
The projection \(\tilde{v} = v \mathbin {\downarrow }Y\) ensures that \(f(Y, \bar{e})\) only depends on \(Y\), i.e., the communication in \(v\) along channels \(Y^\complement \) does not matter. The differentials \((\theta )'\) have a semantics describing the local rate of change of \(\theta \) [30].
The denotational semantics of CHPs [6] combines \(\textsf {d{}L}\)’s Kripke semantics [30] with a linear history semantics [47] and a global notion of time. Denotations are subsets of \(\mathcal {D}= \mathcal {S}\times \mathcal {T}_\text {rec}\times {\mathcal {S}}_\bot \) with \({\mathcal {S}}_\bot = \mathcal {S}\cup \{\bot \}\). Final state \(\bot \) marks an unfinished computation, i.e., it still can be continued or was aborted due to a failing test. If (\({w}' = \bot \) and \(\tau '\preceq \tau \)), where \(\preceq \) is the prefix relation on traces, or \((\tau ', {w}') = (\tau , w)\), then \((\tau ', {w}')\) is a prefix of \((\tau , w)\) written \((\tau ', {w}')\preceq (\tau , w)\). Since (even empty) communication of unfinished computations is still observable, denotations \(D\subseteq \mathcal {D}\) of CHPs are prefix-closed and total, i.e., \((v, \tau , w)\in D\) and \((\tau ', {w}')\preceq (\tau , w)\) implies \((v, \tau ', {w}')\in D\), and \(\bot _\mathcal {D}\subseteq D\) with \(\bot _\mathcal {D}= \mathcal {S}\times \{\epsilon \} \times \{\bot \}\). Moreover, all \((v, \tau , w)\in D\) are chronological, i.e., \(v(\mu ) \le w(\mu )\) and when \(\tau = (\tau _1, \ldots , \tau _k) \ne \epsilon \) and let \(\tau _i(\mu ) = (\langle h_i, \text {ch}{}_i, d_i, s_i \rangle )(\mu ) = s_i\), then \(v(\mu ) \le \tau _1(\mu )\) and if \(w \ne \bot \), then \(\tau _k(\mu ) \le w(\mu )\). Note that \(\tau \) is chronological as all traces are.
The interpretation
 of a program constant
of a program constant
 is a prefix-closed and total set of chronological computations that (i) only communicate along (write) channels \(Y\) and (ii) only bind variables \(\bar{z}\). More precisely, for all
is a prefix-closed and total set of chronological computations that (i) only communicate along (write) channels \(Y\) and (ii) only bind variables \(\bar{z}\). More precisely, for all
 , we have (i) \(\tau \mathbin {\downarrow }Y^\complement = \epsilon \), and (ii) \(v = w\) on \(V_\mathcal {T}\) and \(w \cdot \tau = v\) on \(\bar{z}^\complement \). For \(D, M \subseteq \mathcal {D}\), we define \({D}_\bot = \{ (v, \tau , \bot ) \mid (v, \tau , w)\in D\}\), and \((v, \tau , w)\in D\mathbin {\triangleright }M\) if \((v, \tau _1, u) \in D\) and \((u, \tau _2, w) \in M\) exist with \(\tau = \tau _1 \cdot \tau _2\). For states \(w_\alpha , w_\beta \), the merged state \(w_\alpha \oplus w_\beta \) is \(\bot \) if one of the substates \(w_\alpha \) or \(w_\beta \) is \(\bot \). Otherwise, \(w_\alpha \oplus w_\beta = w_\alpha \) on \(\mathop {\mathsf {B\! V}}(\alpha )\) and \(w_\alpha \oplus w_\beta = w_\beta \) on \(\mathop {\mathsf {B\! V}}(\alpha )^\complement \) (or, equivalently by syntactic well-formedness, on \(\mathop {\mathsf {B\! V}}(\beta )^\complement \) and \(\mathop {\mathsf {B\! V}}(\beta )\), respectively). If \(Y\) is the set of all channel names occurring in \(\alpha \), we write \(\tau \mathbin {\downarrow }\alpha \) for \(\tau \mathbin {\downarrow }Y\).
, we have (i) \(\tau \mathbin {\downarrow }Y^\complement = \epsilon \), and (ii) \(v = w\) on \(V_\mathcal {T}\) and \(w \cdot \tau = v\) on \(\bar{z}^\complement \). For \(D, M \subseteq \mathcal {D}\), we define \({D}_\bot = \{ (v, \tau , \bot ) \mid (v, \tau , w)\in D\}\), and \((v, \tau , w)\in D\mathbin {\triangleright }M\) if \((v, \tau _1, u) \in D\) and \((u, \tau _2, w) \in M\) exist with \(\tau = \tau _1 \cdot \tau _2\). For states \(w_\alpha , w_\beta \), the merged state \(w_\alpha \oplus w_\beta \) is \(\bot \) if one of the substates \(w_\alpha \) or \(w_\beta \) is \(\bot \). Otherwise, \(w_\alpha \oplus w_\beta = w_\alpha \) on \(\mathop {\mathsf {B\! V}}(\alpha )\) and \(w_\alpha \oplus w_\beta = w_\beta \) on \(\mathop {\mathsf {B\! V}}(\alpha )^\complement \) (or, equivalently by syntactic well-formedness, on \(\mathop {\mathsf {B\! V}}(\beta )^\complement \) and \(\mathop {\mathsf {B\! V}}(\beta )\), respectively). If \(Y\) is the set of all channel names occurring in \(\alpha \), we write \(\tau \mathbin {\downarrow }\alpha \) for \(\tau \mathbin {\downarrow }Y\).
Definition 7
(Program semantics). Given an interpretation \(I\), the semantics \(I [\![\alpha ]\!] \subseteq \mathcal {D}\) of a CHP \(\alpha \) is defined as follows, where \(\bot _\mathcal {D}= \mathcal {S}\times \{\epsilon \} \times \{\bot \}\) and \(\vDash \) denotes the satisfaction relation (Definition 8):

The semantics is indeed constructed prefix-closed, total, and chronological. Communication \(\tau \) of \(\alpha _1 \parallel \alpha _2\) is implicitly characterized via its subsequences for the subprograms. By \(\tau = \tau \mathbin {\downarrow }(\alpha _1 \parallel \alpha _2)\), there is no non-causal communication. Joint communication and the whole computation are synchronized in global time by the projections and by \(w_{\alpha _1} = w_{\alpha _2}\) on \(\{ \mu , \mu ' \}\), respectively. Likewise, by projection, communication is synchronously recorded by trace variables.
Definition 8
(Formula semantics). The satisfaction \(Iv \vDash \phi \) of a \({\textsf {d{}L}} {}_{\text {CHP}}\) formula \(\phi \) in interpretation \(I\) and state \(v\) is inductively defined as follows:
-
1.
\(Iv \vDash e_1 {\sim } e_2\) if \(Iv [\![e_1 ]\!] \sim Iv [\![e_2 ]\!] {\quad \mathrm {where\, }\sim \mathrm {\, is\, any\, relation\, symbol}}\)
-
2.
\(Iv \vDash p(Y, e_1, \ldots , e_k)\) if \((I\tilde{v} [\![e_1 ]\!], \ldots , I\tilde{v} [\![e_k ]\!]) \in I(p) {\quad \mathrm {where\, }\tilde{v} = v \mathbin {\downarrow }Y}\)
-
3.
\(Iv \vDash \varphi \wedge \psi \) if \(Iv \vDash \varphi \) and \(Iv \vDash \psi \)
-
4.
\(Iv \vDash \lnot \varphi \) if \(Iv \nvDash \varphi \), i.e., it is not the case that \(Iv \vDash \varphi \)
-
5.
\(Iv \vDash \forall z \, \varphi \) if \(Iv _{z}^{d} \vDash \varphi \) for all \(d \in type(z)\)
-
6.
\(Iv \vDash [ \alpha ] \psi \) if \(Iw \cdot \tau \vDash \psi \) for all \((v, \tau , w)\in I [\![\alpha ]\!]\) with \(w \ne \bot \)
-
7.
\(Iv \vDash [ \alpha ] _{\{\textsf{A}, \textsf{C}\}}\psi \) if for all \((v, \tau , w)\in I [\![\alpha ]\!]\) the following conditions hold:
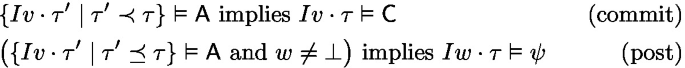
Where \(U \vDash \varphi \) for a set of interpretation-state pairs U and any formula \(\varphi \) if \(Iv \vDash \varphi \) for all \(Iv \in U\). In particular, \(\emptyset \vDash \varphi \).
In item 6 and 7, reachable worlds are built from states \(v\) and \(w\), and communication \(\tau \), as change of state and communication are observable. The strict prefix \(\prec \) for the assumption in case (commit) in item 6 excludes (when \(\textsf{A}\equiv \textsf{C}\)) the circularity that commitment \(\textsf{C}\) can be shown in states where it is assumed.
2.3 Static Semantics
In the uniform substitution process, checks of free and bound variables, as well as accessed and written channels, separate sound from unsound axiom instantiations. As parallelism requires fine-grained control over channels, the static semantics for dL [30] is lifted to a communication-aware static semantics for \({\textsf {d{}L}} {}_{\text {CHP}}\). It uses accessed channels to characterize the subsequence of a communication trace influencing truth of a formula even more precisely than free variables.
To precisely grasp free and bound variables, and accessed and written channels, Definition 9 gives a semantic characterization. In this section, formulas are considered truth-valued, i.e., \(Iv [\![\phi ]\!] = \textbf{tt}\) if \(Iv \vDash \phi \) and \(Iv [\![\phi ]\!] = \textbf{ff}\) if \(Iv \nvDash \phi \).
Definition 9
(Static semantics). For term or formula \(e\), and program \(\alpha \), free variables \(\mathop {\mathsf {F\! V}}(e)\) and \(\mathop {\mathsf {F\! V}}(\alpha )\), bound variables \(\mathop {\mathsf {B\! V}}(\alpha )\), accessed channels \(\mathop {\mathsf {C\! N}}(e)\), and written channels \(\mathop {\mathsf {C\! N}}(\alpha )\) form the static semantics.

The already subtle static semantics of hybrid systems [30] becomes even more subtle with communication and parallelism. For example, CHPs (silently) synchronize with the global time \(\mu \), which is free and bound in ODEs, and the differential \(\mu '\) is bound, i.e.,
 and
and
 if the evolution has a run of non-zero duration, regardless of whether \(\mu \) occurs in x. Since reachable worlds of CHPs consist of communication and state, bound variables \(\mathop {\mathsf {B\! V}}(\alpha )\) of program \(\alpha \) compare \(v\) with the state-trace concatenation \(w \cdot \tau \) instead of missing \(\tau \). Consequently,
if the evolution has a run of non-zero duration, regardless of whether \(\mu \) occurs in x. Since reachable worlds of CHPs consist of communication and state, bound variables \(\mathop {\mathsf {B\! V}}(\alpha )\) of program \(\alpha \) compare \(v\) with the state-trace concatenation \(w \cdot \tau \) instead of missing \(\tau \). Consequently,
 , which also reflects that the initial communication never gets lost.
, which also reflects that the initial communication never gets lost.
Lemma 10
(Bound effect property). The sets \(\mathop {\mathsf {B\! V}}(\alpha )\) and \(\mathop {\mathsf {C\! N}}(\alpha )\) are the smallest sets with the bound effect property for program \(\alpha \). That is, \(v = w\) on \(V_\mathcal {T}\) and \(v = w \cdot \tau \) on \(\mathop {\mathsf {B\! V}}(\alpha )^\complement \) if \(w \ne \bot \), and \(\tau \mathbin {\downarrow }\mathop {\mathsf {C\! N}}(\alpha )^\complement = \epsilon \) for all \((v, \tau , w)\in I [\![\alpha ]\!]\).
By the following communication-aware coincidence property, terms and formulas only depend on their free variables, which for trace variables can be further refined to the subtraces whose channels are accessed. This subtrace-level precision is crucial in the soundness proof of the parallel injection axiom as it allows to drop \(\beta \) from \([ \alpha \parallel \beta ] \psi \) only if \(\beta \) does not write channels of \(\psi \) that are not also written by \(\alpha \). The signature \(\varSigma (\cdot )\) of an expression denotes all occurring symbols.
Lemma 11
(Coincidence for terms and formulas). The sets \(\mathop {\mathsf {F\! V}}(e)\) and \(\mathop {\mathsf {C\! N}}(e)\) are the smallest sets with the communication-aware coincidence property for term or formula \(e\). That is, if \(v \mathbin {\downarrow }\mathop {\mathsf {C\! N}}(e) = \tilde{v} \mathbin {\downarrow }\mathop {\mathsf {C\! N}}(e)\) on \(\mathop {\mathsf {F\! V}}(e)\) and \(I= J\) on \(\varSigma (e)\), then \(Iv [\![e ]\!] = J\tilde{v} [\![e ]\!]\). In particular, for formula \(\phi \): \(Iv \vDash \phi \) iff \(J\tilde{v} \vDash \phi \).
Programs communicate but do not depend on the recorded history, thus the coincidence property for programs is not communication-aware. However, programs can produce the same communication starting from coinciding states.
Lemma 12
(Coincidence for programs). The set \(\mathop {\mathsf {F\! V}}(\alpha )\) is the smallest set with the coincidence property for program \(\alpha \). That is, if \(v = \tilde{v}\) on \(X\supseteq \mathop {\mathsf {F\! V}}(\alpha )\), and \(I= J\) on \(\varSigma (\alpha )\), and \((v, \tau , w)\in I [\![\alpha ]\!]\), then \((\tilde{v}, \tilde{\tau }, \tilde{w})\in J [\![\alpha ]\!]\) exists such that \(w = \tilde{w}\) on \(X\), and \(\tau = \tilde{\tau }\), and (\(w = \bot \) iff \(\tilde{w} = \bot \)).
3 Uniform Substitution for \({\textsf {d{}L}} {}_{\text {CHP}}\)
In \({\textsf {d{}L}} {}_{\text {CHP}}\), a uniform substitution [30] \(\sigma \) maps function and predicate symbols to terms (of equal sort) and formulas, respectively, while substituting the arguments of the symbol for their placeholders in the replacement, and program constants are mapped to CHPs. For example,
 replaces all occurrences of function symbol \(f\) with \(\boldsymbol{\cdot }+ 1\) while the reserved 0-ary function symbol \(\boldsymbol{\cdot }\) marks the positions for the parameter of \(f\) in the replacement. Moreover, \(\sigma \) replaces the program constant \(a\) with the program
replaces all occurrences of function symbol \(f\) with \(\boldsymbol{\cdot }+ 1\) while the reserved 0-ary function symbol \(\boldsymbol{\cdot }\) marks the positions for the parameter of \(f\) in the replacement. Moreover, \(\sigma \) replaces the program constant \(a\) with the program
 .
.
The key to sound uniform substitution is that new free variables must not be introduced into a context where they are bound [8]. In the presence of communication, likewise, new channel access must not be introduced into contexts where the channel is written (B I). For parallelism, substitution must not reveal internals of the parallel context to the local abstraction of a subprogram (B II), and must not violate state disjointness. The one-pass approach [32] used for \({\textsf {d{}L}} {}_{\text {CHP}}\) postpones these checks and simply applies the substitution recursively while collecting written variables and channels as taboo set (Fig. 2), thus operates linearly in the input. Clashes between the taboo, and new free variables and channel access are only checked locally at the replacement site. Likewise, clashes between the permitted channels and variables of a program constant, and its replacement program are checked locally.
The substitution operator \(\sigma ^{{U, W}{}}_{{Z}{}}(\alpha )\) for program \(\alpha \) takes an input taboo \(U\subseteq V\cup \varOmega \) and a parallel context \(W\subseteq V\), and returns, if defined, the substitution result and a set of output taboos \(Z\subseteq V\cup \varOmega \). For terms and formulas, the substitution operator \(\sigma ^{{U}{}}\) only takes a taboo \(U\subseteq V\cup \varOmega \) as input. The substitution process clashes, i.e., prevents unsound instantiation, if it were to introduce a free variable or accessed channel into a context where it is bound (B I) or if it were to write variables and channels violating abstraction (B II). Moreover, substitution preserves well-formedness of programs and formulas, i.e., substitution clashes if replacements were to violate well-formedness.
The side condition \((\mathop {\mathsf {F\! V}}(\sigma f(\boldsymbol{\cdot })) \cup \mathop {\mathsf {C\! N}}(\sigma f(\boldsymbol{\cdot }))) \cap U= \emptyset \) implements locally that the replacement for \(f\) must not introduce free parameters that are tabooed by \(U\) (B I). The substitution \(\{ \boldsymbol{\cdot }\mapsto \sigma ^{{U}{}}(e \mathbin {\downarrow }Y) \}^\emptyset \) is responsible for the argument \(e\),Footnote 3 where \(\emptyset \) suffices as the taboo \(U\) is already checked on \(e\mathbin {\downarrow }Y\). By the projection, \(e\mathbin {\downarrow }Y\) only depends on channels \(Y\). Quantification \(\forall z \,\!\) taboos the bound variable \(z\). Program \(\alpha \) in a box or ac-box has an empty parallel context \(\emptyset \).
The substitution \(\sigma ^{{U, W}{}}_{{Z}{}}(\alpha )\) computes the output taboo \(Z\) by adding the written variables and channels of program \(\alpha \) to \(U\), e.g., real variable x for assignment \(x \mathrel {{:}{=}}\theta \) and for receiving
 additionally channel \(\text {ch}{}\) and trace variable \(h\). The output taboo \(Z\) is passed to ac-formulas and postconditions of boxes and ac-boxes for recursive checks for clashes w.r.t. (B I). Crucially for soundness, Lemma 13 below proves that \(\sigma ^{{U, W}{}}_{{Z}{}}(\cdot )\) correctly computes the output taboo \(Z\).
additionally channel \(\text {ch}{}\) and trace variable \(h\). The output taboo \(Z\) is passed to ac-formulas and postconditions of boxes and ac-boxes for recursive checks for clashes w.r.t. (B I). Crucially for soundness, Lemma 13 below proves that \(\sigma ^{{U, W}{}}_{{Z}{}}(\cdot )\) correctly computes the output taboo \(Z\).
The taboo \(U\cup W\) passed to nested expressions contains the parallel context \(W\) to prevent free variables in replacements of function and predicate symbols that are bound in parallel. This prepares the substitution process to preserve the syntax restrictions for parallel composition from previous work [6].Footnote 4 Substitution for evolution
 considers that the global time \(\mu , \mu '\) is always implicitly bound regardless of whether it occurs in \(x, x'\). The fixpoint notation \(\sigma ^{Z, W}_{Z}{(\alpha )}\) for the replacement of repetition \(\alpha ^*\) ensures that the output taboo of the first iteration is tabooed in the subsequent iterations [32]. Computing the parallel context of \(\alpha \) and \(\beta \) in case \(\alpha \parallel \beta \) requires one additional pass for both subprograms because what they potentially bind after substitution adds to the parallel context of the respective other subprogram.
considers that the global time \(\mu , \mu '\) is always implicitly bound regardless of whether it occurs in \(x, x'\). The fixpoint notation \(\sigma ^{Z, W}_{Z}{(\alpha )}\) for the replacement of repetition \(\alpha ^*\) ensures that the output taboo of the first iteration is tabooed in the subsequent iterations [32]. Computing the parallel context of \(\alpha \) and \(\beta \) in case \(\alpha \parallel \beta \) requires one additional pass for both subprograms because what they potentially bind after substitution adds to the parallel context of the respective other subprogram.
Lemma 13
(Correct output taboo). Application \(\sigma ^{{U, W}{}}_{{Z}{}}(\alpha )\) of uniform substitution retains input taboo \(U\) and correctly adds the bound variables and written channels of program \(\alpha \), i.e., \(Z\supseteq U\cup \mathop {\mathsf {B\! V}}(\sigma ^{{U, W}{}}_{{Z}{}}(\alpha )) \cup \mathop {\mathsf {C\! N}}(\sigma ^{{U, W}{}}_{{Z}{}}(\alpha ))\).
The side condition of
 maintains local abstraction of subprograms (B II) because the replacement cannot bind more than
maintains local abstraction of subprograms (B II) because the replacement cannot bind more than
 , thus cannot bind variables and channels of an abstraction that is independent of
, thus cannot bind variables and channels of an abstraction that is independent of
 . This also preserves state-disjointness (well-formedness) of parallel programs.
. This also preserves state-disjointness (well-formedness) of parallel programs.
3.1 Semantic Effect of Uniform Substitution
The key ingredients for proving soundness of uniform substitution are Lemma 16 and 17 below. They prove that the effect of the syntactic transformation applied by uniform substitution can be equally mimicked by semantically modifying the interpretation of function and predicate symbols, and program constants. This adjoint interpretation \({\sigma _{w}^* I}\) for interpretation \(I\) and state \(w\) changes how symbols are interpreted according to their syntactic replacements in the substitution \(\sigma \).
Definition 14
(Adjoint substitution). For interpretation \(I\) and state \(w\), the adjoint interpretation \({\sigma _{w}^* I}\) changes the meaning of function and predicate symbols, and program constants according to the substitution \(\sigma \) evaluated in state \(w\):

We follow the observation for dGL [32] that the more liberal one-pass substitution requires stronger coincidence between the substitution and the adjoint on neighborhoods of the original state. Where the dGL soundness proof has succeeded by a neighborhood semantics of state on taboos, the \({\textsf {d{}L}} {}_{\text {CHP}}\) proof succeeds with a generalization to a neighborhood semantics of state and communication on taboos. The neighborhood of a state consists of its variations:
Definition 15
(Variation). For a set \(U\subseteq V\cup \varOmega \), a state \(v\) is a \(U\)-variation of state \(w\) if \(v\) and \(w\) only differ on variables or projections onto channels in \(U\), i.e., \(v \mathbin {\downarrow }(U^\complement \cap \varOmega ) = w\mathbin {\downarrow }(U^\complement \cap \varOmega )\) on \(U^\complement \cap V\).
The proofs of Lemma 16 and 17 follow a lexicographic induction on the structure of substitution, and term, formula, or program. In Lemma 17, the induction is mutual for formulas and programs.
Lemma 16
(Semantic uniform substitution). The term \(e\) evaluates equally over \(U\)-variations under uniform substitution \(\sigma ^{{U}{}}\) and adjoint interpretation \({\sigma _{w}^* I}\), i.e., \(Iv [\![\sigma ^{{U}{}}(e) ]\!] = {\sigma _{w}^* I{v}} [\![e ]\!]\) for all \(U\)-variations \(v\) of \(w\).
Lemma 17
(Semantic uniform substitution). The formula \(\phi \) and the program \(\alpha \) have equal truth value and semantics, respectively, over \(U\)-variations under uniform substitution \(\sigma ^{{U}{}}\) and adjoint interpretation \({\sigma _{w}^* I}\), i.e.,
-
1.
for all \(U\)-variations \(v\) of \(w\): \(Iv \vDash \sigma ^{{U}{}}(\phi )\) iff \({\sigma _{w}^* I{v}} \vDash \phi \)
-
2.
for all \((U\cup W)\)-variations \(v\) of \(w\): \((v, \tau , o)\in I [\![\sigma ^{{U, W}{}}_{{Z}{}}(\alpha ) ]\!]\) iff \((v, \tau , o)\in {\sigma _{w}^* I} [\![\alpha ]\!]\)
3.2 Uniform Substitution Proof Rule
The proof rule
 for uniform substitution is the single point of truth for the sound instantiation of axioms (plus renaming of bound variables [30] and written channels, e.g., \([x \mathrel {{:}{=}}\theta ] \psi (x)\) to \([y \mathrel {{:}{=}}\theta ] \psi (y)\) and
for uniform substitution is the single point of truth for the sound instantiation of axioms (plus renaming of bound variables [30] and written channels, e.g., \([x \mathrel {{:}{=}}\theta ] \psi (x)\) to \([y \mathrel {{:}{=}}\theta ] \psi (y)\) and
 to
to
 . Soundness of the rule, i.e., that validity of its premise implies validity of the conclusion, immediately follows from Lemma 17. Since the substitution process starts with no taboos, \(\sigma (\phi )\) is short for \(\sigma ^{\emptyset }({\phi })\). If the substitution clashes, i.e., \(\sigma ^{\emptyset }({\phi })\) is not defined, then rule
. Soundness of the rule, i.e., that validity of its premise implies validity of the conclusion, immediately follows from Lemma 17. Since the substitution process starts with no taboos, \(\sigma (\phi )\) is short for \(\sigma ^{\emptyset }({\phi })\). If the substitution clashes, i.e., \(\sigma ^{\emptyset }({\phi })\) is not defined, then rule
 is not applicable.
is not applicable.
Theorem 18
(
 is sound). The proof rule
is sound). The proof rule
 is sound.
is sound.

Unlike dL [30] and dGL [32], \({\textsf {d{}L}} {}_{\text {CHP}}\) has a context-sensitive syntax for programs and formulas (see Definition 2 and Definition 4). By Proposition 19, uniform substitution, however, preserves syntactic well-formedness. Since all axioms in Sect. 4 will be well-formed, only well-formed formulas can be derived in \({\textsf {d{}L}} {}_{\text {CHP}}\).
Proposition 19
(
 preserves well-formedness). The result \(\sigma ^{{U}{}}(\phi )\) (if defined) of applying uniform substitution to a well-formed formula \(\phi \) is well-formed.
preserves well-formedness). The result \(\sigma ^{{U}{}}(\phi )\) (if defined) of applying uniform substitution to a well-formed formula \(\phi \) is well-formed.
4 Axiomatic Proof Calculus
Figure 3 presents a sound proof calculus for \({\textsf {d{}L}} {}_{\text {CHP}}\). The significant difference to \(\textsf {d{}L}_{\text {CHP}}\)’s schematic calculus [6] is that it completely abandons soundness-critical side conditions, internalizing them syntactically in the axioms. Only axiom
 was adjusted to obtain a symbolic representation and an ac-version
was adjusted to obtain a symbolic representation and an ac-version
 of modal modus ponens is included. Now, distribution of ac-boxes over conjuncts
of modal modus ponens is included. Now, distribution of ac-boxes over conjuncts
 and ac-monotonicity
and ac-monotonicity
 derive from
derive from
 , thus are dropped. Except for the small changes soundness is inherited from the schematic axioms [6].
, thus are dropped. Except for the small changes soundness is inherited from the schematic axioms [6].
Algebraic laws for reasoning about traces [6] can be easily adapted to uniform substitution as well [7]. Decidable first-order real arithmetic [41] and Presburger arithmetic [34] have corresponding oracle proof rules [6].
Remark 20
To obtain a truly finite list of axioms from Fig. 3, symbolic (co)finite sets can be finitely axiomatized as a boolean algebra together with extensionality, which can be unrolled to a finite disjunction for (co)finite sets [7].
Parallel Composition. The parallel injection axiom
 in Fig. 3 decomposes parallel CHPs by local abstraction (B II). Unlike \(\textsf {d{}L}_{\text {CHP}}\)’s [6] and Hoare-style [46, 47] schematic calculi for ac-reasoning, axiom
in Fig. 3 decomposes parallel CHPs by local abstraction (B II). Unlike \(\textsf {d{}L}_{\text {CHP}}\)’s [6] and Hoare-style [46, 47] schematic calculi for ac-reasoning, axiom
 internalizes the noninterference property [6, Def. 7] that determines valid instances of formula
internalizes the noninterference property [6, Def. 7] that determines valid instances of formula
purely syntactically. To focus on noninterference,
 abbreviates well-formed parallel composition
abbreviates well-formed parallel composition
 using operator \(\parallel _\text {wf}\) for program constants
using operator \(\parallel _\text {wf}\) for program constants
 ,
,
 . This notation ensures disjoint parallel state except for the global time \(\mu , \mu '\) and recorder variables \(V_\mathcal {T}\).
. This notation ensures disjoint parallel state except for the global time \(\mu , \mu '\) and recorder variables \(V_\mathcal {T}\).
Intuitively, axiom
 restricts \(\beta \) in Eq. (1) such that \(\alpha \) overapproximates the behavior of \(\alpha \parallel \beta \) influencing \(\textsf{A}\), \(\textsf{C}\), or \(\psi \). For this purpose, noninterference internalized in
restricts \(\beta \) in Eq. (1) such that \(\alpha \) overapproximates the behavior of \(\alpha \parallel \beta \) influencing \(\textsf{A}\), \(\textsf{C}\), or \(\psi \). For this purpose, noninterference internalized in
 forbids \(b\) to bind variables \(\bar{z}\) that are free in the postcondition \(p(Y, \bar{z})\), and \(Y^\complement \) forbids \(b\) to bind channels \(Y\) (except for channels \(Y_a\) written by \(a\) because joint parallel communication can already be observed from \(a\), too). Moreover, parallel programs always agree on the global time \(\mu , \mu '\) and the communication recorded by trace variables \(V_\mathcal {T}\). Therefore, the operator \(\parallel _\text {wf}\) explicitly allows their sharing even if \(\bar{z}^\complement \) disallows it. Note that \(Y_a\) and \(Y\), and \(\bar{z}_a\) and \(\bar{z}\) may overlap but can also be disjoint.
forbids \(b\) to bind variables \(\bar{z}\) that are free in the postcondition \(p(Y, \bar{z})\), and \(Y^\complement \) forbids \(b\) to bind channels \(Y\) (except for channels \(Y_a\) written by \(a\) because joint parallel communication can already be observed from \(a\), too). Moreover, parallel programs always agree on the global time \(\mu , \mu '\) and the communication recorded by trace variables \(V_\mathcal {T}\). Therefore, the operator \(\parallel _\text {wf}\) explicitly allows their sharing even if \(\bar{z}^\complement \) disallows it. Note that \(Y_a\) and \(Y\), and \(\bar{z}_a\) and \(\bar{z}\) may overlap but can also be disjoint.
Despite its asymmetric shape, axiom
 decomposes \([ \alpha {\parallel } \beta ] (\phi \wedge \psi )\) into \([ \alpha ] \phi \) and \([ \beta ] \psi \) (if they mutually do not interfere) via independent proofs for \([ \alpha {\parallel } \beta ] \phi \) and \([ \alpha {\parallel } \beta ] \psi \), which drop either \(\alpha \) or \(\beta \) by
decomposes \([ \alpha {\parallel } \beta ] (\phi \wedge \psi )\) into \([ \alpha ] \phi \) and \([ \beta ] \psi \) (if they mutually do not interfere) via independent proofs for \([ \alpha {\parallel } \beta ] \phi \) and \([ \alpha {\parallel } \beta ] \psi \), which drop either \(\alpha \) or \(\beta \) by
 modulo commutativity.
modulo commutativity.
Axiom System. For each program statement, there is either a dynamic or an ac-axiom because the respective other version derives by axiom
 or
or
 . Axioms
. Axioms
 ,
,
 , and
, and
 are as in dL [30]. Axioms
are as in dL [30]. Axioms
 ,
,
 , and
, and
 for decomposition, and
for decomposition, and
 for induction carefully generalize their versions in differential [30] dynamic [14] logic to ac-reasoning. Sending is handled step-wise via flattening the assumption-commitments by axiom
for induction carefully generalize their versions in differential [30] dynamic [14] logic to ac-reasoning. Sending is handled step-wise via flattening the assumption-commitments by axiom
 and axiom
and axiom
 that executes the effect onto the recorder \(h\). The duality
that executes the effect onto the recorder \(h\). The duality
 turns receiving into arbitrary sending, which only synchronizes if it agrees with the parallel context on the value. Usage of axiom
turns receiving into arbitrary sending, which only synchronizes if it agrees with the parallel context on the value. Usage of axiom
 is for convenience. Axiom
is for convenience. Axiom
 materializes the flow of global time \(\mu \) such that \(\textsf {d{}L}\)’s axiomatization of continuous evolution [30] gets applicable, which requires ODE shape \(\bar{x}' = f^\mathbb {R}(\bar{x})\). The axiomatic proof rules
materializes the flow of global time \(\mu \) such that \(\textsf {d{}L}\)’s axiomatization of continuous evolution [30] gets applicable, which requires ODE shape \(\bar{x}' = f^\mathbb {R}(\bar{x})\). The axiomatic proof rules
 ,
,
 ,
,
 , and
, and
 are an ac-version of Gödels generalization rule, modus ponens, quantifier elimination, and contextual equivalence, respectively.
are an ac-version of Gödels generalization rule, modus ponens, quantifier elimination, and contextual equivalence, respectively.
The axiom
 can weaken assumptions. Its slight change compared to \(\textsf {d{}L}_{\text {CHP}}\)’s schematic calculus [6] exploits that the compositionality condition \(\text {W}_\textsf{A}\) is only required for \(a\)’s reachable worlds. Interestingly, \(\textsf {d{}L}_{\text {CHP}}\)’s monotonicity rule
can weaken assumptions. Its slight change compared to \(\textsf {d{}L}_{\text {CHP}}\)’s schematic calculus [6] exploits that the compositionality condition \(\text {W}_\textsf{A}\) is only required for \(a\)’s reachable worlds. Interestingly, \(\textsf {d{}L}_{\text {CHP}}\)’s monotonicity rule
 [6] does not derive from modal modus ponens
[6] does not derive from modal modus ponens
 and Gödel generalization
and Gödel generalization
 in analogy to dL [30] but needs
in analogy to dL [30] but needs
 handling monotonicity of assumptions, which does not fit into
handling monotonicity of assumptions, which does not fit into
 because necessitating the assumption in
because necessitating the assumption in
 would render the derivation of
would render the derivation of
 by
by
 impossible.
impossible.
Axioms using postcondition \(\text {P}\equiv p(Y, \bar{z})\), e.g., in
 , allow any replacement of \(\text {P}\) since accessed channels \(Y\subseteq \varOmega \) and free variables \(\bar{z}\subseteq V_\mathbb {R}\cup V_\mathcal {T}\) can be arbitrary. Replacements of assumptions \(\text {R}\equiv r(Y, \bar{h})\) and commitments \(\text {Q}\equiv q(Y, \bar{h})\) can instead only mention trace variables \(\bar{h}\subseteq V_\mathcal {T}\) bound in their context. This reflects that trace variables are the only interface between the program \(\alpha \) and the ac-formulas \(\textsf{A}\) and \(\textsf{C}\) in an ac-box \([ \alpha ] _{\{\textsf{A}, \textsf{C}\}}\psi \) (well-formedness).
, allow any replacement of \(\text {P}\) since accessed channels \(Y\subseteq \varOmega \) and free variables \(\bar{z}\subseteq V_\mathbb {R}\cup V_\mathcal {T}\) can be arbitrary. Replacements of assumptions \(\text {R}\equiv r(Y, \bar{h})\) and commitments \(\text {Q}\equiv q(Y, \bar{h})\) can instead only mention trace variables \(\bar{h}\subseteq V_\mathcal {T}\) bound in their context. This reflects that trace variables are the only interface between the program \(\alpha \) and the ac-formulas \(\textsf{A}\) and \(\textsf{C}\) in an ac-box \([ \alpha ] _{\{\textsf{A}, \textsf{C}\}}\psi \) (well-formedness).
Theorem 21
(Soundness). The proof calculus for \({\textsf {d{}L}} {}_{\text {CHP}}\) presented in Fig. 3 is sound as an instantiation of the schematic calculus [6].
Clashes. Clashes sort out unsound instantiations of axioms. Unlike in dL and dGL [30, 32] whose clashes are solely due to tabooed variables in terms and formulas, clashes in \({\textsf {d{}L}} {}_{\text {CHP}}\) can also be due to tabooed channels, and even due to taboos in programs. For example, the substitution
 with \(\psi \equiv | h\mathbin {\downarrow }\text {ch}{} |> 0 \wedge | h\mathbin {\downarrow }\text {dh} | > 0 \wedge y < 0\) clashes below, where \(Y= \{ \text {ch}{}, \text {dh} \}\), and \(\bar{z}\equiv h, y\), and \(\text {R}\equiv r(Y)\), and \(\text {Q}\equiv q(Y)\). Writing channel \(\text {ch}{}\) in the replacement for \(b\) would break the local abstraction of \(a\) as \(\text {ch}{}\) is accessed in \(\psi \) but not written in the replacement for \(a\), thus the clash indeed sorts out an unsound instantiation.
with \(\psi \equiv | h\mathbin {\downarrow }\text {ch}{} |> 0 \wedge | h\mathbin {\downarrow }\text {dh} | > 0 \wedge y < 0\) clashes below, where \(Y= \{ \text {ch}{}, \text {dh} \}\), and \(\bar{z}\equiv h, y\), and \(\text {R}\equiv r(Y)\), and \(\text {Q}\equiv q(Y)\). Writing channel \(\text {ch}{}\) in the replacement for \(b\) would break the local abstraction of \(a\) as \(\text {ch}{}\) is accessed in \(\psi \) but not written in the replacement for \(a\), thus the clash indeed sorts out an unsound instantiation.

In contrast,
 does not clash below, where \(Y= \{ \text {ch}{}, \text {dh} \}\), and \(Y_a = \{ \text {ch}{}, \text {gh} \}\), and other abbreviations are as above, because \(\text {ch}{} \in Y^\complement \cup Y_a = \{ \text {dh} \}^\complement \). Intuitively, the \(\text {ch}{}\)-communication of \(b\) remains observable after dropping \(b\) from the parallel composition as it is joint with \(a\).
does not clash below, where \(Y= \{ \text {ch}{}, \text {dh} \}\), and \(Y_a = \{ \text {ch}{}, \text {gh} \}\), and other abbreviations are as above, because \(\text {ch}{} \in Y^\complement \cup Y_a = \{ \text {dh} \}^\complement \). Intuitively, the \(\text {ch}{}\)-communication of \(b\) remains observable after dropping \(b\) from the parallel composition as it is joint with \(a\).

Also note that by the operator \(\parallel _\text {wf}\) for well-formed parallel composition, the recorder variable \(h\) can be shared without causing a clash above. However, clashes prevent instantiation that would violate syntactic well-formedness of programs (Definition 2) by binding the same state variable in parallel:

Well-formedness of programs and formulas is ensured in the axioms by well-formed parallel composition \(\parallel _\text {wf}\) and limitation to trace variables \(\bar{h}\) in \(\text {R}_j \equiv r_j(Y, \bar{h})\) and \(\text {Q}_j \equiv q_j(Y, \bar{h})\) in ac-boxes \([ \alpha ] _{\{\text {R}_j, \text {Q}_j\}} \psi \) in Fig. 3, respectively. By Proposition 19, uniform substitution always preserves well-formedness.
Example 22
The proof tree below decomposes safety (Example 5) of cruise control (Example 3) into safety
 of controller \(\texttt {ct}\) and branch
of controller \(\texttt {ct}\) and branch
 to be continued to safety of the vehicle ve. The
to be continued to safety of the vehicle ve. The
 introduces the ac-formulas
introduces the ac-formulas
using axiom
 to abstract from the communication between \(\texttt {ct}\) and \(\texttt {ve}\). The
to abstract from the communication between \(\texttt {ct}\) and \(\texttt {ve}\). The
 uses the parallel injection axiom
uses the parallel injection axiom
 to drop \(\texttt {ve}\). Uniform substitution
to drop \(\texttt {ve}\). Uniform substitution
 does not clash as the commitment \(\textsf{C}\) only refers to joint communication of \(\texttt {ct}\) and \(\texttt {ve}\). Other applications of
does not clash as the commitment \(\textsf{C}\) only refers to joint communication of \(\texttt {ct}\) and \(\texttt {ve}\). Other applications of
 (e.g., for
(e.g., for
 ) are omitted. Rule
) are omitted. Rule
 denotes propositional reasoning. Abbreviations are as follows:
denotes propositional reasoning. Abbreviations are as follows:
 , \(\text {R}\equiv r(\text {tar}, h)\), \(\text {Q}\equiv q(\text {tar}, h)\), \(\text {P}\equiv p(\text {tar})\).
, \(\text {R}\equiv r(\text {tar}, h)\), \(\text {Q}\equiv q(\text {tar}, h)\), \(\text {P}\equiv p(\text {tar})\).

5 Related Work
Uniform substitution for differential dynamic logic dL [30] generalizes Church’s uniform substitution for first-order logic [8, §35, 40]. Unlike the lifting from dL to differential game logic dGL [31], \({\textsf {d{}L}} {}_{\text {CHP}}\) generalizes into the complementary direction of communication and parallelism. Unlike schematic calculi [2, 19, 27, 44, 46], whose treacherous schematic simplicity relies on encoding all subtlety of parallel systems in significant soundness-critical side conditions, our development builds upon a minimalistic non-schematic parallel injection axiom and sound instantiation encapsulated in uniform substitution. This provides a new, more atomic and more modular understanding of parallel systems overcoming the root cause for large soundness-critical prover kernels [5, 9, 12, 16, 18, 36]. Usage of uniform substitution reduced the kernel of the theorem prover KeYmaera from 105 kLOC to 2 kLOC in KeYmaera X [23]. We expect \(\textsf {d{}L}_{\text {CHP}}\)’s integration into KeYmaera X to stay in the same order of magnitude.
To the best of our knowledge, assumption-commitment reasoning [22, 46]Footnote 5 has no tool support, which might be due to vast implementation effort. The latter can be underpinned by analogy with tools [5, 9, 16, 18, 36] for verification of shared-variables concurrency, some of which use rely-guarantee reasoning [36, 39]. Unlike uniform substitution for \({\textsf {d{}L}} {}_{\text {CHP}}\) that enables a straightforward implementation of a small prover kernel, they all rely on large soundness-critical code bases. Unlike refinement checking for CSP [12] and discrete-time CSP [4], \({\textsf {d{}L}} {}_{\text {CHP}}\) supports safety properties of dense-time hybrid systems. Contrary to our goal of small prover kernels, implementations of model checkers [12] are inherently large.
Beyond embeddings of concurrency reasoning for discrete systems into proof assistants [3, 25, 26, 38], \({\textsf {d{}L}} {}_{\text {CHP}}\) can verify parallel hybrid systems synchronizing in shared global time. The latter imposes even more complicated binding structures than parallel or hybrid systems alone but \(\textsf {d{}L}_{\text {CHP}}\)’s uniform substitution calculus continues to manage them in a modular way.
The recent tool HHLPy [37] for hybrid CSP (HCSP) [17] is limited to the sequential fragment. Unlike extending HHLPy to parallelism, which would require extensive soundness-critical side conditions and a treatment of the duration calculus, integrating \({\textsf {d{}L}} {}_{\text {CHP}}\) into KeYmaera X [11] boils down to adding a finite list of concrete object level formulas as axioms and only small changes to the uniform substitution process. In contrast to \(\textsf {d{}L}_{\text {CHP}}\)’s compositional parallel systems calculus [6], HCSP calculi [13, 20, 42] are non-compositional [6] as they either unroll exponentially many interleavings from the operational semantics [13, 42] or can only decompose independent parallel components [20] causing limited ability to reason about complex systems. Former HCSP tools [43, 45] only implement a non-compositional calculus [20] reinforcing the significance of our approach for managing parallel hybrid systems reasoning. Other hybrid process algebras defer to model checkers for reasoning [10, 21, 40]. Further discussion of \({\textsf {d{}L}} {}_{\text {CHP}}\) is in [6].
6 Conclusion
This paper introduced a sound one-pass uniform substitution calculus for the dynamic logic of communicating hybrid programs \({\textsf {d{}L}} {}_{\text {CHP}}\) thereby mastering the significant challenge of developing simple sound proof calculi for parallel hybrid systems with communication. Uniform substitution can separate even notoriously complicated binding structures from parallelism with communication in multi-dynamical logics into axioms and their instantiation. In the case of \({\textsf {d{}L}} {}_{\text {CHP}}\), this applies to channel access in predicates and the need for local abstraction of subprograms in parallel statements, and it even turns out that uniform substitution can maintain a context-sensitive syntax along the way. Thanks to uniform substitution, parallel systems reasoning reduces to multiple uses of an asymmetric parallel injection axiom.
Now, with uniform substitution a straightforward implementation of \({\textsf {d{}L}} {}_{\text {CHP}}\) in KeYmaera X is only one step away.
Notes
- 1.
Omitting multiplication results in decidable Presburger arithmetic [34].
- 2.
Previous work [6] disallows reading of variables bound in parallel as their change is not observable. This restriction is conceptually desirable but not soundness-critical. Here we drop it for simplicity, but it could be maintained by
 as well.
as well. - 3.
Extension to vectorial arguments is straightforward.
- 4.
For \(\alpha \parallel \beta \), the restriction is \((\mathop {\textsf{V}}(\alpha ) \cap \mathop {\mathsf {B\! V}}(\beta )) \cup (\mathop {\textsf{V}}(\beta ) \cap \mathop {\mathsf {B\! V}}(\alpha )) \subseteq \{\mu , \mu '\} \cup V_\mathcal {T}\) [6]. However, in this paper, programs obey a less restrictive syntax for simplicity.
- 5.
Assumption-commitment and rely-guarantee reasoning are specific patterns for message-passing and shared variables concurrency, respectively. The broader assume-guarantee principle has been used across diverse areas for various purposes.
References
Apt, K.R., de Boer, F.S., Olderog, E.R.: Verification of Sequential and Concurrent Programs, 3rd edn. Springer, Heidelberg (2010). https://doi.org/10.1007/978-1-84882-745-5
Apt, K.R., Francez, N., de Roever, W.P.: A proof system for communicating sequential processes. ACM Trans. Program. Lang. Syst. 2(3), 359–385 (1980). https://doi.org/10.1145/357103.357110
Armstrong, A., Gomes, V.B.F., Struth, G.: Algebras for program correctness in Isabelle/HOL. In: Höfner, P., Jipsen, P., Kahl, W., Müller, M.E. (eds.) RAMICS 2014. LNCS, vol. 8428, pp. 49–64. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-06251-8_4
Armstrong, P.J., Lowe, G., Ouaknine, J., Roscoe, B.: Model checking timed CSP. In: Voronkov, A., Korovina, M.V. (eds.) HOWARD-60: A Festschrift on the Occasion of Howard Barringer’s 60th Birthday, EPiC Series in Computing, vol. 42, pp. 13–33. EasyChair (2014). https://doi.org/10.29007/6fqk
Blom, S., Darabi, S., Huisman, M., Oortwijn, W.: The VerCors tool set: verification of parallel and concurrent software. In: Polikarpova, N., Schneider, S. (eds.) IFM 2017. LNCS, vol. 10510, pp. 102–110. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66845-1_7
Brieger, M., Mitsch, S., Platzer, A.: Dynamic logic of communicating hybrid programs. CoRR abs/2302.14546 (2023). https://doi.org/10.48550/arXiv.2302.14546
Brieger, M., Mitsch, S., Platzer, A.: Uniform substitution for dynamic logic with communicating hybrid programs. CoRR abs/2303.17333 (2023). https://doi.org/10.48550/arXiv.2303.17333
Church, A.: Introduction to Mathematical Logic. Princeton University Press, Princeton (1956)
Cohen, E., et al.: VCC: a practical system for verifying concurrent C. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 23–42. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03359-9_2
Cong, X., Yu, H., Xu, X.: Verification of hybrid chi model for cyber-physical systems using PHAVer. In: Barolli, L., You, I., Xhafa, F., Leu, F., Chen, H. (eds.) Proceedings of the 7th International Conference on Innovative Mobile and Internet Services in Ubiquitous Computing (IMIS), pp. 122–128. IEEE Computer Society (2013). https://doi.org/10.1109/IMIS.2013.29
Fulton, N., Mitsch, S., Quesel, J.-D., Völp, M., Platzer, A.: KeYmaera X: an axiomatic tactical theorem prover for hybrid systems. In: Felty, A.P., Middeldorp, A. (eds.) CADE 2015. LNCS (LNAI), vol. 9195, pp. 527–538. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21401-6_36
Gibson-Robinson, T., Armstrong, P., Boulgakov, A., Roscoe, A.W.: FDR3—a modern refinement checker for CSP. In: Ábrahám, E., Havelund, K. (eds.) TACAS 2014. LNCS, vol. 8413, pp. 187–201. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54862-8_13
Guelev, D.P., Wang, S., Zhan, N.: Compositional Hoare-style reasoning about hybrid CSP in the duration calculus. In: Larsen, K.G., Sokolsky, O., Wang, J. (eds.) SETTA 2017. LNCS, vol. 10606, pp. 110–127. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-69483-2_7
Harel, D. (ed.): First-Order Dynamic Logic. LNCS, vol. 68. Springer, Heidelberg (1979). https://doi.org/10.1007/3-540-09237-4
Hoare, C.A.R.: Communicating sequential processes. Commun. ACM 21(8), 666–677 (1978). https://doi.org/10.1145/359576.359585
Jacobs, B., Smans, J., Philippaerts, P., Vogels, F., Penninckx, W., Piessens, F.: VeriFast: a powerful, sound, predictable, fast verifier for C and Java. In: Bobaru, M., Havelund, K., Holzmann, G.J., Joshi, R. (eds.) NFM 2011. LNCS, vol. 6617, pp. 41–55. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20398-5_4
Jifeng, H.: From CSP to hybrid systems In: A Classical Mind: Essays in Honour of C. A. R. Hoare, pp. 171–189. Prentice Hall International (1994)
Kirchner, F., Kosmatov, N., Prevosto, V., Signoles, J., Yakobowski, B.: Frama-C: a software analysis perspective. Formal Aspects Comput. 27(3), 573–609 (2015). https://doi.org/10.1007/s00165-014-0326-7
Levin, G., Gries, D.: A proof technique for communicating sequential processes. Acta Informatica 15(3), 281–302 (1981). https://doi.org/10.1007/BF00289266
Liu, J., et al.: A calculus for hybrid CSP. In: Ueda, K. (ed.) APLAS 2010. LNCS, vol. 6461, pp. 1–15. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17164-2_1
Man, K.L., Reniers, M.A., Cuijpers, P.J.L.: Case studies in the hybrid process algebra HyPA. Int. J. Softw. Eng. Knowl. Eng. 15(2), 299–306 (2005). https://doi.org/10.1142/S0218194005002385
Misra, J., Chandy, K.M.: Proofs of networks of processes. IEEE Trans. Softw. Eng. 7(4), 417–426 (1981). https://doi.org/10.1109/TSE.1981.230844
Mitsch, S., Platzer, A.: A retrospective on developing hybrid system provers in the KeYmaera family. In: Ahrendt, W., Beckert, B., Bubel, R., Hähnle, R., Ulbrich, M. (eds.) Deductive Software Verification: Future Perspectives. LNCS, vol. 12345, pp. 21–64. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64354-6_2
Müller, A., Mitsch, S., Retschitzegger, W., Schwinger, W., Platzer, A.: A component-based approach to hybrid systems safety verification. In: Ábrahám, E., Huisman, M. (eds.) IFM 2016. LNCS, vol. 9681, pp. 441–456. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-33693-0_28
Nieto, L.P.: Verification of parallel programs with the Owicki-Gries and Rely-Guarantee methods in Isabelle/HOL. Ph.D. thesis, Technical University Munich, Germany (2002). http://tumb1.biblio.tu-muenchen.de/publ/diss/in/2002/prensa_nieto.html
Nipkow, T., Nieto, L.P.: Owicki/Gries in Isabelle/HOL. In: Finance, J.-P. (ed.) FASE 1999. LNCS, vol. 1577, pp. 188–203. Springer, Heidelberg (1999). https://doi.org/10.1007/978-3-540-49020-3_13
Owicki, S.S., Gries, D.: An axiomatic proof technique for parallel programs I. Acta Informatica 6, 319–340 (1976). https://doi.org/10.1007/BF00268134
Platzer, A.: Differential dynamic logic for hybrid systems. J. Autom. Reas. 41(2), 143–189 (2008). https://doi.org/10.1007/s10817-008-9103-8
Platzer, A.: Differential game logic. ACM Trans. Comput. Log. 17(1), 1:1–1:51 (2015). https://doi.org/10.1145/2817824
Platzer, A.: A complete uniform substitution calculus for differential dynamic logic. J. Autom. Reas. 59(2), 219–265 (2017). https://doi.org/10.1007/s10817-016-9385-1
Platzer, A.: Uniform substitution for differential game logic. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS (LNAI), vol. 10900, pp. 211–227. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_15
Platzer, A.: Uniform substitution at one fell swoop. In: Fontaine, P. (ed.) CADE 2019. LNCS (LNAI), vol. 11716, pp. 425–441. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-29436-6_25
Platzer, A., Tan, Y.K.: Differential equation invariance axiomatization. J. ACM 67(1), 6:1–6:66 (2020). https://doi.org/10.1145/3380825
Presburger, M.: Über die Vollständigkeit eines gewissen Systems der Arithmetik ganzer Zahlen, in welchem die Addition als einzige Operation hervortritt. In: Comptes Rendus du I congrès de Mathématiciens des Pays Slaves (1931)
de Roever, W.P., et al.: Concurrency Verification: Introduction to Compositional and Noncompositional Methods. Cambridge Tracts in Theoretical Computer Science, vol. 54. Cambridge University Press (2001)
Schellhorn, G., Bodenmüller, S., Bitterlich, M., Reif, W.: Software & system verification with KIV. In: Ahrendt, W., Beckert, B., Bubel, R., Johnsen, E.B. (eds.) The Logic of Software. A Tasting Menu of Formal Methods. LNCS, vol. 13360, pp. 408–436. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-08166-8_20
Sheng, H., Bentkamp, A., Zhan, B.: HHLPy: practical verification of hybrid systems using Hoare logic. In: Chechik, M., Katoen, J., Leucker, M. (eds.) FM 2023. LNCS, vol. 14000, pp. 160–178. Springer, Cham (2023). https://doi.org/10.1007/978-3-031-27481-7_11
Shi, L., Zhao, Y., Liu, Y., Sun, J., Dong, J.S., Qin, S.: A UTP semantics for communicating processes with shared variables and its formal encoding in PVS. Formal Aspects Comput. 30(3–4), 351–380 (2018). https://doi.org/10.1007/s00165-018-0453-7
Smans, J., Vanoverberghe, D., Devriese, D., Jacobs, B., Piessens, F.: Shared boxes: rely-guarantee reasoning in VeriFast. Technical report, Katholieke Universiteit Leuven, Netherlands (2014). https://lirias.kuleuven.be/handle/123456789/456819
Song, H., Compton, K.J., Rounds, W.C.: SPHIN: a model checker for reconfigurable hybrid systems based on SPIN. In: Lazic, R., Nagarajan, R. (eds.) Proceedings of the 5th International Workshop Automated Verification of Critical Systems (AVoCS). ENTCS, vol. 145, pp. 167–183. Elsevier (2005). https://doi.org/10.1016/j.entcs.2005.10.011
Tarski, A.: A Decision Method for Elementary Algebra and Geometry, 2nd edn. University of California Press, Berkeley (1951). https://doi.org/10.1525/9780520348097
Wang, S., Zhan, N., Guelev, D.: An assume/guarantee based compositional calculus for hybrid CSP. In: Agrawal, M., Cooper, S.B., Li, A. (eds.) TAMC 2012. LNCS, vol. 7287, pp. 72–83. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29952-0_13
Wang, S., Zhan, N., Zou, L.: An improved HHL prover: an interactive theorem prover for hybrid systems. In: Butler, M., Conchon, S., Zaïdi, F. (eds.) ICFEM 2015. LNCS, vol. 9407, pp. 382–399. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-25423-4_25
Xu, Q., de Roever, W.P., He, J.: The rely-guarantee method for verifying shared variable concurrent programs. Formal Aspects Comput. 9(2), 149–174 (1997). https://doi.org/10.1007/BF01211617
Zou, L., et al.: Verifying Chinese train control system under a combined scenario by theorem proving. In: Cohen, E., Rybalchenko, A. (eds.) VSTTE 2013. LNCS, vol. 8164, pp. 262–280. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54108-7_14
Zwiers, J., de Bruin, A., de Roever, W.P.: A proof system for partial correctness of dynamic networks of processes. In: Clarke, E., Kozen, D. (eds.) Logic of Programs 1983. LNCS, vol. 164, pp. 513–527. Springer, Heidelberg (1984). https://doi.org/10.1007/3-540-12896-4_384
Zwiers, J., de Roever, W.P., van Emde Boas, P.: Compositionality and concurrent networks: soundness and completeness of a proofsystem. In: Brauer, W. (ed.) ICALP 1985. LNCS, vol. 194, pp. 509–519. Springer, Heidelberg (1985). https://doi.org/10.1007/BFb0015776
Acknowledgments
This project was funded in part by the Deutsche Forschungs-gemeinschaft (DFG) – 378803395 (ConVeY), an Alexander von Humboldt Professorship, and by the AFOSR under grant number FA9550-16-1-0288.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Brieger, M., Mitsch, S., Platzer, A. (2023). Uniform Substitution for Dynamic Logic with Communicating Hybrid Programs. In: Pientka, B., Tinelli, C. (eds) Automated Deduction – CADE 29. CADE 2023. Lecture Notes in Computer Science(), vol 14132. Springer, Cham. https://doi.org/10.1007/978-3-031-38499-8_6
Download citation
DOI: https://doi.org/10.1007/978-3-031-38499-8_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-38498-1
Online ISBN: 978-3-031-38499-8
eBook Packages: Computer ScienceComputer Science (R0)






 .
.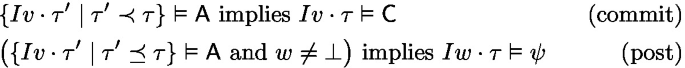

 for any program
for any program 
 as well.
as well.