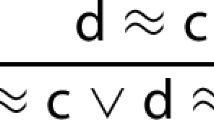Abstract
Resolution and superposition provers rely on the given clause procedure to saturate clause sets. Using Isabelle/HOL, we formally verify four variants of the procedure: the well-known Otter and DISCOUNT loops as well as the newer iProver and Zipperposition loops. For each of the variants, we show that the procedure guarantees saturation, given a fair data structure to store the formulas that wait to be selected. Our formalization of the Zipperposition loop clarifies some fine points previously misunderstood in the literature.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Resolution [13] and superposition [2] provers are based on saturation. In a first approximation, these provers perform all possible inferences between the available clauses. The full truth, however, is more complex: Provers may delete clauses that are considered redundant; for example, with resolution, if \(\textsf{p}(x)\) is in the clause set, then both \(\textsf{p}(\textsf{a})\) and \(\textsf{p}(x) \mathrel \vee \textsf{q}(x)\) are redundant and could be deleted.
The procedure that saturates a set of clauses—or more generally, formulas—up to redundancy is called the given clause procedure [10, Sect. 2.3]. It has several variants. The two main variants are the Otter loop [10] and the DISCOUNT loop [1]. In this paper, we also consider the iProver [8] and Zipperposition loops [17]; they are variants of the Otter and DISCOUNT loops, respectively.
In its simplest form, the procedure distinguishes between passive and active formulas. Formulas start as passive. One passive formula is selected as the given clause.Footnote 1 Deletions and simplifications with respect to other passive and active formulas are then performed; for example, if the given clause is redundant with respect to an active formula, the given clause can be deleted, and if the given clause makes an active formula redundant, that formula can be deleted. Moreover, simplifications can take place; for example, in a superposition prover, if the term order specifies \(\textsf{b} \succ \textsf{a}\), the given clause is \(\textsf{b} \approx \textsf{a}\), and \(\textsf{p}(\textsf{b})\) is an active formula, the active formula can be simplified to \(\textsf{p}(\textsf{a})\) and made passive again.
Next, if the given clause has not been deleted, it is moved to the active set. All inferences between the given clause and formulas in the active set are then performed, and the resulting conclusions are put in the passive set. This procedure is repeated, starting with the selection of a new given clause, until the distinguished formula \(\bot \) is derived or the passive set is empty.
The main metatheorem about this procedure states that if the given clause is chosen fairly (i.e., no passive formula is ignored forever), then the active set will be saturated (up to redundancy) at the limit. As a corollary, if the proof calculus is refutationally complete (i.e., it derives \(\bot \) from any inconsistent set), then the prover based on the calculus will be refutationally complete as well.
We present an Isabelle/HOL [12] formalization of the Otter, DISCOUNT, iProver, and Zipperposition loops, culminating in a statement and proof of the main metatheorem for each one. We build on the pen-and-paper saturation framework developed by Waldmann, Tourret, Robillard, and Blanchette [18, 19] and formalized in Isabelle/HOL by Tourret and Blanchette [16]. The framework is an elaboration of Bachmair–Ganzinger-style saturation [3, Sect. 4]. Waldmann et al. include descriptions of the four “loops” as instances of the framework, as Examples 71, 74, 81, and 82 [19]; our formalization follows these descriptions.
Among the four loops, the oldest one is the Otter loop. It originates from Otter, a resolution-based theorem prover for first-order logic introduced in 1988 [11]. Otter was the first prover to present the given clause algorithm, in its simplest form as described above.
The DISCOUNT loop followed a few years later as a byproduct of the DISCOUNT system [7], itself built to distribute proof tasks among processors. What distinguishes a DISCOUNT loop is that it really treats the passive set as passive. Its formulas serve only as the pool from which to choose the next given clause; they are never involved in deletions or other simplifications. Another key difference between the two loops is the decoupling of the scheduling of an inference and the production of its conclusion, which makes DISCOUNT able to propagate deletions and simplifications to discard inferences before their conclusions enter the passive set. For example, suppose that, in DISCOUNT, an inference

called \(\iota \) is scheduled, in a derivation using first-order resolution. Then suppose that, before \(\iota \) is realized, \(\textsf{p}(\textsf{a})\) is generated (e.g., as the result of the factorization of \(\textsf{p}(x) \vee \textsf{p}(\textsf{a})\)). This triggers the deletion of \(\textsf{p}(x)\vee \textsf{p}(\textsf{a})\), which has become redundant. Then \(\iota \) becomes an orphan inference, since one of its premises is no longer in the active set. It can be deleted without threatening the procedure’s completeness. In contrast, in an Otter loop, if \(\iota \) is scheduled before \(\textsf{p}(\textsf{a})\) is selected as the given clause, \(\iota \)’s conclusion \(\textsf{p}(x)\vee \textsf{q}(y)\) is directly added to the passive set, where it can be simplified.
What we call the iProver loop [8] is an extension of the Otter loop with a transition that removes a formula C if C is made redundant by a formula set M. This terminology is from Waldmann et al. [19, Example 74]. This rule, introduced when iProver was extended to handle the superposition calculus [8], combines an inference step with a step that simplifies the active set.
The last and most elaborate loop variant we present is the Zipperposition loop. Zipperposition is a higher-order theorem prover based on \(\lambda \)-superposition [4]. Its given clause procedure is designed to work with higher-order logic. Due to the explosiveness of higher-order unification, a single pair of premises can yield infinitely many conclusions. For example, the higher-order resolution inference

where y and z are variables, produces infinitely many conclusions of the form \(\textsf{q}\>(\lambda x.\>\textsf{f}^n\,x)\) for \(n \in \mathbb {N}\). Thus, the passive set must be able to store possibly infinite sequences of lazily performed inferences. The Zipperposition loop was described by Vukmirović et al. [17] and by Waldmann et al. [19, Example 82].Footnote 2 Vukmirović et al. describe the loop’s implementation in Zipperposition, which we believe to be correct. In contrast, Waldmann et al. present an abstract version of the loop and connect it, via stepwise refinement, to their saturation framework, obtaining the main metatheorem. However, in the latter work, the details are not worked out. Thanks to the Isabelle formalization, we note and address several issues such that we now have a first rigorous—in fact, fully formal—presentation of the essence of the Zipperposition loop including the metatheorem.
Our work is part of IsaFoL (Isabelle Formalization of Logic), an effort that aims at developing a formal library of results about logic and automated reasoning [6]. The Isabelle files amount to about 7000 lines of code. They were developed using the 2022 edition of Isabelle and are available in the Archive of Formal Proofs (AFP) [5], where they are updated to follow Isabelle’s evolution.
This work joins a long list of verifications of calculi and provers. We refer to Blanchette [6, Sect. 5] for an overview of such works. The most closely related works are the two proofs of completeness of Bachmair and Ganzinger’s resolution prover \(\textsf{RP}\), by Schlichtkrull, Blanchette, Traytel, and Waldmann [14] and by Tourret and Blanchette [16] as well as the proof of completeness of ordered (unfailing) completion by Hirokawa, Middeldorp, Sternagel, and Winkler [9]. Instead of focusing on a single prover, here we consider general prover architectures. Via refinement, our results can be applied to individual provers.
2 Abstract Given Clause Procedures
To prove the main metatheorem for each of the four loops, we build on the saturation framework. The framework defines two highly abstract given clause procedures, called \(\textsf{GC}\) (“given clause”) and \(\textsf{LGC}\) (“lazy given clause”) [19, Sect. 4]. They are formalized in the file Given_Clause_Architectures.thy of the AFP entry Saturation_Framework [15].
\(\textsf{GC}\) is an idealized Otter-style loop. It operates on sets of labeled formulas. Formulas have the generic type \({{'}{f}}\), and labels have the generic type \({{'}{l}}\). One label, \(\textsf{active}\), identifies active formulas, and the other labels correspond to passive formulas. \(\textsf{GC}\) is defined as a two-rule transition system \(\leadsto _\textsf{GC}\). In Isabelle syntax:

When presenting Isabelle code, we will focus on the main ideas and not explain all the Isabelle syntax or all the symbols that occur in the code. We refer to Waldmann et al. [19] for mathematical statements of the key concepts and to the Isabelle theory files for the formal definitions.
Informally, the transition relation \(\leadsto _\textsf{GC}\) is defined as an inductive predicate equipped with two introduction rules, process and infer. Both rules allow a transition from \(N_1\) to \(N_2\) under some conditions:
-
The process rule replaces a subset M of \(N_1\) by \(M'\). This is possible only if the redundancy criterion (\(\textsf{Red}_\textsf{F}\)) justifies the replacement and the formulas in \(M'\) are all made passive (i.e., the active subset of \(M'\) is the empty set). This rule models formula simplification and deletion, but also replacing a passive label by another, “greater” passive label.
-
The infer rule makes a passive formula C active and performs all inferences between this formula and active formulas, yielding M. Strictly speaking, the inferences need not be performed at all; it suffices that M makes the inferences redundant.
The main metatheorem for \(\textsf{GC}\) states that if the set of passive formulas is empty at the limit of a derivation, the active formula set is saturated at the limit.
The lazy variant \(\textsf{LGC}\) generalizes the DISCOUNT loop. It operates on pairs (T, N), where \(T \mathrel {::}{{'}{f}}\> inference \> set \) is a set of inferences that have been scheduled but not yet performed and \(N \mathrel {::}({{'}{f}}\times {{'}{l}})\> set \) is a set of labeled formulas. It consists of four rules that can be summarized as follows:
-
The process rule is essentially as in \(\textsf{GC}\). It leaves the T component unchanged.
-
The schedule_infer rule makes a passive formula active and schedules all the inferences between this formula and active formulas by adding them to the T component.
-
The compute_infer rule actually performs a scheduled inference or otherwise ensures that it is made redundant by adding suitable formulas.
-
The delete_orphan_infers rule can be used to delete a scheduled inference if one of its premises has been deleted.
The main metatheorem for \(\textsf{LGC}\) states that if the set of scheduled inferences and the set of passive formulas are empty at the limit of a derivation starting in an initial state, the active formula set is saturated at the limit.
3 Otter and iProver Loops
The Otter loop [10] works on five-tuples (N, X, P, Y, A), where N is the set of new formulas; X is a subsingleton (i.e., the empty set or a singleton \(\{C\}\)) storing a formula moving from N to P; P is the set of so-called passive formulas (although, strictly speaking, the formulas in N, X, and Y are also passive); Y is a subsingleton storing the given clause, which moves from P to A; and A is the set of active formulas. All the sets are finite in practice.
Initial states have the form \((N, \emptyset , \emptyset , \emptyset , \emptyset )\). Inferences are assumed to be finitary, meaning that the set of inferences with C and formulas from A as premises (formally written \(\mathsf {Inf\_between}\; A\; \{C\}\)) is finite if A is finite. Premiseless inferences are disallowed.
Otter Loop without Fairness. The first version of the Otter loop, formalized in Otter_Loop.thy, does not make any fairness assumption on the choice of the given clause. The guarantee it offers is correspondingly weak: If the sets N, X, P, and Y are empty at the limit of a derivation starting in an initial state, then A is saturated. But there is no guarantee that N, X, P, and Y are empty at the limit. Later in this section, we will show how to ensure this generically.
The transition system \(\leadsto _\textsf{OL}\) for the Otter loop without fairness is as follows:

The \(\textsf{state}\) function converts a five-tuple into a set of labeled formulas—an equivalent representation that is often more convenient formally. The labels are \(\textsf{New}\) (for N), \(\textsf{XX}\) (for X), \(\textsf{Passive}\) (for P), \(\textsf{YY}\) (for Y), and \(\textsf{Active}\) (for A, corresponding to \(\textsf{active}\) in \(\textsf{GC}\)).
The first nine rules all refine \(\textsf{GC}\)’s process rule, whereas the tenth rule, infer, refines \(\textsf{GC}\)’s infer. More precisely: The first rule moves a formula from N to X. The second and third rules delete or simplify the formula in X. The fourth to seventh rules delete or simplify other formulas using the formula in X. The eight rule moves a formula from X to P. The ninth rule moves a formula from P to Y. And the tenth rule moves a formula from Y to A and performs all inferences with formulas in A or otherwise ensures that the inferences are made redundant.
Following Waldmann et al., the rules introducing new formulas—namely, the simplify rules and infer—allow adding arbitrary formulas to the state and are therefore not sound. Since the metatheorems are about completeness, there is no harm in allowing unsound steps, such as skolemization. If desired, soundness can be required simply by adding the assumption \(N \models N'\) for each step \(N \leadsto _\textsf{OL} N'\) in a derivation.
Compared with most descriptions of the Otter loop in the literature, the above formalization (and Example 71 in Waldmann et al. [19] on which it is based) is abstract and nondeterministic, allowing arbitrary interleavings of deletions, simplifications, and inferences. By not commiting to a specific strategy, we keep our code widely applicable: Our abstract Otter loop can be used as the basis of refinement steps targetting a wide range of deterministic procedures implementing specific strategies. We will see the same approach used for all the loops. We note that Bachmair and Ganzinger made a similar choice for their ordered resolution prover RP [3, Sect. 4].
Otter Loop with Fairness. Below we introduce a fair version of the Otter loop, called \(\leadsto _\textsf{OLf}\) and formalized in Fair_Otter_Loop_Def.thy. This new version is closer to an implementation.

The definition of \(\leadsto _\textsf{OLf}\) differs from that of \(\leadsto _\textsf{OL}\) in two main respects:
-
The set P is organized as some form of queue, with operations such as \(\textsf{select}\), which chooses the queue’s next element; \(\textsf{remove}\), which removes all occurrences of an element from the queue; and \(\textsf{elems}\), which returns the set of the queue’s elements. The queue is assumed to be fair, meaning that if \(\textsf{select}\) is called infinitely often, every element in the queue will eventually be chosen and the limit of P will be empty.
-
Simplification (e.g., in simplify_fwd) is allowed only if the simplified formula \(C'\) is smaller than the original formula C according to some given well-founded order \(\prec _\textsf{S}\). In practice, simplifications are usually well founded, so this is not a severe restriction.
Also note that the state is now directly represented as a five-tuple (without the mediation of the \(\textsf{state}\) function), where the subsingletons are of type \({{'}{f}}\> option \), with values of the forms \(\textsf{None}\) and \(\textsf{Some}\; C\).
Formula Queue. The queue that represents the passive formula set P is formalized in its own file, Prover_Queue.thy. The file defines an abstract type of queue and the operations on it (\(\textsf{empty}\), \(\textsf{select}\), \(\textsf{add}\), \(\textsf{remove}\), and \(\textsf{elems}\)). It also expresses the fairness assumption on the \(\textsf{select}\) function:
If a sequence of queue operations starting from an empty queue contains infinitely many removals of the \(\textsf{select}\)ed element, then the queue is empty at the limit.
Moreover, the file contains an example implementation of the queue as a FIFO queue. This ensures that the abstract requirements on the queue, including fairness, are satisfiable.
iProver Loop with Fairness. To obtain an iProver loop from an Otter loop, only one extra rule is needed. The fair version of the iProver loop is formalized in Fair_iProver_Loop.thy as follows:

The first rule, ol, executes any \(\leadsto _\textsf{OLf}\) rule as an iProver loop rule. The second rule, red_by_children, replaces a formula C by a set of formulas M that make it redundant. As M, iProver would use a set of simplified formulas produced by inferences with C as a premise and formulas from \(A \cup \{C\}\) as further premises. The rule is stated in a more general, unsound form.
We prove the main metatheorem first for the iProver loop. Then, since an Otter derivation is an iProver derivation (in which the second rule, red_by_children, is not used), the result carries over directly to the Otter loop. The Isabelle statement, located in Fair_iProver_Loop.thy, is as follows:

Informally, this states that if \( Sts \) is a complete \(\leadsto _\textsf{ILf}\) derivation starting in a state of the form \((N, \textsf{None}, \textsf{empty}, \textsf{None}, \emptyset )\), then the limit is saturated. The limit (strictly speaking, limit inferior) is defined by
where \( Xs \mathrel {!} j\) returns the element at index j of the finite or infinite sequence \( Xs \). In Isabelle, such sequences are represented by the type \({{'}{a}}\> llist \) of “lazy lists.”
This metatheorem is proved within the scope of the passive set queue’s fairness assumption. It is derived from the metatheorem about the transition system \(\leadsto _\textsf{IL}\) without fairness, which is inherited from the abstract procedure \(\textsf{GC}\).
Proof Sketch
The main difficulty is to show that N, X, P, and Y are empty at the limit. Once this is shown, we can apply the main metatheorem for \(\textsf{GC}\), which states that if there are no passive formulas at the limit, the active formula set is saturated.
Let \( St _0 \leadsto _\textsf{IL} St _1 \leadsto _\textsf{IL} \cdots \) be a complete derivation, where \( St _i = (N_i, X_i, P_i, Y_i, A_i)\). If the derivation is finite, it is easy to show that the final state, and hence the limit, must be of the form \((\emptyset , \textsf{None}, \textsf{empty}, \textsf{None}, A)\), as desired.
Otherwise, for an infinite derivation, we assume in turn that the limit of N, X, P, or Y is nonempty and show that this leads to a contradiction. We start with N. Let i be an index such that \(N_i \cap N_{i+1} \cap \cdots \not = \emptyset \), which exists by the definition of limit. This means that \(N_i, N_{i+1}, \dots \) are all nonempty. By invariance, we can show that \(Y_i, Y_{i+1}, \dots \) are all empty. Thus, if we have a transition from \( St _{j}\) to \( St _{j+1}\) for \(j \ge i\), it cannot be infer (via ol) or red_by_children. It can be shown that for the remaining transition rules, we have \( St _i \sqsupset _1 St _{i+1} \sqsupset _1 \cdots \,\), where \(\sqsupset _1\) is the converse of the lexicographic combination \(\sqsubset _1\) of three well-founded relations:
-
the multiset extension \(\prec \!\!\!\prec _\textsf{S}\) of \(\prec _\textsf{S}\) on entire states—i.e., on unions \(N \cup X \cup P \cup Y \cup A\);
-
as a tiebreaker, \(\prec \!\!\!\prec _\textsf{S}\) on N components;
-
as a further tiebreaker, \(\prec \!\!\!\prec _\textsf{S}\) on X components.
Since the lexicographic combination of well-founded relations is well founded, the chain \( St _i \sqsupset _1 St _{i+1} \sqsupset _1 \cdots \,\) cannot be infinite, a contradiction.
Next, we consider the X component. If X is nonempty forever, the only possible transition rules are deletions and simplifications, and both make the entire state decrease with respect to \(\prec \!\!\!\prec _\textsf{S}\). Again, we get a contradiction.
Next, we consider the P component. The fairness assumption for the queue guarantees that P is empty at the limit, at the condition that the choose_p rule is executed infinitely often. Since P is assumed not to be empty at the limit, choose_p must be executed only finitely often. Let i be an index from which no choose_p step takes place. We then have \( St _i \sqsupset _2 St _{i+1} \sqsupset _2 \cdots \,\), where \(\sqsupset _2\) is the converse of the lexicographic combination \(\sqsubset _2\) of two well-founded relations:
-
\(\prec \!\!\!\prec _\textsf{S}\) on Y components;
-
as a tiebreaker, the relation \(\sqsubset _1\) on entire states.
Again, we get a contradiction.
Finally, for Y, the only two transitions possible, infer and red_by_children, are to a state where Y is empty afterward, contradicting the hypothesis that Y is nonempty forever. \(\square \)
4 DISCOUNT Loop
The DISCOUNT loop [1] works on four-tuples (T, P, Y, A), where T is the set of scheduled (“to do”) inferences, P is the set of so-called passive formulas (although, strictly speaking, any formula in Y is also passive); Y is a subsingleton storing the given clause; and A is the set of active formulas. All the sets are finite.
Initial states have the form \((\emptyset , P, \emptyset , \emptyset )\). Inferences are assumed to be finitary. We disallow premiseless inferences. Waldmann et al. [19, Example 81] allow them and let the T component of initial sets consist of all of them. However, in their “reasonable strategy,” they implicitly assume that T is finite, in which case premiseless inferences can be immediately performed and replaced by the resulting formulas inserted in P.
DISCOUNT Loop without Fairness. The first version of the DISCOUNT loop, formalized in DISCOUNT_Loop.thy, does not make any fairness assumption on the choice of the inference to compute or the given clause. There is no guarantee that T, P, and Y are empty at the limit, but if they are, then A is saturated at the limit. Here is an extract of the definition, omitting the delete_bwd and simplify_fwd rules:

The \(\textsf{state}\) function converts a four-tuple (T, P, Y, A) into a pair (T, N), where N is a set of labeled formulas. The labels are \(\textsf{Passive}\) (for P), \(\textsf{YY}\) (for Y), and \(\textsf{Active}\) (for A, corresponding to \(\textsf{active}\) in \(\textsf{LGC}\)). The rules compute_infer, schedule_infer, and delete_orphan_infers refine the \(\textsf{LGC}\) rules of the same names; the other rules refine process.
DISCOUNT Loop with Fairness. In the fair version of the DISCOUNT loop, formalized in Fair_DISCOUNT_Loop.thy, the scheduled inferences and the passive formulas are organized as a single queue. A state is then a triple (P, Y, A), where P is the single queue that merges T and P from the above DISCOUNT loop, and Y and A are as above. Elements of P have the forms \(\mathsf {Passive\_Inference}\; \iota \) and \(\mathsf {Passive\_Formula}\; C\). The \(\textsf{select}\) function of P is assumed to be fair: If \(\textsf{select}\) is called infinitely often, every element in the queue will eventually be chosen and the limit of P will be empty.
The definition of the transition system is as follows:

We note the following:
-
Inferences are added to P by schedule_infer. An inference can be deleted by delete_orphan_infers if one of the premises has been removed since the inference was scheduled.
-
The next element from P is chosen by compute_infer or choose_p, depending on whether it is of the form \(\mathsf {Passive\_Inference}\; \iota \) or \(\mathsf {Passive\_Formula}\; C\).
-
Formulas are added to P by simplify_bwd.
As with the Otter and iProver loops, the most important result is saturation at the limit:

Proof Sketch
The proof amounts to showing that the sets P and Y are empty at the limit. This is easy to show for finite derivations, so we focus on infinite ones. We proceed by contradiction. For P, the fairness assumption for the \(\textsf{select}\) function of the queue guarantees that P is empty at the limit, at the condition that the compute_infer and choose_p rules are collectively executed infinitely often. Since P is assumed not to be empty at the limit, these two rules must be executed only finitely often. Let i be an index from which no compute_infer or choose_p step takes place. We then have \( St _i \sqsupset St _{i+1} \sqsupset \cdots \,\), where \(\sqsupset \) is the converse of the lexicographic combination \(\sqsubset \) of two well-founded relations:
-
< on the cardinality of Y components (0 or 1);
-
as a tiebreaker, the multiset extension \(\prec \!\!\!\prec _\textsf{S}\) of \(\prec _\textsf{S}\) on unions \(P\cup Y\cup A\).
Since the lexicographic combination of well-founded relations is well founded, the chain \( St _i \sqsupset St _{i+1} \sqsupset \cdots \,\) cannot be infinite, a contradiction.
Finally, we consider Y. If Y is nonempty forever, the only possible transitions make the entire state decrease with respect to \(\sqsubset \). This yields a contradiction. \(\square \)
5 Zipperposition Loop
The Zipperposition loop [17] as described by Waldmann et al. [19, Example 82] works on four-tuples (T, P, Y, A), where the components have the same roles as in the DISCOUNT loop: T is the scheduled set, P is the passive set, Y is the given clause, if any, and A is the active set. For technical reasons, we need to enrich the state with a ghost component D (“done”), of type \({{'}{f}}\> inference \> set \), resulting in a five-tuple (T, D, P, Y, A). All the sets are finite.
The hallmark of the Zipperposition loop is that it can handle infinitary inferences. We assume that \(\mathsf {Inf\_between}\; A\; \{C\}\) is countable if A is finite. (This assumption is implicit in Waldmann et al.) To store the infinitely many conclusions of an inference, T contains possibly infinite sequences of inferences, instead of individual inferences. Premiseless inferences are also allowed. Initial states have the form \((T, P, \emptyset , \emptyset , \emptyset )\), where T contains all the premiseless inferences of the underlying proof calculus and only those.
The implementation in Zipperposition by Vukmirović et al. [17] deviates from Waldmann et al. in one important respect: Instead of sequences of inferences, Zipperposition works with sequences of subsingletons of inferences. The special value \(\emptyset \) is returned when no progress is made in computing an inference, to give control back to the given clause procedure. In the setting of Waldmann et al., this special value can be replaced by a tautology (e.g., \(\top \) or \(\top \approx \top \)), which the given clause procedure can delete as redundant.
Zipperposition Loop without Fairness. The first version of the Zipperposition loop, formalized in Zipperposition_Loop.thy, does not make any fairness assumption on the choice of the inference to compute or the given clause. Here is an extract of the definition:

The \(\mathsf {zl\_state}\) function converts a five-tuple (T, D, P, Y, A) into a pair (U, N), where
-
U consists of all the inferences contained in T minus those in D (formally written \(\mathsf {inferences\_of}\; T - D\)); and
-
N is a set of labeled formulas corresponding to P, Y, and A.
We use a multiset for the T component. Waldmann et al. use a set, but this is not very realistic because an implementation cannot in general detect duplicate infinite sequences.
The D component addresses a subtle issue in Waldmann et al. If we did not subtract D in the definition of U, the completeness theorem we would obtain from the \(\textsf{LGC}\) layer above would require the T component to be empty at the limit. However, a given inference \(\iota \) might appear in T multiple times and hence always be present, even if we keep on removing copies of it, if new copies are continuously added. The issue goes away if we add \(\iota \) to D whenever we compute it, in compute_infer—then the inference is not present in U (i.e., \(\mathsf {inferences\_of}\; T - D\)). In other words, computing an inference makes it momentarily disappear, even if there are multiple copies of it in T.
Admittedly, it is not easy to develop a robust intuitive understanding of how D works, but what matters ultimately is that D allows us to obtain a usable main metatheorem. The metatheorem states that if the set of scheduled inferences and the set of passive formulas are empty at the limit of a derivation starting in an initial state, the active formula set is saturated at the limit. We will also see, via an additional refinement layer, that the ghost component is truly a ghost and can be omitted once it has served its purpose.
Zipperposition Loop with Fairness. Unlike the fair DISCOUNT loop, the fair Zipperposition loop, formalized in Fair_Zipperposition_Loop.thy, keeps T and P separate. An extract of the Isabelle definition follows:

The presence of two queues introduces some complications. Waldmann et al. [19, Example 82] claim that “to produce fair derivations, a prover needs to choose the sequence in ComputeInfer fairly and to choose the formula in ChooseP fairly.” However, this does not suffice: A counterexample would apply compute_infer infinitely often in a fair fashion, retrieving elements from some infinite sequences, without ever applying choose_p (whose choice of formula would then be vacuously fair). The solution is to add a fairness assumption stating that compute_infer is applied at most finitely many times before choose_p is applied—or, in other words, that if compute_infer is applied infinitely often, then so is choose_p. This leads to the following main metatheorem:

Proof Sketch
Recall that \(\mathsf {zl\_state}\) maps (T, D, P, Y, A) to a pair (U, N). In the abstract \(\textsf{LGC}\) layer, U and the passive subset of N are required to be empty at the limit. To obtain the same effect in \(\leadsto _\textsf{ZLf}\), we must show that the sets U, P, and Y are empty at the limit. This is easy to show for finite derivations, so we focus on infinite ones. We proceed by contradiction.
We start with U. We first show that there must be infinitely many compute_infer steps. Assume that there are finitely many. Then there exists an index i from which no more compute_infer steps take place. We then have \( St _i \sqsupset St _{i+1} \sqsupset \cdots \,\), where \(\sqsupset \) is the converse of the lexicographic combination \(\sqsubset \) of four well-founded relations:
-
the multiset extension \(\prec \!\!\!\prec _\textsf{S}\) of \(\prec _\textsf{S}\) on unions \(P\cup Y\cup A\);
-
as a tiebreaker, \(\prec \!\!\!\prec _\textsf{S}\) on P components;
-
as a further tiebreaker, \(\prec \!\!\!\prec _\textsf{S}\) on Y components;
-
as a further tiebreaker, < on the cardinality of T components.
We get a contradiction. Having shown that there are infinitely many compute_ infer steps, we exploit the queue’s fairness to show that one of these steps will choose any given inference \(\iota \) from the queue. Thanks to the D trick, \(\iota \) will then momentarily vanish from U, ensuring that it is not in the limit. The same argument applies for any inference \(\iota \), showing that U is empty at the limit.
Next, we show that P is empty at the limit. We start by showing that there must be infinitely many choose_p steps. Assume that there are finitely many. Then, by the third assumption, there must be finitely many compute_infer steps as well. Let i be an index from which no more compute_infer steps take place. We then have \( St _i \sqsupset St _{i+1} \sqsupset \cdots \,\), as above, yielding a contradiction.
Finally, we show that Y is empty at the limit. Let i be an index such that \(Y_i \cap Y_{i+1} \cap \cdots \not = \emptyset \). Since a compute_infer step is possible only if Y is empty, no such steps are possible from index i. Again, we have \( St _i \sqsupset St _{i+1} \sqsupset \cdots \,\), a contradiction. \(\square \)
Queue of Formula Sequences. The queue data structure used for the T component of the Zipperposition loop needs to store a finite number of possibly infinite sequences of inferences. It is formalized in Prover_Lazy_List_Queue.thy. It provides the following operations on abstract queue and element types \({{'}{q}}\) and \({{'}{e}}\):

The fairness requirement on implementations of the abstract queue interface takes the following form:
If a sequence of queue operations contains infinitely many \(\mathsf {pick\_elem}\) steps and \(\iota \) is at the head of one of the sequences stored in the queue, then either the sequence will be entirely removed (by orphan deletion) or \(\iota \) will eventually be chosen.
A syntactically stronger formulation of fairness, where \(\iota \) may occur anywhere in a sequence, is derived as a corollary:
If a sequence of queue operations contains infinitely many \(\mathsf {pick\_elem}\) steps and \(\iota \) occurs in one of the sequences stored in the queue at some index in the sequence, then either the sequence (possibly amputated from its leading elements) will be entirely removed or \(\iota \) will eventually be chosen.
As a proof of concept, the theory file contains an example implementation of the queue as a FIFO queue. The proof that this FIFO queue is fair is the most finicky proof of our entire development.
Zipperposition Loop without Ghost Fields. In the last step of our development, we remove the D state component. D is useful to retrieve a usable main metatheorem for \(\leadsto _\textsf{ZL}\), but it is not explicitly referenced in the metatheorem for the fair variant \(\leadsto _\textsf{ZLf}\). The resulting transition system \(\leadsto _\textsf{ZLfw}\), formalized in Fair_Zipperposition_Loop_without_Ghosts.thy, operates on four-tuples (T, P, Y, A). Each transition is identical to the corresponding \(\leadsto _\textsf{ZLf}\) transition, omitting the D component. The main metatheorem is also essentially the same.
6 Conclusion
We presented an Isabelle/HOL formalization of four variants of the given clause procedure, starting from Tourret and Blanchette’s formalization of two abstract given clause procedures [16]. We relied extensively on stepwise refinement to derive properties of more concrete transition systems from more abstract ones.
Our main findings concern the Zipperposition loop. We found that the refinement proof is not as straightforward as previously thought [19, Example 82] and requires a nontrivial abstraction function. In addition, we discovered a fairness condition—the necessity of avoiding computing inferences forever without selecting a formula—that was not mentioned before in the literature, and we clarified other fine points.
Notes
- 1.
We keep the traditional name “given clause” even though our formulas are not necessarily clauses.
- 2.
Both groups of researchers include Blanchette and Tourret.
References
Avenhaus, J., Denzinger, J., Fuchs, M.: DISCOUNT: a system for distributed equational deduction. In: Hsiang, J. (ed.) RTA 1995. LNCS, vol. 914, pp. 397–402. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-59200-8_72
Bachmair, L., Ganzinger, H.: Rewrite-based equational theorem proving with selection and simplification. J. Log. Comput. 4(3), 217–247 (1994). https://doi.org/10.1093/logcom/4.3.217
Bachmair, L., Ganzinger, H.: Resolution theorem proving. In: Robinson, A., Voronkov, A. (eds.) Handbook of Automated Reasoning, vol. I, pp. 19–99. Elsevier and MIT Press (2001). https://doi.org/10.1016/b978-044450813-3/50004-7
Bentkamp, A., Blanchette, J., Tourret, S., Vukmirović, P.: Superposition for full higher-order logic. In: Platzer, A., Sutcliffe, G. (eds.) CADE 2021. LNCS (LNAI), vol. 12699, pp. 396–412. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-79876-5_23
Blanchette, J., Qiu, Q., Tourret, S.: Given clause loops. Archive of Formal Proofs 2023 (2023). https://www.isa-afp.org/entries/Given_Clause_Loops.html
Blanchette, J.C.: Formalizing the metatheory of logical calculi and automatic provers in Isabelle/HOL (invited talk). In: Mahboubi, A., Myreen, M.O. (eds.) CPP 2019, pp. 1–13. ACM (2019). https://doi.org/10.1145/3293880.3294087
Denzinger, J., Pitz, W.: Das DISCOUNT-System: Benutzerhandbuch. SEKI working paper, Fachbereich Informatik, Univ. Kaiserslautern (1992). https://books.google.fr/books?id=8XwBvwEACAAJ
Duarte, A., Korovin, K.: Implementing superposition in iProver (system description). In: Peltier, N., Sofronie-Stokkermans, V. (eds.) IJCAR 2020. LNCS (LNAI), vol. 12167, pp. 388–397. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-51054-1_24
Hirokawa, N., Middeldorp, A., Sternagel, C., Winkler, S.: Infinite runs in abstract completion. In: Miller, D. (ed.) FSCD 2017. LIPIcs, vol. 84, pp. 19:1–19:16. Schloss Dagstuhl–Leibniz-Zentrum für Informatik (2017). https://doi.org/10.4230/LIPIcs.FSCD.2017.19
McCune, W., Wos, L.: Otter–the CADE-13 competition incarnations. J. Autom. Reason. 18(2), 211–220 (1997). https://doi.org/10.1023/A:1005843632307
McCune, W.W.: OTTER 3.0 reference manual and guide (1994). https://doi.org/10.2172/10129052, https://www.osti.gov/biblio/10129052
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL: A Proof Assistant for Higher-Order Logic. LNCS, vol. 2283. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45949-9
Robinson, J.A.: A machine-oriented logic based on the resolution principle. J. ACM 12(1), 23–41 (1965). https://doi.org/10.1145/321250.321253
Schlichtkrull, A., Blanchette, J., Traytel, D., Waldmann, U.: Formalizing Bachmair and Ganzinger’s Ordered Resolution Prover. J. Autom. Reason. 64(7), 1169–1195 (2020). https://doi.org/10.1007/s10817-020-09561-0
Tourret, S.: A comprehensive framework for saturation theorem proving. Archive of Formal Proofs 2020 (2020). https://www.isa-afp.org/entries/Saturation_Framework.html
Tourret, S., Blanchette, J.: A modular isabelle framework for verifying saturation provers. In: Hritcu, C., Popescu, A. (eds.) CPP 2021, pp. 224–237. ACM (2021). https://doi.org/10.1145/3437992.3439912
Vukmirović, P., Bentkamp, A., Blanchette, J., Cruanes, S., Nummelin, V., Tourret, S.: Making higher-order superposition work. In: Platzer, A., Sutcliffe, G. (eds.) CADE 2021. LNCS (LNAI), vol. 12699, pp. 415–432. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-79876-5_24
Waldmann, U., Tourret, S., Robillard, S., Blanchette, J.: A comprehensive framework for saturation theorem proving. In: Peltier, N., Sofronie-Stokkermans, V. (eds.) IJCAR 2020. LNCS (LNAI), vol. 12166, pp. 316–334. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-51074-9_18
Waldmann, U., Tourret, S., Robillard, S., Blanchette, J.: A comprehensive framework for saturation theorem proving. J. Autom. Reason. 66(4), 499–539 (2022). https://doi.org/10.1007/s10817-022-09621-7
Acknowledgments
We thank Andrei Popescu for helping us with a coinductive proof that arose when removing the ghosts in the Zipperposition loop. We thank Uwe Waldmann for sharing with us his encyclopedic knowledge of the various given clause loops and their history. Finally, we thank Mark Summerfield and the anonymous reviewers for many helpful suggestions.
This research has received funding from the Netherlands Organization for Scientific Research (NWO) under the Vidi program (project No. 016.Vidi.189.037, Lean Forward).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Blanchette, J., Qiu, Q., Tourret, S. (2023). Verified Given Clause Procedures. In: Pientka, B., Tinelli, C. (eds) Automated Deduction – CADE 29. CADE 2023. Lecture Notes in Computer Science(), vol 14132. Springer, Cham. https://doi.org/10.1007/978-3-031-38499-8_4
Download citation
DOI: https://doi.org/10.1007/978-3-031-38499-8_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-38498-1
Online ISBN: 978-3-031-38499-8
eBook Packages: Computer ScienceComputer Science (R0)