Abstract
Using Isabelle/HOL, we verify the state-of-the-art decision procedure for multi-level syllogistic with singleton (MLSS for short), which is a quantifier-free fragment of set theory. We formalise its syntax and semantics as well as a sound and complete tableau calculus for it. We also provide an executable specification of a decision procedure that exhaustively applies the rules of the calculus and prove its termination. Furthermore, we extend the calculus with a lightweight type system that paves the way for an integration of the procedure into Isabelle/HOL.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
In Isabelle/HOL, there are specialised procedures for dealing with e.g. natural numbers, linear arithmetic, and metric spaces. Some of these procedures have been verified in Isabelle/HOL, such as a procedure for Presburger arithmetic [12] that was later extended to mixed real-integer arithmetic [11]. This procedure, though, uses reflection to work on goals in Isabelle/HOL, which, during execution, either sacrifices speed by going through the simplifier or requires trusting the code generator. More recently, Stevens and Nipkow [25] presented a verified decision procedure for orders that produces certificates. This approach offers efficient execution by using generated code as well as soundness because the certificates are replayed through Isabelle’s inference kernel.
This paper focuses on another ubiquitous structure in mathematics, namely sets. To the best of our knowledge, we present the first formally verified decision procedure for (a fragment of) set theory. In particular, we consider a quantifier-free fragment which Cantone and Zarba [9] call multi-level syllogistic with singleton (MLSS). The fragment includes the usual set operations of union, intersection, difference, membership, equality and, in addition, it allows the construction of singleton sets.
Since MLSS admits a tableau calculus, generating certificates will be straightforward. Like with the aforementioned order solver, this paves the way for an integration of the decision procedure into Isabelle, adding to its growing body of verified decision procedures.
1.1 Contributions
We present a formalisation in Isabelle/HOL of a tableau calculus for MLSS due to Cantone and Zarba [9] [7, Chapter 14]. We prove soundness and completeness of the calculus and give an abstract specification of a decision procedure that exhaustively applies the rules of the calculus. To obtain total correctness of the procedure, we prove its termination. Additionally, we naively refine the abstract to an executable specification from which we can generate code. The formalisation initially follows the paper but offers a more thorough account of some important details:
-
We deliver the omitted proof of Lemma 2 in the paper [9], a key building block for the completeness proof of the calculus.
-
The formal proof of completeness reveals that the calculus lacks a rule for eliminating double negation.
-
We derive an explicit upper bound for the number of formulas in a tableau branch.
In the context of Isabelle/HOL, there is one crucial aspect that requires us to modify the calculus in the paper: the calculus works under the assumption that every variable is a set; however, this is not the case in Isabelle/HOL, e.g. consider the expression
 where n is a natural number. We call these variables urelements. To deal with them, we extend the calculus with a lightweight type system and a verified inference algorithm that identifies the urelements.
where n is a natural number. We call these variables urelements. To deal with them, we extend the calculus with a lightweight type system and a verified inference algorithm that identifies the urelements.
The modification of the calculus required non-trivial changes to the completeness proof. Here, the formalisation was instrumental because Isabelle immediately revealed which proofs had been broken. This illustrates the usefulness of ITPs for developing logic calculi: they allow us to confidently make modifications without compromising correctness.
All in all, the formalisation amounts to over 6000 lines of theory. It is part of the Archive of Formal Proofs (AFP) [24]. The entry provides an overview theory MLSS_Proc_All.thy that highlights the (mostly syntactic) differences between paper and formalisation and references the constants and theorems that are introduced in this paper.
1.2 Related Work
Since the literature on decidable fragments of set theory is vast, we only focus on MLSS here. Ferro et al. [14] were the first to show the decidability of the fragment. Subsequent work [6] found the decision problem to be NP-complete. To obtain a practical decision procedure, Cantone [4] proposed a tableau calculus, which was later improved by Beckert and Hartmer [1]. Both of these procedures construct a model during execution that guides the proof search. Beckert and Hartmer also cover an extension of the calculus with uninterpreted functions, which Cantone and Zarba [10] later revisited while avoiding the construction of a model during execution. In this paper, we consider a version of the latter procedure due to Cantone and Zarba [9] that is specialised to MLSS and where the branching rules of the calculus are set up to guarantee the mutual exclusivity of the branches. Later extensions of the calculus added certain interpreted functions, such as monotone functions [8] and the inverse of a function [5]. The latter extension notably includes the Cartesian product. Those extensions, though, did not improve upon the tableau calculus for MLSS.
There is a large body of work at the intersection of ITPs and tableau methods, but to keep with this paper’s theme we only consider formalisations of correctness here. For first-order logic, there are abstract completeness proofs using the Beth-Hintikka style of possibly infinite derivation trees [3] as well as the Henkin style of maximally consistent sets [17]. Both are abstract enough to be instantiated with a wide range of concrete calculi. A more concrete formalisation [19] verifies a sequent calculus for first-order logic whose completeness proof is via a translation to semantic tableau.
Beyond completeness, we target decidability, which is more attainable for propositional logic. There is a verified tableau calculus for the modal logic S5 [2] in Lean and one for hybrid logic [18] in Isabelle/HOL. Both of these do not prove termination but there is a formalisation of a tableau calculus for the temporal logic CTL in Coq [13] that does.
1.3 Notation
Isabelle/HOL [21] conforms to everyday mathematical notation for the most part. We establish notation and in particular some essential data types together with their primitive operations that are specific to Isabelle/HOL.
We write
 to specify that the term t has the type ’a and
to specify that the term t has the type ’a and
 for the space of total functions from type ’a to type
for the space of total functions from type ’a to type
 .
.
Sets with elements of type ’a have the type
 . The cardinality of a set A is denoted by
. The cardinality of a set A is denoted by
 and the image of A under f by
and the image of A under f by
 .
.
We use
 to describe the type of lists, which are constructed using the empty list [] constructor or the infix cons constructor #, and are appended with the infix operator @. The function
to describe the type of lists, which are constructed using the empty list [] constructor or the infix cons constructor #, and are appended with the infix operator @. The function
 converts a list into a set.
converts a list into a set.
We remark that \(\longleftrightarrow \) is equivalent to \(=\) on the type of Booleans
 and \(\equiv \) is definitional equality of the meta-logic of Isabelle/HOL, which is called Isabelle/Pure. Meta-implication is denoted by \(\Longrightarrow \) and a chain of implications
and \(\equiv \) is definitional equality of the meta-logic of Isabelle/HOL, which is called Isabelle/Pure. Meta-implication is denoted by \(\Longrightarrow \) and a chain of implications
 can be abbreviated by
can be abbreviated by
 .
.
2 Syntax and Semantics of MLSS
2.1 Syntax
At the heart of MLSS, we have the type of set terms, which is the disjoint union of the empty set and variables as well as the operations union, intersection, difference, and the singleton set represented by the constructor
 . We keep the type of variables abstract by making it a parameter of the set term data type. The only restriction on the type of variables is that it needs to be infinite. Isabelle/HOL’s data type package automatically defines a function that gives us the set of variables in a set term, which we name
. We keep the type of variables abstract by making it a parameter of the set term data type. The only restriction on the type of variables is that it needs to be infinite. Isabelle/HOL’s data type package automatically defines a function that gives us the set of variables in a set term, which we name
 . In what follows, we will overload the function
. In what follows, we will overload the function
 to also work on set atoms, formulas, and branches.
to also work on set atoms, formulas, and branches.

We can combine two set terms to form a set atom by using the membership or the equality operator.

With the above operators we can also represent the subset operator \(\sqsubseteq _\text {s}\) and enumerate finite sets:
 is equivalent to
is equivalent to
 and a finite set of elements
and a finite set of elements
 can be expressed by
can be expressed by
 .
.
We use the propositional fragment of formulas due to Nipkow [20] with set atoms as propositional atoms to form the quantifier-free fragment MLSS of set theory.

We will often drop the atom constructor
 to reduce clutter. Additionally, we use
to reduce clutter. Additionally, we use
 and
and
 to denote
to denote
 and
and
 , respectively.
, respectively.
Similarly to
 , we get the function
, we get the function
 for free that retrieves all set atoms in a formula. We combine these functions to extract all the variables occurring in a set formula.
for free that retrieves all set atoms in a formula. We combine these functions to extract all the variables occurring in a set formula.

Likewise, we fix the constant
 that is polymorphic in its argument type b. We overload this constant to return the set terms that are subterms of a set term, set atom, or formula, respectively. Lastly, we introduce the function
that is polymorphic in its argument type b. We overload this constant to return the set terms that are subterms of a set term, set atom, or formula, respectively. Lastly, we introduce the function
 that computes the subformulas of a formula. The functions
that computes the subformulas of a formula. The functions
 and
and
 are implemented in the expected way.
are implemented in the expected way.
2.2 Semantics
The original paper [9] bases the semantics of MLSS on the von Neumann hierarchy of sets \(\mathcal {V}\). We instead use the hierarchy of hereditarily finite sets (HF sets) which fulfil all the same axioms as \(\mathcal {V}\) – that is, the axioms of ZF – except for the axiom of infinity. In particular, the membership relation is well-founded. The HF sets, as we will see, are sufficient to construct a model for any satisfiable MLSS formula. In contrast to \(\mathcal {V}\), the HF sets are directly representable in Isabelle/HOL, and indeed, an AFP entry [23] formalises them. The entry defines a type
 that comes with the following functionality:
that comes with the following functionality:
-
The function
 that converts a finite set of HF sets into an HF set.
that converts a finite set of HF sets into an HF set. -
The usual set operations such as equality (\(=\)), membership (\(\boldsymbol{\in }\)), union (\(\sqcup \)), intersection (\(\sqcap \)), and difference (−) are defined.
-
Finally, the empty set coincides with the ordinal 0, so it is denoted by
 .
.
Equipped with the above, we define the interpretation functions
-
 and
and -

in the standard way, i.e. by mapping each syntactic construct to the corresponding operation on HF sets and interpreting variables with respect to a given valuation function
 . For the concrete definition we refer to the formalisation.
. For the concrete definition we refer to the formalisation.
We write M \(\models \phi \) for the judgement that the formula \(\phi \) holds under the valuation function M. The implementation of \(\models \) coincides with the interpretation function of Nipkow [20]. As usual, we call a formula \(\phi \) satisfiable if there exists a model M with M \(\models \phi \). Otherwise, we say that \(\phi \) is unsatisfiable.
3 A Tableau Calculus for MLSS
We formalise the tableau calculus for MLSS as described by Cantone and Zarba [9]. Inspired by the formalisation of a tableau calculus for hybrid logic by From [16], we use lists to represent the branches of the tableau tree. Note that we add formulas to the front of the list during branch expansion, so
 for a branch b is always the formula we are trying to disprove with the tableau. We sometimes call this formula the initial formula.
for a branch b is always the formula we are trying to disprove with the tableau. We sometimes call this formula the initial formula.

We lift the functions
 and
and
 to branches in the expected way.
to branches in the expected way.
In the standard tableau calculus for propositional logic as Fitting [15] describes it, a branch is called closed if it contains both the negation of a formula and the formula itself; conversely, it is called open if it is not closed. For MLSS, we extend the notion of closedness with three additional rules; the first two are straightforward while the last one states that a branch is closed when the branch contains a membership cycle
 .
.

A tableau is called closed if all of its branches are closed.
3.1 Linear Expansion Rules
The calculus considers two kinds of branch expansion rules: linear and branching rules. As the name suggests, branching rules lead to the creation of new branches in the tableau while linear rules only extend a branch b with new formulas
 , which we denote by
, which we denote by
 . Table 1 shows the linear expansion rules. Note that in the first two rules for \(=_\text {s}\), l is a literal occurring in the branch. Furthermore, the term-for-term substitution
. Table 1 shows the linear expansion rules. Note that in the first two rules for \(=_\text {s}\), l is a literal occurring in the branch. Furthermore, the term-for-term substitution
 is restricted to the top-level set terms of l, i.e. the set terms that occur directly under one of the atom constructors \(\in _\text {s}\) or \(=_\text {s}\); for example, given the literal
is restricted to the top-level set terms of l, i.e. the set terms that occur directly under one of the atom constructors \(\in _\text {s}\) or \(=_\text {s}\); for example, given the literal

we have

A more crucial restriction of the linear rules is that no new subterm may be created by their application; for instance, the second rule for \(\in _\text {s}\) is

which formally represents

and may only be used under the condition
 . The purpose of this restriction is to prevent unbounded expansion of the branch. In fact, we give an explicit upper bound for the number of formulas in a branch in Sect. 7.
. The purpose of this restriction is to prevent unbounded expansion of the branch. In fact, we give an explicit upper bound for the number of formulas in a branch in Sect. 7.
Due to boundedness, repeated expansion with linear rules eventually results in a linearly saturated branch, i.e. a branch where no application of linear rules would produce new formulas.

Finally, we remark that the original paper [9] is missing the last propositional rule dealing with double negation. This rule is required for completeness, though, considering that the branch
 is saturated—neither linear nor branching rules apply—and open, but there clearly is no model for the initial formula
is saturated—neither linear nor branching rules apply—and open, but there clearly is no model for the initial formula
 .
.
 here. All rules coincide with the original paper [9] so we only show an illustrative subset.
here. All rules coincide with the original paper [9] so we only show an illustrative subset.3.2 Branching Rules
After running out of linear rules to apply, only the branching rules shown in Table 2 remain. A rule is applicable if its precondition is met and, to prevent unnecessary branching, if it is not subsumed as indicated by the subsumption condition. These rules create multiple branches in the tableau, so we represent the different possibilities
 to expand a branch b as a set and write
to expand a branch b as a set and write
 . Accordingly, we get a new branch
. Accordingly, we get a new branch
 in the tableau for each
in the tableau for each
 .
.
A linearly saturated branch where no further branching is possible is called a saturated branch.

Note that even branching rules are defined such that they never create new subterms, except for the last rule that adds a new variable to the branch. These variables serve to manifest an inequality; hence, we call them witnesses.

4 A Decision Procedure for MLSS
The mechanics of the decision procedure are typical for a procedure based on a tableau calculus: it decides the satisfiability of a given formula \(\phi \) by determining whether the formula has a closed tableau. More specifically, it initialises the tableau with the singleton branch [\(\phi \)] and checks whether this branch can be expanded to a closed tableau.
We only discuss the abstract specification here and refer the reader to the formalisation for the executable specification. The implementation uses a couple of features of Isabelle/HOL’s function package: instead of defining the function via pattern matching, we specify the equations of the function as conditional rewrite rules. This requires us to prove that the assumptions of the equations are non-overlapping, which is done by automation. The other concern is that Isabelle/HOL requires functions to be total, so a recursive function needs to terminate for it to be well-defined; nevertheless, the termination proof is separated from the definition of the function for modularity. The function package maintains the soundness of the definition by introducing a so-called domain predicate
 which characterises the arguments for which the function terminates. Each equation of the function is guarded by an assumption that the predicate holds for the argument. In Sect. 7, we will show that the domain predicate holds for the context in which the function
which characterises the arguments for which the function terminates. Each equation of the function is guarded by an assumption that the predicate holds for the argument. In Sect. 7, we will show that the domain predicate holds for the context in which the function
 is called in. Before we go into more detail on how the termination is proved, we discuss the definition of the function, as shown below.
is called in. Before we go into more detail on how the termination is proved, we discuss the definition of the function, as shown below.

The purpose of the function is to determine whether we can expand a given branch to a closed tableau. As stated before, we first use linear expansion rules in order to prevent premature branching; to this end, we recursively expand the branch with linear rules until the branch is linearly saturated. Note that we use Hilbert’s \(\varepsilon \)-operator in the form of
 Footnote 1 to choose some rule that actually adds new formulas to the branch. As soon as the branch is linearly saturated, we terminate if the branch is closed as the second equation shows. Otherwise, we choose an applicable branching rule and recursively check whether all newly created branches can be closed. The final equation applies once no further branch expansion is possible, in which case we just test for closedness of the branch.
Footnote 1 to choose some rule that actually adds new formulas to the branch. As soon as the branch is linearly saturated, we terminate if the branch is closed as the second equation shows. Otherwise, we choose an applicable branching rule and recursively check whether all newly created branches can be closed. The final equation applies once no further branch expansion is possible, in which case we just test for closedness of the branch.
The procedure
 then calls
then calls
 with a singleton branch [\(\phi \)] to determine the satisfiability of a given formula \(\phi \).
with a singleton branch [\(\phi \)] to determine the satisfiability of a given formula \(\phi \).
Thus, we use
 is only on branches that result from applying the expansion rules. We call this kind of branch well-formed. In the definition below, the expression
is only on branches that result from applying the expansion rules. We call this kind of branch well-formed. In the definition below, the expression
 denotes that b’ is one of the branches that results from applying (potentially zero) expansion rules to b.
denotes that b’ is one of the branches that results from applying (potentially zero) expansion rules to b.

We use this notion in Sect. 7 to state an upper bound for the cardinality of well-formed branches. The upper bound justifies the termination of the decision procedure. Before we come to that, though, we prove soundness and completeness in Sect. 6 and 5, respectively. In Sect. 7, we also show that both properties easily transfer to
 , which, together with termination, establishes that it is a decision procedure.
, which, together with termination, establishes that it is a decision procedure.
5 Completeness of the Calculus
For completeness of the calculus, we need to show that every unsatisfiable formula has a closed tableau or, conversely, that the formula is satisfiable if there is a saturated and open branch in the tableau. To facilitate inductive reasoning, we show a stronger statement by constructing a model M such that M \(\models \phi \) for all
 . At the core of the model, there is a realisation function that maps set terms to sets of type hf. A subset of the witnesses, which we call pure witnesses, receives special treatment from the realisation function for reasons that will become apparent in Sect. 5.1. The collection of set terms of a branch can thus be partitioned into two collections, as defined below.
. At the core of the model, there is a realisation function that maps set terms to sets of type hf. A subset of the witnesses, which we call pure witnesses, receives special treatment from the realisation function for reasons that will become apparent in Sect. 5.1. The collection of set terms of a branch can thus be partitioned into two collections, as defined below.

We aim to construct a syntactic model that we derive from the membership literals
 in the branch. To this end, we construct a graph whose vertices are the disjoint union of the sets above and there is an edge from s to t in the graph if, and only if,
in the branch. To this end, we construct a graph whose vertices are the disjoint union of the sets above and there is an edge from s to t in the graph if, and only if,
 is in b. Note that we use Noschinski’s graph library [22] which represents a graph as a record of vertices, arcs (directed edges), and two functions
is in b. Note that we use Noschinski’s graph library [22] which represents a graph as a record of vertices, arcs (directed edges), and two functions
 and
and
 that map an arc to its source and target vertex, respectively.
that map an arc to its source and target vertex, respectively.

The realisation function is defined relative to this graph. As mentioned before, the realisation function treats the pure witnesses differently than the rest of the set terms. The function evaluates terms in the latter set in accordance to the structure of the graph, i.e. the realisation of a vertex is defined as the union of the realisations of the parent vertices. For the former set, we choose a function I that assigns the pure witnesses pairwise distinct sets with cardinality greater than that of the vertices. We can always choose such a function since we assume an infinite universe of variables. Then, we return the singleton set
 , which, together with the cardinality constraint, guarantees that realisations are distinct between pure witnesses themselves as well as between pure witnesses and set terms. The notation
, which, together with the cardinality constraint, guarantees that realisations are distinct between pure witnesses themselves as well as between pure witnesses and set terms. The notation
 in the definition below indicates that there is an edge from u to s in the graph G.
in the definition below indicates that there is an edge from u to s in the graph G.

Again, we need to ensure that the assumptions of the equations are non-overlapping and that the function terminates. The former is taken care of by automation, leaving us to prove termination. The assumption that b is open implies that there are no membership cycles, thus
 is acyclic. Furthermore, the graph is finite by definition. Thus, we can use the cardinality of the set of ancestors as a measure that decreases in each recursive call.
is acyclic. Furthermore, the graph is finite by definition. Thus, we can use the cardinality of the set of ancestors as a measure that decreases in each recursive call.
Before we prove that the realisation function constitutes a model in Sect. 5.2, we will first explain the significance of the pure witnesses.
5.1 Characterisation of the Pure Witnesses
Recall that the pure witnesses of a branch b are those witnesses that are not related to other subterms in
 by equality. In the context of a well-formed branch, we can strengthen this characterisation to any set term and, in addition, we also get that there is no membership literal where a pure witness is on the right-hand side. Intuitively speaking, the realisation of a pure witness does not depend on the realisation of any other set term.
by equality. In the context of a well-formed branch, we can strengthen this characterisation to any set term and, in addition, we also get that there is no membership literal where a pure witness is on the right-hand side. Intuitively speaking, the realisation of a pure witness does not depend on the realisation of any other set term.

So why are pure witnesses treated differently? According to the definition of
 , it would evaluate the pure witnesses would to the empty set
, it would evaluate the pure witnesses would to the empty set
 , were they not treated separately. To see that this is a problem, consider the branch
, were they not treated separately. To see that this is a problem, consider the branch
 which expands to several open and saturated branches, one of which is
which expands to several open and saturated branches, one of which is

for some fresh x and y. Assigning both
 and
and
 a value of 0 would contradict the literal
a value of 0 would contradict the literal
 . To prevent this, we assign the pure witnesses pairwise different values.
. To prevent this, we assign the pure witnesses pairwise different values.
The proof of lemma_2 is more technical than interesting so we refer the reader to the formalisation.
5.2 Realisation of an Open Branch
Remember that for completeness, we need to show that the realisation function for an open and saturated branch b actually constitutes a model for all formulas in the branch. We start by verifying that the realisation function models all literals in the branch; more formally, the following propositions hold:
-
(1)
We have
 if it holds that
if it holds that
 is in b.
is in b. -
(2)
We have
 if
if
 is in b.
is in b. -
(3)
We have
 if
if
 is in b.
is in b. -
(4)
We have
 if it holds that
if it holds that
 is in b.
is in b.
To illustrate the usefulness of lemma_2, we prove Proposition (2). The proofs of all propositions translate well into Isabelle, so we refer to the original paper [9] for the remaining proofs.
Proof
(Proof of Proposition (2)). Assume that
 is in b. If there exists a
is in b. If there exists a
 where
where
 or
or
 , we arrive at a contradiction due to lemma_2. Therefore, both
, we arrive at a contradiction due to lemma_2. Therefore, both
 and
and
 must hold. Now, assume for contradiction that
must hold. Now, assume for contradiction that
 . Without loss of generality—the other case is symmetric—we obtain an e such that
. Without loss of generality—the other case is symmetric—we obtain an e such that
 and
and
 . Considering that
. Considering that
 and the definition of
and the definition of
 , we obtain a d with
, we obtain a d with
 and
and
 . This, in turn, yields that
. This, in turn, yields that
 must be in b. Together with the assumption
must be in b. Together with the assumption
 and the saturation of b, it follows that
and the saturation of b, it follows that
 must also be in b. But then we have
must also be in b. But then we have
 using Proposition (1), which is a contradiction to the assumption
using Proposition (1), which is a contradiction to the assumption
 .
.
We now lower the results on literals to set terms. All of the proofs are straightforward so we refer the reader to the formalisation.
-
(a)
It holds that
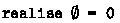 .
. -
(b)
Let
 . If the term
. If the term
 occurs in
occurs in
 , then
, then 
-
(c)
If
 , then
, then 
The final step for obtaining a proper model is to connect the realisation function to the semantics as defined in Sect. 2. For set terms, we can use the Propositions (a)–(c) to prove the lemma below by induction on t.

Lifting the above result to formulas yields the coherence of b, as the original paper [9] calls it. The proof is a tedious but straightforward induction on the the size of the formulas.

The coherence property finishes the proof of completeness of the calculus as it gives us a model for every formula in an open and saturated branch.
6 Soundness of the Calculus
A tableau calculus is sound if the corresponding formula is unsatisfiable for any closed tableau. We prove the following two properties to establish soundness:
-
(1)
It is impossible to satisfy all formulas in a closed branch simultaneously.
-
(2)
The expansion rules maintain satisfiability.
We formalise the first property in Isabelle below.

Proof
It is clear that, for any s, neither does M model
 nor
nor
 . Furthermore, no model can satisfy both \(\phi \) and
. Furthermore, no model can satisfy both \(\phi \) and
 at the same time. Lastly, a membership cycle is impossible since the membership relation of
at the same time. Lastly, a membership cycle is impossible since the membership relation of
 is well-founded.
is well-founded.
We are left with showing that both linear and branching expansion rules preserve satisfiability. As for the linear rules, a straightforward proof by case analysis on
 suffices to obtain the lemma below.
suffices to obtain the lemma below.

A similar argument would work for the branching rules if it were not for the last rule adding new variables. Those variables need to be assigned specific values; hence, we modify the model as shown in the proof below.

Proof
We only consider the case where
 was proved by applying the last branching expansion rule to
was proved by applying the last branching expansion rule to
 for some s and t. We have
for some s and t. We have

for some fresh variable x. Since
 is in b, we have that
is in b, we have that
 because M is a model. Without loss of generality, this inequality manifests itself through some y with
because M is a model. Without loss of generality, this inequality manifests itself through some y with
 and
and
 . We update M to map x to y to obtain the assignment M’. Note that M’ is still a model for formulas in b because x is fresh with respect to b. Furthermore, it is also a model for the first branch in
. We update M to map x to y to obtain the assignment M’. Note that M’ is still a model for formulas in b because x is fresh with respect to b. Furthermore, it is also a model for the first branch in
 , which finishes the proof.
, which finishes the proof.
7 Total Correctness of the Decision Procedure
We first demonstrate the termination of the procedure for well-formed branches, i.e. every well-formed branch is in the domain of
 . To this end, we derive an upper bound for the number of distinct formulas in a branch whose proof we omit here for brevity. We should point out that this bound is not to be construed as the complexity of the procedure as it may create exponentially many branches in general.
. To this end, we derive an upper bound for the number of distinct formulas in a branch whose proof we omit here for brevity. We should point out that this bound is not to be construed as the complexity of the procedure as it may create exponentially many branches in general.

Remember that
 only applies a linear expansion rule to a branch if the application results in new formulas. Moreover, the subsumption conditions of the branching expansion rules ensure that each of the newly created branches contain new formulas. Ultimately, we conclude that the procedure must terminate for well-formed branches because the number of formulas increases in each step but is also bounded.
only applies a linear expansion rule to a branch if the application results in new formulas. Moreover, the subsumption conditions of the branching expansion rules ensure that each of the newly created branches contain new formulas. Ultimately, we conclude that the procedure must terminate for well-formed branches because the number of formulas increases in each step but is also bounded.

The above lemma allows us to utilise the computation induction rule of
 on well-formed branches, which we use to prove soundness and completeness. As both proofs are essentially an application of soundness, respectively completeness, of the calculus, we refer the reader to the formalisation.
on well-formed branches, which we use to prove soundness and completeness. As both proofs are essentially an application of soundness, respectively completeness, of the calculus, we refer the reader to the formalisation.

To finish the proof of total correctness, note that every singleton branch is trivially well-formed; thus, termination, completeness, and soundness easily transfer to
 .
.

8 Dealing with Urelements
In the introduction, we stated the goal of integrating
 as a tactic into Isabelle. For this to work, we must map every branch expansion rule to a corresponding theorem in Isabelle/HOL. This is straightforward for all expansion rules except for the last branching expansion rule. To illustrate, suppose that we are to disprove a statement of the form
as a tactic into Isabelle. For this to work, we must map every branch expansion rule to a corresponding theorem in Isabelle/HOL. This is straightforward for all expansion rules except for the last branching expansion rule. To illustrate, suppose that we are to disprove a statement of the form

in Isabelle/HOL. By way of reification, we convert this to a formula of the shape

in our set syntax for some s’, t’, A’, and B’. When we apply the decision procedure to this formula, it might return a tableau proof that contains an application of the last branching rule to
 . This results in two branches, one of which is
. This results in two branches, one of which is
 ; however, there is no matching rule in Isabelle/HOL since s and t are not sets.
; however, there is no matching rule in Isabelle/HOL since s and t are not sets.
To deal with this problem, we formalise a lightweight type system as displayed in Fig. 1. The type of a set term in this system is just a natural number which we call level. Intuitively speaking, the level l means that the corresponding term t in Isabelle/HOL has type
for some ’a. Note that the constructor \(\emptyset \) now receives an additional argument indicating the level of each instance of \(\emptyset \).
Moreover, the typing judgement extends to set atoms by matching up the levels of its component set terms.
Ultimately, we define
 in order to type formulas.
in order to type formulas.
We can now define the urelements with respect to a formula. An urelement is a set term whose corresponding type in Isabelle/HOL might not be a set.

Using this definition, we make two changes to the specification of the calculus: (1) First and foremost, we require that neither s nor t is an urelement in the precondition of the last branching expansion rule. (2) As mentioned above, we add an argument to the \(\emptyset \) constructor. This argument is only used for the typing judgement; it has no impact on the semantics.
Soundness, of course, is not affected by these changes but we have to make a few amendments to maintain completeness: (1) The first equation of
 now also must account for the urelements. In particular, it has to ensure that urelements receive pairwise different values unless they are related through equality atoms. This does not affect pure witnesses since they can not be related through equality atoms due to lemma_2. (2) We must adjust the completeness proof in those places where it directly refers to the definition of
now also must account for the urelements. In particular, it has to ensure that urelements receive pairwise different values unless they are related through equality atoms. This does not affect pure witnesses since they can not be related through equality atoms due to lemma_2. (2) We must adjust the completeness proof in those places where it directly refers to the definition of
 to account for the case where a given term is an urelement. (3) The completeness theorem receives the additional assumption that \(\varGamma \vdash \phi \) holds for the initial formula \(\phi \). (4) For the completeness proof, we must show that the typing judgement is invariant under branch expansion.
to account for the case where a given term is an urelement. (3) The completeness theorem receives the additional assumption that \(\varGamma \vdash \phi \) holds for the initial formula \(\phi \). (4) For the completeness proof, we must show that the typing judgement is invariant under branch expansion.
The modifications above ensure that the proof can be replayed through Isabelle/HOL. To actually use the calculus, we must determine the urelements of the initial formula \(\phi \), though. In other words, we have to implement an inference algorithm for our lightweight type system. The algorithm is, in essence, a simplified version of Hindley-Milner type inference so it has the same two phases: it generates constraints using syntax directed rules and then passes them to a constraint solver.
Since we are only interested in the level of a term, we can encode all constraints into the theory of 0, the successor function S, and equality (but no disequality). Note that constraints of the form
 can be replaced by
can be replaced by
 with i being a fresh variable. A solver for this theory is straightforward to implement and verify; nevertheless, we have to be careful that it computes the minimum assignment \(\varGamma \) from variables to levels that fulfils the constraints. This guarantees that a set term t is not an urelement if, and only if,
with i being a fresh variable. A solver for this theory is straightforward to implement and verify; nevertheless, we have to be careful that it computes the minimum assignment \(\varGamma \) from variables to levels that fulfils the constraints. This guarantees that a set term t is not an urelement if, and only if,
 . Conversely, all terms s with
. Conversely, all terms s with
 are urelements.
are urelements.
9 Conclusion and Future Work
We developed a formalisation of a tableau calculus for a quantifier-free fragment of set theory called MLSS based on a paper by Cantone and Zarba [9]. The formalisation includes an abstract description of a decision procedure that builds on the calculus. To make the decision procedure compatible with Isabelle/HOL, we extended the calculus with a lightweight type system while maintaining completeness. We also refined the abstract specification to an executable specification from which code can be generated.
In future work, we plan to implement an efficient executable specification in the style of a worklist algorithm. This specification should also generate certificates that can be replayed through Isabelle’s inference kernel to facilitate the integration of the procedure into Isabelle.
Notes
- 1.
In the formalisation, the function
 is actually parametrised by choice functions to allow for refinement.
is actually parametrised by choice functions to allow for refinement.
References
Beckert, B., Hartmer, U.: A tableau calculus for quantifier-free set theoretic formulae. In: de Swart, H. (ed.) TABLEAUX 1998. LNCS (LNAI), vol. 1397, pp. 93–107. Springer, Heidelberg (1998). https://doi.org/10.1007/3-540-69778-0_16
Bentzen, B.: A Henkin-style completeness proof for the modal logic S5. In: Baroni, P., Benzmüller, C., Wáng, Y.N. (eds.) CLAR 2021. LNCS (LNAI), vol. 13040, pp. 459–467. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-89391-0_25
Blanchette, J.C., Popescu, A., Traytel, D.: Soundness and completeness proofs by coinductive methods. J. Autom. Reason. 58(1), 149–179 (2016). https://doi.org/10.1007/s10817-016-9391-3
Cantone, D.: A fast saturation strategy for set-theoretic tableaux. In: Galmiche, D. (ed.) TABLEAUX 1997. LNCS, vol. 1227, pp. 122–137. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0027409
Cantone, D., Longo, C., Asmundo, M.N.: A decision procedure for a two-sorted extension of multi-level syllogistic with the cartesian product and some map constructs. In: Faber, W., Leone, N. (eds.) Italian Conference on Computational Logic, CEUR Workshop Proceedings, vol. 598, CEUR-WS.org (2010). http://ceur-ws.org/Vol-598/paper11.pdf
Cantone, D., Omodeo, E.G., Policriti, A.: The automation of syllogistic. J. Autom. Reasoning 6(2), 173–187 (1990). https://doi.org/10.1007/BF00245817. ISSN 0168-7433
Cantone, D., Omodeo, E.G., Policriti, A.: Set Theory for Computing - From Decision Procedures to Declarative Programming with Sets. Monographs in Computer Science. Springer, Heidelberg (2001). https://doi.org/10.1007/978-1-4757-3452-2
Cantone, D., Schwartz, J.T., Zarba, C.G.: A decision procedure for a sublanguage of set theory involving monotone, additive, and multiplicative functions. Electron. Notes Theor. Comput. Sci. 86(1), 49–60 (2003). https://doi.org/10.1016/S1571-0661(04)80652-2. International Workshop on First-Order Theorem Proving
Cantone, D., Zarba, C.G.: A new fast tableau-based decision procedure for an unquantified fragment of set theory. In: Caferra, R., Salzer, G. (eds.) FTP 1998. LNCS (LNAI), vol. 1761, pp. 126–136. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-46508-1_8
Cantone, D., Zarba, C.G.: A tableau-based decision procedure for a fragment of set theory involving a restricted form of quantification. In: Murray, N.V. (ed.) TABLEAUX 1999. LNCS (LNAI), vol. 1617, pp. 97–112. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48754-9_12
Chaieb, A.: Verifying mixed real-integer quantifier elimination. In: Furbach, U., Shankar, N. (eds.) IJCAR 2006. LNCS (LNAI), vol. 4130, pp. 528–540. Springer, Heidelberg (2006). https://doi.org/10.1007/11814771_43
Chaieb, A., Nipkow, T.: Verifying and reflecting quantifier elimination for presburger arithmetic. In: Sutcliffe, G., Voronkov, A. (eds.) LPAR 2005. LNCS (LNAI), vol. 3835, pp. 367–380. Springer, Heidelberg (2005). https://doi.org/10.1007/11591191_26
Doczkal, C., Smolka, G.: Completeness and decidability results for CTL in Coq. In: Klein, G., Gamboa, R. (eds.) ITP 2014. LNCS, vol. 8558, pp. 226–241. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08970-6_15
Ferro, A., Omodeo, E.G., Schwartz, J.T.: Decision procedures for elementary sublanguages of set theory. I. Multi-level syllogistic and some extensions. Commun. Pure Appl. Math. 33(5), 599–608 (1980). https://doi.org/10.1002/cpa.3160330503
Fitting, M.: Semantic Tableaux and Resolution. Springer, New York (1996). https://doi.org/10.1007/978-1-4612-2360-3_3
From, A.H.: Formalizing a Seligman-style tableau system for hybrid logic. Archive of Formal Proofs (2019). ISSN 2150-914x. https://isa-afp.org/entries/Hybrid_Logic.html. Formal proof development
From, A.H.: Synthetic completeness. Archive of Formal Proofs (2023). ISSN 2150-914x. https://isa-afp.org/entries/Synthetic_Completeness.html. Formal proof development
From, A.H., Blackburn, P., Villadsen, J.: Formalizing a seligman-style tableau system for hybrid logic. In: Peltier, N., Sofronie-Stokkermans, V. (eds.) IJCAR 2020. LNCS (LNAI), vol. 12166, pp. 474–481. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-51074-9_27
From, A.H., Schlichtkrull, A., Villadsen, J.: A sequent calculus for first-order logic formalized in Isabelle/HOL. In: Monica, S., Bergenti, F. (eds.) Proceedings of the 36th Italian Conference on Computational Logic, CEUR Workshop Proceedings, vol. 3002, pp. 107–121. CEUR-WS.org (2021). http://ceur-ws.org/Vol-3002/paper7.pdf
Nipkow, T.: Linear quantifier elimination. In: Armando, A., Baumgartner, P., Dowek, G. (eds.) IJCAR 2008. LNCS (LNAI), vol. 5195, pp. 18–33. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-71070-7_3
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL–A Proof Assistant for Higher-Order Logic. LNCS, vol. 2283. Springer, Heidelberg (2002)
Noschinski, L.: Graph theory. Archive of Formal Proofs (2013). ISSN 2150-914x. https://isa-afp.org/entries/Graph_Theory.html. Formal proof development
Paulson, L.C.: The hereditarily finite sets. Archive of Formal Proofs (2013). ISSN 2150-914x. https://isa-afp.org/entries/HereditarilyFinite.html. Formal proof development
Stevens, L.: MLSS decision procedure. Archive of Formal Proofs (2023). ISSN 2150-914x. https://isa-afp.org/entries/MLSS_Decision_Proc.html. Formal proof development
Stevens, L., Nipkow, T.: A verified decision procedure for orders in Isabelle/HOL. In: Hou, Z., Ganesh, V. (eds.) ATVA 2021. LNCS, vol. 12971, pp. 127–143. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-88885-5_9
Acknowledgements
The author thanks Kevin Kappelmann and Tobias Nipkow for their comments on a draft version of this paper and the anonymous referees for their thorough reviews.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Stevens, L. (2023). Towards a Verified Tableau Prover for a Quantifier-Free Fragment of Set Theory. In: Pientka, B., Tinelli, C. (eds) Automated Deduction – CADE 29. CADE 2023. Lecture Notes in Computer Science(), vol 14132. Springer, Cham. https://doi.org/10.1007/978-3-031-38499-8_28
Download citation
DOI: https://doi.org/10.1007/978-3-031-38499-8_28
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-38498-1
Online ISBN: 978-3-031-38499-8
eBook Packages: Computer ScienceComputer Science (R0)


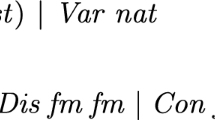


 that converts a finite set of HF sets into an HF set.
that converts a finite set of HF sets into an HF set. .
. and
and
 if it holds that
if it holds that
 is in
is in  if
if
 is in
is in  if
if
 is in
is in  if it holds that
if it holds that
 is in
is in 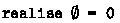 .
. . If the term
. If the term
 occurs in
occurs in
 , then
, then 
 , then
, then 

 is actually parametrised by choice functions to allow for refinement.
is actually parametrised by choice functions to allow for refinement.