Abstract
We revisit AC completion for left-linear term rewrite systems where AC unification is avoided and the normal rewrite relation can be used in order to decide validity questions. To that end, we give a new correctness proof for finite runs and establish a simulation result between the two inference systems known from the literature. Furthermore, we show how left-linear AC completion can be simulated by general AC completion. In particular, this result allows us to switch from the former to the latter at any point during a completion process. Finally, we present experimental results for our implementation of left-linear AC completion in the tool accompll.
Supported by JSPS KAKENHI Grant Number JP22K11900.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Completion has been extensively studied since its introduction in the seminal paper by Knuth and Bendix [10]. One of the main limitations of the original formulation is its inability to deal with equations which cannot be oriented into a terminating rule such as the commutativity axiom. This shortcoming can be resolved by completion modulo an equational theory \(\mathcal {E}\). In the literature, there are two different approaches of achieving this. The general approach [3, 6] requires \(\mathcal {E}\)-unification and allows us to decide validity problems using the rewrite relation \(\rightarrow _{\mathcal {R}/\mathcal {E}}\) which is defined as \(\leftrightarrow _{\mathcal {E}}^{*} \cdot \rightarrow _{\mathcal {R}}^{} \cdot \leftrightarrow _{\mathcal {E}}^{*}\). For left-linear term rewrite systems, however, there is Huet’s approach [5] which avoids \(\mathcal {E}\)-unification and allows us to decide validity problems with the normal rewrite relation \(\rightarrow _{\mathcal {R}}\) and a single check for \(\mathcal {E}\)-equivalence of the computed normal forms. In their respective books, Avenhaus [1] and Bachmair [3] present inference systems for left-linear completion modulo an equational theory. In this paper, we revisit slightly modified versions (\(\textsf{A}\) and \(\textsf{B}\)) of these inference systems for finite runs. In addition to a new correctness proof for \(\textsf{A}\) in the spirit of [4] which does not rely on proof orderings (Sect. 3), we reduce correctness of \(\textsf{B}\) to the correctness of \(\textsf{A}\) by establishing a simulation result between finite runs in these systems (Sect. 4). For the concrete equational theory of associative and commutative (AC) function symbols, we also show the connection between the inference system \(\textsf{A}\) and general AC completion by means of another simulation result (Sect. 5). Finally, we present experimental results obtained from our implementation of \(\textsf{A}\) for AC in the tool accompll which show that the avoidance of AC unification can result in significant performance improvements over general AC completion (Sects. 6 and 7).
2 Preliminaries
We assume familiarity with term rewriting and completion as described e.g. in [2] but recall some central notions. We consider term rewriting systems (TRSs) which operate on terms over a given signature \(\mathcal {F}\). Terms which do not contain the same variable more than once are referred to as linear terms. We say that a TRS is left-linear if \(\ell \) is a linear term for every rule \({\ell \rightarrow r} \in \mathcal {R}\). A TRS \(\mathcal {R}\) is terminating if the associated rewrite relation \(\rightarrow _{\mathcal {R}}\) is well-founded. In that case, we write \(s \rightarrow _{\mathcal {R}}^{!} t\) if t is a normal form of s. A TRS \(\mathcal {R}\) is confluent if different computation paths can always be joined, i.e.,
 . An important sufficient criterion for confluence is the well-known critical pair lemma which states that a terminating TRS is confluent if all non-trivial overlaps between left-hand sides of rules (critical pairs) are joinable. Furthermore, there is the notion of prime critical pairs [8] which further restricts the considered critical peaks
. An important sufficient criterion for confluence is the well-known critical pair lemma which states that a terminating TRS is confluent if all non-trivial overlaps between left-hand sides of rules (critical pairs) are joinable. Furthermore, there is the notion of prime critical pairs [8] which further restricts the considered critical peaks
 to the ones where all proper subterms of \(s|_p\) are irreducible. In particular, terminating TRSs whose prime critical pairs are joinable are also confluent. The set of (prime) critical pairs is denoted by \(\textsf{CP}({\mathcal {R}})\) (\(\textsf{PCP}({\mathcal {R}})\)). We define \(\textsf{CP}({\mathcal {R}_1,\mathcal {R}_2})\) as the set of all critical pairs stemming from local peaks of the form
to the ones where all proper subterms of \(s|_p\) are irreducible. In particular, terminating TRSs whose prime critical pairs are joinable are also confluent. The set of (prime) critical pairs is denoted by \(\textsf{CP}({\mathcal {R}})\) (\(\textsf{PCP}({\mathcal {R}})\)). We define \(\textsf{CP}({\mathcal {R}_1,\mathcal {R}_2})\) as the set of all critical pairs stemming from local peaks of the form
 and \(\textsf{CP}^{\pm }({\mathcal {R}_1,\mathcal {R}_2}) = \textsf{CP}({\mathcal {R}_1,\mathcal {R}_2}) \cup \textsf{CP}({\mathcal {R}_2,\mathcal {R}_1})\). A TRS is complete if it is terminating and confluent. Hence, a complete presentation \(\mathcal {R}\) of an equational system (ES) \(\mathcal {E}\) can be used to decide the validity problem for \(\mathcal {E}\): \(s \leftrightarrow _{\mathcal {E}}^{*} t\) if and only if
and \(\textsf{CP}^{\pm }({\mathcal {R}_1,\mathcal {R}_2}) = \textsf{CP}({\mathcal {R}_1,\mathcal {R}_2}) \cup \textsf{CP}({\mathcal {R}_2,\mathcal {R}_1})\). A TRS is complete if it is terminating and confluent. Hence, a complete presentation \(\mathcal {R}\) of an equational system (ES) \(\mathcal {E}\) can be used to decide the validity problem for \(\mathcal {E}\): \(s \leftrightarrow _{\mathcal {E}}^{*} t\) if and only if
 .
.
We now turn our attention to rewriting modulo AC function symbols. To that end, we start by giving general definitions for abstract rewrite systems (ARSs). Let \(\mathcal {A}= \langle A,{\rightarrow } \rangle \) be an ARS and \(\sim \) an equivalence relation on A. We write \(\Leftrightarrow \) for \(\leftarrow \cup \rightarrow \cup \sim \), \({\rightarrow }/{\sim }\) for \(\sim \cdot \rightarrow \cdot \sim \) and \(\downarrow ^{\sim }\) for
 . Given \(\mathcal {A}\), we denote \(\langle A,{{\rightarrow }/{\sim }} \rangle \) by \({\mathcal {A}}/{\sim }\). The ARS \(\mathcal {A}\) is terminating modulo \(\sim \) if there are no infinite rewrite sequences with \({\rightarrow }/{\sim }\) and Church–Rosser modulo \(\sim \) if \({\Leftrightarrow ^{*}} \subseteq {\downarrow ^{\sim }}\). The ARS \(\mathcal {A}\) is complete modulo \(\sim \) if it is terminating modulo \(\sim \) and Church–Rosser modulo \(\sim \). While there is no distinction for termination modulo \(\sim \) between \(\mathcal {A}\) and \({\mathcal {A}}/{\sim }\) (\({\sim \cdot \sim } = {\sim }\) by transitivity), it makes a considerable difference whether we talk about the Church–Rosser modulo \(\sim \) property and therefore completeness modulo \(\sim \) of \(\mathcal {A}\) or \({\mathcal {A}}/{\sim }\). The following lemma is taken from [1, Lemma 4.1.12]. It establishes an important connection between the Church–Rosser modulo \(\sim \) property of an ARS \(\mathcal {A}\) and \({\mathcal {A}}/{\sim }\).
. Given \(\mathcal {A}\), we denote \(\langle A,{{\rightarrow }/{\sim }} \rangle \) by \({\mathcal {A}}/{\sim }\). The ARS \(\mathcal {A}\) is terminating modulo \(\sim \) if there are no infinite rewrite sequences with \({\rightarrow }/{\sim }\) and Church–Rosser modulo \(\sim \) if \({\Leftrightarrow ^{*}} \subseteq {\downarrow ^{\sim }}\). The ARS \(\mathcal {A}\) is complete modulo \(\sim \) if it is terminating modulo \(\sim \) and Church–Rosser modulo \(\sim \). While there is no distinction for termination modulo \(\sim \) between \(\mathcal {A}\) and \({\mathcal {A}}/{\sim }\) (\({\sim \cdot \sim } = {\sim }\) by transitivity), it makes a considerable difference whether we talk about the Church–Rosser modulo \(\sim \) property and therefore completeness modulo \(\sim \) of \(\mathcal {A}\) or \({\mathcal {A}}/{\sim }\). The following lemma is taken from [1, Lemma 4.1.12]. It establishes an important connection between the Church–Rosser modulo \(\sim \) property of an ARS \(\mathcal {A}\) and \({\mathcal {A}}/{\sim }\).
Lemma 1
Let \(\mathcal {A}= \langle A,{\rightarrow } \rangle \) and \(\mathcal {A}' = \langle A,{\rightharpoonup } \rangle \) be ARSs and \(\sim \) an equivalence relation on A such that \({\rightarrow } \subseteq {\rightharpoonup } \subseteq {{\rightarrow }/{\sim }}\). If \(\mathcal {A}'\) is Church–Rosser modulo \(\sim \) then \({\mathcal {A}}/{\sim }\) is Church–Rosser modulo \(\sim \).
The definitions and results for ARSs carry over to TRSs by replacing the equivalence relation \(\sim \) by the equational theory \(\leftrightarrow _{\mathcal {B}}^{*}\) of an ES \(\mathcal {B}\). Most theoretical results of this paper are not specific to AC but hold for an arbitrary base theory \(\mathcal {B}\) of which we only demand that \(\mathcal {V}\textsf{ar}({\ell }) = \mathcal {V}\textsf{ar}({r})\) for all \({\ell \approx r} \in \mathcal {B}\). We abbreviate \(\leftrightarrow _{\mathcal {B}}^{*}\) by \(\sim _{\mathcal {B}}\) and the rewrite relation \(\rightarrow _{\mathcal {R}/\mathcal {B}}\) is defined as \(\sim _{\mathcal {B}}\cdot \rightarrow _{\mathcal {R}} \cdot \sim _{\mathcal {B}}\). Furthermore, we write \(\downarrow _{\mathcal {R}}^{\sim }\) for the relation
 . Termination modulo \(\mathcal {B}\) is shown by \(\mathcal {B}\)-compatible reduction orders >, i.e., > is well-founded, closed under contexts and substitutions and \({\sim _{\mathcal {B}}\cdot> \cdot \sim _{\mathcal {B}}} \subseteq {>}\). This paper deals with a completion procedure which produces TRSs \(\mathcal {R}\) such that \(\mathcal {R}\) (rather than \(\mathcal {R}/\mathcal {B}\)) is complete modulo \(\mathcal {B}\). In particular, the completion procedure uses the joinability with respect to \(\downarrow _{\mathcal {R}}^{\sim }\) of \(\textsf{CP}({\mathcal {R}}) \cup \textsf{CP}^{\pm }({\mathcal {R},\mathcal {B}^\pm })\) where \(\mathcal {B}^\pm \) denotes \(\mathcal {B}\cup \{r \approx \ell \mid {\ell \approx r} \in \mathcal {B}\}\) as a sufficient and necessary criterion for the Church–Rosser modulo \(\mathcal {B}\) property of a \(\mathcal {B}\)-terminating TRS \(\mathcal {R}\). Note that this criterion works with standard critical pairs and therefore does not need unification modulo \(\mathcal {B}\). However, the criterion is not valid for non-left-linear TRSs as the following example shows.
. Termination modulo \(\mathcal {B}\) is shown by \(\mathcal {B}\)-compatible reduction orders >, i.e., > is well-founded, closed under contexts and substitutions and \({\sim _{\mathcal {B}}\cdot> \cdot \sim _{\mathcal {B}}} \subseteq {>}\). This paper deals with a completion procedure which produces TRSs \(\mathcal {R}\) such that \(\mathcal {R}\) (rather than \(\mathcal {R}/\mathcal {B}\)) is complete modulo \(\mathcal {B}\). In particular, the completion procedure uses the joinability with respect to \(\downarrow _{\mathcal {R}}^{\sim }\) of \(\textsf{CP}({\mathcal {R}}) \cup \textsf{CP}^{\pm }({\mathcal {R},\mathcal {B}^\pm })\) where \(\mathcal {B}^\pm \) denotes \(\mathcal {B}\cup \{r \approx \ell \mid {\ell \approx r} \in \mathcal {B}\}\) as a sufficient and necessary criterion for the Church–Rosser modulo \(\mathcal {B}\) property of a \(\mathcal {B}\)-terminating TRS \(\mathcal {R}\). Note that this criterion works with standard critical pairs and therefore does not need unification modulo \(\mathcal {B}\). However, the criterion is not valid for non-left-linear TRSs as the following example shows.
Example 1
Consider the TRS \(\mathcal {R}\) consisting of the single rule \(\textsf{f}(x,x) \rightarrow x\) with \(+\) as an additional AC function symbol. There are no critical pairs in \(\mathcal {R}\) and between \(\mathcal {R}\) and AC, so \(\textsf{CP}({\mathcal {R}}) = \textsf{CP}^{\pm }({\mathcal {R},\textsf{AC}^\pm }) = \varnothing \). Now consider the conversion \(\textsf{f}(x+y,y+x) \sim _{\textsf{AC}}\textsf{f}(x+y,x+y) \rightarrow _{\mathcal {R}} x+y\). According to the criterion, \(\textsf{f}(x+y,y+x) \downarrow _{\mathcal {R}}^{\sim } x+y\) should hold, but this is clearly not the case.
3 Avenhaus’ Inference System
The idea of completion modulo an equational theory \(\mathcal {B}\) for left-linear systems where the normal rewrite relation can be used to decide validity problems has been put forward by Huet [5]. To the best of our knowledge, inference systems for this approach are only presented in the books by Avenhaus [1] and Bachmair [3]. This section presents a new correctness proof of a version of Avenhaus’ inference system for finite runs in the spirit of [4] which does not rely on proof orderings. Correctness of Bachmair’s system is established by a simulation result in Sect. 4.
3.1 Inference System
Definition 1
The inference system \(\textsf{A}\) is parameterized by a fixed \(\mathcal {B}\)-compatible reduction order > on terms. It transforms pairs consisting of an ES \(\mathcal {E}\) and a TRS \(\mathcal {R}\) over the common signature \(\mathcal {F}\) according to the following inference rules where \(s \mathrel {\dot{\approx }}t\) denotes either \(s \approx t\) or \(t \approx s\):


A step in an inference system I from an ES \(\mathcal {E}\) and a TRS \(\mathcal {R}\) to an ES \(\mathcal {E}'\) and a TRS \(\mathcal {R}'\) is denoted by
 . The parentheses of the pairs are only used when the expression is surrounded by text in order to increase readability. In the following, \(\textsf{PCP}^{\pm }({\mathcal {R},\mathcal {B}^{\pm }})\) denotes the restriction of \(\textsf{CP}^{\pm }({\mathcal {R},\mathcal {B}^{\pm }})\) to prime critical pairs but where irreducibility is always checked with respect to \(\mathcal {R}\), i.e., the critical peaks
. The parentheses of the pairs are only used when the expression is surrounded by text in order to increase readability. In the following, \(\textsf{PCP}^{\pm }({\mathcal {R},\mathcal {B}^{\pm }})\) denotes the restriction of \(\textsf{CP}^{\pm }({\mathcal {R},\mathcal {B}^{\pm }})\) to prime critical pairs but where irreducibility is always checked with respect to \(\mathcal {R}\), i.e., the critical peaks
 and \(t' \leftrightarrow _{\mathcal {B}}^{p} s \rightarrow _{\mathcal {R}}^{\epsilon } u'\) are both prime if all proper subterms of \(s|_p\) are irreducible with respect to \(\mathcal {R}\).
and \(t' \leftrightarrow _{\mathcal {B}}^{p} s \rightarrow _{\mathcal {R}}^{\epsilon } u'\) are both prime if all proper subterms of \(s|_p\) are irreducible with respect to \(\mathcal {R}\).
Definition 2
Let \(\mathcal {E}\) be an ES. A finite sequence
with \(\mathcal {E}_0 = \mathcal {E}\) and \(\mathcal {R}_0 = \varnothing \) is a run for \(\mathcal {E}\). If \(\mathcal {E}_n \ne \varnothing \), the run fails. The run is fair if \(\mathcal {R}_n\) is left-linear and the following inclusions hold:
Intuitively, fair and non-failing runs yield a \(\mathcal {B}\)-complete presentation \(\mathcal {R}_n\) of the initial set of equations \(\mathcal {E}\), i.e., \({\leftrightarrow _{\mathcal {E}\cup \mathcal {B}}^{*}} = {\leftrightarrow _{\mathcal {R}_n \cup \mathcal {B}}^{*}} \subseteq {\downarrow _{\mathcal {R}_n}^{\sim }}\). In particular, the inference rules are designed to preserve the equational theory augmented by \(\mathcal {B}\). The following example shows that deducing local cliffs (
 ) as rules as well as the restriction to \(\rightarrow _{\mathcal {R}}\) in the collapse rule are crucial properties of the inference system.
) as rules as well as the restriction to \(\rightarrow _{\mathcal {R}}\) in the collapse rule are crucial properties of the inference system.
Example 2
Consider the ES \(\mathcal {E}\) consisting of the single equation \(x + \textsf{0}\approx x\) where \(+\) is an AC function symbol. We clearly have \(\textsf{0}+ x \leftrightarrow _{\mathcal {E}\cup \textsf{AC}}^{*} x\), so an AC complete system \(\mathcal {C}\) representing \(\mathcal {E}\) has to satisfy \(\textsf{0}+ x \downarrow _{\mathcal {C}}^{\sim } x\). There is just one way to orient the only equation in \(\mathcal {E}\), which results in the rule \(x + \textsf{0}\rightarrow x\). Since we want our run to be fair, we add the rules stemming from the prime critical pairs between \(x + \textsf{0}\rightarrow x\) and \(\textsf{AC}^\pm \):
If collapsing with \(\rightarrow _{\mathcal {R}/\textsf{AC}}\) is allowed, all these rules become trivial equations and can therefore be deleted. Thus, the modified inference system allows for a fair run which is not complete as \(\textsf{0}+ x \downarrow _{\mathcal {R}}^{\sim } x\) does not hold for \(\mathcal {R}= \{x + \textsf{0}\rightarrow x\}\). Furthermore, if we add pairs of terms stemming from local cliffs as equations, we get the same result by applications of simplify.
The inference system presented in Definition 1 is almost the same as the one presented by Avenhaus in [1]. However, since we only consider finite runs, the encompassment condition for the collapse rule has been removed in the spirit of [13]. The following example shows that this can lead to smaller \(\mathcal {B}\)-complete systems.
Example 3
Consider the ES \(\mathcal {E}= \{\textsf{f}(x+y) \approx \textsf{f}(x) + \textsf{f}(y)\}\) where \(+\) is an AC symbol. The inference system presented in [1] produces the AC complete system
in which either of the rules could be collapsed if it was allowed to collapse with the other rule. In [1] this is prevented by an encompassment condition which essentially forbids to collapse at the root position with a rewrite rule whose left-hand side is a variant of the left-hand side of the rule which should be collapsed. However, this is possible with the system presented in this paper, so for an AC complete representation just one of the two rules suffices.
3.2 Confluence Criterion
The confluence criterion used in the correctness proof of \(\textsf{A}\) is an extended version of the one used in [4] which we dub peak-and-cliff decreasingness. In the following, we assume that equivalence relations \(\sim \) are defined as the reflexive and transitive closure of a symmetric relation
 , so
, so
 . Furthermore, we assume that steps are labeled with labels from a set I, so let \(\mathcal {A}= \langle A, \{\rightarrow _{\alpha }\}_{\alpha \in I} \rangle \) be an ARS and
. Furthermore, we assume that steps are labeled with labels from a set I, so let \(\mathcal {A}= \langle A, \{\rightarrow _{\alpha }\}_{\alpha \in I} \rangle \) be an ARS and
 an equivalence relation on A.
an equivalence relation on A.
Definition 3
The ARS \(\mathcal {A}\) is peak-and-cliff decreasing if there is a well-founded order > on I such that for all \(\alpha , \beta \in I\) the inclusions

hold. Here
 denotes the set \(\{\gamma \in I \mid \alpha> \gamma \,{or}\, \beta > \gamma \}\) and if \(J \subseteq I\) then \(\rightarrow _{J}\) denotes \(\bigcup _{\gamma \in J} \rightarrow _{\gamma }\). We simplify
denotes the set \(\{\gamma \in I \mid \alpha> \gamma \,{or}\, \beta > \gamma \}\) and if \(J \subseteq I\) then \(\rightarrow _{J}\) denotes \(\bigcup _{\gamma \in J} \rightarrow _{\gamma }\). We simplify
 to
to
 .
.
Lemma 2
Every conversion modulo \(\sim \) is either a valley modulo \(\sim \) or contains a local peak or cliff:

The proof of the following theorem is based on a well-founded order on multisets. We denote the multiset extension of an order > by \(>_{\textsf{mul}}\). It is well-known that the multiset extension of a well-founded order is also well-founded.
Theorem 1
If \(\mathcal {A}\) is peak-and-cliff decreasing then \({\mathcal {A}}\) is Church–Rosser modulo \(\sim \).
Proof
With every conversion C we associate a multiset \(M_C\) consisting of labels of its rewrite and equivalence relation steps. Since \(\mathcal {A}\) is peak-and-cliff decreasing, there is a well-founded order > on I which allows us to replace conversions C of the forms
 ,
,
 and
and
 by conversions \(C'\) where \(M_C >_{\textsf{mul}}M_{C'}\). Hence, we prove that \({\mathcal {A}}\) is Church–Rosser modulo \(\sim \), i.e., \({\Leftrightarrow ^{*}} \subseteq {\downarrow ^{\sim }}\), by well-founded induction on \(>_{\textsf{mul}}\). Consider a conversion \(a \Leftrightarrow ^{*} b\) which we call C. By Lemma 2 we either have \(a \downarrow ^{\sim } b\) (which includes the case that C is empty) or one of the following cases holds:
by conversions \(C'\) where \(M_C >_{\textsf{mul}}M_{C'}\). Hence, we prove that \({\mathcal {A}}\) is Church–Rosser modulo \(\sim \), i.e., \({\Leftrightarrow ^{*}} \subseteq {\downarrow ^{\sim }}\), by well-founded induction on \(>_{\textsf{mul}}\). Consider a conversion \(a \Leftrightarrow ^{*} b\) which we call C. By Lemma 2 we either have \(a \downarrow ^{\sim } b\) (which includes the case that C is empty) or one of the following cases holds:

If \(a \downarrow ^{\sim } b\) we are immediately done. In the remaining cases, we have a local peak or cliff with concrete labels \(\alpha \) and \(\beta \), so \(M_C = \varGamma _1 \uplus \{\alpha , \beta \} \uplus \varGamma _2\). Since \(\mathcal {A}\) is peak-and-cliff decreasing, there is a conversion \(C'\) with \(M_{C'} = \varGamma _1 \uplus \varGamma \uplus \varGamma _3\) where \(\{\alpha , \beta \} >_{\textsf{mul}}\varGamma \). Hence, \(M_C >_{\textsf{mul}}M_{C'}\) and we finish the proof by applying the induction hypothesis. \(\square \)
In the following, we connect the joinability of local peaks and cliffs to the joinability of prime critical pairs which allows us to apply peak-and-cliff decreasingness in the correctness proof of \(\textsf{A}\).
Definition 4
Given a TRS \(\mathcal {R}\) and terms s, t and u, we write \(t \mathrel {\triangledown _{s}^{}} u\) if \(s \rightarrow _{\mathcal {R}}^{+} t\), \(s \rightarrow _{\mathcal {R}}^{+} u\), and \(t \downarrow _{\mathcal {R}} u\) or \(t \leftrightarrow _{\textsf{PCP}({\mathcal {R}})} u\). We write \(t \mathrel {\triangledown _{s}^{\smash {\sim }}} u\) if \(s \rightarrow _{\mathcal {R}}^{+} t\), \(s \sim u\) and \(t \downarrow _{\mathcal {R}}^{\sim }u\) or \(t \leftrightarrow _{\textsf{PCP}^{\pm }({\mathcal {R},\mathcal {B}^\pm })} u\). Furthermore,
 .
.
Lemma 3
Let \(\mathcal {R}\) be a left-linear TRS. The following two properties hold:
-
1.
If
 then \(t \mathrel {\triangledown _{s}^{2}} u\).
then \(t \mathrel {\triangledown _{s}^{2}} u\). -
2.
If
 then \(t \mathrel {\triangledown _{s}^{}} \cdot \mathrel {\triangledown _{s}^{\smash {\sim }}} u\).
then \(t \mathrel {\triangledown _{s}^{}} \cdot \mathrel {\triangledown _{s}^{\smash {\sim }}} u\).
3.3 Correctness Proof
We show that every fair and non-failing finite run results in a \(\mathcal {B}\)-complete presentation. To this end, we first verify that inference steps in \(\textsf{A}\) preserve convertibility. We abbreviate \(\mathcal {E}\cup \mathcal {R}\cup \mathcal {B}\) to \(\mathcal {E}\mathcal {R}\mathcal {B}\) and \(\mathcal {E}' \cup \mathcal {R}' \cup \mathcal {B}\) to \(\mathcal {E}\mathcal {R}\mathcal {B}'\).
Lemma 4
If \((\mathcal {E},\mathcal {R}) \vdash _\textsf{A}(\mathcal {E}',\mathcal {R}')\) then the following inclusions hold:

Corollary 1
If \((\mathcal {E},\mathcal {R}) \vdash _\textsf{A}^* (\mathcal {E}',\mathcal {R}')\) then
 .
.
Lemma 5
If \((\mathcal {E},\mathcal {R}) \vdash _\textsf{A}^* (\mathcal {E}',\mathcal {R}')\) and \(\mathcal {R}\subseteq {>}\) then \(\mathcal {R}' \subseteq {>}\).
Definition 5
Let \(\leftrightarrow \) be a rewrite relation or equivalence relation, M a finite multiset of terms and > a \(\mathcal {B}\)-compatible reduction order. We write
 if \(s \leftrightarrow t\) and there exist terms \(s', t' \in M\) such that \(s' \gtrsim s\) and \(t' \gtrsim t\) for \({\gtrsim } = {{>} \cup {\sim _{\mathcal {B}}}}\).
if \(s \leftrightarrow t\) and there exist terms \(s', t' \in M\) such that \(s' \gtrsim s\) and \(t' \gtrsim t\) for \({\gtrsim } = {{>} \cup {\sim _{\mathcal {B}}}}\).
We follow the convention that if a conversion is labeled with M, all single steps can be labeled with M.
Lemma 6
Let \((\mathcal {E},\mathcal {R}) \vdash _\textsf{A}(\mathcal {E}',\mathcal {R}')\) and \(\mathcal {R}' \subseteq {>}\).
-
1.
For any finite multiset M we have
 .
. -
2.
If
 then
then
 with \(\{s\} >_{\textsf{mul}}N\).
with \(\{s\} >_{\textsf{mul}}N\).
Finally, we are able to prove the correctness result for \(\textsf{A}\), i.e., all finite fair and non-failing runs produce a \(\mathcal {B}\)-complete TRS which represents the original set of equations. In contrast to [1] and [3], the proof shows that it suffices to consider prime critical pairs.
Theorem 2
Let \(\mathcal {E}\) be an ES. For every fair and non-failing run
for \(\mathcal {E}\), the TRS \(\mathcal {R}_n\) is a \(\mathcal {B}\)-complete representation of \(\mathcal {E}\).
Proof
Let > be the \(\mathcal {B}\)-compatible reduction order used in the run. From fairness we obtain \(\mathcal {E}_n = \varnothing \) as well as the fact that \(\mathcal {R}_n\) is left-linear. Corollary 1 establishes \({\leftrightarrow _{\mathcal {E}\cup \mathcal {B}}^{*}} = {\leftrightarrow _{\mathcal {R}_n \cup \mathcal {B}}^{*}}\) and termination modulo \(\mathcal {B}\) of \(\mathcal {R}_n\) follows from Lemma 5. It remains to prove that \(\mathcal {R}_n\) is Church–Rosser modulo \(\mathcal {B}\) which we do by showing peak-and-cliff decreasingness. So consider a labeled local peak
 . Lemma 3(1) yields \(t \mathrel {\triangledown _{s}^{2}} u\). Let \(v \mathrel {\triangledown _{s}^{}} w\) appear in this sequence (so \(v = t\) or \(w = u\)). By definition, \(v \downarrow _{\mathcal {R}_n} w\) or \(v \leftrightarrow _{\textsf{PCP}({\mathcal {R}_n})} w\). Together with fairness, the fact that \(\sim _{\mathcal {B}}\) is reflexive as well as closure of rewriting under contexts and substitutions we obtain \(v \downarrow _{\mathcal {R}_n}^{\sim } w\) or \((v,w) \in {\bigcup _{i=0}^n {\leftrightarrow _{\mathcal {E}_i \cup \mathcal {R}_i}}}\). In both cases, it is possible to label all steps between v and w with \(\{v,w\}\). Since \(s > v\) and \(s > w\) we have \(M_1 >_{\textsf{mul}}\{v,w\}\) and \(M_2 >_{\textsf{mul}}\{v,w\}\). Repeated applications of Lemma 6(1) therefore yield a conversion in \(\mathcal {R}_n \cup \mathcal {B}\) between v and w where every step is labeled with a multiset that is smaller than both \(M_1\) and \(M_2\). Hence, the corresponding condition required by peak-and-cliff decreasingness is fulfilled.
. Lemma 3(1) yields \(t \mathrel {\triangledown _{s}^{2}} u\). Let \(v \mathrel {\triangledown _{s}^{}} w\) appear in this sequence (so \(v = t\) or \(w = u\)). By definition, \(v \downarrow _{\mathcal {R}_n} w\) or \(v \leftrightarrow _{\textsf{PCP}({\mathcal {R}_n})} w\). Together with fairness, the fact that \(\sim _{\mathcal {B}}\) is reflexive as well as closure of rewriting under contexts and substitutions we obtain \(v \downarrow _{\mathcal {R}_n}^{\sim } w\) or \((v,w) \in {\bigcup _{i=0}^n {\leftrightarrow _{\mathcal {E}_i \cup \mathcal {R}_i}}}\). In both cases, it is possible to label all steps between v and w with \(\{v,w\}\). Since \(s > v\) and \(s > w\) we have \(M_1 >_{\textsf{mul}}\{v,w\}\) and \(M_2 >_{\textsf{mul}}\{v,w\}\). Repeated applications of Lemma 6(1) therefore yield a conversion in \(\mathcal {R}_n \cup \mathcal {B}\) between v and w where every step is labeled with a multiset that is smaller than both \(M_1\) and \(M_2\). Hence, the corresponding condition required by peak-and-cliff decreasingness is fulfilled.
Next consider a labeled local cliff
 . From Lemma 3(2) we obtain a term v such that \(t \mathrel {\triangledown _{s}^{}} v \mathrel {\triangledown _{s}^{\smash {\sim }}} u\). As in the case for local peaks we obtain a conversion between t and v where each step can be labeled with \(\{t,v\} <_{\textsf{mul}}M_1\). Together with fairness, \(v \mathrel {\triangledown _{s}^{\smash {\sim }}} u\) yields \(v \downarrow _{\mathcal {R}_n}^{\sim } u\) or \((v,u) \in {\bigcup _{i = 0}^n {\leftrightarrow _{\mathcal {R}_i}}}\). In the former case there exists a k such that
. From Lemma 3(2) we obtain a term v such that \(t \mathrel {\triangledown _{s}^{}} v \mathrel {\triangledown _{s}^{\smash {\sim }}} u\). As in the case for local peaks we obtain a conversion between t and v where each step can be labeled with \(\{t,v\} <_{\textsf{mul}}M_1\). Together with fairness, \(v \mathrel {\triangledown _{s}^{\smash {\sim }}} u\) yields \(v \downarrow _{\mathcal {R}_n}^{\sim } u\) or \((v,u) \in {\bigcup _{i = 0}^n {\leftrightarrow _{\mathcal {R}_i}}}\). In the former case there exists a k such that
 . If \(k = 0\) we can label all steps with \(\{v\}\). If \(k > 0\) the conversion is of the form
. If \(k = 0\) we can label all steps with \(\{v\}\). If \(k > 0\) the conversion is of the form
 . We can label the rightmost step with \(M_2\) and the remaining steps with \(\{v,w\}\). Note that \(s > v\). Since > is a \(\mathcal {B}\)-compatible reduction order we also have \(s > w\). Thus, \(M_1 >_{\textsf{mul}}\{v,w\}\) which establishes the corresponding condition required by peak-and-cliff decreasingness for all k. In the remaining case we have \((v,u) \in {\bigcup _{i = 0}^n {\leftrightarrow _{\mathcal {R}_i}}}\), so there is some \(i \leqslant n\) such that \(v \leftrightarrow _{\mathcal {R}_i} u\). Actually, we know that \(u \rightarrow _{\mathcal {R}_i}^{M_2} v\) since otherwise we would have both \(s > v\) and \(v > s\) by the \(\mathcal {B}\)-compatibility of >. Repeated applications of Lemma 6(1,2) therefore yield a conversion between u and v of the form
. We can label the rightmost step with \(M_2\) and the remaining steps with \(\{v,w\}\). Note that \(s > v\). Since > is a \(\mathcal {B}\)-compatible reduction order we also have \(s > w\). Thus, \(M_1 >_{\textsf{mul}}\{v,w\}\) which establishes the corresponding condition required by peak-and-cliff decreasingness for all k. In the remaining case we have \((v,u) \in {\bigcup _{i = 0}^n {\leftrightarrow _{\mathcal {R}_i}}}\), so there is some \(i \leqslant n\) such that \(v \leftrightarrow _{\mathcal {R}_i} u\). Actually, we know that \(u \rightarrow _{\mathcal {R}_i}^{M_2} v\) since otherwise we would have both \(s > v\) and \(v > s\) by the \(\mathcal {B}\)-compatibility of >. Repeated applications of Lemma 6(1,2) therefore yield a conversion between u and v of the form

where \(\{u\} >_{\textsf{mul}}N\). By definition, \(s' \gtrsim u\) for some \(s' \in M_1\) and therefore \(M_1 >_{\textsf{mul}}N\), which means that the corresponding condition required by peak-and-cliff decreasingness is fulfilled. Overall, it follows that \(\mathcal {R}_n\) is peak-and-cliff decreasing and therefore Church–Rosser modulo \(\mathcal {B}\). \(\square \)
Note that the proofs of the previous theorem and Theorem 1 do not require multiset orders induced by quasi-orders but use multiset extensions of proper \(\mathcal {B}\)-compatible reduction orders which are easier to work with. This could be achieved by defining peak-and-cliff decreasingness in such a way that well-founded orders suffice for the abstract setting. However, the usage of multiset orders based on \(\mathcal {B}\)-compatible reduction orders as well as a notion of labeled rewriting which allows us to label steps with \(\mathcal {B}\)-equivalent terms are crucial in order to establish peak-and-cliff decreasingness for TRSs.
4 Bachmair’s Inference System
As already mentioned, the inference system proposed by Avenhaus [1] is essentially the same as \(\textsf{A}\). The only other inference system for \(\mathcal {B}\)-completion for left-linear TRSs is due to Bachmair [3]. We investigate a slightly modified version of this inference system where arbitrary local peaks are deducible and the encompassment condition from the collapse rule is removed as we only consider finite runs and call the resulting system \(\textsf{B}\).
The main difference between \(\textsf{A}\) and \(\textsf{B}\) is that in \(\textsf{B}\) one may only use the standard rewrite relation \(\rightarrow _{\mathcal {R}}\) for simplifying equations and composing rules. This allows us to deduce local cliffs as equations. The goal of this section is to establish correctness of \(\textsf{B}\) via a simulation by \(\textsf{A}\).
Definition 6
The inference system \(\textsf{B}\) is the same as \(\textsf{A}\) but with rewriting in compose and simplify restricted to \(\rightarrow _{\mathcal {R}}\) and the following rule which replaces the two deduction rules of \(\textsf{A}\):

Definition 7
Let \(\mathcal {E}\) be an ES. A finite sequence
with \(\mathcal {E}_0 = \mathcal {E}\) and \(\mathcal {R}_0 = \varnothing \) is a run for \(\mathcal {E}\). If \(\mathcal {E}_n \ne \varnothing \), the run fails. The run is fair if \(\mathcal {R}_n\) is left-linear and the following inclusion holds:
In contrast to Definition 2, the fairness condition is the same for all prime critical pairs since the inference rule deduce of \(\textsf{B}\) never produces rewrite rules.
In the following,
 denotes an application of the rule orient in an inference system I. In order to prove that fair and non-failing runs in \(\textsf{B}\) can be simulated in \(\textsf{A}\), we start with the following technical lemma.
denotes an application of the rule orient in an inference system I. In order to prove that fair and non-failing runs in \(\textsf{B}\) can be simulated in \(\textsf{A}\), we start with the following technical lemma.
Lemma 7
If \((\mathcal {E}_1,\mathcal {R}_1) \vdash _\textsf{B}(\mathcal {E}_2, \mathcal {R}_2)\) and
 then \((\mathcal {E}_1',\mathcal {R}_1') \vdash _\textsf{A}^= (\mathcal {E}_2',\mathcal {R}_2')\) where
then \((\mathcal {E}_1',\mathcal {R}_1') \vdash _\textsf{A}^= (\mathcal {E}_2',\mathcal {R}_2')\) where
 . In a picture:
. In a picture:

For the proof of the simulation result, we need a slightly different form of the previous lemma. Analogous to the notation for rewrite relations, the relation
 denotes the exhaustive application of the inference rule orient.
denotes the exhaustive application of the inference rule orient.
Corollary 2
If \((\mathcal {E}_1,\mathcal {R}_1) \vdash _\textsf{B}(\mathcal {E}_2, \mathcal {R}_2)\) and
 then \((\mathcal {E}_1',\mathcal {R}_1') \vdash _\textsf{A}^* (\mathcal {E}_2',\mathcal {R}_2')\) where
then \((\mathcal {E}_1',\mathcal {R}_1') \vdash _\textsf{A}^* (\mathcal {E}_2',\mathcal {R}_2')\) where
 .
.
Theorem 3
For every fair run \((\mathcal {E}, \varnothing ) \vdash _\textsf{B}^* (\varnothing , \mathcal {R})\) there exists a fair run \((\mathcal {E}, \varnothing ) \vdash _\textsf{A}^* (\varnothing , \mathcal {R})\).
Proof
Assume \((\mathcal {E}_0, \mathcal {R}_0) \vdash _\textsf{B}^n (\mathcal {E}_n, \mathcal {R}_n)\) where \(\mathcal {R}_0 = \mathcal {E}_n = \varnothing \). By n applications of Corollary 2 we arrive at the following situation:

The following two statements hold:
-
1.
For \(0 \leqslant i \leqslant n\), all orientable equations in \(\mathcal {E}_i\) are in \(\mathcal {R}_i'\) (possibly reversed) and the other equations are in \(\mathcal {E}_i'\).
-
2.
\(\textsf{PCP}^{\pm }({\mathcal {R}_n',\mathcal {B}^\pm })\) is a set of orientable equations.
Statement (1) is immediate from the simulation relation
 and statement (2) follows from \(\mathcal {B}\)-compatibility of the used reduction order together with the fact that every (prime) critical pair is connected by one \(\mathcal {R}_n\)-step and one \(\mathcal {B}\)-step. Furthermore, \(\mathcal {E}_n = \varnothing \) implies \(\mathcal {E}_n' = \varnothing \) as well as \(\mathcal {R}_n = \mathcal {R}_n'\). Hence, we obtain fairness of the run in \(\textsf{A}\) by showing the following inclusions:
and statement (2) follows from \(\mathcal {B}\)-compatibility of the used reduction order together with the fact that every (prime) critical pair is connected by one \(\mathcal {R}_n\)-step and one \(\mathcal {B}\)-step. Furthermore, \(\mathcal {E}_n = \varnothing \) implies \(\mathcal {E}_n' = \varnothing \) as well as \(\mathcal {R}_n = \mathcal {R}_n'\). Hence, we obtain fairness of the run in \(\textsf{A}\) by showing the following inclusions:
Let \({s \approx t} \in \textsf{PCP}({\mathcal {R}_n'})\). By fairness of the run in \(\textsf{B}\) we obtain \(s \downarrow _{\mathcal {R}_n'}^{\sim } t\) or \(s \leftrightarrow _{\mathcal {E}_k} t\) for some \(k \leqslant n\). In the former case, we are immediately done. In the latter case we obtain \(s \leftrightarrow _{\mathcal {E}_k' \cup \mathcal {R}_k'} t\) from (1) as desired. Now, let \({s \approx t} \in \textsf{PCP}^{\pm }({\mathcal {R}_n',\mathcal {B}^\pm })\). By fairness of the run in \(\textsf{B}\) we obtain \(s \downarrow _{\mathcal {R}_n'}^{\sim } t\) or \(s \leftrightarrow _{\mathcal {E}_k} t\) for some \(k \leqslant n\). Again, we are immediately done in the former case. In the latter case we have \(s \leftrightarrow _{\mathcal {R}_k'} t\) because of (1) and (2). Therefore, the run in \(\textsf{A}\) is fair. \(\square \)
The previous theorem is an important simulation result which justifies the emphasis on \(\textsf{A}\) in this paper. Moreover, together with Theorem 2 the correctness of the inference system \(\textsf{B}\) is an easy consequence.
Corollary 3
Every fair and non-failing run for \(\mathcal {E}\) in \(\textsf{B}\) produces a \(\mathcal {B}\)-complete presentation of \(\mathcal {E}\).
5 AC Completion
So far, the theoretical results have been generalized by using the equational theory \(\mathcal {B}\) as a placeholder. In practice, however, this paper is concerned with the particular theory AC. The results of this section allow us to assess the effectiveness of the inference system \(\textsf{A}\) in the setting of AC completion.
5.1 Limitations of Left-Linear AC Completion
In addition to the restriction to left-linear rewrite rules, the following example demonstrates another severe limitation of the inference system \(\textsf{A}\) previously unmentioned in the literature.
Example 4
Consider the ES \(\mathcal {E}\) consisting of the equations
where \(\textsf{and}\) is an AC function symbol. There is only one way to orient each equation. Furthermore, there are no critical pairs between the resulting rewrite rules. Hence, using the inference system \(\textsf{A}\) we arrive at the intermediate TRS
where the only possible next step is to deduce local cliffs. We will now show that this has to be done infinitely many times. Note that an AC-complete presentation \(\mathcal {R}\) of \(\mathcal {E}\) has to be able to rewrite any AC-equivalent term of a redex: Consider the infinite family of terms
Clearly, \(s_n \leftrightarrow _{\mathcal {E}\cup \textsf{AC}}^{*} t_n\) for all \(n \in \mathbb {N}\) and therefore also \(s_n \downarrow _{\mathcal {R}}^{\sim } t_n\) for all \(n \in \mathbb {N}\), but this demands infinitely many rules in \(\mathcal {R}\): For each \(s_n\) there is an AC-equivalent term such that the constants \(\textsf{0}\) and \(\textsf{1}\) are next to each other which allows us to rewrite it using the rule \(\textsf{and}(\textsf{0},\textsf{1}) \rightarrow \textsf{0}\). However, with n also the amount of variables between these constants increases which requires \(\mathcal {R}\) to have infinitely many rules since rewrite rules can only be applied before the representation modulo AC is changed.
Note that there is nothing special about this example except the fact that it contains at least one equation which can only be oriented such that the left-hand side contains an AC function symbol where both arguments have “structure”, i.e., both arguments represent more complicated terms than a variable. As a consequence, the necessity of infinite rules applies to all equational systems which have this property. Needless to say, this means that for a large class of equational systems the corresponding AC-canonical presentation (in the left-linear sense) is infinite if it exists. This observation is in stark contrast to the properties of general AC completion as presented in the next section which can complete the ES \(\mathcal {E}\) from Example 4 into a finite AC-canonical TRS by simply orienting all rules from left to right.
5.2 General AC Completion
Inference systems for completion modulo an equational theory which are not restricted to the left-linear case usually need more inference rules than the ones already covered in this paper. For general AC completion, however, there exists a particularly simple inference system which constitutes a special case of normalized completion [12] and can be found in Sarah Winkler’s PhD thesis [16, p. 109].
Definition 8
The inference system \(\textsf{KB}_{\textsf{AC}}\) is the same as \(\textsf{A}\) for the fixed theory AC but with a modified collapse rule which allows us to rewrite with \(\rightarrow _{\mathcal {R}/\textsf{AC}}\) and the following rule which replaces the two deduction rules of \(\textsf{A}\):

The purpose of this section is to show how \(\textsf{A}\) can be simulated by \(\textsf{KB}_{\textsf{AC}}\) in the case of \(\mathcal {B}= \textsf{AC}\). Since local cliffs cannot be deduced in \(\textsf{KB}_{\textsf{AC}}\), the simulation has to work with a potentially smaller set of rewrite rules. Furthermore, during a run, the variants of rules stemming from local cliffs may be in different states with respect to inter-reduction (collapse and compose). Given an intermediate TRS \(\mathcal {R}\) of a run in \(\textsf{A}\) as well as an intermediate TRS \(\mathcal {R}'\) of a run in \(\textsf{KB}_{\textsf{AC}}\), the invariant \(\mathcal {R}\subseteq {\rightarrow _{\mathcal {R}'/\textsf{AC}}^{+}}\) resolves both of the aforementioned problems. The main motivation behind this invariant is the avoidance of compose and collapse in the \(\textsf{KB}_{\textsf{AC}}\) run.
Lemma 8
If \((\mathcal {E}_1,\mathcal {R}_1) \vdash _\textsf{A}(\mathcal {E}_2, \mathcal {R}_2)\) and \(\mathcal {R}_1 \subseteq {\rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+}}\) then there exists a TRS
 and \(\mathcal {R}_2 \subseteq {\rightarrow _{\mathcal {R}'_2/\textsf{AC}}^{+}}\).
and \(\mathcal {R}_2 \subseteq {\rightarrow _{\mathcal {R}'_2/\textsf{AC}}^{+}}\).
Proof
Let > be a fixed AC-compatible reduction order which is used in both \(\textsf{A}\) and \(\textsf{KB}_{\textsf{AC}}\). Suppose \((\mathcal {E}_1,\mathcal {R}_1) \vdash _\textsf{A}(\mathcal {E}_2,\mathcal {R}_2)\) and \(\mathcal {R}_1 \subseteq {\rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+}}\). We proceed by a case analysis on the rule applied in the inference step \((\mathcal {E}_1,\mathcal {R}_1) \vdash _\textsf{A}(\mathcal {E}_2,\mathcal {R}_2)\). The only interesting cases are when deduce, simplify, compose, or collapse is applied.
-
If deduce is applied, we further distinguish whether it was applied to a local peak or cliff. In the case of a local cliff, we have \(\mathcal {E}_1 = \mathcal {E}_2\) and \(\mathcal {R}_2 = \mathcal {R}_1 \cup \{\ell \rightarrow r\}\) with \(\ell \rightarrow _{\mathcal {R}_1/\textsf{AC}} r\). From \(\ell \rightarrow _{\mathcal {R}_1/\textsf{AC}} r\) and \(\mathcal {R}_1 \subseteq {\rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+}}\) we obtain \(\ell \rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+} r\). Thus, \(\mathcal {R}_2 \subseteq {\rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+}}\) holds. As
 is trivial, the claim follows. In the case of a local peak, we have \(\mathcal {R}_1 = \mathcal {R}_2\) and \(\mathcal {E}_2 = \mathcal {E}_1 \cup \{ t \approx u \}\) with
is trivial, the claim follows. In the case of a local peak, we have \(\mathcal {R}_1 = \mathcal {R}_2\) and \(\mathcal {E}_2 = \mathcal {E}_1 \cup \{ t \approx u \}\) with
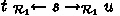 . Since \(\mathcal {R}_1 \subseteq {\rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+}}\) holds, we have
. Since \(\mathcal {R}_1 \subseteq {\rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+}}\) holds, we have
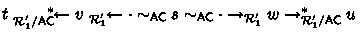 for some v and w. By performing deduce and simplify steps
for some v and w. By performing deduce and simplify steps 
is obtained. As \(\mathcal {R}_1 = \mathcal {R}_2\), the inclusion \(\mathcal {R}_2 \subseteq {\rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+}}\) is trivial. Hence, the claim holds.
-
If simplify is applied, we have \(\mathcal {R}_1 = \mathcal {R}_2\), \(\mathcal {E}_1 = \mathcal {E}_0 \cup \{s \approx t\}\), and \(\mathcal {E}_2 = \mathcal {E}_0 \cup \{s' \approx t'\}\) with \(s \rightarrow _{\mathcal {R}_1}^{=} s'\) and \(t \rightarrow _{\mathcal {R}_1}^{=} t'\). By \(\mathcal {R}_1 \subseteq {\rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+}}\) we have \(s \rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{*} s'\) and \(t \rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{*} t'\). Therefore, performing simplify, we obtain
 . As \(\mathcal {R}_1 = \mathcal {R}_2\), the inclusion \(\mathcal {R}_2 \subseteq {\rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+}}\) is trivial.
. As \(\mathcal {R}_1 = \mathcal {R}_2\), the inclusion \(\mathcal {R}_2 \subseteq {\rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+}}\) is trivial. -
If compose is applied, we can write \(\mathcal {E}_1 = \mathcal {E}_2\),
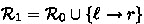 , and \(\mathcal {R}_2 = \mathcal {R}_0 \cup \{\ell \rightarrow r'\}\) with \(r \rightarrow _{\mathcal {R}_0/\textsf{AC}} r'\). We have
, and \(\mathcal {R}_2 = \mathcal {R}_0 \cup \{\ell \rightarrow r'\}\) with \(r \rightarrow _{\mathcal {R}_0/\textsf{AC}} r'\). We have
 . Since the inclusions \(\mathcal {R}_0 \subseteq \mathcal {R}_1 \subseteq {\rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+}}\) yield \(\ell \rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+} r \rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+} r'\), we obtain \(\mathcal {R}_2 \subseteq {\rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+}}\).
. Since the inclusions \(\mathcal {R}_0 \subseteq \mathcal {R}_1 \subseteq {\rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+}}\) yield \(\ell \rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+} r \rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+} r'\), we obtain \(\mathcal {R}_2 \subseteq {\rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+}}\). -
If collapse is applied, we can write \(\mathcal {E}_2 = \mathcal {E}_1 \cup \{\ell ' \approx r\}\) and \(\mathcal {R}_1 = \mathcal {R}_2 \uplus \{\ell \rightarrow r\}\) with \(\ell \rightarrow _{\mathcal {R}_2} \ell '\). By \(\mathcal {R}_2 \subseteq \mathcal {R}_1 \subseteq {\rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+}}\) we have

for some t and u. Performing deduce and simplify, we obtain:

By \(\mathcal {R}_2 \subseteq \mathcal {R}_1 \subseteq {\rightarrow _{\mathcal {R}'_1/\textsf{AC}}^{+}}\) the claim is concluded. \(\square \)
Theorem 4
For every fair run \((\mathcal {E},\varnothing ) \vdash _\textsf{A}^* (\varnothing ,\mathcal {R})\) there exists a run
 such that \(\mathcal {R}'/\textsf{AC}\) is an AC-complete presentation of \(\mathcal {E}\).
such that \(\mathcal {R}'/\textsf{AC}\) is an AC-complete presentation of \(\mathcal {E}\).
Proof
With a straightforward induction argument, we obtain the run
 as well as \({\mathcal {R}} \subseteq {\rightarrow _{\mathcal {R}'/\textsf{AC}}^{+}}\) (\(*\)) from Lemma 8. Furthermore, AC termination of \(\mathcal {R}'\) and \({\leftrightarrow _{\mathcal {E}\cup \textsf{AC}}^{*}} = {\leftrightarrow _{\mathcal {R}' \cup \textsf{AC}}^{*}}\) (\(**\)) are easy consequences from the definition of \(\textsf{KB}_{\textsf{AC}}\). AC-completeness of \(\mathcal {R}\) follows from fairness of the run in \(\textsf{A}\) and Theorem 2. For the Church–Rosser modulo AC property of \(\mathcal {R}'/\textsf{AC}\), consider a conversion \(s \leftrightarrow _{\mathcal {R}' \cup \textsf{AC}}^{*} t\). From (\(**\)) we obtain \(s \leftrightarrow _{\mathcal {E}\cup \textsf{AC}}^{*}\) and therefore
as well as \({\mathcal {R}} \subseteq {\rightarrow _{\mathcal {R}'/\textsf{AC}}^{+}}\) (\(*\)) from Lemma 8. Furthermore, AC termination of \(\mathcal {R}'\) and \({\leftrightarrow _{\mathcal {E}\cup \textsf{AC}}^{*}} = {\leftrightarrow _{\mathcal {R}' \cup \textsf{AC}}^{*}}\) (\(**\)) are easy consequences from the definition of \(\textsf{KB}_{\textsf{AC}}\). AC-completeness of \(\mathcal {R}\) follows from fairness of the run in \(\textsf{A}\) and Theorem 2. For the Church–Rosser modulo AC property of \(\mathcal {R}'/\textsf{AC}\), consider a conversion \(s \leftrightarrow _{\mathcal {R}' \cup \textsf{AC}}^{*} t\). From (\(**\)) we obtain \(s \leftrightarrow _{\mathcal {E}\cup \textsf{AC}}^{*}\) and therefore
 by the fact that \(\mathcal {R}\) is an AC-complete presentation of \(\mathcal {E}\). Finally, (\(*\)) yields
by the fact that \(\mathcal {R}\) is an AC-complete presentation of \(\mathcal {E}\). Finally, (\(*\)) yields
 as desired. Thus, \(\mathcal {R}'/\textsf{AC}\) is an AC-complete presentation of \(\mathcal {E}\). \(\square \)
as desired. Thus, \(\mathcal {R}'/\textsf{AC}\) is an AC-complete presentation of \(\mathcal {E}\). \(\square \)
In addition to the result of the previous theorem, the proof of Lemma 8 provides a procedure to construct a \(\textsf{KB}_{\textsf{AC}}\) run which “corresponds” to a given \(\textsf{A}\) run. In particular, this means that it is possible to switch from \(\textsf{A}\) to \(\textsf{KB}_{\textsf{AC}}\) at any point while performing AC completion. This is of practical relevance: Assume that AC completion is started with \(\textsf{A}\) in order to avoid AC unification. If \(\textsf{A}\) gets stuck due to simplified equations which are not orientable into a left-linear rule or it seems to be the case that the procedure diverges due to the problem described in Example 4, starting from scratch with \(\textsf{KB}_{\textsf{AC}}\) is not necessary. We conclude the section by illustrating the practical relevance of the simulation result with an example.
Example 5
Consider the ES \(\mathcal {E}\) for abelian groups consisting of the equations
where \(\cdot \) is an AC symbol. Note that the well-known completion run for non-abelian group theory is also a run in \(\textsf{A}\): Critical pairs with respect to the associativity axiom are deducible via local cliffs, non-left-linear intermediate rules are allowed and all (intermediate) rules are orientable with e.g. AC-KBO. Hence, we obtain the TRS \(\mathcal {R}'\) consisting of the rules
and switch to \(\textsf{KB}_{\textsf{AC}}\) where we can collapse the redundant rules 4, 6, 7 and 9. A final joinability check of all AC critical pairs reveals that the resulting TRS \(\mathcal {R}\) is an AC-complete presentation of abelian groups. Hence, the simulation result allows to make progress with \(\textsf{A}\) even when it is doomed to fail. In particular, critical pairs between rules whose left-hand sides do not contain AC symbols do not need to be recomputed.
6 Implementation
To the best of our knowledge, our tool accompll is the first implementation of left-linear AC completion. It is written in Haskell and available on its websiteFootnote 1. Instead of expecting explicit AC-compatible reduction orders as input, accompll performs completion with termination tools [15]. In principle, completion with termination tools has to consider all combinations of possible orientations of equations in order to find a complete system. However, traversing the whole search space is rather inefficient. The state of the art for solving this problem efficiently is multi-completion with termination tools due to Winkler et al. [20]. Since the implementation of this method is a major effort, accompll adopts a simple but incomplete strategy presented in [14]: Instead of traversing the whole search space, accompll runs two threads in parallel where one thread prefers to orient equations from left to right and vice versa. If one of the threads finishes successfully, the corresponding result is reported. Completion fails if both threads fail.
As input, the tool expects a file in the WSTFootnote 2 format describing the equational theory on which left-linear AC completion should be performed. The user can choose whether \(\rightarrow _{\mathcal {R}}\) or \(\rightarrow _{\mathcal {R}/\textsf{AC}}\) is used for rewriting in the inference rules simplify and compose. Furthermore, the generation of critical pairs can be restricted to the primality criterion.
Another feature is the validity problem solving mode which solves a given instance of the validity problem for an equational theory \(\mathcal {E}\) upon successful completion of \(\mathcal {E}\). This mode can be triggered by supplying a concrete equation \(s \approx t\) as a command line argument in addition to the file describing \(\mathcal {E}\).
In the tool accompll, external termination tools do much of the heavy lifting. In particular, the user can supply the executable of an arbitrary termination tool as long as the output starts with YES, MAYBE, NO or TIMEOUT (all other cases are treated as an error). The input format for the termination tool can be set by a command line argument. The available options are the WST format as well as the XML format of the Nagoya Termination Tool [21]Footnote 3.
Since starting a new process for every call of the termination tool causes a lot of operating system overhead, the tool supports an interactive mode which allows it to communicate with a single process of the termination tool in a dialogue style. Here, the only constraint for the termination tool is that it accepts a sequence of termination problems separated by the keyword (RUN). This is currently only implemented in an experimental version of Tyrolean Termination Tool 2 (
 ) [11], but we hope that more termination tools will follow as this approach has a positive effect on the runtime of completion with termination tools while demanding comparatively little implementation effort.
) [11], but we hope that more termination tools will follow as this approach has a positive effect on the runtime of completion with termination tools while demanding comparatively little implementation effort.
7 Experimental Results
The problem set used for the experimental results consists of 50 ESs. It is based on the one used in [18] and has been extended by further examples from the literature as well as handcrafted examples. The experiments were performed on an Intel Core i7-7500U running at a clock rate of 2.7 GHz with 15.5 GiB of main memory. Our tool accompll was used with the termination tool
 as well as an experimental version (denoted by
as well as an experimental version (denoted by
 e) which allows our tool to communicate a sequence of termination problems without having to start a new process all the time, as described in the preceding section.
e) which allows our tool to communicate a sequence of termination problems without having to start a new process all the time, as described in the preceding section.
Table 1 shows some interesting results and compares the two configurations of accompll with the normalized completion [12] mode of mkbTT [19] and the AC completion mode of MædMax [17]. The tool mkbTT is the original implementation of multi-completion with termination tools [20]. MædMax, on the other hand, implements maximal completion [9] which makes use of MaxSAT/MaxSMT solvers instead of termination tools in order to avoid using concrete reduction orders as input. To the best of our knowledge, there is no comparable completion tool which supports AC axioms. Since normalized completion subsumes general AC completion, a comparison with the aforementioned modes of both systems allows us to assess the effectiveness of accompll with respect to the state of the art in AC completion. Note that normalized completion uses AC unification.
In Table 1, columns (1) show the execution time in seconds where \(\infty \) denotes that the timeout of 60 s has been reached and \(\bot \) denotes failure of completion. Columns (2) state the number of rules of the completed TRS. The first two problems show that the avoidance of AC unification can indeed have a positive effect on the execution time. However, the third problem indicates that there may also be an opposite effect on small problems. The last two problems show the two main limitations of left-linear AC completion: Abelian groups do not have an AC-complete presentation which is left-linear and Example 2 from [7] is a ground ES which causes left-linear AC completion to suffer from the problem described in Example 4 by definition. The severity of these limitations is reflected in the total number of solved problems. In particular, the problem set does not contain an ES which is completed only by accompll. However, given Theorem 4, this is not unexpected. Another noteworthy but unsurprising fact is that complete systems produced by accompll tend to have more rules since every rule needs different versions of left-hand sides to facilitate rewriting without AC-matching. It would also be interesting to compare the execution times for typical queries of the form \(\mathcal {E}\vDash s \approx t\) as the resulting systems of left-linear AC completion allow for more efficient joinability checks using \(\rightarrow _{\mathcal {R}}\) instead of \(\rightarrow _{\mathcal {R}/\textsf{AC}}\). We leave this for future work.
The complete results are available on the tool’s websiteFootnote 4. We conclude with some additional notes on the results.
-
The results are not cluttered with detailed results for the available options regarding prime critical pairs and the concrete rewrite relation used for simplify and compose since they did not lead to significant runtime differences. Instead, the default options (no prime critical pairs and the rewrite relation \(\rightarrow _{\mathcal {R}}\)) were used for the experiments.
-
The second problem in Table 1 shows the merits of using termination tools as it includes round-up division which cannot be handled by simplification orders.
-
Due to the incompleteness of the used approach for completion with termination tools, some equations in the problems A95_ex4_2_4a.trs as well as sp.trs had to be reversed in order to get appropriate results. Note that this does not distort the experimental results for left-linear AC completion in general as the problem lies in the particular implementation of completion with termination tools.
8 Conclusion
In this paper, we consolidated the existing literature for left-linear AC completion in the case of finite runs and gave new insight into its merits compared to general AC completion. Furthermore, our implementation accompll allowed us to run practical experiments. An extended version of this paper with full proof details and an appendix which describes the original inference systems of Avenhaus and Bachmair is available on the website of accompll (see Footnote 4). We conclude by giving some pointers for future work. First of all, the merits of our novel simulation result for general AC completion could be evaluated experimentally by providing an implementation. Another interesting research direction is normalized completion for the left-linear case. If successful, this would facilitate the treatment of important cases such as abelian groups despite the restriction to left-linear TRSs. Furthermore, a formalization of the established theoretical results is desirable. To that end, the existing Isabelle/HOL formalization from [4] is a perfect starting point as some results of this paper are extensions of the results for standard rewriting presented there.
References
Avenhaus, J.: Reduktionssysteme. Springer, Heidelberg (1995). https://doi.org/10.1007/978-3-642-79351-6. (in German)
Baader, F., Nipkow, T.: Term Rewriting and All That. Cambridge University Press (1998). https://doi.org/10.1017/CBO9781139172752
Bachmair, L.: Canonical Equational Proofs. Progress in Theoretical Computer Science. Birkhäuser, Boston (1991). https://doi.org/10.1007/978-1-4684-7118-2
Hirokawa, N., Middeldorp, A., Sternagel, C., Winkler, S.: Abstract completion, formalized. Logical Methods Comput. Sci. 15(3), 19:1–19:42 (2019). https://doi.org/10.23638/LMCS-15(3:19)2019
Huet, G.: Confluent reductions: abstract properties and applications to term rewriting systems. J. ACM 27(4), 797–821 (1980). https://doi.org/10.1145/322217.322230
Jouannaud, J.P., Kirchner, H.: Completion of a set of rules modulo a set of equations. SIAM J. Comput. 15(4), 1155–1194 (1986). https://doi.org/10.1137/0215084
Kapur, D.: A modular associative commutative (AC) congruence closure algorithm. In: Kobayashi, N. (ed.) Proceedings of the 6th International Conference on Formal Structures for Computation and Deduction. Leibniz International Proceedings in Informatics, vol. 195, pp. 15:1–15:21 (2021). https://doi.org/10.4230/LIPIcs.FSCD.2021.15
Kapur, D., Musser, D.R., Narendran, P.: Only prime superpositions need be considered in the Knuth-Bendix completion procedure. J. Symb. Comput. 6(1), 19–36 (1988). https://doi.org/10.1016/S0747-7171(88)80019-1
Klein, D., Hirokawa, N.: Maximal completion. In: Schmidt-Schauß, M. (ed.) Proceedings of the 22nd International Conference on Rewriting Techniques and Applications. Leibniz International Proceedings in Informatics, vol. 10, pp. 71–80 (2011). https://doi.org/10.4230/LIPIcs.RTA.2011.71
Knuth, D.E., Bendix, P.B.: Simple word problems in universal algebras. In: Leech, J. (ed.) Computational Problems in Abstract Algebra, pp. 263–297. Pergamon Press (1970). https://doi.org/10.1016/B978-0-08-012975-4.50028-X
Korp, M., Sternagel, C., Zankl, H., Middeldorp, A.: Tyrolean Termination Tool 2. In: Treinen, R. (ed.) RTA 2009. LNCS, vol. 5595, pp. 295–304. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02348-4_21
Marché, C.: Normalized rewriting: an alternative to rewriting modulo a set of equations. J. Symb. Comput. 21(3), 253–288 (1996). https://doi.org/10.1006/jsco.1996.0011
Sternagel, C., Thiemann, R.: Formalizing Knuth-Bendix orders and Knuth-Bendix completion. In: Raamsdonk, F. (ed.) Proceedings of the 24th International Conference on Rewriting Techniques and Applications. Leibniz International Proceedings in Informatics, vol. 21, pp. 286–301 (2013). https://doi.org/10.4230/LIPIcs.RTA.2013.287
Sternagel, T., Zankl, H.: KBCV – Knuth-Bendix completion visualizer. In: Gramlich, B., Miller, D., Sattler, U. (eds.) IJCAR 2012. LNCS (LNAI), vol. 7364, pp. 530–536. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31365-3_41
Wehrman, I., Stump, A., Westbrook, E.: Slothrop: Knuth-Bendix completion with a modern termination checker. In: Pfenning, F. (ed.) RTA 2006. LNCS, vol. 4098, pp. 287–296. Springer, Heidelberg (2006). https://doi.org/10.1007/11805618_22
Winkler, S.: Termination tools in automated reasoning. Ph.D. thesis, University of Innsbruck (2013)
Winkler, S.: Extending maximal completion. In: Geuvers, H. (ed.) Proceedings of the 4th International Conference on Formal Structures for Computation and Deduction. Leibniz International Proceedings in Informatics, vol. 131, pp. 3:1–3:15 (2019). https://doi.org/10.4230/LIPIcs.FSCD.2019.3
Winkler, S., Middeldorp, A.: AC completion with termination tools. In: Bjørner, N., Sofronie-Stokkermans, V. (eds.) CADE 2011. LNCS (LNAI), vol. 6803, pp. 492–498. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22438-6_37
Winkler, S., Middeldorp, A.: Normalized completion revisited. In: Raamsdonk, F. (ed.) Proceedings of the 24th International Conference on Rewriting Techniques and Applications. Leibniz International Proceedings in Informatics, vol. 21, pp. 318–333 (2013). https://doi.org/10.4230/LIPIcs.RTA.2013.319
Winkler, S., Sato, H., Middeldorp, A., Kurihara, M.: Multi-completion with termination tools. J. Autom. Reason. 50(3), 317–354 (2013). https://doi.org/10.1007/s10817-012-9249-2
Yamada, A., Kusakari, K., Sakabe, T.: Nagoya Termination Tool. In: Dowek, G. (ed.) RTA 2014. LNCS, vol. 8560, pp. 466–475. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08918-8_32
Acknowledgments
We thank Jonas Schöpf and Fabian Mitterwallner for providing the experimental version of
 as well as the anonymous reviewers for their valuable suggestions.
as well as the anonymous reviewers for their valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Niederhauser, J., Hirokawa, N., Middeldorp, A. (2023). Left-Linear Completion with AC Axioms. In: Pientka, B., Tinelli, C. (eds) Automated Deduction – CADE 29. CADE 2023. Lecture Notes in Computer Science(), vol 14132. Springer, Cham. https://doi.org/10.1007/978-3-031-38499-8_23
Download citation
DOI: https://doi.org/10.1007/978-3-031-38499-8_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-38498-1
Online ISBN: 978-3-031-38499-8
eBook Packages: Computer ScienceComputer Science (R0)





 then
then  then
then  .
. then
then
 with
with  is trivial, the claim follows. In the case of a local peak, we have
is trivial, the claim follows. In the case of a local peak, we have 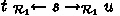 . Since
. Since 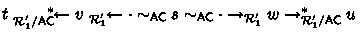 for some v and w. By performing
for some v and w. By performing 
 . As
. As 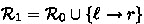 , and
, and  . Since the inclusions
. Since the inclusions 
