Abstract
Dependency pairs are one of the most powerful techniques to analyze termination of term rewrite systems (TRSs) automatically. We adapt the dependency pair framework to the probabilistic setting in order to prove almost-sure innermost termination of probabilistic TRSs. To evaluate its power, we implemented the new framework in our tool AProVE.
Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) - 235950644 (Project GI 274/6-2) and DFG Research Training Group 2236 UnRAVeL.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Techniques and tools to analyze innermost termination of term rewrite systems (TRSs) automatically are successfully used for termination analysis of programs in many languages (e.g., Java [10, 35, 38], Haskell [18], and Prolog [19]). While there exist several classical orderings for proving termination of TRSs (e.g., based on polynomial interpretations [30]), a direct application of these orderings is usually too weak for TRSs that result from actual programs. However, these orderings can be used successfully within the dependency pair (DP) framework [2, 16, 17]. This framework allows for modular termination proofs (e.g., which apply different orderings in different sub-proofs) and is one of the most powerful techniques for termination analysis of TRSs that is used in essentially all current termination tools for TRSs, e.g., AProVE [20], MU-TERM [22], NaTT [40], TTT2 [29], etc.
On the other hand, probabilistic programs are used to describe randomized algorithms and probability distributions, with applications in many areas. To use TRSs also for such programs, probabilistic term rewrite systems (PTRSs) were introduced in [8, 9]. In the probabilistic setting, there are several notions of “termination”. A program is almost-surely terminating (AST) if the probability for termination is 1. As remarked in [24]: “AST is the classical and most widely-studied problem that extends termination of non-probabilistic programs, and is considered as a core problem in the programming languages community”. A strictly stronger notion is positive almost-sure termination (PAST), which requires that the expected runtime is finite. While there exist many automatic approaches to prove (P)AST of imperative programs on numbers (e.g., [1, 4, 11, 15, 21, 24,25,26, 32,33,34, 36]), there are only few automatic approaches for programs with complex non-tail recursive structure [7, 12], and even less approaches which are also suitable for algorithms on recursive data structures [3, 6, 31, 39]. The approach of [39] focuses on algorithms on lists and [31] mainly targets algorithms on trees, but they cannot easily be adjusted to other (possibly user-defined) data structures. The calculus of [6] considers imperative programs with stack, heap, and pointers, but it is not yet automated. Moreover, the approaches of [3, 6, 31, 39] analyze expected runtime, while we focus on AST.
PTRSs can be used to model algorithms (possibly with complex recursive structure) operating on algebraic data types. While PTRSs were introduced in [8, 9], the first (and up to now only) tool to analyze their termination automatically was presented in [3], where orderings based on interpretations were adapted to prove PAST. Moreover, [14] extended general concepts of abstract rewrite systems (e.g., confluence and uniqueness of normal forms) to the probabilistic setting.
As mentioned, already for non-probabilistic TRSs a direct application of orderings (as in [3]) is limited in power. To obtain a powerful approach, one should combine such orderings in a modular way, as in the DP framework. In this paper, we show for the first time that an adaption of dependency pairs to the probabilistic setting is possible and present the first DP framework for probabilistic term rewriting. Since the crucial idea of dependency pairs is the modularization of the termination proof, we analyze AST instead of PAST, because it is well known that AST is compositional, while PAST is not (see, e.g., [25]). We also present a novel adaption of the technique from [3] for the direct application of polynomial interpretations in order to prove AST (instead of PAST) of PTRSs.
We start by briefly recapitulating the DP framework for non-probabilistic TRSs in Sect. 2. Then we recall the definition of PTRSs based on [3, 9, 14] in Sect. 3 and introduce a novel way to prove AST using polynomial interpretations automatically. In Sect. 4 we present our new probabilistic DP framework. The implementation of our approach in the tool AProVE is evaluated in Sect. 5. We refer to [28] for all proofs (which are much more involved than the original proofs for the non-probabilistic DP framework from [2, 16, 17]).
2 The DP Framework
We assume familiarity with term rewriting [5] and regard TRSs over a finite signature \(\varSigma \) and a set of variables \(\mathcal {V}\). A polynomial interpretation \({\text {Pol}}\) is a \(\varSigma \)-algebra with carrier set \(\mathbb {N}\) which maps every function symbol \(f \in \varSigma \) to a polynomial \(f_{{\text {Pol}}} \in \mathbb {N}[\mathcal {V}]\). For a term \(t \in \mathcal {T}\left( \varSigma , \mathcal {V}\right) \), \({\text {Pol}}(t)\) denotes the interpretation of t by the \(\varSigma \)-algebra \({\text {Pol}}\). An arithmetic inequation like \({\text {Pol}}(t_1) > {\text {Pol}}(t_2)\) holds if it is true for all instantiations of its variables by natural numbers.
Theorem 1
(Termination With Polynomial Interpretations [30]). Let \(\mathcal {R}\) be a TRS and let \({\text {Pol}}:\mathcal {T}\left( \varSigma ,\mathcal {V}\right) \rightarrow \mathbb {N}[\mathcal {V}]\) be a monotonic polynomial interpretation (i.e., \(x > y\) implies \(f_{{\text {Pol}}}(\ldots , x, \ldots ) > f_{{\text {Pol}}}(\ldots , y, \ldots )\) for all \(f \in \varSigma \)). If for every \(\ell \rightarrow r \in \mathcal {R}\), we have \({\text {Pol}}(\ell ) > {\text {Pol}}(r)\), then \(\mathcal {R}\) is terminating.
The search for polynomial interpretations is usually automated by SMT solving. Instead of polynomials over the naturals, Theorem 1 (and the other termination criteria in the paper) can also be extended to polynomials over the non-negative reals, by requiring that whenever a term is “strictly decreasing”, then its interpretation decreases at least by a certain fixed amount \(\delta > 0\).
Example 2
Consider the TRS \(\mathcal {R}_{\textsf{div}} = \{(1), \ldots , (4) \}\) for division from [2].

Termination of \(\mathcal {R}_{\textsf{minus}} = \{(1), (2) \}\) can be proved by the polynomial interpretation that maps \(\textsf{minus}(x,y)\) to \(x+y+1\), \(\textsf{s}(x)\) to \(x+1\), and \(\mathcal {O}\) to 0. However, a direct application of classical techniques like polynomial interpretations fails for \(\mathcal {R}_{\textsf{div}}\). These techniques correspond to so-called (quasi-)simplification orderings [13] which cannot handle rules like (4) where the right-hand side is embedded in the left-hand side if y is instantiated with \(\textsf{s}(x)\). In contrast, the dependency pair framework is able to prove termination of \(\mathcal {R}_{\textsf{div}}\) automatically.
We now recapitulate the DP framework and its core processors, and refer to, e.g., [2, 16, 17, 23] for more details. In this paper, we restrict ourselves to the DP framework for innermost rewriting (denoted “
 ”), because our adaption to the probabilistic setting relies on this evaluation strategy (see Sect. 4.1).
”), because our adaption to the probabilistic setting relies on this evaluation strategy (see Sect. 4.1).
Definition 3
(Dependency Pair). Let \(\mathcal {R}\) be a (finite) TRS. We decompose its signature \(\varSigma = \varSigma _{C} \uplus \varSigma _{D}\) such that \(f \in \varSigma _D\) if \(f = {\text {root}}(\ell )\) for some rule \(\ell \rightarrow r \in \mathcal {R}\). The symbols in \(\varSigma _{C}\) and \(\varSigma _{D}\) are called constructors and defined symbols, respectively. For every \(f \in \varSigma _{D}\), we introduce a fresh tuple symbol \(f^{\#}\) of the same arity. Let \(\varSigma ^{\#}\) denote the set of all tuple symbols. To ease readability, we often write \(\textsf{F}\) instead of \(\textsf{f}^\#\). For any term \(t = f(t_1,\ldots ,t_n) \in \mathcal {T}\left( \varSigma ,\mathcal {V}\right) \) with \(f \in \varSigma _{D}\), let \(t^{\#} = f^{\#}(t_1,\ldots ,t_n)\). Moreover, for any \(r \in \mathcal {T}\left( \varSigma ,\mathcal {V}\right) \), let \(\textrm{Sub}_D(r)\) be the set of all subterms of r with defined root symbol. For a rule \(\ell \rightarrow r\) with \(\textrm{Sub}_D(r) = \{ t_1,\ldots ,t_n\}\), one obtains the n dependency pairs (DPs) \(\ell ^\# \rightarrow t_i^\#\) with \(1 \le i \le n\). \(\mathcal{D}\mathcal{P}(\mathcal {R})\) denotes the set of all dependency pairs of \(\mathcal {R}\).
Example 4
For the TRS \(\mathcal {R}_{\textsf{div}}\) from Example 2, we get the following dependency pairs.

The DP framework uses DP problems \((\mathcal {D}, \mathcal {R})\) where \(\mathcal {D}\) is a (finite) set of DPs and \(\mathcal {R}\) is a (finite) TRS. A (possibly infinite) sequence \(t_0^\#, t_1^\#, t_2^\#, \ldots \) with
 for all i is an (innermost) \((\mathcal {D}, \mathcal {R})\)-chain. Here,
for all i is an (innermost) \((\mathcal {D}, \mathcal {R})\)-chain. Here,
 is the restriction of \(\rightarrow _{\mathcal {D}}\) to rewrite steps where the used redex is in normal form w.r.t. \(\mathcal {R}\). A chain represents subsequent “function calls” in evaluations. Between two function calls (corresponding to steps with \(\mathcal {D}\)) one can evaluate the arguments with \(\mathcal {R}\). For example, \(\textsf{D}(\textsf{s}^2(\mathcal {O}), \textsf{s}(\mathcal {O})), \; \textsf{D}(\textsf{s}(\mathcal {O}), \textsf{s}(\mathcal {O}))\) is a \((\mathcal{D}\mathcal{P}(\mathcal {R}_{\textsf{div}}), \mathcal {R}_{\textsf{div}})\)-chain, as \(\textsf{D}(\textsf{s}^2(\mathcal {O}), \textsf{s}(\mathcal {O}))\)
is the restriction of \(\rightarrow _{\mathcal {D}}\) to rewrite steps where the used redex is in normal form w.r.t. \(\mathcal {R}\). A chain represents subsequent “function calls” in evaluations. Between two function calls (corresponding to steps with \(\mathcal {D}\)) one can evaluate the arguments with \(\mathcal {R}\). For example, \(\textsf{D}(\textsf{s}^2(\mathcal {O}), \textsf{s}(\mathcal {O})), \; \textsf{D}(\textsf{s}(\mathcal {O}), \textsf{s}(\mathcal {O}))\) is a \((\mathcal{D}\mathcal{P}(\mathcal {R}_{\textsf{div}}), \mathcal {R}_{\textsf{div}})\)-chain, as \(\textsf{D}(\textsf{s}^2(\mathcal {O}), \textsf{s}(\mathcal {O}))\)
 , where \(\textsf{s}^2(\mathcal {O})\) is \(\textsf{s}(\textsf{s}(\mathcal {O}))\).
, where \(\textsf{s}^2(\mathcal {O})\) is \(\textsf{s}(\textsf{s}(\mathcal {O}))\).
A DP problem \((\mathcal {D}, \mathcal {R})\) is called innermost terminating (iTerm) if there is no infinite innermost \((\mathcal {D}, \mathcal {R})\)-chain. The main result on dependency pairs is the chain criterion which states that a TRS \(\mathcal {R}\) is iTerm iff \((\mathcal{D}\mathcal{P}(\mathcal {R}),\mathcal {R})\) is iTerm. The key idea of the DP framework is a divide-and-conquer approach which applies DP processors to transform DP problems into simpler sub-problems. A DP processor \({\text {Proc}}\) has the form \({\text {Proc}}(\mathcal {D}, \mathcal {R}) = \{(\mathcal {D}_1,\mathcal {R}_1), \ldots , (\mathcal {D}_n,\mathcal {R}_n)\}\), where \(\mathcal {D}, \mathcal {D}_1, \ldots , \mathcal {D}_n\) are sets of dependency pairs and \(\mathcal {R}, \mathcal {R}_1, \ldots , \mathcal {R}_n\) are TRSs. A processor \({\text {Proc}}\) is sound if \((\mathcal {D}, \mathcal {R})\) is iTerm whenever \((\mathcal {D}_i,\mathcal {R}_i)\) is iTerm for all \(1 \le i \le n\). It is complete if \((\mathcal {D}_i,\mathcal {R}_i)\) is iTerm for all \(1 \le i \le n\) whenever \((\mathcal {D}, \mathcal {R})\) is iTerm.
So given a TRS \(\mathcal {R}\), one starts with the initial DP problem \((\mathcal{D}\mathcal{P}(\mathcal {R}), \mathcal {R})\) and applies sound (and preferably complete) DP processors repeatedly until all sub-problems are “solved” (i.e., sound processors transform them to the empty set). This allows for modular termination proofs, since different techniques can be applied on each resulting “sub-problem” \((\mathcal {D}_i,\mathcal {R}_i)\). The following three theorems recapitulate the three most important processors of the DP framework.
The (innermost) \((\mathcal {D}, \mathcal {R})\)-dependency graph is a control flow graph that indicates which dependency pairs can be used after each other in a chain. Its node set is \(\mathcal {D}\) and there is an edge from \(\ell _1^\# \rightarrow t_1^\#\) to \(\ell _2^\# \rightarrow t_2^\#\) if there exist

substitutions \(\sigma _1, \sigma _2\) such that
 , and both \(\ell _1^\# \sigma _1\) and \(\ell _2^\# \sigma _2\) are in normal form w.r.t. \(\mathcal {R}\). Any infinite \((\mathcal {D}, \mathcal {R})\)-chain corresponds to an infinite path in the dependency graph, and since the graph is finite, this infinite path must end in some strongly connected component (SCC).Footnote 1 Hence, it suffices to consider the SCCs of this graph independently. The \((\mathcal{D}\mathcal{P}(\mathcal {R}_{\textsf{div}}), \mathcal {R}_{\textsf{div}})\)-dependency graph can be seen on the right.
, and both \(\ell _1^\# \sigma _1\) and \(\ell _2^\# \sigma _2\) are in normal form w.r.t. \(\mathcal {R}\). Any infinite \((\mathcal {D}, \mathcal {R})\)-chain corresponds to an infinite path in the dependency graph, and since the graph is finite, this infinite path must end in some strongly connected component (SCC).Footnote 1 Hence, it suffices to consider the SCCs of this graph independently. The \((\mathcal{D}\mathcal{P}(\mathcal {R}_{\textsf{div}}), \mathcal {R}_{\textsf{div}})\)-dependency graph can be seen on the right.
Theorem 5
(Dep. Graph Processor). For the SCCs \(\mathcal {D}_1, ..., \mathcal {D}_n\) of the \((\mathcal {D}, \mathcal {R})\)-dependency graph, \({\text {Proc}}_{\texttt{DG}}(\mathcal {D},\mathcal {R}) = \{(\mathcal {D}_1,\mathcal {R}), ..., (\mathcal {D}_n,\mathcal {R})\}\) is sound and complete.
While the exact dependency graph is not computable in general, there are several techniques to over-approximate it automatically, see, e.g., [2, 17, 23]. In our example, applying \({\text {Proc}}_{\texttt{DG}}\) to the initial problem \((\mathcal{D}\mathcal{P}(\mathcal {R}_{\textsf{div}}), \mathcal {R}_{\textsf{div}})\) results in the smaller problems \(\bigl (\{(5)\}, \mathcal {R}_{\textsf{div}}\bigr )\) and \(\bigl (\{(7)\}, \mathcal {R}_{\textsf{div}}\bigr )\) that can be treated separately.
The next processor removes rules that cannot be used to evaluate right-hand sides of dependency pairs when their variables are instantiated with normal forms.
Theorem 6
(Usable Rules Processor). Let \(\mathcal {R}\) be a TRS. For every \(f \in \varSigma \uplus \varSigma ^{\#}\) let \({\text {Rules}}_\mathcal {R}(f) = \{\ell \rightarrow r \in \mathcal {R}\mid {\text {root}}(\ell ) = f\}\). For any \(t \in \mathcal {T}\left( \varSigma \uplus \varSigma ^{\#}, \mathcal {V}\right) \), its usable rules \(\mathcal {U}_\mathcal {R}(t)\) are the smallest set such that \(\mathcal {U}_\mathcal {R}(x) = \varnothing \) for all \(x \in \mathcal {V}\) and \(\mathcal {U}_\mathcal {R}(f(t_1, \ldots , t_n)) = {\text {Rules}}_\mathcal {R}(f) \cup \bigcup _{i = 1}^n \mathcal {U}_\mathcal {R}(t_i) \; \cup \; \bigcup _{\ell \rightarrow r \in {\text {Rules}}_\mathcal {R}(f)} \mathcal {U}_\mathcal {R}(r)\). The usable rules for the DP problem \((\mathcal {D}, \mathcal {R})\) are \(\mathcal {U}(\mathcal {D},\mathcal {R}) = \bigcup _{\ell ^\# \rightarrow t^\# \in \mathcal {D}} \mathcal {U}_\mathcal {R}(t^\#)\). Then \({\text {Proc}}_{\texttt{UR}}(\mathcal {D},\mathcal {R}) = \{(\mathcal {D},\mathcal {U}(\mathcal {D},\mathcal {R}))\}\) is sound but not complete.Footnote 2
For the DP problem \(\bigl (\{(7)\}, \mathcal {R}_{\textsf{div}}\bigr )\) only the \(\textsf{minus}\)-rules are usable and thus \({\text {Proc}}_{\texttt{UR}}\bigl (\{(7)\}, \mathcal {R}_{\textsf{div}}\bigr ) = \{\bigl (\{(7)\}, \{(1), (2)\}\bigr )\}\). For \(\bigl (\{(5)\}, \mathcal {R}_{\textsf{div}}\bigr )\) there are no usable rules at all, and thus \({\text {Proc}}_{\texttt{UR}}\bigl (\{(5)\}, \mathcal {R}_{\textsf{div}}\bigr ) = \{\bigl (\{(5)\}, \varnothing \bigr )\}\).
The last processor adapts classical orderings like polynomial interpretations to DP problems.Footnote 3 In contrast to their direct application in Theorem 1, we may now use weakly monotonic polynomials \(f_{{\text {Pol}}}\) that do not have to depend on all of their arguments. The reduction pair processor requires that all rules and dependency pairs are weakly decreasing and it removes those DPs that are strictly decreasing.
Theorem 7
(Reduction Pair Processor with Polynomial Interpretations). Let \({\text {Pol}}:\mathcal {T}\left( \varSigma \uplus \varSigma ^{\#},\mathcal {V}\right) \rightarrow \mathbb {N}[\mathcal {V}]\) be a weakly monotonic polynomial interpretation (i.e., \(x \ge y\) implies \(f_{{\text {Pol}}}(\ldots , x, \ldots ) \ge f_{{\text {Pol}}}(\ldots , y, \ldots )\) for all \(f \in \varSigma \uplus \varSigma ^\#\)). Let \(\mathcal {D} = \mathcal {D}_{\ge } \uplus \mathcal {D}_{>}\) with \(\mathcal {D}_{>} \ne \varnothing \) such that:
-
(1)
For every \(\ell \rightarrow r \in \mathcal {R}\), we have \({\text {Pol}}(\ell ) \ge {\text {Pol}}(r)\).
-
(2)
For every \(\ell ^\# \rightarrow t^\# \in \mathcal {D}\), we have \({\text {Pol}}(\ell ^\#) \ge {\text {Pol}}(t^\#)\).
-
(3)
For every \(\ell ^\# \rightarrow t^\# \in \mathcal {D}_{>}\), we have \({\text {Pol}}(\ell ^\#) > {\text {Pol}}(t^\#)\).
Then \({\text {Proc}}_{\texttt{RP}}(\mathcal {D},\mathcal {R}) = \{(\mathcal {D}_{\ge },\mathcal {R})\}\) is sound and complete.
The constraints of the reduction pair processor for the remaining DP problems \((\{(7)\}, \{(1), (2)\})\) and \((\{(5)\}, \varnothing )\) are satisfied by the polynomial interpretation which maps \(\mathcal {O}\) to 0, \(\textsf{s}(x)\) to \(x + 1\), and all other non-constant function symbols to the projection on their first arguments. Since (7) and (5) are strictly decreasing, \({\text {Proc}}_{\texttt{RP}}\) transforms both \((\{(7)\}, \{(1), (2)\})\) and \((\{(5)\}, \varnothing )\) into DP problems of the form \((\varnothing , \ldots )\). As \({\text {Proc}}_{\texttt{DG}}(\varnothing , \ldots ) = \varnothing \) and all processors used are sound, this means that there is no infinite innermost chain for the initial DP problem \((\mathcal{D}\mathcal{P}(\mathcal {R}_{\textsf{div}}), \mathcal {R}_{\textsf{div}})\) and thus, \(\mathcal {R}_{\textsf{div}}\) is innermost terminating.
3 Probabilistic Term Rewriting
Now we recapitulate probabilistic TRSs [3, 9, 14] and present a novel criterion to prove almost-sure termination automatically by adapting the direct application of polynomial interpretations from Theorem 1 to PTRSs. In contrast to TRSs, a PTRS has finiteFootnote 4 multi-distributions on the right-hand side of rewrite rules.
Definition 8
(Multi-Distribution). A finite multi-distribution \(\mu \) on a set \(A \ne \varnothing \) is a finite multiset of pairs (p : a), where \(0 < p \le 1\) is a probability and \(a \in A\), such that \(\sum _{(p:a) \in \mu }p = 1\). \({\text {FDist}}(A)\) is the set of all finite multi-distributions on A. For \(\mu \in {\text {FDist}}(A)\), its support is the multiset \({\text {Supp}}(\mu )\!=\!\{a \mid (p\!:\!a)\!\in \!\mu \) for some \(p\}\).
Definition 9
(PTRS). A probabilistic rewrite rule is a pair \(\ell \rightarrow \mu \in \mathcal {T}\left( \varSigma , \mathcal {V}\right) \times {\text {FDist}}(\mathcal {T}\left( \varSigma ,\mathcal {V}\right) )\) such that \(\ell \not \in \mathcal {V}\) and \(\mathcal {V}(r) \subseteq \mathcal {V}(\ell )\) for every \(r \in {\text {Supp}}(\mu )\). A probabilistic TRS (PTRS) is a finite set \(\mathcal {R}\) of probabilistic rewrite rules. Similar to TRSs, the PTRS \(\mathcal {R}\) induces a rewrite relation \({\rightarrow _{\mathcal {R}}} \subseteq \mathcal {T}\left( \varSigma ,\mathcal {V}\right) \times {\text {FDist}}(\mathcal {T}\left( \varSigma ,\mathcal {V}\right) )\) where \(s \rightarrow _{\mathcal {R}} \{p_1:t_1, \ldots , p_k:t_k\}\) if there is a position \(\pi \), a rule \(\ell \rightarrow \{p_1:r_1, \ldots , p_k:r_k\} \in \mathcal {R}\), and a substitution \(\sigma \) such that \(s|_{\pi }=\ell \sigma \) and \(t_j = s[r_j\sigma ]_{\pi }\) for all \(1 \le j \le k\). We call \(s \rightarrow _{\mathcal {R}} \mu \) an innermost rewrite step (denoted
 ) if every proper subterm of the used redex \(\ell \sigma \) is in normal form w.r.t. \(\mathcal {R}\).
) if every proper subterm of the used redex \(\ell \sigma \) is in normal form w.r.t. \(\mathcal {R}\).
Example 10
As an example, consider the PTRS \(\mathcal {R}_{\textsf{rw}}\) with the only rule \(\textsf{g}(x) \rightarrow \{{1}/{2}:x, \; {1}/{2}:\textsf{g}(\textsf{g}(x))\}\), which corresponds to a symmetric random walk.
As proposed in [3], we lift \(\rightarrow _{\mathcal {R}}\) to a rewrite relation between multi-distributions in order to track all probabilistic rewrite sequences (up to non-determinism) at once. For any \(0 < p \le 1\) and any \(\mu \in {\text {FDist}}(A)\), let \(p \cdot \mu = \{ (p\cdot q:a) \mid (q:a) \in \mu \}\).
Definition 11
(Lifting). The lifting \({\rightrightarrows } \subseteq {\text {FDist}}(\mathcal {T}\left( \varSigma ,\mathcal {V}\right) ) \times {\text {FDist}}(\mathcal {T}\left( \varSigma ,\mathcal {V}\right) )\) of a relation \({\rightarrow } \subseteq \mathcal {T}\left( \varSigma ,\mathcal {V}\right) \times {\text {FDist}}(\mathcal {T}\left( \varSigma ,\mathcal {V}\right) )\) is the smallest relation with:
-
If \(t \in \mathcal {T}\left( \varSigma ,\mathcal {V}\right) \) is in normal form w.r.t. \(\rightarrow \), then \(\{1: t\} \rightrightarrows \{1:t\}\).
-
If \(t \rightarrow \mu \), then \(\{1: t\} \rightrightarrows \mu \).
-
If for all \(1 \le j \le k\) there are \(\mu _j, \nu _j \in {\text {FDist}}(\mathcal {T}\left( \varSigma ,\mathcal {V}\right) )\) with \(\mu _j \rightrightarrows \nu _j\) and \(0 < p_j \le 1\) with \(\sum _{1 \le j \le k} p_j = 1\), then \(\bigcup _{1 \le j \le k} p_j \cdot \mu _j \rightrightarrows \bigcup _{1 \le j \le k} p_j \cdot \nu _j\).
For a PTRS \(\mathcal {R}\), we write \(\rightrightarrows _\mathcal {R}\) and
 for the liftings of \(\rightarrow _{\mathcal {R}}\) and
for the liftings of \(\rightarrow _{\mathcal {R}}\) and
 , respectively.
, respectively.
Example 12
For instance, we obtain the following
 -rewrite sequence:
-rewrite sequence:

Note that the two occurrences of \(\mathcal {O}\) and \(\textsf{g}^2(\mathcal {O})\) in the multi-distribution above could be rewritten differently if the PTRS had rules resulting in different terms. So it should be distinguished from \(\{5/8:\mathcal {O}, 1/4:\textsf{g}^2(\mathcal {O}), 1/8:\textsf{g}^4(\mathcal {O}) \}\).
To express the concept of almost-sure termination, one has to determine the probability for normal forms in a multi-distribution.
Definition 13
(\(|\mu |_{\mathcal {R}}\)). For a PTRS \(\mathcal {R}\), \(\texttt{NF}_{\mathcal {R}} \subseteq \mathcal {T}\left( \varSigma ,\mathcal {V}\right) \) denotes the set of all normal forms w.r.t. \(\mathcal {R}\). For any \(\mu \in {\text {FDist}}(\mathcal {T}\left( \varSigma ,\mathcal {V}\right) )\), let \(|\mu |_{\mathcal {R}} = \sum _{(p:t) \in \mu , t \in \texttt{NF}_{\mathcal {R}}} p\).
Example 14
Consider the multi-distribution \(\{ 1/2:\mathcal {O}, 1/8:\mathcal {O}, 1/8:\textsf{g}^2(\mathcal {O}), 1/8:\textsf{g}^2(\mathcal {O}), 1/8:\textsf{g}^4(\mathcal {O}) \}\) from Example 12 and \(\mathcal {R}_{\textsf{rw}}\) from Example 10. Then \(|\mu |_{\mathcal {R}_{\textsf{rw}}} = 1/2 + 1/8 = 5/8\).
Definition 15
((Innermost) AST). Let \(\mathcal {R}\) be a PTRS and \((\mu _n)_{n \in \mathbb {N}}\) be an infinite \(\rightrightarrows _{\mathcal {R}}\)-rewrite sequence, i.e., \(\mu _n \rightrightarrows _{\mathcal {R}} \mu _{n+1}\) for all \(n \in \mathbb {N}\). Note that \(\lim \limits _{n \rightarrow \infty }|\mu _n|_{\mathcal {R}}\) exists, since \(|\mu _n|_{\mathcal {R}} \le |\mu _{n+1}|_{\mathcal {R}}\le 1\) for all \(n \in \mathbb {N}\). \(\mathcal {R}\) is almost-surely terminating (AST) (innermost almost-surely terminating (iAST)) if \(\lim \limits _{n \rightarrow \infty } |\mu _n|_{\mathcal {R}} = 1\) holds for every infinite \(\rightrightarrows _{\mathcal {R}}\)-rewrite sequence (
 -rewrite sequence) \((\mu _n)_{n \in \mathbb {N}}\).
-rewrite sequence) \((\mu _n)_{n \in \mathbb {N}}\).
Example 16
For the (unique) infinite extension of the
 -rewrite sequence \((\mu _n)_{n \in \mathbb {N}}\) in Example 12, we have \(\lim \limits _{n \rightarrow \infty } |\mu _n|_{\mathcal {R}} = 1\). Indeed, \(\mathcal {R}_{\textsf{rw}}\) is AST (but not PAST, i.e., the expected number of rewrite steps is infinite for every term containing \(\textsf{g}\)).
-rewrite sequence \((\mu _n)_{n \in \mathbb {N}}\) in Example 12, we have \(\lim \limits _{n \rightarrow \infty } |\mu _n|_{\mathcal {R}} = 1\). Indeed, \(\mathcal {R}_{\textsf{rw}}\) is AST (but not PAST, i.e., the expected number of rewrite steps is infinite for every term containing \(\textsf{g}\)).
Theorem 17 introduces a novel technique to prove AST automatically using a direct application of polynomial interpretations.
Theorem 17
(Proving AST with Polynomial Interpretations). Let \(\mathcal {R}\) be a PTRS, let \({\text {Pol}}:\mathcal {T}\left( \varSigma ,\mathcal {V}\right) \rightarrow \mathbb {N}[\mathcal {V}]\) be a monotonic, multilinearFootnote 5 polynomial interpretation (i.e., for all \(f \in \varSigma \), all monomials of \(f_{{\text {Pol}}}(x_1,\ldots ,x_n)\) have the form \(c \cdot x_1^{e_1} \cdot \ldots \cdot x_n^{e_n}\) with \(c \in \mathbb {N}\) and \(e_1,\ldots ,e_n \in \{0,1\}\)). If for every rule \(\ell \rightarrow \{p_1:r_1, \ldots , p_k:r_k\} \in \mathcal {R}\),
-
(1)
there exists a \(1 \le j \le k\) with \({\text {Pol}}(\ell ) > {\text {Pol}}(r_j)\) and
-
(2)
\({\text {Pol}}(\ell ) \ge \sum _{1 \le j \le k} \; p_j \cdot {\text {Pol}}(r_j)\),
then \(\mathcal {R}\) is AST.
In [3], it was shown that PAST can be proved by using multilinear polynomials and requiring a strict decrease in the expected value of each rule. In contrast, we only require a weak decrease of the expected value in (2) and in addition, at least one term in the support of the right-hand side must become strictly smaller (1). As mentioned, the proof for Theorem 17 (and for all our other new results and observations) can be found in [28]. The proof idea is based on [32], but it extends their approach from while-programs on integers to terms. However, in contrast to [32], PTRSs can only deal with constant probabilities, since all variables stand for terms, not for numbers. Note that the constraints (1) and (2) of our new criterion in Theorem 17 are equivalent to the constraint of the classical Theorem 1 in the special case where the PTRS is in fact a TRS (i.e., all rules have the form \(\ell \rightarrow \{ 1: r \}\)).
Example 18
To prove that \(\mathcal {R}_{\textsf{rw}}\) is AST with Theorem 17, we can use the polynomial interpretation that maps \(\textsf{g}(x)\) to \(x+1\) and \(\mathcal {O}\) to 0.
4 Probabilistic Dependency Pairs
We introduce our new adaption of DPs to the probabilistic setting in Sect. 4.1. Then we present the processors for the probabilistic DP framework in Sect. 4.2.
4.1 Dependency Tuples and Chains for Probabilistic Term Rewriting
We first show why straightforward adaptions are unsound. A natural idea to define DPs for probabilistic rules \(\ell \rightarrow \{p_1:r_1,\dots , p_k:r_k\} \in \mathcal {R}\) would be (8) or (9):
For (9), if \(\textrm{Sub}_D(r_j) = \varnothing \), then we insert a fresh constructor \(\bot \) into \(\textrm{Sub}_D(r_j)\) that does not occur in \(\mathcal {R}\). So in both (8) and (9), we replace \(r_j\) by a single term \(t_j^\#\) in the right-hand side. The following example shows that this notion of probabilistic DPs does not yield a sound chain criterion. Consider the PTRSs \(\mathcal {R}_1\) and \(\mathcal {R}_2\):
\(\mathcal {R}_1\) is AST since it corresponds to a symmetric random walk stopping at 0, where the number of \(\textsf{g}\)s denotes the current position. In contrast, \(\mathcal {R}_2\) is not AST as it corresponds to a random walk where there is an equal chance of reducing the number of \(\textsf{g}\)s by 1 or increasing it by 2. For both \(\mathcal {R}_1\) and \(\mathcal {R}_2\), (8) and (9) would result in the only dependency pair \(\textsf{G}\rightarrow \{1/2: \mathcal {O}, 1/2: \textsf{G}\}\) and \(\textsf{G}\rightarrow \{1/2: \bot , 1/2: \textsf{G}\}\), resp. Rewriting with this DP is clearly AST, since it corresponds to a program that flips a coin until one gets head and then terminates. So the definitions (8) and (9) would not yield a sound approach for proving AST.
\(\mathcal {R}_1\) and \(\mathcal {R}_2\) show that the number of occurrences of the same subterm in the right-hand side r of a rule matters for AST. Thus, we now regard the multiset \(\textrm{MSub}_D(r)\) of all subterms of r with defined root symbol to ensure that multiple occurrences of the same subterm in r are taken into account. Moreover, instead of pairs we regard dependency tuples which consider all subterms with defined root in r at once. Dependency tuples were already used when adapting DPs for complexity analysis of (non-probabilistic) TRSs [37]. We now adapt them to the probabilistic setting and present a novel rewrite relation for dependency tuples.
Definition 19
(Transformation dp). If \(\textrm{MSub}_D(r) =\{t_{1}, \dots , t_{n}\}\), then we define \(dp(r) = \textsf{c}_{n}(t^\#_1, \ldots , t^\#_n)\). To make dp(r) unique, we use the lexicographic ordering < on positions where \(t_{i} = r|_{\pi _{i}}\) and \(\pi _{1}< \ldots < \pi _{n}\). Here, we extend \(\varSigma _{C}\) by fresh compound constructor symbols \(\textsf{c}_{n}\) of arity n for \(n \in \mathbb {N}\).
When rewriting a subterm \(t^\#_i\) of \(\textsf{c}_{n}(t^\#_1, \ldots , t^\#_n)\) with a dependency tuple, one obtains terms with nested compound symbols. To abstract from nested compound symbols and from the order of their arguments, we introduce the following normalization.
Definition 20
(Normalizing Compound Terms). For any term t, its content \(cont(t)\) is the multiset defined by \(cont(\textsf{c}_{n}(t_1,\ldots ,t_n)) = cont(t_1) \cup \ldots \cup cont(t_n)\) and \(cont(t) = \{t\}\) otherwise. For any term t with \(cont(t) = \{ t_1, \ldots , t_n \}\), the term \(\textsf{c}_{n}(t_1,\ldots ,t_n)\) is a normalization of t. For two terms \(t, t'\), we define \(t \approx t'\) if \(cont(t) = cont(t')\). We define \(\approx \) on multi-distributions in a similar way: whenever \(t_j \approx t_j'\) for all \(1 \le j \le k\), then \(\{p_1:t_1, \ldots , p_k: t_k \} \approx \{p_1:t_1', \ldots , p_k: t_k'\}\).
So for example, \(\textsf{c}_{3}(x, x, y)\) is a normalization of \(\textsf{c}_{2}(\textsf{c}_{1}(x), \textsf{c}_{2}(x,y))\). We do not distinguish between terms and multi-distributions that are equal w.r.t. \(\approx \) and we write \(\textsf{c}_{n}(t_1,\ldots ,t_n)\) for any term t with a compound root symbol where \(cont(t) = \{t_1,\ldots ,t_n\}\), i.e., we consider all such t to be normalized.
For any rule \(\ell \rightarrow \{p_1:r_1,\dots , p_k:r_k\} \in \mathcal {R}\), the natural idea would be to define its dependency tuple (DT) as \(\ell ^{\#} \rightarrow \{p_1:dp(r_1), \dots , p_k:dp(r_k)\}\). Then innermost chains in the probabilistic setting would result from alternating a DT-step with an arbitrary number of \(\mathcal {R}\)-steps (using
 ). However, such chains would not necessarily correspond to the original rewrite sequence and thus, the resulting chain criterion would not be sound.
). However, such chains would not necessarily correspond to the original rewrite sequence and thus, the resulting chain criterion would not be sound.
Example 21
Consider the PTRS \(\mathcal {R}_3 = \{\textsf{f}(\mathcal {O}) \rightarrow \{1: \textsf{f}(\textsf{a}) \}, \textsf{a}\rightarrow \{1/2:\textsf{b}_1, 1/2:\textsf{b}_2\}, \textsf{b}_1 \rightarrow \{1: \mathcal {O}\}, \textsf{b}_2 \rightarrow \{1: \textsf{f}(\textsf{a}) \} \}\). Its DTs would be \(\mathcal {D}_3 = \{\textsf{F}(\mathcal {O}) \rightarrow \{1:\textsf{c}_{2}(\textsf{F}(\textsf{a}), \textsf{A})\}, \textsf{A}\rightarrow \{1/2:\textsf{c}_{1}(\textsf{B}_1), 1/2:\textsf{c}_{1}(\textsf{B}_2) \}, \textsf{B}_1 \rightarrow \{1:\textsf{c}_{0}\}, \textsf{B}_2 \rightarrow \{1:\textsf{c}_{2}(\textsf{F}(\textsf{a}), \textsf{A})\} \}\). \(\mathcal {R}_3\) is not iAST, because one can extend the rewrite sequence

to an infinite sequence without normal forms. The resulting chain starts with

The second and third term in the last distribution do not correspond to terms in the original rewrite sequence (11). After the next \(\mathcal {D}_3\)-step which removes \(\textsf{B}_1\), no further \(\mathcal {D}_3\)-step can be applied to the underlined term anymore, because \(\textsf{b}_2\) cannot be rewritten to \(\mathcal {O}\). Thus, the resulting chain criterion would be unsound, as every chain \((\mu _n)_{n \in \mathbb {N}}\) in this example contains such \(\mathcal {D}_3\)-normal forms and therefore, it is AST (i.e., \(\lim \limits _{n \rightarrow \infty }|\mu _n|_{\mathcal {D}_3} =1\) where \(|\mu _n|_{\mathcal {D}_3}\) is the probability for \(\mathcal {D}_3\)-normal forms in \(\mu _n\)). So we have to ensure that when \(\textsf{A}\) is rewritten to \(\textsf{B}_1\) via a DT from \(\mathcal {D}_3\), then the “copy” \(\textsf{a}\) of the redex \(\textsf{A}\) is rewritten via \(\mathcal {R}_3\) to the corresponding term \(\textsf{b}_1\) instead of \(\textsf{b}_2\). Thus, after the step with
 we should have \(\textsf{c}_{2}(\textsf{F}(\textsf{b}_1), \textsf{B}_1)\) and \(\textsf{c}_{2}(\textsf{F}(\textsf{b}_2), \textsf{B}_2)\), but not \(\textsf{c}_{2}(\textsf{F}(\textsf{b}_2), \textsf{B}_1)\) or \(\textsf{c}_{2}(\textsf{F}(\textsf{b}_1), \textsf{B}_2)\).
we should have \(\textsf{c}_{2}(\textsf{F}(\textsf{b}_1), \textsf{B}_1)\) and \(\textsf{c}_{2}(\textsf{F}(\textsf{b}_2), \textsf{B}_2)\), but not \(\textsf{c}_{2}(\textsf{F}(\textsf{b}_2), \textsf{B}_1)\) or \(\textsf{c}_{2}(\textsf{F}(\textsf{b}_1), \textsf{B}_2)\).
Therefore, for our new adaption of DPs to the probabilistic setting, we operate on pairs. Instead of having a rule \(\ell \rightarrow \{ p_1:r_1, \ldots , p_k:r_k \}\) from \(\mathcal {R}\) and its corresponding dependency tuple \(\ell ^\# \rightarrow \{ p_1:dp(r_1), \ldots , p_k:dp(r_k)\}\) separately, we couple them together to \(\langle \ell ^\#,\ell \rangle \rightarrow \{ p_1:\langle dp(r_1),r_1 \rangle , \ldots , p_k:\langle dp(r_k),r_k \rangle \}\). This type of rewrite system is called a probabilistic pair term rewrite system (PPTRS), and its rules are called coupled dependency tuples. Our new DP framework works on (probabilistic) DP problems \((\mathcal {P},\mathcal {S})\), where \(\mathcal {P}\) is a PPTRS and \(\mathcal {S}\) is a PTRS.
Definition 22
(Coupled Dependency Tuple). Let \(\mathcal {R}\) be a PTRS. For every \(\ell \rightarrow \mu = \{p_1:r_1, \ldots , p_k:r_k\} \in \mathcal {R}\), its coupled dependency tuple (or simply dependency tuple, DT) is \(\mathcal{D}\mathcal{T}(\ell \rightarrow \mu ) = \langle \ell ^\#,\ell \rangle \rightarrow \{ p_1 : \langle dp(r_1),r_1 \rangle , \ldots , p_k : \langle dp(r_k),r_k \rangle \}\). The set of all coupled dependency tuples of \(\mathcal {R}\) is denoted by \(\mathcal{D}\mathcal{T}(\mathcal {R})\).
Example 23
The following PTRS \(\mathcal {R}_{\textsf{pdiv}}\) adapts \(\mathcal {R}_{\textsf{div}}\) to the probabilistic setting.

In (15), we now do the actual rewrite step with a chance of 1/2 or the terms stay the same. Our new probabilistic DP framework can prove automatically that \(\mathcal {R}_{\textsf{pdiv}}\) is iAST, while (as in the non-probabilistic setting) a direct application of polynomial interpretations via Theorem 17 fails. We get \(\mathcal{D}\mathcal{T}(\mathcal {R}_{\textsf{pdiv}}) = \{ (16), \ldots , (19)\}\):
Definition 24
(PPTRS,
 ). Let \(\mathcal {P}\) be a finite set of rules of the form \(\langle \ell ^\#,\ell \rangle \rightarrow \{ p_1:\langle d_1,r_1 \rangle , \ldots , p_k:\langle d_k,r_k \rangle \}\). For every such rule, let \(\textrm{proj}_1(\mathcal {P})\) contain \(\ell ^\# \rightarrow \{ p_1:d_1, \ldots , p_k:d_k \}\) and let \(\textrm{proj}_2(\mathcal {P})\) contain \(\ell \rightarrow \{ p_1:r_1, \ldots , p_k:r_k \}\). If \(\textrm{proj}_2(\mathcal {P})\) is a PTRS and \(cont(d_j) \subseteq cont(dp(r_j))\) holdsFootnote 6 for all \(1 \le j \le k\), then \(\mathcal {P}\) is a probabilistic pair term rewrite system (PPTRS).
). Let \(\mathcal {P}\) be a finite set of rules of the form \(\langle \ell ^\#,\ell \rangle \rightarrow \{ p_1:\langle d_1,r_1 \rangle , \ldots , p_k:\langle d_k,r_k \rangle \}\). For every such rule, let \(\textrm{proj}_1(\mathcal {P})\) contain \(\ell ^\# \rightarrow \{ p_1:d_1, \ldots , p_k:d_k \}\) and let \(\textrm{proj}_2(\mathcal {P})\) contain \(\ell \rightarrow \{ p_1:r_1, \ldots , p_k:r_k \}\). If \(\textrm{proj}_2(\mathcal {P})\) is a PTRS and \(cont(d_j) \subseteq cont(dp(r_j))\) holdsFootnote 6 for all \(1 \le j \le k\), then \(\mathcal {P}\) is a probabilistic pair term rewrite system (PPTRS).
Let \(\mathcal {S}\) be a PTRS. Then a normalized term \(\textsf{c}_{n}(s_1,\ldots ,s_n)\) rewrites with the PPTRS \(\mathcal {P}\) to \(\{p_1:b_1, \ldots , p_k:b_k\}\) w.r.t. \(\mathcal {S}\) (denoted
 ) if there are an \(1 \le i \le n\), an \(\langle \ell ^\#,\ell \rangle \rightarrow \{ p_1:\langle d_1,r_1 \rangle , \ldots , p_k:\langle d_k,r_k \rangle \} \in \mathcal {P}\), a substitution \(\sigma \) with \(s_i = \ell ^\# \sigma \in \texttt{NF}_{\mathcal {S}}\), and for all \(1 \le j \le k\) we have \(b_j = \textsf{c}_{n}(t_1^j,\ldots ,t_n^j)\) where
) if there are an \(1 \le i \le n\), an \(\langle \ell ^\#,\ell \rangle \rightarrow \{ p_1:\langle d_1,r_1 \rangle , \ldots , p_k:\langle d_k,r_k \rangle \} \in \mathcal {P}\), a substitution \(\sigma \) with \(s_i = \ell ^\# \sigma \in \texttt{NF}_{\mathcal {S}}\), and for all \(1 \le j \le k\) we have \(b_j = \textsf{c}_{n}(t_1^j,\ldots ,t_n^j)\) where
-
\(t_i^j = d_j \sigma \) for all \(1 \le j \le k\), i.e., we rewrite the term \(s_i\) using \(\textrm{proj}_1(\mathcal {P})\).
-
For every \(1 \le i' \le n\) with \(i \ne i'\) we have
-
(i)
\(t_{i'}^j = s_{i'}\) for all \(1 \le j \le k\) or
-
(ii)
\(t_{i'}^j = s_{i'}[r_j \sigma ]_{\tau }\) for all \(1 \le j \le k\), if \(s_{i'}|_\tau = \ell \sigma \) for some position \(\tau \) and if \(\ell \rightarrow \{ p_1:r_1, \ldots , p_k:r_k\} \in \mathcal {S}\).
So \(s_{i'}\) stays the same in all \(b_j\) or we can apply the rule from \(\textrm{proj}_2(\mathcal {P})\) to rewrite \(s_{i'}\) in all \(b_j\), provided that this rule is also contained in \(\mathcal {S}\). Note that even if the rule is applicable, the term \(s_{i'}\) can still stay the same in all \(b_j\).
-
(i)
Example 25
For \(\mathcal {R}_3\) from Example 21, the (coupled) dependency tuple for the \(\textsf{f}\)-rule is \(\langle \textsf{F}(\mathcal {O}),\textsf{f}(\mathcal {O})\rangle \rightarrow \{1:\langle \textsf{c}_{2}(\textsf{F}(\textsf{a}), \textsf{A}), \textsf{f}(\textsf{a})\rangle \}\) and the DT for the \(\textsf{a}\)-rule is \(\langle \textsf{A},\textsf{a}\rangle \rightarrow \{1/2:\langle \textsf{c}_{1}(\textsf{B}_1),\textsf{b}_1\rangle , 1/2:\langle \textsf{c}_{1}(\textsf{B}_2),\textsf{b}_2\rangle \}\). With the lifting
 of
of
 , we get the following sequence which corresponds to the rewrite sequence (11) from Example 21.
, we get the following sequence which corresponds to the rewrite sequence (11) from Example 21.

So with the PPTRS, when rewriting \(\textsf{A}\) to \(\textsf{B}_1\) in the second step, we can simultaneously rewrite the inner subterm \(\textsf{a}\) of \(\textsf{F}(\textsf{a})\) to \(\textsf{b}_1\) or keep \(\textsf{a}\) unchanged, but we cannot rewrite \(\textsf{a}\) to \(\textsf{b}_2\). This is ensured by \(\textsf{b}_1\) in the second component of \(\langle \textsf{A},\textsf{a}\rangle \rightarrow \{1/2:\langle \textsf{c}_{1}(\textsf{B}_1),\textsf{b}_1\rangle , \ldots \}\), since by Definition 24, if \(s_{i'}\) contains \(\ell \sigma \) at some arbitrary position \(\tau \), then one can (only) use the rule in the second component of the DT to rewrite \(\ell \sigma \) (i.e., here we have \(s_{i'}=\textsf{F}(\textsf{a})\), \(s_i=\textsf{A}\), and \(s_{i'}|_\tau =\textsf{a}\)). A similar observation holds when rewriting \(\textsf{A}\) to \(\textsf{B}_2\). Recall that with the notion of chains in Example 21, one cannot simulate every possible rewrite sequence, which leads to unsoundness. In contrast, with the notion of coupled DTs and PPTRSs, every possible rewrite sequence can be simulated which ensures soundness of the chain criterion. Of course, due to the ambiguity in (i) and (ii) of Definition 24, one could also create other “unsuitable”
 -sequences where \(\textsf{a}\) is not reduced to \(\textsf{b}_1\) and \(\textsf{b}_2\) in the second step, but is kept unchanged. This does not affect the soundness of the chain criterion, since every rewrite sequence of the original PTRS can be simulated by a “suitable” chain. To obtain completeness of the chain criterion, one would have to avoid such “unsuitable” sequences.
-sequences where \(\textsf{a}\) is not reduced to \(\textsf{b}_1\) and \(\textsf{b}_2\) in the second step, but is kept unchanged. This does not affect the soundness of the chain criterion, since every rewrite sequence of the original PTRS can be simulated by a “suitable” chain. To obtain completeness of the chain criterion, one would have to avoid such “unsuitable” sequences.
We also introduce an analogous rewrite relation for PTRSs, where we can apply the same rule simultaneously to the same subterms in a single rewrite step.
Definition 26
(
 ). For a PTRS \(\mathcal {S}\) and a normalized term \(\textsf{c}_{n}(s_1,\ldots ,s_n)\), we define
). For a PTRS \(\mathcal {S}\) and a normalized term \(\textsf{c}_{n}(s_1,\ldots ,s_n)\), we define
 if there are an \(1\!\le \!i\!\le n\), an \(\ell \!\rightarrow \!\{ p_1\!:\!r_1, \ldots , p_k\!:\!r_k\} \in \mathcal {S}\), a position \(\pi \), a substitution \(\sigma \) with \(s_i|_{\pi }\!=\!\ell \sigma \) such that every proper subterm of \(\ell \sigma \) is in \(\texttt{NF}_{\mathcal {S}}\), and for all \(1\!\le j\!\le k\) we have \(b_j = \textsf{c}_{n}(t_1^j,\ldots ,t_n^j)\) where
if there are an \(1\!\le \!i\!\le n\), an \(\ell \!\rightarrow \!\{ p_1\!:\!r_1, \ldots , p_k\!:\!r_k\} \in \mathcal {S}\), a position \(\pi \), a substitution \(\sigma \) with \(s_i|_{\pi }\!=\!\ell \sigma \) such that every proper subterm of \(\ell \sigma \) is in \(\texttt{NF}_{\mathcal {S}}\), and for all \(1\!\le j\!\le k\) we have \(b_j = \textsf{c}_{n}(t_1^j,\ldots ,t_n^j)\) where
-
\(t_i^j = s_i[r_j \sigma ]_{\pi }\) for all \(1 \le j \le k\), i.e., we rewrite the term \(s_i\) using \(\mathcal {S}\).
-
For every \(1 \le i' \le n\) with \(i \ne i'\) we have
-
(i)
\(t_{i'}^j = s_{i'}\) for all \(1 \le j \le k\) or
-
(ii)
\(t_{i'}^j = s_{i'}[r_j \sigma ]_{\tau }\) for all \(1 \le j \le k\), if \(s_{i'}|_\tau = \ell \sigma \) for some position \(\tau \).
-
(i)
So for example, the lifting
 of
of
 for \(\mathcal {S}= \mathcal {R}_3\) rewrites \(\{1:\textsf{c}_{2}(\textsf{f}(\textsf{a}), \textsf{a})\}\) to both \(\{1/2: \textsf{c}_{2}(\textsf{f}(\textsf{b}_1), \textsf{b}_1), 1/2: \textsf{c}_{2}(\textsf{f}(\textsf{b}_2), \textsf{b}_2) \}\) and \(\{1/2: \textsf{c}_{2}(\textsf{f}(\textsf{a}), \textsf{b}_1), 1/2: \textsf{c}_{2}(\textsf{f}(\textsf{a}), \textsf{b}_2) \}\).
for \(\mathcal {S}= \mathcal {R}_3\) rewrites \(\{1:\textsf{c}_{2}(\textsf{f}(\textsf{a}), \textsf{a})\}\) to both \(\{1/2: \textsf{c}_{2}(\textsf{f}(\textsf{b}_1), \textsf{b}_1), 1/2: \textsf{c}_{2}(\textsf{f}(\textsf{b}_2), \textsf{b}_2) \}\) and \(\{1/2: \textsf{c}_{2}(\textsf{f}(\textsf{a}), \textsf{b}_1), 1/2: \textsf{c}_{2}(\textsf{f}(\textsf{a}), \textsf{b}_2) \}\).
A straightforward adaption of “chains” to the probabilistic setting using
 would force us to use steps with DTs from \(\mathcal {P}\) at the same time for all terms in a multi-distribution. Therefore, instead we view a rewrite sequence on multi-distributions as a tree (e.g., the tree representation of the rewrite sequence 20 from Example 25 is on the right). Regarding the
would force us to use steps with DTs from \(\mathcal {P}\) at the same time for all terms in a multi-distribution. Therefore, instead we view a rewrite sequence on multi-distributions as a tree (e.g., the tree representation of the rewrite sequence 20 from Example 25 is on the right). Regarding the

paths in this tree (which represent rewrite sequences of terms with certain probabilities) allows us to adapt the idea of chains, i.e., that one uses only finitely many \(\mathcal {S}\)-steps before the next step with a DT from \(\mathcal {P}\).
Definition 27
(Chain Tree).\(\mathfrak {T}\!=\!(V,E,L,P)\) is an (innermost) \((\mathcal {P}\!,\mathcal {S})\) -chain tree if
-
1.
\(V \ne \varnothing \) is a possibly infinite set of nodes and \(E \subseteq V \times V\) is a set of directed edges, such that (V, E) is a (possibly infinite) directed tree where \(vE = \{ w \mid (v,w) \in E \}\) is finite for every \(v \in V\).
-
2.
\(L:V\rightarrow (0,1]\times \mathcal {T}\left( \varSigma \uplus \varSigma ^{\#},\mathcal {V}\right) \) labels every node v by a probability \(p_v\) and a term \(t_v\). For the root \(v \in V\) of the tree, we have \(p_v = 1\).
-
3.
\(P \subseteq V \setminus {\text {Leaf}}\) (where \({\text {Leaf}}\) are all leaves) is a subset of the inner nodes to indicate whether we use the PPTRS \(\mathcal {P}\) or the PTRS \(\mathcal {S}\) for the rewrite step. \(S = V \setminus ({\text {Leaf}}\cup P)\) are all inner nodes that are not in P. Thus, \(V = P \,\uplus \, S \,\uplus \, {\text {Leaf}}\).
-
4.
For all \(v \in P\): If \(vE = \{w_1, \ldots , w_k\}\), then
 .
. -
5.
For all \(v \in S\): If \(vE = \{w_1, \ldots , w_k\}\), then
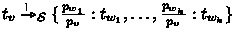 .
. -
6.
Every infinite path in \(\mathfrak {T}\) contains infinitely many nodes from P.
Conditions 1–5 ensure that the tree represents a valid rewrite sequence and the last condition is the main property for chains.
Definition 28
(\(|\mathfrak {T}|_{{\text {Leaf}}}\), iAST). For any innermost \((\mathcal {P},\mathcal {S})\)-chain tree \(\mathfrak {T}\) we define \(|\mathfrak {T}|_{{\text {Leaf}}} = \sum _{v \in {\text {Leaf}}} \,p_v\). We say that \((\mathcal {P},\mathcal {S})\) is iAST if we have \(|\mathfrak {T}|_{{\text {Leaf}}} = 1\) for every innermost \((\mathcal {P},\mathcal {S})\)-chain tree \(\mathfrak {T}\).
While we have \(|\mathfrak {T}|_{{\text {Leaf}}} = 1\) for every finite chain tree \(\mathfrak {T}\), for infinite chain trees \(\mathfrak {T}\) we may have \(|\mathfrak {T}|_{{\text {Leaf}}} <1\) or even \(|\mathfrak {T}|_{{\text {Leaf}}} = 0\) if \(\mathfrak {T}\) has no leaf at all.
With this new type of DTs and chain trees, we now obtain an analogous chain criterion to the non-probabilistic setting.
Theorem 29
(Chain Criterion). A PTRS \(\mathcal {R}\) is iAST if \((\mathcal{D}\mathcal{T}(\mathcal {R}),\mathcal {R})\) is iAST.
In contrast to the non-probabilistic case, our chain criterion as presented in the paper is sound but not complete (i.e., we do not have “iff” in Theorem 29). However, we also developed a refinement where our chain criterion is made complete by also storing the positions of the defined symbols in dp(r) [27]. In this way, one can avoid “unsuitable” chain trees, as discussed at the end of Example 25.
Our notion of DTs and chain trees is only suitable for innermost evaluation. To see this, consider the PTRSs \(\mathcal {R}_1'\) and \(\mathcal {R}_2'\) which both contain \(\textsf{g}\rightarrow \{ 1/2:\mathcal {O}, 1/2:\textsf{h}(\textsf{g}) \}\), but in addition \(\mathcal {R}_1'\) has the rule \(\textsf{h}(x) \rightarrow \{ 1: \textsf{f}(x,x) \}\) and \(\mathcal {R}_2'\) has the rule \(\textsf{h}(x) \rightarrow \{1:\textsf{f}(x,x,x)\}\). Similar to \(\mathcal {R}_1\) and \(\mathcal {R}_2\) in (10), \(\mathcal {R}_1'\) is AST while \(\mathcal {R}_2'\) is not. In contrast, both \(\mathcal {R}_1'\) and \(\mathcal {R}_2'\) are iAST, since the innermost evaluation strategy prevents the application of the \(\textsf{h}\)-rule to terms containing \(\textsf{g}\). Our DP framework handles \(\mathcal {R}_1'\) and \(\mathcal {R}_2'\) in the same way, as both have the same DT \(\langle \textsf{G}, \textsf{g}\rangle \rightarrow \{ 1/2:\langle \textsf{c}_{0}, \mathcal {O}\rangle , 1/2:\langle \textsf{c}_{2}(\textsf{H}(\textsf{g}),\textsf{G}), \textsf{h}(\textsf{g}) \rangle \}\) and a DT \(\langle \textsf{H}(x), \textsf{h}(x) \rangle \rightarrow \{ 1: \langle \textsf{c}_{0}, \textsf{f}(\ldots ) \rangle \}\). Even if we allowed the application of the second DT to terms of the form \(\textsf{H}(\textsf{g})\), we would still obtain \(|\mathfrak {T}|_{{\text {Leaf}}} = 1\) for every chain tree \(\mathfrak {T}\). So a DP framework to analyze “full” instead of innermost AST would be considerably more involved.
4.2 The Probabilistic DP Framework
Now we introduce the probabilistic dependency pair framework which keeps the core ideas of the non-probabilistic framework. So instead of applying one ordering for a PTRS directly as in Theorem 17, we want to benefit from modularity. Now a DP processor \({\text {Proc}}\) is of the form \({\text {Proc}}(\mathcal {P}, \mathcal {S}) = \{(\mathcal {P}_1,\mathcal {S}_1), \ldots , (\mathcal {P}_n,\mathcal {S}_n)\}\), where \(\mathcal {P}, \mathcal {P}_1, \ldots , \mathcal {P}_n\) are PPTRSs and \(\mathcal {S}, \mathcal {S}_1, \ldots , \mathcal {S}_n\) are PTRSs. A processor \({\text {Proc}}\) is sound if \((\mathcal {P}, \mathcal {S})\) is iAST whenever \((\mathcal {P}_i, \mathcal {S}_i)\) is iAST for all \(1 \le i \le n\). It is complete if \((\mathcal {P}_i, \mathcal {S}_i)\) is iAST for all \(1 \le i \le n\) whenever \((\mathcal {P}, \mathcal {S})\) is iAST. In the following, we adapt the three main processors from Theorems 5, 6, and 7 to the probabilistic setting and present two additional processors.
The (innermost) \((\mathcal {P},\mathcal {S})\)-dependency graph indicates which DTs from \(\mathcal {P}\) can rewrite to each other using the PTRS \(\mathcal {S}\). The possibility of rewriting with \(\mathcal {S}\) is not related to the probabilities. Thus, for the dependency graph, we can use the non-probabilistic variant \(\textrm{np}(\mathcal {S}) = \{\ell \rightarrow r_j \mid \ell \rightarrow \{p_1:r_1, \ldots , p_k:r_k\} \in \mathcal {S}, 1 \le j \le k\}\).
Definition 30
(Dep. Graph). The node set of the \((\mathcal {P},\mathcal {S})\)-dependency graph is \(\mathcal {P}\) and there is an edge from \(\langle \ell ^\#_1,\ell _1 \rangle \rightarrow \{ p_1:\langle d_1,r_1 \rangle , \ldots , p_k:\langle d_k,r_k \rangle \}\) to \(\langle \ell ^\#_2, \ell _2 \rangle \rightarrow \ldots \) if there are substitutions \(\sigma _1, \sigma _2\) and \(t^\# \in cont(d_j)\) for some \(1 \le j \le k\) such that
 and both \(\ell _1^\# \sigma _1\) and \(\ell _2^\# \sigma _2\) are in \(\texttt{NF}_{\mathcal {S}}\).
and both \(\ell _1^\# \sigma _1\) and \(\ell _2^\# \sigma _2\) are in \(\texttt{NF}_{\mathcal {S}}\).

For \(\mathcal {R}_{\textsf{pdiv}}\) from Example 23, the \((\mathcal{D}\mathcal{T}(\mathcal {R}_{\textsf{pdiv}}), \mathcal {R}_{\textsf{pdiv}})\)-dependency graph is on the side. In the non-probabilistic DP framework, every step with
 corresponds to an edge in the \((\mathcal {D}, \mathcal {R})\)-dependency graph. Similarly, in the probabilistic setting, every path from one node of P to the next node of P in a \((\mathcal {P},\mathcal {S})\)-chain tree corresponds to an edge in the \((\mathcal {P},\mathcal {S})\)- dependency graph. Since every infinite path in a chain tree contains infinitely many nodes from P, when tracking the arguments of the compound symbols, every such path traverses a cycle of the dependency graph infinitely often. Thus, it again suffices to consider the SCCs of the dependency graph separately. So for our example, we obtain \({\text {Proc}}_{\texttt{DG}}(\mathcal{D}\mathcal{T}(\mathcal {R}_{\textsf{pdiv}}),\mathcal {R}_{\textsf{pdiv}}) = \{(\{(17)\},\mathcal {R}_{\textsf{pdiv}}), (\{(19)\},\mathcal {R}_{\textsf{pdiv}})\}\). To automate the following two processors, the same over-approximation techniques as for the non-probabilistic dependency graph can be used.
corresponds to an edge in the \((\mathcal {D}, \mathcal {R})\)-dependency graph. Similarly, in the probabilistic setting, every path from one node of P to the next node of P in a \((\mathcal {P},\mathcal {S})\)-chain tree corresponds to an edge in the \((\mathcal {P},\mathcal {S})\)- dependency graph. Since every infinite path in a chain tree contains infinitely many nodes from P, when tracking the arguments of the compound symbols, every such path traverses a cycle of the dependency graph infinitely often. Thus, it again suffices to consider the SCCs of the dependency graph separately. So for our example, we obtain \({\text {Proc}}_{\texttt{DG}}(\mathcal{D}\mathcal{T}(\mathcal {R}_{\textsf{pdiv}}),\mathcal {R}_{\textsf{pdiv}}) = \{(\{(17)\},\mathcal {R}_{\textsf{pdiv}}), (\{(19)\},\mathcal {R}_{\textsf{pdiv}})\}\). To automate the following two processors, the same over-approximation techniques as for the non-probabilistic dependency graph can be used.
Theorem 31
(Prob. Dep. Graph Processor). For the SCCs \(\mathcal {P}_1, ..., \mathcal {P}_n\) of the \((\mathcal {P}\!,\mathcal {S})\)-dependency graph, \({\text {Proc}}_{\texttt{DG}}(\mathcal {P}\!,\mathcal {S})\!=\!\{(\mathcal {P}_1,\mathcal {S}), ..., (\mathcal {P}_n,\mathcal {S})\}\) is sound and complete.
Next, we introduce a new usable terms processor (a similar processor was also proposed for the DTs in [37]). Since we regard dependency tuples instead of pairs, after applying \({\text {Proc}}_{\texttt{DG}}\), the right-hand sides of DTs \(\langle \ell ^\#_1, \ell _1 \rangle \rightarrow \ldots \) might still contain terms \(t^\#\) where no instance \(t^\#\sigma _1\) rewrites to an instance \(\ell _2^\#\sigma _2\) of a left-hand side of a DT (where we only consider instantiations such that \(\ell ^\#_1\sigma _1\) and \(\ell ^\#_2\sigma _2\) are in \(\texttt{NF}_{\mathcal {S}}\), because only such instantiations are regarded in chain trees). Then \(t^\#\) can be removed from the right-hand side of the DT. For example, in the DP problem \((\{(19) \},\mathcal {R}_{\textsf{pdiv}})\), the only DT (19) has the left-hand side \(\textsf{D}(\textsf{s}(x),\textsf{s}(y))\). As the term \(\textsf{M}(x,y)\) in (19)’s right-hand side cannot “reach” \(\textsf{D}(\ldots )\), the following processor removes it, i.e., \({\text {Proc}}_{\texttt{UT}}(\{(19)\},\mathcal {R}_{\textsf{pdiv}}) = \{(\{(21)\},\mathcal {R}_{\textsf{pdiv}})\}\), where (21) is
So both Theorems 31 and 32 are needed to fully simulate the dependency graph processor in the probabilistic setting, i.e., they are both necessary to guarantee that the probabilistic DP processors work analogously to the non-probabilistic ones (which in turn ensures that the probabilistic DP framework is similar in power to its non-probabilistic counterpart). This is also confirmed by our experiments in Sect. 5 which show that disabling the processor of Theorem 32 affects the power of our approach. For example, without Theorem 32, the proof that \(\mathcal {R}_{\textsf{pdiv}}\) is iAST in the probabilistic DP framework would require a more complicated polynomial interpretation. In contrast, when using both processors of Theorems 31 and 32, then one can prove iAST of \(\mathcal {R}_{\textsf{pdiv}}\) with the same polynomial interpretation that was used to prove iTerm of \(\mathcal {R}_{\textsf{div}}\) (see Example 36).
Theorem 32
(Usable Terms Processor). Let \(\ell ^\#_1\) be a term and \((\mathcal {P}, \mathcal {S})\) be a DP problem. We call a term \(t^\#\) usable w.r.t. \(\ell ^\#_1\) and \((\mathcal {P}, \mathcal {S})\) if there is a \(\langle \ell ^\#_2,\ell _2 \rangle \rightarrow \ldots \in \mathcal {P}\) and substitutions \(\sigma _1, \sigma _2\) such that
 and both \(\ell ^\#_1 \sigma _1\) and \(\ell ^\#_2 \sigma _2\) are in \(\texttt{NF}_{\mathcal {S}}\). If \(d= \textsf{c}_{n}(t_1^\#, \ldots , t_n^\#)\), then \(\mathcal {U}\mathcal {T}(d)_{\ell ^\#_1\!,\mathcal {P},\mathcal {S}}\) denotes the term \(\textsf{c}_{m}(t_{i_1}^\#, \ldots , t_{i_m}^\#)\), where \(1 \le i_1< \ldots < i_m \le n\) are the indices of all terms \(t^\#_i\) that are usable w.r.t. \(\ell ^\#_1\) and \((\mathcal {P}, \mathcal {S})\). The transformation that removes all non-usable terms in the right-hand sides of dependency tuples is denoted by:
and both \(\ell ^\#_1 \sigma _1\) and \(\ell ^\#_2 \sigma _2\) are in \(\texttt{NF}_{\mathcal {S}}\). If \(d= \textsf{c}_{n}(t_1^\#, \ldots , t_n^\#)\), then \(\mathcal {U}\mathcal {T}(d)_{\ell ^\#_1\!,\mathcal {P},\mathcal {S}}\) denotes the term \(\textsf{c}_{m}(t_{i_1}^\#, \ldots , t_{i_m}^\#)\), where \(1 \le i_1< \ldots < i_m \le n\) are the indices of all terms \(t^\#_i\) that are usable w.r.t. \(\ell ^\#_1\) and \((\mathcal {P}, \mathcal {S})\). The transformation that removes all non-usable terms in the right-hand sides of dependency tuples is denoted by:
Then \({\text {Proc}}_{\texttt{UT}}(\mathcal {P},\mathcal {S}) = \{(\mathcal {T}_\texttt{UT}(\mathcal {P}, \mathcal {S}),\mathcal {S})\}\) is sound and complete.
To adapt the usable rules processor, we adjust the definition of usable rules such that it regards every term in the support of the distribution on the right-hand side of a rule. The usable rules processor only deletes non-usable rules from \(\mathcal {S}\), but not from \(\textrm{proj}_2(\mathcal {P})\). This is sufficient, because according to Definition 24, rules from \(\textrm{proj}_2(\mathcal {P})\) can only be applied if they also occur in \(\mathcal {S}\).
Theorem 33
(Probabilistic Usable Rules Processor). Let \((\mathcal {P}, \mathcal {S})\) be a DP problem. For every \(f \in \varSigma \uplus \varSigma ^{\#}\) let \({\text {Rules}}_\mathcal {S}(f) = \{\ell \rightarrow \mu \in \mathcal {S}\mid {\text {root}}(\ell ) = f\}\). For any term \(t \in \mathcal {T}\left( \varSigma \uplus \varSigma ^{\#}, \mathcal {V}\right) \), its usable rules \(\mathcal {U}_\mathcal {S}(t)\) are the smallest set such that \(\mathcal {U}_\mathcal {S}(x) = \varnothing \) for all \(x \in \mathcal {V}\) and \(\mathcal {U}_\mathcal {S}(f(t_1, \ldots , t_n)) = {\text {Rules}}_\mathcal {S}(f) \cup \bigcup _{i = 1}^n \mathcal {U}_\mathcal {S}(t_i) \cup \; \bigcup _{\ell \rightarrow \mu \in {\text {Rules}}_\mathcal {S}(f), r \in {\text {Supp}}(\mu )} \mathcal {U}_\mathcal {S}(r)\). The usable rules for \((\mathcal {P}, \mathcal {S})\) are \(\mathcal {U}(\mathcal {P},\mathcal {S}) = \bigcup _{\ell ^\# \rightarrow \mu \in \textrm{proj}_1(\mathcal {P}), d \in {\text {Supp}}(\mu )} \mathcal {U}_\mathcal {S}(d)\). Then \({\text {Proc}}_{\texttt{UR}}(\mathcal {P},\mathcal {S}) = \{(\mathcal {P},\mathcal {U}(\mathcal {P},\mathcal {S}))\}\) is sound.
Example 34
For the DP problem \((\{(21)\},\mathcal {R}_{\textsf{pdiv}})\) only the \(\textsf{minus}\)-rules are usable and thus \({\text {Proc}}_{\texttt{UR}}(\{(21)\},\mathcal {R}_{\textsf{pdiv}}) = \{ (\{(21)\},\{(12),(13)\}) \}\). For \((\{(17)\},\mathcal {R}_{\textsf{pdiv}})\) there are no usable rules at all, hence \({\text {Proc}}_{\texttt{UR}}(\{(17)\},\mathcal {R}_{\textsf{pdiv}}) = \{ (\{(17)\},\varnothing )\}\).
For the reduction pair processor, we again restrict ourselves to multilinear polynomials and use analogous constraints as in our new criterion for the direct application of polynomial interpretations to PTRSs (Theorem 17), but adapted to DP problems \((\mathcal {P}, \mathcal {S})\). Moreover, as in the original reduction pair processor of Theorem 7, the polynomials only have to be weakly monotonic. For every rule in \(\mathcal {S}\) or \(\textrm{proj}_1(\mathcal {P})\), we require that the expected value is weakly decreasing. The reduction pair processor then removes those DTs \(\langle \ell ^\#,\ell \rangle \rightarrow \{ p_1:\langle d_1,r_1 \rangle , \ldots ,p_k:\langle d_k,r_k \rangle \}\) from \(\mathcal {P}\) where in addition there is at least one term \(d_j\) that is strictly decreasing. Recall that we can also rewrite with the original rule \(\ell \rightarrow \{ p_1:r_1, \ldots ,p_k:r_k \}\) from \(\textrm{proj}_2(\mathcal {P})\), provided that it is also contained in \(\mathcal {S}\). Therefore, to remove the dependency tuple, we also have to require that the rule \(\ell \rightarrow r_j\) is weakly decreasing. Finally, we have to use \(\textsf{c}_{}\)-additive interpretations (with \({\textsf{c}_{n}}_{{\text {Pol}}}(x_1, \ldots , x_n) = x_1 + \ldots + x_n\)) to handle compound symbols and their normalization correctly.
Theorem 35
(Probabilistic Reduction Pair Processor). Let \({\text {Pol}}: \mathcal {T}(\varSigma \,\uplus \) \(\varSigma ^\#, \mathcal {V}) \rightarrow \mathbb {N}[\mathcal {V}]\) be a weakly monotonic, multilinear, and \(\textsf{c}_{}\)-additive polynomial interpretation. Let \(\mathcal {P}= \mathcal {P}_{\ge } \uplus \mathcal {P}_{>}\) with \(\mathcal {P}_> \ne \varnothing \) such that:
-
(1)
For every \(\ell \rightarrow \{ p_1:r_1, ...,p_k:r_k \} \in \mathcal {S}\), we have \({\text {Pol}}(\ell ) \ge \sum _{1 \le j \le k} p_j \cdot {\text {Pol}}(r_j)\).
-
(2)
For every \(\langle \ell ^\#,\ell \rangle \rightarrow \{ p_1:\langle d_1,r_1 \rangle , \ldots ,p_k:\langle d_k,r_k \rangle \} \in \mathcal {P}\), we have \({\text {Pol}}(\ell ^\#) \ge \sum _{1 \le j \le k} p_j \cdot {\text {Pol}}(d_j)\).
-
(3)
For every \(\langle \ell ^\#,\ell \rangle \rightarrow \{ p_1:\langle d_1,r_1 \rangle , \ldots ,p_k:\langle d_k,r_k \rangle \} \in \mathcal {P}_{>}\), there exists a \(1 \le j \le k\) with \({\text {Pol}}(\ell ^\#) > {\text {Pol}}(d_j)\). If \(\ell \rightarrow \{ p_1:r_1, \ldots ,p_k:r_k \} \in \mathcal {S}\), then we additionally have \({\text {Pol}}(\ell ) \ge {\text {Pol}}(r_j)\).
Then \({\text {Proc}}_{\texttt{RP}}(\mathcal {P},\mathcal {S}) = \{(\mathcal {P}_{\ge },\mathcal {S})\}\) is sound and complete.
Example 36
The constraints of the reduction pair processor for the two DP problems from Example 34 are satisfied by the \(\textsf{c}_{}\)-additive polynomial interpretation which again maps \(\mathcal {O}\) to 0, \(\textsf{s}(x)\) to \(x+1\), and all other non-constant function symbols to the projection on their first arguments. As in the non-probabilistic case, this results in DP problems of the form \((\varnothing , \ldots )\) and subsequently, \({\text {Proc}}_{\texttt{DG}}(\varnothing , \ldots )\) yields \(\varnothing \). By the soundness of all processors, this proves that \(\mathcal {R}_{\textsf{pdiv}}\) is iAST.
So with the new probabilistic DP framework, the proof that \(\mathcal {R}_{\textsf{pdiv}}\) is iAST is analogous to the proof that \(\mathcal {R}_{\textsf{div}}\) is iTerm in the original DP framework (the proofs even use the same polynomial interpretation in the respective reduction pair processors). This indicates that our novel framework for PTRSs has the same essential concepts and advantages as the original DP framework for TRSs. This is different from our previous adaption of dependency pairs for complexity analysis of TRSs, which also relies on dependency tuples [37]. There, the power is considerably restricted, because one does not have full modularity as one cannot decompose the proof according to the SCCs of the dependency graph.
In proofs with the probabilistic DP framework, one may obtain DP problems \((\mathcal {P},\mathcal {S})\) that have a non-probabilistic structure (i.e., every DT in \(\mathcal {P}\) has the form \(\langle \ell ^\#, \ell \rangle \rightarrow \{1:\langle d,r\rangle \}\) and every rule in \(\mathcal {S}\) has the form \(\ell ' \rightarrow \{1:r'\}\)). We now introduce a processor that allows us to switch to the original non-probabilistic DP framework for such (sub-)problems. This is advantageous, because due to the use of dependency tuples instead of pairs in \(\mathcal {P}\), in general the constraints of the probabilistic reduction pair processor of Theorem 35 are harder than the ones of the reduction pair processor of Theorem 7. Moreover, Theorem 7 is not restricted to multilinear polynomial interpretations and the original DP framework has many additional processors that have not yet been adapted to the probabilistic setting.
Theorem 37
(Probability Removal Processor). Let \((\mathcal {P}, \mathcal {S})\) be a probabilistic DP problem where every DT in \(\mathcal {P}\) has the form \(\langle \ell ^\#, \ell \rangle \rightarrow \{1:\langle d,r\rangle \}\) and every rule in \(\mathcal {S}\) has the form \(\ell ' \rightarrow \{1\!:r'\}\). Let \(\textrm{np}(\mathcal {P}) = \{\ell ^\# \rightarrow t^\# \mid \ell ^\# \rightarrow \{1\!:d\} \in \textrm{proj}_1(\mathcal {P}), t^\# \in cont(d) \}\). Then \((\mathcal {P},\mathcal {S})\) is iAST iff the non-probabilistic DP problem \((\textrm{np}(\mathcal {P}), \textrm{np}(\mathcal {S}))\) is iTerm. So if \((\textrm{np}(\mathcal {P}), \textrm{np}(\mathcal {S}))\) is iTerm, then the processor \({\text {Proc}}_{\texttt{PR}}(\mathcal {P},\mathcal {S}) = \varnothing \) is sound and complete.
5 Conclusion and Evaluation
Starting with a new “direct” technique to prove almost-sure termination of probabilistic TRSs (Theorem 17), we presented the first adaption of the dependency pair framework to the probabilistic setting in order to prove innermost AST automatically. This is not at all obvious, since most straightforward ideas for such an adaption are unsound (as discussed in Sect. 4.1). So the challenge was to find a suitable definition of dependency pairs (resp. tuples) and chains (resp. chain trees) such that one can define DP processors which are sound and work analogously to the non-probabilistic setting (in order to obtain a framework which is similar in power to the non-probabilistic one). While the soundness proofs for our new processors are much more involved than in the non-probabilistic case, the new processors themselves are quite analogous to their non-probabilistic counterparts and thus, adapting an existing implementation of the non-probabilistic DP framework to the probabilistic one does not require much effort.
We implemented our contributions in our termination prover AProVE, which yields the first tool to prove almost-sure innermost termination of PTRSs on arbitrary data structures (including PTRSs that are not PAST). In our experiments, we compared the direct application of polynomials for proving AST (via our new Theorem 17) with the probabilistic DP framework. We evaluated AProVE on a collection of 67 PTRSs which includes many typical probabilistic algorithms. For example, it contains the following PTRS \(\mathcal {R}_{\textsf{qs}}\) for probabilistic quicksort.
The \(\textsf{rotate}\)-rules rotate a list randomly often (they are AST, but not terminating). Thus, by choosing the first element of the resulting list, one obtains a random pivot element for the recursive call of quicksort. In addition to the rules above, \(\mathcal {R}_{\textsf{qs}}\) contains rules for list concatenation (\(\textsf{app}\)), and rules such that \(\textsf{low}(x, xs )\) (resp. \(\textsf{high}(x, xs )\)) returns all elements of the list \( xs \) that are smaller (resp. greater or equal) than x, see [28]. Using the probabilistic DP framework, AProVE can prove iAST of \(\mathcal {R}_{\textsf{qs}}\) and many other typical programs.
61 of the 67 examples in our collection are iAST and AProVE can prove iAST for 53 (87%) of them. Here, the DP framework proves iAST for 51 examples and the direct application of polynomial interpretations via Theorem 17 succeeds for 27 examples. (In contrast, proving PAST via the direct application of polynomial interpretations as in [3] only works for 22 examples.) The average runtime of AProVE per example was 2.88 s (where no example took longer than 8 s). So our experiments indicate that the power of the DP framework can now also be used for probabilistic TRSs.
We also performed experiments where we disabled individual processors of the probabilistic DP framework. More precisely, we disabled either the usable terms processor (Theorem 32), both the dependency graph and the usable terms processor (Theorems 31 and 32), or all processors except the reduction pair processor of Theorem 35. Our experiments show that disabling processors indeed affects the power of the approach, in particular for larger examples with several defined symbols (e.g., then AProVE cannot prove iAST of \(\mathcal {R}_{\textsf{qs}}\) anymore). So all of our processors are needed to obtain a powerful technique for termination analysis of PTRSs.
Due to the use of dependency tuples instead of pairs, the probabilistic DP framework does not (yet) subsume the direct application of polynomials completely (two examples in our collection can only be proved by the latter, see [28]). Therefore, currently AProVE uses the direct approach of Theorem 17 in addition to the probabilistic DP framework. In future work, we will adapt further processors of the original DP framework to the probabilistic setting, which will also allow us to integrate the direct approach of Theorem 17 into the probabilistic DP framework in a modular way. Moreover, we will develop processors to prove AST of full (instead of innermost) rewriting. Further work may also include processors to disprove (i)AST and possible extensions to analyze PAST and expected runtimes as well. Finally, one could also modify the formalism of PTRSs in order to allow non-constant probabilities which depend on the sizes of terms.
For details on our experiments and for instructions on how to run our implementation in AProVE via its web interface or locally, we refer to https://aprove-developers.github.io/ProbabilisticTermRewriting/.
Notes
- 1.
Here, a set \(\mathcal {D}'\) of dependency pairs is an SCC if it is a maximal cycle, i.e., it is a maximal set such that for any \(\ell _1^\# \rightarrow t_1^\#\) and \(\ell _2^\# \rightarrow t_2^\#\) in \(\mathcal {D}'\) there is a non-empty path from \(\ell _1^\# \rightarrow t_1^\#\) to \(\ell _2^\# \rightarrow t_2^\#\) which only traverses nodes from \(\mathcal {D}'\).
- 2.
For a complete version of the usable rules processor, one has to use a more involved notion of DP problems with more components that we omit here for readability [16].
- 3.
In this paper, we only regard the reduction pair processor with polynomial interpretations, because for most other classical orderings it is not clear how to extend them to probabilistic TRSs, where one has to consider “expected values of terms”.
- 4.
Since our goal is the automation of termination analysis, in this paper we restrict ourselves to finite PTRSs with finite multi-distributions.
- 5.
As in [3], multilinearity ensures “monotonicity” w.r.t. expected values, since multilinearity implies \(f_{{\text {Pol}}}(\ldots , \sum _{1 \le j \le k}p_j \cdot {\text {Pol}}(r_j), \ldots ) = \sum _{1 \le j \le k}p_j \cdot {\text {Pol}}(f(\ldots , r_j, \ldots ))\).
- 6.
The reason for \(cont(d_j) \subseteq cont(dp(r_j))\) instead of \(cont(d_j) = cont(dp(r_j))\) is that in this way processors can remove terms from the right-hand sides of DTs, see Theorem 32.
References
Agrawal, S., Chatterjee, K., Novotný, P.: Lexicographic ranking supermartingales: an efficient approach to termination of probabilistic programs. Proc. ACM Program. Lang. 2(POPL), 1–32 (2017). https://doi.org/10.1145/3158122
Arts, T., Giesl, J.: Termination of term rewriting using dependency pairs. Theor. Comput. Sci. 236(1–2), 133–178 (2000). https://doi.org/10.1016/S0304-3975(99)00207-8
Avanzini, M., Dal Lago, U., Yamada, A.: On probabilistic term rewriting. Sci. Comput. Program. 185 (2020). https://doi.org/10.1016/j.scico.2019.102338
Avanzini, M., Moser, G., Schaper, M.: A modular cost analysis for probabilistic programs. Proc. ACM Program. Lang. 4(OOPSLA), 1–30 (2020). https://doi.org/10.1145/3428240
Baader, F., Nipkow, T.: Term Rewriting and All That. Cambridge University Press, Cambridge (1998). https://doi.org/10.1017/CBO9781139172752
Batz, K., Kaminski, B.L., Katoen, J.-P., Matheja, C., Verscht, L.: A calculus for amortized expected runtimes. Proc. ACM Program. Lang. 7(POPL), 1957–1986 (2023). https://doi.org/10.1145/3571260
Beutner, R., Ong, L.: On probabilistic termination of functional programs with continuous distributions. In: Freund, S.N., Yahav, E. (eds.) PLDI 2021, pp. 1312–1326 (2021). https://doi.org/10.1145/3453483.3454111
Bournez, O., Kirchner, C.: Probabilistic rewrite strategies. Applications to ELAN. In: Tison, S. (ed.) RTA 2002. LNCS, vol. 2378, pp. 252–266. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45610-4_18
Bournez, O., Garnier, F.: Proving positive almost-sure termination. In: Giesl, J. (ed.) RTA 2005. LNCS, vol. 3467, pp. 323–337. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-32033-3_24
Brockschmidt, M., Musiol, R., Otto, C., Giesl, J.: Automated termination proofs for Java programs with cyclic data. In: Madhusudan, P., Seshia, S.A. (eds.) CAV 2012. LNCS, vol. 7358, pp. 105–122. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31424-7_13
Chatterjee, K., Fu, H., Novotný, P.: Termination analysis of probabilistic programs with martingales. In: Barthe, G., Katoen, J.-P., Silva, A. (eds.) Foundations of Probabilistic Programming, pp. 221–258. Cambridge University Press (2020). https://doi.org/10.1017/9781108770750.008
Dal Lago, U., Grellois, C.: Probabilistic termination by monadic affine sized typing. In: Yang, H. (ed.) ESOP 2017. LNCS, vol. 10201, pp. 393–419. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54434-1_15
Dershowitz, N.: Orderings for term-rewriting systems. Theor. Comput. Sci. 17, 279–301 (1982). https://doi.org/10.1016/0304-3975(82)90026-3
Faggian, C.: Probabilistic rewriting and asymptotic behaviour: on termination and unique normal forms. Log. Methods Comput. Sci. 18(2) (2022). https://doi.org/10.46298/lmcs-18(2:5)2022
Ferrer Fioriti, L.M., Hermanns, H.: Probabilistic termination: soundness, completeness, and compositionality. In: Rajamani, S.K., Walker, D. (eds.) POPL 2015, pp. 489–501 (2015). https://doi.org/10.1145/2676726.2677001
Giesl, J., Thiemann, R., Schneider-Kamp, P.: The dependency pair framework: combining techniques for automated termination proofs. In: Baader, F., Voronkov, A. (eds.) LPAR 2005. LNCS (LNAI), vol. 3452, pp. 301–331. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-32275-7_21
Giesl, J., Thiemann, R., Schneider-Kamp, P., Falke, S.: Mechanizing and improving dependency pairs. J. Autom. Reason. 37(3), 155–203 (2006). https://doi.org/10.1007/s10817-006-9057-7
Giesl, J., Raffelsieper, M., Schneider-Kamp, P., Swiderski, S., Thiemann, R.: Automated termination proofs for Haskell by term rewriting. ACM Trans. Program. Lang. Syst. 33(2), 1–39 (2011). https://doi.org/10.1145/1890028.1890030
Giesl, J., Ströder, T., Schneider-Kamp, P., Emmes, F., Fuhs, C.: Symbolic evaluation graphs and term rewriting: a general methodology for analyzing logic programs. In: De Schreye, D., Janssens, G., King, A. (eds.) PPDP 2012, pp. 1–12 (2012). https://doi.org/10.1145/2370776.2370778
Giesl, J., et al.: Analyzing program termination and complexity automatically with AProVE. J. Autom. Reason. 58(1), 3–31 (2017). https://doi.org/10.1007/s10817-016-9388-y
Giesl, J., Giesl, P., Hark, M.: Computing expected runtimes for constant probability programs. In: Fontaine, P. (ed.) CADE 2019. LNCS (LNAI), vol. 11716, pp. 269–286. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-29436-6_16
Gutiérrez, R., Lucas, S.: MU-TERM: verify termination properties automatically (system description). In: Peltier, N., Sofronie-Stokkermans, V. (eds.) IJCAR 2020. LNCS (LNAI), vol. 12167, pp. 436–447. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-51054-1_28
Hirokawa, N., Middeldorp, A.: Automating the dependency pair method. Inf. Comput. 199(1–2), 172–199 (2005). https://doi.org/10.1016/j.ic.2004.10.004
Huang, M., Fu, H., Chatterjee, K., Goharshady, A.K.: Modular verification for almost-sure termination of probabilistic programs. Proc. ACM Program. Lang. 3(OOPSLA), 1–29 (2019). https://doi.org/10.1145/3360555
Kaminski, B.L., Katoen, J.-P., Matheja, C., Olmedo, F.: Weakest precondition reasoning for expected runtimes of randomized algorithms. J. ACM 65, 1–68 (2018). https://doi.org/10.1145/3208102
Kaminski, B.L., Katoen, J.-P., Matheja, C.: Expected runtime analyis by program verification. In: Barthe, G., Katoen, J.-P., Silva, A. (eds.) Foundations of Probabilistic Programming, pp. 185–220. Cambridge University Press (2020). https://doi.org/10.1017/9781108770750.007
Kassing, J.-C.: Using dependency pairs for proving almost-sure termination of probabilistic term rewriting. MA thesis. RWTH Aachen University (2022). https://verify.rwth-aachen.de/da/Kassing-Masterthesis.pdf
Kassing, J.-C., Giesl, J.: Proving almost-sure innermost termination of probabilistic term rewriting using dependency pairs. CoRR abs/2305.11741 (2023). https://doi.org/10.48550/arXiv.2305.11741
Korp, M., Sternagel, C., Zankl, H., Middeldorp, A.: Tyrolean termination tool 2. In: Treinen, R. (ed.) RTA 2009. LNCS, vol. 5595, pp. 295–304. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02348-4_21
Lankford, D.S.: On proving term rewriting systems are noetherian. Memo MTP-3, Mathematics Department, Louisiana Technical University, Ruston, LA (1979). http://www.ens-lyon.fr/LIP/REWRITING/TERMINATION/LankfordPolyTerm.pdf
Leutgeb, L., Moser, G., Zuleger, F.: Automated expected amortised cost analysis of probabilistic data structures. In: Shoham, S., Vizel, Y. (eds.) CAV 2022. LNCS, vol. 13372, pp. 70–91. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-13188-2_4
McIver, A., Morgan, C., Kaminski, B.L., Katoen, J.-P.: A new proof rule for almost-sure termination. Proc. ACM Program. Lang. 2(POPL), 1–28 (2018). https://doi.org/10.1145/3158121
Meyer, F., Hark, M., Giesl, J.: Inferring expected runtimes of probabilistic integer programs using expected sizes. In: TACAS 2021. LNCS, vol. 12651, pp. 250–269. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-72016-2_14
Moosbrugger, M., Bartocci, E., Katoen, J.-P., Kovács, L.: Automated termination analysis of polynomial probabilistic programs. In: ESOP 2021. LNCS, vol. 12648, pp. 491–518. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-72019-3_18
Moser, G., Schaper, M.: From Jinja bytecode to term rewriting: a complexity reflecting transformation. Inf. Comput. 261, 116–143 (2018). https://doi.org/10.1016/j.ic.2018.05.007
Ngo, V.C., Carbonneaux, Q., Hoffmann, J.: Bounded expectations: resource analysis for probabilistic programs. In: Foster, J.S., Grossman, D. (eds.) PLDI 2018, pp. 496–512 (2018). https://doi.org/10.1145/3192366.3192394
Noschinski, L., Emmes, F., Giesl, J.: Analyzing innermost runtime complexity of term rewriting by dependency pairs. J. Autom. Reason. 51, 27–56 (2013). https://doi.org/10.1007/978-3-642-22438-6_32
Otto, C., Brockschmidt, M., von Essen, C., Giesl, J.: Automated termination analysis of Java bytecode by term rewriting. In: Lynch, C. (ed.) RTA 2010. LIPIcs 6, pp. 259–276 (2010). https://doi.org/10.4230/LIPIcs.RTA.2010.259
Wang, D., Kahn, D.M., Hoffmann, J.: Raising expectations: automating expected cost analysis with types. Proc. ACM Program. Lang. 4(ICFP), 1–31 (2020). https://doi.org/10.1145/3408992
Yamada, A., Kusakari, K., Sakabe, T.: Nagoya termination tool. In: Dowek, G. (ed.) RTA-TLCA 2014. LNCS, vol. 8560, pp. 466–475. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08918-8_32
Acknowledgements
We are grateful to Marcel Hark, Dominik Meier, and Florian Frohn for help and advice.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Kassing, JC., Giesl, J. (2023). Proving Almost-Sure Innermost Termination of Probabilistic Term Rewriting Using Dependency Pairs. In: Pientka, B., Tinelli, C. (eds) Automated Deduction – CADE 29. CADE 2023. Lecture Notes in Computer Science(), vol 14132. Springer, Cham. https://doi.org/10.1007/978-3-031-38499-8_20
Download citation
DOI: https://doi.org/10.1007/978-3-031-38499-8_20
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-38498-1
Online ISBN: 978-3-031-38499-8
eBook Packages: Computer ScienceComputer Science (R0)




 .
.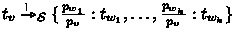 .
.