A Uniform Formalisation of Three-Valued Logics in Bisequent Calculus

Abstract

We present a uniform characterisation of three-valued logics by means of bisequent calculus (BSC). It is a generalised form of sequent calculus (SC) where rules operate on the ordered pairs of ordinary sequents. BSC may be treated as the weakest kind of system in the rich family of generalised SC operating on items being some collections of ordinary sequents. This family covers several forms of hypersequent and nested sequent calculi introduced to provide decent SC for several non-classical logics. It seems that for many non-classical logics, including some many-valued, paraconsistent and modal logics, this reasonably modest generalization of standard SC is sufficient. In this paper we examine a variety of three-valued logics and show how they can be formalised in the framework of bisequent calculus. All provided systems are cut-free and satisfy the subformula property. Also the interpolation theorem is constructively proved for some logics.

Funded by the European Union (ERC, ExtenDD, project number: 101054714). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them.

1 Introduction

The aim of this paper is to provide a uniform characterization of a variety of three-valued logics by means of a simple cut-free generalised sequent calculus (SC) called bisequent calculus (BSC). It is the weakest kind of system in the rich family of generalised sequent calculi operating on collections of ordinary sequents [23]. If we restrict our interest to structures built of two sequents only, we obtain a limiting case of either hypersequent or nested sequent calculi; it is what we call bisequent calculus.

Is such restricted calculus of any use? Hypersequent calculi already may be seen as a quite restrictive form of generalised SC, yet they were shown to be useful in many fields (see, e.g., [25] for a survey of applications of hypersequent calculi in modal logic, and [37] for their use in fuzzy logic). BSC is even more restrictive but preliminary work on its application is promising. It was already successfully applied to first-order modal logic S5 [23] and to the class of four-valued quasi-relevant logics [27]. In what follows we will focus on another application of such minimal framework – to three-valued logics.

Several proof systems of different kinds were proposed so far for many-valued logics (see e.g. Hähnle [20] for a survey). The most direct and popular approach to construction of many-valued sequent or tableau systems is based on the idea of syntactic representation of n values either by means of n-sided sequents (e.g. [8, 45, 56]) or by n labels attached to formulae or sets of formulae (e.g. [11, 53, 55]). This solution was presented by many authors and despite its popularity has many drawbacks (see [25] for discussion). Significant improvement in the construction of efficient SC or tableau systems for many-valued logic was proposed independently by Doherty [15] and Hähnle [19], where labels correspond not to single values but to their sets (sets-as signs). Among other proof-theoretic approaches to many-valued logics let us mention Caleiro and Marcelino’s [10] analytic calculi for many-valued non-deterministic logics as well as the result by Grätz [18] who has recently developed analytic tableau systems based on sets-as-signs DNF representations with a correspondence to canonical sequent calculi.

Although BSC is a strictly syntactical calculus its semantical interpretation makes it similar to set-as-signs approach. A fuller discussion of this issue is provided in [27]. BSC is uniform in the sense that all three-valued logics are characterised by the same set of axiomatic sequents, and in the case of logics having the same set of connectives (i.e. defined in the same way) the rules are identical even if the set of designated values or the consequence relation is defined in different way. In this sense BSC is more uniform than several other approaches where either the set of axioms must be changed or rules for connectives must be different (even if described by means of the same table). In particular, BSC is superior in this respect to the generalised calculus presented in [25].

Section 2 has rather encyclopaedic character and provides self-contained description of a representative selection of three-valued logics. Section 3 contains a case study of BSC for K$_3$ and LP. In Sect. 4 we provide rules for connectives of all logics introduced in Sect. 2. Section 5 shows how BSC can be applied to prove interpolation for some three-valued paraconsistent and paracomplete logics. We finish with remarks on possible extensions and comparison with other approaches to formalisation of many-valued logics.

2 Logics

We will examine several three-valued propositional logics determined by three element matrices with classical-like connectives (negation, disjunction, conjunction, and implication, plus the usual three-valued modal-style connectives); we are not going to consider other types of connectives because of the lack of space. The languages of these logics are freely generated algebras similar to three element algebras of values. Logics are interpreted by homomorphisms from languages to algebras such that $h(c^n(\varphi _1, \ldots , \varphi _n))= \underline{c}(h(\varphi _1), \ldots , h(\varphi _n))$ for every $n-$ary connective c and the corresponding operation $\underline{c}$.

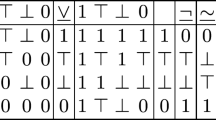
Let us consider as the starting point two three element Kleene’s algebras of the form: $\mathfrak {A}_3 = \langle A, O\rangle$ where $A=\{0, u, 1\}$ and O contains an unary operation $\underline{\lnot }:A\longrightarrow A$ and binary operations $\odot : A\times A\longrightarrow A$, where $\odot \in \{\underline{\wedge }, \underline{\vee } , \underline{\rightarrow } \}$. The operations are defined by the following truth tables in the strong and weak Kleene algebra; the latter considered also by Bochvar [9] (negation is the same in both):

We obtain four matrices by specifying a set of designated values D either as $\{ 1 \}$ or $\{1, u \}$. These are called $\mathfrak {SM}_1^3$, $\mathfrak {SM}_2^3$, $\mathfrak {WM}_1^3$ and $\mathfrak {WM}_2^3$ (where $\mathfrak {S}$ stands for strong, $\mathfrak {W}$ for weak, 1 and 2 indicate the amount of designated values). In general we will call matrices with $D = \{ 1 \}$ 1-matrices, and with $D= \{1, u \}$ – 2-matrices. Accordingly we will also call logics determined by 1-matrices and 2-matrices, 1- and 2-logics respectively. For any matrix we define a relation of matrix consequence in the standard way:

$$\varGamma \models _M\varphi \text { iff for any homomorphism } h: \text { if } h(\varGamma )\subseteq D, \text { then } h(\varphi )\in D.$$

Logics are identified with their matrix consequences. In particular, logics determined by these matrices are K$_3$ (strong Kleene 1-logic) [31], LP – the logic of paradox of Asenjo and Priest (corresponding 2-logic) [2, 42], K$_3^\textbf{w}$ (weak Kleene 1-logic) [31], PWK (paraconsistent weak Kleene 2-logic) of Halldén [21].

Let us consider a few modifications of strong and weak Kleene logics. Here is McCarthy’s logic K$_3^\rightarrow$ [36] (also called Kleene’s sequential and studied by Fitting [16]) and its interesting modification presented by Komendantskaya [32] under the name K$_3^\leftarrow$ by means of the following truth tables (again, negation is unchanged):

Both K$_3^\rightarrow$ and K$_3^\leftarrow$ are logics determined by 1-matrices. An important property of K$_3$, K$_3^\textbf{w}$, K$_3^\rightarrow$, and K$_3^\leftarrow$ is that they are the only three-valued logics with one designated value which produce partial recursive predicates (see [31, 32] for more details).

Several other important logics are obtained by changing the definitions of $\rightarrow$ and $\lnot$. Consider Łukasiewicz’s [34], Słupecki’s [49], Heyting’s [22] implications as well as Heyting’s [22], Bochvar’s [9], Post’s and dual Post’s [41] negations. Let us also consider yet another pair of additive conjunction and disjunction, arising in Łukasiewicz’s logic:

$\mathfrak {SM}_1^3$ with Łukasiewicz’s implication (instead of Kleene’s one) yields famous Łukasiewicz’s Ł$_3$, the first many-valued logic. In Ł$_3$ we may deal with two pairs of conjunction and disjunction. We have: $\varphi \vee \psi =(\varphi \rightarrow _L\psi )\rightarrow _L\psi$ and $\varphi \wedge \psi =\lnot (\lnot \varphi \vee \lnot \psi )$, but $\varphi \wedge _L\psi =\lnot (\varphi \rightarrow _L\lnot \psi )$ and $\varphi \vee _L\psi =\lnot \varphi \rightarrow _L \psi$. $\mathfrak {SM}_1^3$ with Słupecki’s implication is an alternative to Ł$_3$ having the deduction theorem. It was studied by Słupecki, Bryll, and Prucnal [49] as well as Avron [4], under the name GM$_3$. If we change negation and implication of $\mathfrak {SM}_1^3$ to Heyting’s ones, then we get Heyting’s [22] logic G$_3$, a close relative of intuitionistic logic (the name after Gödel who also studied it [17]; this logic was investigated by Jaśkowski as well [29]). The disjunction of $\mathfrak {SM}_1^3$ and Post’s cyclic negation from Post’s logic P$_3$ [41] which is known for being functionally complete in the three-valued setting. In [40], a dual cyclic negation $\lnot _{ DP }$ was suggested (it reverses the direction of cyclicality of Post’s negation). $\mathfrak {SM}_2^3$ with Heyting’s implication and Bochvar’s negation was investigated by Osorio and Carballido [38] under the name G$_3^\prime$. In the case of $\mathfrak {SM}_2^3$ the following connectives are interesting as well: Sobociński’s [51] conjunction, disjunction, and implications as well as D’Ottaviano/DaCosta/Jaśkowski/Słupecki’s implication [13, 30, 48]:

Sobociński’s logic S$_3$ is obtained from $\mathfrak {SM}_2^3$ by the replacement of all binary connectives of this matrix with Sobociński’s original ones. This logic may be treated as a relevant logic. However, a more popular three-valued relevant logic is Anderson and Belnap’s RM$_3$ [1] which is obtained from $\mathfrak {SM}_2^3$ only by the replacement of its implication with Sobociński’s one. Note that earlier Sobociński [50] considered yet another implication $\rightarrow _S^\prime$. $\mathfrak {SM}_2^3$ with the implication due to D’Ottaviano/DaCosta/Jaśkowski/Słupecki (first mentioned by Słupecki [48]) instead of Kleene’s one was independently studied by several authors: D’Ottaviano and da Costa themselves [13, 14], Asenjo and Tamburino [3], Batens [7] (under the name PI$^s$), Avron [5] (under the name RM$_3^\supset$), and Rozonoer [44] (under the name PCont). An important extension of this logic is J$_3$ by D’Ottaviano and da Costa [13]. It has an additional connective which is Łukasiewicz’s tabular possibility operator (see below; we also present Łukasiewicz’s tabular necessity operator).

As it is easy to guess, since RM$_3$ may be viewed as a relevant logic, it should be paraconsistent as well. Moreover, J$_3$, S$_3$, LP, and many other three-valued logics with two designated values are paraconsistent (in contrast, three-valued logics with one designated value are paracomplete). One of the most famous three-valued paraconsistent logics is Sette’s logic P$^1$ [47]. It has Bochvar’s negation and the above presented binary connectives (both 1 and u are designated). There is a version of P$^1$ with Kleene’s negation introduced by Carnielli and Marcos [12, 35] and called P$^2$. A paracomplete companion of P$^1$, the logic I$^1$, was presented by Sette and Carnielli [46]: it has Heyting’s negation and presented below binary connectives (the implication has been first introduced by Bochvar [9]). Its version with Kleene’s negation is I$^2$ due to Marcos [35]. Both I$^1$ and I$^2$ have one designated value.

Last but not least, let us mention Rescher’s [43] and Tomova’s [57] implications (added above). These implications can be added to $\mathfrak {SM}_1^3$. Tomova [57] introduced the concept of natural implication. In three-valued case with one designated value there are only 6 natural implications: Łukasiewicz’s, Słupecki’s, Heyting’s, Bochvar’s, Rescher’s, and Tomova’s. In the case with two designated values there are 24 natural implications, including Heyting’s and Rescher’s as well as D’Ottaviano/DaCosta/Jaśkowski/Słupecki’s implication, both Sobociński’s implications, and Sette’s implication.

3 Bisequent Calculus for K$_3$ (and LP)

Bisequents in BSC are ordered pairs of sequents $\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma$, where $\varGamma , \varDelta , \varPi , \varSigma$ are finite (possibly empty) multisets of formulae. We will call the left component of a bisequent as 1-sequent and the right as 2-sequent respectively. Bisequents with all elements being atomic will be also called atomic. In what follows B stands for arbitrary bisequents and S for sequents.

Let us define the calculus BSC-K$_3$ which provides an adequate formalisation of K$_3$. A bisequent $\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma$ is axiomatic iff it has nonempty $\varGamma \cap \varSigma$ or $\varGamma \cap \varDelta$ or $\varPi \cap \varSigma$. In fact this set of axioms is fixed for all considered calculi. If constants $\top , \bot , U$ (the last for fixed undefined proposition) are added we must add axioms of the form: $\varGamma \Rightarrow \varDelta , \top \mid \varPi \Rightarrow \varSigma$; $\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \top$; $\bot , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma$; $\varGamma \Rightarrow \varDelta \mid \bot , \varPi \Rightarrow \varSigma$; $U, \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma$ and $\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , U$.

The set of rules characterising the operations of the strong Kleene algebra consists of the following schemata:

$$\begin{array}{ll} (\mathord {\lnot }\mathord {\Rightarrow \mid }) \ \dfrac{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi }{\lnot \varphi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma } &{} (\mathord {\Rightarrow }\mathord {\lnot \mid }) \ \dfrac{\varGamma \Rightarrow \varDelta \mid \varphi , \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta , \lnot \varphi \mid \varPi \Rightarrow \varSigma }\\ (\mathord {\mid \lnot }\mathord {\Rightarrow }) \ \dfrac{\varGamma \Rightarrow \varDelta , \varphi \mid \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta \mid \lnot \varphi , \varPi \Rightarrow \varSigma } &{} (\mathord {\mid \Rightarrow }\mathord {\lnot }) \ \dfrac{\varphi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \lnot \varphi }\\ \end{array}$$

$$\begin{array}{ll} (\mathord {\wedge }\mathord {\Rightarrow \mid }) \ \dfrac{\varphi , \psi , \varGamma \Rightarrow \varDelta \mid S}{\varphi \wedge \psi , \varGamma \Rightarrow \varDelta \mid S} &{} (\mathord {\Rightarrow }\mathord {\wedge \mid }) \ \dfrac{\varGamma \Rightarrow \varDelta , \varphi \mid S \qquad \varGamma \Rightarrow \varDelta , \psi \mid S}{\varGamma \Rightarrow \varDelta , \varphi \wedge \psi \mid S}\\ (\mathord {\mid \wedge }\mathord {\Rightarrow }) \ \dfrac{S \mid \varphi , \psi , \varGamma \Rightarrow \varDelta }{S \mid \varphi \wedge \psi , \varGamma \Rightarrow \varDelta } &{} (\mathord {\mid \Rightarrow }\mathord {\wedge }) \ \dfrac{S\mid \varGamma \Rightarrow \varDelta , \varphi \qquad S\mid \varGamma \Rightarrow \varDelta , \psi }{S\mid \varGamma \Rightarrow \varDelta , \varphi \wedge \psi }\\ \end{array}$$

$$\begin{array}{ll} (\mathord {\Rightarrow }\mathord {\vee }\mid ) \ \dfrac{\varGamma \Rightarrow \varDelta , \varphi ,\psi \mid S}{\varGamma \Rightarrow \varDelta , \varphi \vee \psi \mid S} &{} (\mathord {\vee }\mathord {\Rightarrow }\mid ) \ \dfrac{\varphi , \varGamma \Rightarrow \varDelta \mid S \qquad \psi , \varGamma \Rightarrow \varDelta \mid S}{\varphi \vee \psi , \varGamma \Rightarrow \varDelta \mid S}\\ (\mathord {\mid \Rightarrow }\mathord {\vee }) \ \dfrac{S\mid \varGamma \Rightarrow \varDelta , \varphi ,\psi }{S\mid \varGamma \Rightarrow \varDelta , \varphi \vee \psi } &{} (\mathord {\mid \vee }\mathord {\Rightarrow }) \ \dfrac{S\mid \varphi , \varGamma \Rightarrow \varDelta \qquad S\mid \psi , \varGamma \Rightarrow \varDelta }{S\mid \varphi \vee \psi , \varGamma \Rightarrow \varDelta }\\ \end{array}$$

$(\mathord {\Rightarrow }\mathord {\rightarrow }\mid )$   $\dfrac{\varGamma \Rightarrow \varDelta , \psi \mid \varphi , \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta , \varphi \rightarrow \psi \mid \varPi \Rightarrow \varSigma }$      $(\mathord {\mid \Rightarrow }\mathord {\rightarrow })$   $\dfrac{\varphi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \psi }{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi \rightarrow \psi }$

$(\mathord {\rightarrow }\mathord {\Rightarrow }\mid )$   $\dfrac{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi \quad \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma }{\varphi \rightarrow \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma }$

$(\mathord {\mid \rightarrow }\mathord {\Rightarrow })$   $\dfrac{\varGamma \Rightarrow \varDelta , \varphi \mid \varPi \Rightarrow \varSigma \quad \varGamma \Rightarrow \varDelta \mid \psi , \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta \mid \varphi \rightarrow \psi , \varPi \Rightarrow \varSigma }$

Note that all rules satisfy the subformula property and other desirable properties of well-behaved SC. In particular, they are context independent in the sense that validity-preservation of rules is intact by deletion or addition of the same parameters in the premisses and conclusion. This feature will be of special importance for the proof of the interpolation theorem. One may easily observe that in case of the rules for strong $\wedge , \vee$ we have just standard G3 rules but repeated in both components. Rules for negation and implication have different character since side and principal formula are in different sequents in all cases.

Bisequents as such do not directly correspond to standard consequence relations in suitable matrices. Hence before we define the notion of a proof in BSC-K$_3$ (or any other logic) it is better to start with more general concept. A proof-search tree for a bisequent B in BSC-L, where L is any logic, is a tree of bisequents with B as the root and nodes generated by rules of BSC-L. A proof-search tree is complete iff every leaf is atomic, and it is axiomatic iff all leaves are axiomatic. The height of a proof-search tree is defined as the length of the maximal branches. A simple consequence of the subformula property of rules is:

Proposition 1

Every proof-search tree may be extended to a complete proof-search tree.

The notion of a proof in BSC-K$_3$ is introduced not only by restricting the class of proof-search trees in BSC-K$_3$ to axiomatic ones but also by restricting the class of admissible roots. In general the rationale for bisequents is that 1-sequent corresponds to consequence relation in 1-matrices and 2-sequent to consequence relation in 2-matrices. Since K$_3$ is characterised by 1-matrix we have:

BSC-K$_3 \vdash B$ iff there is an axiomatic proof-search tree for $B := \varGamma \Rightarrow \varphi \mid \Rightarrow$.

We define the L-validity (L-satisfiability) of bisequents in the following way:

L $\models \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma$ iff every homomorphism h satisfies $\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma$. The latter holds for h iff for some $\varphi$: either ($\varphi \in \varGamma$ and $h(\varphi )\ne 1$) or ($\varphi \in \varDelta$ and $h(\varphi )=1$) or ($\varphi \in \varPi$ and $h(\varphi )=0$) or ($\varphi \in \varSigma$ and $h(\varphi )\ne 0$).

Clearly L $\not \models \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma$ iff for some h, all elements of $\varGamma$ are true, all elements of $\varDelta$ are either false or undefined, all elements of $\varPi$ are either true or undefined and all elements of $\varSigma$ are false. In this case we say that h falsifies this sequent.

Obviously, all axiomatic bisequents are valid for any logic L. As for the rules they are not only sound (i.e. validity-preserving) but also invertible; namely it holds:

Theorem 1

For all rules of BSC-K$_3$, all premisses are K$_3$-valid iff the conclusion is K$_3$-valid.

Proof

Straightforward proof by tedious checking.    $\square$

A simple consequence of this theorem is that for every rule the conclusion is falsified by some h iff at least one premiss is falsified by the same h.

Theorem 2 (Soundness)

If BSC-K$_3 \vdash \varGamma \Rightarrow \varphi \mid \,\Rightarrow$, then $\varGamma \models _{K_3}\varphi$

Proof

By induction on the height of the proof, use Theorem 1.    $\square$

Invertibility of all rules implies that proof search process is confluent, i.e. that the order of applications of rules does not affect the result. In particular, B is provable iff every proof-search tree may be extended to obtain a proof.

Theorem 3 (Completeness)

If $\varGamma \models _{K_3}\varphi$, then BSC-K$_3 \vdash \varGamma \Rightarrow \varphi \mid \,\Rightarrow$.

Proof

Assume that $\varGamma \models _{K_3}\varphi$ but BSC-K$_3 \nvdash \varGamma \Rightarrow \varphi \mid \,\Rightarrow$. Hence in every complete proof-search tree for $\varGamma \Rightarrow \varphi \mid \,\Rightarrow$ there is at least one branch starting with non-axiomatic atomic bisequent falsified by some h. Since all rules inherit this valuation, then the root is also falsified contrary to our assumption.    $\square$

As a simple consequence we obtain also a decision procedure for K$_3$ (and for other logics L with complete BSC-L). Another by-product of our proof is that the following cut rules are admissible in BSC-K$_3$ (and other logics):

$(Cut\mid )$ $\dfrac{\varGamma \Rightarrow \varDelta , \varphi \mid \Lambda \Rightarrow \varTheta \qquad \varphi , \varPi \Rightarrow \varSigma \mid \varXi \Rightarrow \varOmega }{\varGamma , \varPi \Rightarrow \varDelta , \varSigma \mid \Lambda , \varXi \Rightarrow \varTheta , \varOmega }$

$(\mid Cut)$ $\dfrac{\varGamma \Rightarrow \varDelta \mid \Lambda \Rightarrow \varTheta , \varphi \qquad \varPi \Rightarrow \varSigma \mid \varphi , \varXi \Rightarrow \varOmega }{\varGamma , \varPi \Rightarrow \varDelta , \varSigma \mid \Lambda , \varXi \Rightarrow \varTheta , \varOmega }$

Moreover, we can constructively prove that these cut rules are admissible in the same way as it is done for four-valued logics in [27]. Due to lack of space we omit this issue here.

Note that the rules stated above provide BSC not only for K$_3$ but also for LP. The only difference is that in LP we consider as provable all bisequents of the form $\Rightarrow \mid \varGamma \Rightarrow \varphi$, which is a consequence of the fact that it is determined by 2-matrix. All the results established for BSC-K$_3$ hold for BSC-LP.

4 Bisequent Calculi for Other Logics

We provide sets of rules adequate for all logics described in Sect. 2. Every operation will be characterised by four rules of introduction to antecedents and consequents of 1- and 2-sequent. The rules are devised on the basis of geometrical insights based on the tabular representation of the respective connective: to establish the premisses for the rule with the principal formula in one of the four positions in a bisequent, we just examine its tabular representation. For example, if indicated values of the arguments form a rectangle, one premiss is enough, in case of more complex shapes, two or three premisses are required. Since the process of construction of rules on the basis of tables is not deterministic we do not propose any algorithm for that aim, however by the end of this section we will illustrated the method with one example. In every case it holds that either:

$\varGamma \models _L \varphi$ iff BSC-L $\vdash \varGamma \Rightarrow \varphi \mid \,\Rightarrow$ or $\varGamma \models _L \varphi$ iff BSC-L $\vdash \ \Rightarrow \mid \varGamma \Rightarrow \varphi$

depending on the fact whether $\models _L$ denotes consequence relation for logics characterised by 1-matrices or by 2-matrices. Adequacy of BSC-L for all concrete logics is proved in the same way as for BSC-K$_3$. Therefore we limit our presentation to systematic characterisation of rules from which the BSC for suitable logic can be composed.

We start with rules for respective unary operations (including Łukasiewicz’s modalities):

$$\begin{array}{ll} (\mathord {\mid \Rightarrow }\mathord {\lnot _P}) \ \dfrac{\varGamma \Rightarrow \varDelta , \varphi \mid \varphi , \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \lnot \varphi }&(\mathord {\lnot _{DP}}\mathord {\Rightarrow \mid }) \ \dfrac{\varGamma \Rightarrow \varDelta , \varphi \mid \varphi , \varPi \Rightarrow \varSigma }{\lnot \varphi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma } \end{array}$$

The remaining rules in each case (namely , , , , , and ) are like respective rules of BSC-K$_3$. Consider premisses of and displaying two occurrences of the same side formula: in semantical terms it gives the effect of evaluating $\varphi$ as undefined.

Not surprisingly rules introducing modal formula to antecedents or to succedents of 1- and 2-sequents have the same premisses; this is a consequence of the fact that such formula is never undefined. The same remark applies to rules for $\lnot _H$ and $\lnot _B$.

The set of rules for weak $\wedge , \vee , \rightarrow$ is also partly identical with those for BSC-K$_3$. The identical rules are $(\mathord {\wedge _w}\mathord {\Rightarrow \mid })$, $(\mathord {\Rightarrow }\mathord {\wedge _w\mid })$, $(\mathord {\mid \Rightarrow }\mathord {\vee _w})$, $(\mathord {\mid \vee _w}\mathord {\Rightarrow })$, $(\mathord {\mid \Rightarrow }\mathord {\rightarrow _w})$ and $(\mathord {\mid \rightarrow _w}\mathord {\Rightarrow })$. In the remaining cases we have three premiss rules:

$(\mathord {\mid \wedge _w}\mathord {\Rightarrow })$ $\dfrac{\varGamma \Rightarrow \varDelta \mid \varphi , \psi , \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta , \varphi \mid \varphi , \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta , \psi \mid \psi , \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta \mid \varphi \wedge \psi , \varPi \Rightarrow \varSigma }$

$(\mathord {\mid \Rightarrow }\mathord {\wedge _w})$ $\dfrac{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi , \psi \qquad \varphi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \psi \qquad \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi }{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi \wedge \psi }$

$(\mathord {\Rightarrow }\mathord {\vee _w}\mid )$ $\dfrac{\varGamma \Rightarrow \varDelta , \varphi , \psi \mid \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta , \varphi \mid \varphi , \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta , \psi \mid \psi , \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta , \varphi \vee \psi \mid \varPi \Rightarrow \varSigma }$

$(\mathord {\vee _w}\mathord {\Rightarrow }\mid )$ $\dfrac{\varphi , \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma \qquad \varphi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \psi \qquad \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi }{\varphi \vee \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma }$

$(\mathord {\Rightarrow }\mathord {\rightarrow _w}\mid )$ $\dfrac{\varGamma \Rightarrow \varDelta , \psi \mid \varphi , \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta , \varphi \mid \varphi , \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta , \psi \mid \psi , \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta , \varphi \rightarrow \psi \mid \varPi \Rightarrow \varSigma }$

$(\mathord {\rightarrow _w}\mathord {\Rightarrow }\mid )$ $\dfrac{\varphi , \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi , \psi \qquad \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi }{\varphi \rightarrow \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma }$

In the case of K$_3^\rightarrow$ and K$_3^\leftarrow$ the specific rules are:

$(\mid \mathord {\Rightarrow }\mathord {\wedge _{mC}})$ $\dfrac{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi \qquad \varphi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \psi }{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi \wedge \psi }$

$(\mid \mathord {\wedge }\mathord {\Rightarrow _{mC}})$ $\dfrac{\varGamma \Rightarrow \varDelta \mid \varphi , \psi , \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta , \varphi \mid \varphi , \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta \mid \varphi \wedge \psi , \varPi \Rightarrow \varSigma }$

$(\mathord {\vee }\mathord {\Rightarrow _{mC}}\mid )$ $\dfrac{\varphi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma \qquad \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi }{\varphi \vee \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma }$

$(\mathord {\Rightarrow }\mathord {\vee _{mC}}\mid )$ $\dfrac{\varGamma \Rightarrow \varDelta , \varphi , \psi \mid \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta , \varphi \mid \varphi , \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta , \varphi \vee \psi \mid \varPi \Rightarrow \varSigma }$

$(\mathord {\Rightarrow }\mathord {\rightarrow _{mC}}\mid )$ $\dfrac{\varGamma \Rightarrow \varDelta , \psi \mid \varphi , \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta , \varphi \mid \varphi , \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta , \varphi \rightarrow \psi \mid \varPi \Rightarrow \varSigma }$

$(\mathord {\rightarrow }\mathord {\Rightarrow _{mC}}\mid )$ $\dfrac{\varphi , \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi }{\varphi \rightarrow \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma }$

$(\mid \mathord {\Rightarrow }\mathord {\wedge _K})$ $\dfrac{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \psi \qquad \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi }{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi \wedge \psi }$

$(\mid \mathord {\wedge }\mathord {\Rightarrow _K})$ $\dfrac{\varGamma \Rightarrow \varDelta \mid \varphi , \psi , \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta , \psi \mid \psi , \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta \mid \varphi \wedge \psi , \varPi \Rightarrow \varSigma }$

$(\mathord {\vee }\mathord {\Rightarrow _K}\mid )$ $\dfrac{\varphi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \psi \qquad \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma }{\varphi \vee \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma }$

$(\mathord {\Rightarrow }\mathord {\vee _K}\mid )$ $\dfrac{\varGamma \Rightarrow \varDelta , \varphi , \psi \mid \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta , \psi \mid \psi , \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta , \varphi \vee \psi \mid \varPi \Rightarrow \varSigma }$

$(\mathord {\Rightarrow }\mathord {\rightarrow _K}\mid )$ $\dfrac{\varGamma \Rightarrow \varDelta , \psi \mid \varphi , \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta , \psi \mid \psi , \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta , \varphi \rightarrow \psi \mid \varPi \Rightarrow \varSigma }$

$(\mathord {\rightarrow }\mathord {\Rightarrow _K}\mid )$ $\dfrac{\psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi , \psi }{\varphi \rightarrow \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma }$

The remaining rules in both cases are identical with $(\mathord {\wedge }\mathord {\Rightarrow \mid })$, $(\mathord {\Rightarrow }\mathord {\wedge \mid })$, $(\mathord {\mid \Rightarrow }\mathord {\vee })$, $(\mathord {\mid \vee }\mathord {\Rightarrow })$, $(\mid \mathord {\Rightarrow }\mathord {\rightarrow })$ and $(\mid \mathord {\rightarrow }\mathord {\Rightarrow })$ from BSC-K$_3$.

The implication of Łukasiewicz [34] and his specific additive $\wedge _L$ and $\vee _L$ are characterised by the following rules:

$(\mid \mathord {\wedge _L\Rightarrow })$ $\dfrac{\varphi , \varGamma \Rightarrow \varDelta \mid \psi , \varPi \Rightarrow \varSigma \qquad \psi , \varGamma \Rightarrow \varDelta \mid \varphi , \varPi \Rightarrow \varSigma }{ \varGamma \Rightarrow \varDelta \mid \varphi \wedge \psi ,\varPi \Rightarrow \varSigma }$

$(\mid \mathord {\Rightarrow \wedge _L})$ $\dfrac{\varGamma \Rightarrow \varDelta , \varphi , \psi \mid \varPi \Rightarrow \varSigma \qquad \varphi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \psi \qquad \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi }{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi \wedge \psi }$

$(\mathord {\mid \vee _L\Rightarrow })$ $\dfrac{\varphi , \varGamma \Rightarrow \varDelta \mid \psi , \varPi \Rightarrow \varSigma \qquad \psi , \varGamma \Rightarrow \varDelta \mid \varphi , \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta \mid \varphi \vee \psi , \varPi \Rightarrow \varSigma }$

$(\mathord {\mid \Rightarrow \vee _L})$ $\dfrac{\varGamma \Rightarrow \varDelta , \varphi , \psi \mid \varPi \Rightarrow \varSigma \qquad \varphi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \psi \qquad \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi }{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi \vee \psi }$

$(\mathord {\Rightarrow }\mathord {\rightarrow _L}\mid )$ $\dfrac{\varphi , \varGamma \Rightarrow \varDelta , \psi \mid \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta \mid \varphi , \varPi \Rightarrow \varSigma , \psi }{\varGamma \Rightarrow \varDelta , \varphi \rightarrow \psi \mid \varPi \Rightarrow \varSigma }$

$(\mathord {\rightarrow _L}\mathord {\Rightarrow }\mid )$ $\dfrac{\varGamma \Rightarrow \varDelta , \varphi \mid \psi , \varPi \Rightarrow \varSigma \qquad \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi }{\varphi \rightarrow \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma }$

The remaining rules are identical with $(\mathord {\wedge }\mathord {\Rightarrow \mid })$, $(\mathord {\Rightarrow }\mathord {\wedge \mid })$, $(\mathord {\Rightarrow }\mathord {\vee \mid })$, $(\mathord {\vee }\mathord {\Rightarrow \mid })$, $(\mid \mathord {\Rightarrow }\mathord {\rightarrow })$ and $(\mid \mathord {\rightarrow }\mathord {\Rightarrow })$ from BSC-K$_3$.

For Sobociński’s connectives we have:

$(\mathord {\wedge _S\Rightarrow }\mid )$ $\dfrac{\varphi , \varGamma \Rightarrow \varDelta \mid \psi , \varPi \Rightarrow \varSigma \qquad \psi , \varGamma \Rightarrow \varDelta \mid \varphi , \varPi \Rightarrow \varSigma }{\varphi \wedge \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma }$

$(\mathord {\Rightarrow \wedge _S}\mid )$ $\dfrac{\varGamma \Rightarrow \varDelta , \varphi , \psi \mid \varPi \Rightarrow \varSigma \qquad \varphi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \psi \qquad \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi }{\varGamma \Rightarrow \varDelta , \varphi \wedge \psi \mid \varPi \Rightarrow \varSigma }$

$(\mathord {\mid \Rightarrow }\mathord {\vee _S})$ $\dfrac{\varGamma \Rightarrow \varDelta , \varphi \mid \varPi \Rightarrow \varSigma , \psi \qquad \varGamma \Rightarrow \varDelta , \psi \mid \varPi \Rightarrow \varSigma , \varphi }{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi \vee \psi }$

$(\mathord {\mid \vee _S}\mathord {\Rightarrow })$ $\dfrac{\varGamma \Rightarrow \varDelta \mid \varphi , \psi , \varPi \Rightarrow \varSigma \qquad \varphi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \psi \qquad \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi }{\varGamma \Rightarrow \varDelta \mid \varphi \vee \psi , \varPi \Rightarrow \varSigma }$

$(\mathord {\mid \Rightarrow }\mathord {\rightarrow _S})$ $\dfrac{\varphi , \varGamma \Rightarrow \varDelta , \psi \mid \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta \mid \varphi , \varPi \Rightarrow \varSigma , \psi }{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi \rightarrow \psi }$

$(\mathord {\mid \rightarrow _S}\mathord {\Rightarrow })$ $\dfrac{\varGamma \Rightarrow \varDelta , \varphi \mid \psi , \varPi \Rightarrow \varSigma \qquad \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi }{\varGamma \Rightarrow \varDelta \mid \varphi \rightarrow \psi , \varPi \Rightarrow \varSigma }$

The remaining rules look like in BSC-K$_3$.

Sette’s connectives are characterised by the following rules:

$(\mathord {\Rightarrow }\mathord {\wedge _{ Se }\mid })$ $\dfrac{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi \;\quad \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \psi }{\varGamma \Rightarrow \varDelta , \varphi \wedge \psi \mid \varPi \Rightarrow \varSigma }$

  ,   , ,   are like in BSC-K$_3$.

Finally Carnielli and Sette connectives characterising $\mathbf{I^1}$ and $\mathbf{I^2}$:

$(\mathord {\mid \Rightarrow }\mathord {\wedge _C})$ $\dfrac{\varGamma \Rightarrow \varDelta , \varphi \mid \varPi \Rightarrow \varSigma \quad \varGamma \Rightarrow \varDelta , \psi \mid \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi \wedge \psi }$

$$\begin{array}{ll} (\mathord {{\mid }\wedge _C}\mathord {\Rightarrow }) \dfrac{\varphi , \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma }{ \varGamma \Rightarrow \varDelta \mid \varphi \wedge \psi , \varPi \Rightarrow \varSigma } &{} (\mathord {\mid \Rightarrow }\mathord {\vee _C}) \dfrac{\varGamma \Rightarrow \varDelta , \varphi , \psi \mid \varPi \Rightarrow \varSigma }{ \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi \vee \psi }\\[16pt] \end{array}$$

$(\mathord {{\mid }\vee _C}\mathord {\Rightarrow })$ $\dfrac{\varphi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma \quad \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta \mid \varphi \vee \psi , \varPi \Rightarrow \varSigma }$

$(\mathord {\mid \rightarrow _C}\mathord {\Rightarrow })$ $\dfrac{\varGamma \Rightarrow \varDelta , \varphi \mid \varPi \Rightarrow \varSigma \quad \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta \mid \varphi \rightarrow \psi , \varPi \Rightarrow \varSigma }$

$$\begin{array}{ll} (\mathord {\mid \Rightarrow }\mathord {\rightarrow _C}) \dfrac{\varphi , \varGamma \Rightarrow \varDelta , \psi \mid \varPi \Rightarrow \varSigma }{\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi \rightarrow \psi } &{} (\mathord {\Rightarrow }\mathord {\rightarrow _C\mid }) \ \dfrac{\varphi , \varGamma \Rightarrow \varDelta , \psi \mid S}{\varGamma \Rightarrow \varDelta , \varphi \rightarrow \psi \mid S}\\[16pt] \end{array}$$

$(\mathord {\rightarrow _C}\mathord {\Rightarrow \mid })$ $\dfrac{\varGamma \Rightarrow \varDelta , \varphi \mid S \qquad \psi , \varGamma \Rightarrow \varDelta \mid S }{\varphi \rightarrow \psi , \varGamma \Rightarrow \varDelta \mid S}$

$(\mathord {\wedge _C}\mathord {\Rightarrow }\mid )$, $(\mathord {\Rightarrow }\mathord {\wedge _C}\mid )$, $(\mathord {\Rightarrow }\mathord {\vee _C}\mid )$, $(\mathord {\vee _C}\mathord {\Rightarrow }\mid )$ are like in BSC-K$_3$.

We finish with the characterisation of the remaining implications introduced in Sect. 2. In most cases it is obtained by combining rules which were previously introduced. In particular:

Słupecki’s [49] implication is characterised by means of: $(\mathord {\mid \Rightarrow }\mathord {\rightarrow })$ and $(\mathord {\mid \rightarrow }\mathord {\Rightarrow })$ from BSC-K$_3$ as well as $(\mathord {\Rightarrow }\mathord {\rightarrow _C}\mid )$ and $(\mathord {\rightarrow _C}\mathord {\Rightarrow }\mid )$.

Heyting’s implication [22] is characterised by means of: $(\mathord {\rightarrow _L}\mathord {\Rightarrow }\mid )$, $(\mathord {\Rightarrow }\mathord {\rightarrow _L}\mid )$, $(\mathord {\mid \Rightarrow }\mathord {\rightarrow _{Se}})$,$(\mathord {\mid \rightarrow _{Se}}\mathord {\Rightarrow })$.

D’Ottaviano/DaCosta/Jaśkowski/Słupecki’s implication [13, 30, 48] is characterised by means of: $(\mathord {\rightarrow }\mathord {\Rightarrow }\mid )$, $(\mathord {\Rightarrow }\mathord {\rightarrow }\mid )$, $(\mathord {\mid \Rightarrow }\mathord {\rightarrow _{Se}})$,$(\mathord {\mid \rightarrow _{Se}}\mathord {\Rightarrow })$.

Rescher’s implication [43] is characterised by means of: $(\mathord {\rightarrow _L}\mathord {\Rightarrow }\mid )$, $(\mathord {\Rightarrow }\mathord {\rightarrow _L}\mid )$, $(\mathord {\mid \Rightarrow }\mathord {\rightarrow _{S}})$,$(\mathord {\mid \rightarrow _{S}}\mathord {\Rightarrow })$.

Tomova’s implication [22] is characterised by means of: $(\mathord {\rightarrow _L}\mathord {\Rightarrow }\mid )$, $(\mathord {\Rightarrow }\mathord {\rightarrow _L}\mid )$, $(\mathord {\mid \Rightarrow }\mathord {\rightarrow _{C}})$,$(\mathord {\mid \rightarrow _{C}}\mathord {\Rightarrow })$.

Only in case of Sobociński’s implication $\rightarrow _S'$ we have a pair of new rules:

$(\mathord {\rightarrow _S'}\mathord {\Rightarrow \mid })$ $\dfrac{\psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma \qquad \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi , \psi \qquad \varGamma \Rightarrow \varDelta , \varphi \mid \varphi , \psi , \varPi \Rightarrow \varSigma }{\varphi \rightarrow \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma }$

$(\mathord {\Rightarrow }\mathord {\rightarrow _S'\mid })$ $\dfrac{\varphi , \varGamma \Rightarrow \varDelta , \psi \mid \varPi \Rightarrow \varSigma \;\quad \varGamma \Rightarrow \varDelta \mid \varphi , \varPi \Rightarrow \varSigma , \psi \;\quad \varGamma \Rightarrow \varDelta , \psi \mid \psi , \varPi \Rightarrow \varSigma , \varphi }{\varGamma \Rightarrow \varDelta , \varphi \rightarrow \psi \mid \varPi \Rightarrow \varSigma }$

The remaining two rules are: $(\mathord {\mid \Rightarrow }\mathord {\rightarrow _{Se}})$ and $(\mathord {\mid \rightarrow _{Se}}\mathord {\Rightarrow })$.

Let us show how $(\mathord {\Rightarrow }\mathord {\rightarrow _S'\mid })$ was obtained on the basis of the table for $\rightarrow '_S$ from p. 4. $\varphi \rightarrow \psi$ is either false or undefined which corresponds to four cells:

The remaining premiss covers the cell with 0 in the first and second rows attributed to $\psi$ while $\varphi$ is 1 or u. Note that since the left premiss covers the first row and the right premiss covers the last row we could alternatively formulate the middle premiss as $\varGamma \Rightarrow \varDelta , \varphi \mid \varphi , \varPi \Rightarrow \varSigma , \psi$ to cover exactly the cell with 0 in the second row (here $\varphi$ is just u) but since $\psi$ is 0 in two rows where $\varphi$ is 1 or u we can be more economical here. A reader can check that many rules can be formulated in alternative way. We always tried to find the most economical representation which can be used easily also for proving syntactically the cut elimination theorem (which will be shown in the extended version of this paper).

Now, consider an arbitrary connective c of the logic L, the corresponding operation $\underline{c}$ as characterised by suitable matrix determining L in Sect. 2, and the four rules for c. It holds:

Theorem 4

For all presented rules characterising arbitrary c of any L: all premisses are L-valid iff the conclusion is L-valid.

Proof

This is an analogue of Theorem 1 for any considered logic L which implies adequacy of respective BSC-L.    $\square$

5 Interpolation

We present a constructive proof of the interpolation theorem for some logics based on the strategy proposed by Muskens and Wintein [58]. It was originally applied in tableau setting for Belnap-Dunn four-valued logic as well as for $\mathbf{K_3}$ and LP. Here we demonstrate that BSC can be also used for showing that interpolation holds for some paracomplete and paraconsistent logics. Let $\textbf{L}\in \{\mathbf{I^1, I^2, P^1, P^2}\}$.

Theorem 5

For any contingent formulae $\varphi , \psi$, if $\varphi \models _L\psi$, then we can construct an interpolant for $\mathbf{I^1, I^2}$ on the basis of proof-search trees for $\varphi \Rightarrow \mid \Rightarrow$ and $\Rightarrow \psi \mid \Rightarrow$ and an interpolant for $\mathbf{P^1, P^2}$ on the basis of proof-search trees for $\Rightarrow \mid \varphi \Rightarrow$ and $\Rightarrow \mid \Rightarrow \psi$ in suitable BSC-L.

Proof

We will demonstrate the case of BSC-I$^1$; the case of BSC-I$^2$ is identical and the cases of BSC-P$^1$ and BSC-P$^2$ are dual, so we only comment on them in the key points. Assume that $\varphi \models _{I^1}\psi$; hence by completeness we have a cut-free proof of $\varphi \Rightarrow \psi \mid \Rightarrow$ in BSC-I$^1$. Now produce complete proof-search trees for $\varphi \Rightarrow \mid \Rightarrow$ and $\Rightarrow \psi \mid \Rightarrow$. Since $\varphi , \psi$ are contingent, they have some non-axiomatic leaves. Let $\varGamma _1\Rightarrow \varDelta _1\mid \varPi _1\Rightarrow \varSigma _1, \ldots , \varGamma _k\Rightarrow \varDelta _k\mid \varPi _k\Rightarrow \varSigma _k$ be the list of non-axiomatic atomic leaves of the proof-search tree for $\varphi \Rightarrow \mid \Rightarrow$ and $\varTheta _1\Rightarrow \Lambda _1\mid \varXi _1\Rightarrow \varOmega _1, \ldots , \varTheta _n\Rightarrow \Lambda _n\mid \varXi _n\Rightarrow \varOmega _n$ such a list taken from the proof-search tree for $\Rightarrow \psi \mid \Rightarrow$. It holds:

Claim (1)

For any $i\le k$ and $j\le n$, $\varGamma _i, \varTheta _j\Rightarrow \varDelta _i, \Lambda _j\mid \varPi _i, \varXi _j\Rightarrow \varSigma _i, \varOmega _j$ is an axiomatic atomic bisequent.

To see this take a tree for $\varphi \Rightarrow \mid \Rightarrow$ and add $\psi$ to succedents of all 1-sequents in the tree. Due to context independence of all rules it is a correct proof-search tree. Now for each leaf $\varGamma _i\Rightarrow \varDelta _i, \psi \mid \varPi _i\Rightarrow \varSigma _i$ append a tree of $\Rightarrow \psi \mid \Rightarrow$ but with $\varGamma _i$ added to each antecedent and $\varDelta _i$ added to each succedent of 1-sequents, and similarly with $\varPi _i$ and $\varSigma _i$ in all 2-sequents. In the resulting proof-search tree we have leaves of the form $\varGamma _i, \varTheta _j\Rightarrow \varDelta _i, \Lambda _j\mid \varPi _i, \varXi _j\Rightarrow \varSigma _i, \varOmega _j$ for all $i\le k$ and $j\le n$. If at least one of them is not axiomatic, then $\nvdash \varphi \Rightarrow \psi \mid \Rightarrow$.    $\square$

Next for every $\varGamma _i\Rightarrow \varDelta _i\mid \varPi _i\Rightarrow \varSigma _i, i\le k$, define the following sets:

$\varGamma _i' = \varGamma _i\cap (\bigcup \Lambda _j\cup \bigcup \varOmega _j)$ for $j\le n$

$\varDelta _i' = \varDelta _i\cap \bigcup \varTheta _j$ for $j\le n$

$\varPi _i' = \varPi _i\cap \bigcup \varOmega _j$ for $j\le n$

$\varSigma _i' = \varSigma _i\cap (\bigcup \varTheta _j\cup \bigcup \varXi _j)$ for $j\le n$

Since every $\varGamma _i, \varTheta _j\Rightarrow \varDelta _i, \Lambda _j\mid \varPi _i, \varXi _j\Rightarrow \varSigma _i, \varOmega _j$ is axiomatic we are guaranteed that $\varGamma _i'\cup \varDelta _i'\cup \varPi _i'\cup \varSigma _i'\ne \varnothing$. Note also that $AT(\varGamma _i'\cup \varDelta _i'\cup \varPi _i'\cup \varSigma _i') \subseteq AT(\varphi )\cap AT(\psi )$, where AT stands for the set of atoms. Now define an interpolant $Int(\varphi , \psi )$ for considered logics. For $\mathbf{I^1, I^2}$ it has the same form:

$\bigwedge \varGamma _1' \wedge \bigwedge \lnot \varSigma _1'\wedge \lnot \big (\bigvee \lnot \varPi _1'\vee \bigvee \varDelta _1'\big ) \ \vee \ldots \vee \ \bigwedge \varGamma _k' \wedge \bigwedge \lnot \varSigma _k'\wedge \lnot \big (\bigvee \lnot \varPi _k'\vee \bigvee \varDelta _k'\big )$,

where $\lnot \varPi$ means the set of negations of all elements in $\varPi$.

For $\mathbf{P^1, P^2}$ $Int(\varphi , \psi )$ is defined as:

$\bigwedge \varPi _1' \wedge \bigwedge \lnot \varDelta _1'\wedge \lnot \big (\bigvee \lnot \varGamma _1'\vee \bigvee \varSigma _1'\big ) \ \vee \ldots \vee \ \bigwedge \varPi _k' \wedge \bigwedge \lnot \varDelta _k'\wedge \lnot \big (\bigvee \lnot \varGamma _k'\vee \bigvee \varSigma _k'\big )$

We can show that:

Claim (2)

$Int(\varphi , \psi )$ is an interpolant for $\varphi \models _L\psi$.

Proof

As an example, we present the proof for BSC-I$^1$. For the sake of proof let us recall that BSC-I$^1$ consists of the rules characterising $\wedge _C, \vee _C, \rightarrow _C$ and $\lnot _H$. However, most of the rules necessary for conducting the proof are identical with respective rules from BSC-K$_3$, so the label C in their names will be omitted in these cases for easier recognition where the specific rules (concretely $(\mid \vee _C\Rightarrow )$ and $(\mid \Rightarrow \vee _C)$) are required.

Since for every $\bigwedge \varGamma _i'\wedge \bigwedge \lnot \varSigma _i'\wedge \lnot (\bigvee \lnot \varPi _i'\vee \bigvee \varDelta _i')$ all (negated) atoms are by definition taken from $AT(\varphi )\cap AT(\psi )$, we must only prove that BSC-I$^1$ $\vdash \varphi \Rightarrow Int(\varphi , \psi )\mid \Rightarrow$, and BSC-I$^1$ $\vdash Int(\varphi , \psi ) \Rightarrow \psi \mid \Rightarrow$ (the same for BSC-I$^2$), and BSC-P$^1$ $\vdash \Rightarrow \mid \varphi \Rightarrow Int(\varphi , \psi )$ and BSC-P$^1$ $\vdash \Rightarrow \mid Int(\varphi , \psi ) \Rightarrow \psi$ (and the same for BSC-P$^2$).

Again take a complete proof-search tree for $\varphi \Rightarrow \mid \Rightarrow$ and add $Int(\varphi , \psi )$ to every succedent of 1-sequent. For every $\varGamma _i\Rightarrow \varDelta _i, Int(\varphi , \psi )\mid \varPi _i\Rightarrow \varSigma _i$ apply $(\Rightarrow \vee \mid )$ to get

$$\varGamma _i\Rightarrow \varDelta _i, \bigwedge \varGamma _i'\wedge \bigwedge \lnot \varSigma _i'\wedge \lnot (\bigvee \lnot \varPi _i'\vee \bigvee \varDelta _i'), Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i,$$

where $Int(\varphi , \psi )^{-i}$ is the rest of the disjunction (if any). Applying $(\Rightarrow \wedge \mid )$ we obtain three bisequents:

(a) $\varGamma _i\Rightarrow \varDelta _i, \bigwedge \varGamma _i', Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i$

(b) $\varGamma _i\Rightarrow \varDelta _i, \bigwedge \lnot \varSigma _i', Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i$

(c) $\varGamma _i\Rightarrow \varDelta _i, \lnot (\bigvee \lnot \varPi _i'\vee \bigvee \varDelta _i'), Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i$.

Systematically applying $(\Rightarrow \wedge \mid )$ to (a) we obtain $\varGamma _i\Rightarrow \varDelta _i, p, Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i$ for each $p\in \varGamma _i'$ and since $\varGamma _i'\subseteq \varGamma _i$ they are all axiomatic. Similarly with (b) but now we first obtain $\varGamma _i\Rightarrow \varDelta _i, \lnot p, Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i$ for each $p\in \varSigma _i'$. After the application of $(\Rightarrow \lnot \mid )$ we obtain $\varGamma _i\Rightarrow \varDelta _i, Int(\varphi , \psi )^{-i}\mid p, \varPi _i\Rightarrow \varSigma _i$ which is axiomatic since $\varSigma _i'\subseteq \varSigma _i$. For (c) we first apply $(\Rightarrow \lnot \mid )$ and obtain $\varGamma _i\Rightarrow \varDelta _i, Int(\varphi , \psi )^{-i}\mid \bigvee \lnot \varPi _i'\vee \bigvee \varDelta _i', \varPi _i\Rightarrow \varSigma _i$. By $(\mid \vee _C\Rightarrow )$ we obtain: $\bigvee \lnot \varPi _i', \varGamma _i\Rightarrow \varDelta _i, Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i$ and $\bigvee \varDelta _i',\varGamma _i\Rightarrow \varDelta _i, Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i$. Systematic application of $(\vee \Rightarrow \mid )$ to the latter produces axiomatic bisequents $p,\varGamma _i\Rightarrow \varDelta _i, Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i$ for each $p\in \varDelta _i'$. Systematic application of $(\vee \Rightarrow \mid )$ to the former produces $\lnot p,\varGamma _i\Rightarrow \varDelta _i, Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i$ for each $p\in \varPi _i'$. After application of $(\lnot \Rightarrow \mid )$ they also yield axiomatic sequents. Hence we have a proof of $\varphi \Rightarrow Int(\varphi , \psi )\mid \Rightarrow$.

We have to do the same with a complete proof-search tree for $\Rightarrow \psi \mid \Rightarrow$ but now adding $Int(\varphi , \psi )$ to every antecedent of all 1-sequents in the tree. For every leaf $Int(\varphi , \psi ), \varTheta _j\Rightarrow \Lambda _j\mid \varXi _j\Rightarrow \varOmega _j$ we apply $(\vee \Rightarrow |)$ to each disjunct of $Int(\varphi , \psi )$ until we get leaves: $\bigwedge \varGamma _1'\wedge \bigwedge \lnot \varSigma _1'\wedge \lnot (\bigvee \lnot \varPi _1'\vee \bigvee \varDelta _1'), \varTheta _j\Rightarrow \Lambda _j\mid \varXi _j\Rightarrow \varOmega _j$ ...$\bigwedge \varGamma _k'\wedge \bigwedge \lnot \varSigma _k'\wedge \lnot (\bigvee \lnot \varPi _k'\vee \bigvee \varDelta _k'), \varTheta _j\Rightarrow \Lambda _j\mid \varXi _j\Rightarrow \varOmega _j$. To each such leaf we apply $(\wedge \Rightarrow \mid )$ obtaining bisequents of the form $\varGamma _i', \lnot \varSigma _i', \lnot (\bigvee \lnot \varPi _i'\vee \bigvee \varDelta _i'), \varTheta _j\Rightarrow \Lambda _j\mid \varXi _j\Rightarrow \varOmega _j$ for $i\le k, j\le n$. In each case the application of $(\lnot \Rightarrow \mid )$ yields $\varGamma _i', \varTheta _j\Rightarrow \Lambda _j\mid \varXi _j\Rightarrow \varOmega _j, \varSigma _i', \bigvee \lnot \varPi _i'\vee \bigvee \varDelta _i'$. The application of $(\mid \Rightarrow \vee _C)$ to $\bigvee \lnot \varPi _i'\vee \bigvee \varDelta _i'$ yields $\varGamma _i', \varTheta _j\Rightarrow \Lambda _j, \bigvee \lnot \varPi _i', \bigvee \varDelta _i'\mid \varXi _j\Rightarrow \varOmega _j, \varSigma _i'$. Systematic application of $(\Rightarrow \vee \mid )$ and $(\Rightarrow \lnot \mid )$ gives leaves of the form $\varGamma _i', \varTheta _j\Rightarrow \Lambda _j, \varDelta _i'\mid \varPi _i', \varXi _j\Rightarrow \varOmega _j, \varSigma _i'$. Since for every $i\le k, j\le n$, $\varGamma _i, \varTheta _j\Rightarrow \varDelta _i, \Lambda _j\mid \varPi _i, \varXi _j\Rightarrow \varSigma _i, \varOmega _j$ is axiomatic these primed versions are axiomatic too. Assume the contrary, then it must be e.g. some $p\notin \varGamma _i'$ such that either $p\in \varGamma _i\cap \Lambda _j$ or $p\in \varGamma _i\cap \varOmega _j$ (or for other pairs generating axioms). But it is impossible since by definition $\varGamma _i'$ must contain such p (and the same for other cases of primed sets).    $\square$

The proof for BSC-I$^2$ is identical since the only difference between these two logics is that $\mathbf{I^1}$ has Heyting’s negation whereas in $\mathbf{I^2}$ it is Kleene’s negation. But the two BSC rules for negation which are used in the proof are common to both negations. The proof for $\mathbf{P^1, P^2}$ is dual to the above and uses slightly different definition of $Int(\varphi , \psi )$ specified above. Again the two logics differ only with respect to negations, but the rules used in the proof are common to Bochvar’s and Kleene’s one.

Eventually note that this proof may be applied also to other logics but in some cases it is convenient to extend their languages. For example, interpolants for some logics can be defined as disjunctions of the following formulae:

For $\mathbf{K_3}$ – $\bigwedge \varGamma _i' \wedge \bigwedge \lnot \varSigma _i'\wedge \bigwedge \lnot _B\varDelta _i'\wedge \bigwedge \lnot _B\lnot \varPi _i'$

For LP – $\bigwedge \varPi _i'\wedge \bigwedge \lnot \varDelta _i'\wedge \bigwedge \lnot _H\varSigma _i'\wedge \bigwedge \lnot _H\lnot \varGamma _i'$

For $\mathbf{G_3}$ – $\bigwedge \varGamma _i' \wedge \lnot _H(\bigwedge \varPi _i'\rightarrow \bigvee \varSigma _i')\wedge \bigwedge \lnot _B\varDelta _i'$

For $\mathbf{G_3'}$ – $\bigwedge \varPi _i'\wedge \bigwedge \lnot _B\varDelta _i'\wedge \bigwedge \lnot _H\varSigma _i'\wedge \bigwedge \lnot _B\lnot _B\varGamma _i'$

6 Conclusion

Bisequent calculi can be seen as one of the possible syntactical realizations of so called Suszko’s thesis [54] in the treatment of many-valued logics. According to Suszko every logic is two-valued in the sense that all values are divided into designated and non-designated and this is reflected in the definition of consequence relation. In the case of bisequent calculi it is additionally made evident that two possible choices of designated values can be made. However, on a deep level a BSC is similar to some other proposed formalisations mentioned in the Introduction. On one hand bisequents resemble several labelled approaches where labels denote sets of values; a difference is that instead of labels a position of a formula in a bisequent is crucial, hence the method is strictly syntactical. On the other hand, there is a similarity with Avron’s [4] and Avron, Ben-Naim, and Konikowska’s [6] sequent calculi with special rules defined for negated formulae; a difference is that BSC satisfies ordinary subformula property and purity conditions to the effect that in schemata of rules only one (occurrence of a) connective is involved. The price is that instead of standard sequents we use a pair of them.

As we mentioned in the Introduction there is one more general difference. In the case of labelled calculi or Avron’s SC we have the same input for 1- and 2-logics, whereas in BSC a different input for both classes of logics is defined; a 1- or a 2-sequent in a bisequent. A consequence of our choice is that for every pair of 1- and 2-logic with the same connectives (like e.g. K$_3$ and LP) the rules and axioms are identical. In contrast, in other mentioned approaches for such pairs of related logics, the respective calculi must differ either with respect to some axioms (closure conditions in tableaux) or to rules. It seems that the present solution where systems differ only with respect to the input is more economical and uniform. In fact we can consider also logics determined by different notions of consequence relations while still keeping the rules and axioms intact. Two relations considered in the text express informally the situation where either truth is preserved or non-falsity is preserved. But two other possibilities are open as well: $\varGamma \Rightarrow \,\mid \, \Rightarrow \psi$ corresponds to the notion of no-counterexample consequence (see e.g. Lehmann [33], Paoli [39]), whereas $\Rightarrow \varphi \mid \varGamma \Rightarrow$ corresponds to the liberal consequence which leads from non-falsity to truth. This level of uniformity follows from the fact that rules of BSC are not computed on the basis of any normal (disjunctive or conjunctive) form, like in other approaches, but on the basis of geometrical insights illustrated in Sect. 4.

Finally notice that the application of BSC may be extended easily to first-order languages. It is quite obvious how to define suitable rules for quantifiers. But the proof of adequacy requires more refined methods than those applied here so for the lack of space we limited ourselves to propositional case. However, we finish the paper with one more problem for further investigation: the application of first-order BSC to formalisation of neutral free logics, and in particular to specific theories of definite descriptions based on some Fregean ideas (see e.g. Lehmann [33], Stenlund [52]). Since sequent and tableau calculi for such theories built on positive and negative free logics were already provided in [24, 26, 28], this paper offers a proper ground for extension of these results to neutral free logics.