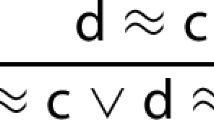Program Synthesis in Saturation

Abstract

We present an automated reasoning framework for synthesizing recursion-free programs using saturation-based theorem proving. Given a functional specification encoded as a first-order logical formula, we use a first-order theorem prover to both establish validity of this formula and discover program fragments satisfying the specification. As a result, when deriving a proof of program correctness, we also synthesize a program that is correct with respect to the given specification. We describe properties of the calculus that a saturation-based prover capable of synthesis should employ, and extend the superposition calculus in a corresponding way. We implemented our work in the first-order prover Vampire, extending the successful applicability of first-order proving to program synthesis.

1 Introduction

Program synthesis constructs code from a given specification. In this work we focus on synthesis using functional specifications summarized by valid first-order formulas [1, 14], ensuring that our programs are provably correct. While being a powerful alternative to formal verification [20], synthesis faces intrinsic computational challenges. One of these challenges is posed to the reasoning backend used for handling program specifications, as the latter typically include first-order quantifier alternations and interpreted theory symbols. As such, efficient reasoning with both theories and quantifiers is imperative for any effort towards program synthesis.

In this paper we address this demand for recursion-free programs. We advocate the use of first-order theorem proving for extracting code from correctness proofs of functional specifications given as first-order formulas $\forall \overline{x} . \exists y. F[\overline{x},y]$. These formulas state that “for all (program) inputs $\overline{x}$ there exists an output y such that the input-output relation (program computation) $F[\overline{x}, y]$ is valid”. Given such a specification, we synthesize a recursion-free program while also deriving a proof certifying that the program satisfies the specification.

The programs we synthesize are built using first-order theory terms extended with $\texttt{if}\!-\!\texttt{then}\!-\!\texttt{else}$ constructors. To ensure that our programs yield computational models, i.e., that they can be evaluated for given values of input variables $\overline{x}$, we restrict the programs we synthesize to only contain computable symbols.

Our Approach in a Nutshell. In order to synthesize a recursion-free program, we prove its functional specification using saturation-based theorem proving [11, 15]. We extend saturation-based proof search with answer literals [5], allowing us to track substitutions into the output variable y of the specification. These substitutions correspond to the sought program fragments and are conditioned on clauses they are associated with in the proof. When we derive a clause corresponding to a program branch $\texttt{if}\ C\ \texttt{then}\ r$, where C is a condition and r a term and both C, r are computable, we store it and continue proof search assuming that $\lnot C$ holds; we refer to such conditions C as (program) branch conditions. The saturation process for both proof search and code construction terminates when the conjunction of negations of the collected branch conditions becomes unsatisfiable. Then we synthesize the final program satisfying the given (and proved) specification by assembling the recorded program branches (see e.g. Examples 1–3).

The main challenges of making our approach effective come with (i) integrating the construction of the programs with $\texttt{if}\!-\!\texttt{then}\!-\!\texttt{else}$ into the proof search, turning thus proof search into program search/synthesis, and (ii) guiding program synthesis to only computable branch conditions and programs.

Contributions. We bring the next contributions solving the above challenges:¹

• We formalize the semantics for clauses with answer literals and introduce a saturation-based algorithm for program synthesis based on this semantics. We prove that, given a sound inference system, our saturation algorithm derives correct and computable programs (Sect. 4).

• We define properties of a sound inference calculus in order to make the calculus suitable for our saturation-based algorithm for program synthesis. We accordingly extend the superposition calculus and define a class of substitutions to be used within the extended calculus; we refer to these substitutions as computable unifiers (Sect. 5).

• We extend a first-order unification algorithm to find computable unifiers (Sect. 6) to be further used in saturation-based program synthesis.

• We implement our work in the Vampire prover [11] and evaluate our synthesis approach on a number of examples, complementing other techniques in the area (Sect. 7). For example, our results demonstrate the applicability of our work on synthesizing programs for specifications that cannot be even encoded in the SyGuS syntax [16].

2 Preliminaries

We assume familiarity with standard multi-sorted first-order logic with equality. We denote variables by x, y, terms by s, t, atoms by A, literals by L, clauses by C, D, formulas by F, G, all possibly with indices. Further, we write $\sigma$ for Skolem constants. We reserve the symbol $\square$ for the empty clause which is logically equivalent to $\bot$. Formulas and clauses with free variables are considered implicitly universally quantified (i.e. we consider closed formulas). By $\simeq$ we denote the equality predicate and write $t\not \simeq s$ as a shorthand for $\lnot t\simeq s$. We use a distinguished integer sort, denoted by $\mathbb {Z}$. When we use standard integer predicates <, $\le$, >, $\ge$, functions $+, -, \dots$ and constants $0, 1, \dots$, we assume that they denote the corresponding interpreted integer predicates and functions with their standard interpretations. Additionally, we include a conditional term constructor $\texttt{if}\!-\!\texttt{then}\!-\!\texttt{else}$ in the language, as follows: given a formula F and terms s, t of the same sort, we write $\texttt{if}\ F\ \texttt{then}\ s\ \texttt{else}\ t$ to denote the term s if F is valid and t otherwise.

An expression is a term, literal, clause or formula. We write E[t] to denote that the expression E contains the term t. For simplicity, E[s] denotes the expression E where all occurrences of t are replaced by the term s. A substitution $\theta$ is a mapping from variables to terms. A substitution $\theta$ is a unifier of two expressions E and $E'$ if $E\theta = E'\theta$, and is a most general unifier (mgu) if for every unifier $\eta$ of E and $E'$, there exists substitution $\mu$ such that $\eta =\theta \mu$. We denote the mgu of E and $E'$ with $\texttt{mgu}(E,E')$. We write $F_1,\ldots ,F_n \vdash G_1,\ldots ,G_m$ to denote that $F_1 \wedge \ldots \wedge F_n \rightarrow G_1{\vee }\ldots {\vee } G_m$ is valid, and extend the notation also to validity modulo a theory T. Symbols occurring in a theory T are interpreted and all other symbols are uninterpreted.

2.1 Computable Symbols and Programs

We distinguish between computable and uncomputable symbols in the signature. The set of computable symbols is given as part of the specification. Intuitively, a symbol is computable if it can be evaluated and hence is allowed to occur in a synthesized program. A term or a literal is computable if all symbols it contains are computable. A symbol, term or literal is uncomputable if it is not computable.

A functional specification, or simply just a specification, is a formula

$$\begin{aligned} {\forall \overline{x} . \exists y. F[\overline{x},y].} \end{aligned}$$

(1)

The variables $\overline{x}$ of a specification (1) are called input variables. Note that while we use specifications with a single variable y, our work can analogously be used with a tuple of variables $\overline{y}$ in (1).

Let $\overline{\sigma }$ denote a tuple of Skolem constants. Consider a computable term $r[\overline{\sigma }]$ such that the instance $F[\overline{\sigma }, r[\overline{\sigma }]]$ of (1) holds. Since $\overline{\sigma }$ are fresh Skolem constants, the formula $\forall \overline{x} . F[\overline{x},r[\overline{x}]]$ also holds; we call such $r[\overline{x}]$ a program for (1) and say that the program $r[\overline{x}]$ computes a witness of (1).

Further, if $\forall \overline{x}. (F_1\wedge \ldots \wedge F_n \rightarrow F[\overline{x},r[\overline{x}]])$ holds for computable formulas $F_1, \dots , F_n$, we write $\langle {r[\overline{x}]}, {\bigwedge _{i=1}^n F_i}\rangle$ to refer to a program with conditions $F_1,\dots ,F_n$ for (1). In the sequel, we refer to (parts of) programs with conditions also as conditional branches. In Sect. 4 we show how to build programs for (1) by composing programs with conditions for (1) (see Corollary 3).

2.2 Saturation and Superposition

Saturation-based proof search implements proving by refutation [11]: to prove validity of F, a saturation algorithm establishes unsatisfiability of $\lnot F$. First-order theorem provers work with clauses, rather than with arbitrary formulas. To prove a formula F, first-order provers negate F which is further skolemized and converted to clausal normal form (CNF). The CNF of $\lnot F$ is denoted by $\texttt{cnf}(\lnot F)$ and represents a set S of initial clauses. First-order provers then saturate S by computing logical consequences of S with respect to a sound inference system $\mathcal {I}$. The saturated set of S is called the closure of S and the process of computing the closure of S is called saturation. If the closure of S contains the empty clause $\square$, the original set S of clauses is unsatisfiable, and hence the formula F is valid.

We may extend the set S of initial clauses with additional clauses $C_1,\dots ,C_n$. If C is derived by saturating this extended set, we say C is derived from S under additional assumptions $C_1,\dots ,C_n$.

Fig. 1.

The superposition calculus $\mathbb {S}\text {up}$ .

The superposition calculus, denoted as $\mathbb {S}\text {up}$ and given in Fig. 1, is the most common inference system used by saturation-based provers for first-order logic with equality [15]. The $\mathbb {S}\text {up}$ calculus is parametrized by a simplification ordering $\succ$ on terms and a selection function, which selects in each non-empty clause a non-empty subset of literals (possibly also positive literals). We denote selected literals by underlining them. An inference rule can be applied on the given premise(s) if the literals that are underlined in the rule are also selected in the premise(s). For a certain class of selection functions, the superposition calculus $\mathbb {S}\text {up}$ is sound (if $\square$ is derived from F, then F is unsatisfiable) and refutationally complete (if F is unsatisfiable, then $\square$ can be derived from it).

2.3 Answer Literals

Answer literals [5] provide a question answering technique for tracking substitutions into given variables throughout the proof. Suppose we want to find a witness for the validity of the formula

$$\begin{aligned} \exists y.F[y]. \end{aligned}$$

(2)

Within saturation-based proving, we first derive the skolemized negation of (2) and add an answer literal using a fresh predicate $\texttt{ans}$ with argument y, yielding

$$\begin{aligned} \forall y.(\lnot F[y]{\vee } \texttt{ans}(y)). \end{aligned}$$

(3)

We then saturate the CNF of (3), while ensuring that answer literals are not selected for performing inferences. If the clause $\texttt{ans}(t_1){\vee }\ldots {\vee }\texttt{ans}(t_m)$ is derived during saturation, note that this clause contains only answer literals in addition to the empty clause; hence, in this case we proved unsatisfiability of $\forall y.\lnot F[y]$, implying validity of (2). Moreover, $t_1,\dots ,t_m$ provides a disjuntive answer, i.e. witness, for the validity of (2); that is, $F[t_1]{\vee }\ldots {\vee } F[t_m]$ holds [12]. In particular, if we derive the clause $\texttt{ans}(t)$ during saturation, we found a definite answer t for (2), namely F[t] is valid.

Answer Literals with $\texttt{if}\!-\!\texttt{then}\!-\!\texttt{else}$. The derivation of disjunctive answers can be avoided by modifying the inference rules to only derive clauses containing at most one answer literal. One such modification is given within the $\text {A}(R)$-calculus for binary resolution [22], where R is a so-called strongly liftable term restriction. The $\text {A}(R)$-calculus replaces the binary resolution rule when both premises contain an answer literal by the following A-resolution rule:

where $\theta :=\texttt{mgu}(A,A^\prime )$ and the restriction $R(\texttt{if}\ A\ \texttt{then}\ r^\prime \ \texttt{else}\ r)$ holds.

In our work we go beyond the A-resolution rule and modify both the superposition calculus and the saturation algorithm to reason not only about answer literals but also about their use of $\texttt{if}\!-\!\texttt{then}\!-\!\texttt{else}$ terms (see Sects. 4–5).

3 Illustrative Example

Let us illustrate our approach to program synthesis. We use answer literals in saturation to construct programs with conditions while proving specifications (1). By adding an answer literal to the skolemized negation of (1), we obtain

$$\begin{aligned} \forall y. (\lnot F[\overline{\sigma },y] {\vee }\texttt{ans}(y)), \end{aligned}$$

where $\overline{\sigma }$ are the skolemized input variables x. When we derive a unit clause $\texttt{ans}(r[\overline{\sigma }])$ during saturation, where $r[\overline{\sigma }]$ is a computable term, we construct a program for (1) from the definite answer $r[\overline{\sigma }]$ by replacing $\overline{\sigma }$ with the input variables $\overline{x}$, obtaining the program $r[\overline{x}]$. Hence, deriving computable definite answers by saturation allows us to synthesize programs for specifications.

Fig. 2.

Axioms defining a group. Uninterpreted function symbols $i(\cdot ), e, *$ represent the inverse, the identity element, and the group operation, respectively.

Example 1

Consider the group theory axioms (A1)–(A3) of Fig. 2. We are interested in synthesizing a program for the following specification:

$$\begin{aligned} {\forall x.\exists y.\ x*y \simeq e} \end{aligned}$$

(4)

In this example we assume that all symbols are computable. To synthesize a program for (4), we add an answer literal to the skolemized negation of (4) and convert the resulting formula to CNF (preprocessing). We consider the set S of clauses containing the obtained CNF and the axioms (A1)-(A3). We saturate S using $\mathbb {S}\text {up}$ and obtain the following derivation:²

• 1. $\sigma *y\not \simeq e {\vee } \texttt{ans}(y)$                         [preprocessed specification]

• 2. $i(x)*(x*y) \simeq e*y$                                        [Sup A1, A3]

• 3. $i(x)*(x*y) \simeq y$                                              [Sup A2, 2.]

• 4. $x*y \simeq i(i(x))*y$                                              [Sup 3., 3.]

• 5. $e \simeq x*i(x)$                                                    [Sup 4., A1]

• 6. $\texttt{ans}(i(\sigma ))$                                                          [BR 5., 1.]

Using the above derivation, we construct a program for the functional specification (4) as follows: we replace $\sigma$ in the definite answer $i(\sigma )$ by x, yielding the program i(x). Note that for each input x, our synthesized program computes the inverse i(x) of x as an output. In other words, our synthesized program for (4) ensures that each group element x has a right inverse i(x).

While Example 1 yields a definite answer within saturation-based proof search, our work supports the synthesis of more complex recursion-free programs (see Examples 2–3) by composing program fragments derived in the program search (Sect. 4) as well as by using answer literals with $\texttt{if}\!-\!\texttt{then}\!-\!\texttt{else}$ to effectively handle disjunctive answers (Sect. 5).

4 Program Synthesis with Answer Literals

We now introduce our approach to saturation-based program synthesis using answer literals (Algorithm 1). We focus on recursion-free program synthesis and present our work in a more general setting. Namely, we consider functional specifications whose validity may depend on additional assumptions (e.g. additional program requirements) $A_1,\dots ,A_n$, where each $A_i$ is a closed formula:

$$\begin{aligned} A_1\wedge \ldots \wedge A_n\rightarrow \forall \overline{x}.\exists y. F[\overline{x}, y] \end{aligned}$$

(5)

Note that specification (1) is a special case of (5). However, since $A_1,\dots ,A_n$ are closed formulas, (5) is equivalent to $\forall \overline{x}.\exists y.(A_1\wedge \ldots \wedge A_n\rightarrow F[\overline{x}, y])$, which is a special case of (1).

Given a functional specification (5), we use answer literals to synthesize programs with conditions (Sect. 4.1) and extend saturation-based proof search to reason about answer literals (Sect. 4.2). For doing so, we add the answer literal $\texttt{ans}(y)$ to the skolemized negation of (5) and obtain

$$\begin{aligned} A_1\wedge \ldots \wedge A_n\wedge \forall y. (\lnot F[\overline{\sigma }, y] {\vee }\texttt{ans}(y)). \end{aligned}$$

(6)

We saturate the CNF of (6), while ensuring that answer literals are not selected within the inference rules used in saturation. We guide saturation-based proof search to derive clauses $C[\overline{\sigma }]{\vee }\texttt{ans}(r[\overline{\sigma }])$, where $C[\overline{\sigma }]$ and $r[\overline{\sigma }]$ are computable.

4.1 From Answer Literals to Programs

Our next result ensures that, if we derive the clause $C[\overline{\sigma }]{\vee }\texttt{ans}(r[\overline{\sigma }])$, the term $r[\overline{\sigma }]$ is a definite answer under the assumption $\lnot C[\overline{\sigma }]$ (Theorem 1). We note that we do not terminate saturation-based program synthesis once a clause $C[\overline{\sigma }]{\vee }\texttt{ans}(r[\overline{\sigma }])$ is derived. We rather record the program $r[\overline{x}]$ with condition $\lnot C[\overline{x}]$ (and possibly also other conditions), replace clause $C[\overline{\sigma }]{\vee }\texttt{ans}(r[\overline{\sigma }])$ by $C[\overline{\sigma }]$, and continue saturation (Corollary 2). As a result, upon establishing validity of (5), we synthesized a program for (5) (Corollary 3).

Theorem 1

[Semantics of Clauses with Answer Literals]. Let C be a clause not containing an answer literal. Assume that, using a saturation algorithm based on a sound inference system $\mathcal {I}$, the clause $C{\vee } \texttt{ans}(r[\overline{\sigma }])$ is derived from the set of clauses consisting of initial assumptions $A_1,\dots ,A_n$, the clausified formula $\texttt{cnf}(\lnot F[\overline{\sigma }, y]{\vee }\texttt{ans}(y))$ and additional assumptions $C_1,\dots ,C_m$. Then,

$$\begin{aligned} A_1,\dots ,A_n,C_1,\dots ,C_m\vdash C, F[\overline{\sigma }, r[\overline{\sigma }]]. \end{aligned}$$

That is, under the assumptions $C_1, \ldots , C_m,\lnot C$, the computable term $r[\overline{\sigma }]$ provides a definite answer to (5).

We further use Theorem 1 to synthesize programs with conditions for (5).

Corollary 2

[Programs with Conditions]. Let $r[\overline{\sigma }]$ be a computable term and $C[\overline{\sigma }]$ a ground computable clause not containing an answer literal. Assume that clause $C[\overline{\sigma }]{\vee } \texttt{ans}(r[\overline{\sigma }])$ is derived from the set of initial clauses $A_1,\dots ,A_n$, the clausified formula $\texttt{cnf}(\lnot F[\overline{\sigma }, y]{\vee }\texttt{ans}(y))$ and additional ground computable assumptions $C_1[\overline{\sigma }],\dots ,C_m[\overline{\sigma }]$, by using saturation based on a sound inference system $\mathcal {I}$. Then,

$$\langle {r[\overline{x}]}, {\bigwedge _{j=1}^{m}C_j[\overline{x}]\wedge \lnot C[\overline{x}]}\rangle $$

is a program with conditions for (5).

Note that a program with conditions $\langle {r[\overline{x}]}, {\bigwedge _{j=1}^{m}C_j[\overline{x}]\wedge \lnot C[\overline{x}]}\rangle$ corresponds to a conditional (program) branch $\texttt{if}\ \bigwedge _{j=1}^{m}C_j[\overline{x}]\wedge \lnot C[\overline{x}]\ \texttt{then}\ r[\overline{x}]$: only if the condition $\bigwedge _{j=1}^{m}C_j[\overline{x}]\wedge \lnot C[\overline{x}]$ is valid, then $r[\overline{x}]$ is computed for (5).

We use programs with conditions $\langle {r[\overline{x}]}, {\bigwedge _{j=1}^{m}C_j[\overline{x}]\wedge \lnot C[\overline{x}]}\rangle$ to finally synthesize a program for (5). To this end, we use Corollary 2 to derive programs with conditions, and once their conditions cover all possible cases given the initial assumptions $A_1,\dots ,A_n$, we compose them into a program for (5).

Corollary 3

[From Programs with Conditions to Programs for (5)]. Let $P_1[\overline{x}],\dots , P_k[\overline{x}]$, where $P_i[\overline{x}] = \langle {r_i[\overline{x}]}, {\bigwedge _{j=1}^{i-1}C_j[\overline{x}]\wedge \lnot C_i[\overline{x}]}\rangle$, be programs with conditions for (5), such that $\bigwedge _{i=1}^n A_i\wedge \bigwedge _{i=1}^k C_i[\overline{x}]$ is unsatisfiable. Then $P[\overline{x}]$, given by

$$\begin{aligned} \begin{aligned} P[\overline{x}] := \ {}&\texttt{if}\ \lnot C_1[\overline{x}]\ \texttt{then}\ r_1[\overline{x}] \\&\texttt{else}\ \texttt{if}\ \lnot C_2[\overline{x}]\ \texttt{then}\ r_2[\overline{x}] \\&\qquad \dots \\&\texttt{else}\ \texttt{if}\ \lnot C_{k-1}[\overline{x}]\ \texttt{then}\ r_{k-1}[\overline{x}] \\&\texttt{else}\ r_k[\overline{x}], \end{aligned} \end{aligned}$$

(7)

is a program for (5).

Note that since the conditional branches of (7) cover all possible cases to be considered over $\overline{x}$, we do not need the condition $\texttt{if}\ \lnot C_k$. In particular, if $k=1$, i.e. $\bigwedge _{i=1}^n A_i\wedge C_1[\overline{x}]$ is unsatisfiable, then the synthesized program for (5) is $r_1[\overline{x}]$.

4.2 Saturation-Based Program Synthesis

Our program synthesis results from Theorem 1, Corollary 2 and Corollary 3 rely upon a saturation algorithm using a sound (but not necessarily complete) inference system $\mathcal {I}$. In this section, we present our modifications to extend state-of-the-art saturation algorithms with answer literal reasoning, allowing to derive clauses $C[\overline{\sigma }]{\vee } \texttt{ans}(r[\overline{\sigma }])$, where both $C[\overline{\sigma }]$ and $r[\overline{\sigma }]$ are computable. In Sects. 5–6 we then describe modifications of the inference system $\mathcal {I}$ to implement rules over clauses with answer literals.

Our saturation algorithm is given in Algorithm 1. In a nutshell, we use Corollary 2 to construct programs from clauses $C[\overline{\sigma }]{\vee }\texttt{ans}(r[\overline{\sigma }])$ and replace clauses $C[\overline{\sigma }]{\vee }\texttt{ans}(r[\overline{\sigma }])$ by $C[\overline{\sigma }]$ (lines 7–10 of Algorithm 1). The newly added computable assumptions $C[\overline{\sigma }]$ are used to guide saturation towards deriving programs with conditions where the conditions contain $C[\overline{x}]$; these programs with conditions are used for synthesizing programs for (5), as given in Corollary 3.

Compared to a standard saturation algorithm used in first-order theorem proving (e.g. lines 4–5 of Algorithm 1), Algorithm 1 implements additional steps for processing newly derived clauses $C[\overline{\sigma }]{\vee }\texttt{ans}(r[\overline{\sigma }])$ with answer literals (lines 6–10). As a result, Algorithm 1 establishes not only the validity of the specification (5) but also synthesizes a program (lines 12–13). Throughout the algorithm, we maintain a set $\mathcal {P}$ of programs with conditions derived so far and a set $\mathcal {C}$ of additional assumptions. For each new clause $C_i$, we check if it is in the form $C[\overline{\sigma }]{\vee }\texttt{ans}(r[\overline{\sigma }])$ where $C[\overline{\sigma }]$ is ground and computable (line 7). If yes, we construct a program with conditions $\langle {r[\overline{x}]}, {\bigwedge _{C'\in \mathcal {C}}C'\wedge \lnot C[\overline{x}]}\rangle$, extend $\mathcal {C}$ with the additional assumption $C[\overline{x}]$, and replace $C_i$ by $C[\overline{\sigma }]$ (lines 8–10). Then, when we derive the empty clause, we construct the final program as follows. We first collect all clauses that participated in the derivation of $\square$. We use this clause collection to filter the programs in $\mathcal {P}$ – we only keep a program originating from a clause $C[\overline{\sigma }]{\vee }\texttt{ans}(r[\overline{\sigma }])$ if the condition $C[\overline{\sigma }]$ was used in the proof, obtaining programs $P_1,\dots ,P_k$. From $P_1,\dots ,P_k$ we then synthesize the final program P using the construction (7) from Corollary 3.

Remark 1

Compared to [22] where potentially large programs (with conditions) are tracked in answer literals, Algorithm 1 removes answer literals from clauses and constructs the final program only after saturation found a refutation of the negated (5). Our approach has two advantages: first, we do not have to keep track of potentially many large terms using $\texttt{if}\!-\!\texttt{then}\!-\!\texttt{else}$, which might slow down saturation-based program synthesis. Second, our work can naturally be integrated with clause splitting techniques within saturation (see Sect. 7).

5 Superposition with Answer Literals

We note that our saturation-based program synthesis approach is not restricted to a specific calculus. Algorithm 1 can thus be used with any sound set of inference rules, including theory-specific inference rules, e.g. [10], as long as the rules allow derivation of clauses in the form $C {\vee } \texttt{ans}(r)$, where C, r are computable and C is ground. I.e., the rules should only derive clauses with at most one answer literal, and should not introduce uncomputable symbols into answer literals.

In this section we present changes tailored to the superposition calculus $\mathbb {S}\text {up}$ , yet, without changing the underlying saturation process of Algorithm 1. We first introduce the notion of an abstract unifier [17] and define a computable unifier – a mechanism for dealing with the uncomputable symbols in the reasoning instead of introducing them into the programs. The use of such a unifier in any sound calculus is explained, with particular focus on the $\mathbb {S}\text {up}$ calculus.

Definition 1

(Abstract unifier [17]). An abstract unifier of two expressions $E_1, E_2$ is a pair $(\theta , D)$ such that:

• 1. $\theta$ is a substitution and D is a (possibly empty) disjunction of disequalities,

• 2. $(D{\vee } E_1\simeq E_2)\theta$ is valid in the underlying theory.

Intuitively speaking, an abstract unifier combines disequality constraints D with a substitution $\theta$ such that the substitution is a unifier of $E_1, E_2$ if the constraints D are not satisfied.

Definition 2

(Computable unifier). A computable unifier of two expressions $E_1, E_2$ with respect to an expression $E_3$ is an abstract unifier $(\theta , D)$ of $E_1, E_2$ such that the expression $E_3\theta$ is computable.

For example, let f be computable and g uncomputable. Then $(\{y\mapsto f(z)\}, z \not \simeq g(x))$ is a computable unifier of the terms f(g(x)), y with respect to f(y). Further, $(\{y\mapsto f(g(x))\}, \emptyset )$ is an abstract unifier of the same terms, but not a computable unifier with respect to f(y).

Ensuring Computability of Answer Literal Arguments. We modify the rules of a sound inference system $\mathcal {I}$ to use computable unifiers with respect to the answer literal argument instead of unifiers. Since a computable unifier may entail disequality constraints D, we add D to the conclusions of the inference rules. That is, for an inference rule of $\mathcal {I}$ as below

(8)

where $\theta$ is a substitution such that $E\theta \simeq E^\prime \theta$ holds for some expressions $E, E^\prime$, we extend $\mathcal {I}$ with the following n inference rules with computable unifiers:

(9)

where $(\theta ', D)$ is a computable unifier of $E, E^\prime$ with respect to r and none of $C_1,\dots ,C_n$ contains an answer literal. We obtain the following result.

Lemma 4

[Soundness of Inferences with Answer Literals]. If the rule (8) is sound, the rules (9) are sound as well.

Fig. 3.

Selected rules of the extended superposition calculus $\mathbb {S}\text {up}$ for reasoning with answer literals, with underlined literals being selected.

We note that we keep the original rule (8) in $\mathcal {I}$, but impose that none of its premises $C_1,\dots ,C_n$ contains an answer literal. Clearly, neither the such modified rule (8) nor the new rules (9) introduce uncomputable symbols into answer literals. Rather, these rules add disequality constraints D into their conclusions and immediately select D for further applications of inference rules. Such a selection guides the saturation process in Algorithm 1 to first discharge the constraints D containing uncomputable symbols with the aim of deriving a clause $C^\prime {\vee }\texttt{ans}(r^\prime )$ where $C^\prime$ is computable. The clause $C^\prime {\vee }\texttt{ans}(r^\prime )$ is then converted into a program with conditions using Corollary 2.

Superposition with Answer Literals. We make the inference rule modifications (8), together with the addition of new rules (9), for each inference rule of the $\mathbb {S}\text {up}$ calculus from Fig. 1. Further, we also ensure that rules with multiple premises, when applied on several premises containing answer literals, derive clauses with at most one answer literal. We therefore introduce the following two rule modifications. (i) We use the $\texttt{if}\!-\!\texttt{then}\!-\!\texttt{else}$ constructor to combine answer literals of premises, by adapting the use of $\texttt{if}\!-\!\texttt{then}\!-\!\texttt{else}$ within binary resolution [13, 14, 22] to superposition rules. (ii) We use an answer literal from only one of the rule premises in the rule conclusion and add new disequality constraint $r\not \simeq r'$ between the premises’ answer literal arguments, similar to the constraints D of the computable unifier. Analogously to the computable unifier constraints, we immediately select this disequality constraint $r\not \simeq r'$.

The resulting extension of the $\mathbb {S}\text {up}$ calculus with answer literals is given in Fig. 3. In addition to the rules of Fig. 3, the extended calculus contains rules constructed as (9) for superposition and binary resolution rules of Fig. 1. Using Lemma 4, we conclude the following.

Lemma 5

[Soundness of $\mathbb {S}$up with Answer Literals]. The inference rules from Fig. 3 of the extended $\mathbb {S}\text {up}$ calculus with answer literals are sound.

By the soundness results of Lemmas 4–5, Corollaries 2–3 imply that, when applying the calculus of Fig. 3 in the saturation-based program synthesis approach of Algorithm 1, we construct correct programs.

Example 2

We illustrate the use of Algorithm 1 with the extended $\mathbb {S}\text {up}$ calculus of Fig. 3, strengthening our motivation from Sect. 3 with $\texttt{if}\!-\!\texttt{then}\!-\!\texttt{else}$ reasoning. To this end, consider the functional specification over group theory:

$$\begin{aligned} {\forall x,y.\exists z.(x*y\not \simeq y*x \rightarrow z*z\not \simeq e),} \end{aligned}$$

(10)

asserting that, if the group is not commutative, there is an element whose square is not e. In addition to the axioms (A1)–(A3) of Fig. 2, we also use the right identity axiom (A2’) $\forall x.\ x*e\simeq x$.³ Based on Algorithm 1, we obtain the following derivation of the program for (10):

• 1. $\sigma _1*\sigma _2\not \simeq \sigma _2 * \sigma _1 {\vee } \texttt{ans}(z)$                         [preprocessed specification]

• 2. $e \simeq z*z {\vee } \texttt{ans}(z)$                               [preprocessed specification]

• 3. $\sigma _1*\sigma _2\not \simeq \sigma _2 * \sigma _1$       [answer literal removal 1. (Algorithm 1, line 10)]

• 4. $x*(x*y) \simeq e*y {\vee }\texttt{ans}(x)$                         [Sup 2., A3]

• 5. $e \simeq x*(y*(x*y)){\vee }\texttt{ans}(x*y)$                   [Sup A3, 2.]

• 6. $x*(x*y) \simeq y{\vee }\texttt{ans}(x)$                            [Sup 4., A2]

• 7. $x*e \simeq y*(x*y){\vee }\texttt{ans}(\texttt{if}\ e \simeq x*(y*(x*y))\ \texttt{then}\ x\ \texttt{else}\ x*y)$                               [Sup 6., 5.]

• 8. $y*(x*y) \simeq x{\vee }\texttt{ans}(\texttt{if}\ e \simeq x*(y*(x*y))\ \texttt{then}\ x\ \texttt{else}\ x*y)$                               [Sup 7., A2’]

• 9. $x*y \simeq y*x {\vee }\texttt{ans}(\texttt{if}\ x*(y*x)\simeq y\ \texttt{then}\ x\ \texttt{else}\ \texttt{if}\ e \simeq x*(y*(x*y))\ \texttt{then}\ x\ \texttt{else}\ x*y)$       [Sup 6., 8.]

• 10. $\texttt{ans}(\texttt{if}\ \sigma _1*(\sigma _2*\sigma _1)\simeq \sigma _2\ \texttt{then}\ \sigma _1\ \texttt{else}\ \texttt{if}\ e \simeq \sigma _1*(\sigma _2*(\sigma _1*\sigma _2))\ \texttt{then}\ \sigma _1\ \texttt{else}\ \sigma _1*\sigma _2)$       [BR 9., 3.]

• 11. $\square$                         [answer literal removal 11. (Algorithm 1, line 10)]

The programs with conditions collected during saturation-based program synthesis, in particular corresponding to steps 3. and 11. above, are:

$$\begin{aligned} P_1[x,y] :=&\ \langle z, x*y \simeq y*x \rangle \\ P_2[x,y] :=&\ \langle \texttt{if}\ x*(y*x)\simeq y\ \texttt{then}\ x\ \texttt{else}\ (\texttt{if}\ e \simeq x*(y*(x*y))\ \texttt{then}\ x\ \texttt{else}\ x*y), \\&\;\; x*y \not \simeq y*x \rangle \end{aligned}$$

Note the variable z, representing an arbitrary witness, in $P_1[x, y]$. An arbitrary value is a correct witness in case $x*y\simeq y*x$ holds, as in this case (10) is trivially satisfied. Thus, we do not need to consider the case $x*y\simeq y*x$ separately. Hence, we construct the final program P[x, y] only from $P_2[x,y]$ and obtain:

$$\begin{aligned} P[x,y] :=&\ \texttt{if}\ x\!*\!(y\!*\!x)\!\simeq \! x\ \texttt{then}\ x\ \texttt{else}\ (\texttt{if}\ e\!\simeq \! x\!*\!(y\!*\!(x\!*\!y))\ \texttt{then}\ x\ \texttt{else}\ x\!*\!y) \end{aligned}$$

We conclude this section by illustrating the benefits of computable unifiers.

Example 3

Consider the group theory specification

$$\begin{aligned} \forall x, y.\exists z.\ z*(i(x)*i(y)) = e, \end{aligned}$$

(11)

describing the inverse element z of $i(x)*i(y)$. We annotate the inverse $i(\cdot )$ as uncomputable to disallow the trivial solution $i(i(x)*i(y))$. Using computable unifiers, we synthesize the program $y*x$; that is, a program computing $y*x$ as the inverse of $i(x)*i(y)$.

6 Computable Unification with Abstraction

When compared to the $\mathbb {S}\text {up}$ calculus of Fig. 1, our extended $\mathbb {S}\text {up}$ calculus with answer literals from Fig. 3 uses computable unifiers instead of mgus. To find computable unifiers, we introduce Algorithm 2 by extending a standard unification algorithm [7, 18] and an algorithm for unification with abstraction of [17]. Algorithm 2 combines computable unifiers with mgu computation, resulting in the computable unifier $\theta :=\mathtt {mgu_{comp}}(E_1, E_2, E_3)$ to be further used in Fig. 3.

Algorithm 2 modifies a standard unification algorithm to ensure computability of $E_3\theta$. Changes compared to a standard unification algorithm are highlighted. Algorithm 2 does not add $s \mapsto t$ to $\theta$ if s is a variable in $E_3$ and t is uncomputable. Instead, if t is $f(t_1,\dots ,t_n)$ where f is computable but not all $t_1,\dots ,t_n$ are computable, we extend $\theta$ by $s\mapsto f(x_1,\dots ,x_n)$ and then add equations $x_1=t_1,\dots ,x_n=t_n$ to the set of equations $\mathcal {E}$ to be processed. Otherwise, f is uncomputable and we perform an abstraction: we consider s and t to be unified under the condition that $s \simeq t$ holds. Therefore we add a constraint $s \not \simeq t$ to the set of literals $\mathcal {D}$ which will be added to any clause invoking the computable unifier. To discharge the literal $s \not \simeq t$, one must prove $s \simeq t$. While s can be later substituted for other terms, as long as we use $\mathtt {mgu_{comp}}$, s will never be substituted for an uncomputable term. Thus, we conclude the following result.

Theorem 6

Let $E_1, E_2, E_3$ be expressions. Then $(\theta , D) := \mathtt {mgu_{comp}}(E_1, E_2, E_3)$ is a computable unifier.

7 Implementation and Experiments

Implementation. We implemented our saturation-based program synthesis approach in the Vampire prover [11]. We used Algorithm 1 with the extended $\mathbb {S}\text {up}$ calculus of Fig. 3. The implementation, consisting of approximately 1100 lines of C++ code, is available at https://github.com/vprover/vampire/tree/synthesis-pr. The synthesis functionality can be turned on using the option –question_answering synthesis.

Vampire accepts functional specifications in an extension of the SMT-LIB2 format [4], by using the new command assert-not to mark the specification. We consider interpreted theory symbols to be computable. Uninterpreted symbols can be annotated as uncomputable via the command (set-option :uncomputable (symbol1 ... symbolN)).

Our implementation also integrates Algorithm 1 with the AVATAR architecture [26]. We modified the AVATAR framework to only allow splitting over ground computable clauses that do not contain answer literals. Further, if we derive a clause $C[\overline{\sigma }]{\vee }\texttt{ans}(r[\overline{\sigma }])$ with AVATAR assertions $C_1[\overline{\sigma }],\dots ,C_m[\overline{\sigma }]$, where $C[\overline{\sigma }]$ is ground and computable, we replace it by the clause $C[\overline{\sigma }]{\vee }\bigvee _{i=1}^m \lnot C_i[\overline{\sigma }]{\vee }\texttt{ans}(r[\overline{\sigma }])$ without any assertions. We then immediately record a program with conditions $\langle {r[\overline{x}]}, {\lnot C[\overline{x}]\wedge \bigwedge _{i=1}^m C_i[\overline{x}]}\rangle$, and replace the clause by $C[\overline{\sigma }]{\vee }\bigvee _{i=1}^m \lnot C_i[\overline{\sigma }]$ (see lines 7–10 of Algorithm 1), which may be then further split by AVATAR.

Finally, our implementation simplifies the programs we synthesize. If during Algorithm 1 we record a program $\langle z, F\rangle$ where z is a variable, we do not use this program in the final program construction (line 12 of Algorithm 1) even if F occurs in the derivation of $\square$ (see Example 2).

Examples and Experimental Setup. The goal of our experimental evaluation is to showcase the benefits of our approach on problems that are deemed to be hard, even unsolvable, by state-of-the-art synthesis techniques. We therefore focused on first–order theory reasoning and evaluated our work on the group theory problems of Examples 1–3, as well as on integer arithmetic problems.

As the SMT-LIB2 format can easily be translated into the SyGuS 2.1 syntax [16], we compared our results to cvc5 1.0.4 [3], supporting SyGuS-based synthesis [2]. Our experiments were run on an AMD Epyc 7502, 2.5 GHz CPU with 1 TB RAM, using a 5 min time limit per example. Our benchmarks as well as the configurations for our experiments are available at: https://github.com/vprover/vampire_benchmarks/tree/master/synthesis

Experimental Results with Group Theory Properties. Vampire synthesizes the solutions of the Examples 1–3 in 0.01, 13, and 0.03 s, respectively. Since these examples use uninterpreted functions, they cannot be encoded in the SyGuS 2.1 syntax, showcasing the limits of other synthesis tools.

Experimental Results with Maximum of $n\ge 2$ Integers. For the maximum of 2 integers, the specification is $\forall x_1, x_2\in \mathbb {Z}.\ \exists y\in \mathbb {Z}.\big (y\ge x_1 \wedge y\ge x_2 \wedge (y=x_1 {\vee } y=x_2)\big )$, and the program we synthesize is $\texttt{if}\ x_1<x_2\ \texttt{then}\ x_2\ \texttt{else}\ x_1$. Both our work and cvc5 are able to synthesize programs choosing the maximal value for up to $n=23$ input variables, as summarized below. For $n> 23$, both Vampire and cvc5 time out.

Number n of variables for which max is synthesized	2	5	10	15	20	22	23
Vampire	0.03	0.03	0.05	1	13	55	215
cvc5	0.01	0.03	0.6	6.8	88	188	257

Experimental Results with Polynomial Equations. Vampire can synthesize the solution of polynomial equations; for example, for $\forall x_1, x_2 \in \mathbb {Z}.\exists y \in \mathbb {Z}. (y^2 = x_1^2 + 2x_1x_2 + x_2^2)$, we synthesize $x_1+x_2$. Vampire finds the corresponding program in 26 s using simple first-order reasoning, while cvc5 fails in our setup.

8 Related Work

Our work builds upon deductive synthesis [14] adapted for the resolution calculus [13, 22]. We extend this line of work with saturation-based program synthesis, by using adjustments of the superposition calculus.

Component-based synthesis of recursion-free programs [21] from logical specifications is addressed in [6, 21, 24]. The work of [21] uses first-order theorem proving to prove specifications and extract programs from proofs. In [6, 24], $\exists \forall$ formulas are produced to capture specifications over component properties and SMT solving is applied to find a term satisfying the formula, corresponding to a straight-line program. We complement [21] with saturation-based superposition proving and avoid template-based SMT solving from [6, 24].

A prominent line of research comes with syntax guided synthesis (SyGuS) [1], where functional specifications are given using a context-free grammar. This grammar yields program templates to be synthesized via an enumerative search procedure based on SMT solving [3, 9]. We believe our work is complementary to SyGuS, by strengthening first-order reasoning for program synthesis, as evidenced by Examples 1–3.

The sketching technique [19, 25] synthesizes program assignments to variables, using an alternative framework to the program synthesis setting we rely upon. In particular, sketching addresses domains that do not involve input logical formulas as functional specifications, such as example-guided synthesis [23].

9 Conclusions

We extend saturation-based proof search to saturation-based program synthesis, aiming to derive recursion-free programs from specifications. We integrate answer literals with saturation, and modify the superposition calculus and unification to synthesize computable programs. Our initial experiments show that a first-order theorem prover becomes an efficient program synthesizer, potentially opening up interesting avenues toward recursive program synthesis, for example using saturation-based proving with induction.