Policy Synthesis and Reinforcement Learning for Discounted LTL

Abstract

The difficulty of manually specifying reward functions has led to an interest in using linear temporal logic (LTL) to express objectives for reinforcement learning (RL). However, LTL has the downside that it is sensitive to small perturbations in the transition probabilities, which prevents probably approximately correct (PAC) learning without additional assumptions. Time discounting provides a way of removing this sensitivity, while retaining the high expressivity of the logic. We study the use of discounted LTL for policy synthesis in Markov decision processes with unknown transition probabilities, and show how to reduce discounted LTL to discounted-sum reward via a reward machine when all discount factors are identical.

This research was partially supported by ONR award N00014-20-1-2115, NSF grant CCF-2009022, and NSF CAREER award CCF-2146563.

1 Introduction

Reinforcement learning [39] (RL) is a sampling-based approach to synthesis in systems with unknown dynamics where an agent seeks to maximize its accumulated reward. This reward is typically a real-valued feedback that the agent receives on the quality of its behavior at each step. However, designing a reward function that captures the user’s intent can be tedious and error prone, and misspecified rewards can lead to undesired behavior, called reward hacking [5].

Due to the aforementioned difficulty, recent research [8, 17, 23, 31, 35] has shown interest in utilizing high-level logical specifications, particularly linear temporal logic [7] (LTL), to express intent. However, a significant challenge arises due to the sensitivity of LTL, similar to other infinite-horizon objectives like average reward and safety, to small changes in transition probabilities. Even slight modifications in transition probabilities can lead to significant impacts on the value, such as enabling previously unreachable states to become reachable. Without additional information on the transition probabilities, such as the minimum nonzero transition probability, LTL is proven to be not probably approximately correct (PAC) [29] learnable [3, 43]. Ideally, it is desirable to maintain PAC learnability while still keeping the benefits of a highly expressive temporal logic.

Discounting can serve as a solution to this problem. Typically, discounting is used to encode time-sensitive rewards (i.e., a payoff is worth more today than tomorrow), but it has a useful secondary effect that payoffs received in the distant future have small impact on the accumulated reward today. This insensitivity enables PAC learning without requiring any prior knowledge of the transition probabilities. In RL, discounted reward is commonly used and has numerous associated PAC learning algorithms [29].

Fig. 1.

Example showing non-robustness of safety specifications.

In this work, we examine the discounted LTL of [2] for policy synthesis in Markov decision processes (MDPs) with unknown transition probabilities. We refer to such MDPs as “unknown MDPs” throughout the paper. This logic maintains the syntax of LTL, but discounts the temporal operators. Discounted LTL gives a quantitative preference to traces that satisfy the objective sooner, and those that delay failure as long as possible. The authors of [2] examined discounted LTL in the model checking setting. Exploring policy synthesis and learnability for discounted LTL specifications is novel to this paper.

To illustrate how discounting affects learnability, consider the example [32] MDP shown in Fig. 1. It consists of a safe state $s_0$, two sink states $s_1,s_2$, and two actions $a_1,a_2$. Taking action $a_i$ in $s_0$ leads to a sink state with probability $p_i$ and stays in $s_0$ with probability $1-p_i$. Suppose we are interested in learning a policy to make sure that the system always stays in the state $s_0$. Now consider two scenarios—one in which $p_1 = 0$ and $p_2 = \delta$ and another in which $p_2=0$ and $p_1=\delta$ where $\delta >0$ is a small positive value. In the former case, the optimal policy is to always choose $a_1$ in $s_0$ and in the latter case, we need to choose $a_2$ in $s_0$. Furthermore, it can be shown that a near-optimal policy in one case is not near-optimal in another. However, we cannot select a finite number of samples needed to distinguish between the two cases (with high probability) without knowledge of $\delta$. In contrast, the time-discounted semantics of the safety property evaluates to $1-\lambda ^k$ where k is the number of time steps spent in the state $s_0$. Then, for sufficiently small $\delta$, any policy achieves a high value w.r.t. the discounted safety property in both scenarios. In general, small changes to the transition probabilities do not have drastic effects on the nature of near-optimal policies for discounted interpretations of LTL properties.

Table 1. Policy synthesis in MDPs for different classes of specifications.

Contributions. Table 1 summarizes results of this paper in the context of known results regarding policy synthesis for various classes of specifications. We consider three key properties of specifications, namely, (1) whether there is a finite-state optimal policy and whether there are known algorithms for (2) computing an optimal policy when the MDP is known, as well as for (3) learning a near-optimal policy when the transition probabilities are unknown (without additional assumptions). The classes of specifications include reward machines with discounted-sum rewards [24], linear temporal logic (LTL) [7], discounted LTL and a variant of discounted LTL in which all discount factors are identical, which we call uniformly discounted LTL. In this paper, we show the following.

• In general, finite-memory optimal policies may not exist for discounted LTL specifications.

• There exists a PAC learning algorithm to learn policies for discounted LTL specifications.

• There is a reward machine for any uniformly discounted LTL specification such that the discounted-sum rewards capture the semantics of the specification. From this we infer that for any given MDP finite-memory optimal policies exist and can be computed.

Related Work. Linear temporal logic (LTL) is a popular and expressive formalism to unambiguously express qualitative safety and progress requirements of Kripke structures and MDPs [7]. The standard approach to model check LTL formulas against MDPs is the automata-theoretic approach where the LTL formulas are first translated to a class of good-for-MDP automata [20], such as limit-deterministic Büchi automata [18, 36, 37, 40], and then, efficient graph-theoretic techniques (computing accepting end-component and then maximizing the probability to reach states in such components) [13, 30, 40] over the product of the automaton with the MDP can be used to compute optimal satisfaction probabilities and strategies. Since LTL formulas can be translated into (deterministic) automata in doubly exponential time, the probabilistic model checking problem is in 2EXPTIME with a matching lower bound [11].

Several variants of LTL have been proposed that provide discounted temporal modalities. De Alfaro et al. [15] proposed an extension of $\mu$-calculus with discounting and showed [14] the decidability of model-checking over finite MDPs. Mandrali [33] introduced discounting in LTL by taking a discounted sum interpretation of logic over a trace. Littman et al. [32] proposed geometric LTL as a logic to express learning objectives in RL. However, this logic has unclear semantics for nesting operators. Discounted LTL was proposed by Almagor, Boker, and Kupferman [2], which considers discounting without accumulation. The decidability of the policy synthesis problem for discounted LTL against MDPs is an open problem.

An alternative approach to discounting that ensuring PAC learnability is to introduce a fixed time horizon, along with a temporal logic for finite traces. In this setting, the logic $\text {LTL}_f$ is the most popular [10, 16]. Using $\text {LTL}_f$ with a finite horizon yields simple algorithms [41], finite automata suffice for checking properties, but at the expense of the expressivity of the logic, formulas like $\textbf{G}\textbf{F}p$ and $\textbf{F}\textbf{G}p$ both mean that p occurs at the end of the trace.

There has been a lot of recent work on reinforcement learning from temporal specifications [1, 9, 16, 19, 21, 22, 24,25,26,27,28, 31, 32, 42, 44]. Such approaches often lack strong convergence guarantees. Some methods have been developed to reduce LTL properties to discounted-sum rewards [8, 19] while preserving optimal policies; however they rely on the knowledge of certain parameters that depend on the transition probabilities of the unknown MDP. Recent work [3, 32, 43] has shown that PAC algorithms that do not depend on the transition probabilities do not exist for the class of LTL specifications. There has also been work on learning algorithms for LTL specifications that provide guarantees when additional information about the MDP (e.g., the smallest nonzero transition probability) is available [6, 12, 17].

2 Problem Definition

An alphabet $\varSigma$ is a finite set of letters. A finite word (resp. $\omega$-word) over $\varSigma$ is defined as a finite sequence (resp. $\omega$-sequence) of letters from $\varSigma$. We write $\varSigma ^*$ and $\varSigma ^\omega$ for the set of finite and $\omega$-words over $\varSigma$.

A probability distribution over a finite set S is a function $d :S {\rightarrow } [0, 1]$ such that $\sum _{s \in S} d(s) = 1$. Let $\mathcal {D}(S)$ denote the set of all discrete distributions over S.

Markov Decision Processes. A Markov Decision Process (MDP) is a tuple $\mathcal {M}= (S, A, s_0, P)$, where S is a finite set of states, $s_0$ is the initial state, A is a finite set of actions, and $P:S \times A \rightarrow \mathcal {D}(S)$ is the transition probability function. An infinite run $\psi \in (S\times A)^{\omega }$ is a sequence $\psi = s_0{a_0}s_1{a_1}\ldots$, where $s_i \in S$ and $a_i\in A$ for all $i\in \mathbb {Z}_{\ge 0}$. For any run $\psi$ and any $i\le j$, we let $\psi _{i:j}$ denote the subsequence $s_i{a_i}s_{i+1}{a_{i+1}}\ldots {a_{j-1}}s_j$. Similarly, a finite run $h\in (S\times A)^*\times S$ is a finite sequence $h = s_0{a_0}s_1{a_1}\ldots a_{t-1}s_t$. We use $\mathcal {Z}(S,A) = (S\times A)^{\omega }$ and $\mathcal {Z}_f(S,A) = (S\times A)^*\times S$ to denote the set of infinite and finite runs, respectively.

A policy $\pi :\mathcal {Z}_f(S,A)\rightarrow \mathcal {D}(A)$ maps a finite run $h\in \mathcal {Z}_f(S,A)$ to a distribution $\pi (h)$ over actions. We denote by $\varPi (S,A)$ the set of all such policies. A policy $\pi$ is deterministic if, for all finite runs $h\in \mathcal {Z}_f(S,A)$, there is an action $a\in A$ with $\pi (h)(a) = 1$.

Given a finite run $h=s_0a_0\ldots a_{t-1}s_t$, the cylinder of h, denoted by ${\texttt {Cyl}}(h)$, is the set of all infinite runs with prefix h. Given an MDP $\mathcal {M}$ and a policy $\pi \in \varPi (S,A)$, we define the probability of the cylinder set by $\mathcal {D}^{\mathcal {M}}_{\pi }({\texttt {Cyl}}(h)) = \prod _{i=0}^{t-1}\pi (h_{0:i})(a_i)P(s_i, a_i, s_{i+1})$. It is known that $\mathcal {D}_{\pi }^{\mathcal {M}}$ can be uniquely extended to a probability measure over the $\sigma$-algebra generated by all cylinder sets. Let $\mathcal {P}$ be a finite set of atomic propositions and $\varSigma =2^{\mathcal {P}}$ denote the set of all valuations of propositions in $\mathcal {P}$. An infinite word $\rho \in \varSigma ^\omega$ is a map $\rho :\mathbb {Z}_{\ge 0}\rightarrow \varSigma$.

Definition 1 (Discounted LTL)

Given a set of atomic propositions $\mathcal {P}$, discounted LTL formulas over $\mathcal {P}$ are given by the grammar

$$\varphi := b \in \mathcal {P}\mid \lnot \varphi \mid \varphi \vee \varphi \mid \textbf{X}_{\lambda }\varphi \mid \varphi ~\textbf{U}_{\lambda }\varphi $$

where $\lambda \in [0,1)$. Note that, in general, different temporal operators within the same formula may have different discount factors $\lambda$. For a formula $\varphi$ and a word $\rho =\sigma _0\sigma _1\ldots \in (2^{\mathcal {P}})^\omega$, the semantics ${\llbracket \varphi ,\rho \rrbracket }\in [0,1]$ is given by

$$\begin{aligned} {\llbracket b,\rho \rrbracket }&= \mathbbm {1}\big (b\in \sigma _0\big )\\ {\llbracket \lnot \varphi ,\rho \rrbracket }&= 1-{\llbracket \varphi ,\rho \rrbracket }\\ {\llbracket \varphi _1\vee \varphi _2,\rho \rrbracket }&= \max \big \{{\llbracket \varphi _1,\rho \rrbracket },{\llbracket \varphi _2,\rho \rrbracket }\big \}\\ {\llbracket \textbf{X}_{\lambda }\varphi ,\rho \rrbracket }&= \lambda \cdot {\llbracket \varphi ,\rho _{1:\infty } \rrbracket }\\ {\llbracket \varphi _1\textbf{U}_{\lambda }\varphi _2,\rho \rrbracket }&= \underset{i \ge 0}{\sup }\ \left\{ \min \Big \{\lambda ^i [\![\varphi _2, \rho _{i:\infty }]\!], \underset{0\le j< i}{\min }\{\lambda ^j [\![\varphi _1, \rho _{j:\infty }]\!]\}\Big \}\right\} \end{aligned}$$

where $\rho _{i:\infty }=\sigma _i\sigma _{i+1}\ldots$ denotes the infinite word starting at position i.

Conjunction is defined using $\varphi _1\wedge \varphi _2 = \lnot (\lnot \varphi _1\vee \lnot \varphi _2)$. We use $\textbf{F}_\lambda \varphi = {\texttt {true}}\textbf{U}_\lambda \varphi$ and $\textbf{G}_\lambda \varphi = \lnot \textbf{F}_\lambda \lnot \varphi$ to denote the discounted versions of finally and globally operators respectively. Note that when all discount factors equal 1, the semantics corresponds to the usual semantics of LTL.

For this paper, we consider the case of strict discounting, where $\lambda < 1$. We refer to the case where the discount factor is the same for all temporal operators as uniform discounting. Our definition differs from [2] in two ways: 1) we discount the next operator, and 2) we enforce strict, exponential discounting.

Example Discounted LTL Specifications. To develop an intuition of the semantics of discounted LTL, we now present a few example formulas and their meaning.

• $\textbf{F}_\lambda \, p$ obtains a value of $\lambda ^n$ where n is the first index where p becomes true in a trace, and 0 if p is never true. An optimal policy attempts to reach a p-state as soon as possible.

• $\textbf{G}_\lambda \, p$ obtains a value of $1-\lambda ^n$ where n is the first index that a $\lnot p$ occurs in a trace, and 1 if p always holds. An optimal policy attempts to delay reaching a $\lnot p$-state as long as possible.

• $\textbf{X}_\lambda \, p$ obtains a value of $\lambda$ if p is in the second position and 0 otherwise.

• $p \vee \textbf{X}_\lambda \, q$ obtains a value of 1 if p is in the first position of the trace, a value of $\lambda$ if the trace begins with $\lnot p$ followed by q, and a value of 0 otherwise.

• $\textbf{F}_\lambda \, p \,\wedge \, \textbf{G}_\lambda \, q$ evaluates to the minimum of $\lambda ^n$ and $(1-\lambda ^m)$, where n is the first position where p becomes true in a trace and m is the first position where q becomes false. If $n^*= { l og}_\lambda 0.5$ is the index where these two competing objectives coincide, then the optimal policy attempts to stay within q-states for the first $n^*$ steps and then attempts to reach a p-state as soon as possible.

• Consider the formula $\textbf{F}_{\lambda _1} \textbf{G}_{\lambda _2} p$. Given a trace, consider a p-block of length m starting at position n, that is, p holds at all positions from n to $n+m-1$, and does not hold at position $n-1$ (or n is the initial position). The value of such a block is $\lambda _1^n(1-\lambda _2^m)$. The value of the trace is then the maximum over values of all such p-blocks. The optimal policy attempts to have as long a p-block as possible as early as possible. The discount factor $\lambda _1$ indicates the preference for the p-block to occur sooner and the discount factor $\lambda _2$ indicates the preference for the p-block to be longer.

• $\textbf{G}_{\lambda _1} \textbf{F}_{\lambda _2} p$ obtains a value equivalent to $\lnot \textbf{F}_{\lambda _1} \textbf{G}_{\lambda _2} \lnot p$. Traces which contain more p’s at shorter intervals are preferred. The discount factor $\lambda _1$ indicates the preference for the total number of p’s to be larger and $\lambda _2$ indicates the preference for the interval between the consecutive p’s to be shorter.

Policy Synthesis Problem. Given an MDP $\mathcal {M}= (S,A,s_0,P)$, we assume that we have access to a labelling function $L:S\rightarrow \varSigma$ that maps each state to the set of propositions that hold true in that state. Given any run $\psi = s_0a_0s_1a_1\ldots$ we can define an infinite word $L(\psi ) = L(s_0)L(s_1)\ldots$ that denotes the corresponding sequence of labels. Given a policy $\pi$ for $\mathcal {M}$, we define the value of $\pi$ with respect to a discounted LTL formula $\varphi$ as

$$\begin{aligned} \mathcal {J}^{\mathcal {M}}(\pi , \varphi ) = \displaystyle \underset{\rho \sim \mathcal {D}^{\mathcal {M}}_{\pi }}{\mathbb {E}}{\llbracket \varphi , \rho \rrbracket } \end{aligned}$$

(1)

and the optimal value for $\mathcal {M}$ with respect to $\varphi$ as $\mathcal {J}^*(\mathcal {M},\varphi ) = \sup _{\pi }\mathcal {J}^{\mathcal {M}}(\pi ,\varphi )$. We say that a policy $\pi$ is optimal for $\varphi$ if $\mathcal {J}^{\mathcal {M}}(\pi ,\varphi ) = \mathcal {J}^*(\mathcal {M},\varphi )$. Let $\varPi _{\text {opt}}(\mathcal {M},\varphi )$ denote the set of optimal policies. Given an MDP $\mathcal {M}$, a labelling function L and a discounted LTL formula $\varphi$, the policy synthesis problem is to compute an optimal policy $\pi \in \varPi _{\text {opt}}(\mathcal {M},\varphi )$ when one exists.

Reinforcement Learning Problem. In reinforcement learning, the transition probabilities P are unknown. Therefore, we need to interact with the environment to learn a policy for a given specification. In this case, it is sufficient to learn an $\varepsilon$-optimal policy $\pi$ that satisfies $\mathcal {J}^{\mathcal {M}}(\pi ,\varphi ) \ge \mathcal {J}^*(\mathcal {M},\varphi )-\varepsilon$. We use $\varPi _{\text {opt}}^{\varepsilon }(\mathcal {M},\varphi )$ to denote the set of $\varepsilon$-optimal policies. Formally, a learning algorithm $\mathcal {A}$ is an iterative process which, in every iteration n, (i) takes a step in $\mathcal {M}$ from the current state, (ii) outputs a policy $\pi _n$ and (iii) optionally resets the current state to $s_0$. We are interested in probably-approximately correct (PAC) learning algorithms.

Definition 2 (PAC-MDP)

A learning algorithm $\mathcal {A}$ is said to be PAC-MDP for a class of specifications $\mathcal {C}$ if, there is a function $\eta$ such that for any $p>0$, $\varepsilon >0$, MDP $\mathcal {M}=(S,A,s_0,P)$, labelling function L, and specification $\varphi \in \mathcal {C}$, taking $N=\eta (|S|,|A|,|\varphi |,\frac{1}{p}, \frac{1}{\varepsilon })$, with probability at least $1-p$, we have

$$\Big |\Big \{n\mid \pi _n\notin \varPi _{\text {opt}}^{\varepsilon }(\mathcal {M},\varphi ) \Big \}\Big |\le N.$$

It has been shown that there does not exist PAC-MDP algorithms for LTL specifications. Therefore, we are interested in the class of discounted LTL specifications that are strictly discounted, i.e. $\lambda < 1$ for every temporal operator.

3 Properties of Discounted LTL

In this section, we discuss important properties of discounted LTL regarding the nature of optimal policies. We first show that, under uniform discounting, the amount of memory required for the optimal policy may increase with the discount factor. We then show that, in general, allowing multiple discount factors may result in optimal policies requiring infinite memory. This motivates our restriction to the uniform discounting case in Sect. 4. We end this section by introducing a PAC learning algorithm for discounted LTL.

3.1 Nature of Optimal Policies

It is known that for any (undiscounted) LTL formula $\varphi$ and any MDP $\mathcal {M}$, there exists a finite memory policy that is optimal—i.e., the policy stores only a finite amount of information about the history. Formally, given an MDP $\mathcal {M}=(S,A,s_0,P)$, a finite memory policy $\pi = (M,\delta _M,\mu ,m_0)$ consists of a finite set of memory states M, a transition function $\delta _M:M\times S\times A\rightarrow M$ and an action function $\mu :M\times S\rightarrow \mathcal {D}(A)$. Given a finite run $h = s_0a_0\ldots s_t = h's_t$, the policy’s action is sampled from $\mu (\delta _M(m_0,h'), s_t)$ where $\delta _M$ is also used to represent the transition function extended to sequences of state-action pairs. We use $\varPi _f(S,A)$ to denote the set of finite memory policies. In this paper, we will show that uniformly discounted LTL admits finite memory optimal policies, but that infinite memory may be required for the general case.

Unlike (undiscounted) LTL, discounted LTL allows a notion of satisfaction quality. In discounted LTL, traces which satisfy a reachability objective sooner are given a higher value, and are thus preferred. If an LTL formula cannot be satisfied, the corresponding discounted LTL formula will assign higher values to traces which delay failure as long as possible. These properties of discounted LTL are desirable for enabling notions of promptness, but may yield more complex strategies which try to balance the values of multiple competing subformulas.

Example 1

Consider the discounted LTL formula $\varphi = \textbf{G}_\lambda p \wedge \textbf{F}_\lambda \lnot p$. This formula contains two competing objectives that cannot both be completely satisfied. Increasing the value of $\textbf{G}_\lambda p$ by increasing the number of p’s at the beginning of the trace before the first $\lnot p$ decreases the value of $\textbf{F}_\lambda \lnot p$. Under the semantics of conjunction, the value of $\varphi$ is the minimum of the two subformulas. Specifically, the value of $\varphi$ w.r.t. a word $\rho$ is

$$\begin{aligned}{}[\![ \textbf{G}_{\lambda } p \wedge \textbf{F}_{\lambda } \lnot p,\rho ]\!]&= [\![ \lnot \textbf{F}_{\lambda } \lnot p \wedge \textbf{F}_{\lambda } \lnot p, \rho ]\!] \\&= [\![ \lnot ( \textbf{F}_{\lambda } \lnot p \vee \lnot \textbf{F}_{\lambda } \lnot p ),\rho ]\!] \\&= 1 - \max \{ [\![\textbf{F}_{\lambda } \lnot p ,\rho ]\!] , [\![ \lnot \textbf{F}_{\lambda } \lnot p ,\rho ]\!] \} \\&= 1 - \max \left\{ \sup _{i \ge 0} \{ \lambda ^i [\![ \lnot p,\rho _{i:\infty } ]\!] \} , 1 - \sup _{i \ge 0} \{ \lambda ^i [\![ \lnot p,\rho _{i:\infty } ]\!] \} \right\} . \end{aligned}$$

where $\rho _{i:\infty }$ is the trace starting from index i. Now consider a two state (deterministic) MDP with two states $S =\{s_1,s_2\}$ and two actions $A=\{a_1,a_2\}$ in which the agent can decide to either stay in $s_1$ or move to $s_2$ at any step and the system stays in $s_2$ upon reaching $s_2$. This MDP can be seen in Fig. 2. We have one proposition p which holds in state $s_1$ and not in $s_2$. Note that all runs produced by the example MDP are either of the form $s_1^\omega$ or $s_1^k s_2^\omega$. The discounted LTL value of runs of the form $s_1^\omega$ is 0. The value of runs of the form $\psi = s_1^k s_2^\omega$ is

$$ v(k) = {\llbracket \varphi ,L(\psi ) \rrbracket } = 1 - \max \{ \lambda ^k, 1 - \lambda ^k \}. $$

A finite memory policy stays in $s_1$ for k steps will yield this value. Since $\lambda ^k$ is decreasing in k and $1-\lambda ^k$ is increasing in k, the integer value of k that maximizes v(k) lies in the interval $[\gamma -1,\gamma +1]$ where $\gamma \in \mathbb {R}$ satisfies $\lambda ^\gamma = 1-\lambda ^\gamma$. Figure 2 shows this graphically. We have that $\gamma = \frac{\log (0.5)}{\log (\lambda )}$ which is increasing in $\lambda$. Hence, the amount of memory required increases with increase in $\lambda$.

Fig. 2.

An example showing that memory requirements for optimal policies may depend on the discount factor. The red line is $\lambda ^k$, the blue line is $1 - \lambda ^k$ and the solid black line is $v(k) = 1 - \max \{ \lambda ^n, 1 - \lambda ^n \}$, where k is the number of time steps one remains in $s_0$. The dashed vertical line shows the value $\gamma$ where v(k) is maximized. We have set $\lambda = 0.99$. Note that changing the value of $\lambda$ corresponds to rescaling the x-axis. (Color figure online)

The optimal strategy in the example above tries to balance the value of two competing subformula. We will now show that extending this idea to the general case of multiple discount factors requires balancing quantities that are decaying at different speeds. This balancing may require remembering an arbitrarily long history of the trace—infinite memory is required.

Theorem 1

There exists an MDP $\mathcal {M}= (S,A,s_0,P)$, a labelling function L and a discounted LTL formula $\varphi$ such that for all $\pi \in \varPi _f(S,A)$ we have $J^{\mathcal {M}}(\pi ,\varphi ) < \mathcal {J}^*(\mathcal {M},\varphi ).$

Proof

Consider the MDP $\mathcal {M}$ depicted in Fig. 3. It consists of three states $S=\{s_0,s_1,s_2\}$ and two actions $A=\{a_1,a_2\}$. The edges are labelled with actions and the corresponding transition probabilities. There are two propositions $\mathcal {P}=\{p_1,p_2\}$ and $p_1$ holds true in state $s_1$ and $p_2$ holds true in state $s_2$. The specification is given by $\varphi = \textbf{F}_{\lambda _1}\textbf{G}_{\lambda _2}p_1\wedge \textbf{F}_{\lambda _2}p_2$ where $\lambda _1< \lambda _2 < 1$.

Fig. 3.

The need for infinite memory for achieving optimality in discounted LTL.

For any run $\psi$ that never visits $s_2$, we have ${\llbracket \varphi , L(\psi ) \rrbracket } = 0$ since ${\llbracket \textbf{F}_{\lambda _2}p_2,L(\psi ) \rrbracket } = 0$. Otherwise the run has the form $\psi =s_0^{k_0} s_1^{k_1} s_2^{\omega }$ where $k_0$ is stochastic and $k_1$ is a strategic choice by the agent. To show that this requires an infinite amount of memory to play optimally, one just has to show that the optimal choice of $k_1$ increases with $k_0$. This means that the agent must remember $k_0$, the number of steps spent in the initial state, via an unbounded counter. Note that every value of $k_0$ has a non-zero probability in $\mathcal {M}$ and therefore choosing a suboptimal $k_1$ for even a single value of $k_0$ causes a decrease in value from the policy that always chooses optimal $k_1$.

The value of the run $\psi$ is ${\llbracket \varphi ,L(\psi ) \rrbracket }=\min ( \lambda _1^{k_0} (1 - \lambda _2^{k_1}) , \lambda _2^{k_0+k_1} )$. Note that $\lambda _1^{k_0} (1 - \lambda _2^{k_1})$ increases with increase in $k_1$ and $\lambda _2^{k_0+k_1}$ decreases with increase in $k_1$. Therefore taking $\gamma \in \mathbb {R}$ to be such that $\lambda _1^{k_0} (1 - \lambda _2^{\gamma }) = \lambda _2^{k_0+\gamma }$, the optimal choice of $k_1$ lies in the interval $[\gamma -1,\gamma +1]$. Now $\gamma$ satisfies $1 = \big ((\lambda _2 / \lambda _1)^{k_0} + 1\big )\lambda _2^{\gamma }$. Since $\lambda _1<\lambda _2<1$ we must have that $\gamma$ increases with increase in $k_0$. Therefore, $k_1$ also increases with increase in $k_0$.    $\square$

3.2 PAC Learning

In the above discussion, we showed that one might need infinite memory to act optimally w.r.t a discounted LTL formula. However, it can be shown that for any MDP $\mathcal {M}$, labelling function L, discounted LTL formula $\varphi$ and any $\varepsilon >0$, there is a finite-memory policy $\pi$ that is $\varepsilon$-optimal for $\varphi$. In fact, we can show that this class of discounted LTL formulas admit a PAC-MDP learning algorithm.

Theorem 2 (Existence of PAC-MDP)

There exists a PAC-MDP learning algorithm for discounted LTL specifications.

Proof (sketch)

Our approach to compute $\varepsilon$-optimal policies for discounted LTL is to compute a policy which is optimal for T steps. The policy will depend on the entire history of atomic propositions that has occured so far.

Given discounted LTL specification $\varphi$, the first step of the algorithm is to determine T. We select T such that for any two infinite words $\alpha$ and $\beta$ where the first $T+1$ indices match, i.e. $\alpha _{0:T} = \beta _{0:T}$, we have that $\big |[\![ \varphi ,\alpha ]\!] - [\![ \varphi ,\beta ]\!]\big | \le \varepsilon$. Say that the maximum discount factor appearing in all temporal operators is $\lambda _{\max {}}$. Due to the strict discounting of discounted LTL, selecting $T \ge \frac{\log \varepsilon }{\log \lambda _{\max }}$ ensures that $\big |[\![ \varphi ,\alpha ]\!] - [\![ \varphi ,\beta ]\!]\big | \le \lambda ^n \le \varepsilon$.

Now we unroll the MDP for T steps. We include the history of the atomic proposition sequence in the state. Given an MDP $\mathcal {M}= (S, A, s_0, P)$ and a labeling $L: S \rightarrow \varSigma$, the unrolled MDP $\mathcal {M}_T = (S', A', s_0', P')$ is such that

$$ S' = \bigcup _{t = 0}^T S \times \underbrace{\varSigma \times \ldots \times \varSigma }_{t\text { times}}, $$

$A' = A$, $P'((s, \sigma _0, \ldots , \sigma _{t-1}), a, (s', \sigma _0, \ldots , \sigma _{t-1}, \sigma _t)) = P(s, a, s')$ if $0 \le t \le T$ and $\sigma _t = L(s')$, and is 0 otherwise (the MDP goes to a sink state if $t>T$). The leaves of the unrolled MDP are the states where T timesteps have elapsed. In these states, there is an associated finite word of length T. For a finite word of length T, we define the value of any formula $\varphi$ to be zero beyond the end of the trace, i.e. $[\![ \varphi ,\rho _{j:\infty } ]\!] = 0$ for any $j > T$. We then compute the value of the finite words associated with the leaves which is then considered as the reward at the final step. We can use existing PAC algorithms to compute an $\varepsilon$-optimal policy w.r.t. this reward for the finite horizon MDP $\mathcal {M}_T$ from which we can obtain a $2\varepsilon$-optimal policy for $\mathcal {M}$ w.r.t the specification $\varphi$.   $\square$

4 Uniformly Discounted LTL to Reward Machines

In general, optimal strategies for discounted LTL require infinite memory (Theorem 1). However, producing such an example required the use of multiple, varied discount factors. In this section, we will show that finite memory is sufficient for optimal policies under uniform discounting, where the discount factors for all temporal operators in the formula are the same. We will also provide an algorithm for computing these strategies.

Our approach is to reduce uniformly discounted LTL formulas to reward machines, which are finite state machines in which each transition is associated with a reward. We show that the value of a given discounted LTL formula $\varphi$ for an infinite word $\rho$ is the discounted-sum reward computed by a corresponding reward machine.

Formally, a reward machine is a tuple $\mathcal {R}= (Q, \delta , r, q_0, \lambda )$ where Q is a finite set of states, $\delta : Q\times \varSigma \rightarrow Q$ is the transition function, $r:Q\times \varSigma \rightarrow \mathbb {R}$ is the reward function, $q_0\in Q$ is the initial state, and $\lambda \in [0,1)$ is the discount factor. With any infinite word $\rho =\sigma _0\sigma _1\ldots \in \varSigma ^\omega$, we can associate a sequence of rewards $c_0c_1\ldots$ where $c_t = r(q_t,\sigma _t)$ with $q_t = \delta (q_{t-1}, \sigma _{t-1})$ for $t>0$. We use $\mathcal {R}(\rho )$ to denote the discounted reward achieved by $\rho$,

$$\mathcal {R}(\rho ) = \sum _{t=0}^\infty \lambda ^tc_t,$$

and $\mathcal {R}(w)$ to denotes the partial discounted reward achieved by the finite word $w=\sigma _0\sigma _1\ldots \sigma _T\in \varSigma ^*$—i.e., $\mathcal {R}(w) = \sum _{t=0}^T\lambda ^tc_t$ where $c_t$ is the reward at time t.

Given a reward machine $\mathcal {R}$ and an MDP $\mathcal {M}$, our objective is to maximize the expected value $\mathcal {R}(\rho )$ from the reward machine reading the word $\rho$ produced by the MDP. Specifically, the value for a policy $\pi$ for $\mathcal {M}$ is

$$ \mathcal {J}^{\mathcal {M}}(\pi , \mathcal {R}) = \displaystyle \underset{\rho \sim \mathcal {D}^{\mathcal {M}}_{\pi }}{\mathbb {E}}[\mathcal {R}(\rho )] $$

where $\pi$ is optimal if $\mathcal {J}^{\mathcal {M}}(\pi , \mathcal {R}) = \sup _{\pi } \mathcal {J}^{\mathcal {M}}(\pi , \mathcal {R})$. Finding such an optimal policy is straightforward: we consider the product of the reward machine $\mathcal {R}$ with the MDP $\mathcal {M}$ to form a product MDP with a discounted reward objective. In the corresponding product MDP, we can compute optimal policies for maximizing the expected discounted-sum reward using standard techniques such as policy iteration and linear programming. If the transition function of the MDP is unknown, this product can be formed on-the-fly and any RL algorithm for discounted reward can be applied. Using the state space of the reward machine as memory, we can then obtain a finite-memory policy that is optimal for $\mathcal {R}$.

We have the following theorem showing that we can construct a reward machine $\mathcal {R}_{\varphi }$ for every uniformly discounted LTL formula $\varphi$.

Theorem 3

For any uniformly discounted LTL formula $\varphi$, in which all temporal operators use a common discount factor $\lambda$, we can construct a reward machine $\mathcal {R}_\varphi = (Q, \delta , r, q_0, \lambda )$ such that for any $\rho \in \varSigma ^\omega$, we have $\mathcal {R}_\varphi (\rho ) = {\llbracket \rho , \varphi \rrbracket }$.

We provide the reward machine construction for Theorem 3 in the next subsection. Using this theorem, one can use a reward machine $\mathcal {R}_\varphi$ that matches the value of a particular uniformly discounted LTL formula $\varphi$, and then apply the procedure outlined above for computing optimal finite-memory policies for reward machines.

Corollary 1

For any MDP $\mathcal {M}$, labelling function L and a discounted LTL formula $\varphi$ in which all temporal operators use a common discount factor $\lambda$, there exists a finite-memory optimal policy $\pi \in \varPi _{\text {opt}}(\mathcal {M},\varphi )$. Furthermore, there is an algorithm to compute such a policy.

4.1 Reward Machine Construction

For our construction, we examine the case of uniformly discounted LTL formula with positive discount factors $\lambda \in (0, 1)$. This allows us to divide by $\lambda$ in our construction. We note that the case of uniformly discounted LTL formula with $\lambda = 0$ can be evaluated after reading the initial letter of the word, and thus have trivial reward machines.

The reward machine $\mathcal {R}_\varphi$ constructed for the uniformly discounted LTL formula $\varphi$ exhibits a special structure. Specifically, all edges within any given strongly-connected component (SCC) of $\mathcal {R}_{\varphi }$ share the same reward, which is either 0 or $1-\lambda$, while all other rewards fall within the range of $[0,1-\lambda ]$. We present an inductive construction of the reward machines over the syntax of discounted LTL that maintains these invariants.

Lemma 1

For any uniformly discounted LTL formula $\varphi$ there exists a reward machine $\mathcal {R}_\varphi = (Q, \delta , r, q_0, \lambda )$ such that following hold:

$I_1$.:

For any $\rho \in \varSigma ^\omega$, we have $\mathcal {R}_\varphi (\rho ) = {\llbracket \rho , \varphi \rrbracket }$.

$I_2$.:

There is a partition of the states $Q = \bigcup _{\ell =1}^L Q_\ell$ and a type mapping $\chi :[L]\rightarrow \{0, 1-\lambda \}$ such that for any $q\in Q_\ell$ and $\sigma \in \varSigma$,

(a):

$\delta (q,\sigma )\in \bigcup _{m=\ell }^L Q_m$, and

(b):

if $\delta (q,\sigma )\in Q_\ell$ then $r(q, \sigma ) = \chi (\ell )$.

$I_3$.:

For any $q\in Q$ and $\sigma \in \varSigma$, we have $0\le r(q,\sigma )\le 1-\lambda$.

Our construction proceeds inductively. We define the reward machine for the base case of a single atomic proposition, i.e. $\varphi = p$, and then the construction for negation, the next operator, disjunction, the eventually operator (for ease of presentation), and the until operator. The ideas used in the constructions for disjunction, the eventually operator, and the until operator build off of each other, as they all involve keeping track of the maximum/minimum value over a set of subformulas. We use properties $I_1$ and $I_3$ to show correctness, and properties $I_2$ and $I_3$ to show finiteness. A summary of the construction and detailed proofs can be found in the full version of this paper [4].

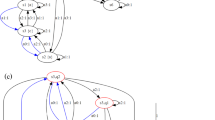
Atomic Propositions. Let ${\varphi = p}$ for some $p\in \mathcal {P}$. The reward machine $\mathcal {R}_\varphi = (Q, \delta , r, q_0, \lambda )$ for $\varphi$ is such that $Q=\{q_0, q_1, q_2\}$ and $\delta (q,\sigma ) = q$ for all $q\in \{q_1,q_2\}$ and $\sigma \in \varSigma$. The reward machine is shown in Fig. 4 where edges are labelled with propositions and rewards. If $p\in \sigma$, $\delta (q_0, \sigma ) = q_1$ and $r(q_0, \sigma ) = 1-\lambda$. If $p\notin \sigma$, $\delta (q_0, \sigma ) = q_2$ and $r(q_0, \sigma ) = 0$. Finally, $r(q_1, \sigma ) = 1-\lambda$ and $r(q_2, \sigma ) = 0$ for all $\sigma \in \varSigma$. It is clear to see that $I_1$, $I_2$, and $I_3$ hold.

Fig. 4.

Reward machines for $\varphi = p$ (left) and $\varphi = \textbf{X}_\lambda q$ (right). The transitions are labeled by the guard and reward.

Negation. Let $\varphi = \lnot \varphi _1$ for some LTL formula $\varphi _1$ and let $\mathcal {R}_{\varphi _1} = (Q, \delta , r, q_0, \lambda )$ be the reward machine for $\varphi _1$. Notice that the reward machine for $\varphi$ can be constructed from $\mathcal {R}_{\varphi _1}$ by simply replacing every reward c with $(1-\lambda ) - c$ as $\sum _{i=0}^\infty \lambda ^i(1-\lambda ) = 1$. Formally, $\mathcal {R}_{\varphi } = (Q, \delta , r', q_0, \lambda )$ where $r'(q, \sigma ) = (1-\lambda ) - r(q, \sigma )$ for all $q\in Q$ and $\sigma \in \varSigma$. Again, assuming that invariants $I_1$, $I_2$, and $I_3$ hold for $\mathcal {R}_{\varphi _1}$, it easily follows that they hold for $\mathcal {R}_{\varphi }$.

Next Operator. Let $\varphi = \textbf{X}_{\lambda }\varphi _1$ for some $\varphi _1$ and let $\mathcal {R}_{\varphi _1} = (Q, \delta , r, q_0, \lambda )$ be the reward machine for $\varphi _1$. The reward machine for $\varphi$ can be constructed from $\mathcal {R}_{\varphi _1}$ by adding a new initial state $q_0'$ and a transition in the first step from it to the initial state of $\mathcal {R}_{\varphi _1}$. From the next step $\mathcal {R}_{\varphi }$ simulates $\mathcal {R}_{\varphi _1}$. This has the resulting effect of skipping the first letter, and decreasing the value by $\lambda$. Formally, $\mathcal {R}_{\varphi } = (\{q_0'\}\sqcup Q, \delta ', r', q_0', \lambda )$ where $\delta '(q_0', \sigma ) = q_0$ and $\delta '(q, \sigma )=\delta (q,\sigma )$ for all $q\in Q$ and $\sigma \in \varSigma$. Similarly, $r'(q_0', \sigma ) = 0$ and $r'(q,\sigma ) = r(q, \sigma )$ for all $q\in Q$ and $\sigma \in \varSigma$. Assuming that invariants $I_1$, $I_2$, and $I_3$ hold for $\mathcal {R}_{\varphi _1}$, it follows that they hold for $\mathcal {R}_{\varphi }$.

Disjunction. Let $\varphi = \varphi _1\vee \varphi _2$ for some $\varphi _1,\varphi _2$ and let $\mathcal {R}_{\varphi _1} = (Q_1, \delta _1, r_1, q_0^1, \lambda )$ and $\mathcal {R}_{\varphi _2} = (Q_2, \delta _2, r_2, q_0^2, \lambda )$ be the reward machines for $\varphi _1$ and $\varphi _2$, respectively. The reward machine $\mathcal {R}_{\varphi } = (Q, \delta , r, q_0, \lambda )$ is constructed $\mathcal {R}_{\varphi _1}$ and $\mathcal {R}_{\varphi _2}$ such that for any finite word it maintains the invariant that the discounted reward is the maximum of the reward provided by $\mathcal {R}_{\varphi _1}$ and $\mathcal {R}_{\varphi _2}$. Moreover, once it is ascertained that the reward provided by one machine cannot be overtaken by the other for any suffix, $\mathcal {R}_{\varphi }$ begins simulating the reward machine with higher reward.

The construction involves a product construction along with a real-valued component that stores a scaled difference between the total accumulated reward for $\varphi _1$ and $\varphi _2$. In particular, $Q = (Q_1\times Q_2\times \mathbb {R})\sqcup Q_1\sqcup Q_2$ and $q_0=(q_0^1, q_0^2, 0)$. The reward deficit $\zeta$ of a state $q = (q_1,q_2,\zeta )$ denotes the difference between the total accumulated reward for $\varphi _1$ and $\varphi _2$ divided by $\lambda ^{n}$ where n is the total number of steps taken to reach q. The reward function is defined as follows.

• For $q = (q_1,q_2,\zeta )$, we let $f(q,\sigma ) = r_1(q_1, \sigma ) - r_2(q_2, \sigma ) + \zeta$ denote the new (scaled) difference between the discounted-sum rewards accumulated by $\mathcal {R}_{\varphi _1}$ and $\mathcal {R}_{\varphi _2}$. The current reward depends on whether $f(q,\sigma )$ is positive (accumulated reward from $\mathcal {R}_{\varphi _1}$ is higher) or negative and whether the sign is different from $\zeta$. Formally,

  $$\begin{aligned} r(q, \sigma ) = {\left\{ \begin{array}{ll} r_1(q_1,\sigma ) + \min \{0, \zeta \} &{}\text {if}\ f(q,\sigma ) \ge 0\\ r_2(q_2,\sigma ) - \max \{0, \zeta \} &{}\text {if}\ f(q,\sigma ) < 0 \end{array}\right. } \end{aligned}$$

• For a state $q_i\in Q_i$ we have $r(q_i, \sigma ) = r_i(q_i, \sigma )$.

Now we need to make sure that $\zeta$ is updated correctly. We also want the transition function to be such that the (reachable) state space is finite and the reward machine satisfies $I_1,I_2$ and $I_3$.

• First, we make sure that, when the difference $\zeta$ is too large, the machine transitions to the appropriate state in $Q_1$ or $Q_2$. For a state $q = (q_1, q_2, \zeta )$ with $|\zeta | \ge 1$, we have

  $$\begin{aligned} \delta (q, \sigma ) = {\left\{ \begin{array}{ll} \delta _1(q_1, \sigma ) &{}\text {if}\ \zeta \ge 1\\ \delta _2(q_2, \sigma ) &{}\text {if}\ \zeta \le -1. \end{array}\right. } \end{aligned}$$

• For states with $|\zeta |< 1$, we simply advance both the states and update $\zeta$ accordingly. Letting $f(q,\sigma ) = r_1(q_1, \sigma )-r_2(q_2, \sigma )+\zeta$, we have that for a state $q = (q_1, q_2, \zeta )$ with $|\zeta | < 1$,

  $$\begin{aligned} \delta (q, \sigma )&= (\delta _1(q_1, \sigma ), \delta _2(q_2,\sigma ), f(q,\sigma )/\lambda ). \end{aligned}$$

  (2)

• Finally, for $q_i\in Q_i$, $\delta (q_i,\sigma ) = \delta _i(q_i, \sigma )$.

Finiteness. We argue that the (reachable) state space of $\mathcal {R}_{\varphi }$ is finite. Let $Q_i = \bigcup _{\ell =1}^{L_i} Q_\ell ^i$ for $i\in \{1,2\}$ be the SCC decompositions of $Q_1$ and $Q_2$ that satisfy property $I_2$ for $\mathcal {R}_{\varphi _1}$ and $\mathcal {R}_{\varphi _2}$ respectively. Intuitively, if $\mathcal {R}_{\varphi }$ stays within $Q_{\ell }^1\times Q_{m}^2\times \mathbb {R}$ for some $\ell \le L_1$ and $m\le L_2$, then the rewards from $\mathcal {R}_{\varphi _1}$ and $\mathcal {R}_{\varphi _2}$ are constant; this enables us to infer the reward machine ($\mathcal {R}_{\varphi _1}$ and $\mathcal {R}_{\varphi _2}$) with the higher total accumulated reward in a finite amount of time after which we transition to $Q_1$ or $Q_2$. Hence the set of all possible values of $\zeta$ in a reachable state $(q_1,q_2,\zeta )\in Q_{\ell }^1\times Q_{m}^2\times \mathbb {R}$ is finite. This can be shown by induction.

Property $I_1$. Intuitively, it suffices to show that $\mathcal {R}_{\varphi }(w) = \max \{\mathcal {R}_{\varphi _1}(w),\mathcal {R}_{\varphi _2}(w)\}$ for every finite word $w\in \varSigma ^*$. We show this property along with the fact that for any $w\in \varSigma ^*$ of length n, if the reward machine reaches a state $(q_1,q_2,\zeta )$, then $\zeta = (\mathcal {R}_{\varphi _1}(w) - \mathcal {R}_{\varphi _2}(w))/\lambda ^{n}$. This can be proved using induction on n.

Property $I_2$. This property is true if and only if for every SCC $\mathcal {C}$ of $\mathcal {R}_{\varphi }$ there is a type $c\in \{0,1-\lambda \}$ such that if $\delta (q,\sigma ) = q'$ for some $q,q'\in \mathcal {C}$ and $\sigma \in \varSigma$, we have $r(q,\sigma ) = c$. From the definition of the transition function $\delta$, $\mathcal {C}$ cannot contain two states where one is of the form $(q_1,q_2,\zeta )\in Q_1\times Q_2\times \mathbb {R}$ and the other is $q_i\in Q_i$ for some $i\in \{1,2\}$. Now if $\mathcal {C}$ is completely contained in $Q_i$ for some i, we can conclude from the inductive hypothesis that the rewards within $\mathcal {C}$ are constant (and they are all either 0 or $1-\lambda$). When all states of $\mathcal {C}$ are contained in $Q_1\times Q_2\times \mathbb {R}$, they must be contained in $\bar{Q}_1\times \bar{Q}_2\times \mathbb {R}$ where $\bar{Q}_i$ is some SCC of $\mathcal {R}_{\varphi _i}$. In such a case, we can show that $|\mathcal {C}|=1$ and in the presence of a self loop on a state within $\mathcal {C}$, the reward must be either 0 or $1-\lambda$.

Property $I_3$. We now show that all rewards are bounded between 0 and $(1-\lambda )$. Let $q = (q_1,q_2,\zeta )$ and $f(q,\sigma ) = r_1(q_1,\sigma ) - r_2(q_2,\sigma ) + \zeta$. We show the bound for the case when $f(q,\sigma )\ge 0$ and the other case is similar. If $\zeta \ge 0$, then $r(q,\sigma ) = r_1(q_1,\sigma ) \in [0,1-\lambda ]$. If $\zeta < 0$, then $r(q,\sigma )\le r_1(q_1,\sigma )\le 1-\lambda$ and

$$ r(q,\sigma ) = r_1(q_1,\sigma ) + \zeta = f(q,\sigma ) + r_2(q_2,\sigma ) \ge 0. $$

This concludes the construction for $\varphi _1\vee \varphi _2$.

Eventually Operator. For ease of presentation, we treat the until operator as a generalization of the eventually operator $\textbf{F}_{\lambda }$ and present it first. We have that $\varphi = \textbf{F}\varphi _1$ for some $\varphi _1$. Let $\mathcal {R}_{\varphi _1} = (Q_1, \delta _1, r_1, q_0^1, \lambda )$ be the reward machine for $\varphi _1$. Let $\textbf{X}_\lambda ^i$ denote the operator $\textbf{X}_\lambda$ applied i times. We begin by noting that

$$ \textbf{F}_\lambda \varphi _1 \equiv \bigvee _{i\ge 0} \textbf{X}_\lambda ^i \varphi _1 = \varphi _1 \vee \textbf{X}_\lambda \varphi _1 \vee \textbf{X}_\lambda ^2 \varphi _1 \vee \ldots . $$

The idea of the construction is to keep track of the unrolling of this formula up to the current timestep n,

$$\begin{aligned} \textbf{F}_\lambda ^n \varphi _1&= \bigvee _{n \ge i\ge 0} \textbf{X}_\lambda ^i \varphi _1 = \varphi _1 \vee \textbf{X}_\lambda \varphi _1 \vee \textbf{X}_\lambda ^2 \varphi _1 \vee \ldots \vee \textbf{X}_\lambda ^n \varphi _1. \end{aligned}$$

For this, we will generalize the construction for disjunction. In the disjunction construction, there were states of the form $(q_1, q_2, \zeta )$ where $\zeta$ was a bookkeeping parameter that kept track of the difference between $\mathcal {R}_{\varphi _1}(w)$ and $\mathcal {R}_{\varphi _2}(w)$, namely, $\zeta = (\mathcal {R}_{\varphi _1}(w) - \mathcal {R}_{\varphi _2}(w))/\lambda ^n$ where $w \in \varSigma ^*$ is some finite word of length n. To generalize this notion to make a reward machine for $\max \{\mathcal {R}_{1}, \ldots , \mathcal {R}_{k}\}$, we will have states of the form $\{(q_1, \zeta _1), \ldots , (q_n, \zeta _n)\}$ where $\zeta _i = (\mathcal {R}_{i}(w) - \max _{j}\mathcal {R}_{j}(w))/\lambda ^n$. When $\zeta _i \le -1$ then $\mathcal {R}_{i}(w) + \lambda ^n \le \max _{j}\mathcal {R}_{j}(w)$ and we know that the associated reward machine $\mathcal {R}_{i}$ cannot be the maximum, so we drop it from our set. We also note that the value of $\textbf{X}_\lambda ^i \varphi _1$ can be determined by simply waiting i steps before starting the reward machine $\mathcal {R}_{\varphi _1}$, i.e. $\lambda ^i \mathcal {R}_{\varphi _1} (\rho _{i:\infty }) = \mathcal {R}_{\textbf{X}_\lambda ^i \varphi _1} (\rho )$. This allows us to perform a subset construction for this operator.

For a finite word $w=\sigma _0\sigma _1\ldots \sigma _n \in \varSigma ^*$ and a nonnegative integer k, let $w_{k:\infty }$ denote the subword $\sigma _k\ldots \sigma _n$ which equals the empty word $\epsilon$ if $k {>} n$. We use the notation ${\llbracket \textbf{X}_\lambda ^k \varphi _1, w \rrbracket } = \lambda ^k \mathcal {R}_{\varphi _1}(w_{k:\infty })$ and define ${\llbracket \textbf{F}_\lambda ^k \varphi _1, w \rrbracket } = \max _{k \ge i \ge 0} {\llbracket \textbf{X}_\lambda ^k \varphi _1, w \rrbracket }$ which represents the maximum value accumulated by the reward machine of some formula of the form $\textbf{X}_\lambda ^i\varphi _1$ with $i\le k$ on a finite word w. The reward machine for $\textbf{F}_\lambda \varphi _1$ will consist of states of the form (v, S), containing a value v for bookkeeping and a set S that keeps track of the states of all $\mathcal {R}_{\textbf{X}_\lambda ^i\varphi _1}$ that may still obtain the maximum given a finite prefix w of length n, i.e. reward machine states of all subformulas $\textbf{X}_\lambda ^i \varphi _1$ for $n \ge i \ge 0$ that satisfy ${\llbracket \textbf{X}_\lambda ^i \varphi _1, w \rrbracket } + \lambda ^n > {\llbracket \textbf{F}_\lambda ^n \varphi _1, w \rrbracket }$ since $\lambda ^n$ is the maximum additional reward obtainable by any $\rho \in \varSigma ^\omega$ with prefix w. The subset S consists of elements of the form $(q_i, \zeta _i) \in S$ where $q_i = \delta _1(q_0^1, w_{i:\infty })$ and $\zeta _i = ({\llbracket \textbf{X}_\lambda ^i \varphi _1, w \rrbracket } - {\llbracket \textbf{F}_\lambda ^n \varphi _1, w \rrbracket })/\lambda ^n$ corresponding to each subformula $\textbf{X}_\lambda ^i \varphi _1$. The value $v = \max \{-1, -{\llbracket \textbf{F}_\lambda ^n \varphi _1, w \rrbracket }/\lambda ^n\}$ is a bookkeeping parameter used to initialize new elements in the set S and to stop adding elements to S when $v \le -1$. We now present the construction formally.

We form a reward machine $\mathcal {R}_\varphi = (Q, \delta , r, q_0, \lambda )$ where $Q = \mathbb {R} \times 2^{Q_1 \times \mathbb {R}}$ and $q_0 = (0, \{(q_0^1, 0)\})$. We define a few functions that ease defining our transition function. Let $f(\zeta , q, \sigma ) = r_1(q, \sigma ) + \zeta$ and $m(S, \sigma ) = \max \limits _{(q_i, \zeta _i) \in S} f(\zeta _i, q_i, \sigma )$. For the subset construction, we define

$$ \varDelta (S, \sigma ) = \bigcup _{(q, \zeta ) \in S} \{(\delta _1(q, \sigma ), \zeta ') : \zeta ' = \big ((f(\zeta , q, \sigma ) - m(S,\sigma ))/\lambda \big )> -1\} $$

The transition function is

$$ \delta ((v, S), \sigma ) = {\left\{ \begin{array}{ll} \Big (v'(S,v,\sigma ),\ \varDelta (S, \sigma ) \sqcup \big (q_0^1, v'(S,v,\sigma )\big )\Big ) &{} \text {if}\ v'(S,v,\sigma ) > -1 \\ (-1,\ \varDelta (S, \sigma )) &{} \text {if}\ v'(S,v,\sigma ) \le -1 \end{array}\right. } $$

where $v'(S,v,\sigma ) = (v - m(S,\sigma ))/\lambda$. The reward function is $r((v, S), \sigma ) = m(S, \sigma )$.

We now argue that $\mathcal {R}_{\varphi }$ satisfies properties $I_1$, $I_2$ and $I_3$ and the set of reachable states in $\mathcal {R}_{\varphi }$ is finite assuming $\mathcal {R}_{\varphi _1}$ satisfies $I_1$, $I_2$ and $I_3$.

Finiteness. Consider states of the form $(v, S) \in Q$. If $v = 0$, then it must be that $\zeta _i = 0$ for all $(q_i, \zeta _i) \in S$ since receiving a non-zero reward causes the value of v to become negative. There are only finitely many such states. If $-1< v < 0$, then we will reach a state $(v', S') \in Q$ with $v' = -1$ in at most n steps, where n is such that $v/\lambda ^n \le -1$. Therefore, the number of reachable states (v, S) with $-1<v<0$ is also finite. Also, the number of states of the form $(-1,S)$ that can be initially reached (via paths consisting only of states of the form $(v,S')$ with $v>-1$) is finite. Furthermore, upon reaching such a state $(-1,S)$, the reward machine is similar to that of a disjunction (maximum) of |S| reward machines. From this we can conclude that the full reachable state space is finite.

Property $I_1$. The transition function is designed so that the following holds true: for any finite word $w \in \varSigma ^*$ of length n and letter $\sigma \in \varSigma$, if $\delta (q_0, w) = (v, S)$, then $m(S, \sigma ) = ({\llbracket \textbf{F}_\lambda ^{n+1} \varphi _1, w\sigma \rrbracket } - {\llbracket \textbf{F}_\lambda ^n \varphi _1, w \rrbracket })/\lambda ^n$. Since $r((v, S), \sigma ) = m(S, \sigma )$, we get that $\mathcal {R}_\varphi (w) = {\llbracket \textbf{F}_\lambda ^n \varphi _1, w \rrbracket }$. Thus, $\mathcal {R}_\varphi (\rho ) = {\llbracket \textbf{F}_\lambda \varphi _1, \rho \rrbracket }$ for any infinite word $\rho \in \varSigma ^\omega$. This property for $m(S, \sigma )$ follows from the preservation of all the properties outlined in the above description of the construction.

Property $I_2$. Consider an SCC $\mathcal {C}$ in $\mathcal {R}_\varphi$ such that $(v, S) = \delta ((v,S), w)$ for some $(v, S) \in \mathcal {C}$ and $w \in \varSigma ^*$ of length $n > 0$. Note that if $-1< v < 0$, then $(v', S') = \delta ((v, S), w)$ is such that $v' < v$. Thus, it must be that $v = 0$ or $v = -1$. If $v = 0$, then all the reward must be zero, since any nonzero rewards result in $v < 0$. If $v = -1$, then it must be that for any $(q_i, \zeta _i) \in S$, $q_i$ is in an SCC $\mathcal {C}_1^i$ in $\mathcal {R}_{\varphi _1}$ with some reward type $c_i \in \{0, 1-\lambda \}$. For all $\zeta _i$ to remain fixed (which is necessary as otherwise some $\zeta _i$ strictly increases or decreases), it must be that all $c_i$ are the same, say c. Thus, the reward type in $\mathcal {R}_{\varphi _1}$ for SCC $\mathcal {C}$ equals c.

Property $I_3$. We can show that for any finite word $w \in \varSigma ^*$ of length n and letter $\sigma \in \varSigma$, if $\delta (q_0, w) = (v, S)$, then the reward is $r((v, S), \sigma ) = m(S, \sigma ) = ({\llbracket \textbf{F}_\lambda ^{n+1} \varphi _1, w\sigma \rrbracket } - {\llbracket \textbf{F}_\lambda ^n \varphi _1, w \rrbracket })/\lambda ^n$ using induction on n. Since property $I_3$ holds for $\mathcal {R}_{\varphi _1}$, we have that $0 \le ({\llbracket \textbf{F}_\lambda ^{n+1} \varphi _1, w\sigma \rrbracket } - {\llbracket \textbf{F}_\lambda ^n \varphi _1, w \rrbracket }) \le (1-\lambda )\lambda ^n$.

Until Operator. We now present the until operator, generalizing the ideas presented for the eventually operator. We have that $\varphi = \varphi _1 \textbf{U}_\lambda \varphi _2$ for some $\varphi _1$ and $\varphi _2$. Let $\mathcal {R}_{\varphi _1} = (Q_1, \delta _1, r_1, q_0^1, \lambda )$ and $\mathcal {R}_{\varphi _2} = (Q_2, \delta _2, r_2, q_0^2, \lambda )$. Note that

$$\begin{aligned} \varphi _1 \textbf{U}_\lambda \varphi _2&= \bigvee _{i\ge 0} ( \textbf{X}_\lambda ^i \varphi _2 \wedge \varphi _1 \wedge \textbf{X}_\lambda \varphi _1 \wedge \ldots \wedge \textbf{X}_\lambda ^{i-1} \varphi _1) \\&= \varphi _2 \vee (\textbf{X}_\lambda \varphi _2 \wedge \varphi _1) \vee (\textbf{X}_\lambda ^2 \varphi _2 \wedge \varphi _1 \wedge \textbf{X}_\lambda \varphi _1) \vee \ldots . \end{aligned}$$

The goal of the construction is to keep track of the unrolling of this formula up to the current timestep n,

$$\begin{aligned} \varphi _1 \textbf{U}_\lambda ^n \varphi _2&= \bigvee _{n\ge i\ge 0} (\textbf{X}_\lambda ^i \varphi _2 \wedge \varphi _1 \wedge \textbf{X}_\lambda \varphi _1 \wedge \ldots \wedge \textbf{X}_\lambda ^{i-1} \varphi _1) = \bigvee _{n\ge i\ge 0} \psi _i . \end{aligned}$$

Each $\psi _i$ requires a subset construction in the style of the eventually operator construction to maintain the minimum. We then nest another subset construction in the style of the eventually operator construction to maintain the maximum over $\psi _i$. For a finite word $w \in \varSigma ^*$, we use the notation ${\llbracket \psi _i, w \rrbracket }$ and ${\llbracket \varphi _1 \textbf{U}_\lambda ^{k} \varphi _2, w \rrbracket }$ for the value accumulated by reward machine corresponding to these formula on the word w, i.e. ${\llbracket \psi _i, w \rrbracket } = \min \{{\llbracket \textbf{X}_\lambda ^i \varphi _2 \rrbracket }, \min _{i > j \ge 0} \{ {\llbracket \textbf{X}_\lambda ^j \varphi _1, w \rrbracket } \}$ and ${\llbracket \varphi _1 \textbf{U}_\lambda ^{k} \varphi _2, w \rrbracket } = \max _{k \ge i \ge 0} {\llbracket \psi _i, w \rrbracket }$.

Let $\mathcal {S} = 2^{(Q_1 \sqcup Q_2) \times \mathbb {R}}$ be the set of subsets containing $(q, \zeta )$ pairs, where q may be from either $Q_1$ or $Q_2$. The reward machine consists of states of the form $(v, I, \mathcal {X})$ where the value $v \in \mathbb {R}$ and the subset $I \in \mathcal {S}$ are for bookkeeping, and $\mathcal {X} \in 2^{\mathcal {S}}$ is a subset of subsets for each $\psi _i$. Specifically, each element of $\mathcal {X}$ is a subset S corresponding to a particular $\psi _i$ which may still obtain the maximum, i.e. ${\llbracket \psi _i, w \rrbracket } + \lambda ^n > {\llbracket \varphi _1 \textbf{U}_\lambda ^{n} \varphi _2, w \rrbracket }$. Each element of S is of the form $(q, \zeta )$. We have that $q \in Q_2$ for at most one element where $q = \delta _2(q_0^2, w_{k:\infty })$ and $\zeta = ({\llbracket \textbf{X}_\lambda ^k \varphi _2, w \rrbracket } - {\llbracket \varphi _1 \textbf{U}_\lambda ^{n} \varphi _2, w \rrbracket })/\lambda ^n$. For the other elements of S, we have that $q \in Q_1$ with $q = \delta _1(q_0^1, w_{k:\infty })$ and $\zeta = ({\llbracket \textbf{X}_\lambda ^k \varphi _1, w \rrbracket } - {\llbracket \varphi _1 \textbf{U}_\lambda ^{n} \varphi _2, w \rrbracket })/\lambda ^n$. If for any of these elements, the value of its corresponding formula becomes too large to be the minimum for the conjunction forming $\psi _i$, i.e. ${\llbracket \psi _i, w \rrbracket } + \lambda ^n \le {\llbracket \varphi _1 \textbf{U}_\lambda ^{n} \varphi _2, w \rrbracket } + \lambda ^n \le {\llbracket \textbf{X}_\lambda ^k \varphi _t, w \rrbracket }$ which occurs when $\zeta \ge 1$, that element is dropped from S. In order to update $\mathcal {X}$, we add a new S corresponding to $\psi _n$ on the next timestep. The value $v = \max \{-1, {\llbracket \varphi _1 \textbf{U}_\lambda ^{n} \varphi _2, w \rrbracket }\}$ is a bookkeeping parameter for initializing new elements in the subsets and for stopping the addition of new elements when $v \le -1$. The subset I is a bookkeeping parameter that keeps track of the subset construction for $\bigwedge _{n > i \ge 0} \textbf{X}_\lambda ^i \varphi _1$, which is used to initialize the addition of a subset corresponding to $\psi _n = \textbf{X}_\lambda ^n \varphi _2 \wedge (\bigwedge _{n > i \ge 0} \textbf{X}_\lambda ^i \varphi _1)$. We now define the reward machine formally.

We define a few functions that ease defining our transition function. We define $\delta _*(q, \sigma ) = \delta _i(q, \sigma )$ and $f_*(\zeta , q, \sigma )= r_i(q, \sigma ) + \zeta$ if $q \in Q_i$ for $i \in \{1, 2\}$. We also define $n(S, \sigma ) = \min _{(q_i, \zeta _i) \in S} f_*(\zeta _i, q_i, \sigma )$ and $m(\mathcal {X}, \sigma ) = \max _{S \in \mathcal {X}} n(S, \sigma )$. For the subset construction, we define

$$ \varDelta (S, \sigma , m) = \bigcup _{(q, \zeta ) \in S} \{(\delta _*(q, \sigma ), \zeta ') : \zeta ' < 1\} $$

where $\zeta ' = (f_*(\zeta , q, \sigma ) - m)/\lambda$ and

$$ T(\mathcal {X}, \sigma , m) = \bigcup _{ S \in \mathcal {X}}\{\varDelta (S, \sigma ,m ) : n(S, \sigma ) > -1\} . $$

We form a reward machine $\mathcal {R}_\varphi = (Q, \delta , r, q_0, \lambda )$ where $Q = \mathbb {R} \times \mathcal {S} \times 2^\mathcal {S}$ and $q_0 = (0, \emptyset , \{\{(q_0^2, 0)\}\})$. The transition function is

$$ \delta ((v, I, \mathcal {X}), \sigma ) = {\left\{ \begin{array}{ll} \Big (v',\ I',\ T(\mathcal {X}, \sigma , m) \sqcup \big (I' \sqcup (q_0^2, v')\big )\Big ) &{} \text {if}\ v' > -1 \\ (-1,\ \emptyset ,\ T(\mathcal {X}, \sigma , m)) &{} \text {if}\ v' \le -1 \end{array}\right. } $$

where $m = m(\mathcal {X},\sigma )$, $v' = (v - m)/\lambda$, and $I' = \varDelta (I \sqcup (q_0^1, v'), \sigma , m)$. The reward function is $r((v, I, \mathcal {X}), \sigma ) = m(\mathcal {X}, \sigma )$.

We now show a sketch of correctness, which mimics the proof for the eventually operator closely.

Finiteness. Consider states of the form $(v, I, \mathcal {X}) \in Q$. If $v = 0$, then for all $S \in \mathcal {X}$ and $(q_i, \zeta _i) \in S$ it must be that $\zeta _i = 0$ since receiving a non-zero reward causes the value of v to become negative. Similarly, all $\zeta _i = 0$ for $(q_i, \zeta _i) \in I$ when $v = 0$. There are only finitely many such states. If $-1< v < 0$, then we will reach a state $(v', I', \mathcal {X}') \in Q$ with $v' = -1$ in at most n steps, where n is such that $v/\lambda ^n \le -1$. Therefore, the number of reachable states $-1<v<0$ is also finite. Additionally, the number of states where $v = -1$ that can be initially reached is finite. Upon reaching such a state $(-1,\emptyset ,\mathcal {X}')$, the reward machine is similar to that of the finite disjunction of reward machines for finite conjunctions.

Property $I_1$. The transition function is designed so that the following holds true: for any finite word $w \in \varSigma ^*$ of length n and letter $\sigma \in \varSigma$, if $\delta (q_0, w) = (v, I, \mathcal {X})$, then $m(\mathcal {X}, \sigma ) = ({\llbracket \varphi _1 \textbf{U}_\lambda ^{n+1} \varphi _2, w\sigma \rrbracket } - {\llbracket \varphi _1 \textbf{U}_\lambda ^n \varphi _2, w \rrbracket })/\lambda ^n$. Since $r((v, I, \mathcal {X}), \sigma ) = m(\mathcal {X}, \sigma )$, we get that $\mathcal {R}_\varphi (w) = {\llbracket \varphi _1 \textbf{U}_\lambda ^n \varphi _2, w \rrbracket }$. Thus, $\mathcal {R}_\varphi (\rho ) = {\llbracket \varphi _1 \textbf{U}_\lambda \varphi _2, \rho \rrbracket }$ for any infinite word $\rho \in \varSigma ^\omega$. This property for $m(\mathcal {X},\sigma )$ follows from the properties outlined in the construction, which can be shown inductively.

Property $I_2$. Consider an SCC $\mathcal {C}$ of $\mathcal {R}_{\varphi }$ and a state $(v, I, \mathcal {X}) \in \mathcal {C}$. If $v = 0$, then we must receive zero reward because non-zero reward causes the value of v to become negative. It cannot be that $-1< v < 0$ since if $v < 0$, we reach a state $(v', I', \mathcal {X}') \in Q$ with $v' = -1$ in at most n steps, where n is such that $v/\lambda ^n \le -1$. If $v = -1$, then we have a state of the form $(-1, \emptyset , \mathcal {X})$. For this to be an SCC, all elements of the form $(q_k, \zeta _k) \in S$ for $S \in \mathcal {X}$ must be such that $q_k$ is in an SCC of its respective reward machine (either $\mathcal {R}_{\varphi _1}$ or $\mathcal {R}_{\varphi _2}$) with reward type $t_k \in \{0, 1-\lambda \}$. Additionally, there cannot be a $t_k' \ne t_k$ otherwise there would be a $\zeta _k$ that changes following a cycle in the SCC $\mathcal {C}$. Thus, the reward for this SCC $\mathcal {C}$ is $t_k$.

Property $I_3$. This property can be shown by recalling the property above that $r((v, I, \mathcal {X}), \sigma ) = m(\mathcal {X}, \sigma ) = ({\llbracket \varphi _1 \textbf{U}_\lambda ^{n+1} \varphi _2, w\sigma \rrbracket } - {\llbracket \varphi _1 \textbf{U}_\lambda ^n \varphi _2, w \rrbracket })/\lambda ^n$.

5 Conclusion

This paper studied policy synthesis for discounted LTL in MDPs with unknown transition probabilities. Unlike LTL, discounted LTL provides an insensitivity to small perturbations of the transitions probabilities which enables PAC learning without additional assumptions. We outlined a PAC learning algorithm for discounted LTL that uses finite memory. We showed that optimal strategies for discounted LTL require infinite memory in general due to the need to balance the values of multiple competing objectives. To avoid this infinite memory, we examined the case of uniformly discounted LTL, where the discount factors for all temporal operators are identical. We showed how to translate uniformly discounted LTL formula to finite state reward machines. This construction shows that finite memory is sufficient, and provides an avenue to use discounted reward algorithms, such as reinforcement learning, for computing optimal policies for uniformly discounted LTL formulas.