Abstract
Rely-guarantee (RG) is a highly influential compositional proof technique for concurrent programs, which was originally developed assuming a sequentially consistent shared memory. In this paper, we first generalize RG to make it parametric with respect to the underlying memory model by introducing an RG framework that is applicable to any model axiomatically characterized by Hoare triples. Second, we instantiate this framework for reasoning about concurrent programs under causally consistent memory, which is formulated using a recently proposed potential-based operational semantics, thereby providing the first reasoning technique for such semantics. The proposed program logic, which we call \({\textsf{Piccolo}}\), employs a novel assertion language allowing one to specify ordered sequences of states that each thread may reach. We employ \({\textsf{Piccolo}}\) for multiple litmus tests, as well as for an adaptation of Peterson’s algorithm for mutual exclusion to causally consistent memory.
Lahav is supported by the Israel Science Foundation (grants 1566/18 and 814/22) and by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 851811). Dongol is supported by EPSRC grants EP/X015149/1, EP/V038915/1, EP/R025134/2, VeTSS, and ARC Discovery Grant DP190102142. Wehrheim is supported by the German Research Council DFG (project no. 467386514).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others


1 Introduction
Rely-guarantee (RG) is a fundamental compositional proof technique for concurrent programs [21, 48]. Each program component P is specified using rely and guarantee conditions, which means that P can tolerate any environment interference that follows its rely condition, and generate only interference included in its guarantee condition. Two components can be composed in parallel provided that the rely of each component agrees with the guarantee of the other.
The original RG framework and its soundness proof have assumed a sequentially consistent (SC) memory [33], which is unrealistic in modern processor architectures and programming languages. Nevertheless, the main principles behind RG are not at all specific for SC. Accordingly, our first main contribution, is to formally decouple the underlying memory model from the RG proof principles, by proposing a generic RG framework parametric in the input memory model. To do so, we assume that the underlying memory model is axiomatized by Hoare triples specifying pre- and postconditions on memory states for each primitive operation (e.g., loads and stores). This enables the formal development of RG-based logics for different shared memory models as instances of one framework, where all build on a uniform soundness infrastructure of the RG rules (e.g., for sequential and parallel composition), but employ different specialized assertions to describe the possible memory states, where specific soundness arguments are only needed for primitive memory operations.
The second contribution of this paper is an instance of the general RG framework for causally consistent shared memory. The latter stands for a family of wide-spread and well-studied memory models weaker than SC, which are sufficiently strong for implementing a variety of synchronization idioms [6, 12, 26]. Intuitively, unlike SC, causal consistency allows different threads to observe writes to memory in different orders, as long as they agree on the order of writes that are causally related. This concept can be formalized in multiple ways, and here we target a strong form of causal consistency, called strong release-acquire (SRA) [28, 31] (and equivalent to “causal convergence” from [12]), which is a slight strengthening of the well-known release-acquire (RA) model (used by C/C++11). (The variants of causal consistency only differ for programs with write/write races [10, 28], which are rather rare in practice.)
Our starting point for axiomatizing SRA as Hoare triples is the potential-based operational semantics of SRA, which was recently introduced with the goal of establishing the decidability of control state reachability under this model [27, 28] (in contrast to undecidability under RA [1]). Unlike more standard presentations of weak memory models whose states record information about the past (e.g., in the form of store buffers containing executed writes before they are globally visible [36], partially ordered execution graphs [8, 20, 31], or collections of timestamped messages and thread views [11, 16, 17, 23, 25, 47]), the states of the potential-based model track possible futures ascribing what sequences of observations each thread can perform. We find this approach to be a particularly appealing candidate for Hoare-style reasoning which would naturally generalize SC-based reasoning. Intuitively, while an assertion in SC specifies possible observations at a given program point, an assertion in a potential-based model should specify possible sequences of observations.
To pursue this direction, we introduce a novel assertion language, resembling temporal logics, which allows one to express properties of sequences of states. For instance, our assertions can express that a certain thread may currently read \(\texttt{x}=0\), but it will have to read \(\texttt{x}=1\) once it reads \(\texttt{y}=1\). Then, we provide Hoare triples for SRA in this assertion language, and incorporate them in the general RG framework. The resulting program logic, which we call \({\textsf{Piccolo}}\), provides a novel approach to reason on concurrent programs under causal consistency, which allows for simple and direct proofs, and, we believe, may constitute a basis for automation in the future.
2 Motivating Example
To make our discussion concrete, consider the message passing program (MP) in Figs. 1 and 2, comprising shared variables \(\texttt{x}\) and \(\texttt{y}\) and local registers \(\texttt{a}\) and \(\texttt{b}\). The proof outline in Fig. 1 assumes SC, whereas Fig. 2 assumes SRA. In both cases, at the end of the execution, we show that if \(\texttt{a}\) is 1, then \(\texttt{b}\) must also be 1. We use these examples to explain the two main concepts introduced in this paper: (i) a generic RG framework and (ii) its instantiation with a potential-focused assertion system that enables reasoning under SRA.
Rely-Guarantee. The proof outline in Fig. 1 can be read as an RG derivation:
-
1.
Thread \(\texttt{T}_1\) locally establishes its postcondition when starting from any state that satisfies its precondition. This is trivial since its postcondition is \( True \).
-
2.
Thread \(\texttt{T}_1\) relies on the fact that its used assertions are stable w.r.t. interference from its environment. We formally capture this condition by a rely set \(\mathcal {R}_1 \triangleq \{{ True , \texttt{x} = 1}\}\).
-
3.
Thread \(\texttt{T}_1\) guarantees to its concurrent environment that its only interferences are
 and
and  , and furthermore that
, and furthermore that  is only performed when \(\texttt{x} = 1\) holds. We formally capture this condition by a guarantee set
is only performed when \(\texttt{x} = 1\) holds. We formally capture this condition by a guarantee set  , where each element is a command guarded by a precondition.
, where each element is a command guarded by a precondition. -
4.
Thread \(\texttt{T}_2\) locally establishes its postcondition when starting from any state that satisfies its precondition. This is straightforward using standard Hoare rules for assignment and sequential composition.
-
5.
Thread \(\texttt{T}_2\)’s rely set is again obtained by collecting all the assertions used in its proof: \(\mathcal {R}_2 \triangleq \{{\texttt{y} = 1 \Rightarrow \texttt{x} = 1, \texttt{a} = 1 \Rightarrow \texttt{x} = 1, \texttt{a} = 1 \Rightarrow \texttt{b} = 1}\}\). Indeed, the local reasoning for \(\texttt{T}_2\) needs all these assertions to be stable under the environment interference.
-
6.
Thread \(\texttt{T}_2\)’s guarantee set is given by:
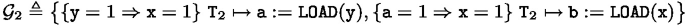
-
7.
To perform the parallel composition, \({\langle {\mathcal {R}_1, \mathcal {G}_1}\rangle }\) and \({\langle {\mathcal {R}_2, \mathcal {G}_2}\rangle }\) should be non-interfering. This involves showing that each \(R \in \mathcal {R}_i\) is stable under each \(G \in \mathcal {G}_j\) for \(i \ne j\). That is, if \(G = \{P\} \; {\tau }\mapsto c\), we require the Hoare triple \(\{P \cap R\}\;{{\tau }\mapsto c}\;\{R\}\) to hold. In this case, these proof obligations are straightforward to discharge using Hoare’s assignment axiom (and is trivial for \(i=1\) and \(j=2\) since load instructions leave the memory intact).
Remark 1
Classical treatments of RG involve two related ideas [21]: (1) specifying a component by rely and guarantee conditions (together with standard pre- and postconditions); and (2) taking the relies and guarantees to be binary relations over states. Our approach adopts (1) but not (2). Thus, it can be seen as an RG presentation of the Owicki-Gries method [37], as was previously done in [32]. We have not observed an advantage for using binary relations in our examples, but the framework can be straightforwardly modified to do so.
Now, observe that substantial aspects of the above reasoning are not directly tied with SC. This includes the Hoare rules for compound commands (such as sequential composition above), the idea of specifying a thread using collections of stable rely assertions and guaranteed guarded primitive commands, and the non-interference condition for parallel composition. To carry out this generalization, we assume that we are provided an assertion language whose assertions are interpreted as sets of memory states (which can be much more involved than simple mappings of variables to values), and a set of valid Hoare triples for the primitive instructions. The latter is used for checking validity of primitive triples, (e.g.,  ), as well as non-interference conditions (e.g.,
), as well as non-interference conditions (e.g.,  ). In Sect. 4, we present this generalization, and establish the soundness of RG principles independently of the memory model.
). In Sect. 4, we present this generalization, and establish the soundness of RG principles independently of the memory model.
Potential-Based Reasoning. The second contribution of our work is an application of the above to develop a logic for a potential-based operational semantics that captures SRA. In this semantics every memory state records sequences of store mappings (from shared variables to values) that each thread may observe. For example, assuming all variables are initialized to 0, if \(\texttt{T}_1\) executed its code until completion before \(\texttt{T}_2\) even started (so under SC the memory state is the store \(\{{\texttt{x}\mapsto 1, \texttt{y} \mapsto 1}\}\)), we may reach the SRA state in which \(\texttt{T}_1\)’s potential consists of one store \(\{{\texttt{x}\mapsto 1, \texttt{y} \mapsto 1}\}\), and \(\texttt{T}_2\)’s potential is the sequence of stores:
which captures the stores that \(\texttt{T}_2\) may observe in the order it may observe them. Naturally, potentials are lossy allowing threads to non-deterministically lose a subsequence of the current store sequence, so they can progress in their sequences. Thus, \(\texttt{T}_2\) can read 1 from \(\texttt{y}\) only after it loses the first two stores in its potential, and from this point on it can only read 1 from \(\texttt{x}\). Now, one can see that all potentials of \(\texttt{T}_2\) at its initial program point are, in fact, subsequences of the above sequence (regardless of where \(\texttt{T}_1\) is), and conclude that \(\texttt{a} = 1 \Rightarrow \texttt{b} = 1\) holds when \(\texttt{T}_2\) terminates.
To capture the above informal reasoning in a Hoare logic, we designed a new form of assertions capturing possible locally observable sequences of stores, rather than one global store, which can be seen as a restricted fragment of linear temporal logic. The proof outline using these assertions is given in Fig. 2. In particular, \([\texttt{x} = 1]\) is satisfied by all store sequences in which every store maps \(\texttt{x}\) to 1, whereas \([\texttt{y} \ne 1] \mathbin {;}[\texttt{x} = 1]\) is satisfied by all store sequences that can be split into a (possibly empty) prefix whose value for \(\texttt{y}\) is not 1 followed by a (possibly empty) suffix whose value for \(\texttt{x}\) is 1. Assertions of the form  state that the potential of thread \({\tau }\) includes only store sequences that satisfy \(I\).
state that the potential of thread \({\tau }\) includes only store sequences that satisfy \(I\).
The first assertion of \(\texttt{T}_2\) is implied by the initial condition, \({\texttt{T}_0} \!\ltimes \! [ \texttt{y} \ne 1] \), since the potential of the parent thread \(\texttt{T}_0\) is inherited by the forked child threads and \({\texttt{T}_2} \!\ltimes \! [ \texttt{y} \ne 1] \) implies \({\texttt{T}_2} \!\ltimes \! [ \texttt{y} \ne 1] \mathbin {;}I \) for any \(I\). Moreover, \({\texttt{T}_2} \!\ltimes \! [ \texttt{y} \ne 1] \mathbin {;}[\texttt{x} = 1] \) is preserved by (i) line 1 because writing 1 to \(\texttt{x}\) leaves \([\texttt{y} \ne 1]\) unchanged and re-establishes \([\texttt{x} = 1]\); and (ii) line 2 because the semantics for SRA ensures that after reading 1 from \(\texttt{y}\) by \(\texttt{T}_2\), the thread \(\texttt{T}_2\) is confined by \(\texttt{T}_1\)’s potential just before it wrote 1 to \(\texttt{y}\), which has to satisfy the precondition \({\texttt{T}_1} \!\ltimes \! [ \texttt{x}=1] \). (SRA allows to update the other threads’ potential only when the suffix of the potential after the update is observable by the writer thread.)
In Sect. 6 we formalize these arguments as Hoare rules for the primitive instructions, whose soundness is checked using the potential-based operational semantics and the interpretation of the assertion language. Finally, \({\textsf{Piccolo}}\) is obtained by incorporating these Hoare rules in the general RG framework.
Remark 2
Our presentation of the potential-based semantics for SRA (fully presented in Sect. 5) deviates from the original one in [28], where it was called  . The most crucial difference is that while
. The most crucial difference is that while  potentials consist of lists of per-location read options, our potentials consist of lists of stores assigning a value to every variable. (This is similar in spirit to the adaptation of load buffers for TSO [4, 5] to snapshot buffers in [2]). Additionally, unlike
potentials consist of lists of per-location read options, our potentials consist of lists of stores assigning a value to every variable. (This is similar in spirit to the adaptation of load buffers for TSO [4, 5] to snapshot buffers in [2]). Additionally, unlike  , we disallow empty potential lists, require that the potentials of the different threads agree on the very last value to each location, and handle read-modify-write (RMW) instructions differently. We employed these modifications to
, we disallow empty potential lists, require that the potentials of the different threads agree on the very last value to each location, and handle read-modify-write (RMW) instructions differently. We employed these modifications to  as we observed that direct reasoning on
as we observed that direct reasoning on  states is rather unnatural and counterintuitive, as
states is rather unnatural and counterintuitive, as  allows traces that block a thread from reading any value from certain locations (which cannot happen in the version we formulate). For example, a direct interpretation of our assertions over
allows traces that block a thread from reading any value from certain locations (which cannot happen in the version we formulate). For example, a direct interpretation of our assertions over  states would allow states in which \({{\tau }} \!\ltimes \! [{x}=v] \) and \({{\tau }} \!\ltimes \! [{x}\ne v] \) both hold (when \({\tau }\) does not have any option to read from \({x}\)), while these assertions are naturally contradictory when interpreted on top of our modified SRA semantics. To establish confidence in the new potential-based semantics we have proved in Coq its equivalence to the standard execution-graph based semantics of SRA (over 5K lines of Coq proofs) [29].
states would allow states in which \({{\tau }} \!\ltimes \! [{x}=v] \) and \({{\tau }} \!\ltimes \! [{x}\ne v] \) both hold (when \({\tau }\) does not have any option to read from \({x}\)), while these assertions are naturally contradictory when interpreted on top of our modified SRA semantics. To establish confidence in the new potential-based semantics we have proved in Coq its equivalence to the standard execution-graph based semantics of SRA (over 5K lines of Coq proofs) [29].
3 Preliminaries: Syntax and Semantics
In this section we describe the underlying program language, leaving the shared-memory semantics parametric.
Syntax. The syntax of programs, given in Fig. 3, is mostly standard, comprising primitive (atomic) commands \(c\) and compound commands \(C\). The non-standard components are instrumented commands \(\tilde{c}\), which are meant to atomically execute a primitive command \(c\) and a (multiple) assignment \(\mathbf {{r}}\;{:=}\;\mathbf {{e}}\). Such instructions are needed to support auxiliary (a.k.a. ghost) variables in RG proofs. In addition,  (a.k.a. atomic exchange) is an example of an RMW instruction. For brevity, other standard RMW instructions, such as
(a.k.a. atomic exchange) is an example of an RMW instruction. For brevity, other standard RMW instructions, such as  and
and  , are omitted.
, are omitted.
Unlike many weak memory models that only support top-level parallelism, we include dynamic thread creation via commands of the form  that forks two threads named \({\tau }_1\) and \({\tau }_2\) that execute the commands \(C_1\) and \(C_2\), respectively. Each \(C_i\) may itself comprise further parallel compositions. Since thread identifiers are explicit, we require commands to be well formed. Let \(\textsf{Tid}(C)\) be the set of all thread identifiers that appear in \(C\). A command \(C\) is well formed, denoted \(\textsf{wf}(C)\), if parallel compositions inside employ disjoint sets of thread identifiers. This notion is formally defined by induction on the structure of commands, with the only interesting case being
that forks two threads named \({\tau }_1\) and \({\tau }_2\) that execute the commands \(C_1\) and \(C_2\), respectively. Each \(C_i\) may itself comprise further parallel compositions. Since thread identifiers are explicit, we require commands to be well formed. Let \(\textsf{Tid}(C)\) be the set of all thread identifiers that appear in \(C\). A command \(C\) is well formed, denoted \(\textsf{wf}(C)\), if parallel compositions inside employ disjoint sets of thread identifiers. This notion is formally defined by induction on the structure of commands, with the only interesting case being  if \(\textsf{wf}(C_1) \wedge \textsf{wf}(C_2) \wedge {\tau }_1 \ne {\tau }_2 \wedge \textsf{Tid}(C_1) \cap \textsf{Tid}(C_2) =\emptyset \).
if \(\textsf{wf}(C_1) \wedge \textsf{wf}(C_2) \wedge {\tau }_1 \ne {\tau }_2 \wedge \textsf{Tid}(C_1) \cap \textsf{Tid}(C_2) =\emptyset \).
Program Semantics. We provide small-step operational semantics to commands independently of the memory system. To connect this semantics to a given memory system, its steps are instrumented with labels, as defined next.
Definition 1
A label \({l}\) takes one of the following forms: a read \({{\texttt{R}}}^{}({{x}},{v_{\texttt{R}}})\), a write \({{\texttt{W}}}^{}({{x}},{v_{\texttt{W}}})\), a read-modify-write \({{\texttt{RMW}}}^{}({{x}},{v_{\texttt{R}}},{v_{\texttt{W}}})\), a fork \({{\texttt{FORK}}}({{\tau }_1},{{\tau }_2})\), or a join \({{\texttt{JOIN}}}({{\tau }_1},{{\tau }_2})\), where \({x}\in \textsf{Loc}\), \(v_{\texttt{R}},v_{\texttt{W}}\in \textsf{Val}\), and \({\tau }_1,{\tau }_2\in \textsf{Tid}\). We denote by \(\textsf{Lab}\) the set of all labels.
Definition 2
A register store is a mapping \({\gamma }: \textsf{Reg}\rightarrow \textsf{Val}\). Register stores are extended to expressions as expected. We denote by \({\mathsf {\Gamma }}\) the set of all register stores.
The semantics of (instrumented) primitive commands is given in Fig. 4. Using this definition, the semantics of commands is given in Fig. 5. Its steps are of the form  where \(C\) and \(C'\) are commands, \({\gamma }\) and \({\gamma }'\) are register stores, and \({l}_\varepsilon \in \textsf{Lab}\cup \{{\varepsilon }\}\) (\(\varepsilon \) denotes a thread internal step). We lift this semantics to command pools as follows.
where \(C\) and \(C'\) are commands, \({\gamma }\) and \({\gamma }'\) are register stores, and \({l}_\varepsilon \in \textsf{Lab}\cup \{{\varepsilon }\}\) (\(\varepsilon \) denotes a thread internal step). We lift this semantics to command pools as follows.
Definition 3
A command pool is a non-empty partial function \(\mathcal {C}\) from thread identifiers to commands, such that the following hold:
-
1.
\(\textsf{Tid}(\mathcal {C}({\tau }_1)) \cap \textsf{Tid}(\mathcal {C}({\tau }_2)) = \emptyset \) for every \({\tau }_{1} \ne {\tau }_{2}\) in \(\textit{dom}{({\mathcal {C}})}\).
-
2.
\({\tau }\not \in \textsf{Tid}(\mathcal {C}({\tau }))\) for every \({\tau }\in \textit{dom}{({\mathcal {C}})}\).
We write command pools as sets of the form  .
.
Steps for command pools are given in Fig. 6. They take the form  , where \(\mathcal {C}\) and \(\mathcal {C}'\) are command pools, \({\gamma }\) and \({\gamma }'\) are register stores, and \({\langle {{{\tau }}:{{l}_\varepsilon }}\rangle }\) (with \({\tau }\in \textsf{Tid}\) and \({l}_\varepsilon \in \textsf{Lab}\cup \{{\varepsilon }\}\)) is a command transition label.
, where \(\mathcal {C}\) and \(\mathcal {C}'\) are command pools, \({\gamma }\) and \({\gamma }'\) are register stores, and \({\langle {{{\tau }}:{{l}_\varepsilon }}\rangle }\) (with \({\tau }\in \textsf{Tid}\) and \({l}_\varepsilon \in \textsf{Lab}\cup \{{\varepsilon }\}\)) is a command transition label.
Memory Semantics. To give semantics to programs under a memory model, we synchronize the transitions of a command \(C\) with a memory system. We leave the memory system parametric, and assume that it is represented by a labeled transition system (LTS) \(\mathcal {M}\) with set of states denoted by \(\mathcal {M}.{\texttt{Q}}\), and steps denoted by  . The transition labels of general memory system \(\mathcal {M}\) consist of non-silent program transition labels (elements of \(\textsf{Tid}\times \textsf{Lab}\)) and a (disjoint) set \(\mathcal {M}.{\mathbf {\Theta }}\) of internal memory actions, which is again left parametric (used, e.g., for memory-internal propagation of values).
. The transition labels of general memory system \(\mathcal {M}\) consist of non-silent program transition labels (elements of \(\textsf{Tid}\times \textsf{Lab}\)) and a (disjoint) set \(\mathcal {M}.{\mathbf {\Theta }}\) of internal memory actions, which is again left parametric (used, e.g., for memory-internal propagation of values).
Example 1
The simple memory system that guarantees sequential consistency is denoted here by \({\textsf{SC}}\). This memory system tracks the most recent value written to each variable and has no internal transitions (\({\textsf{SC}}.{\mathbf {\Theta }}=\emptyset \)). Formally, it is defined by \({\textsf{SC}}.{\texttt{Q}}\triangleq \textsf{Loc}\rightarrow \textsf{Val}\) and  is given by:
is given by:

The composition of a program with a general memory system is defined next.
Definition 4
The concurrent system induced by a memory system \(\mathcal {M}\), denoted by \(\overline{\mathcal {M}}\), is the LTS whose transition labels are the elements of \((\textsf{Tid}\times (\textsf{Lab}\cup \{{\varepsilon }\})) \uplus \mathcal {M}.{\mathbf {\Theta }}\); states are triples of the form  where \(\mathcal {C}\) is a command pool, \({\gamma }\) is a register store, and \({m}\in \mathcal {M}.{\texttt{Q}}\); and the transitions are “synchronized transitions” of the program and the memory system, using labels to decide what to synchronize on, formally given by:
where \(\mathcal {C}\) is a command pool, \({\gamma }\) is a register store, and \({m}\in \mathcal {M}.{\texttt{Q}}\); and the transitions are “synchronized transitions” of the program and the memory system, using labels to decide what to synchronize on, formally given by:

4 Generic Rely-Guarantee Reasoning
In this section we present our generic RG framework. Rather than committing to a specific assertion language, our reasoning principles apply on the semantic level, using sets of states instead of syntactic assertions. The structure of proofs still follows program structure, thereby retaining RG’s compositionality. By doing so, we decouple the semantic insights of RG reasoning from a concrete syntax. Next, we present proof rules serving as blueprints for memory model specific proof systems. An instantiation of this blueprint requires lifting the semantic principles to syntactic ones. More specifically, it requires
-
1.
a language with (a) concrete assertions for specifying sets of states and (b) operators that match operations on sets of states (like \(\wedge \) matches \(\cap \)); and
-
2.
sound Hoare triples for primitive commands.
Thus, each instance of the framework (for a specific memory system) is left with the task of identifying useful abstractions on states, as well as a suitable formalism, for making the generic semantic framework into a proof system.
RG Judgments. We let \(\mathcal {M}\) be an arbitrary memory system and \(\varSigma _\mathcal {M}\triangleq {\mathsf {\Gamma }}\times \mathcal {M}.{\texttt{Q}}\). Properties of programs \(\mathcal {C}\) are stated via RG judgments:
where \(P,Q\subseteq \varSigma _\mathcal {M}\), \(\mathcal {R}\subseteq \mathcal {P}({\varSigma _\mathcal {M}})\), and \(\mathcal {G}\) is a set of guarded commands, each of which takes the form \(\{{G}\} \; {\tau }\mapsto \alpha \), where \({G}\subseteq \varSigma _\mathcal {M}\) and \(\alpha \) is either an (instrumented) primitive command \(\tilde{c}\) or a fork/join label (of the form \({{\texttt{FORK}}}({{\tau }_1},{{\tau }_2})\) or \({{\texttt{JOIN}}}({{\tau }_1},{{\tau }_2})\)). The latter is needed for considering the effect of forks and joins on the memory state.
Interpretation of RG Judgments. RG judgments \(\mathcal {C}\ \underline{sat}_\mathcal {M}\ ( P,\mathcal {R},\mathcal {G}, Q)\) state that a terminating run of \(\mathcal {C}\) starting from a state in \(P\), under any concurrent context whose transitions preserve each of the sets of states in \(\mathcal {R}\), will end in a state in \(Q\) and perform only transitions contained in \(\mathcal {G}\). To formally define this statement, following the standard model for RG, these judgments are interpreted on computations of programs. Computations arise from runs of the concurrent system (see Definition 4) by abstracting away from concrete transition labels and including arbitrary “environment transitions” representing steps of the concurrent context. We have:
-
Component transitions of the form
 .
. -
Memory transitions, which correspond to internal memory steps (labeled with \({\theta }\in \mathcal {M}.{\mathbf {\Theta }}\)), of the form
 .
. -
Environment transitions of the form
 .
.
Note that memory transitions do not occur in the classical RG presentation (since \({\textsf{SC}}\) does not have internal memory actions).
A computation is a (potentially infinite) sequence

with  . We let \({\langle {\mathcal {C}_{\textsf{last}(\xi )},{\gamma }_{\textsf{last}(\xi )},{m}_{\textsf{last}(\xi )}}\rangle }\) denotes its last element, when \(\xi \) is finite. We say that \(\xi \) is a computation of a command pool \(\mathcal {C}\) when \(\mathcal {C}_0=\mathcal {C}\) and for every \(i\ge 0\):
. We let \({\langle {\mathcal {C}_{\textsf{last}(\xi )},{\gamma }_{\textsf{last}(\xi )},{m}_{\textsf{last}(\xi )}}\rangle }\) denotes its last element, when \(\xi \) is finite. We say that \(\xi \) is a computation of a command pool \(\mathcal {C}\) when \(\mathcal {C}_0=\mathcal {C}\) and for every \(i\ge 0\):
-
If \(a_i=\texttt{cmp}\), then
 for some \({\tau }\in \textsf{Tid}\) and \({l}_\varepsilon \in \textsf{Lab}\cup \{{\varepsilon }\}\).
for some \({\tau }\in \textsf{Tid}\) and \({l}_\varepsilon \in \textsf{Lab}\cup \{{\varepsilon }\}\). -
If \(a_i=\texttt{mem}\), then
 for some \({\theta }\in \mathcal {M}.{\mathbf {\Theta }}\).
for some \({\theta }\in \mathcal {M}.{\mathbf {\Theta }}\).
We denote by \( Comp (\mathcal {C})\) the set of all computations of a command pool \(\mathcal {C}\).
To define validity of RG judgments, we use the following definition.
Definition 5
Let  be a computation, and \(\mathcal {C}\ \underline{sat}_\mathcal {M}\ ( P,\mathcal {R},\mathcal {G}, Q)\) an RG-judgment.
be a computation, and \(\mathcal {C}\ \underline{sat}_\mathcal {M}\ ( P,\mathcal {R},\mathcal {G}, Q)\) an RG-judgment.
-
\(\xi \) admits \(P\) if \({\langle {{\gamma }_0,{m}_0}\rangle }\in P\).
-
\(\xi \) admits \(\mathcal {R}\) if \({\langle {{\gamma }_i,{m}_i}\rangle } \in R\Rightarrow {\langle {{\gamma }_{i+1},{m}_{i+1}}\rangle }\in R\) for every \(R\in \mathcal {R}\) and \(i\ge 0\) with \(a_{i+1}=\texttt{env}\).
-
\(\xi \) admits \(\mathcal {G}\) if for every \(i\ge 0\) with \(a_{i+1}=\texttt{cmp}\) and \({\langle {{\gamma }_i,{m}_i}\rangle } \ne {\langle {{\gamma }_{i+1},{m}_{i+1}}\rangle }\) there exists \(\{{P}\} \; {\tau }\mapsto \alpha \in \mathcal {G}\) such that \({\langle {{\gamma }_i,{m}_i}\rangle } \in {P}\) and
-
if \(\alpha =\tilde{c}\) is an instrumented primitive command, then for some \({l}_\varepsilon \in \textsf{Lab}\cup \{{\varepsilon }\}\), we have

-
if \(\alpha \in \{{{{\texttt{FORK}}}({{\tau }_1},{{\tau }_2}),{{\texttt{JOIN}}}({{\tau }_1},{{\tau }_2})}\}\), then
 .
.
-
-
\(\xi \) admits \(Q\) if \({\langle {{\gamma }_{\textsf{last}(\xi )},{m}_{\textsf{last}(\xi )}}\rangle }\in Q\) whenever \(\xi \) is finite and
 for every \({\tau }\in \textit{dom}{({\mathcal {C}_{\textsf{last}(\xi )}})}\).
for every \({\tau }\in \textit{dom}{({\mathcal {C}_{\textsf{last}(\xi )}})}\).
We denote by \(\textsf{Assume}(P,\mathcal {R})\) the set of all computations that admit \(P\) and \(\mathcal {R}\), and by \(\textsf{Commit}(\mathcal {G},Q)\) the set of all computations that admit \(\mathcal {G}\) and \(Q\).
Then, validity of a judgment if defined as
Memory Triples. Our proof rules build on memory triples, which specify pre- and postconditions for primitive commands for a memory system \(\mathcal {M}\).
Definition 6
A memory triple for a memory system \(\mathcal {M}\) is a tuple of the form \(\{P\}\;{{\tau }\mapsto \alpha }\;\{Q\}\), where \(P,Q\subseteq \varSigma _\mathcal {M}\), \({\tau }\in \textsf{Tid}\), and \(\alpha \) is either an instrumented primitive command, a fork label, or a join label. A memory triple for \(\mathcal {M}\) is valid, denoted by \(\mathcal {M}\vDash \{P\}\;{{\tau }\mapsto \alpha }\;\{Q\}\), if the following hold for every \({\langle {{\gamma },{m}}\rangle }\in P\), \({\gamma }'\in {\mathsf {\Gamma }}\) and \({m}'\in \mathcal {M}.{\texttt{Q}}\):
-
if \(\alpha \) is an instrumented primitive command and
 for some \({l}_\varepsilon \in \textsf{Lab}\cup \{{\varepsilon }\}\), then \({\langle {{\gamma }',{m}'}\rangle }\in Q\).
for some \({l}_\varepsilon \in \textsf{Lab}\cup \{{\varepsilon }\}\), then \({\langle {{\gamma }',{m}'}\rangle }\in Q\). -
If \(\alpha \in \{{{{\texttt{FORK}}}({{\tau }_1},{{\tau }_2}),{{\texttt{JOIN}}}({{\tau }_1},{{\tau }_2})}\}\) and
 , then \({\langle {{\gamma },{m}'}\rangle }\in Q\).
, then \({\langle {{\gamma },{m}'}\rangle }\in Q\).
Example 2
For the memory system \({\textsf{SC}} \) introduced in Example 1, we have, e.g., memory triples of the form  (where \({e}({r}:={x})\) is the expression \({e}\) with all occurrences of \({r}\) replaced by \({x}\)).
(where \({e}({r}:={x})\) is the expression \({e}\) with all occurrences of \({r}\) replaced by \({x}\)).
RG Proof Rules. We aim at proof rules deriving valid RG judgments. Figure 7 lists (semantic) proof rules based on externally provided memory triples. These rules basically follows RG reasoning for sequential consistency. For example, rule seq states that RG judgments of commands \(C_1\) and \(C_2\) can be combined when the postcondition of \(C_1\) and the precondition of \(C_2\) agree, thereby uniting their relies and guarantees. Rule com builds on memory triples. The rule par for parallel composition combines judgments for two components when their relies and guarantees are non-interfering. Intuitively speaking, this means that each of the assertions that each thread relied on for establishing its proof is preserved when applying any of the assignments collected in the guarantee set of the other thread. An example of non-interfering rely-guarantee pairs is given in step 7 in Sect. 2. Formally, non-interference is defined as follows:
Definition 7
Rely-guarantee pairs \({\langle {\mathcal {R}_1,\mathcal {G}_1}\rangle }\) and \({\langle {\mathcal {R}_2,\mathcal {G}_2}\rangle }\) are non-interfering if \(\mathcal {M}\vDash \{R\cap {P}\}\;{{\tau }\mapsto \alpha }\;\{R\}\) holds for every \(R\in \mathcal {R}_1\) and \(\{{P}\} \; {\tau }\mapsto \alpha \in \mathcal {G}_2\), and similarly for every \(R\in \mathcal {R}_2\) and \(\{{P}\} \; {\tau }\mapsto \alpha \in \mathcal {G}_1\).
In turn, fork-join combines the proof of a parallel composition with proofs of fork and join steps (which may also affect the memory state). Note that the guarantees also involve guarded commands with \({\texttt{FORK}}\) and \({\texttt{JOIN}}\) labels.
Additional rules for consequence and introduction of auxiliary variables are elided here (they are similar to their \({\textsf{SC}}\) counterparts), and provided in the extended version of this paper [30].
Soundness.
To establish soundness of the above system we need an additional requirement regarding the internal memory transitions (for \({\textsf{SC}}\) this closure vacuously holds as there are no such transitions). We require all relies in \(\mathcal {R}\) to be stable under internal memory transitions, i.e. for \(R\in \mathcal {R}\) we require

This condition is needed since the memory system can non-deterministically take its internal steps, and the component’s proof has to be stable under such steps.
Theorem 1 (Soundness)
\({\vdash }\,{C}{\ \underline{sat}_\mathcal {M}\ ({P},{\mathcal {R}},{\mathcal {G}},{Q})}\,{\Longrightarrow }\,{\vDash }\,{C}{\ \underline{sat}_\mathcal {M}\ ({P},{\mathcal {R}},{\mathcal {G}},{Q})}\).
With this requirement, we are able to establish soundness. The proof, which generally follows [48] is given in the extended version of this paper [30]. We write \(\vdash \mathcal {C}\ \underline{sat}_\mathcal {M}\ (P,\mathcal {R},\mathcal {G}, Q)\) for provability of a judgment using the semantic rules presented above.
5 Potential-Based Memory System for SRA
In this section we present the potential-based semantics for Strong Release-Acquire (\({\textsf{SRA}}\)), for which we develop a novel RG logic. Our semantics is based on the one in [27, 28], with certain adaptations to make it better suited for Hoare-style reasoning (see Remark 2).
In weak memory models, threads typically have different views of the shared memory. In \({\textsf{SRA}}\), we refer to a memory snapshot that a thread may observe as a potential store:
Definition 8
A potential store is a function \(\delta : \textsf{Loc}\rightarrow \textsf{Val}\times \{{{\texttt{R}},{\texttt{RMW}}}\} \times \textsf{Tid}\). We write \({\texttt{val}}(\delta ({x}))\), \({\texttt{rmw}}(\delta ({x}))\), and \({\texttt{tid}}(\delta ({x}))\) to retrieve the different components of \(\delta ({x})\). We denote by \(\mathsf {\Delta }\) the set of all potential stores.
Having \(\delta ({x})={\langle {v,{\texttt{R}},{\tau }}\rangle }\) allows to read the value \(v\) from \({x}\) (and further ascribes that this read reads from a write performed by thread \({\tau }\), which is technically needed to properly characterize the SRA model). In turn, having \(\delta ({x})={\langle {v,{\texttt{RMW}},{\tau }}\rangle }\) further allows to perform an RMW instruction that atomically reads and modifies \({x}\).
Potential stores are collected in potential store lists describing the values which can (potentially) be read and in what order.
Notation 9
Lists over an alphabet A are written as \(L = a_1 \cdot \!\ldots \!\cdot a_n\) where \(a_1 {,}\ldots {,}a_n\in A\). We also use \(\cdot \) to concatenate lists, and write L[i] for the i’th element of L and \(|{L}|\) for the length of L.
A (potential) store list is a finite sequence of potential stores ascribing a possible sequence of stores that a thread can observe, in the order it will observe them. The RMW-flags in these lists have to satisfy certain conditions: once the flag for a location is set, it remains set in the rest of the list; and the flag must be set at the end of the list. Formally, store lists are defined as follows.
Definition 10
A store list \(L\in {\mathcal {{L}}}\) is a non-empty finite sequence of potential stores with monotone RMW-flags ending with an \({\texttt{RMW}}\), that is: for all \({x}\in \textsf{Loc}\),
-
1.
if \({\texttt{rmw}}(L[i]({x}))={\texttt{RMW}}\), then \({\texttt{rmw}}(L[j]({x}))={\texttt{RMW}}\) for every \(i < j \le |{L}|\), and
-
2.
\({\texttt{rmw}}(L[|{L}|]({x}))={\texttt{RMW}}\).
Now, SRA states (\({\textsf{SRA}}.{\texttt{Q}}\)) consist of potential mappings that assign potentials to threads as defined next.
Definition 11
A potential \(D\) is a non-empty set of potential store lists. A potential mapping is a function \({\mathcal {{D}}}: \textsf{Tid}\rightharpoonup \mathcal {P}({{\mathcal {{L}}}}) \setminus \{{\emptyset }\}\) that maps thread identifiers to potentials such that all lists agree on the very final potential store (that is: \(L_1[|{L_1}|]= L_2[|{L_2}|]\) whenever \(L_1 \in {\mathcal {{D}}}({\tau }_1)\) and \(L_2 \in {\mathcal {{D}}}({\tau }_2)\)).
These potential mappings are “lossy” meaning that potential stores can be arbitrarily dropped. In particular, dropping the first store in a list enables reading from the second. This is formally done by transitioning from a state \({\mathcal {{D}}}\) to a “smaller” state \({\mathcal {{D}}}'\) as defined next.
Definition 12
The (overloaded) partial order \(\sqsubseteq \) is defined as follows:
-
1.
on potential store lists: \(L' \sqsubseteq L\) if \(L'\) is a nonempty subsequence of \(L\);
-
2.
on potentials: \(D' \sqsubseteq D\) if \(\forall L'\in D'.\; \exists L\in D.\; L' \sqsubseteq L\);
-
3.
on potential mappings: \({\mathcal {{D}}}' \sqsubseteq {\mathcal {{D}}}\) if \({\mathcal {{D}}}'({\tau })\sqsubseteq {\mathcal {{D}}}({\tau })\) for every \({\tau }\in \textit{dom}{({{\mathcal {{D}}}})}\).
Steps of \({\textsf{SRA}} \) (defining \(\delta [{x}\mapsto {\langle {v,u,{\tau }}\rangle }]({y}) = {\langle {v,u,{\tau }}\rangle }\) if \({y}= {x}\) and \(\delta ({y})\) else, and \(\delta [{x}\mapsto {\texttt{R}}]\) to set all RMW-flags for \({x}\) to \({\texttt{R}}\); both pointwise lifted to lists)
We also define \(L\preceq L'\) if \(L'\) is obtained from \(L\) by duplication of some stores (e.g., \(\delta _1 \cdot \delta _2 \cdot \delta _3 \preceq \delta _1 \cdot \delta _2 \cdot \delta _2 \cdot \delta _3\)). This is lifted to potential mappings as expected.
Figure 8 defines the transitions of \({\textsf{SRA}} \). The lose and dup steps account for losing and duplication in potentials. Note that these are both internal memory transitions (required to preserve relies as of ()). The fork and join steps distribute potentials on forked threads and join them at the end. The read step obtains its value from the first store in the lists of the potential of the reader, provided that all these lists agree on that value and the writer thread identifier. rmw steps atomically perform a read and a write step where the read is restricted to an \({\texttt{RMW}}\)-marked entry.
Most of the complexity is left for the write step. It updates to the new written value for the writer thread \({\tau }\). For every other thread, it updates a suffix ( ) of the store list with the new value. For guaranteeing causal consistency this updated suffix cannot be arbitrary: it has to be in the potential of the writer thread (
) of the store list with the new value. For guaranteeing causal consistency this updated suffix cannot be arbitrary: it has to be in the potential of the writer thread ( ). This is the key to achieving the “shared-memory causality principle” of [28], which ensures causal consistency.
). This is the key to achieving the “shared-memory causality principle” of [28], which ensures causal consistency.
Example 3
Consider again the MP program from Fig. 2. After the initial fork step, threads \(\texttt{T}_1\) and \(\texttt{T}_2\) may have the following store list in their potentials:

Then,  by \(\texttt{T}_1\) can generate the following store list for \(\texttt{T}_2\):
by \(\texttt{T}_1\) can generate the following store list for \(\texttt{T}_2\):

Thus \(\texttt{T}_2\) keeps the possibility of reading the “old” value of \(\texttt{x}\). For \(\texttt{T}_1\) this is different: the model allows the writing thread to only see its new value of \(\texttt{x}\) and all entries for \(\texttt{x}\) in the store list are updated. Thus, for \(\texttt{T}_1\) we obtain store list

Next, when \(\texttt{T}_1\) executes  , again, the value for \(\texttt{y}\) has to be updated to 1 in \(\texttt{T}_1\) yielding
, again, the value for \(\texttt{y}\) has to be updated to 1 in \(\texttt{T}_1\) yielding

For \(\texttt{T}_2\) the write step may change \(\mathtt {L_2}\) to

Thus, thread \(\texttt{T}_2\) can still see the old values, or lose the prefix of its list and see the new values. Importantly, it cannot read 1 from \(\texttt{y}\) and then 0 from \(\texttt{x}\). Note that  by \(\texttt{T}_1\) cannot modify \(\mathtt {L_2}\) to the list
by \(\texttt{T}_1\) cannot modify \(\mathtt {L_2}\) to the list

as it requires \(\texttt{T}_1\) to have \(\mathtt {L_2}\) in its own potential. This models the intended semantics of message passing under causal consistency.
The next theorem establishes the equivalence of \({\textsf{SRA}}\) as defined above and opSRA from [28], which is an (operational version of) the standard strong release-acquire declarative semantics [26, 31]. (As a corollary, we obtain the equivalence between the potential-based system from [28] and the variant we define in this paper.)
Our notion of equivalence employed in the theorem is trace equivalence. We let a trace of a memory system be a sequence of transition labels, ignoring \(\varepsilon \) transitions, and consider traces of \({\textsf{SRA}}\) starting from an initial state  and traces of opSRA starting from the initial execution graph that consists of a write event to every location writing 0 by a distinguished initialization thread \(\texttt{T}_0\).
and traces of opSRA starting from the initial execution graph that consists of a write event to every location writing 0 by a distinguished initialization thread \(\texttt{T}_0\).
Theorem 2
A trace is generated by \({\textsf{SRA}}\) iff it is generated by opSRA.
The proof is of this theorem is by simulation arguments (forward simulation in one direction and backward for the converse). It is mechanized in Coq [29]. The mechanized proof does not consider fork and join steps, but they can be straightforwardly added.
6 Program Logic
For the instantiation of our RG framework to \({\textsf{SRA}}\), we next (1) introduce the assertions of the logic \({\textsf{Piccolo}}\) and (2) specify memory triples for \({\textsf{Piccolo}}\). Our logic is inspired by interval logics like Moszkowski’s ITL [35] or duration calculus [13].
Syntax and Semantics. Figure 9 gives the grammar of \({\textsf{Piccolo}}\). We base it on extended expressions which—besides registers—can also involve locations as well as expressions of the form \({\texttt{R}}({x})\) (to indicate RMW-flag \({\texttt{R}}\)). Extended expressions \(E\) can hold on entire intervals of a store list (denoted \([E]\)). Store lists can be split into intervals satisfying different interval expressions (\(I_1 \mathbin {;}\ldots \mathbin {;}I_n\)) using the “\(\mathbin {;}\)” operator (called “chop”). In turn, \({{\tau }} \!\ltimes \! I \) means that all store lists in \({\tau }\)’s potential satisfy \(I\). For an assertion \(\varphi \), we let \( fv (\varphi ) \subseteq \textsf{Reg}\cup \textsf{Loc}\cup \textsf{Tid}\) be the set of registers, locations and thread identifiers occurring in \(\varphi \), and write \({\texttt{R}}({x}) \in \varphi \) to indicate that the term \({\texttt{R}}({x})\) occurs in \(\varphi \).
As an example consider again MP (Fig. 2). We would like to express that \(\texttt{T}_2\) upon seeing \(\texttt{y}\) to be 1 cannot see the old value 0 of \(\texttt{x}\) anymore. In \({\textsf{Piccolo}}\) this is expressed as \({\texttt{T}_2} \!\ltimes \! [\texttt{y} \ne 1] \mathbin {;}[\texttt{x} = 1] \): the store lists of \(\texttt{T}_2\) can be split into two intervals (one possibly empty), the first satisfying \(\texttt{y} \ne 1\) and the second \(\texttt{x}=1\).
Formally, an assertion \(\varphi \) describes register stores coupled with \({\textsf{SRA}}\) states:
Definition 13
Let \({\gamma }\) be a register store, \(\delta \) a potential store, \(L\) a store list, and \({\mathcal {{D}}}\) a potential mapping. We let \(\llbracket {e} \rrbracket _{{\langle {{\gamma },\delta }\rangle }} = {\gamma }({e})\), \(\llbracket {x} \rrbracket _{{\langle {{\gamma },\delta }\rangle }} = \delta ({x})\), and \(\llbracket {\texttt{R}}({x}) \rrbracket _{{\langle {{\gamma },\delta }\rangle }} = \textsf{if}\ {\texttt{rmw}}(\delta ({x})) = {\texttt{R}}\ \textsf{then} \ true \ \textsf{else}\ false \). The extension of this notation to any extended expression \(E\) is standard. The validity of assertions in \({\langle {{\gamma },{\mathcal {{D}}}}\rangle }\), denoted by \({\langle {{\gamma },{\mathcal {{D}}}}\rangle } \models \varphi \), is defined as follows:
-
1.
\({\langle {{\gamma },L}\rangle } \models {[E]}\) if \(\llbracket E \rrbracket _{{\langle {{\gamma },\delta }\rangle }} = true \) for every \(\delta \in L\).
-
2.
\({\langle {{\gamma },L}\rangle } \models {I_1 \mathbin {;}I_2}\) if \({\langle {{\gamma },L_1}\rangle } \models I_1\) and \({\langle {{\gamma },L_2}\rangle } \models I_2\) for some (possibly empty) \(L_1\) and \(L_2\) such that \(L=L_1 \cdot L_2\).
-
3.
\({\langle {{\gamma },L}\rangle } \models {I_1 \wedge I_2}\) if \({\langle {{\gamma },L}\rangle } \models I_1\) and \({\langle {{\gamma },L}\rangle } \models I_2\) (similarly for \(\vee \)).
-
4.
\({\langle {{\gamma },{\mathcal {{D}}}}\rangle } \models {{\tau }} \!\ltimes \! I \) if \({\langle {{\gamma },L}\rangle } \models I\) for every \(L\in {\mathcal {{D}}}({\tau })\).
-
5.
\({\langle {{\gamma },{\mathcal {{D}}}}\rangle } \models {e}\) if \({\gamma }({e})= true \).
-
6.
\({\langle {{\gamma }, {\mathcal {{D}}}}\rangle } \models \varphi _1 \wedge \varphi _2\) if \({\langle {{\gamma }, {\mathcal {{D}}}}\rangle } \models \varphi _1\) and \({\langle {{\gamma }, {\mathcal {{D}}}}\rangle } \models \varphi _2\) (similarly for \(\vee \)).
Note that with \(\wedge \) and \(\vee \) as well as negation on expressions,Footnote 1 the logic provides the operators on sets of states necessary for an instantiation of our RG framework. Further, the requirements from \({\textsf{SRA}}\) states guarantee certain properties:
-
For \(\varphi _1 = {{\tau }} \!\ltimes \! [E^{\tau }_1]\mathbin {;}\ldots \mathbin {;}[E^{\tau }_n] \) and \(\varphi _2 = {{\pi }} \!\ltimes \! [E^{\pi }_1]\mathbin {;}\ldots \mathbin {;}[E^{\pi }_m] \): if \(E^{\tau }_i \wedge E^{\pi }_j \Rightarrow False \) for all \(1 \le i\le n\) and \(1 \le j \le m\), then \(\varphi _1 \wedge \varphi _2 \Rightarrow False \) (follows from the fact that all lists in potentials are non-empty and agree on the last store).
-
If \({\langle {{\gamma }, {\mathcal {{D}}}}\rangle } \models {{\tau }} \!\ltimes \! [{\texttt{R}}({x})]\mathbin {;}[E] \), then every list \(L\in {\mathcal {{D}}}({\tau })\) contains a non-empty suffix satisfying \(E\) (since all lists have to end with RMW-flags set on).
All assertions are preserved by steps lose and dup. This stability is required by our RG framework (Condition ())Footnote 2. Stability is achieved here because negations occur on the level of (simple) expressions only (e.g., we cannot have \(\lnot ({{\tau }} \!\ltimes \! [{x}= v]) \), meaning that \({\tau }\) must have a store in its potential whose value for \({x}\) is not \(v\), which would not be stable under lose).
Proposition 1
If \({\langle {{\gamma }, {\mathcal {{D}}}}\rangle } \models \varphi \) and  , then \({\langle {{\gamma }, {\mathcal {{D}}}'}\rangle } \models \varphi \).
, then \({\langle {{\gamma }, {\mathcal {{D}}}'}\rangle } \models \varphi \).
Memory Triples. Assertions in \({\textsf{Piccolo}}\) describe sets of states, thus can be used to formulate memory triples. Figure 10 gives the base triples for the different primitive instructions.
We see the standard \({\textsf{SC}}\) rule of assignment (Subst-asgn) for registers followed by a number of stability rules detailing when assertions are not affected by instructions. Axioms Fork and Join describe the transfer of properties from forking thread to forked threads and back.
The next four axioms in the table concern write instructions (either  or
or  ). They reflect the semantics of writing in \({\textsf{SRA}}\): (1) In the writer thread \({\tau }\) all stores in all lists get updated (axiom Wr-own). Other threads \({\pi }\) will have (2) their lists being split into “old” values for \({x}\) with \({\texttt{R}}\) flag and the new value for \({x}\) (Wr-other-1), (3) properties (expressed as \(I_{\tau }\)) of suffixes of lists being preserved when the writing thread satisfies the same properties (Wr-other-2) and (4) their lists consisting of \({\texttt{R}}\)-accesses to \({x}\) followed by properties of the writer (Wr-other-3). The last axiom concerns
). They reflect the semantics of writing in \({\textsf{SRA}}\): (1) In the writer thread \({\tau }\) all stores in all lists get updated (axiom Wr-own). Other threads \({\pi }\) will have (2) their lists being split into “old” values for \({x}\) with \({\texttt{R}}\) flag and the new value for \({x}\) (Wr-other-1), (3) properties (expressed as \(I_{\tau }\)) of suffixes of lists being preserved when the writing thread satisfies the same properties (Wr-other-2) and (4) their lists consisting of \({\texttt{R}}\)-accesses to \({x}\) followed by properties of the writer (Wr-other-3). The last axiom concerns  only: as it can only read from store entries marked as \({\texttt{RMW}}\) it discards intervals satisfying \([{\texttt{R}}({x})]\).
only: as it can only read from store entries marked as \({\texttt{RMW}}\) it discards intervals satisfying \([{\texttt{R}}({x})]\).
Example 4
We employ the axioms for showing one proof step for MP, namely one pair in the non-interference check of the rely \(\mathcal {R}_2\) of \(\texttt{T}_2\) with respect to the guarantees \(\mathcal {G}_1\) of \(\texttt{T}_1\):

By taking \(I_{\tau }\) to be \([\texttt{x}=1]\), this is an instance of Wr-other-2.
In addition to the axioms above, we use a shift rule for load instructions:

A load instruction reads from the first store in the lists, however, if the list satisfying \([ ({e}\wedge E)({r}:={x})]\) in \([ ({e}\wedge E)({r}:={x})] \mathbin {;}I\) is empty, it reads from a list satisfying \(I\). The shift rule for  puts this shifting to next stores into a proof rule. Like the standard Hoare rule Subst-asgn, Ld-shift employs backward substitution.
puts this shifting to next stores into a proof rule. Like the standard Hoare rule Subst-asgn, Ld-shift employs backward substitution.
Example 5
We exemplify rule Ld-shift on another proof step of example MP, one for local correctness of \(\texttt{T}_2\):  From axiom Stable-ld we get
From axiom Stable-ld we get  . We obtain
. We obtain  using the former as premise forLd-shift.
using the former as premise forLd-shift.
In addition, we include the standard conjunction, disjunction and consequence rules of Hoare logic. For instrumented primitive commands we employ the following rule:

Finally, it can be shown that all triples derivable from axioms and rules are valid memory triples.
Lemma 1
If a \({\textsf{Piccolo}}\) memory triple is derivable,  , then \({\textsf{SRA}} \vDash \{\{{{\langle {{\gamma },{\mathcal {{D}}}}\rangle } \; | \;{\langle {{\gamma },{\mathcal {{D}}}}\rangle } \models \varphi }\}\}\;{{\tau }\mapsto \alpha }\;\{\{{{\langle {{\gamma },{\mathcal {{D}}}}\rangle } \; | \;{\langle {{\gamma },{\mathcal {{D}}}}\rangle } \models \psi }\}\}\).
, then \({\textsf{SRA}} \vDash \{\{{{\langle {{\gamma },{\mathcal {{D}}}}\rangle } \; | \;{\langle {{\gamma },{\mathcal {{D}}}}\rangle } \models \varphi }\}\}\;{{\tau }\mapsto \alpha }\;\{\{{{\langle {{\gamma },{\mathcal {{D}}}}\rangle } \; | \;{\langle {{\gamma },{\mathcal {{D}}}}\rangle } \models \psi }\}\}\).
7 Examples
We discuss examples verified in \({\textsf{Piccolo}}\). Additional examples can be found in the extended version of this paper [30].
Coherence. We provide two coherence examples in Figs. 11 and 12, using the notation \(I^{x}_{v_1 v_2 \dots v_n} = [x=v_1] \mathbin {;}[{x}=v_2] \mathbin {;}\ldots \mathbin {;}[{x}=v_n]\). Figure 11 enforces an ordering on writes to the shared location \(\texttt{x}\) on thread \(\texttt{T}_1\). The postcondition guarantees that after reading the second write, thread \(\texttt{T}_2\) cannot read from the first. Figure 12 is similar, but the writes to \(\texttt{x}\) occur on two different threads. The postcondition of the program guarantees that the two different threads agree on the order of the writes. In particular if one reading thread (here \(\texttt{T}_3\)) sees the value 2 then 1, it is impossible for the other reading thread (here \(\texttt{T}_4\)) to see 1 then 2.
Potential assertions provide a compact and intuitive mechanism for reasoning, e.g., in Fig. 11, the precondition of line 3 precisely expresses the order of values available to thread \(\texttt{T}_2\). This presents an improvement over view-based assertions [16], which required a separate set of assertions to encode write order.
Peterson’s Algorithm. Figure 13 shows Peterson’s algorithm for implementing mutual exclusion for two threads [38] together with \({\textsf{Piccolo}}\) assertions. We depict only the code of thread \(\texttt{T}_1\). Thread \(\texttt{T}_2\) is symmetric. A third thread \(\texttt{T}_3\) is assumed stopping the other two threads at an arbitrary point in time. We use \(\texttt {do } C\texttt { until } {e}\) as a shorthand for  . For correctness under \({\textsf{SRA}}\), all accesses to the shared variable \(\texttt{turn}\) are via a
. For correctness under \({\textsf{SRA}}\), all accesses to the shared variable \(\texttt{turn}\) are via a  , which ensures that \(\texttt{turn}\) behaves like an \({\textsf{SC}} \) variable.
, which ensures that \(\texttt{turn}\) behaves like an \({\textsf{SC}} \) variable.
Correctness is encoded via registers \(\mathtt {mx_1}\) and \( \mathtt {mx_2}\) into which the contents of shared variable \(\texttt{cs}\) is loaded. Mutual exclusion should guarantee both registers to be 0. Thus neither threads should ever be able to read \(\texttt{cs}\) to be \(\bot \) (as stored in line 7). The proof (like the associated \({\textsf{SC}} \) proof in [9]) introduces auxiliary variables \(\mathtt {a_1}\) and \(\mathtt {a_2}\). Variable \(\texttt{a}_i\) is initially \( false \), set to \( true \) when a thread \(\texttt{T}_i\) has performed its swap, and back to \( false \) when \(\texttt{T}_i\) completes.
Once again potentials provide convenient mechanisms for reasoning about the interactions between the two threads. For example, the assertion \({\texttt{T}_1} \!\ltimes \! [ {\texttt{R}}(\texttt{turn}) ]\mathbin {;}[\texttt{flag}_2] \) in the precondition of line 2 encapsulates the idea that an RMW on \(\texttt{turn}\) (via  ) must read from a state in which \(\texttt{flag}_2\) holds, allowing us to establish \({\texttt{T}_1} \!\ltimes \! [ \texttt{flag}_2 ] \) as a postcondition (using the axiom Swap-skip). We obtain disjunct
) must read from a state in which \(\texttt{flag}_2\) holds, allowing us to establish \({\texttt{T}_1} \!\ltimes \! [ \texttt{flag}_2 ] \) as a postcondition (using the axiom Swap-skip). We obtain disjunct  after additionally applying Wr-own.
after additionally applying Wr-own.
8 Discussion, Related and Future Work
Previous RG-like logics provided ad-hoc solutions for other concrete memory models such as x86-TSO and C/C++11 [11, 16, 17, 32, 39, 40, 47]. These approaches established soundness of the proposed logic with an ad-hoc proof that couples together memory and thread transitions. We believe that these logics can be formulated in our proposed general RG framework (which will require extensions to other memory operations such as fences).
Moreover, Owicki-Gries logics for different fragments of the C11 memory model [16, 17, 47] used specialized assertions over the underlying view-based semantics. These include conditional-view assertion (enabling reasoning about MP), and value-order (enabling reasoning about coherence). Both types of assertions are special cases of the potential-based assertions of \({\textsf{Piccolo}}\).
Ridge [40] presents an RG reasoning technique tailored to x86-TSO, treating the write buffers in TSO architectures as threads whose steps have to preserve relies. This is similar to our notion of stability of relies under internal memory transitions. Ridge moreover allows to have memory-model specific assertions (e.g., on the contents of write buffers).
The OGRA logic [32] for Release-Acquire (which is slightly weaker form of causal consistency compared to SRA studied in this paper) takes a different approach, which cannot be directly handled in our framework. It employs simple SC-like assertions at the price of having a non-standard non-interference condition which require a stronger form of stability.
Coughlin et al. [14, 15] provide an RG reasoning technique for weak memory models with a semantics defined in terms of reordering relations (on instructions). They study both multicopy and non-multicopy atomic architectures, but in all models, the rely-guarantee assertions are interpreted over SC.
Schellhorn et al. [41] develop a framework that extends ITL with a compositional interleaving operator, enabling proof decomposition using RG rules. Each interval represents a sequence of states, strictly alternating between program and environment actions (which may be a skip action). This work is radically different from ours since (1) their states are interpreted using a standard SC semantics, and (2) their intervals represent an entire execution of a command as well the interference from the environment while executing that command.
Under SC, rely-guarantee was combined with separation logic [44, 46], which allows the powerful synergy of reasoning using stable invariants (as in rely-guarantee) and ownership transfer (as in concurrent separation logic). It is interesting to study a combination of our RG framework with concurrent separation logics for weak memory models, such as [43, 45].
Other works have studied the decidability of verification for causal consistency models. In work preceding the potential-based SRA model [28], Abdulla et al. [1] show that verification under RA is undecidable. In other work, Abdulla et al. [3] show that the reachability problem under TSO remains decidable for systems with dynamic thread creation. Investigating this question under SRA is an interesting topic for future work.
Finally, the spirit of our generic approach is similar to Iris [22], Views [18], Ogre and Pythia [7], the work of Ponce de León et al. [34], and recent axiomatic characterizations of weak memory reasoning [19], which all aim to provide a generic framework that can be instantiated to underlying semantics.
In the future we are interested in automating the reasoning in \({\textsf{Piccolo}}\), starting from automatically checking for validity of program derivations (using, e.g., SMT solvers for specialised theories of sequences or strings [24, 42]), and, including, more ambitiously, synthesizing appropriate \({\textsf{Piccolo}}\) invariants.
Notes
- 1.
Negation just occurs on the level of simple expressions \({e}\) which is sufficient for calculating \(P\setminus \llbracket {e} \rrbracket \) required in rules if and while.
- 2.
Such stability requirements are also common to other reasoning techniques for weak memory models, e.g., [19].
References
Abdulla, P.A., Arora, J., Atig, M.F., Krishna, S.N.: Verification of programs under the release-acquire semantics. In: PLDI, pp. 1117–1132. ACM (2019). https://doi.org/10.1145/3314221.3314649
Abdulla, P.A., Atig, M.F., Bouajjani, A., Kumar, K.N., Saivasan, P.: Deciding reachability under persistent x86-TSO. Proc. ACM Program. Lang. 5(POPL), 1–32 (2021). https://doi.org/10.1145/3434337
Abdulla, P.A., Atig, M.F., Bouajjani, A., Narayan Kumar, K., Saivasan, P.: Verifying reachability for TSO programs with dynamic thread creation. In: Koulali, M.A., Mezini, M. (eds.) Networked Systems, NETYS 2022. LNCS, vol. 13464. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-17436-0_19
Abdulla, P.A., Atig, M.F., Bouajjani, A., Ngo, T.P.: The benefits of duality in verifying concurrent programs under TSO. In: CONCUR. LIPIcs, vol. 59, pp. 5:1–5:15. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2016). https://doi.org/10.4230/LIPIcs.CONCUR.2016.5
Abdulla, P.A., Atig, M.F., Bouajjani, A., Ngo, T.P.: A load-buffer semantics for total store ordering. Log. Methods Comput. Sci. 14(1) (2018). https://doi.org/10.23638/LMCS-14(1:9)2018
Ahamad, M., Neiger, G., Burns, J.E., Kohli, P., Hutto, P.W.: Causal memory: definitions, implementation, and programming. Distrib. Comput. 9(1), 37–49 (1995). https://doi.org/10.1007/BF01784241
Alglave, J., Cousot, P.: Ogre and Pythia: an invariance proof method for weak consistency models. In: Castagna, G., Gordon, A.D. (eds.) POPL, pp. 3–18. ACM (2017). https://doi.org/10.1145/3009837.3009883
Alglave, J., Maranget, L., Tautschnig, M.: Herding cats: modelling, simulation, testing, and data mining for weak memory. ACM Trans. Program. Lang. Syst. 36(2), 7:1–7:74 (2014). https://doi.org/10.1145/2627752
Apt, K.R., de Boer, F.S., Olderog, E.: Verification of Sequential and Concurrent Programs. Texts in Computer Science. Springer, Heidelberg (2009). https://doi.org/10.1007/978-1-84882-745-5
Beillahi, S.M., Bouajjani, A., Enea, C.: Robustness against transactional causal consistency. Log. Meth. Comput. Sci. 17(1) (2021). http://lmcs.episciences.org/7149
Bila, E.V., Dongol, B., Lahav, O., Raad, A., Wickerson, J.: View-based Owicki–Gries reasoning for persistent x86-TSO. In: ESOP 2022. LNCS, vol. 13240, pp. 234–261. Springer, Cham (2022). https://doi.org/10.1007/978-3-030-99336-8_9
Bouajjani, A., Enea, C., Guerraoui, R., Hamza, J.: On verifying causal consistency. In: POPL, pp. 626–638. ACM (2017). https://doi.org/10.1145/3009837.3009888
Chaochen, Z., Hoare, C.A.R., Ravn, A.P.: A calculus of durations. Inf. Process. Lett. 40(5), 269–276 (1991). https://doi.org/10.1016/0020-0190(91)90122-X
Coughlin, N., Winter, K., Smith, G.: Rely/guarantee reasoning for multicopy atomic weak memory models. In: Huisman, M., Păsăreanu, C., Zhan, N. (eds.) FM 2021. LNCS, vol. 13047, pp. 292–310. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-90870-6_16
Coughlin, N., Winter, K., Smith, G.: Compositional reasoning for non-multicopy atomic architectures. Form. Asp. Comput. (2022). https://doi.org/10.1145/3574137
Dalvandi, S., Doherty, S., Dongol, B., Wehrheim, H.: Owicki-Gries reasoning for C11 RAR. In: ECOOP. LIPIcs, vol. 166, pp. 11:1–11:26. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2020). https://doi.org/10.4230/LIPIcs.ECOOP.2020.11
Dalvandi, S., Dongol, B., Doherty, S., Wehrheim, H.: Integrating Owicki-Gries for C11-style memory models into Isabelle/HOL. J. Autom. Reason. 66(1), 141–171 (2022). https://doi.org/10.1007/s10817-021-09610-2
Dinsdale-Young, T., Birkedal, L., Gardner, P., Parkinson, M.J., Yang, H.: Views: compositional reasoning for concurrent programs. In: POPL, pp. 287–300. ACM (2013). https://doi.org/10.1145/2429069.2429104
Doherty, S., Dalvandi, S., Dongol, B., Wehrheim, H.: Unifying operational weak memory verification: an axiomatic approach. ACM Trans. Comput. Log. 23(4), 27:1–27:39 (2022). https://doi.org/10.1145/3545117
Doherty, S., Dongol, B., Wehrheim, H., Derrick, J.: Verifying C11 programs operationally. In: PPoPP, pp. 355–365. ACM (2019). https://doi.org/10.1145/3293883.3295702
Jones, C.B.: Tentative steps toward a development method for interfering programs. ACM Trans. Program. Lang. Syst. 5(4), 596–619 (1983). https://doi.org/10.1145/69575.69577
Jung, R., Krebbers, R., Jourdan, J., Bizjak, A., Birkedal, L., Dreyer, D.: Iris from the ground up: A modular foundation for higher-order concurrent separation logic. J. Funct. Program. 28, e20 (2018). https://doi.org/10.1017/S0956796818000151
Kaiser, J., Dang, H., Dreyer, D., Lahav, O., Vafeiadis, V.: Strong logic for weak memory: reasoning about release-acquire consistency in Iris. In: ECOOP. LIPIcs, vol. 74, pp. 17:1–17:29. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2017). https://doi.org/10.4230/LIPIcs.ECOOP.2017.17
Kan, S., Lin, A.W., Rümmer, P., Schrader, M.: CertiStr: a certified string solver. In: CPP, pp. 210–224. ACM (2022). https://doi.org/10.1145/3497775.3503691
Kang, J., Hur, C., Lahav, O., Vafeiadis, V., Dreyer, D.: A promising semantics for relaxed-memory concurrency. In: POPL, pp. 175–189. ACM (2017). https://doi.org/10.1145/3009837.3009850
Lahav, O.: Verification under causally consistent shared memory. ACM SIGLOG News 6(2), 43–56 (2019). https://doi.org/10.1145/3326938.3326942
Lahav, O., Boker, U.: Decidable verification under a causally consistent shared memory. In: PLDI, pp. 211–226. ACM (2020). https://doi.org/10.1145/3385412.3385966
Lahav, O., Boker, U.: What’s decidable about causally consistent shared memory? ACM Trans. Program. Lang. Syst. 44(2), 8:1–8:55 (2022). https://doi.org/10.1145/3505273
Lahav, O., Dongol, B., Wehrheim, H.: Artifact: rely-guarantee reasoning for causally consistent shared memory. Zenodo (2023). https://doi.org/10.5281/zenodo.7929646
Lahav, O., Dongol, B., Wehrheim, H.: Rely-guarantee reasoning for causally consistent shared memory (extended version) (2023). https://doi.org/10.48550/arXiv.2305.08486
Lahav, O., Giannarakis, N., Vafeiadis, V.: Taming release-acquire consistency. In: POPL, pp. 649–662. ACM (2016). https://doi.org/10.1145/2837614.2837643
Lahav, O., Vafeiadis, V.: Owicki-Gries reasoning for weak memory models. In: Halldórsson, M.M., Iwama, K., Kobayashi, N., Speckmann, B. (eds.) ICALP 2015. LNCS, vol. 9135, pp. 311–323. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47666-6_25
Lamport, L.: How to make a multiprocessor computer that correctly executes multiprocess programs. IEEE Trans. Comput. 28(9), 690–691 (1979). https://doi.org/10.1109/TC.1979.1675439
de León, H.P., Furbach, F., Heljanko, K., Meyer, R.: BMC with memory models as modules. In: FMCAD, pp. 1–9. IEEE (2018). https://doi.org/10.23919/FMCAD.2018.8603021
Moszkowski, B.C.: A complete axiom system for propositional interval temporal logic with infinite time. Log. Meth. Comput. Sci. 8(3) (2012). https://doi.org/10.2168/LMCS-8(3:10)2012
Owens, S., Sarkar, S., Sewell, P.: A better x86 memory model: x86-TSO. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 391–407. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03359-9_27
Owicki, S.S., Gries, D.: An axiomatic proof technique for parallel programs I. Acta Informatica 6, 319–340 (1976). https://doi.org/10.1007/BF00268134
Peterson, G.L.: Myths about the mutual exclusion problem. Inf. Process. Lett. 12(3), 115–116 (1981)
Raad, A., Lahav, O., Vafeiadis, V.: Persistent Owicki-Gries reasoning: a program logic for reasoning about persistent programs on Intel-x86. Proc. ACM Program. Lang. 4(OOPSLA), 151:1–151:28 (2020). https://doi.org/10.1145/3428219
Ridge, T.: A rely-guarantee proof system for x86-TSO. In: Leavens, G.T., O’Hearn, P., Rajamani, S.K. (eds.) VSTTE 2010. LNCS, vol. 6217, pp. 55–70. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15057-9_4
Schellhorn, G., Tofan, B., Ernst, G., Pfähler, J., Reif, W.: RGITL: a temporal logic framework for compositional reasoning about interleaved programs. Ann. Math. Artif. Intell. 71(1–3), 131–174 (2014). https://doi.org/10.1007/s10472-013-9389-z
Sheng, Y., et al.: Reasoning about vectors using an SMT theory of sequences. In: Blanchette, J., Kováics, L., Pattinson, D. (eds.) Automated Reasoning, IJCAR 2022. LNCS, vol. 13385, pp. pp. 125–143. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-10769-6_9
Svendsen, K., Pichon-Pharabod, J., Doko, M., Lahav, O., Vafeiadis, V.: A separation logic for a promising semantics. In: Ahmed, A. (ed.) ESOP 2018. LNCS, vol. 10801, pp. 357–384. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89884-1_13
Vafeiadis, V.: Modular fine-grained concurrency verification. Ph.D. thesis, University of Cambridge, UK (2008). https://ethos.bl.uk/OrderDetails.do?uin=uk.bl.ethos.612221
Vafeiadis, V., Narayan, C.: Relaxed separation logic: a program logic for C11 concurrency. In: OOPSLA, pp. 867–884. ACM (2013). https://doi.org/10.1145/2509136.2509532
Vafeiadis, V., Parkinson, M.: A marriage of rely/guarantee and separation logic. In: Caires, L., Vasconcelos, V.T. (eds.) CONCUR 2007. LNCS, vol. 4703, pp. 256–271. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74407-8_18
Wright, D., Batty, M., Dongol, B.: Owicki-Gries reasoning for C11 programs with relaxed dependencies. In: Huisman, M., Păsăreanu, C., Zhan, N. (eds.) FM 2021. LNCS, vol. 13047, pp. 237–254. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-90870-6_13
Xu, Q., de Roever, W.P., He, J.: The rely-guarantee method for verifying shared variable concurrent programs. Formal Aspects Comput. 9(2), 149–174 (1997). https://doi.org/10.1007/BF01211617
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Lahav, O., Dongol, B., Wehrheim, H. (2023). Rely-Guarantee Reasoning for Causally Consistent Shared Memory. In: Enea, C., Lal, A. (eds) Computer Aided Verification. CAV 2023. Lecture Notes in Computer Science, vol 13964. Springer, Cham. https://doi.org/10.1007/978-3-031-37706-8_11
Download citation
DOI: https://doi.org/10.1007/978-3-031-37706-8_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-37705-1
Online ISBN: 978-3-031-37706-8
eBook Packages: Computer ScienceComputer Science (R0)







 and
and  , and furthermore that
, and furthermore that  is only performed when
is only performed when  , where each element is a command guarded by a precondition.
, where each element is a command guarded by a precondition.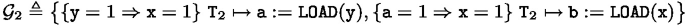


 )
)
 )
)
 )
) .
. .
. .
. for some
for some  for some
for some 
 .
. for every
for every 
 for some
for some  , then
, then 


 and assuming
and assuming 

