Searching for i-Good Lemmas to Accelerate Safety Model Checking

Abstract

IC3/PDR and its variants have been the prominent approaches to safety model checking in recent years. Compared to the previous model-checking algorithms like BMC (Bounded Model Checking) and IMC (Interpolation Model Checking), IC3/PDR is attractive due to its completeness (vs. BMC) and scalability (vs. IMC). IC3/PDR maintains an over-approximate state sequence for proving the correctness. Although the sequence refinement methodology is known to be crucial for performance, the literature lacks a systematic analysis of the problem. We propose an approach based on the definition of i- good lemmas, and the introduction of two kinds of heuristics, i.e., branching and refer-skipping, to steer the search towards the construction of $i$-good lemmas. The approach is applicable to IC3 and its variant CAR (Complementary Approximate Reachability), and it is very easy to integrate within existing systems. We implemented the heuristics into two open-source model checkers, IC3Ref and SimpleCAR, as well as into the mature nuXmv platform, and carried out an extensive experimental evaluation on HWMCC benchmarks. The results show that the proposed heuristics can effectively compute more $i$-good lemmas, and thus improve the performance of all the above checkers.

1 Introduction

Safety model checking is a fundamental problem in verification. The goal is to prove that all the reachable states of the transition system $\langle I,T \rangle$ satisfy a property P. The field has been dominated by SAT-based techniques since the introduction of Bounded Model Checking (BMC) [9]. The first wave of SAT-based model-checking algorithms, including BMC, k-induction [31] and Interpolation-based Model Checking [25] have been superseded by the research deriving from the seminal work of Bradley [11]. The IC3 algorithm maintains an over-approximate state sequence for proving the correctness; it avoids unrolling the transition relation by localizing reasoning to frames, used to incrementally build an inductive invariant by discovering inductive clauses.

IC3 (also known as PDR  [17]) has spawned several variants, including those that attempt to combine forward and backward search [29]. Particularly relevant in this paper is CAR (Complementary Approximate Reachability), which combines the forward overapproximation with a backward underapproximation [23].

It has been noted that different ways to refine the over-approximating sequence can impact the performance of the algorithm. For example, [21] attempts to discover good lemmas, that can be “pushed to the top” since they are inductive. In this paper, we propose an alternative way to drive the refinement of the over-approximating sequence. We identify i- good lemmas, i.e. lemmas that are inductive with respect to the i-th overapproximating level. The intuition is that such $i$-good lemmas are useful in the search since they are fundamental to reach a fix point in the safe case. In order to guide the search towards the discovery of $i$-good lemmas, we propose a heuristic approach based on two key insights, i.e., branching and refer-skipping. First, with branching we try to control the way the SAT solver extracts unsatisfiable cores by privileging variables occurring in $i$-good lemmas. Second, we control lemma generalization by avoiding dropping literals occurring in a subsuming lemma in the previous layer (refer-skipping).

The proposed approach is applicable both to IC3/PDR and CAR, and it is very simple to implement. Yet, it appears to be quite effective in practice. We implemented the $i$-good lemma heuristics in two open-source implementations of IC3 and CAR, and also in the mature, state-of-the-art IC3 implementation available inside the nuXmv model checker [12], and we carried out an extensive experimental evaluation on Hardware Model Checking Competition (HWMCC) benchmarks. Analysis of the results suggests that increasing the ratio of $i$-good lemmas leads to an increase in performance, and the heuristics appear to be quite effective in driving the search towards $i$-good lemmas. In terms of performance, this results in significant improvements for all the tools when equipped with the proposed approach.

This paper is structured as follows. In Sect. 2 we present the problem and the IC3/PDR and CAR algorithms. In Sect. 3 we present the intuition underlying $i$-good lemmas and the algorithms to find them. In Sect. 4 we overview the related work. In Sect. 5 we present the experimental evaluation. In Sect. 6 we draw some conclusions and present directions for future work.

2 Preliminaries

2.1 Boolean Transition System

A Boolean transition system $Sys$ is a tuple $\langle X, Y, I, T\rangle$, where X and $X'$ denote the set of state variables in the present state and the next state, respectively, and Y denotes the set of input variables. The state space of $Sys$ is the set of possible assignments to X. I(X) is a Boolean formula corresponding to the set of initial states, and $T(X, Y, X')$ is a Boolean formula representing the transition relation. State $s_{2}$ is a successor of state $s_{1}$ with input y iff $s_{1} \wedge y \wedge s_{2}' \models T$, which is also denoted by $(s_1,y,s_2)\in T$. In the following, we will also write $(s_1, s_2)\in T$ meaning that $(s_1,y,s_2) \in T$ for some assignment y to the input variables. A path of length k is a finite state sequence $s_{1}, s_{2}, \dots , s_{k}$, where $(s_{i}, s_{i+1})\in T$ holds for $(1\le i \le k -1)$. A state t is reachable from s in k steps if there is a path of length k from s to t. Let S be a set of states in $Sys$. We overload T and denote the set of successors of states in S as $T(S) = \{t \mid (s,t) \in T, s \in S\}$. Conversely, we define the set of predecessors of states in S as $T^{-1}(S) = \{s \mid (s,t) \in T, t \in S\}$. Recursively, we define $T^{0}(S) = S$ and $T^{i+1}(S) = T(T^{i}(S))$ where $i \ge 0$; the notation $T^{-i}(S)$ is defined analogously. In short, $T^{i}(S)$ denotes the states that are reachable from S in i steps, and $T^{-i}(S)$ denotes the states that can reach S in i steps.

2.2 Safety Checking and Reachability Analysis

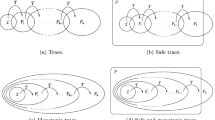
Given a transition system $Sys =\langle X,Y,I,T \rangle$ and a safety property P, which is a Boolean formula over X, a model checker either proves that P holds for any state reachable from an initial state in I, or disproves P by producing a counterexample. In the former case, we say that the system is safe, while in the latter case, it is unsafe. A counterexample is a finite path from an initial state s to a state t violating P, i.e., $t \in \lnot P$, and such a state is called a bad state. In symbolic model checking, safety checking is reduced to symbolic reachability analysis. Reachability analysis can be performed in a forward or backward search. Forward search starts from initial states I and searches for bad states by computing $T^{i}(I)$ with increasing values of i, while backward search begins with states in $\lnot P$ and searches for initial states by computing $T^{-i}(\lnot P)$ with increasing values of i. Table 1 gives the corresponding formal definitions.

Table 1. Exact reachability analysis.

For forward search, $F_i$ denotes the set of states that are reachable from I within i steps, which is computed by iteratively applying T. At each iteration, we first compute a new $F_i$, and then perform safe checking and unsafe checking. If the safe/unsafe checking hits, the search terminates. Intuitively, unsafe checking $F_i\cap \lnot P \ne \emptyset$ indicates some bad states are within $F_i$ and safe checking $F_{i+1}\subseteq \bigcup _{0\le j\le i} F_j$ indicates that all reachable states from I have been checked and none of them violate P. For backward search, $B_i$ is the set of states that can reach $\lnot P$ in i steps, and the search procedure is analogous to the forward one.

Notations. A literal is an atomic variable or its negation. If l is a literal, we denote its corresponding variable with var(l). A cube (resp. clause) is a conjunction (resp. disjunction) of literals. The negation of a clause is a cube and vice versa. A formula in Conjunctive Normal Form (CNF) is a conjunction of clauses. For simplicity, we also treat a CNF formula $\phi$ as a set of clauses and make no difference between the formula and its set representation. Similarly, a cube or a clause c can be treated as a set of literals or a Boolean formula, depending on the context.

We say a CNF formula $\phi$ is satisfiable if there exists an assignment of its Boolean variables, called a model, that makes $\phi$ true; otherwise, $\phi$ is unsatisfiable. A SAT solver is a tool that can decide the satisfiability of a CNF formula $\phi$. In addition to providing a yes/no answer, modern SAT solvers can also produce models for satisfiable formulas, and unsatisfiable cores (UC), i.e. a reason for unsatisfiability, for unsatisfiable ones. More precisely, in the following we shall assume to have a SAT solver that supports the following API (which is standard in state-of-the-art SAT solvers based on the CDCL algorithm [24]):

• is_SAT($\phi , \mathcal {A}$) checks the satisfiability of $\phi$ under the given assumptions $\mathcal {A}$, which is a list of literals. This is logically equivalent to checking the satisfiability of $\phi \wedge \bigwedge \mathcal {A}$, but is typically more efficient;

• get_UC() retrieves an UC of the assumption literals of the previous SAT call when the formula $\phi \wedge \bigwedge \mathcal {A}$ is unsatisfiable. That is, the result is a set $uc \subseteq \mathcal {A}$ such that $\phi \wedge \bigwedge uc$ is unsatisfiable;

• get_model() retrieves the model of the formula $\phi \wedge \bigwedge \mathcal {A}$ of the previous SAT call, if the formula is satisfiable.

2.3 Overview of IC3 and CAR

IC3 is a SAT-based and complete safety model checking algorithm proposed in [11], which only needs to unroll the system at most once. PDR  [17] is a re-implementation of IC3 which optimizes the original version in different aspects. To prove the correctness of a given system $Sys = \langle X, Y, I, T \rangle$ w.r.t. the safety property P, IC3/PDR maintains a monotone over-approximate state sequence O such that (1) $O_0 = I$ and (2) $O_{i+1}\supseteq O_i \cup T(O_i)$ for $i\ge 0$. From the perspective of reachability analysis, IC3 performs as shown in the left part of Table 2. Since O is monotone, the states search can converge as soon as $O_{i+1}= O_i$ holds for some $i\ge 0$. Otherwise, a state path (counterexample) starting from I to some state in $\lnot P$ can be detected ($T^{-i}(\lnot P)\cap I \not = \emptyset$).

Table 2. A high-level description of IC3 (left) and (Forward) CAR (right).

CAR [23] is a recently proposed algorithm, which can be considered as a general version of IC3. The main points CAR differs from IC3 are as follows:

• The over-approximate state sequence O in CAR is not necessarily monotone. Therefore, CAR has to apply the standard invariant-checking approach, i.e., finding a position $i\ge 0$ such that $O_{i+1}\subseteq \bigcup _{0\le j\le i} O_j$ holds, as shown in the right part of Table 2.

• Besides the O sequence, CAR also maintains an under-approximate state sequence U that stores reachable (real) states from $\lnot P$, see Table 2. The motivation to introduce the U sequence is to re-use the intermediate states that are computed during proving. Although it is straightforward for IC3 to introduce such a sequence, the effect on the performance remains unknown.

• CAR can be performed in both forward, i.e., proving from I while searching states back from $\lnot P$, and backward, i.e., proving back from $\lnot P$ while searching states from I. Although Backward CAR is not good at proving, it is advantageous in finding bugs, i.e., checking unsafety [16, 22]. Relevant work on reverse IC3/PDR  [28], which corresponds to Backward CAR, has been studied but the results did not clearly support its advantage on bug-finding.

An overview of IC3 and (forward) CAR is shown in Algorithm 1 and Algorithm 2 respectively. At a high level, both algorithms have a similar structure, consisting of an alternation of two phases: unsafe check and safe check. The unsafe check (line 14 of Algorithm 1, line 14 of Algorithm 2) tries to find a state sequence that is a path between I and $\lnot P$; if such a sequence can be found, then it is a counterexample witnessing the violation of P; otherwise, the $O_i$ are strengthened with additional clauses until $O_k$ is strong enough to imply P.¹ The safe check (line 25 of Algorithm 1, line 26 of Algorithm 2) tries to propagate the clauses in $O_i$ to $O_{i+1}$ and check if a fixpoint is reached. If so then the algorithm terminates. Both algorithms make use of similar additional procedures, which will be detailed in the following section, when we introduce our novel heuristics.

3 Finding i-Good Lemmas

In this section, we introduce the concept of i-good lemmas, define the heuristics to steer the search towards i-good lemmas and describe the IC3 and CAR algorithms enhanced with i-good lemmas. For the sake of convenient description, we fix the input system $Sys = \langle X, Y, I, T \rangle$ and the property P to be verified. In describing the implementation of our heuristics, we shall necessarily assume that the reader has some familiarity with the low-level details of IC3 and CAR, for which we refer to [11, 17, 23]. Specifically, we shall use pseudo-code descriptions of the main components of the algorithms (Algorithm 3, 4, and 5), in which the modifications required to implement our heuristics are highlighted in blue.

3.1 What Are i-good Lemmas

The over-approximate state sequence O in IC3 (resp. CAR) is a finite sequence, in which every element $O_i$ ($0\le i<|O|$), namely frame i, is an over-approximation of the states of the system that are reachable in up to (resp. exactly) i steps from I, and which is strong enough to imply P. Such sequence O has the form of $P\wedge C$, where C is a CNF, and each clause in C is called a lemma. For both algorithms, the goal is that of transforming the sequence O to construct an over-approximation of all the reachable states of the system (over an unbounded horizon) that still implies P. When this happens, such over-approximation is an inductive invariant that proves P. The key idea, common to both IC3 and to CAR, is to construct the invariant incrementally and by reasoning in a localized manner, by (i) considering increasingly-long sequences of overapproximations, and by (ii) trying to propagate forward individual lemmas from a frame $O_i$ to its successor $O_{i+1}$, until a fixpoint is reached². The forward propagation procedure is crucial for ensuring the convergence of the algorithm in practice: for IC3 (resp. CAR), it checks whether a lemma c at frame i represents also an overapproximation of all the states reachable in up to (resp. exactly) $i+1$ steps, and therefore can be added to frame $i+1$. It is immediate to see that the successful propagation of all lemmas from i to $i+1$, for some i, is a sufficient condition for the termination of both IC3 and CAR with a safe result. In fact, for IC3, this is also a necessary condition.

We now introduce the notion of i-good lemma.

Definition 1

(i-Good Lemma). Let c be a lemma that was added at frame i by IC3/CAR (at some previous step in the execution of the algorithm), i.e. $O_i\models c$. We say that c is $i$-good if c now holds also at frame $i+1$, i.e. $O_{i+1}\models c$.

The following theorems are then consequences of the definition.

Theorem 1

IC3 terminates with safe at frame i ($i>0$), if and only if every lemma at frame i is i-good.

Theorem 2

CAR terminates with safe at frame i ($i>0$), if every lemma at frame i is i-good.

Such theorems provide the theoretical foundation on which we base our main conjecture: the computation of $i$-good lemmas can be helpful for both IC3 and CAR to accelerate the convergence in proving properties. Intuitively, an i-good lemma shows the promise of being independent of the reachability layer, and hence holds in general.

3.2 Searching for $i$-good Lemmas

Our conjecture is that there exists, on average, a positive correlation between the ratio of $i$-good lemmas vs the total amount of lemmas computed by IC3/CAR during generalization and the efficiency of the algorithm.

Ensuring that only $i$-good lemmas are produced is as hard as solving the verification problem itself, since this is essentially equivalent to synthesizing an inductive invariant which implies P. However, there are two situations in which it is easy to identify $i$-good lemmas, for both IC3 and CAR:

• 1. In the propagation procedure, if a lemma c can be successfully pushed from frame i to frame $i+1$, then c is $i$-good;

• 2. In the generalize procedure, if the current lemma c at frame i is generalized to a lemma $p \subseteq c$ such that $p \in O_{i-1}$, then p is $(i-1)$-good; additionally, if we can guide the generalization of c so that it produces p, then p becomes $(i-1)$-good.

Therefore, we do not attempt to compute only $i$-good lemmas, but rather, our main idea is to use some (cheap) heuristics to increase the probability of producing $i$-good lemmas during the normal execution of IC3 and CAR.

We exploit the above observations to design two heuristics that try to bias the search for lemmas towards those that are more likely to be $i$-good, which we call respectively branching and refer-skipping.

Branching. The branching strategy [26] is an important feature of modern CDCL (Conflict-Driven Clause Learning) SAT solvers [7]. Traditional scoring schemes for branching such as VSIDS and EVSIDS have been extensively evaluated in [10]. In CDCL SAT solvers, decision variables are selected according to their priority. Whenever a conflict occurs, the priority of each variable in the clause is increased. To this end, variables that have recently been involved in conflicts are more likely to be selected as decision variables.

We adopt a similar idea in our branching heuristic for IC3/CAR to bias the unsatisfiable cores produced by the SAT solver, by ordering the assumptions in SAT queries according to their score. This is based on the fact that modern SAT solvers based on CDCL apply the assumption literals in the order given by the user, and (as a consequence of how CDCL works) the unsatisfiable core produced when the formula is unsatisfiable depends on such order, with literals occurring earlier in the assumption list being more likely to be included in the core. For example, assume the SAT query is is_SAT($\lnot 1\wedge (2 \vee \lnot 3)$, $1\wedge \lnot 2\wedge 3$), which is unsatisfiable, then the returned UC from the SAT solver, e.g., Minisat  [5, 18], will be $\{1\}$. If the order of assumptions is changed to $3\wedge \lnot 2\wedge 1$, then the UC will be $\{3,\lnot 2\}$.

Since UC s are the source for lemmas in both IC3 and CAR, the first idea of our branching heuristic is that of sorting the assumption literals in SAT queries according to how often they occur in recent i- good lemmas. Concretely, this is implemented as follows:

• We introduce a mapping $S_{[v]}:v\rightarrow score_v, v\in X$ from each variable to its score (priority). Initially, all variables have the same score of 0.

• Before each SAT query in which a (negated) lemma c (or its next-state version $c'$) is part of the assumptions, c is sorted in descending order of $S_{[var(l)]}$, where $l\in c$, to give higher priority to assumption literals with higher scores. This corresponds to the calls to the function sort(c) in the pseudo-code description of the main components of IC3 and CAR: at the beginning of Unsafecheck (Algorithm 1 and 2), in Get_predecessor (line 6 of Algorithm 4, line 6 of Algorithm 5), and in Generalization (line 25 of Algorithm 4, line 23 of Algorithm 5).

• Whenever IC3 or CAR discovers an $i$-good lemma c, all the variables in c are rewarded by increasing their score. A lemma c is determined to be $i$-good either when it is propagated forward from frame i to frame $i+1$ (function propagation of Algorithm 4 and 5) or when c is the result of a generalization from $d \supseteq c$ at frame $i+1$ such that c is already in frame i (function generalize, Algorithm 3). In the pseudo-code, the reward steps correspond to the calls to the function reward(c) at line 12 of Algorithm 3, line 42 of Algorithm 4, and line 37 of Algorithm 5. The reward function first decays the scores of all the variables in $S_{[v]}$ by a small amount (we multiply by 0.99 in our implementation), and then increments the score of all the variables in c (by 1 in our implementation). In order to determine whether generalize produced an $i$-good lemma, we also use the function get_parentnode(c) (line 3 of Algorithm 3), which returns a cube p in frame $i-1$ such that $p \subseteq c$ when c belongs to frame i. (If multiple such p exist, the one with the highest score is returned).

• When performing inductive generalization of a lemma c at frame i (Algorithm 3), in which c is strengthened by trying to drop literals from it as long as the result is still a valid lemma for frame i, the literals of c are sorted in increasing order of $S_{[var(l)]}$, with $l\in c$. This corresponds to the call to the function reverse_sort(c) at line 2 of Algorithm 3 in the pseudo-code.

Skipping Literals by Reference. Lemma generalization is a crucial process in IC3/CAR that affects performance significantly. Given the original lemma c to be added into frame i ($i>0$), the generalize procedure tries to compute a new lemma g such that $g\subseteq c$ and g is also valid to be added to frame i ($O_i$). The main idea of generalization is to try to drop literals in the original lemma one by one, to see whether the left part can still be a valid lemma.

There are several generalization algorithms with different trade-offs between efficiency (in terms of the number of SAT queries) and effectiveness (in terms of the potential reduction in the size of the generalized lemma), e.g. [11, 17, 20]. More in general, there might be multiple different ways in which a lemma c can be generalized, with results of uncomparable strength (i.e. there might be both $g_1 \subseteq c$ and $g_2 \subseteq c$ such that $g_1 \not \subseteq g_2$ and $g_2 \not \subseteq g_1$).

The main idea of the refer-skipping heuristic is to bias the generalization to increase the likelihood that the result g is a $(i-1)$-good lemma. Consider the generalization of lemma $c = \lnot 1 \vee 2 \vee \lnot 3$ at frame i ($i>1$). If there is already a lemma $g = \lnot 1 \vee \lnot 3$ at frame $i-1$, we say that g is a candidate $(i-1)$-good lemma for the generalization of c. In order to drive the generalization of c towards g, we blacklist the literals of g, so that generalize will never attempt to drop them from c. As such, we call g a reference for skipping generalization. In general, there might be multiple references for a given lemma. Currently, our strategy in refer-skipping is to just pick the one first found.

The implementation of refer-skipping is based on existing generalization algorithms and only needs to add less than 10 lines in the pseudo-code (see line 4-10 of Algorithm 3). As shown in the algorithm, a variable set req is maintained to store variables that fail to be dropped so that they are not tried to be removed again later. In order to use refer-skipping, we simply initialize req with the variables occurring in the candidate $(i-1)$-good lemma that is returned by the get_parentnode procedure (line 3 of Algorithm 3).

Finally, note that although in our pseudo-code (and in our implementation) we use the CTG algorithm of [20], the idea discussed here can be applied also to the other variants of generalization just as easily.

4 Related Work

In the field of safety model checking, after the introduction of IC3  [11], several variants have been presented: [20] presents the counterexample-guided generalization (CTG) of a lemma by blocking states that interfere with it, which significantly improves the performance of IC3; AVY  [33] introduces the ideas of IC3 into IMC (Interpolant Model Checking) [25] to induce a better model checking algorithm; its upgrade version kAVY  [32] uses k-induction to guide the interpolation and IC3/PDR generalization inside; [28] proposes to combine IC3/PDR with reverse IC3/PDR; the subsequent work [29] interleaves a forward and a backward execution of IC3 and strengthens one frame sequence by leveraging the proof-obligations from the other; IC3-INN [15] enables IC3 to leverage the internal signal information of the system to induce a variant of IC3 that can perform better on certain industrial benchmarks; [30] introduces under-approximation in PDR to improve the performance of bug-finding.

The importance of discovering inductive lemmas for improving convergence is first noted in [17]. In PDR terminology, inductive lemmas are the ones belonging to frame $O_\infty$, as they represent an over-approximation of all the reachable states.

The most relevant related work is [21], where a variant of IC3 named QUIP is proposed for implementing the pushing of the discovered lemmas to $O_\infty$. At its essence, QUIP adds the negation of a discovered lemma c as a may-proof-obligation, hence trying to push c to the next frame. Counterexamples of may-proof-obligations represent an under-approximation of the reachable states and are stored to disprove the inductiveness of other lemmas. In QUIP terminology, such lemmas are classified as bad lemmas, as they have no chance of being part of the inductive invariant. Since the pushing is not limited to the current number of frames, inductive lemmas are discovered when all the clauses of a frame can be pushed ($O_k \setminus O_{k+1} = \emptyset$ for a level k), and then added in $O_\infty$. In QUIP terminology, lemmas belonging to $O_\infty$ are classified as good lemmas, and are always kept during the algorithm. Observe that the concept of good lemma in [21] is a stronger version of Definition 1, which instead is local to a frame i and characterizes lemmas that can be propagated one frame ahead.

Both QUIP and our heuristic try to accomplish a similar task, which is prioritizing the use of already discovered lemmas during the generalization. There are however several differences: QUIP proceeds by adding additional proof-obligations to the queue and by progressively proving the inductiveness of a lemma relative to any frame. Our approach, on the other hand, is based on a cheap heuristic strategy that locally guides the generalization prioritizing the locally good lemmas. Some $i$-good lemmas computed may not be part of the final invariant and can not be pushed later; in QUIP, such lemmas would not be considered good. In our view, pushing them is not necessarily a waste of effort, because they still strengthen the frames and their presence might be necessary to deduce the final invariant. Finally, it is worth mentioning that our heuristic is much simpler to implement and integrate into different PDR-based engines.

The idea of ordering literals when performing inductive generalization is already proposed in [11] and adopted, as a default strategy, in several implementations of IC3 [3, 17, 19], yielding modest improvements on HWMCC benchmarks, however without clear trends identified (see [17, 19]). Compared to such works, our approach has two main differences. First, these heuristics favor literals occurring more frequently in all previous frames, whereas our approach is driven by the role of lemmas and prefers the variables occurring only in those are $i$-good. Second, our use of ordering heuristics is more pervasive: unlike in previous works, where variable ordering heuristics are only used during the lemma generalization, we use ordering everywhere the SAT results affect search direction, which makes it more effective to bias the search.

5 Evaluation

5.1 Experimental Setup

We integrated the branching and refer-skipping heuristics into three systems: the IC3Ref  [3] and SimpleCAR  [6] (open-source) model checkers, which implement the IC3 and (Forward and Backward³) CAR algorithms respectively, and the mature, state-of-the-art implementation of IC3 available inside the nuXmv model checker [12]. We make our implementations and data for reproducing the experiments available at https://github.com/youyusama/i-Good_Lemmas_MC.

Since our approach is related to QUIP [21], we include the evaluation of QUIP, and IC3 (mainly as the baseline for QUIP), as implemented⁴ in IIMC  [4]. We also consider the PDR implementation in the ABC model checker [1], which is state-of-the-art in hardware model checking.

Table 3. Tools and algorithms evaluated in the experiments.

Table 3 summarizes the tested tools, algorithms, and their flags. We use the flag “-br” to enable the branching heuristic and “-rs” to enable refer-skipping. Furthermore, we evaluate also another configuration (denoted as “-sh”), in which the calls to sort() functions in Algorithms 4 and 5 are replaced by random shuffles, thus simulating a strategy that orders variables randomly. When no flag is active, IC3Ref runs the instances with its own strategy of sorting variables, present in the original implementation.

We evaluate all the tools on 749 benchmarks, in aiger format, of the SINGLE safety property track of the 2015 and 2017 editions of HWMCC [8]⁵. We ran the experiments on a cluster, which consists of 2304 2.5GHz CPUs in 240 nodes running RedHat 4.8.5 with a total of 96GB RAM. For each test, we set the memory limit to 8GB and the time limit to 5 h. During the experiments, each model-checking run has exclusive access to a dedicated node.

To increase our confidence in the correctness of the results, we compare the results of the solvers to make sure they are all consistent (modulo timeouts). For the cases with unsafe results, we also check the provided counterexample with the aigsim tool from the Aiger package [2]. We have no discrepancies in the results, and all unsafe cases successfully pass the aigsim check.

5.2 Experimental Results

Overview. The results of the experimental evaluation are discussed below. We first consider the aggregated results, as reported in Table 4. For each tool, we group the results obtained with the various configurations; we report the total number of benchmarks solved, distinguishing between safe and unsafe benchmarks; we also report the benchmarks gained and lost by the configurations with branching and/or refer-skipping active, relative to the baseline where branching and refer-skipping are not active. We can draw the following conclusions.

• The proposed heuristics are in general effective in improving performance. Each of the model checkers, with at least one of branching and refer-skipping active, consistently outperforms the respective baseline in terms of the number of benchmarks solved.

• The same holds within the safe instances, with the exception of refer-skipping in nuXmv that solves two safe benchmarks less than the baseline.

• The heuristics also yield a uniform improvement over the baseline in the unsafe instances.

• The combination of branching and refer-skipping gives further improvements over a single technique, with the exception of nuXmv with branching, which cumulatively solves 5 more benchmarks than nuXmv with branching and refer-skipping.

• The gain is not uniform across the instances. For example, nuXmv with branching gains 52 benchmarks (44 safe and 8 unsafe) that are not solved by nuXmv baseline, while losing 13 (safe) benchmarks. This level of variability can be expected, given a heuristic approach, but further investigation is needed to assess the underlying phenomena.

• The performance of using the heuristics guided by random variable ordering does not differ significantly from the baseline in terms of aggregate results. There are some differences (as expected) at the level of individual instances, especially for CAR, but no clear trend emerges overall.

• The comparison also shows that the considered systems compare well against the state-of-the-art system ABC, and QUIP; QUIP turns out to be quite inefficient and is disregarded in the following. Note that the original implementation of QUIP is not available; the fact that the available version of QUIP implemented on top of IIMC does not seem to achieve the same improvements reported in the original paper [21] (the code for which is unfortunately not available) suggests that the QUIP is far from trivial to implement. As the reference, QUIP performs even worse than the IC3 implementation in IIMC, whose performance is similar to the IC3Ref baseline, see Table 4.

Table 4. Summary of overall results among different configurations.

Similar insights can be obtained from Fig. 1, which clearly shows the positive effect of improvements in performance.

Detailed Statistics. As shown in Table 4 and Fig. 1, nuXmv is highly optimized and has a much better performance than other open-source IC3 implementations, but enabling both heuristics is still useful to improve its overall performance by solving 34 more instances. For IC3Ref and SimpleCAR, the increased numbers of solved cases are 19 and 53, respectively. Moreover, from Table 4, nuXmv/IC3Ref/SimpleCAR is able to solve 24/14/43 more safe and 10/5/10 more unsafe instances with both heuristics.

A comparison of the performance of the tools with and without the heuristics is shown in Fig. 2. All three solvers are able to reduce their time cost when equipping with branching and refer-skipping (see the last row of the figure). Explicitly, 67.8% of the instances cost less or equal to check by ‘nuXmv -br -rs’, and the corresponding portions for ‘ic3 -br -rs’ and ‘fcar -br -rs’ are 77.9% and 87.0%. The variability occurs when considering only a single heuristic, which needs to be explored in the future. For example, ‘fcar -br’ and ‘nuXmv -rs’ generally cost slightly more time than ‘fcar’ and ‘nuXmv ’, respectively.

Fig. 1.

Comparisons among the implementations of IC3, PDR and CAR under different configurations. (To make the figure more readable, we skip the results with a single heuristic, which are still shown in Table 4.)

According to Table 4, either branching or refer-skipping is effective for improving nuXmv, IC3Ref, and SimpleCAR. For nuXmv and SimpleCAR, branching is more useful, considering that ‘nuXmv -br’ (resp. ‘fcar -br’) solves 39 (resp. 38) more instances than ‘nuXmv ’ (resp. ‘fcar’), with 31 (resp. 32) safe and 8 (resp. 6) unsafe. For IC3Ref, the improvement with either heuristic seems relatively modest, i.e., ‘ic3 -br’ solves 8 more instances than ‘ic3’, with 3 safe and 5 unsafe, while ‘ic3 -rs’ solves 10 more instances than ‘ic3’, with 9 safe and 1 unsafe.

Fig. 2.

Time comparison between IC3/CAR with and without two heuristics on safe-unsafe cases. The baseline is always on the y-axis. Points above the diagonal indicate better performance with the heuristics active. Points on the borders indicate timeouts (18000 s).

As listed above, ‘ic3 -br -rs’ loses only 6 instances that are solved by ‘ic3’, while ‘fcar -br -rs’ even loses only 1 instance that is solved by ‘fcar’, which indicates the performance domination of ‘fcar -br -rs’ over ‘fcar’. For ‘nuXmv -br -rs’, the number of lost cases is 15, which is still modest when compared to the gain of 49. So enabling branching and refer-skipping together makes the checkers pay a limited cost. The same applies to the situations when equipping with only one single heuristic for the checkers, see Table 4.

Fig. 3.

Comparison on the success rate (sr) to compute i-good lemmas between IC3/CAR with and without branching and refer-skipping.

5.3 Why Do branching and refer-skipping Work?

To measure why branching and refer-skipping work, we introduce sr, i.e. the success rate in computing $i$-good lemmas. Formally, $sr = N_g/N$ where $N_g$ is the number of generalizations that successfully return i-good lemmas, while N is the total number of generalization calls. We instrumented the two open-source checkers IC3Ref and SimpleCAR in order to compute sr for each terminating run (including each run with/without a returned result at timeout).

• Consider the results presented in Fig. 3. The figure shows the comparison of the success rate in computing i-good lemmas between IC3/CAR with and without the heuristics. ‘ic3 -br -rs’ computes more i-good lemmas than ‘ic3’ on 54% tested instances, while ‘fcar -br -rs’ computes more i-good lemmas than ‘fcar’ on 67% tested instances, the portion of which is even higher. This supports the conjecture that enabling branching and refer-skipping makes IC3/CAR compute more $i$-good lemmas.

• Now consider Fig. 4. The figure shows the comparison between the deviation of success rate to compute $i$-good lemmas (Y axis) and the deviation of checking (CPU) time (X axis) for IC3/CAR with and without the heuristics. The meaning of each point in the plot is explained in the title of the figure. In general, the more points located in the first quadrant, the better our claim can be supported. Clearly, the plot for both IC3 and CAR in Fig. 4 supports the conjecture that searching more i-good lemmas can help achieve better model-checking performance (time cost).

Fig. 4.

Comparison between the deviation of the success rate (sr) to compute i-good lemmas (Y axis) and the deviation of checking (CPU) time (X axis) for IC3/CAR with and without the heuristics. For each instance, let the checking time of ‘ic3’/‘fcar’ be t and that of ‘ic3 -br -rs’/‘fcar -br -rs’ be $t'$. Each point has $t-t'$ as the x value and $sr'-sr$ as the y value.

Finally, we argue that computing as many i-good lemmas as possible is the direction to take to improve the performance of IC3 and its variants. branching and refer-skipping are two heuristics that can enable IC3/CAR to compute more i-good lemmas. However, there can be more efficient ways to compute i-good lemmas, which is left for our future work.

6 Conclusions and Future Work

In this paper, we proposed a heuristic-based approach to improve the performance of IC3-based safety model checking. The idea is to steer the search of the over-approximation sequence towards $i$-good lemmas, i.e. lemmas that can be pushed from frame i to frame $i+1$. On the one side, we attempt to control the way the SAT solver extracts the unsat cores, by privileging variables occurring in $i$-good lemmas (branching); on the other, we control lemma generalization by avoiding dropping literals that occur in a subsuming lemma in the previous layer (refer-skipping). The approach is very simple to implement and has been integrated into two open-source model checkers and an industrial-strength, closed-source model checker. The experimental evaluation, carried out on a wide set of benchmarks, shows that the approach yields computational benefits on all the implementations. Further analysis shows a correlation between $i$-good lemmas and performance improvements and suggests that the proposed heuristics are effective in finding more $i$-good lemmas.

In the future, we plan to investigate the reasons for performance improvement/degradation at the level of the single benchmarks. We will also attempt to integrate the proposed ideas with the ideas in QUIP, explore different kinds of heuristics, and lift this approach to the safety checking of infinite-state systems [13, 14].