Keywords

3.1 Introduction

Soil hydraulic properties are very important for predicting the subsurface behavior of fluids, including light nonaqueous phase liquids (LNAPLs) that may accumulate above the water-saturated zone and potentially result in groundwater contamination. Accounting for pore-size distributions and fluid properties is critical. Relatively small differences in either may produce erroneous predictions. Models that predict subsurface LNAPL behavior commonly use capillary pressure–saturation (S-P) relations to describe fluid saturations and to estimate fluid relative permeabilities. S-P relationships and the size distribution of pores govern subsurface LNAPL volumes. Two of the most common S-P functions are those by Brooks and Corey (1964) and van Genuchten (1980), both of which were developed initially for porous media having normal or lognormal pore-size distributions.

Integrating LNAPL saturations over a vertical slice of the subsurface yields subsurface LNAPL-specific volumes, which are important for planning remedial cleanup activities (Wickramanayaque et al. 1991). Governmental regulatory agencies commonly require removing the LNAPL mass to the maximum extent practicable. Both the volume and architecture of the LNAPL body influence the performance of any remediation effort. Several authors have proposed methods to calculate subsurface LNAPL-specific volumes following accidental spills on the soil surface or by leaking underground storage tanks, mostly by utilizing fluid levels measured in monitoring wells (e.g., Charbeneau et al. 2000; Farr et al. 1990; Lenhard and Parker 1990; Lenhard et al. 2017; Sleep et al. 2000). Closed-form analytical equations are obtained when the Brooks and Corey S-P model is used to predict subsurface LNAPL-specific volumes (Farr et al. 1990; Lenhard and Parker 1990). Numerical integration, on the other hand, is needed when the van Genuchten S-P model is employed to predict subsurface LNAPL volumes (Parker and Lenhard 1989). Throughout this chapter, we will use the terms soils and porous media interchangeably, noting that pedogenesis processes may substantially influence hydraulic properties (Fogg and Zhang 2016).

An unresolved issue still is that all porous media do not necessarily have normal or lognormal pore-size distributions. Many natural porous media have multimodal pore-size distributions as shown by Peters and Klavetter (1988), Durner (1994), Romano et al. (2011), Wijaya and Leong (2016), Madi et al. (2018), among many others. The focus of this chapter is comparing predictions of subsurface LNAPL distributions in porous media when unimodal and multimodal pore-size distributions are assumed. We present our results after discussing the literature and data used for our calculations.

3.2 Pore Structures

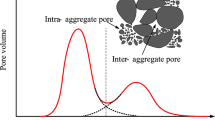
Soils are made up of mostly mineral particles of different sizes (e.g., sand, silt, and clay). In their natural state, these components are often aggregated by means of a series of physical, chemical, and/or biological processes to create structures of different shapes and sizes. The aggregates commonly possess internal voids or pores of varying sizes, leading to a dual-porosity porous medium. Such a medium typically has larger (interaggregate) pores between the aggregates and smaller (intra-aggregate) pores within the aggregates. Pore sizes may range from macropores (larger than 50 nm) to mesopores (between 2 and 50 nm) to micropores (smaller than 2 nm) according to the International Union of Pure and Applied Chemistry (IUPAC).

Pore sizes in soils can be measured by various techniques as described by Dane and Topp (2002), such as mercury porosimetry, thermal porosimetry, nitrogen sorption, microscopy or x-ray tomography. Soils typically have a normal or lognormal pore-size distribution, generally leading to unimodal characteristics since most soils are made up of well-graded particles. However, many soils have more complex pore systems with bimodal or multimodal pore-size distributions (Peters and Klavetter 1988; Romano et al. 2011; Wijaya and Leong 2016; Madi et al. 2018).

Pore sizes govern the ability of porous media to retain fluids against fluid pressures. For example, fine-textured soils with their higher percentages of clay (> 50%) can drain water at low capillary pressures (0.01 MPa) similar as coarser-textured soils. This behavior is more related to the pore-size distribution than the grain size of the porous media. Bimodal or multimodal pore-size distributions can be found also in structured soils and fractured rocks containing large pores (fractures) interspersed with smaller and less permeable micropores of the soil or rock matrix (Peters and Klavetter 1988; Gerke and van Genuchten 1993). Multimodal pore-size distributions occur because of irregular particle-size distributions, the creation of secondary porosity as a result of genetic or other processes (such as physical or chemical aggregation, or biological processes), and/or the effects of glaciation (moraine) or solifluction. Many tropical soils (such as Ultisols and Oxisols) and volcanic soils (Andisols) frequently exhibit multimodal pore-size distributions (Spohrer et al. 2006; Alfaro Soto et al. 2008; Rudiyanto et al. 2013; Seki et al. 2021).

Pore sizes and their geometry affect S-P relations. Soils with unimodal and multimodal pore-size distributions often have very dissimilar S-P relationships. Mathematical functions used to describe unimodal pore-size distributions, hence, may be inadequate for describing multimodal pore-size distributions without adjustments. The standard Brooks and Corey (1964) and van Genuchten (1980) S-P models are applicable to media having normal or lognormal pore-size distributions, but may be inappropriate for predicting LNAPL distributions in porous media having multimodal pore- or particle-size distributions.

3.3 Water and LNAPL Saturations

In this section, several fluid and soil properties such as interfacial tensions, wettability, and capillary pressures are described briefly since they are important for calculating subsurface fluid saturation distributions. Additional information can be found in Chap. 2. Our discussion refers to continuous fluid phases (no fluid entrapment or fluid films).

When more than one fluid phase exists in a porous medium, interfaces will develop between the immiscible fluid phases. At the interfaces, there will likely be an imbalance of attractive forces causing the interfaces to contract, thus forming an interfacial tension (commonly called surface tension when between a gas and a liquid). A difference in fluid pressure across the interfaces will cause them to have a curvature with the convex side having the greater fluid pressure. The degree of curvature depends on the magnitude of the pressure difference between the immiscible fluid phases.

Wettability is the preference of a fluid to spread or adhere to a surface. Generally, the surface is considered to be a solid (porous media grains and/or aggregates). Several different types of wettability may exist, such as fractional wettability and mixed wettability (Tiab and Donaldson 1996), but these will not be discussed in this chapter. We will focus on porous media having a singular or constant wettability. Fluids that wet solid surfaces in preference to other fluids will make a contact angle less than 90 degrees when measured from the solid surface, and are then referred to as the wetting fluid. When a fluid spreads completely on a solid surface, the contact angle is 0 degrees. Different levels of wetting have been recognized. Strong wetting is when the contact angle is less than 30 degrees, moderate wetting when the contact angle is 30°–75°, and neutral wetting when the contact angle is 75°–105°. The other fluid in a two-fluid system is then referred to as the nonwetting fluid.

In porous media containing three fluids (e.g., air, a LNAPL, and water), wettability preference can refer also to which fluid will spread on another fluid (Parker et al. 1987; Tiab and Donaldson 1996). The fluid that wets the solids is the wetting fluid. The fluid that wets the wetting fluid is typically referred to as having intermediate wettability. The fluid wetting the intermediate wetting fluid is referred to as the nonwetting fluid. Neglecting fluid films, wettability dictates which fluid will preferentially occupy what pore sizes. The wetting fluid will generally occupy the smallest pores and the nonwetting fluid the largest pores. Fluids with intermediate wettability will occupy the intermediate-sized pores.

The fluid pressure difference across the interface of immiscible fluid phases is called the capillary pressure. If the capillary pressure is 0, then the interface will not be curved (such as a LNAPL on top of water in a jar). If the capillary pressure is greater than 0, then the interfaces will be curved with the relative wetting fluid on the concave side of the curvature. For example, water will be on the concave side of a curved air–water interface in a capillary tube inserted in a pool of water. Water would be the wetting fluid at a sub-atmospheric pressure, and air would be the nonwetting fluid at atmospheric pressure. The capillary pressure across interfaces is related to the interfacial tension between the relative wetting and nonwetting fluids and the radii of curvature of the interfaces in the orthogonal directions. This relationship is called the Laplace equation of capillarity (Corey 1994):

$$P_{c} = \sigma \left( {\frac{1}{{R_{1} }} + \frac{1}{{R_{2} }}} \right)$$
(3.1)

where \(\sigma\) is the interfacial tension of the fluid pair at the interface, and \(R_{1}\) and \(R_{2}\) are the radii of curvature of the interface in orthogonal directions.

The radii of curvature of the interfaces (\(R\)) can be related to pore radii by the contact angle the wetting fluid makes with the porous media solids such as

$$R = r/\cos \gamma$$
(3.2)

where \(r\) is the pore radius and \(\gamma\) the contact angle. If the cross-sectional area across a fluid interface is assumed to be circular, in which case \(R_{1} = R_{2}\), the Laplace equation reduces to

$$P_{c} = 2\sigma \cos \gamma /r$$
(3.3)

which is commonly given in textbooks. The above shows that the capillary pressure can be used to index pore sizes in which fluid interfaces occur, and to determine fluid saturations.

3.4 Capillary Pressure–Saturation Curves

If two immiscible fluids are present in a porous medium, fluid interfaces only occur between the two fluids. For an air–water fluid system, the fluid interfaces are between air and water. The degree of curvature of the air–water interfaces (i.e., the air–water capillary pressure) can index what pore sizes are occupied by which fluids (the Laplace equation of capillarity and wettability). The capillary pressure will then index the fluid saturations. Air–LNAPL–water fluid systems, where water is the wetting fluid and LNAPL has intermediate wettability between air and water, will have two types of fluid interfaces: one set of interfaces between the LNAPL and water and one set between air and the LNAPL. The radii of curvature of the two sets of interfaces (i.e., the capillary pressures) will be different because the fluids will occupy different pore sizes. Under this wettability (water is the wetting fluid), the LNAPL–water capillary pressure has long been known to index the water saturation. The air–LNAPL capillary pressure then indexes the total-liquid (LNAPL plus water) saturation as advanced by Leverett (1941). The difference between total-liquid saturation and water saturation is the LNAPL saturation.

The relationships between capillary pressure and saturation can be measured by either increasing or decreasing the capillary pressure or the fluid saturation and measuring the changes in fluid saturation or capillary pressure. When the air–water (for a two-fluid system) or LNAPL–water (for a three-fluid system) capillary pressure in water-wet porous media is increased from the completely water-saturated state, the resulting saturation path is called a drying (or drainage) process with regard to the wetting fluid. When the air–water (two-fluid system) or LNAPL–water (three-fluid system) capillary pressure is decreased, it is a wetting (or imbibition) process with regard to the wetting fluid. An example of an S-P curve for an air–water system is shown in Fig. 3.1 for a unimodal pore-size distribution when water is the wetting fluid. For the water drainage curve beginning at Sw = 1, the water saturation, at which there is no further water drainage when the air–water capillary pressure is increased, is shown as Swr. Commonly, Swr is called the residual (or irreducible) water saturation. For the water wetting (imbibition) curve beginning at Swr, air can be occluded by water during water imbibition (i.e., air can become discontinuous by being surrounded by water). The maximum occluded nonwetting fluid saturation (i.e., air) at a capillary pressure of 0 is shown as Snr. In the petroleum industry, the occluded nonwetting fluid is also called residual saturation, but its use generally is restricted to two-fluid systems (i.e., brine oil reservoirs). In the hydrology literature, Snr is also called a residual saturation. In air–LNAPL–water systems, however, LNAPL can become occluded by water and, also, can become essentially irreducible in pore wedges and bypassed pores following LNAPL drainage in the vadose zone. To distinguish between these two processes, Parker and Lenhard (1987) called discontinuous LNAPL occluded by water as entrapped LNAPL, and referred to essentially irreducible LNAPL in the vadose zone as residual LNAPL, which is similar to water residual saturation (i.e., irreducible saturations as the capillary pressures are increased). One can have be entrapped LNAPL in both the vadose and the water-saturated zones.

Fig. 3.1
A scatterplot of capillary pressure versus saturation. It has plots for the imbibition curve and drainage curve with a downward and an upward arrow, respectively, around them.

Hypothetical capillary pressure–saturation (S-P) curve when water is the wetting fluid

Full size image

The water drainage curve beginning at Sw = 1 in Fig. 3.1 and the water wetting curve beginning at Sw = Swr have been called main curves. Any wetting fluid drainage curve initiated from Sw < 1 or wetting process initiated from Sw > Swr is called a scanning curve. We note here also that S-P relationships are not unique. They are usually subject to hysteresis, which means that different S-P relations will occur depending on whether the fluids are draining or wetting. Nonwetting fluid entrapment, contact angle changes, and pore-size contrasts (the “ink-bottle effect” as described by Hillel 1980) are some reasons for hysteresis in S-P relations.

Mathematical models are often used to describe the S-P relationships. Common models are those by Brooks and Corey (1964), van Genuchten (1980), and Kosugi (1996). Here, we limit ourselves to van Genuchten’s formulation given by

$$\overline{S} = \left[ {1 + \left( {\alpha h_{c} } \right)^{n} } \right]^{ - m}$$
(3.4)

in which \(\alpha\), n, and m are quasi-empirical shape parameters, hc is the capillary pressure head, and \(\overline{S}\) is the effective wetting-fluid saturation given by:

$$\overline{S} = \left( {S - S_{r} } \right)/\left( {1 - S_{r} } \right)$$
(3.5)

where S is the actual wetting-fluid saturation and Sr the residual (or irreducible) wetting-fluid saturation. Equation (3.5) is generic for any fluid system and assumes that no entrapped (residual) nonwetting fluid is present (e.g., entrapped air in an air–water system).

For air–LNAPL–water fluid systems where water is the wetting fluid and LNAPL has intermediate wettability between air and water, two S-P relations are needed. One is the LNAPL–water S-P relationship, which relates the LNAPL–water capillary pressure to the water saturation. The second is the air–LNAPL S-P relationship, which relates the air–LNAPL capillary pressure to the total-liquid saturation. Both are needed to determine LNAPL saturations. When not considering entrapment of air and LNAPL, the effective water and effective total-liquid saturations in three-fluid air–LNAPL–water systems can be determined similarly to Eq. (3.5). The effective water saturation (\(\overline{S}_{\text{w}}\)) can be determined by replacing S and Sr in Eq. (3.5) by water saturation (Sw) and the residual water saturation (\(\overline{S}_{\text{wr}}\)), respectively, as

$$\overline{S}_{{{\text{w}}}} = \left( {S_{w} - S_{{{\text{wr}}}} } \right)/\left( {1 - S_{{{\text{wr}}}} } \right)$$
(3.6)

The effective total-liquid saturation (\(\overline{S}_{t}\)) can be determined by replacing S and Sr in Eq. (3.5) by the total-liquid saturation (St), which is the sum of the water and LNAPL saturations, and the residual water saturation (Swr), respectively, as

$$\overline{S}_{{{\text{t}}}} = \left( {S_{t} - S_{{{\text{wr}}}} } \right)/\left( {1 - S_{{{\text{wr}}}} } \right)$$
(3.7)

Figure 3.1 is typical for porous media having unimodal pore-size distributions. Alfaro Soto et al. (2008) measured the air–water capillary pressure–water content relations of soils from the state of São Paulo, Brazil that showed characteristics of bimodal or trimodal pore-size distributions (Fig. 3.2a). The curves are different from the unimodal curve shown in Fig. 3.1. Many formulations for multimodal S-P curves have been proposed over the years (Ragab et al. 1981; Smettem and Kirkby 1990; Othmer et al. 1991; Mallants et al. 1997; Alfaro Soto et al. 2008; Rudiyanto et al. 2013; Li et al. 2014). One of the best-known models was formulated by Durner (1994), based on van Genuchten's (1980) unimodal S-P model:

$$\overline{S} = \mathop \sum \limits_{i = 1}^{j} w_{i} \left[ {1 + \left( {\alpha_{i} h_{c} } \right)^{{n_{i} }} } \right]^{{ - m_{i} }}$$
(3.8)
Fig. 3.2
A graph of pressure head versus gravimetric water content. It has curves for soils 1, 2, 3, and 4 V G in a decreasing trend with fluctuations. A graph of the frequency distribution of pores versus pressure heads has fluctuating curves for soils 1, 2, 3, and 4.

Multimodal characteristics of soils from the state of São Paul, Brazil: a Capillary pressure–saturation curves, b pore-size distribution curves

Full size image

where j represents the number of subsystems composing the total pore distribution; wi are subcurve weight factors varying between 0 and 1, which sum to unity; and \(\alpha_{i}\), ni, and mi are the van Genuchten parameters of each subsystem. Similar combinations can be constructed using Brooks and Corey (1964) type subfunctions, including a mixture of different types of subfunctions (e.g., Zhang and Chen 2005; Dexter et al. 2008; Li 2014; Seki 2021). The fitted curves in Fig. 3.2a were obtained using multiple van Genuchten (1980) subcurves as expressed by Eq. (3.8).

The differences between the various curves in Fig. 3.2a are more clearly shown by their equivalent lognormal pore-size distributions given by P(hc) = dS(hc)/dlog(h) (Fig. 3.2b). The plots reflect the bimodal and trimodal structures of the soils. Figure 3.2a highlights the limitations of standard unimodal models (Fig. 3.1) when describing S-P relationships of aggregated soils or fractured rocks.

To investigate how the predictions of subsurface LNAPL distributions may differ using unimodal and multimodal S-P formulations, we considered two lateritic soils with multimodal pore structures. Alfaro Soto et al. (2019) extracted data for these two soils (Soils A and F) from Mallants et al. (1997). Figure 3.3 shows the air–water capillary pressure data and best-fit unimodal and multimodal S-P curves for both soils. The unimodal S-P curves are based on Eq. (3.4), and the multimodal curves (bi- and trimodal) are based on Eq. (3.8). Figure 3.4 further shows the lognormal pore-size distributions, obtained again using P(S) = dS(h)/dlog(h), for the soils in Fig. 3.3 as a function of pF = log (hc) with hc in cm. The two figures exhibit clear differences between the unimodal and multimodal curves.

Fig. 3.3
Two graphs of capillary pressure head versus water saturation. A, sandy loam, Rio Claro, Brazil, and B, silty clay, Sao Carlos, Brazil. Both have experimental data, unimodal, bimodal, and trimodal are in downward trend with fluctuations.

Measured capillary pressure head–saturation data and optimized (best-fit) curves assuming unimodal, bimodal, and trimodal pore-size distributions for a A sandy loam soil from Rio Claro, Brazil, and b a silty clay soil from São Carlos, Brazil (Alfaro Soto et al. 2019)

Full size image
Fig. 3.4
Two graphs of pore-size density versus capillary pressure head. A, sandy loam, Rio Claro, Brazil, and B, silty clay, Sao Carlos, Brazil, with fluctuating curves for unimodal, bimodal, and trimodal. Trimodal and bimodal have the highest peaks in graphs 1 and 2, respectively.

Relative pore-size distributions assuming unimodal, bimodal, and trimodal pore systems for (a) A sandy loam from Rio Claro, Brazil and (b) a silty clay from São Carlos, Brazil (Alfaro Soto et al. 2019)

Full size image

Figure 3.3a shows that the unimodal and multimodal S-P curves of the sandy loam soil are very similar (Fig. 3.3a) for capillary heads less than about 0.55 m (pF = 1.75). Between capillary heads of about 0.55–1.6 m (pF = 1.75–2.2), the multimodal S-P curves are slightly to the left of the unimodal S-P curve, indicating a somewhat greater volume of relatively large pores for the multimodal pore-size predictions within the range of corresponding pore sizes. The unimodal and multimodal S-P curves match again at a capillary head of around 1.6 m (pF = 2.2). At this point, the volume of pores larger than sizes corresponding to a capillary head of about 1.6 m is the same for the unimodal and multimodal S-P curves. Figure 3.4a shows the calculated pore-size density distributions of the sandy loam soil for the unimodal and bimodal sols, with the predicted distributions for the multimodal S-P formulation showing a greater density of pores with sizes corresponding to capillary heads of 0.55–1.6 m (pF = 1.75–2,2). Hence, a larger volume of pores is predicted (Fig. 3.4a) with the multimodal S-P curves in Fig. 3.3a for capillary heads between 0.55 and 1.6 m (Fig. 3.3a).

The smaller pores between capillary pressure heads of about 1.6 m (pF = 2.2) and 1000 m (pF = 5) occupy less volume when predicted with the unimodal S-P curve as compared to the multimodal S-P curves. For the range of pore sizes corresponding to capillary heads between 1.6 and 100 m (pF = 2.2–4.0), Fig. 3.4a shows a higher pore density for the unimodal S-P curve, but much less than the pore densities corresponding to capillary heads between 0.55 and 1.6 m. At a pF of about 4.0 in Fig. 3.4a, the pore densities predicted for the unimodal S-P curve show very low or negligible values to the end of the analyses, while the densities for the multimodal S-P curves increase again at a pF of 4.5, thus starting to form a second section of higher pore densities. After a pF of approximately 5, the pore densities of the multimodal distributions then begin decreasing until a pF of 6 (Fig. 3.4a), which is the end of the analyses. Still, based on the vertical shape of the unimodal S-P curve in Fig. 3.3a between capillary heads of 100 and 10,000 m, many pores smaller than those corresponding to a capillary head of 10,000 m are assumed to be present. For the multimodal S-P curves, almost all pores are larger than a size corresponding to a capillary head of 10,000 m since the associated water saturation value approaches zero.

For the silty clay soil, the unimodal and multimodal S-P curves are mostly very similar (Fig. 3.3b), except for capillary heads between 0.1 m and about 10 m (pF = 1–3). The multimodal S-P curves predicted larger volume of pore sizes within the range corresponding to capillary heads of 0.1 to 10 m (pF = 1–3), with the trimodal curve predicting a higher volume of these pores than the bimodal curve. Figure 3.4b shows that the predictions from the unimodal and multimodal S-P curves for the silty clay soil are very different for the pF range 1–3, clearly reflecting the different unimodal and multimodal pore structures. Within the pF range 1–3 (Fig. 3.4b), the multimodal curves show higher pore densities than the unimodal curve, especially in the larger pore sizes (i.e., lower pF values). Therefore, the multimodal S-P curves predict a higher volume of larger pores than the unimodal S-P curve here.

As noted by Mallants et al. (1997), the sandy loam soil showed a system of secondary (interaggregate) pores, and the silty clay soil a system of smaller primary (intra-aggregate) pores. The question is whether the differences in using unimodal pore-size S-P curves will yield dissimilar predictions of fluid behavior and subsurface LNAPL distributions, when using multimodal pore-size S-P curves. Whereas the unimodal and multimodal S-P curves are similar in some respects, will the differences yield dissimilar predictions, which will be investigated in the following section. This is addressed next.

3.5 Estimating LNAPL Saturations and Volumes from In-Well Thickness

The S-P relationships of porous media are useful for predicting the subsurface behavior of LNAPLs and for assessing subsurface LNAPL distributions to aid in designing LNAPL remedial operations. The relationships can be used in numerical multiphase flow and transport models for predicting transient fluid behavior. Assuming vertical equilibrium conditions, fluid levels in nearby monitoring wells can be employed to predict subsurface LNAPL distributions from S-P relationships. The predicted LNAPL and water saturations could then be utilized to predict LNAPL relative permeabilities and transmissivity as discussed in Chaps. 2 and 12.

Early approaches to calculate subsurface LNAPL volumes assumed that the LNAPL thickness in the subsurface is equal to that in the monitoring well. Later investigations, however, showed that the LNAPL thickness in a well is not a direct measurement of the LNAPL thickness in the subsurface (de Pastrovich et al. 1979; Mercer and Cohen 1990). Furthermore, using simple ratios of the LNAPL thickness in the subsurface to the LNAPL thickness in a well do not provide accurate predictions of actual LNAPL subsurface volumes (e.g., Hampton and Miller 1988).

Parker and Lenhard (1989), Farr et al. (1990) and Lenhard and Parker (1990) were the first to develop equations for calculating the volume of LNAPL in a vertical slice (the LNAPL-specific volume) of water-wet porous media using capillary pressure–saturation relationships, fluid and porous media properties, and the LNAPL thickness in a well. Parker and Lenhard (1989) also proposed equations for estimating the subsurface LNAPL transmissivity. The approach assumes good contact between the fluids in the subsurface and the well, and that the fluids are vertically static. Parker and Lenhard (1989), Farr et al. (1990), and Lenhard and Parker (1990) assumed all of the LNAPL to be mobile and continuous (i.e., nonhysteretic conditions). Later, API (2007), Jeong and Charbeneau (2014), Lenhard et al, (2017), and Wadill and Parker (1997) developed models accounting for immobile LNAPL in the unsaturated vadose and liquid-saturated zones.

The early and later models assumed applicability of unimodal pore-size distribution S-P models, such as the Brooks and Cory (1964) and van Genuchten (1980) equations. To show potential differences in the predictions of LNAPL saturation distributions when unimodal versus multimodal pore-size S-P formulations are used, Alfaro Soto et al. (2019) modified the API (2007) predictive model to include multimodal pore-size S-P formulation. They incorporated Durner’s model for the multimodal pore-size S-P formulations. For further details of the modifications, readers are referred to Alfaro Soto et al. (2019).

Figure 3.5 shows predicted air, LNAPL, and water saturations as determined from fluid levels in a nearby monitoring well using the API (2007) model assuming a unimodal pore-size S-P formulation and the modified API (2007) model with a multimodal pore-size S-P formulation for a hypothetical soil with a heterogeneous pore system (i.e., the multimodal pore-size distribution). Figure 3.5a shows the hypothetical fluid levels in the monitoring well, and Fig. 3.5b, c show predicted fluid saturations using the unimodal pore-size S-P formulation and multimodal pore-size S-P formulation, respectively. As noted earlier, porous media with heterogeneous pore systems containing secondary porosity or multiple systems of pores may not be correctly represented by sigmoidal-type capillary pressure curves.

Fig. 3.5
A 3-part illustration. A. A schematic of a well with levels labeled z o w, z a w, and z a o. B and C. 2 Graphs of saturation plot 2 curve and the segments are L N A P L saturation, potentiometric surface, air-L N A P L interface, air-L N A P L capillary pressure curve, and L N A P L saturation.

(Adapted from Alfaro Soto et al. 2019)

a Schematic of the elevation of fluids in a monitoring well. The elevations zgs, zao, zow, and zaw correspond to a datum located at or below zow, the height of the air–LNAPL interface in the well, the height of the LNAPL–water interface in the well, and the height of the water table without a LNAPL, respectively, bo represents the thickness of the LNAPL layer in the well, and ho and hw are the distance between the reference level and zao and zaw, respectively (after Farr et al. 1990); b representative distribution of LNAPL in a unimodal porosity medium; c representative distribution of LNAPL in a trimodal porosity medium.

Full size image

Alfaro Soto et al. (2019) calculated fluid saturations for a hypothetical scenario as a function of elevation using the API (2007) model for 2 m of LNAPL in nearby wells. They assumed air–water, air–LNAPL and LNAPL–water interfacial tensions of 65, 25, and 15 mN m−1, respectively, and a LNAPL specific gravity of 0.8. In the API (2007) model, they used parameters for both unimodal and multimodal pore-size S-P formulations obtained by curve fitting to measured data (Fig. 3.3). Figure 3.6 shows the predicted fluid distributions for the sandy loam soil, while predictions for the silty clay soil are shown in Fig. 3.7. In both Figs. 3.6 and 3.7, the upper plots (a) reflect predictions for the unimodal pore-size S-P formulation, and the lower plots (b) reflect the multimodal pore-size S-P formulation. The dashed lines in Figs. 3.6 and 3.7 furthermore indicate the elevation of the water table (i.e., where the water pressure is atmospheric) in a well screened only in the water-saturated zone.

Fig. 3.6
Two graphs of elevation versus saturation. The curves for S o, S o r, S w, and Z a w are in a fluctuating downward trend. The water table remains constant at an elevation of 2.0 and the L N A P L thickness on the y-axis is between 0.0 and 2.5. Values are approximated.

Calculated LNAPL, water, and immobile LNAPL saturation profiles for the sandy loam soil in Figs. 3.3 and 3.4 using a Unimodal and b multimodal pore-size distributions based on the fitted optimized S-P curves (modified from Alfaro Soto et al. 2019)

Full size image
Fig. 3.7
Two graphs of elevation versus saturation. The curves for S o, S o r, S w, and Z a w are in a fluctuating downward trend. The water table remains constant at an elevation of 2.0 and the L N A P L thickness on the y-axis is between 0.0 and 2.5. Values are approximated.

Calculated LNAPL, water, and immobile LNAPL saturation profiles for the silty clay soil in Figs. 3.3 and 3.4 using a Unimodal and b multimodal pore-size distributions based on the fitted optimized S-P curves (modified from Alfaro Soto et al. 2019)

Full size image

Examination of Figs. 3.6 and 3.7 shows that the elevations of the LNAPL–water and air–LNAPL interfaces in the well are approximately 0.38 and 2.4 m, respectively. Using these values, the elevation of the air–water interface in a well screened only in the water-saturated zone can be calculated following Lenhard and Parker (1990) as

$$z_{{{\text{aw}}}} = \left( {1 - \rho_{{{\text{ro}}}} } \right)z_{{{\text{ow}}}} + \rho_{{{\text{ro}}}} z_{{{\text{ao}}}}$$
(3.9)

where \(z_{{{\text{aw}}}}\), \(z_{{{\text{ow}}}}\), and \(z_{{{\text{ao}}}}\) are the elevations of the air–water, LNAPL–water, and air–LNAPL interfaces in wells, respectively, and \(\rho_{{{\text{ro}}}}\) is the LNAPL-specific gravity. From Eq. (3.9), the elevation of the air–water interface in the well is predicted to be 2.00, which agrees with Fig. 3.6 and 3.7 and confirms the estimates of the LNAPL–water and air–LNAPL interface elevations in the well.

LNAPL–water and air–LNAPL capillary heads can be calculated as a function of elevation and fluid levels in a well for equilibrium (static) conditions following Lenhard and Parker (1990) as

$$h_{{{\text{ow}}}} = \left( {1 - \rho_{{{\text{ro}}}} } \right)\left( {z - z_{{{\text{ow}}}} } \right)$$
(3.10)
$$h_{{{\text{ao}}}} = \rho_{{{\text{ro}}}} \left( {z - z_{{{\text{ao}}}} } \right)$$
(3.11)

where \(h_{{{\text{ow}}}}\) is the LNAPL–water capillary head, \(h_{{{\text{ao}}}}\) is the air–LNAPL capillary head, and z is elevation. The LNAPL–water and air–LNAPL capillary heads can then be scaled to yield equivalent air–water capillary heads (Parker et al. 1987). The scaling factors as estimated in API (2007) follow Lenhard and Parker (1987). An alternative scaling format is presented in Lenhard et al. (2017). The scaled LNAPL–water capillary heads estimate water saturations and the scaled air–LNAPL capillary heads total-liquid saturations using an air–water S-P curve, such as in Fig. 3.3.

Figure 3.6 shows that the unimodal and multimodal pore-size S-P formulations yield different predictions of subsurface fluid saturations above the water-saturated zone for the sandy loam soil. We assume the predicted fluid distributions in Figs. 3.6 and 3.7 are equilibrium (static) distributions so calculated scaled capillary heads can predict fluid distributions using Fig. 3.3. At an elevation of 2.5 m in Fig. 3.6a for the unimodal pore-size saturation distribution, which is only slightly higher than the LNAPL free surface, the LNAPL saturation is about 0.56 and the water saturation is about 0.44 for a total-liquid saturation of 1. The air–LNAPL capillary head at the 2.5 m elevation is 0.08 m [using Eq. (3.11)]. The scaled air–LNAPL capillary head is between 0.2 to 0.3 m, depending on the scaling format used. Based on the unimodal S-P curve in Fig. 3.3, the total-liquid saturation (\(S_{t}\)) should be 1 for these scaled air–LNAPL capillary heads. The LNAPL–water capillary head at 2.5-m elevation is 0.42 m [using Eq. (3.10)]. The scaled LNAPL–water capillary head is between 1.1 and 1.6 m. For this scaled LNAPL–water capillary head range, the water saturation (\(S_{w}\)) should be between about 0.46 and 0.56 using Fig. 3.3. Therefore, the LNAPL saturation should be between 0.44 (i.e., \(S_{t} - S_{w} = 1 - 0.56\)) and 0.54 (i.e., \(S_{t} - S_{w} = 1 - 0.46\)) using the scaled capillary pressures and Fig. 3.3, which is close to that estimated from Fig. 3.6a.

At 50 cm higher (elevation 3.0 m) in Fig. 3.6a, the LNAPL saturation is about 0.15 and the water saturation is about the same as for the 2.5-m elevation (i.e., 0.44) for a total-liquid saturation of about 0.59. It is not clear why the water saturation is not predicted to be lower in Fig. 3.6a at the 3.0 m-elevation because the LNAPL–water capillary head is greater than at the 2.5-m elevation. The air–LNAPL capillary head at the 3.0 m elevation is 0.48 m. The scaled air–LNAPL capillary head is between 0.8 and 1.25 m. For this scaled air–LNAPL capillary head range, the total-liquid saturation should be between about 0.52 and 0.72. The LNAPL–water capillary head at 3.0-m elevation is 0.52 m. The scaled LNAPL–water capillary head is between 1.4 and 2.25 m. For this scaled LNAPL–water capillary head range, the water saturation should be between about 0.42 and 0.54. The total-liquid, LNAPL, and water saturations from using the scaled capillary pressures and Fig. 3.3 agree with those estimated from Fig. 3.6a.

For the multimodal pore-size saturation distribution (Fig. 3.6b), the calculated air–LNAPL and LNAPL–water capillary heads and scaled capillary heads at the 2.5- and 3.0-m elevations are the same as for the unimodal pore-size saturation distribution (Fig. 3.6a) because \(z_{{{\text{ow}}}}\) and \(z_{{{\text{ao}}}}\) are unchanged. At an elevation of 2.5 m in Fig. 3.6b for the multimodal pore-size distribution, the LNAPL saturation is about 0.63 and the water saturation about 0.37 for a total-liquid saturation of 1. The scaled air–LNAPL capillary head, which is equal to an equivalent air–water capillary head, is between 0.2 and 0.3 m. For this scaled air–LNAPL capillary head range, the total-liquid saturation should be 1 using Fig. 3.3. The scaled LNAPL–water capillary head is between 1.1 and 1.6 m. For this scaled LNAPL–water capillary head range, the water saturation should be between about 0.44 and 0.5.

At 50 cm higher (elevation 3.0 m), the LNAPL saturation is about 0.08 and the water saturation is about 0.42 for a total-liquid saturation of about 0.5. The air–LNAPL capillary head at the 3.0-m elevation is 0.48 m. The scaled air–LNAPL capillary head is between 0.8 and 1.25 m. For this scaled air–LNAPL capillary head range, the total-liquid saturation should be between about 0.48 and 0.72. The LNAPL–water capillary head at 3.0-m elevation is 0.52 m. The scaled LNAPL–water capillary head is between 1.4 and 2.25 m. For this scaled LNAPL–water capillary head range, the water saturation should be between about 0.42 and 0.5. The total-liquid, LNAPL, and water saturations from using the scaled capillary pressures and Fig. 3.3 agree with those estimated from Fig. 3.6b.

There is reasonable agreement between the unimodal and multimodal pore-size saturation distributions in Fig. 3.6 and saturations estimated from calculated scaled capillary heads using Fig. 3.3. This because the S-P curves are relatively similar for air–water (scaled) capillary heads less than a few meters. However, because the multimodal S-P curve in Fig. 3.3 is slightly to the left of the unimodal S-P curve for the scaled capillary head range of 0.55–1.6 m, water saturations are less for the multimodal pore-size saturation distribution than the unimodal pore-size saturation distribution, which results in a larger LNAPL saturation for the multimodal pore-size saturation distribution when total-liquid saturation is 1. The slight differences in the unimodal and multimodal S-P curves can yield differences in predictions of subsurface LNAPL distributions, especially if the differences involve larger pores. When LNAPL accumulates above the water-saturated zone, LNAPL will always occupy the larger pores if it has intermediate wettability between water and air.

The differences between the unimodal and multimodal predictions in Fig. 3.6 can be explained also in another way. For equilibrium (static) conditions, the air–LNAPL capillary head is related to the LNAPL–water capillary head at a given elevation using Eqs. (3.10) and (3.11), i.e., for static \(z_{{{\text{ow}}}}\) and \(z_{{{\text{ao}}}}\). Consider Fig. 3.3 at an air–water capillary head of 1 m where the unimodal and multimodal S-P curves begin to show differences. From the scaling format of Parker et al. (1987), the air–water capillary head is the scaled capillary head, which can be used to calculate the LNAPL–water capillary head (\(h_{{{\text{ow}}}}\)) by dividing by the LNAPL–water scaling factor. This leads to a value of 0.23 m for \(h_{{{\text{ow}}}}\) when the Lenhard and Parker (1987) and API (2007) LNAPL–water scaling factor is used, and a value of 0.37 m for \(h_{{{\text{ow}}}}\) when the Lenhard et al. (2017) LNAPL–water scaling factor is used. Using these values in Eq. (3.11) gives either an elevation (z) of 1.53 m for the Lenhard and Parker (1987) and API (2007) LNAPL–water scaling factor or an elevation (z) of 2.25 m for Lenhard et al. (2017) LNAPL–water scaling. Both of these elevations are below the air–LNAPL interface elevation in the well at 2.4 m; therefore, the sandy loam soil would be total-liquid saturated at these elevations. The same results are obtained when both elevations are used in Eq. (3.10), i.e., negative air–LNAPL capillary heads result, which indicate that the total-liquid saturation would be 1. For the scaled LNAPL–water capillary head of 1 m, water saturation would be approximately 0.6 for the unimodal S-P curve and approximately 0.54 for the multimodal S-P curves, which shows that higher LNAPL saturations result when using multimodal S-P relations as shown in Fig. 3.6. Even though the unimodal and multimodal S-P curves are generally similar for about 5 m above the water-saturated zone (Fig. 3.3), the slight differences for the larger pores still produced marked differences in the subsurface LNAPL saturation predictions. This may be important for planning remedial operations.

Figure 3.7 shows that the unimodal and multimodal pore-size S-P formulations yield significantly different saturation distributions for the silty clay soil. The calculated air–LNAPL and LNAPL–water capillary heads and scaled capillary heads at the 2.5- and 3.0-m elevations for Fig. 3.7 are the same as for Fig. 3.6, because, \(z_{{{\text{ow}}}}\) and \(z_{{{\text{ao}}}}\) are at the same elevations. For the unimodal pore-size distribution (Fig. 3.7a), the LNAPL saturation at the 2.5-m elevation is about 0.25 and the water saturation about 0.72 for a total-liquid saturation of 0.97. The scaled air–LNAPL capillary head is between 0.2 and 0.3 m. For this scaled air–LNAPL capillary head range, the total-liquid saturation should be close to 1 (i.e., 0.98–1) using Fig. 3.3. The scaled LNAPL–water capillary head is between 1.1 and 1.6 m. For this scaled LNAPL–water capillary head range, water saturation should be between about 0.78 and 0.82.

At a point 50 cm higher (elevation 3.0 m), the LNAPL saturation is about 0.13 and the water saturation about 0.7 for a total-liquid saturation of about 0.83. The air–LNAPL capillary head at 3.0-m elevation is 0.48 m. The scaled air–LNAPL capillary head is between 0.8 and 1.25 m. For this scaled air–LNAPL capillary head range, the total-liquid saturation should be between about 0.8 and 0.9. The LNAPL–water capillary head at 3.0-m elevation is 0.52 m. The scaled LNAPL–water capillary head is between 1.4 and 2.25 m. For this scaled LNAPL–water capillary head range, water saturation should be between about 0.7 and 0.74. The total-liquid, LNAPL and water saturations from using the scaled capillary pressures and Fig. 3.3 agree with those estimated from Fig. 3.7a.

For the multimodal pore-size saturation distribution (Fig. 3.7b), the LNAPL saturation at the 2.5-m elevation is about 0.14 and the water saturation is about 0.69, giving a total-liquid saturation of 0.83. The scaled air–LNAPL capillary head is between 0.2 and 0.3 m. For this scaled air–LNAPL capillary head range, the total-liquid saturation should be between about 0.87 and 0.91 using Fig. 3.3. The scaled LNAPL–water capillary head is between 1.1 and 1.6 m. For this scaled LNAPL–water capillary head range, the water saturation will be between about 0.67 and 0.7. The total-liquid, LNAPL, and water saturations from using the scaled capillary pressures and Fig. 3.3 are relatively close to those estimated using Fig. 3.7b.

At 50 cm higher (elevation 3.0 m), the LNAPL saturation is about 0.03 and the water saturation about 0.66, for a total-liquid saturation of about 0.69. The air–LNAPL capillary head at the 3.0-m elevation is 0.48 m. The scaled air–LNAPL capillary head is between 0.8 and 1.25 m. For this scaled air–LNAPL capillary head range, the total-liquid saturation should be between about 0.69 and 0.74. The LNAPL–water capillary head at 3.0-m elevation is 0.52 m. The scaled LNAPL–water capillary head is between 1.4 and 2.25 m. For this scaled LNAPL–water capillary head range, the water saturation is then between about 0.66 and 0.58. The total-liquid, LNAPL, and water saturations from using the scaled capillary pressures and Fig. 3.3 agree with those estimated using Fig. 3.7b.

There is again a reasonable agreement between the unimodal and multimodal pore-size saturation distributions in Fig. 3.7 and saturations estimated from calculated scaled capillary heads using Fig. 3.3. The differences between the unimodal and multimodal S-P curves in Fig. 3.3 show that the multimodal pore-size distribution predicts a larger volume of larger pores. The larger pores will contain more LNAPL and produce the differences in predicted LNAPL distributions seen in Figs. 3.6 and 3.7. When predicting subsurface LNAPL distributions, the size and volume of larger pores have a significant effect on the predictions. Significantly greater amounts of LNAPL can be predicted for relatively small differences in S-P curves. It is important to understand the potential distribution of pore sizes, especially larger pores. The multimodal pore-size S-P formulations were able to capture these effects of the larger pores in the sandy loam and silty clay soils when predicting subsurface LNAPL distributions above the water-saturated zone.

It should be noted that the symbol Sor in Figs. 3.6 and 3.7 denotes relatively immobile LNAPL saturation in the vadose and liquid-saturated zones present in the form of entrapped LNAPL, LNAPL films, and LNAPL wedges. As discussed in Chap. 2, the model by Lenhard et al. (2017) differentiates between relatively immobile LNAPL not occluded by water (residual LNAPL) and LNAPL occluded by water (entrapped LNAPL). The current version of the API (2007) model does not differentiate between the residual and entrapped LNAPL fractions and defines both as “residual LNAPL”.

3.6 Conclusions

Knowing the hydraulic properties of porous media is very important for predicting subsurface LNAPL distributions. Correctly characterizing the pore-size distribution, especially the larger pores, is essential for accurately predicting LNAPL saturations. Appropriate S-P formulations hence must be used to capture multimodal pore-size structures. Our investigations show that unimodal and multimodal S-P formations yield different subsurface LNAPL saturations when LNAPL collects above the water-saturated zone, even when the S-P curves appear to be similar at scaled capillary pressures less than a couple of meters, especially for the sandy loam soil. If the larger pores are not properly characterized, then significant differences in predicted LNAPL saturations will be obtained. Our results suggest that the efficiency of certain technologies for recovering LNAPL released to groundwater will depend on the pore structure (i.e., unimodal versus multimodal distributions) of the subsurface. Erroneous predictions of potential LNAPL recoveries using conventional techniques hence may result if the pore system is not defined correctly.

Although more research is needed to identify the influential parameters in the distribution of multimodal pores, it is necessary to recognize that in practice, during the soil characterization and field contamination stages, efforts should be made to identify potential pore structures. Soil aggregate development, minerality, and degree of weathering are important factors. Additionally, the implementation of multimodal formulations is recommended to fully capture the effects of subsurface heterogeneity on the LNAPL distribution. Multimodal pore-size distributions can also affect relative permeability and LNAPL transmissivity estimates, which will impact potential LNAPL recoverability and such processes as vapor migration, mass partitioning, and natural source-zone depletion.