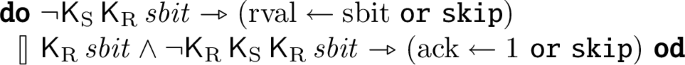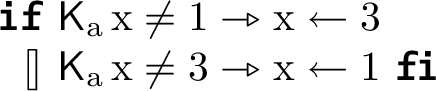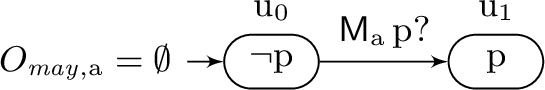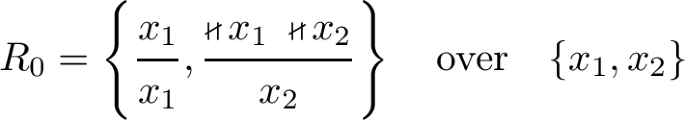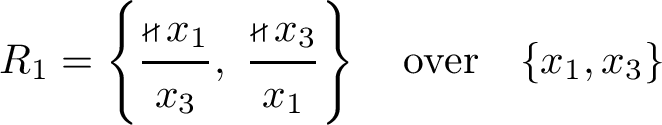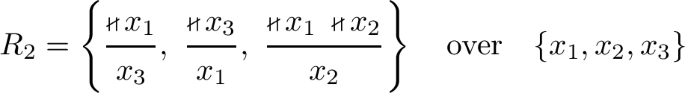Interpreting Knowledge-based Programs

Abstract

Knowledge-based programs specify multi-agent protocols with epistemic guards that abstract from how agents learn and record facts or information about other agents and the environment. Their interpretation involves a non-monotone mutual dependency between the evaluation of epistemic guards over the reachable states and the derivation of the reachable states depending on the evaluation of epistemic guards. We apply the technique of a must/cannot analysis invented for synchronous programming languages to the interpretation problem of knowledge-based programs and demonstrate that the resulting constructive interpretation is monotone and has a least fixed point. We relate our approach with existing interpretation schemes for both synchronous and asynchronous programs. Finally, we describe an implementation of the constructive interpretation and illustrate the procedure by several examples and an application to the Java memory model.

1 Introduction

Knowledge-based programs [14] describe multi-agent systems based on explicit knowledge tests on what an agent knows or does not know about itself, other agents, and the environment: Extending standard programs, an agent may look beyond what it can directly observe by reasoning about the possible states of the other agents and the environment in all possible program executions. Such non-local, epistemic conditions abstract from how an agent may learn and record particular environmental facts or information about other agents. Thus knowledge-based programs rather are specifications of (multi-agent) protocols that may be implemented by standard, directly executable programs. For being implementable in the first place, however, it has to be ensured that the knowledge guards can be resolved consistently given all possible program executions.

Consider for example a bit transmission [14, Ex. 4.1.1, Ex. 7.1.1], where a sender S has to transmit a bit ${\textrm{sbit}}$ over a lossy channel to a receiver R who has to acknowledge the reception, again over a lossy channel. This can be modelled by a knowledge-based program over the state variables ${\textrm{sbit}} \in \{ 0, 1 \}$, ${\textrm{rval}} \in \{ \bot , 0, 1 \}$, and ${\textrm{ack}} \in \{ 0, 1 \}$ as follows: S can only directly observe (read) ${\textrm{sbit}}$ and ${\textrm{ack}}$, and R only ${\textrm{rval}}$ (but both may write all variables); $( \textsf{K} _{\textrm{R}}\!\mathop {}{\textrm{sbit}} = 0) \vee ( \textsf{K} _{\textrm{R}}\!\mathop {}{\textrm{sbit}} = 1)$ expresses that R knows ${\textrm{sbit}}$’s value and is abbreviated by $\textsf{K} _{\textrm{R}}\!\mathop {} sbit$. The behaviour description consists of a looping guarded command with two branches that is started with ${\textrm{rval}} = \bot$ and ${\textrm{ack}} = 0$, but ${\textrm{sbit}}$ left undetermined:

The guarded branches are separated by a , or means a non-deterministic choice, and skip doing nothing: ${\textrm{S}}$ sends the bit as long as it does not know that ${\textrm{R}}$ received it, and ${\textrm{R}}$ keeps acknowledging once it has learnt the bit and does not know that ${\textrm{S}}$ knows this fact. The epistemic formulæ $\textsf{K} _{{\mathrm {}}}\!\mathop {}\varphi$ in the program are to be interpreted as in classical Kripke semantics: $\varphi$ holds in all states (or worlds) that agent a currently deems possible. Which states these are is regulated on the one hand by what a can observe: any state that is indistinguishable from the current one by the available observations is possible for the agent. In the example only ${\textrm{S}}$ can observe ${\textrm{sbit}}$, though, due to the protocol, it should be possible that eventually ${\textrm{R}}$ knows its value. On the other hand, the possible states depend on which runs of the knowledge-based program may actually happen, i.e., which states are reachable taking epistemically guarded transitions: If only the actions of the program are taken, it is impossible to reach a state satisfying both ${\textrm{rval}} \ne \bot$ and ${\textrm{rval}} \ne {\textrm{sbit}}$, which, however, is present in the global state space; but it is decisive that it is not reachable in any execution in order to have some execution where $\textsf{K} _{{\textrm{R}}}\!\mathop {} sbit$ can become true.

The interpretation of knowledge-based programs hinges precisely on this mutual dependency between the evaluation of epistemic guards over the reachable states and the derivation of the reachable states depending on the evaluation of the epistemic guards. This implicit definition of the epistemic state of the agents by the observables and the reachable states of the commonly known protocol is in stark contrast to Baltag’s epistemic action models [4, 31], where the epistemic state is given and manipulated explicitly. In many cases, including the bit transmission protocol, the reachable state space may be computed using static analysis techniques without taking into account the epistemic nature of the guards. However, the interplay between knowledge and reachability may sometimes become more intricate: The more states are reachable the less is known definitely, and the guards will in turn influence what is reachable positively or negatively.

Consider, for another example, a variable setting problem [14, Exc. 7.5] involving a single agent ${\textrm{a}}$ and a single state variable ${\textrm{x}} \in \{ 0, 1, 2, 3 \}$, where ${\textrm{a}}$ cannot observe ${\textrm{x}}$ directly. The agent executes the following guarded command starting with ${\textrm{x}} = 0$:

Being an initial condition, ${\textrm{x}} = 0$ is reachable, whereas ${\textrm{x}} = 2$ is not reachable as 2 is never assigned. However, two different sets of reachable states make for a consistent interpretation of the knowledge guards for the remaining values: $\{ {\textrm{x}} = 0, {\textrm{x}} = 1 \}$, where $\textsf{K} _{{\textrm{a}}}\!\mathop {}{\textrm{x}} \ne 1$ is false and $\textsf{K} _{{\textrm{a}}}\!\mathop {}{\textrm{x}} \ne 3$ is true, and $\{ {\textrm{x}} = 0, {\textrm{x}} = 3 \}$, with the opposite results. The singleton set $\{ {\textrm{x}} = 0 \}$ is ruled out, since both guards would be true such that ${\textrm{x}} = 3$ and ${\textrm{x}} = 1$ are reachable; and $\{ {\textrm{x}} = 0, {\textrm{x}} = 1, {\textrm{x}} = 3 \}$ is impossible, since both guards are false and thus neither ${\textrm{x}} = 1$ nor ${\textrm{x}} = 3$ are reachable. Breaking this cycle by making one of the transitions unconditional on knowledge as, e.g., in

yields a knowledge-based program with the unique consistent interpretation $\{ {\textrm{x}} = 1, {\textrm{x}} = 2 \}$. For computing its behaviour, however, several steps are needed, first reasoning that ${\textrm{x}} = 1$ is reachable, then that ${\textrm{x}} = 3$ is not reachable, and, finally, that ${\textrm{x}} = 2$ is reachable.

Related Work. In their introduction and seminal treatise on knowledge-based programs [13, 14], Fagin et al. characterise the unique interpretability of such programs by their “dependence on the past” w.r.t. some non-empty class of transition systems: The evaluation of knowledge guards in a state coincides for all interpretations in the class that share a common past of the state. A sufficient condition for this dependence is that the program “provides epistemic witnesses” for all interpretations of the class such that not knowing something at some point in time has a counter example in the past. A sufficient condition for this provision, in turn, is that the program is “synchronous”, i.e., that all agents can determine the global time from their local states. For example, the bit transmission protocol provides epistemic witnesses and thus is uniquely interpretable; but it is not synchronous. The cycle-breaking variable setting program is also uniquely interpretable, but does not provide epistemic witnesses. For “asynchronous” knowledge-based programs, De Haan et al. [10] suggest to rely on classical iteration of the non-monotone reachability functional that interprets the knowledge modalities according to what currently is assumed to be reachable. The computation process is started with all states assumed to be reachable and stops when some set of states is repeated. This approach fixes some semantics for all knowledge-based programs, also for those which are cyclic and contradictory or only self-fulfilling.

The problem of mutual dependence of guard evaluation and reachability has also occurred in the design of synchronous programming languages [6] for embedded systems, like Esterel [7] or Lustre [18], which rely on “perfect synchrony”: a step for reacting to some inputs takes zero time and output signals are produced at exactly the same time as the input signals. Since thus the status of a signal to be produced can be queried at the same time, this requires “logical coherence” saying that a (non-input) signal is present in a step of execution if, and only if, a command emitting this signal is executed in this step. Whereas Lustre forbids cyclic programs on a syntactic basis, Berry’s approach to the semantics of Esterel [8] singles out “reactive” — at least one execution — and “determinate” — at most one execution — programs using a static executability analysis: It is computed which signals must be present, i.e., have to occur inevitably, and which signals cannot be present, i.e., have no emitting execution. This is also referred to as must/cannot analysis and has to be performed several times for finding a fixed point of all the signal statuses.

In logic programming involving “negation as failure” under- and over-approximations in terms of three- and four-valued logics lead to the “Kripke-Kleene fixpoint” and “well-founded” models; see [11] for an overview. There, however, the temporal dimension of reachability or executability is not involved. The “stable model semantics” [5, 16] stresses the rational inclusion or exclusion of atoms: A set of atoms M is “stable” for a logic program $\varPi$ if it coincides with the minimal set of atoms inferable from the “reduct” $\varPi _M$ which is obtained from $\varPi$ by deleting each clause that has a negative literal $\lnot p$ in its body with $p \in M$, and all negative literals in the bodies of the remaining clauses. The definition is not algorithmic or constructive; the minimality condition rules out self-fulfilling solutions, the reduction process avoids contradictions. Gelfond’s “epistemic specifications” [15] extend (disjunctive) logic programs with a modality $\textsf{K}$ for “subjective literals” for representing incomplete information in programs with several stable models.

Contributions. We apply the principles of the must/cannot analysis to the interpretability problem of knowledge-based programs. After recalling some basic notions of epistemic logic and epistemic transition structures (Sect. 2), we first recapitulate the approaches by Fagin et al. [14] and De Haan et al. [10] in terms of epistemically guarded transition systems, a syntax-agnostic format for knowledge-based programs (Sect. 3). For a more direct analysis, our account of those designs is state-based rather than run-based. We demonstrate the results and the limits of both interpretation schemes by several examples that illustrate (a-)synchronicity and non-monotone interpretation for cyclic, contradictory, or self-fulfilling programs. The latter behaviour is the main motivation for our reformulation of the interpretation problem in terms of epistemic must/can transition structures which offer lower and upper bounds on the behaviour of a knowledge-based program (Sect. 4). We show that this constructive interpretation is always monotone and yields a least fixed point. However, lower and upper bound of the fixed point need not always coincide and we relate decided fixed points with the notions of “providing epistemic witnesses” and synchronicity. We then derive a representation of the behaviour of a knowledge-based program as a general rule system with not only positive but also negative premisses (Sect. 5). Such rule systems correspond to logic programs involving “negation as failure” and the intended solutions form “stable models”. The must/can approximation technique, its monotonicity, and it fixed point properties directly transfer to such rule systems. We finally describe an implementation of our constructive interpretation approach in the “Temporal Epistemic Model Interpreter and Checker” (tEmIc, Sect. 6). For model checking interpreted knowledge-based programs, the tool supports CTLK, the combination of “Computational Tree Logic” (CTL) with epistemic logic. Moreover, this logic can also be used in program guards; the interpretation of such temporal-epistemic programs extends the previous approaches. We give some applications to the analysis of the Java memory model.

2 Epistemic Logic and Epistemic Transition Structures

We briefly summarise the basic notions of epistemic logic for expressing knowledge guards [30, 31]. We then define epistemic transition structures as the domain of interpretation of knowledge-based programs. These transition structures combine the temporal dimension of executing a program with the epistemic dimension for evaluating what agents know. Both the logic and the transition structures are built over an epistemic signature $\varSigma = ( P , { A })$ that consists of a set of propositions $P$ and a set of agents ${ A }$.

2.1 Epistemic Logic

An epistemic structure $K = (W, R, L)$ over $( P , { A })$ is given by a set of worlds W, an ${ A }$-family of epistemic accessibility relations $R = (R_{{\mathrm {}}} \subseteq W \times W)_{{\mathrm {}}\in { A }}$, and a labelling $L : W \rightarrow \wp P$ assigning each world a set of propositions. In concrete examples, we will require $R_{{\mathrm {}}}$ to be an equivalence relation such that if $(w_1, w_2) \in R_{{\mathrm {}}}$, then agent a cannot distinguish between the two worlds $w_1$ and $w_2$. The epistemic formulæ $\varphi \in \varPhi _{P, A}$ over $( P , { A })$ are defined by the following grammar:

$$\begin{aligned} \varphi&{\;{:}{:}\!\!=\;}\begin{array}{@{}l@{}} {\mathrm {}}\;|\; \textrm{false}\;|\; \lnot \varphi \;|\; \varphi _1 \wedge \varphi _2\;|\; \textsf{K} _{{\mathrm {}}}\!\mathop {}\varphi \end{array} \end{aligned}$$

where ${\mathrm {}}\in P$ and ${\mathrm {}}\in { A }$. The epistemic formula $\textsf{K} _{{\mathrm {}}}\!\mathop {}\varphi$ is to be read as “agent a knows $\varphi$”. We use the usual propositional abbreviations $\textrm{true}$ for $\lnot \textrm{false}$ and $\varphi _1 \vee \varphi _2$ for $\lnot (\lnot \varphi _1 \wedge \lnot \varphi _2)$. Furthermore, we consider the epistemic modality $\textsf{M}$ as the dual of $\textsf{K}$, such that $\textsf{M} _{{\mathrm {}}}\!\mathop {}\varphi$ abbreviates $\lnot \textsf{K} _{{\mathrm {}}}\!\mathop {}\lnot \varphi$ and is to be read as “agent a deems $\varphi$ possible”. The satisfaction relation of an epistemic formula $\varphi \in \varPhi _{P, A}$ over an epistemic structure $K = (W, R, L)$ over $( P , { A })$ at a world $w \in W$, written $K, w \models \varphi$, is inductively defined by

$$\begin{aligned} K, w&\models {\mathrm {}}\iff {\mathrm {}}\in L(w) \\ K, w&\not \models \textrm{false}\\ K, w&\models \lnot \varphi \iff K, w \not \models \varphi \\ K, w&\models \varphi _1 \wedge \varphi _2 \iff K, w \models \varphi _1 \text { and } K, w \models \varphi _2 \\ K, w&\models \textsf{K} _{{\mathrm {}}}\!\mathop {}\varphi \iff K, w' \models \varphi \text { f. a. } w' \in W \text { with } (w, w') \in R_{{\mathrm {}}} \end{aligned}$$

2.2 Epistemic Transition Structures

An epistemic transition structure combines a temporal transition relation with an epistemic accessibility relation over a common set of states. The transitions describe which states can be reached from a set of initial states, the accessibilities specify which states are indistinguishable. Knowledge formulæ are evaluated over the associated global epistemic structure. This derived structure has the reachable states as its worlds and reuses the accessibility relation and the labelling but restricted to the reachable states.

Formally, an epistemic transition structure $M = (S, E, L, S_0, T)$ over $( P , { A })$ is given by an epistemic structure (S, E, L), a set of temporally initial states $S_0 \subseteq S$, and a temporal transition relation $T \subseteq S \times S$. We write $S(M)$ for S, $T(M)$ for T, etc. The (temporally) reachable states ${S_{\omega }}(M) = \bigcup _{0 \le k} {S_{\omega }}(M)$ and transition relation ${T_{\omega }}(M) = \bigcup _{0 \le k} {T_{\omega }}(M)$ of M are inductively defined by

$$\begin{aligned}{} & {} {S_{\omega }}(M) = S_0 \text {,}\quad {S_{\omega }}(M) = {S_{\omega }}(M) \cup \{ s' \;| \text { ex. } s \in {S_{\omega }}(M) \text { s. t. } (s, s') \in T \} \ \text {;} \\{} & {} {T_{\omega }}(M) = \emptyset \text {,}\quad {T_{\omega }}(M) = {T_{\omega }}(M) \cup \{ (s, s') \in T \;|\; s \in {S_{\omega }}(M) \} \ \text {.} \end{aligned}$$

The associated epistemic structure of M is given by

$$\begin{aligned} K(M) = ({S_{\omega }}(M),E \cap {S_{\omega }}(M)^2,L \upharpoonright {S_{\omega }}(M)) \end{aligned}$$

where ${S_{\omega }}(M)^2$ abbreviates ${S_{\omega }}(M) \times {S_{\omega }}(M)$ and $L \upharpoonright {S_{\omega }}(M)$ denotes labelling L restricted to domain ${S_{\omega }}(M)$. The satisfaction relation of an epistemic formula $\varphi \in \varPhi _{P, A}$ over M at an $s \in {S_{\omega }}(M)$, written $M, s \models \varphi$, is defined as

$$\begin{aligned} M, s \models \varphi \iff K(M), s \models \varphi \ \text {.} \end{aligned}$$

The set of epistemic transition structures over $\varSigma = ( P , { A })$ sharing the same epistemic state basis $\textsf{B}= (S,E,L,S_0)$ is denoted by $\mathscr {M}_{\varSigma }(\textsf{B})$. We say that $M_1 \subseteq M_2$ for $M_1, M_2 \in \mathscr {M}_{\varSigma }(\textsf{B})$ if $T(M_1) \subseteq T(M_2)$ and similarly extend union and intersection from transition relations to epistemic transition structures.

3 Knowledge-based Programs

Knowledge-based programs extend standard programs by explicit knowledge tests. Their interpretation involves a cycle: the evaluation of the epistemic guards depends on the program’s reachable states, the derivation of the reachable states on the evaluation of the program’s epistemic guards.

We render knowledge-based programs in a syntax-agnostic format as epistemically guarded transition systems. Like epistemic transition structures, these guarded systems operate on a global set of states with epistemic accessibilities and a propositional labelling. All program steps are represented as knowledge-guarded actions of the form $\varphi \supset B$ with $\varphi$ an epistemic formula and B a relation on the semantic states. Knowledge-independent decisions are obtained by choosing $\varphi = \textrm{true}$, and any kind of program control structure can be expressed by a judicious choice of guarded actions.

Breaking up the cyclic step of assigning meaning to a knowledge-based program, an epistemically guarded transition system $\varGamma$ is interpreted over an epistemic transition structure M yielding another epistemic transition structure $\varGamma ^M$. A guarded action $\varphi \supset B$ of $\varGamma$ contributes those $(s, s') \in B$ for which $M, s \models \varphi$, where, in particular, s is reachable in M. What is sought for is a consistent interpretation with $\varGamma ^M = M$ such that reachability and knowledge are mutually justified. Finding such a balanced structure is complicated by the fact that the interpretation functional is not monotone in general: The more is reachable the less is known and this may make more or less states reachable.

After introducing and illustrating our format of knowledge-based programs we summarise and adapt two existing approaches to their interpretation that have been devised for run-based rather than state-based systems: De Haan et al. [10] propose to iterate the interpretation functional starting from an epistemic transition structure where all states are reachable. Iteration stops when either a fixed point is reached or, due to non-monotonicity, a contradiction is found. In this way all knowledge-based programs are assigned some semantics and there is no distinction between meaningful and contradictory or just self-fulfilling programs. The original approach by Fagin et al. [13, 14] characterises knowledge-based programs that admit a unique consistent interpretation by the notion of dependence on the past. A sufficient condition of providing epistemic witnesses is developed which, in particular, applies to the subclass of synchronous knowledge-based programs.

3.1 Epistemically Guarded Transition Systems

An epistemically guarded transition system $\varGamma = (S, E, L, S_0, \mathcal {T})$ over $( P , { A })$ is given by an epistemic state basis $(S, E, L, S_0)$ over $( P , { A })$ and a set $\mathcal {T}$ of epistemically guarded actions $\varphi \supset B$ consisting of an epistemic formula $\varphi \in \varPhi _{P, A}$ as guard and a transition relation $B \subseteq S \times S$.

Example 1

• (a) Consider the bit transmission problem of the introduction:

  

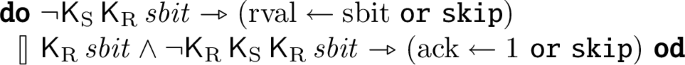
A sender agent ${\textrm{S}}$ sends a bit ${\textrm{sbit}} \in \{ 0, 1 \}$ to a receiver agent ${\textrm{R}}$ over an unreliable channel by setting ${\textrm{rval}} \in \{ \bot , 0, 1 \}$; and ${\textrm{R}}$ acknowledges the reception over an unreliable channel by setting ${\textrm{ack}} \in \{ 0, 1 \}$. Again, we abbreviate $( \textsf{K} _{{\textrm{R}}}\!\mathop {}\lnot {\textrm{sbit}}) \vee ( \textsf{K} _{{\textrm{R}}}\!\mathop {}{\textrm{sbit}})$ expressing that the receiver knows the bit to be sent by $\textsf{K} _{{\textrm{R}}}\!\mathop {} sbit$. We concretise the problem into an epistemically guarded transition system $\varGamma _{ bt } = (\textsf{B}_{ bt }, \mathcal {T}_{ bt })$ with $\textsf{B}_{ bt } = (S_{ bt }, E_{ bt }, L_{ bt }, S_{ bt , 0})$ over $\varSigma [bt] = ( P , { A })$ with $P = \{ {\textrm{sbit}}, {\textrm{rbit}}, {\textrm{snt}}, {\textrm{ack}} \}$ and ${ A } = \{ {\textrm{S}}, {\textrm{R}} \}$. Since we use a propositional encoding, we represent ${\textrm{rval}} \in \{ \bot , 0, 1 \}$ by a proposition ${\textrm{rbit}}$ for the transmitted bit and a proposition ${\textrm{snt}}$ for the validity of ${\textrm{rbit}}$. Further abbreviating the knowledge guards $\textsf{K} _{{\textrm{R}}}\!\mathop {} sbit$ by $\textsf{k}_{ r }$, $\textsf{K} _{{\textrm{S}}}\!\mathop {} \textsf{K} _{{\textrm{R}}}\!\mathop {} sbit$ by $\textsf{k}_{ sr }$, and $\textsf{K} _{{\textrm{R}}}\!\mathop {} \textsf{K} _{{\textrm{S}}}\!\mathop {} \textsf{K} _{{\textrm{R}}}\!\mathop {} sbit$ by $\textsf{k}_{ rsr }$, the transition system $\varGamma _{ bt }$ is graphically given by

The states $S_{ bt }$ comprise of $\{ {\mathrm {z_0}}, {\mathrm {z_1}}, \ldots , {\mathrm {z_7}} \}$ with $L_{ bt }({\mathrm {z_0}}) = \emptyset$, $L_{ bt }({\mathrm {z_1}}) = \{ {\textrm{snt}} \}$, ..., $L_{ bt }({\mathrm {z_7}}) = \{ {\textrm{sbit}}, {\textrm{rbit}}, {\textrm{snt}}, {\textrm{ack}} \}$ as outlined in the graph above; the set of initial states is $S_{ bt , 0} = \{ {\mathrm {z_0}}, {\mathrm {z_4}} \}$. The epistemic accessibility relations $E_{ bt , {\mathrm {}}}$ for ${\mathrm {}}\in { A }$ are given by observability sets $O_{ bt , {\mathrm {}}}$ that declare two states $s_1, s_2 \in S_{ bt }$ to be $O_{ bt , {\mathrm {}}}$-indistinguishable, written as $s_1 \mathrel {\sim _{O_{ bt , {\mathrm {}}}}} s_2$, if for all $p \in O_{ bt , {\mathrm {}}}$ it holds that $p \in L_{ bt }(s_1) \iff p \in L_{ bt }(s_2)$, and consequently $E_{ bt , {\mathrm {}}} = {\mathrel {\sim _{O_{ bt , {\mathrm {}}}}}}$, such that $E_{ bt , {\mathrm {}}}$ forms an equivalence relation. Due to ${\textrm{sbit}} \notin O_{ bt , {\textrm{R}}}$, the receiver ${\textrm{R}}$ cannot “see” ${\textrm{sbit}}$ and hence cannot distinguish between states ${\mathrm {z_0}}$ and ${\mathrm {z_4}}$, but ${\textrm{S}}$ can. On the other hand, ${\textrm{R}}$ can distinguish between ${\mathrm {z_1}}$ and ${\mathrm {z_5}}$ as ${\textrm{R}}$ has access to ${\textrm{rbit}}$. Finally, $\mathcal {T}_{ bt }$ consists of two epistemically guarded actions

$$\begin{aligned}{} & {} \lnot \textsf{K} _{{\textrm{S}}}\!\mathop {} \textsf{K} _{{\textrm{R}}}\!\mathop {} sbit \supset \{ ({\mathrm {z_{\text {i}}}}, {\mathrm {z_{\text {i}}}}) \;|\; 0 \le i \le 7 \} \cup \{ ({\mathrm {z_0}}, {\mathrm {z_1}}), ({\mathrm {z_2}}, {\mathrm {z_3}}), ({\mathrm {z_4}}, {\mathrm {z_5}}), ({\mathrm {z_6}}, {\mathrm {z_7}}) \} \ \ \text {and}\\{} & {} \textsf{K} _{{\textrm{R}}}\!\mathop {} sbit \wedge \lnot \textsf{K} _{{\textrm{R}}}\!\mathop {} \textsf{K} _{{\textrm{S}}}\!\mathop {} \textsf{K} _{{\textrm{R}}}\!\mathop {} sbit \supset {\begin{array}{@{}l@{}}\{ ({\mathrm {z_{\text {i}}}}, {\mathrm {z_{\text {i}}}}) \;|\; 0 \le i \le 7 \} \cup {}\end{array}}\\ {}{} & {} \qquad \qquad \qquad \qquad \qquad \quad \quad \{ ({\mathrm {z_0}}, {\mathrm {z_2}}), ({\mathrm {z_1}}, {\mathrm {z_3}}), ({\mathrm {z_4}}, {\mathrm {z_6}}), ({\mathrm {z_5}}, {\mathrm {z_7}}) \}\ \text {,} \end{aligned}$$

which directly reflect the sending and acknowledging actions of the bit transmission problem: The system can only advance from ${\mathrm {z_0}}$ to ${\mathrm {z_1}}$ (and ${\mathrm {z_4}}$ to ${\mathrm {z_5}}$), where sending has been done successfully, if ${\textrm{S}}$ does not know that ${\textrm{R}}$ knows the bit; but it need not make such progress, i.e., sending can be unsuccessful. Similarly, the system can only advance from ${\mathrm {z_1}}$ to ${\mathrm {z_3}}$ (and ${\mathrm {z_5}}$ to ${\mathrm {z_7}}$), where an acknowledgement has been sent successfully, if ${\textrm{R}}$ knows the bit and ${\textrm{R}}$ does not know that ${\textrm{S}}$ knows that ${\textrm{R}}$ knows the bit.

• (b) Consider the variable setting problem of the introduction for a single agent ${\textrm{a}}$:

  

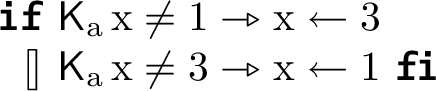
Encoding the integer $x \in \{ 0, 1, 2, 3 \}$ by two bits ${\mathrm {q_1}}$ and ${\mathrm {q_2}}$, we model the problem as the following epistemically guarded transition system $\varGamma _{ vs } = (\textsf{B}[vs], \mathcal {T}_{ vs })$ with $\textsf{B}[vs] = (S_{ vs },E_{ vs },L_{ vs },S_{ vs , 0})$ over $\varSigma [vs] = ( P , { A })$ with $P = \{ {\mathrm {q_1}}, {\mathrm {q_2}} \}$ and ${ A } = \{ {\textrm{a}} \}$:

$O_{ vs , {\textrm{a}}}$ represents a “blind” agent ${\textrm{a}}$ that deems all states equally accessible. State ${\mathrm {s_3}}$ is definitely not reachable. $\mathcal {T}_{ vs }$ consists of the epistemically guarded actions

$$\begin{aligned}\begin{gathered} \textsf{K} _{{\textrm{a}}}\!\mathop {}\lnot ({\mathrm {q_1}} \wedge \lnot {\mathrm {q_2}}) \supset \{ ({\mathrm {s_0}}, {\mathrm {s_1}}) \} \quad \text {and}\quad \textsf{K} _{{\textrm{a}}}\!\mathop {}\lnot (\lnot {\mathrm {q_1}} \wedge {\mathrm {q_2}}) \supset \{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \} \ \text {.} \end{gathered}\end{aligned}$$

   $\square$

3.2 Interpreting Epistemically Guarded Transition Systems

An epistemically guarded transition system $\varGamma = (S, E, L, S_0, \mathcal {T})$ over $( P , { A })$ is interpreted over an epistemic transition structure $M \in \mathscr {M}_{ P , { A }}(S, E, L, S_0)$ by interpreting each guarded action $(\varphi \supset B) \in \mathcal {T}$ w.r.t. M as

$$\begin{aligned}\textstyle {(\varphi \supset B)}^{M} = \{ (s, s') \in B \;|\; s \in {S_{\omega }}(M) \text { and } M, s \models \varphi \} \ \text {,} \end{aligned}$$

and combining these interpretations into the epistemic transition structure

$$\begin{aligned}\textstyle {\varGamma }^{M} = (S, E, L, S_0, \bigcup _{\tau \in \mathcal {T}} {\tau }^{M}) \ \text {.} \end{aligned}$$

We call M a solution for $\varGamma$ if ${\varGamma }^{M} = M$.

Example 2

For the bit transmission problem as described in Ex. 1(a), the epistemic transition structure $M_{ bt } = (\textsf{B}_{ bt }, T_{ bt })$ with $T_{ bt } = \{ ({\mathrm {z_{\text {i}}}}, {\mathrm {z_{\text {i}}}}) \;|\; i \in \{ 0,1,3,4,5,7 \} \} \cup \{ ({\mathrm {z_0}}, {\mathrm {z_1}}),({\mathrm {z_1}}, {\mathrm {z_3}}),({\mathrm {z_4}}, {\mathrm {z_5}}),({\mathrm {z_5}}, {\mathrm {z_7}}) \}$ satisfies ${\varGamma _{ bt }}^{M_{ bt }} = M_{ bt }$. This structure just omits the states ${\mathrm {z_2}}$ and ${\mathrm {z_6}}$ with $L_{ bt }({\mathrm {z_2}}) = \{ {\textrm{ack}} \}$ and $L_{ bt }({\mathrm {z_6}}) = \{ {\textrm{sbit}}, {\textrm{ack}} \}$ which are definitely not reachable, as $\textsf{K} _{{\textrm{R}}}\!\mathop {} sbit$ is false in ${\mathrm {z_0}} \sim _{O_{ bt , {\textrm{R}}}} {\mathrm {z_4}}$. Indeed,

$$\begin{aligned}{} & {} M_{ bt }, s \models \lnot \textsf{K} _{{\textrm{S}}}\!\mathop {} \textsf{K} _{{\textrm{R}}}\!\mathop {} sbit \iff s \in \{ {\mathrm {z_0}}, {\mathrm {z_1}}, {\mathrm {z_4}}, {\mathrm {z_5}} \} \\{} & {} M_{ bt }, s \models \textsf{K} _{{\textrm{R}}}\!\mathop {} sbit \iff s \in \{ {\mathrm {z_1}}, {\mathrm {z_3}}, {\mathrm {z_5}}, {\mathrm {z_7}} \} \\{} & {} M_{ bt }, s \models \lnot \textsf{K} _{{\textrm{R}}}\!\mathop {} \textsf{K} _{{\textrm{S}}}\!\mathop {} \textsf{K} _{{\textrm{R}}}\!\mathop {} sbit \iff s \in \{ {\mathrm {z_0}}, {\mathrm {z_1}}, {\mathrm {z_3}}, {\mathrm {z_4}}, {\mathrm {z_5}}, {\mathrm {z_7}} \} \end{aligned}$$

   $\square$

However, finding a solution is complicated by the fact that the functional of interpreting an epistemically guarded transition system over an epistemic transition structure is not monotone, in general, as illustrated by the following examples.

Example 3

• (a) Continuing Ex. 1(b) for the variable setting problem $\varGamma _{ vs }$, consider the epistemic transition structure $M_{ vs , 0} \in \mathscr {M}_{\varSigma [vs]}(\textsf{B}[vs])$ with the empty transition relation $T(M_{ vs , 0}) = \emptyset$, and hence ${S_{\omega }}(M_{ vs , 0}) = \{ {\mathrm {s_0}} \}$. Setting $M_{ vs , i+1} = {\varGamma _{ vs }}^{M_{ vs , i}}$ for $0 \le i \le 2$ we obtain successively

  $\tau$	${\tau }^{M_{ vs , 0}}$	${\tau }^{M_{ vs , 1}}$	${\tau }^{M_{ vs , 2}}$
  $\textsf{K} _{{\textrm{a}}}\!\mathop {}\lnot ({\mathrm {q_1}} \wedge \lnot {\mathrm {q_2}}) \supset \{ ({\mathrm {s_0}}, {\mathrm {s_1}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_1}}) \}$	$\emptyset$	$\{ ({\mathrm {s_0}}, {\mathrm {s_1}}) \}$
  $\textsf{K} _{{\textrm{a}}}\!\mathop {}\lnot (\lnot {\mathrm {q_1}} \wedge {\mathrm {q_2}}) \supset \{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$	$\emptyset$	$\{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$

  In particular, $M_{ vs , 2} = {\varGamma _{ vs }}^{M_{ vs , 1}} = {\varGamma _{ vs }}^{{\varGamma _{ vs }}^{M_{ vs , 0}}} = M_{ vs , 0}$. However, for $M_{ vs , 4}, M_{ vs , 5} \in \mathscr {M}_{\varSigma [vs]}(\textsf{B}[vs])$ with $T(M_{ vs , 4}) = \{ (\textrm{s}_0, \textrm{s}_1) \}$ and $T(M_{ vs , 5}) = \{ (\textrm{s}_0, \textrm{s}_2) \}$ we obtain that ${\varGamma _{ vs }}^{M_{ vs , 4}} = M_{ vs , 4}$ and ${\varGamma _{ vs }}^{M_{ vs , 5}} = M_{ vs , 5}$.

• (b) For capturing the cycle-breaking variable setting of the introduction consider the following epistemically guarded transition system $\varGamma _{ vsb } = (\textsf{B}_{ vs }, \mathcal {T}_{ vsb })$ over $\varSigma [vs]$ that shares the epistemic state basis $\textsf{B}[vs]$ with Ex. 1(b):

For $M_{ vsb , 0} = (\textsf{B}[vs], \emptyset )$ with ${S_{\omega }}(M_{ vsb , 0}) = \{ {\mathrm {s_0}} \}$, and setting $M_{ vsb , i+1} = {\varGamma _{ vsb }}^{M_{ vsb , i}}$ for $0 \le i \le 3$ we obtain successively

$\tau$	${\tau }^{M_{ vsb , 0}}$	${\tau }^{M_{ vsb , 1}}$	${\tau }^{M_{ vsb , 2}}$	${\tau }^{M_{ vsb , 3}}$
$\textsf{K} _{{\textrm{a}}}\!\mathop {}\lnot ({\mathrm {q_1}} \wedge \lnot {\mathrm {q_2}}) \supset \{ ({\mathrm {s_0}}, {\mathrm {s_1}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_1}}) \}$	$\emptyset$	$\emptyset$	$\emptyset$
$\textrm{true} \supset \{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$
$\textsf{K} _{{\textrm{a}}}\!\mathop {}\lnot (\lnot {\mathrm {q_1}} \wedge {\mathrm {q_2}}) \supset \{ ({\mathrm {s_0}}, {\mathrm {s_3}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_3}}) \}$	$\emptyset$	$\{ ({\mathrm {s_0}}, {\mathrm {s_3}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_3}}) \}$

For $M_{ vsb , 3}$ with ${S_{\omega }}(M_{ vsb , 3}) = \{ {\mathrm {s_0}}, {\mathrm {s_1}}, {\mathrm {s_3}} \}$ it finally holds that ${\varGamma _{ vsb }}^{M_{ vsb , 3}} = M_{ vsb , 3}$.    $\square$

3.3 Iteration Semantics

For illustrating the non-monotonicity of the interpretation functional we have started the interpretation sequence for $\varGamma$ with the smallest epistemic transition structure which suggests to look for a smallest fixed point — which need not exist. De Haan et al. [10] argue that a substitute consisting of the greatest fixed point would be more liberal. They construct a transfinite approximation sequence starting from an $N_0$ having all states reachable. For a successor ordinal $\alpha + 1$, the approximation $N_{\alpha +1}$ is just the interpretation of $\varGamma$ in $N_{\alpha }$; for a limit ordinal $\lambda$, the approximation $N_{\lambda } = \bigcap _{\alpha< \lambda } \bigcup _{\alpha \le \beta < \lambda } N_{\beta }$ is “the intersection of unions of approximations that are sufficiently close to the limit” [10, p. 269]. The latter is preferred over a union of intersections as it includes more states which implies less knowledge, such that “agents [know] facts only when there are good reasons for them” (ibid.). Due to cardinality reasons, the ordinal $\eta _{\varGamma } = \inf \{ \alpha \;|\; \text {ex. } \beta \text { s. t. } \alpha < \beta \text { and }N_{\alpha } = N_{\beta } \}$ exists. If $N_{\alpha +1} \subseteq N_{\alpha }$ for all $\alpha \ge \eta _{\varGamma }$, then $N_{\eta _{\varGamma }+1} = N_{\eta _{\varGamma }}$; otherwise there is some $\alpha \ge \eta _{\varGamma }$ such that $N_{\alpha +1} \not \subseteq N_{\alpha }$. Thus $\alpha _{\varGamma } = \inf \{ \alpha \;|\; \eta _{\varGamma } \le \alpha \text { and } (N_{\alpha } = N_{\alpha +1} \text { or } N_{\alpha +1} \not \subseteq N_{\alpha }) \}$ exists and the iteration semantics of $\varGamma$ is defined as $N_{\alpha _{\varGamma }}$. This yields the greatest fixed point if the interpretation functional is monotone.

Example 4

• (a) For the variable setting problem $\varGamma _{ vs }$ of Ex. 1(b) the interpretation sequence $(N_{ vs , \alpha })_{0 \le \alpha }$ starts with $N_{ vs , 0}$ showing $T(N_{ vs , 0}) = S_{ vs } \times S_{ vs }$. Using the epistemic transition structures from Ex. 3(a) it holds that $N_{ vs , k+1} = {\varGamma _{ vs }}^{N_{ vs , k}} = M_{ vs , 2}$ for k even and $N_{ vs , k+1} = M_{ vs , 1}$ for $k \ge 1$ odd. Thus, $N_{ vs , 1} = N_{ vs , 3}$ such that $\eta _{\varGamma _{ vs }} = 1 = \alpha _{\varGamma _{ vs }}$, since $T(N_{ vs , 2}) = \{ ({\mathrm {s_0}}, {\mathrm {s_0}}), ({\mathrm {s_0}}, {\mathrm {s_1}}), ({\mathrm {s_0}}, {\mathrm {s_2}}) \} \not \subseteq \emptyset = T(N_{ vs , 1})$. Hence the iteration semantics of $\varGamma _{ vs }$ is given by $N_{ vs , 1} = M_{ vs , 2}$; since its transition relation is empty, $\varGamma _{ vs }$ has the same iteration semantics as an epistemically guarded transition system without any guarded actions.

• (b) Computing the iteration semantics sequence $(N_{ vsb , \alpha })_{0 \le k}$ of the cycle-breaking variable setting $\varGamma _{ vsb }$ of Ex. 3(b) proceeds as $N_{ vsb , k} = M_{ vsb , k+1}$. Since this time the functional is monotone from $\alpha = 1$ onwards, the iteration semantics is $N_{ vsb , 2}$.

• (c) Consider the following epistemically guarded transition system $\varGamma _{ nc } = (\textsf{B}_{ vs },\mathcal {T}_{ nc })$ over $\varSigma _{ vs }$ that shares the epistemic basis $\textsf{B}[vs]$ with the variable setting problem $\varGamma _{ vs }$ of (a) and only adds the guarded action $\textsf{K} _{{\textrm{a}}}\!\mathop {}\lnot {\mathrm {q_2}} \supset \{ ({\mathrm {s_0}}, {\mathrm {s_3}}) \}$:

The interpretation process runs as for $\varGamma _{ vs }$, and the epistemic transition structure with the empty transition relation is also the iteration semantics of $\varGamma _{ nc }$. This time, however, there is a unique non-empty interpretation, viz. the transition structure consisting only of $({\mathrm {s_0}}, {\mathrm {s_1}})$. Finding this solution is not constructive and some speculation is necessary: there is no solution where ${\mathrm {s_2}}$ is reachable; if ${\mathrm {s_2}}$ were reachable, then ${\mathrm {s_1}}$ would be reachable leading to a contradiction due to the (non-)reachability of ${\mathrm {s_3}}$. Thus only the possibility of ${\mathrm {s_0}}$ and ${\mathrm {s_1}}$ being reachable, and ${\mathrm {s_2}}$ and ${\mathrm {s_3}}$ unreachable, remains.

• (d) For the epistemically guarded transition system $\varGamma _{ may }$ over $(\{ {\textrm{p}} \}, \{ {\textrm{a}} \})$ given by

  

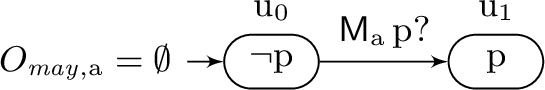
  the iteration process when started with $N_{ may , 0}$ having $T(N_{ may , 0}) = \{ {\mathrm {u_0}}, {\mathrm {u_1}} \} \times \{ {\mathrm {u_0}}, {\mathrm {u_1}} \}$ evaluates $\textsf{M} _{{\textrm{a}}}\!\mathop {}{\textrm{p}}$ to true and we obtain $N_{ may , 1}$ with $T(N_{ may , 1}) = \{ ({\mathrm {u_0}}, {\mathrm {u_1}}) \}$ which in turn is confirmed by the next iteration yielding a fixed point. This iteration semantics, however, has a touch of a “vaticinium ex eventu”: ${\textrm{p}}$ can be reached since ${\textrm{p}}$ may be reached.    $\square$

3.4 Unique Interpretation Solutions

A knowledge-based program can be executed reliably just step by step if each knowledge guard can be stably decided based on what has been computed up to the current point of execution. In particular, in order to obtain a solution by execution, knowledge must not be invalidated by information only to be gained later on. Conversely, if all knowledge guards can be decided by just looking to the past, there is at most a single solution.

Based on this observation, Fagin et al. [13, 14] develop a formal characterisation of unique interpretability by capturing the notion that solutions “depend on the past”. They then show that “providing epistemic witnesses” is a sufficient criterion for “dependence on the past”, which in turn always holds for “synchronous” programs. We briefly summarise their main line of argument adapting the demonstration from their run-based account for knowledge-based programs to our state-based epistemically guarded transition systems.¹

An epistemic formula $\varphi \in \varPhi _{P, A}$ is said to depend on the past w.r.t. a class of epistemic transition structures $\mathcal {M} \subseteq \mathscr {M}_{ P , { A }}(\textsf{B})$ if for all $M_1, M_2\in \mathcal {M}$ and all $k \in \mathbb {N}$ it holds that ${T_{\omega }}(M_1) = {T_{\omega }}(M_2)$ implies $M_1, s \models \varphi \mathrel {\iff } M_2, s \models \varphi$ for all $s \in {S_{\omega }}(M_1)\cap {S_{\omega }}(M_2)$; an epistemically guarded transition system $\varGamma = (\textsf{B}, \mathcal {T})$ over $( P , { A })$ is depending on the past w.r.t. $\mathcal {M}$ if every $\varphi$ in $(\varphi \supset B) \in \mathcal {T}$ depends on the past w.r.t. $\mathcal {M}$.

Example 5

For Ex. 3(a) neither $\textsf{K} _{{\textrm{a}}}\!\mathop {}\lnot ({\mathrm {q_1 }} \wedge \lnot {\mathrm {q_2}})$ nor $\textsf{K} _{{\textrm{a}}}\!\mathop {}\lnot (\lnot {\mathrm {q_1}} \wedge {\mathrm {q_2}})$ depends on the past w.r.t. $\{ M_{ vs , 0}, M_{ vs , 1} \}$. In particular, ${T_{\omega }}(M_{ vs , 0}) = \emptyset = {T_{\omega }}(M_{ vs , 1})$ and ${S_{\omega }}(M_{ vs , 0}) = \{ {\mathrm {s_0}} \} = {S_{\omega }}(M_{ vs , 1})$, but $M_{ vs , 0}, {\mathrm {s_0}} \models \textsf{K} _{{\textrm{a}}}\!\mathop {}\lnot ({\mathrm {q_1}} \wedge \lnot {\mathrm {q_2}})$ and $M_{ vs , 1}, {\mathrm {s_0}} \not \models \textsf{K} _{{\textrm{a}}}\!\mathop {}\lnot ({\mathrm {q_1}} \wedge \lnot {\mathrm {q_2}})$. Similarly for Ex. 3(b), these two formulæ do not depend on the past w.r.t. $\{ M_{ vsb , 0},M_{ vsb , 1},M_{ vsb , 2},M_{ vsb , 3} \}$, but they do w.r.t. $\{ M_{ vsb , 1},M_{ vsb , 2},M_{ vsb , 3} \}$.

An epistemically guarded transition system $\varGamma$ has at most one solution if, and only if, it depends on the past w.r.t. all its solutions. Due to the dependence on the past the successive reachable transition relations ${T_{\omega }}(M)$ of all solutions $M = {\varGamma }^{M}$, i.e., their pasts, coincide.

Proposition 1

Let $\varGamma = (\textsf{B}, \mathcal {T})$ be an epistemically guarded transition system over $\varSigma$. Then $\varGamma$ has at most one solution if, and only if, there is an $\mathcal {M} \subseteq \mathscr {M}_{\varSigma }(\textsf{B})$ with $\{ M \in \mathscr {M}_{\varSigma }(\textsf{B}) \;|\; {\varGamma }^{M} = M \} \subseteq \mathcal {M}$ such that $\varGamma$ depends on the past w.r.t. $\mathcal {M}$.

In order to obtain a solution of $\varGamma$ by execution, the system is interpreted repeatedly to construct the approximations $(M_k)_{0 \le k}$ with $M_{k+1} = {\varGamma }^{M_k}$ for $k \ge -1$ starting with some $M_{-1}$. Each approximation $M_k$ with $k \ge 0$ contributes a transition relation ${T_{\omega }}(M_k)$ which can be combined into a limit $M_{\omega }$. If $\varGamma$ depends on the past w.r.t. the class of epistemic transition structures from which the approximands are constructed and which also contains the limit, then the interpretation of the limit $M_{\omega }$ yields a fixed point.

Proposition 2

Let $\varGamma = (\textsf{B}, \mathcal {T})$ be an epistemically guarded transition system over $\varSigma$, let $\mathcal {M} \subseteq \mathscr {M}_{\varSigma }(\textsf{B})$ such that ${\varGamma }^{M} \in \mathcal {M}$ for every $M \in \mathcal {M}$ and $(\textsf{B}, \bigcup _{0 \le k} {T_{\omega }}(M_k)) \in \mathcal {M}$ for all $(M_k)_{0 \le k} \subseteq \mathcal {M}$ with ${T_{\omega }}(M_{k'}) = {T_{\omega }}(M_k)$ for all $k' \ge k \ge 0$, and let $\varGamma$ depend on the past w.r.t. $\mathcal {M}$. Let $M_{-1} \in \mathcal {M}$, $M_{i+1} = {\varGamma }^{M_i}$ for all $i \ge -1$, and $M_{\omega } = (\textsf{B}, \bigcup _{0 \le k} {T_{\omega }}(M_k))$. Then ${\varGamma }^{M_{\omega }} = {\varGamma }^{{\varGamma }^{M_{\omega }}}$.

A sufficient criterion for obtaining a comprehensive class of epistemic transition structures $\mathcal {M}$ such that $\varGamma$ depends on the past w.r.t. $\mathcal {M}$ is provided by epistemic witnesses: If some knowledge formula $\textsf{K} _{{\mathrm {}}}\!\mathop {}\varphi$ of $\varGamma$ does not hold at some state of an interpreting epistemic transition structure there is evidence in the past of this structure why it does not hold. Formally, a structure $M \in \mathscr {M}_{ P , { A }}(\textsf{B})$ provides epistemic witnesses for a formula $\textsf{K} _{{\mathrm {}}}\!\mathop {}\varphi \in \varPhi _{P, A}$ if for all $k \ge 0$, $s \in {S_{\omega }}(M)$ it holds that if $M, s \not \models \textsf{K} _{{\mathrm {}}}\!\mathop {}\varphi$, then there is an $s' \in {S_{\omega }}(M)$ with $(s, s') \in E_{{\mathrm {}}}$ and $M, s' \not \models \varphi$.

Lemma 1

Let $\varGamma = (\textsf{B}, \mathcal {T})$ be an epistemically guarded transition system over $\varSigma$ and let $\mathcal {M} \subseteq \mathscr {M}_{\varSigma }(\textsf{B})$ such that all $M \in \mathcal {M}$ provide epistemic witnesses for all knowledge guards in $\varGamma$. Then $\varGamma$ is depending on the past w.r.t. $\mathcal {M}$.

A sufficient criterion, in turn, for a structure $M \in \mathscr {M}_{ P , { A }}(S,E,L,S_0)$ to provide epistemic witnesses is M being synchronous: if for all ${\mathrm {}}\in { A }$ and all reachable $s_1 \in {S_{\omega }}(M)$ and $s_2 \in {S_{\omega }}(M)$ with $(s_1, s_2) \in E_{{\mathrm {}}}$ it holds that $s_1, s_2 \in {S_{\omega }}(M)$. In a synchronous structure the temporal and the epistemic dimension for each agent are hence tightly coupled and agents cannot access the future, but also do not need to know the future.

Example 6

The interpretation $M_{ bt }$ of the bit transmission problem given in Ex. 2 provides epistemic witnesses, but is not synchronous: the sender ${\textrm{S}}$ cannot distinguish ${\mathrm {z_0}}$ reachable at depth 0 of $M_{ bt }$ from ${\mathrm {z_1}}$ that is only reachable at depth 1, and similarly the receiver ${\textrm{R}}$ cannot distinguish ${\mathrm {z_1}}$ from ${\mathrm {z_3}}$ at the respective depths of 1 and 2.

An epistemically guarded transition system $\varGamma = (\textsf{B}, \mathcal {T})$ over $\varSigma$ provides epistemic witnesses if for each $M \in \mathscr {M}_{\varSigma }(\textsf{B})$ the interpretation ${\varGamma }^{M}$ provides epistemic witnesses for all knowledge formulæ occurring in some of the action guards of $\varGamma$; $\varGamma$ is synchronous if each ${\varGamma }^{M}$ is synchronous. Moreover, $\varGamma$ can syntactically be seen to be synchronous (cf. [14, p. 135]) if it is round-based where all agents perform some action in each round and record locally which actions they have taken.

4 (Re-)Interpreting Knowledge-based Programs

The results by Fagin et al. [13, 14] guarantee a unique interpretation for all synchronous knowledge-based programs; the approach by De Haan et al. [10] aims at extending the interpretation to asynchronous programs, but assigns semantics also to contradictory or self-fulfilling programs.

The necessity of avoiding contradictory or self-fulfilling behaviour already occurs in the design of synchronous programming languages [6]: Their underlying principle is “perfect synchrony”, that any reaction of a program takes zero time and that thus whatever is output in reaction to some input is already present at the same time as the input. Since the presence or absence of signals can be tested, this requires “logical coherence” saying that a (non-input) signal is present in a reaction if, and only if, this signal is emitted in this very reaction. A program needs to be both reactive in the sense of leading to some logically coherent signal status, and determinate, i.e., not showing several such statuses. For example, in Esterel [7], the program fragment

is not reactive, but contradictory: signal S is only emitted if it is not emitted; and

is not determinate, but self-fulfilling: S is emitted if it is emitted, and it is not emitted if it is not. Such programs can be revealed by using a cycle-detecting static analysis, as is done in Lustre [18], or, for including more intricate cases, by Berry’s “constructive semantics” as for Esterel [8]. Building on a “logical semantics” recording what is emitted in each step of execution, a must/cannot analysis is performed: what must/cannot be emitted, which branch must/cannot be executed. It is then required that for each signal it can be decided whether it must be present or it cannot be present. For example, in the parallel execution

both signals can be emitted — if S1 is assumed to be present, and S2 absent —, but none must be emitted. Thus the constructive semantics does not reach a decision of what must/cannot be present and the program is not constructive. Intriguingly, however, there is exactly one coherent signal status that can be reached by execution: S1 and S2 absent.

We adapt Berry’s constructive semantics approach to knowledge-based programs. In fact, the first, non-reactive Esterel program fragment resembles the variable setting problem described in Ex. 3(a), the second, non-determinate fragment directly corresponds to Ex. 4(d), and the last, combined fragment is essentially the same as Ex. 4(c). We first define a must/can version of epistemic transition structures with a lower (must) and an upper bound (can). Based on a positive (must) and negative (cannot) satisfaction relation of epistemic formulæ over these structures we show how an epistemically guarded transition system can be interpreted yielding another epistemic must/can transition structure. For uniformity, we rephrase this interpretation in terms of the negation normal form of formulæ and demonstrate that the constructive interpretation is always monotone and leads to a least fixed point. For any knowledge-based program, this fixed point soundly shows which executions are necessary and which are possible. However, the fixed point need not be decided, and more can be possible than is necessary. We show that synchronous programs always lead to decided fixed points.

4.1 Epistemic Must/Can Transition Structures

An epistemic must/can transition structure $Y = (S, E, L, S_0, (T_{\mu }, T_{\nu }))$ over $\varSigma = ( P , { A })$ is given by an epistemic state basis $\textsf{B}= (S, E, L, S_0)$ and two lower and upper transition relations $T_{\mu }, T_{\nu } \subseteq S \times S$ with $T_{\mu } \subseteq T_{\nu }$. In particular, $Y_{\mu } = (\textsf{B}, T_{\mu })$ and $Y_{\nu } = (\textsf{B},T_{\nu })$ are epistemic transition structures over $\varSigma$ with $Y_{\mu } \subseteq Y_{\nu }$.

The positive and negative satisfaction relations of an epistemic formula $\varphi \in \varPhi _{P, A}$ over the epistemic must/can transition structure Y at a state $s \in {S_{\omega }}(Y_{\nu })$, written $Y, s \models _{\text { p}}\varphi$ and $Y, s \models _{\text { n}}\varphi$, are defined as follows:

A formula is positively satisfied over Y if it must be true given the upper bound $Y_{\nu }$ of possible behaviour, it is negatively satisfied if it cannot be true given the lower bound $Y_{\mu }$ of necessary behaviour. In fact, it holds that what must be true can also be true:²

Lemma 2

Let $Y = (S, E, L, S_0, (T_{\mu }, T_{\nu }))$ be an epistemic must/can transition structure over $( P , { A })$ and $\varphi \in \varPhi _{P, A}$. Then for all $s \in {S_{\omega }}(Y_{\nu })$, $Y, s \models _{\text { p}}\varphi$ implies $Y, s \not \models _{\text { n}}\varphi$.

The set of epistemic must/can transition structures over $\varSigma$ and the epistemic state basis $\textsf{B}$ is denoted by $\mathscr {Y}_{\varSigma }(\textsf{B})$. We say that $Y_1 \sqsubseteq Y_2$ for $Y_1, Y_2 \in \mathscr {Y}_{\varSigma }(\textsf{B})$ if $Y_{1, \mu } \subseteq Y_{2, \mu }$ and $Y_{1, \nu } \supseteq Y_{2, \nu }$: an extension raises the lower bound and reduces the upper bound.

As with epistemic transition structures, an epistemically guarded transition system $\varGamma = (S, E, L, S_0, \mathcal {T})$ over $( P , { A })$ can be interpreted over an epistemic must/can transition structure $Y \in \mathscr {Y}_{ P , { A }}(S, E, L, S_0)$: The interpretation of a guarded action $(\varphi \supset B) \in \mathcal {T}$ w.r.t. to Y is given by the pair ${(\varphi \supset B)}^{Y} = ({(\varphi \supset B)}^{Y, \mu }, {(\varphi \supset B)}^{Y, \nu })$ with

$$\begin{aligned}\begin{gathered} {(\varphi \supset B)}^{Y, \mu } = \{ (s, s') \in B \;|\; s \in {S_{\omega }}(Y_{\mu }) \text { and } Y, s \models _{\text { p}}\varphi \} \ \text {,}\\ {(\varphi \supset B)}^{Y, \nu } = \{ (s, s') \in B \;|\; s \in {S_{\omega }}(Y_{\nu }) \text { and } Y, s \not \models _{\text { n}}\varphi \} \ \text {.} \end{gathered}\end{aligned}$$

By Lem. 2 it holds that ${\tau }^{Y, \mu } \subseteq {\tau }^{Y, \nu }$ for each $\tau \in \mathcal {T}$. The constructive interpretation of $\varGamma$ w.r.t. Y is given by the epistemic must/can transition structure

$$\begin{aligned}\textstyle {\varGamma }^{Y} = (S, E, L, S_0, (\bigcup _{\tau \in \mathcal {T}} {\tau }^{Y, \mu }, \bigcup _{\tau \in \mathcal {T}} {\tau }^{Y, \nu })) \ \text {.} \end{aligned}$$

This is well defined, i.e., $({\varGamma }^{Y})_{\mu } \subseteq ({\varGamma }^{Y})_{\nu }$. We call Y a constructive solution for $\varGamma$ if ${\varGamma }^{Y} = Y$; a constructive solution is decided if $Y_{\mu } = Y_{\nu }$.

Again as with epistemic transition structures, this interpretation over epistemic must/can transition structures can be iterated for finally reaching a stable structure — and this time interpretation turns out to be monotone.

Example 7

• (a) Re-consider the cycle-breaking variable setting problem of Ex. 3(b). We start the interpretation in $Y_{ vsb , 0} = (\textsf{B}[vs], (\emptyset , S_{ vs }^2))$ and successively obtain the following epistemic must/can transition structures:

  $\tau$	${\tau }^{Y_{ vsb , 0}}$	${\tau }^{Y_{ vsb , 1}}$	${\tau }^{Y_{ vsb , 2}}$	${\tau }^{Y_{ vsb , 3}}$
  $\textsf{K} _{{\textrm{a}}}\!\mathop {}\lnot ({\mathrm {q_1}} \wedge \lnot {\mathrm {q_2}}) \supset \{ ({\mathrm {s_0}}, {\mathrm {s_1}}) \}$	$\emptyset$	$\emptyset$	$\emptyset$	$\emptyset$
  	$\{ ({\mathrm {s_0}}, {\mathrm {s_1}}) \}$	$\emptyset$	$\emptyset$	$\emptyset$
  $\textrm{true} \supset \{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$
  	$\{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$
  $\textsf{K} _{{\textrm{a}}}\!\mathop {}\lnot (\lnot {\mathrm {q_1}} \wedge {\mathrm {q_2}}) \supset \{ ({\mathrm {s_0}}, {\mathrm {s_3}}) \}$	$\emptyset$	$\emptyset$	$\{ ({\mathrm {s_0}}, {\mathrm {s_3}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_3}}) \}$
  	$\{ ({\mathrm {s_0}}, {\mathrm {s_3}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_3}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_3}}) \}$	$\{ ({\mathrm {s_0}}, {\mathrm {s_3}}) \}$

  Not only does it hold that ${\varGamma _{ vsb }}^{Y_{ vsb , 3}} = Y_{ vsb , 3}$, but the interpretations indeed evolve monotonically w.r.t. $\sqsubseteq$. Moreover, the structure $Y_{ vsb , 3}$ is decided and everything what can happen also must happen, i.e., $(Y_{ vsb , 3})_{\mu } = (Y_{ vsb , 3})_{\nu }$.

• (b) For the cyclic variable setting problem, see Ex. 1(b) and Ex. 3(a), the interpretation process is monotone, but only yields

  $\tau$	${\tau }^{Y_{ vs , 0}}$	${\tau }^{Y_{ vs , 1}}$
  $\textsf{K} _{{\textrm{a}}}\!\mathop {}\lnot ({\mathrm {q_1}} \wedge \lnot {\mathrm {q_2}}) \supset \{ ({\mathrm {s_0}}, {\mathrm {s_1}}) \}$	$(\emptyset , \{ ({\mathrm {s_0}}, {\mathrm {s_1}}) \})$	$(\emptyset , \{ ({\mathrm {s_0}}, {\mathrm {s_1}}) \})$
  $\textsf{K} _{{\textrm{a}}}\!\mathop {}\lnot (\lnot {\mathrm {q_1}} \wedge {\mathrm {q_2}}) \supset \{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \}$	$(\emptyset , \{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \})$	$(\emptyset , \{ ({\mathrm {s_0}}, {\mathrm {s_2}}) \})$

  The epistemic must/can transition structure $Y_{ vs , 1}$ is not decided, and indeed there are two solutions of $\varGamma _{ vs }$ in terms of epistemic transition structures. However, the same undecidedness holds true for $\varGamma _{ nc }$ of Ex. 4(c), that is, the unique solution is also missed by the constructive interpretation.    $\square$

4.2 Constructive Interpretation

The separated positive (must) and negative (cannot) satisfaction relations over an epistemic must/can transition structure $Y \in \mathscr {Y}_{ P , { A }}(S, E, L, S_0)$ can be merged into a single, uniform satisfaction relation relying on the negation normal form of epistemic formulæ where negation only occurs in front of propositions. For an arbitrary $\varphi \in \varPhi _{P, A}$ there exists an equivalent ${{\,\textrm{nnf}\,}}(\varphi ) \in \varPhi _{P, A}$ in negation normal form, such that, in particular

$$\begin{aligned}&{{\,\textrm{nnf}\,}}(\lnot {\mathrm {}}) = \lnot {\mathrm {}}\qquad \qquad \quad {{\,\textrm{nnf}\,}}(\lnot \lnot \varphi ) = {{\,\textrm{nnf}\,}}(\varphi )\\&{{\,\textrm{nnf}\,}}(\lnot \textrm{false}) = \textrm{true}\qquad {{\,\textrm{nnf}\,}}(\lnot (\varphi _1 \wedge \varphi _2)) = {{\,\textrm{nnf}\,}}(\lnot \varphi _1) \vee {{\,\textrm{nnf}\,}}(\lnot \varphi _2)\\&\qquad \qquad \qquad \qquad \quad \quad \,\, {{\,\textrm{nnf}\,}}(\lnot \textsf{K} _{{\mathrm {}}}\!\mathop {}\varphi ) = \textsf{M} _{{\mathrm {}}}\!\mathop {}{{\,\textrm{nnf}\,}}(\lnot \varphi ) \end{aligned}$$

The constructive satisfaction relation $Y, s \models \varphi$ for a state $s \in {S_{\omega }}(Y_{\nu })$ and an epistemic formula $\varphi \in \varPhi _{P, A}$ in negation normal form is defined just as for arbitrary epistemic formulæ, but using the upper bound $Y_{\nu }$ for the universal quantifier of $\textsf{K} _{{\mathrm {}}}\!\mathop {}$ and the lower bound $Y_{\mu }$ for the existential quantifier of $\textsf{M} _{{\mathrm {}}}\!\mathop {}$; in particular,

$$\begin{aligned}{} & {} Y, s \models \lnot p \iff p \notin L(s) \\{} & {} Y, s \models \textsf{K} _{{\mathrm {}}}\!\mathop {}\varphi \iff Y, s' \models \varphi \text { f. a. } s' \in {S_{\omega }}(Y_{\nu }) \text { with } (s, s') \in E_{{\mathrm {}}} \\{} & {} Y, s \models \textsf{M} _{{\mathrm {}}}\!\mathop {}\varphi \iff \text {ex.} s' \in {S_{\omega }}(Y_{\mu }) \text { s. t. } (s, s') \in E_{{\mathrm {}}} \text { and } Y, s' \models \varphi \end{aligned}$$

The constructive satisfaction relation indeed combines $\models _{\text { p}}$ and $\models _{\text { n}}$:

Lemma 3

Let $Y \in \mathscr {Y}_{ P , { A }}(\textsf{B})$, $\varphi \in \varPhi _{P, A}$, and $s \in {S_{\omega }}(Y_{\nu })$. Then $Y, s \models _{\text { p}}\varphi$ iff $Y, s \models {{\,\textrm{nnf}\,}}(\varphi )$ and $Y, s \models _{\text { n}}\varphi$ iff $Y, s \models {{\,\textrm{nnf}\,}}(\lnot \varphi )$.

It follows that if $Y_{\mu } = Y_{\nu }$, then $Y, s \models \varphi$ if, and only if, $Y_{\mu }, s \models \varphi$ or, equivalently, $Y_{\nu }, s \models \varphi$. We also obtain that constructive satisfaction is preserved when extending epistemic must/can transition structures:

Lemma 4

Let $Y, Y' \in \mathscr {Y}_{ P , { A }}(\textsf{B})$ with $Y \sqsubseteq Y'$ and let $\varphi \in \varPhi _{P, A}$. Then $Y, s \models {{\,\textrm{nnf}\,}}(\varphi )$ implies $Y', s \models {{\,\textrm{nnf}\,}}(\varphi )$ for all $s \in {S_{\omega }}(Y'_{\nu })$.

This preservation of satisfaction yields that constructive interpretation is monotone.

Proposition 3

Let $\varGamma = (\textsf{B}, \mathcal {T})$ be an epistemically guarded transition system over $\varSigma$ and $Y, Y' \in \mathscr {Y}_{\varSigma }(\textsf{B})$ such that $Y \sqsubseteq Y'$. Then ${\varGamma }^{Y} \sqsubseteq {\varGamma }^{Y'}$.

Finally, we can observe that $\mathscr {Y}_{\varSigma }(\textsf{B})$ for $\textsf{B}= (S, E, L, S_0)$ with the ordering $\sqsubseteq$ is an inductive partial order: each directed subset $\varDelta \subseteq \mathscr {Y}_{\varSigma }(\textsf{B})$ has a least upper bound $\bigsqcup \varDelta$ w.r.t. $\sqsubseteq$, where directed means that every two $Y_1, Y_2 \in \varDelta$ have an upper bound $Y \in \varDelta$ such that $Y_1 \sqsubseteq Y$ and $Y_2 \sqsubseteq Y$; and there is also a bottom or least element $\bot _{\varSigma , \textsf{B}} = (S, E, L, S_0, (\emptyset , S \times S)) \in \mathscr {Y}_{\varSigma }(\textsf{B})$.

Proposition 4

$(\mathscr {Y}_{\varSigma }(\textsf{B}), {\sqsubseteq }, \bot _{\varSigma , \textsf{B}})$ is an inductive partial order.

Pataraia’s fixed-point theorem [9, §8.22] now guarantees that the monotone operator $Y \mapsto {\varGamma }^{Y}$ for each epistemically guarded transition system $\varGamma = (\textsf{B}, \mathcal {T})$ has a least fixed point in the inductive partial order. It can be computed by, possibly transfinite, iterated application of constructive interpretation to $\bot _{\varSigma , \textsf{B}}$, that is, $Y_0 = \bot _{\varSigma , \textsf{B}}$, $Y_{\alpha +1} = {\varGamma }^{Y_{\alpha }}$ for a successor ordinal $\alpha +1$, and $Y_{\lambda } = \bigsqcup _{\alpha < \lambda } Y_{\alpha }$ until equality [9, Exc. 8.19]. Compared to the iteration semantics of Sect. 3.3, the computation of the constructive semantics thus does not have to record all previous approximations in order to find a repetition.

4.3 (Un-)Decided Constructive Fixed Points

If any constructive fixed point $Y = {\varGamma }^{Y}$ with $Y \in \mathscr {Y}_{\varSigma }(\textsf{B})$ is decided, then there is the solution $Y_{\mu } = {\varGamma }^{Y_{\mu }} = {\varGamma }^{Y_{\nu }} = Y_{\nu }$ in terms of epistemic transition structures, and $\varGamma$ is not contradictory. Even if it is not decided, the must/can structures $Y_{\mu \mu } = (\textsf{B},(T(Y_{\mu }), T(Y_{\mu }))) \in \mathscr {Y}_{\varSigma }(\textsf{B})$ and $Y_{\nu \nu } = (\textsf{B},(T(Y_{\nu }), T(Y_{\nu }))) \in \mathscr {Y}_{\varSigma }(\textsf{B})$ satisfy $Y \sqsubseteq Y_{\mu \mu }$ and $Y \sqsubseteq Y_{\nu \nu }$, such that by Prop. 3 we obtain $Y = {\varGamma }^{Y} \sqsubseteq {\varGamma }^{Y_{\mu \mu }}, {\varGamma }^{Y_{\nu \nu }}$ which yields $Y_{\mu } \subseteq {\varGamma }^{Y_{\mu }}$ and ${\varGamma }^{Y_{\nu }} \subseteq Y_{\nu }$, but not equality, in general. For the least constructive fixed point $\mu \varGamma$, any solution $M = {\varGamma }^{M}$ thus satisfies $(\mu \varGamma )_{\mu } \subseteq M \subseteq (\mu \varGamma )_{\nu }$, always giving sound lower and upper bounds and, if $\mu \varGamma$ is decided, moreover unique solvability:

Proposition 5

Let $\varGamma = (\textsf{B}, \mathcal {T})$ be an epistemically guarded transition system over $\varSigma$ and assume $\mu \varGamma \in \mathscr {Y}_{\varSigma }(\textsf{B})$ is decided. Then $\varGamma$ has a unique solution in $\mathscr {M}_{\varSigma }(\textsf{B})$.

Still, even for epistemically guarded transition systems that provide epistemic witnesses it is not guaranteed that the least constructive fixed point is decided:

Example 8

Consider the following epistemically guarded transition system $\varGamma _{ nd } = (\textsf{B}[ nd ],\mathcal {T}_{ nd })$ over $\varSigma [nd] = ( P , { A })$ with $P = \{ {\textrm{p}}, {\textrm{q}} \}$ and ${ A } = \{ {\textrm{a}}, {\textrm{b}} \}$:

Constructive interpretation yields the non-decided fixed point $Y_{ nd }$ with $T(Y_{ nd , \mu }) = \emptyset$ and $T(Y_{ nd , \nu }) = \{ ({\mathrm {u_0}}, {\mathrm {u_1}}) \}$, as $Y_{ nd }, {\mathrm {u_0}} \not \models \textsf{K} _{{\textrm{b}}}\!\mathop {} \textsf{M} _{{\textrm{a}}}\!\mathop {}{\textrm{p}}$, but also $Y_{ nd }, {\mathrm {u_0}} \not \models \textsf{M} _{{\textrm{b}}}\!\mathop {} \textsf{K} _{{\textrm{a}}}\!\mathop {}\lnot {\textrm{p}}$: the states ${\mathrm {u_0}}$ and ${\mathrm {u_1}}$ can be distinguished by agent ${\textrm{a}}$, and agent ${\textrm{b}}$ cannot tell whether a step has been taken. In ${\mathrm {u_0}}$ the formula $\textsf{M} _{{\textrm{a}}}\!\mathop {}{\textrm{p}}$ holds w.r.t. $Y_{ nd }$, but in ${\mathrm {u_1}}$ it does not, since $({\mathrm {u_1}},{\mathrm {u_0}})\not \in E_{ nd ,a}$. On the other hand, $\varGamma _{ nd }$ provides epistemic witnesses pathologically, since ${\varGamma _{ nd }}^{M}, s \models \textsf{K} _{{\textrm{b}}}\!\mathop {} \textsf{M} _{{\textrm{a}}}\!\mathop {}{\textrm{p}}$ for any $M \in \mathscr {M}_{\varSigma [nd]}(\textsf{B}[nd])$ and any $s \in {S_{\omega }}({\varGamma _{ nd }}^{M})$, and hence has a unique interpretation, which in this case is ${\varGamma _{ nd }}^{Y_{ nd , \mu }} = Y_{ nd , \nu } = {\varGamma _{ nd }}^{Y_{ nd , \nu }}$.

For synchronous epistemically guarded transition systems, however, the least fixed point is decided, since all knowledge refers to a past that must have happened:

Lemma 5

Let $\varGamma = (\textsf{B}, \mathcal {T})$ be an epistemically guarded transition system over $\varSigma$ that is synchronous. Let $Y \in \mathscr {Y}_{\varSigma }(\textsf{B})$ satisfy ${\varGamma }^{Y} = Y$. Then Y is decided.

Summing up, the constructive approach to interpreting knowledge-based programs subsumes the solutions for synchronous programs and provides a sound procedure for obtaining lower and upper bounds for the execution of both synchronous and asynchronous programs. The approach, however, is not complete: If the least constructive fixed point $\mu \varGamma$ is undecided, a system $\varGamma$ may be contradictory without any solution (see Ex. 3(a)), self-fulfilling with several solutions (see Ex. 4(d)), or it may have a unique solution in terms of epistemic transition structures (see Ex. 4(c)). One strategy that suggests itself for analysing $\varGamma$ further is to check whether an interpretation using the lower bound $(\mu \varGamma )_{\mu }$ of the least fixed point satisfies ${\varGamma }^{(\mu \varGamma )_{\mu }} = (\mu \varGamma )_{\nu } = {\varGamma }^{(\mu \varGamma )_{\nu }}$, which means that when executing according to what must happen all what can happen is already covered (see Ex. 8).

5 Knowledge-based Programs as Rule Systems

The “executions” of an epistemically guarded transition system $\varGamma$ can be captured as derivations of two mutually dependent inductive rule systems, like used for inductive definitions [1, 19]. One rule system defines the reachability in $\varGamma$, the other one the satisfaction of knowledge formulæ in negation normal form over $\varGamma$. When $\varGamma$ provides epistemic witnesses, the mutual dependence can be resolved by stratifying the rule system for reachability according to the depth of the execution. In the general case, the non-monotone dependence of the formula satisfaction system on the reachability system — the more states are reachable, the less is known — can be mitigated by extending the notion of rule systems to include also negative premisses: The conclusion of a rule is derivable if all its (positive) premisses are derivable, but none of its negative premisses. When applied to knowledge formulæ, negative premisses express that no counterexample is reachable.

The general rule systems can also be read as logic programs with “negation as failure” [11]. A direct application of the must/can approximation technique to the general rule system or, equivalently, the logic program resulting from a knowledge-based program reconstructs the Kripke-Kleene fixed point; the possible solutions correspond to “stable models” [16].

5.1 Inductive Rule Systems

An inductive rule system R consists of rules of the form X/y where the premisses $X \subseteq U$ and the conclusion $y \in U$ are drawn from some universe of judgements U. A rule X/y is interpreted as “if all X can be inferred, then y can be inferred”. The derivations in R together with their sets of premisses and conclusions are inductively defined as follows:

• a $y \in U$ is itself a derivation; its set of premisses is $\{ y \}$, its conclusion is y;

• if $X/y \in R$ and $(d_x)_{x \in X}$ a family of derivations with conclusions $(x)_{x \in X}$, then $(d_x)_{x \in X}/y$ is a derivation; its set of premisses is the union of the premisses of $(d_x)_{x \in X}$, its conclusion is y.

A $y \in U$ is derivable in R if there is a derivation in R with the empty set of premisses and conclusion y. The set of derivable conclusions of R coincides with the least fixed point $\mu \hat{R}$ of $\hat{R} : \wp U \rightarrow \wp U$ defined by $\hat{R}(P) = \{ y \in U \;|\; \text {ex. } X/y \in R \text { s. t. } X \subseteq P \}$.

In logic programming terms, a rule $X/y \in R$ yields a Horn clause $y \leftarrow X$ [11]. The least fixed point $\mu \hat{R}$ coincides with minimal Herbrand model of the logic program corresponding to R and thus with the single stable model, as no negation is involved [11, 16].

For expressing reachability and the satisfaction of knowledge formulæ in an epistemically guarded transition system $\varGamma = (S, E, L, S_0, \mathcal {T})$ over $( P , { A })$ as inductive rule systems, we use two types of judgements, one of the form $s \in ^{\varGamma } {S_{\omega }}$ with $s \in S$ for “state s is reachable in $\varGamma$”, and one of the form $s \models ^{\varGamma } \varphi$ with $s \in S$ and $\varphi \in \varPhi _{P, A}$ in negation normal form for “state s satisfies formula $\varphi$ in $\varGamma$”. The rules for reachability read:

where $s \models ^{\varGamma } \varphi$ in the side condition of the second rule requires this judgement to be derivable in the rule system for satisfaction. The rules for this system read:

Here, the last rule for satisfaction in fact is not monotone w.r.t. reachability: In order to infer $s \models ^{\varGamma } \textsf{K} _{a}\!\mathop {}\varphi$ it is not necessary to infer $s' \models ^{\varGamma } \varphi$ for all $s'$ with $(s, s') \in E_a$, but only for those for which $s' \in ^{\varGamma } {S_{\omega }}$ can be deduced — and also for all of those.

The notion of providing epistemic witnesses allows to stratify the inductive rule systems according to the involved depth $k \ge 0$: We specialise the judgement $s \in ^{\varGamma } {S_{\omega }}$ into $s \in ^{\varGamma } {S_{\omega }}$ meaning “state s is reachable in $\varGamma$ in up to k steps” and, similarly, the judgement $s \models ^{\varGamma } \varphi$ into $s \models ^{\varGamma }_k \varphi$ meaning “formula $\varphi$ is satisfied in $\varGamma$ at state s considering states reachable in up to k steps”. The rules for reachability become for all $k \ge 0$:

Analogously the rules for satisfaction become for all $k \ge 0$:

In particular, the rules for $s \models ^{\varGamma }_k \textsf{M} _{a}\!\mathop {}\varphi$ and $s \models ^{\varGamma }_k \textsf{K} _{a}\!\mathop {}\varphi$ are sound for epistemically guarded transition systems providing epistemic witnesses. The notion of “providing epistemic witnesses” requires that, if $\textsf{K} _{{\mathrm {}}}\!\mathop {}\varphi$ does not hold at depth k, there is a counterexample to $\varphi$ at depth $\le k$. The general case can be covered by dropping the depths and taking into account that $\textsf{K} _{{\mathrm {}}}\!\mathop {}\varphi$ does not hold at some state s if, and only if, there is some reachable, a-indistinguishable state $s'$ at which $\varphi$ does not hold. Therefore, in order to derive that $\textsf{K} _{{\mathrm {}}}\!\mathop {}\varphi$ indeed holds at some reachable state s, it is necessary and sufficient to show that it is not possible to derive that $\lnot \varphi$ holds at some reachable, a-indistinguishable state $s'$.

5.2 General Rule Systems with Positive and Negative Premisses

For expressing negative information in terms of a rule system, we complement the positive premisses of the rules by negative ones: We consider general rule systems R over a universe U consisting of rules of the form $(X, \mathop {\boldsymbol{\nshortparallel }}Z)/y$ where $X, Z \subseteq U$ are the positive and negative premisses, and $y \in U$ is the conclusion; it is interpreted as “if all X can be inferred but no Z, then y can be inferred”. The derivations in R together with their sets of positive and negative premisses and conclusions are again inductively defined as follows:

• a $y \in U$ is itself a derivation; its set of positive premisses is $\{ y \}$, its set of negative premisses is $\emptyset$, and its conclusion is y;

• if $(X, \mathop {\boldsymbol{\nshortparallel }}Z)/y \in R$ and $(d_x)_{x \in X}$ a family of derivations with conclusions $(x)_{x \in X}$, then $((d_x)_{x \in X}, \mathop {\boldsymbol{\nshortparallel }}Z)/y$ is a derivation; its set of positive premisses is the union of the positive premisses of $(d_x)_{x \in X}$, its set of negative premisses is the union of the negative premisses of $(d_x)_{x \in X}$ together with Z, and its conclusion is y.

For a $B \subseteq U$, let $\bar{R}(B)$ be all those $y \in U$ such that there is a derivation of y in R with the empty set of positive premisses and no negative premisses in B. The set of derivable conclusions of R is given by the least fixed point of $\bar{R}$ if it exists.

From the logic programming perspective, a general rule $(X, \mathop {\boldsymbol{\nshortparallel }}Z)/y \in R$ can be seen as a clause of the form $y \leftarrow X, \mathop {\boldsymbol{\nshortparallel }}Z$ with $\mathop {\boldsymbol{\nshortparallel }}$ read as “negation as failure” [5, 11]. Checking that a $B \subseteq U$ is a “stable model” of the logic program obtained from R in this way corresponds to the following process on general rule systems: first the reduct $R_B$ is formed by disregarding all rules $(X, \mathop {\boldsymbol{\nshortparallel }}Z)/y \in R$ with $B \cap Z \ne \emptyset$ and transforming the remaining rules $(X, \mathop {\boldsymbol{\nshortparallel }}Z)/y \in R$ into $X/y \in R_B$; then $R_B$ is an inductive rule system and B is stable if $B = \mu \hat{R}_B$. In particular, the stable models correspond to the solutions of $\bar{R}(B) = B$.

With this generalised notion of rule systems we can reformulate and combine the two inference systems for reachability and satisfaction in an epistemically guarded transition system $\varGamma = (S, E, L, S_0, \mathcal {T})$ over $( P , { A })$ by using a single judgement $s \models ^{\varGamma }_{\omega } \varphi$ for “state s satisfies $\varphi$ in $\varGamma$ and state s is reachable in $\varGamma$”. A negative premiss $\mathop {\boldsymbol{\nshortparallel }}(s \models ^{\varGamma }_{\omega } \textrm{true})$ thus stands for “$s \in ^{\varGamma } {S_{\omega }}$ cannot be deduced”. The new rules with also negative premisses read:

The rule for $s \models ^{\varGamma }_{\omega } \textsf{K} _{{\mathrm {}}}\!\mathop {}\varphi$ checks that s is reachable, but that no counterexample to $\varphi$ can be reached at an a-undistinguishable state.

Using general rule systems, the solvability of an epistemically guarded transition system is shifted to computing derivable conclusions. As for knowledge-based programs, it is not obvious from just the rules of a system R whether there are solutions of $\bar{R}(B) = B$ at all, and whether there is a least one.

Example 9

• (a) The general rule system

  

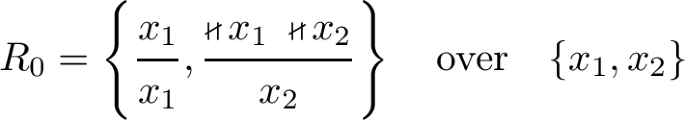
has no set of derivable conclusions, since $\bar{R}_0$ has no fixed point; in particular, $\bar{R}_0(\emptyset ) = \{ x_2 \}$ and $\bar{R}_0(\{ x_1 \}) = \emptyset = \bar{R}_0(\{ x_2 \})$. In terms of stable models, computing $\bar{R}_0(\emptyset )$ amounts to removing the negative premisses from the rule $(\emptyset , \mathop {\boldsymbol{\nshortparallel }}\{ x_1, x_2 \})/x_2$, such that the inductive rules $\{ x_1 \}/x_1$ and $\emptyset /x_2$ remain; and computing $\bar{R}_0(\{ x_i \})$ leads to the single inductive rule $\{ x_1 \}/x_1$ for $i \in \{ 1, 2 \}$.

$R_0$ also demonstrates that the set of derivable conclusions of a general rule system R need not coincide with the least fixed point of the operator $\hat{R} : \wp U \rightarrow \wp U$ when transferred from inductive rule systems by now setting $\hat{R}(P) = \{ y \in U \;|\; \text {ex. } (X, \mathop {\boldsymbol{\nshortparallel }}Z)/y \in R\ \text {s.t. } X \subseteq P\text {, } P \cap Z = \emptyset \}$: $\mu \hat{R}_0 = \{ x_1 \}$.

On the other hand, in view of the general rule system for epistemically guarded transition systems $R_0$ can also be rephrased as a knowledge-based program with a single agent ${\textrm{a}}$ and a single variable ${\textrm{x}} \in \{ 0, 1, 2 \}$, which ${\textrm{a}}$ cannot observe, started with ${\textrm{x}} = 0$:

• (b) There may be several solutions of a general rule system, but no least one:

  

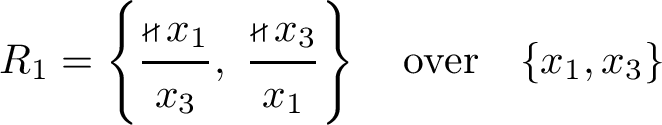
has the solutions $\{ x_1 \}$ and $\{ x_3 \}$, but $\emptyset$ is no solution. It corresponds to the “variable setting” knowledge-based program of the introduction, see Ex. 1(b):

• (c) Combining a contradictory rule $(\emptyset , \mathop {\boldsymbol{\nshortparallel }}\{ x_1, x_2 \})/x_2$ with the non-determined rules of $R_1$ we obtain the rule system

  

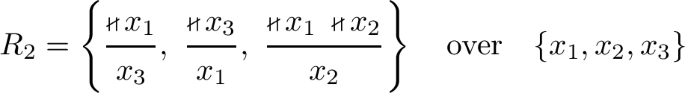
  which has the unique solution $\{ x_1 \}$: if $x_3$ were inferable, i.e., $x_1$ not inferable, this would trigger the contradictory rule for $x_2$ (see Ex. 4(c)).    $\square$

5.3 Solving General Rule Systems

The observations and definitions for epistemic must/can transition structures and constructive interpretation, see Sect. 4.2, can now readily be transferred to a more abstract account for general rule systems. In fact, this reconstructs the “Kripke-Kleene fixpoint” using under- and over-approximations [11], though now using an inductive partial order. We also relate the case where the constructive interpretation is not only monotone, but continuous to knowledge-based programs.

Define, for a universe U, the set $\wp ^{\pm } U$ as $\{ (P, Q) \in \wp U \times \wp U \;|\; P \subseteq Q \}$ and the relation ${\subseteq ^{\pm }} \subseteq \wp ^{\pm } U \times \wp ^{\pm } U$ as $(P, Q) \subseteq ^{\pm } (P', Q')$ if, and only if, $P \subseteq P'$ and $Q \supseteq Q'$.

Lemma 6

$( \wp ^{\pm } U, {\subseteq ^{\pm }}, \bot ^{\pm }_U)$ with $\bot ^{\pm }_U = (\emptyset , U)$ is an inductive partial order.

For a general rule system R over U with positive and negative premisses define the operator $\check{R} : \wp ^{\pm } U \rightarrow \wp ^{\pm } U$ that describes what must and what can be derived given what is assumed to be definitely and potentially derivable:

$$\begin{aligned}&\check{R}(P, Q) = (\{ y \in U \;|\; \text {ex. } (X, \mathop {\boldsymbol{\nshortparallel }}Z)/y \in R \text { s. t. } X \subseteq P,\ Q \cap Z = \emptyset \},\\&\qquad \quad \qquad \, \{ y \in U \;|\; \text {ex. } (X, \mathop {\boldsymbol{\nshortparallel }}Z)/y \in R \text { s. t. } X \subseteq Q,\ P \cap Z = \emptyset \}) \end{aligned}$$

This is well-defined: if $(P, Q) \in \wp ^{\pm } U$, then $\check{R}(P, Q) \in \wp ^{\pm } U$, since for $P \subseteq Q$ and each $(X, \mathop {\boldsymbol{\nshortparallel }}Z)/y \in R$ with $X \subseteq P$ and $Q \cap Z = \emptyset$ it holds that $X \subseteq Q$ and $P \cap Z = \emptyset$. The operator is always monotone:

Lemma 7

Let R be a rule system over U. If $(P_1, Q_1) \subseteq ^{\pm } (P_2, Q_2)$, then $\check{R}(P_1, Q_1) \subseteq ^{\pm } \check{R}(P_2, Q_2)$.

As for constructive interpretation, Pataraia’s fixed-point theorem now guarantees that the monotone operator $\check{R}$ on the inductive partial order $( \wp ^{\pm } U, {\subseteq ^{\pm }}, \bot _U^{\pm })$ has a least fixed point. Again, it can be “computed” by possibly transfinite iterated application of $\check{R}$ to $\bot _U^{\pm }$. If, however, $\check{R}$ is even continuous, then, by Kleene’s fixed-point theorem, it suffices to consider all finite approximations, i.e., $\mu \check{R} = \bigcup ^{\pm }_{n \in \mathbb {N}} \check{R}^{n}(\bot _U^{\pm })$; that $\check{R}$ is continuous means that if $\varDelta \subseteq \wp ^{\pm } U$ is directed, then $\bigcup ^{\pm } \check{R}(\varDelta ) = \check{R}(\bigcup ^{\pm } \varDelta )$.

Lemma 8

Let R be a rule system over U such that every rule of R has only finitely many positive and negative premisses. Then $\check{R}$ is continuous.

The rule system for an epistemically guarded transition system $\varGamma = (S, E, L, S_0, \mathcal {T})$ over $( P , { A })$ always has only finitely many positive premisses; if for each $s \in S$ and each ${\mathrm {}}\in { A }$ the set $\{ s' \in S \;|\; (s, s') \in E_{{\mathrm {}}} \}$ is finite, then there are also only finitely many negative premisses, such that the corresponding must/can operator is continuous.

6 Reasoning About Knowledge-based Programs

We have implemented the constructive interpretation of knowledge-based programs in the prototypical “Temporal Epistemic Model Interpreter and Checker” (tEmIc³). The tool first computes the least constructive fixed point of a (finite state) epistemically guarded transition system. If the least fixed point is decided, the least solution in terms of epistemic transition structures has been found; otherwise it is checked whether the re-interpretation using the lower bound of the undecided least fixed point yields a solution. If either succeeds, properties of the resulting model can be checked. These properties can be expressed in CTLK, the combination of the branching “Computation Tree Logic” (CTL) and epistemic logic [21]. What is more, CTLK can also be used in tEmIc for the action guards. The constructive interpretation just evaluates each universal quantifier of a CTL formula — $\textsf{A}$ for “on all paths” — over the upper bound and each existential quantifier — $\textsf{E}$ for “on some path” — over the lower bound. This adds the temporal dimension to the domain of application of knowledge-based programs. For the run-based interpreted systems of Fagin et al. [13], Van der Hoek and Woolridge [20] and Su [27] provide transformations for linear-time model checking based on local propositions, though for a fixed set of runs that does not depend on the evaluation of knowledge guards. The CTLK-model checker MCMAS [21] similarly operates on a fixed, predetermined model. In dynamic epistemic logic and its model checker DEMO [31], the transition structure is given by epistemic actions.

We first recapitulate briefly CTLK and then show its constructive evaluation over epistemic must/can transition structures. We next describe tEmIc by means of the bit transmission problem and the small paradoxical exercise of the “unexpected examination”; the tEmIc distribution also contains specifications for the well-known problems “Muddy Children” [31, pp. 93ff.] and “Sum-and-Product” [31, pp. 96f.]. Finally, we proceed to an application where CTLK is also used in the action guards: the Java memory model.

6.1 CTLK

The CTLK-formulæ over $( P , { A })$ are defined by the following grammar:

$$\begin{aligned} \varphi&{\;{:}{:}\!\!=\;} {\mathrm {}}\;|\; \textrm{false}\;|\; \lnot \varphi \;|\; \varphi _1 \wedge \varphi _2\;|\; \textsf{K} _{a}\!\mathop {}\varphi \;|\; \textsf{E}\textsf{X} \!\mathop {}\varphi \;|\; \textsf{E}\textsf{G} \!\mathop {}\varphi \;|\; \textsf{E} [\varphi _1\mathbin {\textsf{U}}\varphi _2] \end{aligned}$$

where $p \in P$ and $a \in A$. The path quantifier $\textsf{E}$ is interpreted as “there is a path”, the temporal modality $\textsf{X}$ as “in the next step”, $\textsf{G}$ as “always”, and $\textsf{U}$ as “until”. We also consider the path quantifier $\textsf{A}$ for “on all paths” and the modalities $\textsf{F}$ for “eventually” and $\textsf{R}$ for “release”, such that $\lnot \textsf{E}\textsf{G} \!\mathop {}\lnot \varphi$ is abbreviated by $\textsf{A}\textsf{F} \!\mathop {}\varphi$ and $\lnot \textsf{E} [\lnot \varphi _1\mathbin {\textsf{U}}\lnot \varphi _2]$ by $\textsf{A} [\varphi _1\mathbin {\textsf{R}}\varphi _2]$. The satisfaction relation $M, s \models \varphi$ of a CTLK-formula $\varphi$ over $( P , { A })$ at state $s \in S$ of an epistemic transition structure $M = (S, E, L, S_0, T)$ over $( P , { A })$ conservatively extends the satisfaction relation of epistemic formulæ by

where $\mathscr {P}(M, s)$ denotes all paths of M, i.e., the infinite state sequences $s_0, s_1, \ldots \in S$ with $s_0 = s$ and $(s_i, s_{i+1}) \in T$ for all $i \in \mathbb {N}$. A CTLK-formula $\varphi$ is valid in M, written $M \models \varphi$, if it is satisfied in all initial states, i.e., $M, s_0 \models \varphi$ for all $s_0 \in S_0(M)$.

For a direct definition of the satisfaction of CTLK-formulæ with an $\textsf{A}$, the existential path quantification for $\textsf{E}$ has to be replaced by universal path quantification. As for simple epistemic logic, CTLK including $\textsf{A}\textsf{X} \!\mathop {}\varphi$, $\textsf{A}\textsf{G} \!\mathop {}\varphi$ etc. admits a negation normal form (see, e.g., [3, pp. 333f.]). The constructive satisfaction relation of a CTLK-formula in negation normal form over an epistemic must/can transition structure $Y = (S, E, L, S_0, \mathcal {T})$ over $( P , { A })$ at a state $s \in {S_{\omega }}(Y_{\nu })$, written $Y, s \models \varphi$, conservatively extends the constructive satisfaction relation of epistemic formulæ and interprets $\textsf{E}$ over the lower bound $Y_{\mu }$ and $\textsf{A}$ over the upper bound $Y_{\nu }$ such that, in particular,

$$\begin{aligned}{} & {} Y, s \models \textsf{E}\textsf{F} \!\mathop {}\varphi \iff \begin{array}{@{}l@{}} \text {ex.} s_0, s_1, \ldots \in \mathscr {P}(Y_{\mu }, s) \text { and } i \in \mathbb {N}\text { s. t. } Y, s_i \models \varphi \end{array} \\{} & {} Y, s \models \textsf{A}\textsf{F} \!\mathop {}\varphi \iff \begin{array}{@{}l@{}} \text {f. a. } s_0, s_1, \ldots \in \mathscr {P}(Y_{\nu }, s) \text { ex. } i \in \mathbb {N}\text { s. t. } Y, s_i \models \varphi \end{array} \end{aligned}$$

6.2 tEmIc

tEmIc is a symbolic model interpreter and checker for epistemically guarded transition systems using CTLK. It is written in Java and uses binary decision diagrams for state space representation [28]; it also supports bounded integers and their arithmetic. Given a specification, tEmIc first computes the least constructive fixed point by iterated must/can interpretation. If this fixed point is not decided it checks whether another interpretation using the lower bound of the fixed point yields a solution. If either succeeds, tEmIc proceeds with model checking given properties; these statements can be specified as CTLK-formulæ which have to hold in all initial states or as a reachability query. Reachable deadlock states without outgoing transitions result in a warning.

For example, the bit transmission problem of the introduction as formalised in Ex. 1(a) can be represented as a tEmIc specification as follows (rules are introduced by keyword action followed by a name of the rule and the rule definition):

Constructive interpretation yields in a few milliseconds the decided least fixed point of Ex. 2, over which some CTLK-properties can be checked:

The first two are reported to hold, but the last does not since agent ${\textrm{R}}$ cannot gather enough information to be sure that the bit has been received by agent ${\textrm{S}}$.

For another example, consider the “unexpected examination” paradox [10, Sect. 4.7, there called “unexpected hanging”] (for a detailed account see, e.g., [26, Sects. 5.2f.]): A class is told that within the next week there will be an exam, but it will be a surprise. The class might reason that the exam cannot happen on Friday, because if there has been no exam up to Thursday it will not be a surprise on Friday any more; by backward induction it might reason that there cannot be a surprise exam in the next week at all. This problem statement can be readily expressed as a tEmIc specification:

Again, constructive interpretation yields in a few milliseconds a decided least fixed point. Over this epistemic transition structure we can check that on, e.g., Wednesday the exam can be written and still is indeed a surprise:

For such a reachability check tEmIc also provides a witness that tells that is executed twice after which follows. The following CTLK-property, however, is not satisfied, as it would have to hold in all initial states — and with being 4 the class cannot be surprised any more:

6.3 Memory Models

Memory models regulate the interaction between threads, their caches, and the main memory [23]. The original Java memory model — one of the first formal such models — has been harshly criticised for making several compiler optimisations impossible and has subsequently been superseded by a more liberal model [17, Ch. 17]. Keeping strong guarantees for sequentially consistent, well-synchronised programs, reorderings of data-independent statements or early, “prescient” reads from other threads are allowed for programs with data races. Still, some limits, like consistency with data or control flow dependencies or no “out-of-thin-air” values, should be in force [2, 25].

For example, in the following two-threaded Java-like program to the left it should be possible that both thread-local registers r1 and r2 are assigned the value 1 when reading the global, shared variables x and y: A compiler could reorder the data-independent statements in both threads. This behaviour, however, should be forbidden in the example to the right, since there is a symmetric data dependence.

We want to capture the behaviour of a multi-threaded (Java) program with a liberal memory model without having to check all possible compiler transformations — the correctness of such transformations would actually depend on the program semantics including the memory model. In fact, in the current Java memory model out-of-order executions have to be justified by other legal executions. We interpret these justifications as witnesses in terms of knowledge-based programs; our current exposition, however, neglects synchronisation. We first represent the state space of a two-threaded (Java) program like the ones above by the following tEmIc declarations:

The thread agents and can only observe their local registers and their program counters. The program steps for both threads are turned into actions like

Additionally, we allow for a “prescient reading” of the value v from the main memory variable x by thread $\theta$ into the local variable r at step s by the following action:

The thread $\theta$ can read v from x into r early on if it knows that there is an execution where x has value v without dependence on already setting r to v, and, furthermore, that there is an execution where the early setting is confirmed. The statement of the first thread is expanded into three read actions , , and plus the plain reading action . With this encoding, tEmIc reports that for the first example to the left it is indeed possible to obtain $\texttt {r1} = \texttt {r2} = 1$ in the least constructive fixed point, but that this is impossible for the example to the right.

A more intriguing case is presented by the following two examples: According to Manson et al. [23, pp. 35f.] (cf. also [2]), the program to the left can result in $\texttt {r1} = \texttt {r2} = \texttt {r3} = 1$:

A compiler could see that only 0 and 1 are possible for x and y and “can then replace r2 = x by r2 = 1, because either 1 was read from x on line 1 and there is no intervening write, or 0 was read from x on line 1, 1 was assigned to x on line 3, and there was no intervening write”; this definite assignment can be used to transform the last line to y = 1; which finally can be made the first action of the first thread, as there are no dependencies. But the same transformation is not possible for the program to the right, and there the same behaviour should be disallowed. Still, the left program is the result of inlining the second thread into the first. Our encoding of the two programs in tEmIc confirms these considerations and the witness for the left program indeed first sets to 1 and confirms this only in the last step setting to 1.

7 Conclusions and Future Work

We have introduced a must/can analysis for the interpretation of knowledge-based programs inspired by the constructive semantics of synchronous programming languages. The resulting constructive interpretation provides lower and upper bounds for the possible executions. This interpretation has been shown to be monotone and to yield a least fixed point. We have also transformed knowledge-based programs to general rule systems with positive and negative premisses. Finally, we have described our tool tEmIc for constructive interpretation and temporal-epistemic model checking over CTLK and demonstrated some applications of interpreting knowledge-based programs including CTLK-guards.

Our epistemic logic could be complemented by group knowledge [14, Ch. 6], like common or distributed knowledge. The temporal dimension could be extended to “Linear-Time Logic” (LTL), and, more importantly, to include some notion of fairness. Criteria for ensuring decided least fixed points for the must/can interpretation beyond synchronicity would be desirable. Also a comparison with non-monotone inductive definitions [12], SOS rules with negative premisses [24], and solution strategies for epistemic specifications [5], would be of interest. On the other hand, the general constructive approach may be useful to complement existing intuitionistic approaches to the semantics of synchronous programming languages [22]. Finally, the domain of memory models should be covered more comprehensively by interpreting knowledge-based programs.