1 Introduction

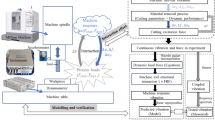
To meet the demands of shorter product life cycles and higher quality requirements, considerable flexibility and dependability in manufacturing are required on an ongoing basis. Furthermore, product complexity and the number of product varieties are increasing as markets and production become more globalized. The use of new manufacturing technologies, as well as their digitization and automation, has become critical in this respect. Using simulation technology, in particular, is becoming increasingly important across the product life cycle. Modeling complex systems, such as machine tools and machining processes, improves production and product development efficiency in terms of both time and cost. Particularly, the need for a trial-and-error process to test a novel approach on actual process and machinery is replaced by simulation. The implementation of more sustainable manufacturing practices can be therefore facilitated.

In this work, a simulation model predicting cutting forces and milling process vibrations has been constructed and experimentally verified in order to analyze the dynamic behavior of milling processes with varied parameters. The milling process model, when combined with the model of the cascade controlled feed drives, allows for a more comprehensive investigation of the nonlinear dynamics of AC electric motors and the mechanical vibrations of machining processes. Subsequently, a correlation study of the control parameters and the process vibrations has been performed based on the experimental and simulation results.

2 State of the Art

First, based on the literature, the current state of research on modeling cutting forces and vibration in machining operations, is briefly presented in this part. Second, various techniques of reducing process vibrations are characterized and compared.

2.1 Cutting Forces and Vibration Modeling

Analytical approaches are used to calculate the forces and vibrations generated by the machining operations. The depth of cut in the simulation techniques in [1, 2] was calculated by taking into account both the static and dynamic components resulting from the tool geometry and process kinematics, as well as the dynamic vibrations. By converting forces into cutting edge coordinates for turning, drilling, and milling procedures, Kaymakci et al. established a unified cutting force model in [3]. Smith and Tlusty [4] introduced the time marching methods for simulating process states at discrete time periods. The time-discrete estimation of cutting forces for five-axis milling operations was verified by Lazoglu et al. in [5]. In the time-domain simulation system with improved computing time in [6], a model of chip formation of each tooth feed was developed utilizing the CSG (constructive solid geometry) modeling method. For a more comprehensive assessment of virtual systems of machining processes, the reader is directed to the literature [7].

2.2 Process Vibration Reducing Techniques

Munoa et al. gave a critical review of the evolution of each approach and the relevant industrial application while demonstrating several chatter reduction strategies in [8]. Modifying the process parameters and the spindle speed based on the stability lobe diagram (SLD) is one technique to reduce chatter. Intensive research on process stability utilizing SLD has been undertaken over the last 15 years, including process damping modeling [9], thin wall machining [10], multitask operations [11], SLD accuracy enhancement [12], and new ways for monitoring dynamic parameters [13]. Spindle speed variation methods are another effective way for decreasing chatter. These strategies focus on adjusting the tool cutting edge passing period to vary the period between the modulations, as the modulations in chip thickness induce regenerative instability [8].

Despite many methodologies and applications for modeling machining processes, understanding of the relationship between motion control parameters and machining process dynamics remains restricted. Furthermore, minimizing process vibrations and, as a result, optimizing the process outputs without extra costly software or hardware change is a study issue that requires further investigation. In comparison to external software solutions, an independently built simulation model of the machining process with integrated motion control simulation allows for greater flexibility for fundamental scientific research. Moreover, it enables a more thorough assessment of the assigned variables and applied functions. Last but not least, the established model allows for the reproducible investigation of interdependencies between control and process parameters in an enclosed system.

3 Milling Process Modeling with Cascade Control

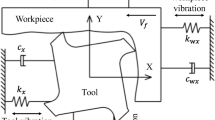
The specifically developed simulation system [14] is used to investigate the influence of control parameter variation on the process vibration amplitudes. The schematic structure of the model is shown in Fig. 1.

The NC-file is initially converted into a matrix consisting of discrete time steps, the set coordinates of the tool path, the spindle speed, the feed rate as well as the logical values for the cutting operation. The motion control model receives the position coordinates as input for the cascade control. Subsequently, with the assistance of the configured PMSM (Permanent-Magnet Synchronous Motor) model and the model of torsional oscillators as the analytical representation of the mechanical elements, the actual position values are calculated and sent to the two dimensional process sub-model. In the process sub-model, the chip thickness is calculated as the distance between the instantaneous cutting edge and the semi-finished workpiece polygon contour at each time step. By subtracting the simulated chip polygon, the workpiece geometry is incrementally updated. Based on the Kienzle formula, the process forces and load torques are calculated and fed back to the PMSM model. The output vibration amplitudes are generated from the mechanics model, which contain the forced vibrations resulted from the periodically varying cutting forces computed in the process sub-model. These are plotted and analyzed for the model validation in Sect. 4.2.

Fig. 1.
figure 1

Schematic structure simulation system

Full size image

4 Experimental Results and Model Validation

In order to verify and validate the simulation model presented in Sect. 3, experimental tests have been carried out at the Institute of Resource and Energy Efficient Production Systems at the Friedrich-Alexander-Universität Erlangen-Nürnberg in Germany. In this section, firstly, the experimental setup of the milling process vibration measurement is specified. Subsequently, the simulation results of the milling process model with different motion control configurations are verified by comparing to the experimental results.

4.1 Experimental Setup

A series of milling operations has been performed in the DNM 500 vertical machining center fabricated by Doosan Machine Tools Co., Ltd. The workpiece clamping setup and its schematic representation are shown in Fig. 2a and Fig. 2b respectively. The workpiece composed of stainless steel X2CrNiMo17-12-2 measures 60 mm in length and width. The milling cutter used is a corner milling cutter from Walter AG, model M4132-040-B16-05-09, with five inserts SDMT09T320-F57 WSP45S. The machine vice is turned 45\(^\circ \)C clockwise to examine the coordinated motion control of the two feed axes using a predetermined straight milling tool path. The tri-axial acceleration sensor W356B11/NC and the Apollo light measurement system are used to record the vibration amplitudes during the milling process.

Fig. 2.
figure 2

Experimental setup

Full size image

4.2 Comparison of Experimental and Simulation Results

The process parameters selected both in the experimental and simulated milling process are listed in Table 1. In Fig. 3, a 0.3-second section of the time sequence of the vibration amplitudes is extracted for the visualized comparison of the experimental and simulation results. The thick lines in solid red and long-dashed blue represent the envelopes of the vibration signals practically measured and simulated respectively. Using Fast Fourier Transform (FFT), the corresponding spectral analysis of the vibration signals up 200 Hz is shown in Fig. 4. It can be observed that the simulation result to a great extent agree with the experimental result. The tooth passing frequency, which is proportional to the rotational frequency of the spindle, can be clearly identified in the experimental and simulation signal spectra, at 66.1 Hz and 65.6 Hz respectively.

Table 1. Process parameters
Full size table
Fig. 3.
figure 3

Comparison experimental and simulation results

Full size image
Fig. 4.
figure 4

Spectral analysis vibration amplitudes

Full size image

In order to further verify the plausibility and validity of the motion control sub-model, the process vibration behavior under various position controller configurations has been practically and simulationally evaluated. For each variation of the proportional gain factor \(K_v\), the root mean square (RMS) of the vibration amplitudes over the complete milling process is calculated and compared (see Fig. 5). Fifteen experimental iterations have been carried out respectively with \(K_v = 6, 11,\) and 20. The corresponding standard deviations are demonstrated as error bars in the diagram. Based on the reproducibility of the simulation results, the standard deviations of the simulated vibration amplitudes remain zero. The simulation model and the experimental tests yield comparable results with percent errors between 1 to 5%. Both experimental and simulated results indicate that a higher \(K_v\)-value, representing a more dynamic motion control configuration, lead to more active vibration behavior.

Fig. 5.
figure 5

Comparison RMS with \(K_v = 6, 11, 20\)

Full size image

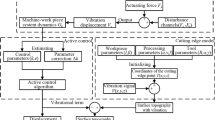
5 Correlation Analysis of Control Parameters and Vibration Amplitudes

In this section, the validated simulation model is implemented to efficiently evaluate the correlational relationship between the motion control parameters and the process vibration behavior. The process parameters utilized for executing the simulation are identical as listed in Table 1. The examined control parameters in this paper are the proportional gain factor of the position controller \(K_v\) and that of the P-part of the speed PI controller \(K_p\). In the first test series, the \(K_v\)-value has been configured from 1 to 20, with a sampling interval of 1, where the speed controller remains unchanged, with \(K_p = 9\), and the reset time of the I-part \(T_n = 0.004\). Analogously, in the second test series, \(K_v\) and \(T_n\) remain constant, with the values of 6 and 0.004 respectively, where the \(K_p\)-value increases from 0.5 to 10, with an interval of 0.5. For each simulated milling process, the RMS of the process vibration amplitudes is calculated. The simulation results of the first and second test series are shown in Fig. 6a and Fig. 6b. It can be observed that both vibration-\(K_v\) and vibration-\(K_p\) curves are monotonic. To quantify the monotonic correlational relationship between two variables, the Spearman’s rank correlation coefficient \(r_s\) is calculated according to Eq. (1)

$$\begin{aligned} r_s = \frac{cov(R(X),R(Y))}{\sigma _{R(X)}\sigma _{R(Y)}}, \end{aligned}$$
(1)

where cov(R(X), R(Y)) is the covariance of the rank variables R(X) and R(Y), \(\sigma _{R(X)}\) and \(\sigma _{R(Y)}\) are the standard deviations of the rank variables [15]. The value of \(r_s\) for the variables vibration amplitude and \(K_v\)-factor equals 0.989, demonstrating a very strong positive monotonic correlation. On the other hand, \(r_s\) for vibration amplitude and \(K_p\)-factor indicates a very strong negative monotonic correlation, with the value of –1.

Fig. 6.
figure 6

Simulation results process vibration RMS

Full size image

6 Summary and Outlook

This paper proposes a novel milling process model integrated with motion control simulation with electrical feed drives. The interactions between the nonlinear behaviors of the electrical motors and the milling process vibrations are computationally reproduced. The functionality and the accuracy of the simulation model have been verified by conducting multiple experimental tests. The results demonstrate that the simulation model accurately calculates the tooth passing frequency with a margin of error of less than 1%. The RMS of the process vibration amplitudes features percent errors less than 5%. Moreover, based on the Spearman’s correlation method, the correlational relationship between the control parameters, \(K_v\) and \(K_p\), and the process vibrations is identified as very strong monotonic. The focus of future study will be on the improvement and the extension of the simulation model for a more comprehensive representation of the physical machine tool, especially for the computation of a wide-spectrum and high-resolution spectral analysis of the process vibration signals. A model extension into the third dimension with prediction of the surface finish of the workpiece is inevitable for the computation of the self-excited chatter vibrations. Furthermore, a thorough investigation on the configuration of vibration-reducing control parameters should be carried out.