Keywords

1 Introduction

At the present time, many communication devices such as smartphones are being produced. According to a survey conducted by IDC, the number of smartphones shipped worldwide reached 1.35 billion in 2021 [1]. Such large-scale product distribution is not only associated with significant economic benefits, but also has a major environmental impact. According to the research of SHARP [2], the CO2 emissions sometimes account for more than 90% of the CO2 emissions for electric products and home appliances in supply chains consisting of parts/materials manufacturing, assembly manufacturing, and logistics stages. Therefore, the CO2 emissions of original material production should be concerned, and the end-of-life (EOL) products should be recycled for a significant reduction in greenhouse gas (GHG) emissions by replacing new products with recycled ones [3].

Nevertheless, the smartphones currently on the market undergo very little recycling. For example, the smartphone recycling rate is only 17% in Japan [4]. This fact means that most of the smartphones are not recycled. One of the reasons for the low recycling rate is that manufactures require the additional costs such as recycling, transportation, and recovery facility costs to construct the reverse supply chain network. The costs of reverse supply chain are based on the network configuration, and the company decides the network for reducing costs. When the reverse supply chain network is changed, the amount of recycling or disposal EOL products is also changed. One of the reasons is that the recycling EOL smartphones is a difficult challenge because the material composition of these devices is complicated. It includes valuable metals that can be recycled but also plastics with no recycling value. The selling prices obtained from recycled materials are different depending on the material type. This makes it difficult for decision-makers (DMs) at manufacturers to design a reverse supply chain network that takes into account the costs associated with recycling processes (e.g., collection, disassembly, and transportation), and the prices (value) of each recycled material. Furthermore, recycling more EOL products and reducing cost for the reverse supply chain are in a trade-off relationship. Therefore, the DMs need to design a reverse supply chain network [5] that is not only environmentally friendly but also economically feasible by performing a complicated profit and cost calculation.

Thies et al. [6] reviewed 142 papers on sustainably assessment related products applied operations research. They showed more than 50% literatures used multi-criteria decision making methods. However, they concluded that there were few attentions for using the model of operations research to sustainability assessment of products. Aldoukhi and Gupta [7] designed a global closed-loop supply chain considering to minimize total cost a carbon emission and to maximize service level of retailers. However, they did not consider materials such as plastic and aluminum obtained from recycling EOL products. In an effort to evaluate GHG emissions from smartphones, Joshi et al. [3] investigated the GHG emissions caused by a smartphone over all its life stages. However, the economic efficiency of the reverse supply chain network was not evaluated.

In order to consider both GHG emissions and economic efficiency, Ijuin et al. [8] have applied linear physical programming (LPP) [9] to a reverse supply chain network in the case of vacuum cleaners. LPP is one of the multi-criteria decision-making methods that enable us to not only optimize the network taking into account the trade-off problem between GHG emissions and economic efficiency, but also to determine weights among objective functions by applying the LPP weight algorithm. According to Ijuin et al. [8], one of the benefits is that LPP can find one satisfied solution among multi objective functions such as the minimizing total cost and total GHG emissions based on the preferences of the DM with a lower number of experimental trials. The limitation of the LPP approach is that alternative and multiple results from pareto solution cannot be obtained to see the trade-offs.

On the other hand, while smartphones are composed of different components, they are usually made in a single country, but the sourcing country for the components varies from smartphone to smartphone. Since the GHG emissions of components and devices in production differ among countries [10], the GHG emissions associated with a particular smartphone are different depending on the country. Therefore, the differences in the reverse supply chain network should be considered in relation to the country manufacturing the components.

This study applies a bi-objective reverse supply chain network design to the GHG volume and costs using LPP for the case of smartphones. First, the reverse supply chain network is modeled for recycling EOL smartphones, and a case study based on literatures and life cycle assessment (LCA) are prepared. Next, the objective functions are set and formulated to minimize the total GHG volume and the total cost using LPP and integer programming. Finally, numerical experiments on the reverse supply chain are conducted and evaluated.

2 Model and Formulation

2.1 Model

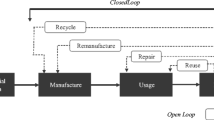
Figure 1 shows the reverse supply chain network modeled for recycling EOL smartphones. Similar to Ijuin et al. [11], the model consists of collection centers G, recovery facilities R, and disposal facilities H.

In the collection center \(g( \in \left\{ {1, \ldots ,\left| G \right|} \right\})\), EOL smartphones are collected with the status \(k\left( { \in \left\{ {1, \ldots ,\left| K \right|} \right\}} \right)\). The status k determines the GHG recovery weight \(GHG_k^{\text{R}}\) and the recycling cost \(C_k^{{\text{RC}}}\) for recycling. The GHG recovery weight \(GHG_k^{\text{R}}\) refers to the GHG recovery amounts during the recycling stage. The recycling cost \(C_k^{{\text{RC}}}\) is the difference between the cost incurred for disassembly of the EOL product and the sales revenue made from the sale of the recovered materials.

The EOL smartphone with status k is transported from collection center g to the recovery facility \(r\left( { \in \left\{ {1, \ldots ,\left| R \right|} \right\}} \right)\) or disposal facility \(h\left( { \in \left\{ {1, \ldots ,\left| H \right|} \right\}} \right)\), with a transportation cost of \(C_{gr}^{{\text{LC}}}\) and \(C_{gh}^{{\text{LC}}}\), respectively. These transportation costs are determined by the distance between the collection center g and recovery facility r, or g and the disposal facility h. In the recovery facility r, the smartphone with status k is recycled with a recycling cost \(C_k^{{\text{RC}}}\). This is the cost to disassemble the EOL smartphone and takes the sales price of the recycled smartphone into account. When the smartphone is recycled, the amount of GHG volume is also reduced proportional to weight \(GHG_k^{\text{R}}\). In the disposal facility h, there are no recycling costs or recovery of GHG emissions.

Fig. 1.
figure 1

Reverse supply chain network model in the case of smartphones.

Full size image

2.2 Variables and Parameters

Based on Ijuin et al. [11], the GHG volume TGHG and the total cost TC as objective functions are set using integer programming [12]. The number of products with status k transported from the collection center g to the recovery facility r and the disposal facility h is represented by vgrk and vghk, respectively. The binary value ur is the decision variable to open a recovery facility r. Total cost TC is calculated by using the transportation numbers vgrk and vghk, and the decision variable to open recovery facilities. The number of collected EOL products at collection center g is represented by \(Q_g^{CQ}\) while the number of products with status k and recycled at the recovery facility r is represented by \(x_{kr}\).

The total cost TC is calculated by summing the recycling cost \(C_k^{{\text{RC}}}\), transportation cost \(C_{gr}^{{\text{LC}}}\) and, \(C_{gh}^{{\text{LC}}}\) for an EOL product, and the cost for opening recovery facility \(C_r^{{\text{FC}}}\) in the reverse supply chain network as shown in Eq. (1).The total GHG volume TGHG is calculated by subtracting the GHG recovery weight of a product with status k \(GHG_k^{\text{R}}\) and GHG emissions \(GHG^{\text{E}}\), which is the GHG emissions weight in the manufacturing stage as shown in Eq. (2).

$$ \begin{array}{*{20}c} {TC = \sum\nolimits_{g \in G}^G {\sum\nolimits_{r \in R}^R {\sum\nolimits_{k \in K}^K {\left( {C_k^{{\text{RC}}} + C_{gr}^{{\text{LC}}} } \right)v_{grk} } } } + \sum\nolimits_{g \in G}^G {\sum\nolimits_{h \in H}^H {\sum\nolimits_{k \in K}^K {C_{gh}^{{\text{LC}}} v_{ghk} } } } } \\ {+ \sum\nolimits_{r \in R}^R {C_r^{{\text{FC}}} u_r } } \\ \end{array} $$
(1)
$$ TGHG = \mathop \sum \nolimits_{g \in G}^G GHG^{\text{E}} Q_g^{{\text{CQ}}} - \mathop \sum \nolimits_{r \in R}^R \mathop \sum \nolimits_{k \in K}^K GHG_k^{\text{R}} x_{kr} $$
(2)

To apply LPP [9] to a reverse supply chain network, two objective functions, related to the total material-based GHG volume TGHG and total cost TC, are aggregated into a single function as shown in Eq. (3). Each objective function i is divided into five limits \(t_{i,s}^+\)(s = 1, 2, 3, 4, 5), where, based on the divided ranges, six ranges referred to as “Ideal” (Under \(t_{i,1}^+\)), “Desirable” (\(t_{i,1}^+\)  ~ \(t_{i,2}^+\)), “Tolerable” (\(t_{i,2}^+\)  ~ \(t_{i,3}^+\)), “Undesirable” (\(t_{i,3}^+\)  ~ \(t_{i,4}^+\)), “Highly Undesirable” (\(t_{i,4}^+\)  ~ \(t_{i,5}^+\)), and “Unacceptable” ( Over \(t_{i,5}^+\)) are decided. In Eq. (3), \(\tilde{w}_{is}^+\) is the weight parameter for objective function i and range s based on each limit \(t_{i,s}^+\). The regression value for all objective functions is multiplied by the deviation \(d_{is}^+\) and weight parameter \(\tilde{w}_{is}^+\) for each objective function.

$$ \sum\nolimits_{i \in I} {\sum\nolimits_{s = \left\{ {2,3,4,5} \right.\} } {\tilde{w}_{i,s}^+ d_{i,s}^+ } } \to min $$
(3)

As the first objective function, the 1st deviation \(d_{1,s}^+\) of the total cost TC is determined under the constraint Eq. (4), where the total cost TC needs to be lower than the limit of unacceptable (Over \(t_{1,5}^+\)), as shown in Eq. (5). In the literature of LPP definition [9], the constraint of the derivation is mentioned as “s = 2,…, 5”. Equations (4) and (6) evaluate the difference among each objective function and aspiration levels. Since s = 1 means the aspiration level of ideal representing best solution range, the difference of each objective function is not required to be evaluated.

$$ TC - d_{1,s}^+ \le t_{1,s - 1}^+ .\quad s = 2, \ldots ,5 $$
(4)
$$ TC \le t_{1,5}^+ . $$
(5)

As the second objective function, the 2nd deviation \(d_{2,s}^+\) for the total GHG volume TGHG is determined from the constraint Eq. (6), where the total GHG volume TGHG needs to be lower than the limit of unacceptable \(t_{2,5}^+\), as shown in Eq. (7).

$$ TGHG - d_{2,s}^+ \le t_{2,s - 1}^+. \quad s = 2, \ldots ,5$$
(6)
$$ TGHG \le t_{2,5}^+.$$
(7)

3 Case Study

To design a reverse supply chain network for collecting and recycling smartphones using LPP, following assumptions are prepared based on the study of Ijuin et al. [11].

  • Product example and global material scenario

    • In a material manufacturing stage, types and weight of materials are assumed within a smartphone based on a survey and material-based GHG emissions visualization tool [13]. There are mainly four materials contained in the products [14] as follows: copper (Cu), ABS, glass, and a lithium ion battery (LIB). By using the material-based GHG emissions visualization tool developed by Umeta et al. [13], GHG emissions when manufacturing the materials depending on countries within smartphone’s components are estimated by life cycle assessment [15].

    • As global material scenarios, there are two global scenarios are assumed and compared depending on material manufacturing country as follows.

      Scenario 1: Materials within components of a smartphone are manufactured in country A, where material-based GHG emissions are lower while procurement costs are higher than them manufactured in country B.

      Scenario 2: Materials within components of a smartphone are manufactured in country B, where material-based GHG emissions are higher but procurement costs are lower than them manufactured in country A.

    • In recycling stage for an EOL smartphone, three product statuses are assumed for their GHG recovery volume \(GHG_k^{\text{R}}\) and recycling cost \(C_k^{{\text{RC}}}\), as shown in Table 1. The recycling cost \(C_k^{{\text{RC}}}\) is the difference between the disassembly cost and the sales revenue of the recovered material.

  • Reverse supply chain example

    • Similar to Ijuin et al. [11], it is assumed that there are two collection centers (G = {1, 2}), three recovery facilities (R = {1, 2, 3}) and one disposal facility (H = {1}) as an example of facilities.

    • Each collection center has 3,000 EOL smartphones with each status (K = {1, 2, 3}), thus, total 9,000 (\(Q_g^{CQ}\) = 9,000) EOL products exist. Each recovery facility has recyclable EOL products depending on the EOL product status.

Table 1. Recycling cost and GHG recovery volume for each status
Full size table

4 Result

To evaluate the values of total GHG volume TGHG and total cost TC for a reverse supply chain network design, a numerical experiment is conducted using the LPP developed in Sect. 2 for the two scenarios described in Sect. 3.

Figure 2 shows the result of the total GHG volume and total cost on countries A and B in the case of smartphones, while Table 2 represents the obtained aspiration level for each objective function. In the case of country A, GHG emissions for components are less than the GHG emissions in country B. Even if all EOL products having status 1 are not recycled, the aspiration level for the GHG volume became “Tolerable”. Therefore, since recovery facility 1, which can recycle EOL products having status 1, is not operating, the preference level of total cost came within the “Desirable” range. In the case of country B, due to the opening of recovery facility 1, the total cost is by 94% higher than one in country A. However, the GHG volume in country B is by 8% lower than one in country A.

Additionally, the total transportation cost between countries A and B is different as shown in Fig. 2. Since material-based GHG emissions for the products manufactured in country B are higher than ones in country A, a larger number of the EOL products manufactured in country B should be collected and recycled to increase the total GHG recovery volumes. However, due to the production capacity at each facility, some of the EOL products manufactured in country B should be transported to a far recovery facility for recycling. Therefore, the transportation and recycling cost for the smartphones manufactured in country B become higher by 65% and 96%, respectively, than ones in country A.

Fig. 2.
figure 2

Result of the total GHG volume and total cost on countries A and B

Full size image
Table 2. Aspiration level for each objective function for countries A and B
Full size table

Regarding the EOL product having status 1, 74% (4,416 out of 6,000 EOL smartphones having status 1 are recycled) of EOL products manufactured solely in country B are recycled. One of the reasons is that the GHG emissions of a product \(GHG^{\text{E}}\) in country B are by 45% higher than ones in country A. All EOL products having status 2 are recycled in the recovery facility 2, which is closer from collection centers than the recovery facility 1. For EOL products with the status 3, only those near the recovery facility 3 are recycled from the collection center, and the others are disposed of.

5 Conclusion

This study applied a bi-objective reverse supply chain network design to the GHG volume and costs applying LPP to the case of smartphones. For EOL smartphones, it was found that the EOL products with high GHG emissions should be transported to a far recovery facility for recycling. One of the managerial insights is that the products manufactured in the country with low GHG emissions are economical than ones in the country with high GHG emissions when considering the recycling stage. Regarding the reverse supply chain network, the EOL products need to be recycled in a nearby facility due to transportation costs.

Future studies should consider recycling mixed products in a reverse supply chain scenario and measure the reverse supply chain network by using net present value (NPV).