Keywords

1 Introduction

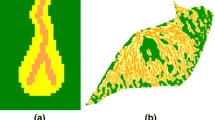
Point bars (Fig. 1) are fluvial sediments that accumulate at the inner bends of channel meanders by deposition of eroded sediments as the channel migrates outwards [1, 20, 37]. Point bars have great economic significance [7], as they can serve as large storage reservoirs [14, 24]. The McMurray Formation in Alberta, Canada, which hosts large accumulations of bitumen is predominantly composed of point bar deposits [36]. Other examples are those of the Widuri Field [6] and the Little Creek Field in southwestern Mississippi [35].

Fig. 1
figure 1

Point bar deposit, formed by erosion of sediments from the outer bend (cutbank), and deposition of the eroded sediments at the inner bend, adapted from [15]

Full size image

However, point bars exhibit complex spatial distribution of heterogeneities [12, 24, 33]. As an example, [34] identified different forms of depositional trends in different directions within point bar deposits. Some of these directional trends include fining upwards, fining along downstream direction and fining in the direction perpendicular to the inclined layers (called inclined heterolithic stratification (IHS)). These trends can affect the exploitation of the subsurface for hydrocarbon production and geological storage of CO2. For example, point bar heterogeneities like shale drapes along the IHS surfaces act as flow barriers, compartmentalize the reservoir and decrease storage capacity [16, 17]. Therefore, developing modeling methods for representing point bars is of economic consequence.

Several studies have used different methods to develop point bar models. Some of these methods are process-based (e.g., [29, 32], object-based (e.g., [4, 11, 39], surface-based (e.g., [26, 30], and geostatistical simulation methods like sequential indicator simulation (e.g., [9]. The geostatistical-based methods remain popular among researchers and modelers. More recently, [8] combined geometric modeling with geostatistical computations to represent point bar geometries and their petrophysical property distribution. This included the use of sine generation function (SGF) to model the aerial dimension of the point bar, to capture the lateral accretions. The main drawback of their study is that the use of the SGF may not yield realistic approximations for point bars with asymmetric geometries.

In this study, a cubic spline function is used to develop a smooth geometric model of the point bar that captures the lateral accretions, while a sigmoidal function is used to model the inclined heterolithic stratifications (IHS). A key element of the modeling approach is the incorporation of a computationally inexpensive grid generation scheme that preserves the point bar curvilinear architecture.

2 An Overview of Point Bar Geometry

The main heterogeneities in the point bars are the lateral accretions and the inclined heterolithic stratifications (IHS). These heterogeneities are formed by episodic migration of meandering channels, due to the erosion of sediments from the outer bend of the channel, and deposition of the eroded sediments into the inner bend. If one moves along section AB in Fig. 2a, a channel is first encountered. A further progression towards point B shows some curvy structures. Those are the lateral accretions, which are traces of past channel migrations, the vertical component of which is the IHS as captured in Fig. 2b.

Fig. 2
figure 2

Point bar schematic, showing a the lateral accretions and b the inclined heterolithic stratifications (IHS). Adapted from [31, 34]

Full size image

3 Modeling Approach

The workflow for modeling the point bar is as summarized in Fig. 3. This would be discussed in detail in subsequent sections.

Fig. 3
figure 3

Proposed workflow for modeling the point bar reservoir

Full size image

4 Channel and Point Bar Facies Identification

Channel and point bar facies can be identified using well log information. Previously, Spontaneous Potential (SP) logs have been used to accomplish this task (e.g., [25, 27], where a bell shape signal has been interpreted to be a point bar while a blocky or cylindrical shape has been interpreted as a channel (Fig. 4).

Fig. 4
figure 4

SP log profiles for point bar and channel identification. Blocky or cylindrical shape is an indication of a channel while a bell shape is an indication of a point bar. Adapted from [38]

Full size image

5 Channel Path Recreation

The workflow for channel path recreation is as summarized in Fig. 5. We begin by identifying facies and classifying them as either point bars or channels, using well log information (Fig. 5a). Since this is a synthetic workflow for demonstration purpose, we assume that all the blue points are channel well locations and the red ones are point bar locations. We then establish the direction of channel progression. This can be done either by using Gamma ray log readings, which increases in the downstream direction (because of increasing clay content), or by inferring from the variation in channel thickness, which decreases in the downstream direction [5, 28]. In this synthetic workflow, the facies have been sorted from left to right (Fig. 5b), because it has been assumed that the channel progresses easterly. The channel path recreation begins in Fig. 5c, where we honor the geological phenomenon of point bars forming at the concave side of a channel meander. This is done by conditioning the channel path to go through the channel nodes sequentially, and bend to accommodate the point bar nodes on the concave side of the bend. This process continues until the entire well data is accommodated (Fig. 5d).

Fig. 5
figure 5

Synthetic procedure for channel path recreation. a Identifying facies and classifying them into channels (blue) and point bars (red), b Sorting facies in the direction of channel flow (East–West direction), c Channel path recreation begins. Channel path goes through channel nodes sequentially, and bend to accommodate the point bars on the concave side, and d Full channel path accommodating all the well data

Full size image

The channel meander path is approximated by a parametric natural cubic spline which passes through a given sequence of channel nodes. The basic form of a cubic spline, with coefficients \(a, b, c,\) and \(d\) is defined as:

$$P(t) = at_{j}^{3} + bt_{j}^{2} + ct_{j} + d$$
(1)

The parameter value \(t\) for the \(j th\) channel node, denoted \({t}_{j}\) is the cumulative sum of the square root of chord length defined according to the centripetal scheme by [18], and it is expressed as:

$$t_{j} = \sum\nolimits_{{i < j}} {\sqrt {\parallel channel\,nodes_{{i + 1}} - channel\,nodes_{i} \parallel _{2} } }$$
(2)

The coefficients (\(a, b, c, d\)), which are weights for interpolating the channel nodes, could be determined from [22].

6 Channel Path Migration

The migration process basically involves using today’s channel meander path (i.e., the current channel meander path) to recreate the ancient channel path (i.e., initial channel meander path). This process allows us to capture the entire aerial extent of point bar and its lateral accretions. We can conceptually explain this process by using any of the concave regions of the channel meander path in Fig. 5d. Assuming the point bar associated with the first concave region in Fig. 5d is of interest, we isolate the channel path in that portion. This extracted channel meander path becomes the current channel path (Fig. 6a). Perturbing the spline coefficients to recreate this initial channel meander path is problematic, because ensuring that the spline coefficients exhibit consistency among themselves is extremely difficult. Instead, we accomplish the migration task by defining a focal point that controls \(n\) possible channel meander paths as shown in Fig. 6b. That is, if there are \(p\) points along the current channel path (with coordinates \(x_{i} ,\,y_{i} ,\,\,i = 1,\,2,\, \ldots p\), then \(n\) possible points \(\left({{x}_{i}}_{j},{{y}_{i}}_{j}, j=\mathrm{1,2}..,n\right)\) can be generated corresponding to each of these \(p\) points and the focal point \(\left( {x_{f} ,y_{f} } \right)\), using Eq. 3:

$$\left( {x_{{i_{j} }} ,\,y_{{i_{j} }} } \right) = \left( {x_{i} + (j - 1) \cdot \frac{{\left( {x_{i} - x_{f} } \right)}}{n - 1},\,y_{i} + (j - 1) \cdot \frac{{\left( {y_{i} - y_{f} } \right)}}{(n - 1)}} \right)$$
(3)
Fig. 6
figure 6

Migration of current channel path to recreate initial channel path. a Current channel path, b Current channel path migrated backwards to recreate possible initial channel meander paths, (arrow indicates the direction of backward migration, i.e., migration starting from today’s channel path to the ancient path), c Area covered by the Current channel path and the pre-migration path and d Current channel path and the most probable initial channel path

Full size image

where \(i = \mathrm{1,2},3\dots p\); \(j = \mathrm{1,2},3\dots n\); \({x}_{i}\) and \({y}_{i}\) are respectively, the \(x\) and \(y\) coordinates of each point at node \(i\) along the current channel path, and \(\left({x}_{f},{y}_{f}\right)\) are defined as:

$$\left({x}_{f},{y}_{f}\right)=\left\{\begin{array}{c}\left({x|}_{\frac{dy}{dx} =0},\mathrm{max}\left({y}_{i}, i=1,\dots ,p\right)\right), if \,channel\, concaves\, up\\ \\ \left({x|}_{\frac{dy}{dx} =0},\mathrm{min}\left({y}_{i,} i=1,\dots ,p\right)\right), if\, channel\, concaves\, down\end{array}\right.$$
(4)

\({x|}_{\frac{dy}{dx} =0}\) is the x-coordinate at the bend where the slope of the channel path is zero. Please note that in all our discussions, it is assumed that the channel progresses in the E-W direction. In a case where the channel path is oblique, a coordinate rotation is necessary for the formulations discussed herein to work.

Applying Eq. 3 and 4 yields the focal point (red point) and the possible initial channel meander paths in Fig. 6b. To select the most probable initial meander path, we make use of the concept of erosion coefficients for each of the possible initial channel meander path. The use of erosion coefficients is guided by the observation that before lateral migration of the channel, the channel path is linear. The channel begins to bend when erosion begins to occur. Therefore, the extent of channel curvature is an indication of the degree of erosion. Thus, we can capture the extent of curvature or erosion coefficient (\(\alpha\)), by using the area bounded by the curves (i.e., the channel paths), as shown in Eq. 5. If knowledge or field data about the erosion co-efficient is available, we can select the initial meander path as the one that yields the closest match to the erosion coefficient from field data, after applying Eq. 5. Otherwise, one can assume equal likelihood of occurrence for each of the paths and randomly select one of the generated initial channel meander paths. In this demonstration, we used the latter to obtain the initial meander path (see Fig. 6d).

$$\alpha = 1 - \frac{{A^{\prime}}}{A}$$
(5)

where \(A\) is the area bounded by the pre-migration channel path and the current channel path (Fig. 6c), and \(A^{\prime}\) is area bounded by the initial meander path and the current channel path (Fig. 6d).

As the channel migrates, it leaves behind lateral accretion surfaces that extend from the initial channel position to the current location of the channel. The encircled portion in Fig. 7 illustrates a point bar deposit that extends up to the banks of the current channel. To capture the full extent of the point bar, we need to account for this lateral extension. If the channel has a width \(W\), then the distance \(d\) to which the point bar laterally extends can be computed as [2]:

$$d = \frac{W}{1.5}$$
(6)
Fig. 7
figure 7

Illustration of the of point bar deposit extending into the channel, adapted from [23]

Full size image

As an approximation, [19] demonstrated that \(W\) can be computed as:

$$W = \sqrt[{1.01}]{{\frac{{\lambda_{m} }}{10.9}}}$$
(7)

The parameter \({\lambda }_{m}\) is the wavelength of the channel (units in m), which is the distance between point \(T\) and \(K\) as illustrated in Fig. 7. In our case, it is equivalent to the length of the pre-migration path in Fig. 6c.

Using these pieces of information, we can delineate the full lateral extent of the initial and current channel meander paths, by computing the coordinates at the points of extension for the initial and current channel paths. If there are \(p\) points on each channel path, then for each point \(i\) on the initial or current channel path, we can compute these coordinates \(\left({x}_{pb,i},{y}_{pb,i}\right)\), using Eq. 8.

$$\left( {x_{pb,i} ,\,y_{pb,\,i} } \right) = \left( {\left( {x_{ch,i} \pm d \cdot \cos \beta_{i} } \right),\,\left( {y_{ch,i} \pm d \cdot \sin \beta_{i} } \right)} \right)$$
(8)

where \(i=\mathrm{1,2},3\dots p\), \({\beta }_{i}\) is the angle between a point at node \(i\) on the channel path, and the focal point discussed earlier. The focal point is illustrated as \(F\) in Fig. 7. The signs in Eq. 8 depend on whether \({\beta }_{i}\) is positive or negative. Applying Eq. 8, yields the path extensions for the current and initial channel meanders paths in Fig. 8.

Fig. 8
figure 8

Demarcation of the lateral extents of a the current channel path, and b the initial channel path

Full size image

7 Modeling the IHS Geometry

As described by [34], the inclined heterolithic surfaces (IHS) are approximately sigmoidal. These surfaces represent the vertical sequence of sediments that are deposited as the channel migrates. We modeled the geometry of the IHS by solving the sigmoidal equation along the IHS surfaces, using Eq. 9.

$$z^{ \circ } = \circ \frac{h}{{1 + e^{ - as} }}$$
(9)

where \(h\) is the vertical thickness of the point bar (see Fig. 7) and \(a\) is the slope of an IHS over a horizontal distance \(s\). As illustrated in this Fig. 7, \(s=d\) for the current channel path. Applying Eq. 9 for the current channel path yields Fig. 9.

Fig. 9
figure 9

Sigmoidal representation of the IHS for the current channel path

Full size image

8 Grid Generation

The task of gridding the complex 3D geometry of a point bar was simplified somewhat by first discretizing the initial and current channel paths, and later combining them with their corresponding IHS grids, to generate 3D gridded surfaces. Finally, the region between the 3D gridded surfaces for the current and initial meander paths are infilled to complete the gridding of the entire point bar.

The procedure is such that, a domain of interest is initially defined, as depicted in Fig. 10a as the region between the current channel path and the migrated path. Assuming the number of grid nodes along each channel path is \(nx\), and \(L\) is the length along the channel, we can compute the cumulative distance \(l\) at every node \(i\) along the channel path using Eq. 10, and use it determine the coordinates of the grid nodes at every division along the channel path (see Fig. 10b). To generate the coordinates of the grid nodes across the channel, Eq. 11 is used by specifying the number of grid nodes across the channel (\(ny\)), to produce Fig. 10c. The equivalent curvilinear grid for the current channel is displayed in Fig. 10d.

$$l_{i}^{ \circ } = \circ \frac{L}{nx} \circ \cdot (i - 1)$$
(10)
$$\left( {u_{i,j} ,v_{i,j} } \right) = \left( {x_{i,j} + \left( {j - 1} \right) \cdot \frac{{x_{i,j} - x^{\prime}_{i,j} }}{ny - 1},y_{i,j} + (j - 1) \cdot \frac{{y_{i,j} - y^{\prime}_{i,j} }}{ny - 1}} \right)$$
(11)
Fig. 10.
figure 10

2D Grid generation process for the current channel path. a Domain to be gridded, b grid nodes generated along the channel, c grid nodes generated across the channel and d equivalent curvilinear grid for the current channel path

Full size image

where \(i = \mathrm{1,2},3\dots nx\); \(j = \mathrm{1,2},3\dots ny\); \(\left({u}_{i,j},{v}_{i,j}\right)\) is the coordinate of the grid at node \(i,j\) across the channel. \(({x}_{i,j},{y}_{i,j})\) and \({{({x}^{^{\prime}}}_{i,j}, {y}^{^{\prime}}}_{i,j})\) are the respective coordinates of the grid nodes generated along the channel paths (Fig. 10b).

For a point bar of constant vertical thickness, \(h\), as illustrated previously, if we know the z-coordinates of the grid nodes for a section across the channel \(\left({\mathbb{Z}}_{i=constant ,j,k}\right)\), the remaining z-coordinates of the grid nodes at the other locations \(\left({z}_{i,j,k}\right)\) can be easily replicated. Thus, by specifying \(nz\) (i.e., the number of grid nodes along the z-axis), we can repeat the procedure used to generate grid nodes along the channel to generate grid nodes along the IHS at a particular section (Fig. 11).

Fig. 11
figure 11

a Current channel path, and section taken across it (red line), and b Grid nodes generated for the IHS across this section for the current channel path

Full size image

We are now ready to project the gridded channel paths into 3D gridded surfaces. Figure 12a shows the 3D gridded surface for the current channel path. Repeating the above procedure for the initial channel path yields Fig. 12b. To generate a grid for the entire point bar, the overlap region between the two 3D gridded surfaces, as illustrated in Fig. 12c is gridded, using Eq. 12. Figure 12d represents the 3D grid for the entire point bar.

$$\begin{gathered} \left( {X_{ijk} ,X_{ijk} ,Z_{ijk} } \right) = \left( {u_{i,j,k} + \left( {j - 1} \right) \cdot \frac{{u_{i,j,k} - u^{\prime}_{i,j,k} }}{ny - 1},v_{i,j,k} } \right. \hfill \\ \left. { + \left( {j - 1} \right) \cdot \frac{{v_{i,j,k} - v^{\prime}_{i,j,k} }}{ny - 1},z_{i,j,k} + \left( {j - 1} \right) \cdot \frac{{z_{i,j,k} - z^{\prime}_{i,j,k} }}{ny - 1}} \right) \hfill \\ \end{gathered}$$
(12)
Fig. 12.
figure 12

3D Grid generation process for the entire point bar. a 3D grid for the current channel, b 3D grid for the initial channel, c overlap of the 3D grids for the current and initial channel paths, showing the overlap region to be gridded d equivalent 3D curvilinear grid for the entire point bar

Full size image

where \(\left({u}_{i,j,k},{v}_{i,j,k},{z}_{i,j,k}\right)\) and \((u^{\prime}_{i,j,k} ,\,v^{\prime}_{i,j,k} ,z^{\prime}_{i,j,k} )\) are the coordinates of the grid nodes along the 3D gridded channels in Fig. 12a and b respectively.

9 Preservation of Point Bar Architecture and Its Internal Heterogeneity

Generating a grid that preserves the point bar reservoir architecture is important, as it is critical to the preservation of the internal heterogeneities in geostatistical simulation. As can be seen in Fig. 13, horizontal (Fig. 13a) and vertical sections (Fig. 13b) taken across the point bar show that the curvilinear architecture of the reservoir is preserved by the gridding scheme implemented.

Fig. 13
figure 13

a horizontal slice, and b vertical slice taken arbitrarily across the point bar to demonstrate the preservation of the curvilinear architecture of the point bar

Full size image

While geostatistical simulation methods like multiple point statistics (MPS) [13, 21] can offer excellent approximation of reservoir architecture and its internal properties, the grid resolution required to capture some of the fine scale variations in a point may render the MPS approach computationally burdensome. As can be seen in Fig. 13, the gridding scheme incorporated in the workflow does not necessarily require many grid cells to sufficiently approximate the point bar curvilinear geometry. The proposed approach is therefore a less computationally expensive method for modeling point bar reservoirs.

To model the point bar properties, the direct use of the conventional geostatistical simulation methods like the Sequential Gaussian Simulation [10] may yield suboptimal results. This is because these methods are implemented within a rectilinear grid system and cannot capture the curvilinear continuity of the point bar properties. Therefore, implementing a grid transformation scheme is necessary. In the grid transformation, the curvilinear grid can be transformed into an equivalent rectilinear grid within which the properties can be modeled, after which the properties can be mapped back into the original curvilinear grid. The idea is to ensure that estimates of the properties proceed in a manner that preserves the point bar reservoir heterogeneity.

10 Concluding Remarks

A systematic method for modeling asymmetric point bar geometries has been proposed. The method incorporates a computationally inexpensive gridding scheme that accounts for the point bar curvilinear architecture. The inexpensive gridding scheme incorporated in the workflow makes the proposed method a promising technique for modeling point bars, especially when a flow simulation study is to be conducted on a large ensemble of point bar models.