Keywords

1 Introduction

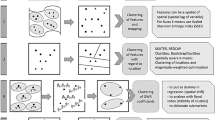
Machine learning (ML) algorithms have gained space in the mineral resource’s modeling process [4, 9, 12]. One motivational aspect of such increase in data-driven models use is the claim that ML methods generate non-stationary estimates and help solve the issue of non-stationary domains ([12, 14]), but care must be taken in making such claims. If a model is developed to predict block values from blast area A, can the model be used with confidence on blast area B? The answer to this question is not obvious and highlights practical issues that stem from data-driven models. When ML is used, specifically supervised learning, the goal is to infer an underlying relationship between input variables and target variables [13] so that values at unsampled locations are predicted from the modeled relationship. Nonetheless, it is assumed that the multivariate distributions of the training stage and the test stage are identical. In geological settings non-stationarity leads to changes within modeling domains and can generate a phenomenon known as dataset shift in ML, which compromises model performance. Therefore, to obtain an accurate and representative model, the presence of dataset shift should be verified [1, 3, 5, 11] and, if present, accounted for. To that end, two algorithms are proposed: the first detects and maps the dataset shift present in geological settings,the second is proposed to handle dataset shift and provide accurate final predictions. The results demonstrate the sub-optimality of ML methods in non-stationary geological domains when dataset shift is not accounted for.

2 Materials and Methods

Herein, two algorithms are developed to detect and handle dataset shift in geospatial context. The proposed algorithm to detect dataset shift is based on the assumptions presented by Gözüaçik et al. [7]. It considers a variable of interest \(Y\) in domain \(A\), with a local neighborhood \(W\) of fixed size. The samples contained in \(W\) are compared to (1) the global data distribution and (2) local samples in an adjacent neighborhood, \(K.\) The algorithm is performed in two steps: first, the algorithm compares the data from two adjacent neighborhoods (\(W\) and \(K\)). Samples within \(W\) are classified as 0 and samples within \(K\) as 1. The size of the neighborhoods can be defined as a fixed radius from an anchor point. Samples from both neighborhoods are merged to create a binary slack variable (\(\zeta\)). Classification of the merged data is attempted using logistic regression, where Y is used to classify \(\zeta\), the classifier is fit to predict the class (0 or 1) based on the sample values. The classifier’s ability to distinguish between classes is measured with the area under the receiver operator characteristic curve (AUC). \(AUC\approx 0.5\) indicates that the classifier is unable to separate the two classes, samples in the two neighborhoods are not shifted. \(AUC\approx 1.0\) indicates that the classifier can separate the two classes, the data distributions do not overlap and are shifted. Intermediate \(AUC\) values indicate the distributions partially overlap; typically, a threshold of \(AUC>0.7\) is used to determine if the distributions are shifted [7]. The second step of the algorithm considers a two sample Kolmogorv-Smirnov test (2 K-S test) [10] on samples in W and K. The nonparametric 2 K-S test verifies if two samples come from the same distribution. The common way to report and interpret the 2 K-S test is through the P-value. A critical region is calculated such that the probability of wrongfully rejecting the hypothesis that the samples originate from the same distribution is not more than a predetermined threshold (\(\alpha )\). If the P-value is lower than the threshold (\(\alpha )\), the distinctions are significant, and the hypothesis is rejected. To detect shift relative to the global distribution, the rational is the same as with two neighborhoods,however, a random sampling of the global distribution is considered to obtain a representative subset with a similar number of samples as the local neighborhood to avoid affecting classifier performance due oversampling one class. For the 2 K-S test, the local neighborhood must contain enough samples to reliably estimate the distributions. Combining the results of the discriminative classifier and the 2 K-S test results in 3 possible scenarios:

$$\left\{\begin{array}{l}2, if AUC>{\tau }_{1}\,and\,p-value<{\tau }_{2} , agreement\,and\,shift\,is\,likely\\ 1, if AUC>{\tau }_{1}\,and\,p-value>{\tau }_{2}\,or\,AUC<{\tau }_{1}\,and\,p-value< {\tau }_{2},disagreement\,and\,shift\,is\,possible\\ 0, if\,AUC<{\tau }_{1}\,and\,p-value>{\tau }_{2} , agreement\,and\,shift\,is\,unlikely\end{array}\right.$$

where \({\tau }_{1}\) is the threshold on AUC for the discriminative classifier, and \({\tau }_{2}\) is the P-value for the 2 K-S test.

The algorithm proposed to account for dataset shift is locally weighted support vector regression (LWSVR), aiming to adjust the training process to specific properties of sub-regions in the input space [2]. This is performed by assigning different importance to data most relevant to the location being predicted. Based on the principals of local models and weighting training data based on relevance, Ellatar et al. [6] proposed an algorithm in which the SVR risk function is modified to account for data relevance. In SVR traditional formulation \(C\) is a fixed regularization parameter defined a priori by the user, however, generalization error changes if \(C\) is modified according to a metric of relevance. The LWSVR risk function becomes:

$$min\frac{1}{2}{\| \omega \| }^{2}+{C}_{i}{\sum }_{n=1}^{N}\left({\xi }_{n}+{\xi }_{n}^{*}\right), {C}_{i}=\Omega \left(\mathbf{d}\right)C$$
(1)

\(\Omega \left(\mathbf{d}\right)\) is the weight calculated for each local neighborhood according to function dependent on the Mahalanobis distance considered inside each search neighborhood and a smoothing factor that controls the generalization range.

3 Results and Discussion

The workflow is demonstrated on the Walker Lake sample set containing 470 samples from variable V [8]. First the database is inspected for dataset shift, then the standard SVR approach and the proposed LWSVR algorithm are applied to make spatial predictions and quantify improvement in the presence of dataset shift. Then, simple kriging (SK) and SK with locally varying means (SK with LVM) are considered to draw a parallel analysis to the ML approaches. The shift detection algorithm is applied to the Walker Lake sample set to detect regions where dataset shift occurs. The global shift analysis compares local windowed distributions to the global distribution while the local shift analysis compares local windowed distributions to other nearby local windowed distributions. To that end, consider a set of local neighborhoods, \({W}_{i}, i=1,\dots ,n\), of fixed size of 60 m and \(n\) samples,compare this distribution to either the global distribution or an adjacent subregion (\(K)\) with 30 m overlap. Choice of threshold to determine a binary, shift versus no shift, decision is dataset specific. In this case study, a sensitivity analysis leads to a threshold for the AUC of 0.8 and P-value of 0.05. The dataset shift detection algorithm demonstrated regions where the dataset shift occurs between local and global distributions. Such regions may benefit from trend modeling in case of a geostatistical approach, or a lazy learning algorithm in ML context. Given that dataset shift is detected, the LWSVR and SVR algorithms are applied and evaluated. The SVR model is optimized with a grid search considering \(1{e}^{-5}<C<100\); \(1{e}^{-5}<\epsilon <0.1\) and \(1{e}^{-5}<\gamma <10\). Optimal SVR parameters are: \(C=0.53\), \(\gamma =6.57\) and \(\epsilon =0.0017\). For LWSVR, the \(C\) parameter is dependent on the closest data samples to the location being predicted. The number of samples retained for the LWSVR model is 5, while \(\gamma\) and \(\epsilon\) are held constant at 1.0 and \(0.1\), respectively. For both LWSVR and SVR the input variables for the predictions are the X and Y sample coordinates and the target variable is V.

The results show SVR obtained a smoother estimate than the LWSVR algorithm which reduced bias in the under sampled low valued regions (Table 1). Similarly, SK does not explicitly account for non-stationarity and produces a smoother estimate than SK with LVM. Bias in the predicted mean is evaluated using the exhaustive database, statistics are compared to the true statistics rather than the declustered data (Table 1); SK with LVM and LWSVR have lower bias in the mean as they better honor local features. As expected, SK with LVM is more variable than SK, similarly LWSVR is more variable than SVR (Table 1). Models’ performance is evaluated with a \(10\)-fold cross validation considering root mean squared error (RMSE) for each fold. Both local methods, LWSVR and SK with LVM, outperform their global counterparts. LWSVR results in a 25% RMSE improvement over SVR. It would be tempting to compare LWSVR to SK with LVM, but that comparison is inappropriate as SK honors data and provides a different modeling paradigm than ML algorithms. Because SK honors data, the impact of non-stationarity on geostatistical algorithms (3% improvement in RMSE) is much less than the impact of dataset shift on ML algorithms (25% improvement in RMSE) (Table 2).

Table 1 Comparison of model statistics relative to the true exhaustive statistics
Full size table
Table 2 Ten–fold cross validation
Full size table

The case study analysis reflects the nature of supervised ML algorithms, and objectively demonstrate the impact of dataset shift generated from non-stationarities in geospatial data. If the statistics change significantly between the training locations and where the modeling is deployed to obtain predictions, the relations previously learned are inefficient and lead to a final model that is not representative of the true geological phenomena. In this case, non-stationarities have to be explicitly (i.e. a trend model) or implicitly (i.e. local learning) accounted for; one such model, LWSVR, was proposed to consider this. The algorithm proposed to map dataset shift helps improve the modeling framework by identifying areas of interest where global algorithms are likely to underperform. However, some limitations persist. Applying the automated shift detection algorithm in sparse settings is sensitive to neighborhood search parameterization and the number of samples. The discriminative classifier is optimized for local neighborhoods, requiring that each labeled class have sufficient samples to form a training and test set. The choice of number of samples for LWSVR to generate a prediction is important and impacts conditional bias. The weighting function used in LWSVR also impacts performance. If sampling is dense, the penalty C applied on LWSVR is higher and can lead to overfit local models; while the search strategy and weight function can be easily modified, it may require tuning. Another aspect that must be considered is 3-dimensional data; the search strategy, anisotropy, and the implementation of the weight function should be modified accordingly. Finally, the impact of local optimization of \(\gamma\) and \(\epsilon\) should be considered, this study focused on local optimization of C.

4 Conclusions

Clear benefits of data-driven algorithms include reduced parameterization and fewer subjective modeling decisions; however, non-stationary spatial features often result in dataset shift within spatial modeling domains of interest. In this case, the impact of dataset shift on spatial modeling shows the importance of local learning. Practitioners must account for nonstationary spatial features of interest and understand how algorithms learning processes are affected by dataset shift and sparse sampling. Many algorithms do not have analogous lazy learning spatial implementations, as presented herein for SVR; it is the responsibility of the practitioner to understand the limitations of the chosen algorithm and investigate the appropriateness of associated lazy learning implementations.