Observation-Based Noise Calibration: An Efficient Dynamics for the Ensemble Kalman Filter

Abstract

We investigate the calibration of the stochastic noise in order to guide the realizations towards the observational data used for the assimilation. This is done in the context of the stochastic parametrization under Location Uncertainty (LU) and data assimilation. The new methodology is rigorously justified by the use of the Girsanov theorem, and yields significant improvements in the experiments carried out on the Surface Quasi Geostrophic (SQG) model, when applied to Ensemble Kalman filters. The particular test case studied here shows improvements of the peak MSE from 85% to 93%.

1 Introduction

Sequential data assimilation uses observational data to correct a set of realizations given by a numerical model. In the case of both high-dimensional data and model, the data assimilation methodology can be facilitated via a procedure allowing to guide the realizations towards the available observations. This is particularly helpful in high dimensions as it enables the ensemble to focus on a restricted set of the state space. That is what we intend to put forward in this paper. This work relies on a stochastic parametrization of the underlying dynamical system based on the Location Uncertainty (LU) principles, which rely on a decomposition of the Lagrangian velocity into a large-scale smooth component and a random time-uncorrelated component. In this setting, a stochastic transport operator plays the role of the usual material derivative, see [1] for more details. This work aims at adding the feature of a noise specifically calibrated to play a guiding role for the realizations.

In a previous data assimilation study on the Surface Quasi Geostrophic (SQG) model, the stochastic forecast was shown to provide better results than deterministic techniques like variance inflation with perturbation on the initial condition, see [2] for details. The current study is a continuation of [2]. The noise calibration presented here further improves the results presented in [2], particularly when the system starts from poor or badly estimated initial conditions (for instance resulting from initial estimations relying on regularized inverse problems). For such initial conditions, which are generally too smooth and inaccurate, classical ensemble methods are likely to be put in difficulties. In this short paper, we will first briefly recall the principles of Location Uncertainty and how it applies to the SQG model. Then we will detail the procedure leading to the noise calibration, and finally detail and assess the numerical experiments performed.

2 The Stochastic SQG Model Under Location Uncertainty (LU)

The analysis in this paper is carried out on the 2D Surface Quasi-Geostrophic (SQG) model. The SQG equations model an idealized dynamics for surface oceanic currents. It involves many realistic non-linear features such as fronts or strong multiscale eddies (see [3, 4] for details). The deterministic SQG model couples a transport equation of the buoyancy field b, a kinematic condition and a 2D divergence-free constraint:

$$\displaystyle \begin{aligned} \mathrm{D}_t b=0~~;~~b=\frac{N_{strat}}{f_0}(- \varDelta)^{\frac{1}{2}}\psi~~;~~v=\nabla^\perp\psi, {} \end{aligned} $$

(1)

expressed on ψ the stream function and v the velocity, where D_t is the material derivative. The kinematic condition depends on the stratification N _strat and the Coriolis frequency f ₀.

The corresponding stochastic dynamics is derived from the Location Uncertainty (LU) principles described in [1]. The full description and numerical analysis of the LU-SQG model can be found in [5, 6]. This stochastic formalism models the impact of the small scales on the flow component that is initially smooth in time. It relies on the decomposition of the Lagrangian velocity of a fluid particle positioned at x _t in a spatial domain $\varOmega \subset \mathbb {R}^2$:

$$\displaystyle \begin{aligned} \mathrm{d} x_t=v(x_t,t)\mathrm{d} t+\sigma(x_t,t)\mathrm{d} B_t, {} \end{aligned} $$

(2)

in terms of a resolved component v (referred to as the large-scale component in the following) and σdB _t, an unresolved highly oscillating random component, built from a (cylindrical) Wiener process B _t (ie a well-defined Brownian motion taking values in a functional space) [7]. The increments of the latter component are time-independent. Due to the lack of smoothness of the solution x _t, we rigorously derive (2) in its integral form.

The random perturbation of velocity is Gaussian and has the following distribution:

$$\displaystyle \begin{aligned} \sigma \mathrm{d} B_t\sim\mathcal{N}(0,Q\mathrm{d}t), \end{aligned} $$

(3)

where Q is the covariance operator. This operator admits an orthonormal eigenfunction basis {ϕ _n(⋅, t)}_{n ∈N} with non-negative eigenvalues (λ _n(t))_{n ∈N}. This generates a convenient spectral definition of the noise as

$$\displaystyle \begin{aligned} \sigma(x,t)\mathrm{d} B_t=\sum_{n\in\mathrm{N}}\sqrt{\lambda_n(t)}\phi_n(x,t)\mathrm{d}\beta^n_t, {} \end{aligned} $$

(4)

where the β ⁿ are i.i.d standard one dimensional Brownian motions. From Eq. (4), the noise variance tensor a is then defined by

$$\displaystyle \begin{aligned} a(x,t)=\sum_{n\in\mathrm{N}}\lambda_n(t)\phi_n(x,t)\phi_n(x,t)^T. \end{aligned} $$

(5)

It can be noticed the variance tensor has the physical dimension of a viscosity (ie m ²∕s). Indeed, as σdB _t is a distance, then a(x, t)dt = E[σdB _t(σdB _t)^T] is a squared distance. The procedure used to generate the orthonormal basis functions determines the spatial structure of the noise. The one used in our experiments will be presented later in this section.

While a deterministically transported tracer Θ has zero material derivative: D_t Θ = ∂ _t Θ + v ⋅∇Θ = 0, in the LU framework, a stochastically transported tracer cancels a related stochastic transport operator defined as:

$$\displaystyle \begin{aligned} {\mathbf{D}}_t \varTheta:=\mathrm{d}_t \varTheta+(v^* \mathrm{d} t+\sigma \mathrm{d} B_t)\boldsymbol{\cdot}\nabla \varTheta-\frac{1}{2}\nabla\boldsymbol{\cdot}(a\nabla \varTheta)\mathrm{d} t, {} \end{aligned} $$

(6)

where

$$\displaystyle \begin{aligned} \mathrm{d}_t\varTheta:=\varTheta(x,t+ \mathrm{d}t)-\varTheta(x,t) \end{aligned} $$

(7)

is the infinitesimal forward time increment of the tracer. The effective advection velocity is defined by

$$\displaystyle \begin{aligned} v^*=v-\frac{1}{2}\nabla\boldsymbol{\cdot} a, {} \end{aligned} $$

(8)

the term σdB _t ⋅∇Θ is a non-Gaussian multiplicative noise corresponding to the tracer’s transport by the small-scale flow, and the last term in (6) is a diffusion term, as the variance tensor a is definite positive. The expression of the stochastic transport operator comes from a generalized Itô formula (Itô-Wentzell formula), see [5] for more details.

The stochastic version of the SQG model is obtained by replacing the material derivative D_t b in Eq. (1) with the stochastic transport operator D _t b:

$$\displaystyle \begin{aligned} {\mathbf{D}}_t b=\mathrm{d}_t b+(v^* \mathrm{d}t+\sigma \mathrm{d}B_t)\boldsymbol{\cdot}\nabla b-\frac{1}{2}\nabla\boldsymbol{\cdot}(a\nabla b)\mathrm{d} t=0, {} \end{aligned} $$

(9)

and an additional compressibility constraint on the noise:

$$\displaystyle \begin{aligned} \nabla\boldsymbol{\cdot}\sigma\mathrm{d} B_t=0. \end{aligned} $$

(10)

In the case of a compressible random field, the modified advection incorporates an additional term in Eq. (8) related to the noise divergence [5]. One essential property of LU (for a divergence-free noise component) is the conservation of energy for the transported random tracer, under the same ideal boundary conditions as in the deterministic case:

$$\displaystyle \begin{aligned} \mathrm{d} \int_\varOmega \varTheta^2(x) \mathrm{d} x = 0, \end{aligned} $$

(11)

and, very importantly, this energy conservation property holds pathwise (i.e for any realization of the Brownian noise), see [5, 8] for details. This property highlights the strong relation between the LU-SQG version and the deterministic one.

Noise Generation

The method used to generate the noise in this study relies on a data-driven method called proper orthogonal decomposition (POD) to estimate the empirical orthogonal functions in the spectral representation of Eq. (4). By a slight abuse of notation in the following, this noise will be referred to as POD noise. We give some brief details in what follows.

Considering a series of snapshots of the velocity field, this method consists in the computation of the covariance tensor around the temporal mean of the series of snapshots. Then its eigenvectors and eigenfunctions can be estimated in order to reconstruct the large-scale variability (the first“modes” or eigenfunctions), and the small-scale one (the smaller modes). In practice, this procedure is applied to coarse-grained high-resolution snapshots of deterministic simulations. The latter modes will be the ones on which the noise is decomposed. These modes are divergence-free and stationary by construction, so the global structure of the noise will not vary in time. In case of chaotic geophysical models like this one, we can also use online-computed noises as the one used in our previous work [2] which have much better uncertainty quantification, but are also much more expensive. An extension of this work to this noise is currently at work. We refer to [6] for a precise description of this procedure.

3 Girsanov Theorem and Noise Calibration

3.1 Change of Measure

Ensemble-based sequential data assimilation filters are composed of a forecasting step of the ensemble to provide a sampling of the forecast distribution, and an analysis step correcting the departure from the observations. The purpose of the proposed noise calibration is to modify the forecast distribution, taking into account the upcoming observation, in order to guide the forecast towards it. In the context of transport equations such as in the SQG model, this extra guiding term is an added drift in the noise σdB _t, which was initially built to have zero mean. Allowing σdB _t to have a non-zero mean entails a modification of the transport equation in order to rewrite it in terms of a centered noise. This is called the Girsanov transform, and it consists in a change of underlying measure so that a non-centered noise becomes centered under a new probability measure, up to a drift term accounting for this change of measure. For now, σdB _t is defined on a probability space $(\Omega ,\mathcal {F},\mathrm {P})$ and we define $(\mathcal {F}_t)_t$ the filtration adapted to σdB _t.

The Girsanov theorem (see [7] for details) states that if (Y _t)_0≤t≤T is a stochastic process such that:

• (Y _t)_0≤t≤T is adapted with respect to the Wiener filtration $(\mathcal {F}_t)_{0\leq t\leq T}$.

• For the current probability measure P, we have, P-almost surely,

  $$\displaystyle \begin{aligned} \int_0^T Y_t^2 \mathrm{d} t <\infty.\end{aligned}$$

• The process (Z _t)_0≤t≤T defined by

  $$\displaystyle \begin{aligned} Z_t=\exp\left(\int_0^t Y_s \mathrm{d} B_s -\frac{1}{2}\int_0^t Y_s^2 \mathrm{d} s\right) \end{aligned} $$

  (12)

  is a $\mathcal {F}_t$-martingale,

then there exists a probability measure $\tilde {\mathrm {P}}$ under which:

• The process $(\tilde {B}_t)_{0\leq t\leq T}$ defined by

  $$\displaystyle \begin{aligned} \tilde{B}_t=B_t-\int_0^t Y_s \mathrm{d} s {}\end{aligned} $$

  (13)

  is a standard cylindrical Wiener process.

• The Radon-Nikodym derivative of $\tilde {\mathrm {P}}$ with respect to P is Z _T.

Let us denote by (Γ _t)_0≤t≤T the drift we intend to add to the noise. With such a change of measure, let us see how Eq. (9) is modified. According to Eq. (13), we have

$$\displaystyle \begin{aligned} \mathrm{d} B_t=\mathrm{d} \tilde{B}_t+\varGamma_t \mathrm{d} t, \end{aligned} $$

(14)

so the stochastic transport operator rewrites

$$\displaystyle \begin{aligned} \mathrm{D}_t b=\mathrm{d}_t b+(v^* \mathrm{d} t+\sigma [\mathrm{d} \tilde{B}_t+\varGamma_t \mathrm{d} t])\boldsymbol{\cdot}\nabla b-\frac{1}{2}\nabla\boldsymbol{\cdot}(a\nabla b)\mathrm{d} t \end{aligned} $$

(15a)

$$\displaystyle \begin{aligned} =\mathrm{d} _t b+(v^* \mathrm{d} t+ v_\varGamma \mathrm{d} t + \sigma \mathrm{d} \tilde{B}_t)\boldsymbol{\cdot}\nabla b-\frac{1}{2}\nabla\boldsymbol{\cdot}(a\nabla b)\mathrm{d} t, {} \end{aligned} $$

(15b)

where

$$\displaystyle \begin{aligned} v_\varGamma=\sum_{k=1}^K\gamma_k\phi_k {} \end{aligned} $$

(16)

is the velocity drift entailed by the Girsanov transform and we assume that Γ _t = Γ = (γ ₁, …, γ _K) is constant on a small time step dt, which will be the case for the discretized numerical scheme that we use.

As a result, under the probability measure $\tilde {\mathrm {P}}$, (15) presents the same form as Eq. (9) since $\tilde {B}$ is indeed a centered cylindrical Wiener process under $\tilde {\mathrm {P}}$, but with an added drifted advection velocity.

3.2 Computation of the Girsanov Drift

We now describe how to compute Γ in order to guide the forecast towards the next observation.

Let us start from a given time t ₁ where a complete buoyancy and velocity field is available. The next observation b ^obs(⋅, t ₂) is assumed to be available at time t ₂ and L numerical time steps are performed until then (t ₂ − t ₁ = Lδ _t, where δ _t is the time discretization step).

At time t ₁, a rough prediction of the velocity at time t ₂ can be estimated with the current velocity (which, more precisely, comes from previous stochastic iterations, but is $\mathcal {F}_{t_1}$-measurable), namely

$$\displaystyle \begin{aligned} b^{obs}\left(x+v(x,t_1)L\delta_t,t_2\right):=\tilde{b}(x,t_2), \end{aligned} $$

(17)

that stands for the backward-registered observation with respect to the current deterministic velocity. This way the error made is

$$\displaystyle \begin{aligned} \varDelta_t\tilde{b}(x)=\tilde{b}(x,t_2)-b(x,t_1). {} \end{aligned} $$

(18)

So $\tilde {b}(x,t_2)$ is a value taken in a modified observation field, because b ^obs is advected by the current velocity v(⋅, t ₁). For this reason we consider that the backward-registered observation used for the calibration does not have the same nature as the raw observation used for data assimilation. It constitutes a pseudo-observation, for which we can consider that the error due to the imprecision of the backward-registration (ensuing in particular from successive bilinear interpolations) is way bigger than the observation noise, and almost uncorrelated to the latter. In the second case, only the raw observation is used for the Kalman filter, corresponding only to the observation noise. The aim is now to calibrate the current velocity by adding a Girsanov drift $v_\varGamma =\sum _{k=1}^K\gamma _k\phi _k$, such that the solution of the following transport equation

$$\displaystyle \begin{aligned} b\left(x+v(x,t_1)L\delta_t+v_\varGamma L\delta_t+\sum_{k=1}^K(\sqrt{\delta_t}\phi_k) (\sqrt{L\delta_t}\beta_k),t_2\right)=b(x,t_1). \end{aligned} $$

(19)

is approximated in a least square sense. In other words, we solve the following minimization problem:

(20)

This can be rewritten as

$$\displaystyle \begin{aligned} \min_\varGamma \int_\varOmega\left[ \varDelta_t\tilde{b}+\nabla\tilde{b}\boldsymbol{\cdot} v_\varGamma L\delta_t-\frac{1}{2}\nabla\tilde{b}\boldsymbol{\cdot}\nabla aL\delta_t-\frac{1}{2}\nabla\boldsymbol{\cdot}(a\nabla\tilde{b})L\delta_t\right]^2 \mathrm{d}x.\end{aligned}$$

Using the identities

$$\displaystyle \begin{aligned} \nabla\boldsymbol{\cdot}a=\sum_{k=1}^K (\phi_k\boldsymbol{\cdot}\nabla)\phi_k~~;~~\nabla\boldsymbol{\cdot}(a\nabla b)=\sum_{k=1}^K (\phi_k\boldsymbol{\cdot}\nabla)(\phi_k\boldsymbol{\cdot}\nabla b), \end{aligned} $$

(21)

we rewrite the minimization problem as

$$\displaystyle \begin{aligned} \min_\varGamma \int_\varOmega\left[ \varDelta_t\tilde{b}+\nabla\tilde{b}\boldsymbol{\cdot}\left(\sum_{k=1}^K\gamma_k\phi_k\right)L\delta_t-\frac{1}{2}\sum_{k=1}^K(\nabla\tilde{b}\boldsymbol{\cdot} F_k+G_k(\tilde{b}))L\delta_t\right]^2 \mathrm{d}x {} \end{aligned} $$

(22)

where

$$\displaystyle \begin{aligned} F_k=(\phi_k\boldsymbol{\cdot}\nabla)\phi_k~~;~~G_k(\tilde{b})=(\phi_k\boldsymbol{\cdot} \nabla)(\phi_k\boldsymbol{\cdot}\nabla\tilde{b}). \end{aligned}$$

Denoting by J the integrand, we have

$$\displaystyle \begin{aligned} \begin{array}{rcl} & &\displaystyle \frac{\partial J}{\partial \gamma_i}=2\int_\varOmega(\nabla\tilde{b}\boldsymbol{\cdot}\phi_i)L\delta_t\left[\varDelta_t\tilde{b}+\nabla\tilde{b}\boldsymbol{\cdot}\left(\sum_{k=1}^K\gamma_k\phi_k\right)L\delta_t\right.\\ & &\displaystyle -\left.\frac{1}{2}\sum_{k=1}^K(\nabla\tilde{b}\boldsymbol{\cdot} F_k+G_k(\tilde{b}))L\delta_t\right]\mathrm{d}x. \end{array} \end{aligned} $$

(23)

Finally, we add a regularization term $\alpha \vert \vert v_\varGamma \vert \vert _2^2= \alpha \sum _{k=1}^K\gamma _k^2\lambda _k$, where λ _k is the eigenvalue of the Q-eigenfunction ϕ _k in Eq. (22) to ensure the uniqueness of the solution of the proposed minimization problem, where α needs to be tuned properly.

As a result, the minimization problem can be written as an inverse problem

$$\displaystyle \begin{aligned} A\varGamma=c \end{aligned} $$

(24)

where

$$\displaystyle \begin{aligned} A_{ik}:=2\int_\varOmega(\nabla\tilde{b}\boldsymbol{\cdot}\phi_i)(\nabla\tilde{b}\boldsymbol{\cdot}\phi_k)+2\alpha\lambda_k\delta_{ik} \end{aligned} $$

(25a)

$$\displaystyle \begin{aligned} c_i:=\int_\varOmega(\nabla\tilde{b}\boldsymbol{\cdot}\phi_i)\left[2\varDelta_t\tilde{b}-\sum_{k=1}^K(\nabla\tilde{b}\boldsymbol{\cdot} F_k+G_k(\tilde{b}))\right]\mathrm{d}x.\end{aligned} $$

(25b)

The parameter α is a priori fixed in order to control the resulting euclidian norm of v _Γ, ||v _Γ||₂. Large values of α lead to very small corrections (Γ tends to (0, …, 0) when α goes to + ∞) whereas small values yield very strong and noisy drifts, as we get closer to an ill-posed problem. For now, we use an empirical iterative way to tune α, we increase it until the resulting norm of v _Γ is under a given threshold.

4 Experiments

This section details the numerical experiments carried out in this work. The goal is to study the benefits brought by a noise-calibrated forecast in an up-to-date version of a localized ensemble Kalman filter. In particular we wish to observe whether or not the noise calibration brings by itself an efficient and practical improvement of the assimilation step.

Ensemble Kalman filters (see e.g. [9] for details) constitute a well-known family of data assimilation methods. They rely on an ensemble of realizations (called ensemble members) of a dynamical system $(x^f_n)_{n=1,\ldots ,N}$ coming from the forecast step, and give as an output another set of members $(x^a_n)_{n=1,\ldots ,N}$. Each posterior ensemble member $x^a_n$ is obtained as a linear combination of the prior ensemble members $(x^f_n)_{n=1,\ldots ,N}$ in order to minimize the distance between the ensemble and the observation in some sense.

One important assumption of the classical EnKF is to consider that the observation and model noise are uncorrelated. This observation-calibrated forecast could imply that the latter assumption no longer holds. Still, the discussion following Eq. (18) on the observation nature explains why we can consider the uncorrelation between the forecast and observation noise. If this assumption appears to be not valid, we refer to the work made in [10] to rigorously justify the introduction of an observation-dependent forecast. In this work, both Kalman and particle filter equations were rewritten in terms of the conditional expectation with respect to the underlying sequence of current and past observations. The stochastic simulations are run on a double-periodic simulation grid, G _s, of size 64 × 64 points and of physical size 1000 km × 1000 km, meaning that two neighbor points are approximately 15 km apart. An observation is assumed to be available every day (i.e. every 600 time steps of the dynamics) on a coarser observation grid, G _o, which is a subset of G _s of size 16 × 16. It is generated as follows: a trajectory of buoyancy (z _t)_t is run from the deterministic model (PDE) at a very fine resolution grid G _f, of size 512 × 512. Then a convolution-decimation procedure D is applied in order to fit to the targeted simulation grid G _s. It consists in the composition of a Gaussian filter and a decimation operator subsampling one pixel out of two. It has to be iterated three times in our case to fit the correct resolution. This is done in order to respect Shannon’s theorem and to avoid spectrum folding. A projection operator P is applied from G _s to G _o, and we finally add an observation noise to get the observation

$$\displaystyle \begin{aligned} b^{obs}(\cdot,t)=P\circ D(z_t)+\eta_t~~;~~\eta_t\sim\mathcal{N}(\mathbf{0},R)~~\mathrm{and}~~R=r^2 I_M, {} \end{aligned} $$

(26)

where R is the diagonal observation covariance matrix and M is the number of points on the observation grid.

Numerical Setup

The simulations have been performed with a pseudo-spectral code in space (see [6] for details). The time-scheme is a fourth-order Runge-Kutta scheme for the deterministic PDE, and an Euler-Maruyama scheme for the SPDEs. We use a standard hyperviscosity model to dissipate the energy at the resolution cut-off with a hyperviscosity coefficient $\beta =(5\times 10^{29}\, \text{m}^8.\text{s}^{-1})M_x^{-8}$, where M _x is the grid resolution [6].

The test case considered in this study is the following: an ensemble of N = 100 ensemble members is started from the very same initial condition at day 0, which consists in two cold vortices to the north and two warm vortices to the south. However, the amplitude of the initial vortices is underestimated compared to the initial condition used for the deterministic run (considered as the truth) by 20%, as shown in Fig. 1. We refer to [2] for a mathematical expression of this field.

Fig. 1

Initial conditions for the truth (on the left) and for each stochastic run (on the right, common to all ensemble members). We enforce an underestimation of the amplitude of the initial vortices of 20%

In this experiment, we study the differences of efficiency of the localized Ensemble Square Root Filter (an up-to-date version of the Ensemble Kalman filter, see for instance [11] for details of the square root filters (ESRF) and [12] for a description of the observation covariance localization procedure) with both noise-calibrated forecast and classical stochastic simulations. We also refer to [13] for the extension of the square root filter for additive forecast noise based on covariance transformation, where the advantages of additional model error in the forecast step are shown.

In both cases, starting from the underestimated initial condition, the stochastic dynamics is simulated using the POD noise with K = 10 modes. An observation is provided each day (i.e. every 600 time steps of the SPDE), with an observation error covariance set to r = 10⁻⁵ in (26), which corresponds to a weak (but not negligible, 1% of the maximum amplitude in the initial buoyancy field) noise on the observation. The localization radius is set to l _obs here, where l _obs ≃ 60 km denotes the distance between two neighboring observational sites, as it provided the best results for both cases.

The typical behaviour of the vortices, at least at the beginning of the simulation, is to spin with no translation of the cores. In our case, the true vortices will spin much faster than those in the biased stochastic runs. The goal of calibration is then to speed these vortices up in order to get them closer to the truth.

The forecast is calibrated at each time step of the SPDE, using the upcoming observation to do it. Multiple parameters were tried for the regularization parameter α, or alternatively for the upper bound allowed for the L ²-norm of the Girsanov drift v _Γ. Figure 2 compares the MSE along time for all the range of parameters tested here, with also the same experiment without noise calibration. For this latter, the LESRF has a difficult task, as it tries to find linear combinations of the prior ensemble members, which all have an underestimated velocity, to get closer to the observation. This is a general issue for ensemble methods (as well as for particle filters), which are not able and designed to correct the bias if this correction is not made in the forecast. By contrast, the LU calibration offers an additional degree of freedom to guide the ensemble towards the observation. This procedure significantly improves the results in terms of MSE. At day 13, when the MSE is maximal for the usual case, we observe an improvement from 85% to 93% depending on the parameters tested. The case of the underestimation is an example, but we expect this procedure to be efficient in any situation in which all ensemble members have a similar problem of bias, bad amplitude estimation, artefacts, unsymmetrical features, etc. With a reasonably small ensemble size, which is generally the case in practice, this is likely to occur if the initial conditions have such features.

Fig. 2

Comparison of MSE along time between the non calibrated forecast (in black) and all the different parameters tested here for the noise calibration. The snapshots shown in Fig. 3 are taken at day 15 (black dashed line)

As explained previously, the regularization term α controls the amplitude of the allowed correction drift. In our experiments, all parameters tested yield significant improvements compared to the classical case, still a good trade-off seems to be found with a control of ||v _Γ||₂ between 70 and 150. Starting from 150, we observe higher MSE in the very first days, certainly due to a lack of constraint on the inverse problem. In addition to the MSE results, we show in Fig. 3 a more visual example of what calibration does. At day 15, the configuration of the truth is that all four vortices are horizontal. Without calibration (first row), the vortices are slanted because of the initial underestimation of the velocity. The velocity field has not been properly corrected. On the other hand, the LU calibration offers a more reliable prediction, as we recovered the global shape of the vortices, with additional spread around the mean.

Fig. 3

Comparison between the ensemble mean (left) and the ensemble standard deviation (right) maps, with and without calibration, at day 15 with the high-resolution truth

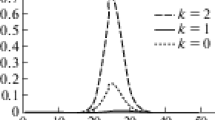
Finally, we show in Fig. 4 an insight of how the Girsanov correction v _Γ behaves in time. As the structure of the noise is stationary, so is the structure of v _Γ because it relies on the same modes as the noise. What is interesting is the evolution of the amplitude of this field, which decreases in time, meaning that most of the calibration work is done in the very first days of simulation, and once the forecast manages to get closer to the truth, the need for calibration is less crucial and the Girsanov correction gets weaker.

Fig. 4

Vorticity of the Girsanov drift v _Γ computed for one ensemble member at the first time step after the initial condition (left) and at the first time step after day 17 (right)

5 Conclusion

The findings of this paper show the ability of a data-driven noise calibration procedure to improve significantly the assimilation by EnKF of a system initialized with an underestimated initial condition.

As already mentioned in Sect. 2, we intend to extend this setting to non-stationary noises, as they were shown to be associated to a better quantification of the uncertainty (see [6] for details). Regarding computational effort, the calibration procedure is intrinsically paralellizable ensemble-wise, and the techniques used are close to optical flow estimation procedures, for which efficient solutions exist. The tuning step of α is the more expensive step for now, for which more sophisticated methods could be envisaged.