1 Introduction

A fundamental challenge in observational sciences, such as weather forecasting and climate change predictions, is the modelling of uncertainty due, for example, to unknown or neglected physical effects, and incomplete information in both the data and the formulation of the theoretical models for prediction. Various dynamical parameterisation approaches have been proposed to tackle this challenge, see e.g. [6], [4], [11], [5], [1]. Of particular interest are the recently developed Data Driven models, that accommodate uncertainty by predicting both the expected future measurement values and their uncertainties, based on input from measurements and statistical analysis of the initial data. To effectively incorporate uncertainty in the data driven approach, such predictions are made in a probabilistic sense. Additionally, a data assimilation procedure is used to take into account the time integrated information obtained from the data being observed along the solution path during the forecast interval as “in flight corrections”.

In the geoscience community, data assimilation (DA) refers to a set of methodologies designed to efficiently combine past knowledge of a geophysical system (in the form of a numerical model) with new information about that system (in the form of observations). DA is a central component of Numerical Weather Prediction where it is used to improve forecasting by adjusting the model parameters and reducing the uncertainties. To achieve this, a stochastic feedback loop between the model and the observation may be introduced: the assimilation of more data during the prediction interval will then decrease the uncertainty of the forecasts based on the initial data, by selecting the more likely paths as more observational data is collected. This is the basis of the so-called ensemble data assimilation which uses a set of model trajectories that are intermittently updated according to data.

A key step for ensuring the successful application of the combined stochastic parameterisation and data assimilation procedure, is the “correct” calibration of stochastic model parameters. For Stochastic Advection by Lie Transport (SALT) and Location Uncertainty (LU) models, current numerical methods for calibration, see [4], [1], [5], [12], have largely been inspired by the physical interpretation of the models derivations. More specifically on the assumption that the flow map is decoupled into a slow scale mean part and a fast scale fluctuating part. In the references mentioned before, it was shown that these methods are effective and led to successful combination of data driven models and state of the art data assimilation techniques.

In this work, we wish to investigate the feasibility and viability of probabilistic pathwise approach for calibration. Our general aim is to explore such ideas for a wide class of nonlinear stochastic transport models. This will be very useful in data assimilation problems, as in real world applications the signal is usually observed through discrete observations, but no results of this type for SALT or LU models have been obtained before. Currently, Lagrangian particle trajectories are simulated starting from each point on both the physical grid and its refined version, then the differences between the particle positions are used to calibrate the noise. This is computationally expensive and not fully justified from a theoretical perspective. In the same spirit as [3] but with a more complicated noise term and without any smoothing effects of a Laplacian, we propose an approach which uses high-frequency in time and low-frequency in space observations of a single path of the solution, to rigorously infer properties of the stochastic parameters. The knowledge of the noise is crucial for determining the behaviour of the solution and for assessing to what degree the solution of the coarse resolution SPDE deviates from the solution of the fine resolution PDE in the model reduction procedure, so an optimal calibration of the noise parameters is relevant from both a theoretical and an applied perspective.

In this work we look at stochastic calibration for the two-dimensional incompressible Euler equation in vorticity form. This stochastic equation models the local rotation of a fluid flow in the presence of spatial uncertainties and it has been derived from fundamental principles in [6]. This equation is a key ingredient in modelling phenomena in oceanography and in order to ensure that it efficiently encodes the small-scale variability in the upper part of the ocean, one needs to specify the stochastic parameters based on real observations. One of the main issues in parameter estimation using real data is the fact that the model parameters do not map to observations in a unique way (model identifiability problem, see e.g. [2]). For this reason, we believe that a probabilistic approach is much more suitable.

The 2D Euler equation in the form derived in [6] and studied in [4], [5] and [8] is given by:

$$\displaystyle \begin{array}{llll} d{\omega }_{t}+u_{t}\cdot \nabla {\omega }_{t}dt+\displaystyle\sum_{i=1}^{\infty}\xi_i \cdot \nabla {\omega }_{t}\circ dW_{t}=0 \end{array} $$
(1)

where u = (u 1, u 2) is the fluid velocity, ω = curl u = ∂ 2 u 1 − ∂ 1 u 2 is the vorticity, (ξ i)i are divergence-free time-independent vector fields such that

$$\displaystyle \begin{array}{llll} \displaystyle\sum_{i=1}^{\infty} \|\xi_i\|{}_{k+1,\infty}^2 < \infty \end{array} $$
(2)

and \((W^{i})_{i \in \mathbb {N}}\) is a sequence of independent Brownian motions. Global well-posedness for Eq. (1) has been proven in [8] and the numerical and data assimilation perspective has been studied in [4] and [5]. In [8] the authors have shown that Eq. (1) admits a unique pathwise solution which belongs to the Sobolev space \(\mathcal {W}^{k,2}(\mathbb {T}^2) \ (k\geq 2)\) when \(\omega _0 \in \mathcal {W}^{k,2}(\mathbb {T}^2)\) and which can be extended to \(L^{\infty }(\mathbb {T}^2)\) when \(\omega _0 \in L^{\infty }(\mathbb {T}^2)\).

In this paper we consider the following SPDE on the two-dimensional torus \(\mathbb {T}^{2}=\mathbb {R}^{2}/\mathbb {Z}^{2}\), driven by a 1-dimensional Brownian motion W:

$$\displaystyle \begin{array}{llll} d{\omega }_{t}+u_{t}\cdot \nabla {\omega }_{t}dt+\xi \cdot \nabla {\omega }_{t}\circ dW_{t}=0 \end{array} $$
(3)

where u and ω are as above and ∘ denotes Stratonovich integration. We impose the following condition on the stochastic parameter ξ, in the same spirit as (2):

$$\displaystyle \begin{array}{llll} \|\xi\|{}_{k+1,\infty}^2 < \infty \end{array} $$
(4)

with k > 4. This condition ensures that for any \(f \in \mathcal {W}^{2,2}(\mathbb {T}^2) \cap \mathcal {W}^{2,\infty }(\mathbb {T}^2)\),

$$\displaystyle \begin{array}{llll} \|\xi\cdot\nabla f\|{}_{2}^2 \leq C\|f\|{}_{1,2}^2 \ \ \ \ \ \ \ \|\xi\cdot\nabla(\xi\cdot\nabla f)\|{}_2^2 \leq C\|f\|{}_{2,2}^2 \end{array} $$
(5)
$$\displaystyle \begin{array}{llll} \|\xi\cdot\nabla f\|{}_{\infty}^2 \leq C\|f\|{}_{1,\infty}^2 \ \ \ \ \ \ \ \|\xi\cdot\nabla(\xi\cdot\nabla f)\|{}_{\infty}^2 \leq C\|f\|{}_{2,\infty}^2. \end{array} $$
(6)

Remark 1

We can view the stochastic part as a space-time noise (ξ, W) where the spatial component is given by ξ and the time component is a standard Brownian motion. This perspective is many times useful in numerical applications where (ξ ∘ dW t) ⋅∇ is implemented as a random operator applied to the solution ω.

The problem of parameter estimation, known also as statistical inference, is technically challenging for such (infinite-dimensional) SPDEs driven by transport noise, as most methods used in the literature benefit from a diagonalizable structure of the underlying space-covariance matrices. This structure is specific for additive noise and therefore it does not apply in our case. Also, most results are obtained for stochastic variations of the heat equation, which contain a smoothing Laplace operator (see for instance [3]). Our model does not contain a Laplacian a priori, and therefore we cannot exploit the properties of a heat kernel. These makes the analysis much harder.

Contributions of the Paper

In this work, we focus on Eq. (3) from two perspectives:

  • First, we show that the driving stochastic parameter ξ can be calibrated in an optimal way to match a set of high-frequency in time given data. This is done using a forced and damped version of the equation and a parametric form of the stream function and the corresponding stochastic parameter which is implemented using an orthonormal basis. Our technique can be explicitly applied to calibrate the 2D Euler model using real oceanic data and we intend to do this in coming work.

  • Second, we show that the original 2D Euler model is robust with respect to the stochastic parameters ξ in the sense that if we consider two couples (ω 1, ξ 1) and (ω 2, ξ 2) which solve Eq. (3), then the L 2 distance between ω 1 and ω 2 can be controlled using the initial conditions and the difference between ξ 1 and ξ 2 only (see Sect. 4). This is important in applications as it shows that if we consider approximate values for ξ, the corresponding model solution remains close to the true solution.

Structure of the Paper

In Sect. 2 below we present the problem formulation. In Sect. 3 we introduce the methodology. In Sect. 4 we prove the robustness of the original model and in Sect. 5 we present the numerical results.

2 Problem Formulation

Let \((\Omega , \mathcal {F}, (\mathcal {F}_t)_{t\geq 0}, \mathbb {P})\) be a filtered probability space and W a one-dimensional Brownian motion adapted to the complete and right-continuous filtration \((\mathcal {F}_t)_{t\geq 0}\).

Let \(h:{\mathbb R}\rightarrow {\mathbb R}\) be a smooth function representing some observation map. We assume we have available a finite sequence of high frequency in time snapshots of observed vorticity fields, that are denoted by \(h(\omega ^*)_{t_i}(x) := h(\omega ^*_{t_i})(x)\), i = 1, …, N, and are adapted to \((\mathcal {F}_t)_{t\geq 0}\). We take the view that the \(h(\omega ^*)_{t_i}\)’s are the given observation data. We further assume that \(\omega ^*_{t_i} \in \mathcal {W}^{k,2}({\mathbb T^2}), k>4\).

Writing ω ξ to denote solutions to the model (3) for a given vector field ξ, the generic problem we are interested in is to find a ξ so that solutions to (3) matches the data as best as possible, i.e.

$$\displaystyle \begin{array}{llll} \displaystyle\arg\min_{\xi}\|\omega^{*} - \omega_\xi\| \end{array} $$
(7)

for some suitable norm.Footnote 1

The dimension of the observations currently coincides with the number of sources of noise, that is we have a determined system. However, in practice this is not always a realistic assumption and in future work we will look at underdetermined or overcomplete systems i.e. when the number of noise sources is larger than the dimension of the observation operator.

In general, the infinite dimensional optimisation problem (7) may be too hard to solve in practice. We thus make concrete the form of ξ. Let \(({\mathfrak {e}}_{j})_{j\in \mathbb {N}}\) be an orthonormal basis in \(L^2(\mathbb {T}^2)\). We assume the following parametric form for the stream function of ξ, which is henceforth denoted by ζ,

$$\displaystyle \begin{array}{llll} \zeta(x) = \sum_{j=1}^\infty \alpha_j {\mathfrak{e}}_j, \end{array} $$
(8)

where α j are reals. Then

$$\displaystyle \begin{array}{llll} \xi(x) = \nabla^\perp \zeta(x) = \sum_{j=1}^\infty \alpha_j \nabla^\perp {\mathfrak{e}}_j(x) \end{array} $$
(9)

and the optimisation problem (7) then reduces to finding the coefficients α j.

3 Methodology

For a stochastic process X t defined on a filtered probability space, its quadratic variation is defined by

$$\displaystyle \begin{array}{llll}{}[X]_t := \lim_{\max_j\Delta t_j\rightarrow 0}\sum_{i=1}^n |X_{t_i} - X_{t_{i-1}}|{}^2,\end{array} $$
(10)

where t 0 = 0 < t 1 < ⋯ < t n = t is a partition of the interval [0, t], Δt i := |t i − t i−1|, and the convergence is in the sense of probability (see e.g. [7]).

From (3) and (9) we have

$$\displaystyle \begin{array}{llll} \omega_t(x) = \omega_0(x) - \displaystyle\int_0^t B_s(x;\omega) \ ds - \displaystyle\int_0^t \displaystyle\sum_j \alpha_j \nabla^\perp {\mathfrak{e}}_j(x) \cdot \nabla \omega_t(x) \circ dW_t \end{array} $$
(11)

in which for notation simplicity, we have introduced B s(x;ω) := u s(x) ⋅∇ω s(x).

Using Itô’s lemma, and following standard results on the quadratic variation of semimartingales, it is straightforward to show that

$$\displaystyle \begin{array}{llll}{}[h(\omega)]_t = \sum_{i,j=1}^\infty \alpha_i \alpha_j \int_0^t \langle h'(\omega_s),\ \nabla^\perp {\mathfrak{e}}_i\cdot\nabla \omega_s\rangle \ \langle h'(\omega_s),\ \nabla^\perp {\mathfrak{e}}_j\cdot\nabla \omega_s \rangle \ ds. \end{array} $$
(12)

Due to global existence and uniqueness of solutions to (3), [h(ω)]t exists globally \(\mathbb {P}\)-almost surely. Thus the right hand side of (23) can be arbitrarily well approximated by its truncation for all t i.e. for a given 𝜖 > 0, there exists M 𝜖 such that

$$\displaystyle \begin{array}{llll} \left | [h(\omega)]_t - \sum_{i,j=1}^{M_\epsilon} \alpha_i\alpha_j \int_0^t \langle h'(\omega_s),\ \nabla^\perp {\mathfrak{e}}_i\cdot\nabla \omega_s\rangle \ \langle h'(\omega_s),\ \nabla^\perp {\mathfrak{e}}_j\cdot\nabla \omega_s \rangle \ ds \right | < \epsilon. \end{array} $$
(13)

Additionally, from the computational perspective, for any fixed M 𝜖, the linear map

$$\displaystyle \begin{array}{llll} {\mathbf{A}}_{ij} := \int_0^t \langle h'(\omega_s),\ \nabla^\perp {\mathfrak{e}}_i\cdot\nabla \omega_s\rangle \ \langle h'(\omega_s),\ \nabla^\perp {\mathfrak{e}}_j\cdot\nabla \omega_s \rangle \ ds \end{array} $$
(14)

that defines the truncated quadratic form is symmetric and positive definite,Footnote 2 and thus can be diagonalised by a unitary linear map. Doing so, we obtain the following linear problem

$$\displaystyle \begin{array}{llll}{}[h(\omega)]_t = \sum_{j=1}^{M_\epsilon} \tilde{\alpha}_j^2 \lambda_j + \epsilon', \end{array} $$
(15)

where 𝜖′ denotes the truncation error of (23), λ j are the eigenvalues of the associated linear map, and \(\tilde {\alpha }_j\)’s are the original α values which get rescaled by the unitary matrix from the diagonalisation.

We can estimate [h(ω)]t using the high frequency in time data h(ω ∗) and (10), assuming the discrete sum converges fast enough,

$$\displaystyle \begin{array}{llll}{}[h(\omega)]_t \approx \widehat{[h(\omega)]}_{t,N} := \sum_{i=1}^N |h(\omega^*)_{t_i} - h(\omega^*)_{t_{i-1}}|{}^2 . \end{array} $$
(16)

The estimate \(\widehat {[h(\omega )]}_{t,N}\) could then be used in (15) to get an estimate for the \(\tilde {\alpha }\). One could then recover the original α’s by applying the unitary linear map that’s associated with the diagonalisation of A ij.

Example 1

Let h be the identity map. Let \({\mathfrak {e}}_\kappa = e^{i\kappa \cdot x}\) be the Fourier basis. Then we have

$$\displaystyle \begin{array}{llll} \widehat{[\omega]}_{t,N} = \sum_{\substack{i,j=1 \\ \text{with }\kappa_i, \kappa_j \in \mathbb{Z}^2 }}^\infty \alpha_i \alpha_j \int_0^t {\mathfrak{e}}_{\kappa_i}{\mathfrak{e}}_{\kappa_j} (\kappa_i^\perp \cdot \nabla \omega_s) \ ( \kappa_j^\perp \cdot \nabla \omega_s ) \ ds. \end{array} $$
(17)

In Sect. 5 we test numerically Eq. (17) for an idealised example, and show we can adequately recover the basis coefficients using our methodology.

Example 2

In this example, we assume the data are the kinetic energy of the flow,

$$\displaystyle \begin{array}{llll} \mathrm{E}_t := \frac {12 }{\int_{\mathbb T^2}} |{\mathbf{u}}_t|{}^2 d\mathbf{x}. \end{array} $$
(18)

Thus the data are “indirect” information about the vorticity. Note that the energy data is feasible for SALT models as energy is not a conserved quantity of SALT.

Below, we avoid calculating the pressure term of the Euler system by utilising the Biot-Savart operator K that links the velocity field to the vorticity field in Eq. (3). For further discussions on this topic see [9] or [10]. We have

$$\begin{array}{llll} \mathbf{u}(\mathbf{x}) = (K \star \omega)(\mathbf{x}) = \int_{\mathbb{T}^2} K(\mathbf{x}-\mathbf{y})\omega(\mathbf{y})d\mathbf{y} \end{array} $$
(19)

where

$$ \begin{array}{llll} K(\mathbf{x}) = \sum_{\kappa \in \mathbb{Z}^2\setminus \{0\}} \frac{i\kappa^{\perp}}{\|\kappa\|{}^2}e^{i\kappa \cdot \mathbf{x}}. \end{array} $$
(20)

It is known that, for any k ≥ 0, there exists a constant C k,2, that is independent of u, and such that

$$\displaystyle \begin{array}{llll} \|\mathbf{u}\|{}_{k+1, 2} \leq C_{k,2}\|\omega\|{}_{k,2}. \end{array}$$

If \(\psi : \mathbb {T}^2 \times [0, \infty ) \rightarrow \mathbb {R}\) is a solution for Δψ = −ω then u = ∇⊥ ψ solves ω = curl u, so u = −∇⊥ Δ−1 ω. The reconstruction of u from ω is ensured by the incompressibility condition ∇⋅u = 0 and a periodic, distributional solution of Δψ = −ω is given by

$$\displaystyle \begin{array}{llll} \psi(\mathbf{x}) = (G \star \omega)(\mathbf{x}) \end{array}$$

where G is the Green’s function of the operator − Δ on \(\mathbb {T}^2\)

$$ \begin{array}{llll} G(\mathbf{x}) = \sum_{\kappa \in \mathbb{Z}^2\setminus \{0\}} \frac{e^{i\kappa \cdot \mathbf{x}}}{\|\kappa\|{}^2} \end{array}$$

and κ = (κ 1, κ 2), κ ⊥ = (κ 2, −κ 1).

Combining (11) with the Biot-Savart law (19) we obtain

$$ \begin{array}{llll} {\mathbf{u}}_t(\mathbf{x}) &= {\mathbf{u}}_0(\mathbf{x}) - \int_0^t \int_{\mathbb T^2} K(\mathbf{x}-\mathbf{y}) B_s(\mathbf{y};\omega) d\mathbf{y} ds - \int_0^t \int_{\mathbb T^2} K(\mathbf{x}-\mathbf{y}) \xi(\mathbf{y})\cdot\nabla \omega_s(\mathbf{y}) d \mathbf{y} \circ dW_s \end{array} $$
(21)

Using Itô’s lemma, we obtain

$$\displaystyle \begin{array}{llll} \mathrm{E}_t - \mathrm{E}_0 = - \int_0^t \langle {\mathbf{u}}_s, K \star (B_s - \frac{1}{2}\xi \cdot \nabla(\xi\cdot\nabla \omega_s)) \rangle ds - \int_0^t \langle {\mathbf{u}}_s, K\star (\xi \cdot \nabla \omega_s)\rangle\ dW_s \end{array} $$
(22)

where 〈⋅, ⋅〉 is the standard \(L^2({\mathbb T^2})\) pairing. Thus

$$\displaystyle \begin{array}{llll} {[}\mathrm{E}{]}_t &= \sum_{i,j=1}^\infty \alpha_i \alpha_j \int_0^t \langle {\mathbf{u}}_s, K\star (\nabla^\perp {\mathfrak{e}}_j \cdot \nabla \omega_s)\rangle \langle {\mathbf{u}}_s, K\star (\nabla^\perp {\mathfrak{e}}_i \cdot \nabla \omega_s)\rangle \ ds. \end{array} $$
(23)

4 Robustness

Theorem 2

Let ω 1, ω 2 be two solutions of the 2D Euler equation (3) and ξ 1, ξ 2 the corresponding stochastic parameters for each of these two solutions. More precisely, (ω ℓ, ξ ℓ) for ℓ = 1, 2 solves

$$\displaystyle \begin{array}{llll} d{\omega}_{t}^{\ell}+u_{t}^{\ell}\cdot \nabla {\omega }_{t}^{\ell}dt+\xi^{\ell} \cdot \nabla {\omega }_{t}^{\ell} dW_{t}=\frac{1}{2}\xi^{\ell} \cdot \nabla\left( \xi^{\ell} \cdot \nabla\omega_t^{\ell}\right). \end{array} $$
(24)

Then for any p ≥ 2 there exist some constants Footnote 3 C = C(p, T), C 1,p, C 2,p , such that

$$\displaystyle \begin{array}{llll} \mathbb{E}\left[ \displaystyle\sup_{t\in[0,T]}e^{-\gamma(t)}\|\omega_t^1-\omega_t^2\|{}_2^{2p}\right] \leq C_{p,T} \left ( \|\omega_0^1-\omega_0^2\|{}_2^{2p} + \|\xi^1-\xi^2\|{}_2^{2p} +\|\xi^1-\xi^2\|{}_{1,2}^{2p}\right) \end{array} $$
(25)

where

$$\displaystyle \begin{array}{llll} \gamma(t):= C_{1,p}\displaystyle\int_0^t\| \omega_r^1\|{}_{k,2}^2dr + C_{2,p}t \end{array}$$

and k > 4.

Proof of Theorem 2

Let \(\bar {\omega }:= \omega ^1 - \omega ^2, \bar {u} = u^1-u^2, \bar {\xi } =\xi ^1 - \xi ^2\). Then \(\bar {\omega }\) satisfies

$$\displaystyle \begin{array}{llll} &d{\bar{\omega}}_t + (\bar{u}_t\cdot\nabla\omega_t^1 + u_t^2 \cdot \nabla {\bar{\omega}_t}) dt + \left( \xi^1\cdot\nabla\omega_t^1 - \xi^2\cdot\nabla\omega_t^2 \right) dW_t \\ &\quad =\frac{1}{2}\left( \xi^1\cdot\nabla(\xi^1\cdot\nabla\omega_t^1) - \xi^2\cdot\nabla(\xi^2\cdot\nabla\omega_t^2) \right)dt. \end{array} $$

By the Itô formula:

$$\displaystyle \begin{array}{llll} d\|\bar{\omega}_t\|{}_2^2=&-2\langle \bar{\omega}_t, \xi^1\cdot\nabla\omega_t^1 - \xi^2\cdot\nabla\omega_t^2\rangle dW_t-2\langle \bar{\omega}_t, \bar{u}_t \cdot \nabla \omega_t^1 + u_t^2 \cdot \nabla {\bar{\omega}_t}\rangle dt \\ &+ \left(\langle \bar{\omega}_t, \xi^1\cdot\nabla(\xi^1\cdot\nabla\omega_t^1) - \xi^2\cdot\nabla(\xi^2\cdot\nabla\omega_t^2) \rangle \right.\\ &\left.+ \langle \xi^1\cdot\nabla\omega_t^1 - \xi^2\cdot\nabla\omega_t^2, \xi^1\cdot\nabla\omega_t^1 - \xi^2\cdot\nabla\omega_t^2 \rangle\right) dt. \end{array} $$
(26)

We make the following notations

$$\displaystyle \begin{array}{llll} m_t := \|\bar{\omega}_t\|{}_2^2 \ \ \ \ \ \ \ \ \ \ \ \ Z: = \|\bar{\xi}\|{}_2^2 \ \ \ \ \ \ \ \ \ \ \ \ L:= \|\bar{\xi}\|{}_{1,2}^2 \end{array}$$
$$\displaystyle \begin{array}{llll} A_t := -2\langle \bar{\omega}_t, \bar{u}_t \cdot \nabla \omega_t^1 & + u_t^2 \cdot \nabla {\bar{\omega}_t}\rangle + \langle \bar{\omega}_t, \xi^1\cdot\nabla(\xi^1\cdot\nabla\omega_t^1) - \xi^2\cdot\nabla(\xi^2\cdot\nabla\omega_t^2) \rangle \\ & + \langle \xi^1\cdot\nabla\omega_t^1 - \xi^2\cdot\nabla\omega_t^2, \xi^1\cdot\nabla\omega_t^1 - \xi^2\cdot\nabla\omega_t^2 \rangle \end{array}$$
$$\displaystyle \begin{array}{llll} & D_t : = \displaystyle\int_0^t\langle \bar{\omega}_s, \xi^1\cdot\nabla\omega_s^1 - \xi^2\cdot\nabla\omega_s^2\rangle dW_s \\ & \phi(t) := C\|\omega_t^1\|{}_{k,2}^2 + C \\ & \psi(t) := (C\|\omega_t^1\|{}_{k,2}^2 + C)Z + C\|\omega_t^1\|{}_{k,2}^2L\\ & \tilde{Z}:= C\|\omega_t^1\|{}_{k,2}^2Z \end{array}$$

Then we can write (26) as

$$\displaystyle \begin{array}{llll} dm_t = A_tdt - 2dD_t \end{array}$$

We want to estimate each of the terms which appear in (26). The difference of the nonlinear terms is analysed explicitly in [8] pp. 9:

$$\displaystyle \begin{array}{llll} \langle \bar{\omega}_t, \bar{u}_t \cdot \nabla\omega_t^1 \rangle \leq \|\bar{\omega}_t\|{}_2\|\bar{u}_t\|{}_{4}\|\nabla\omega_t^1\|{}_{4} \leq C\|\bar{\omega}_t\|{}_2^2\|\omega_t^1\|{}_{k,2} = C\|\omega_t^1\|{}_{k,2}^2m_t \end{array}$$

We used here that \(\|\nabla \omega _{t}^1\|{ }_{4} \leq C \|\omega _t^1\|{ }_{k,2}\) and \(\|\bar {u}_t\|{ }_{4} \leq C\|\bar {u}_t\|{ }_{1,2} \leq C \|\bar {\omega }_t\|{ }_{2}\). Also, since u 2 is divergence-free, \(\langle \bar {\omega }_t, u_t^2 \cdot \nabla {\bar {\omega }_t}\rangle =-\frac {1}{2} \displaystyle \int _{\mathbb {T}^2} (\nabla \cdot u_t^2) (\bar {\omega }_t)^2 dx =0 \). We estimate the difference terms which include ξ 1 and ξ 2 in Lemma 3 below. Note here that the term \(\langle \bar {\omega }_t, \xi ^2 \cdot \nabla \left ( \xi ^2\cdot \nabla \bar {\omega }_t\right )\rangle \) is negative. Using these estimates and Lemma 3 below we have that

$$\displaystyle \begin{array}{llll} A_tdt \leq \psi(t) dt + \phi(t)m_t dt. \end{array}$$

Then

$$\displaystyle \begin{array}{llll} d\left( e^{-\displaystyle\int_0^t \phi(s)ds}m_t\right) & = e^{-\displaystyle\int_0^t\phi(s)ds}\left( dm_t - \phi(t)m_tdt\right) \\ & \leq e^{-\displaystyle\int_0^t \phi(s)ds} \left( \psi(t)dt -2dD_t \right). \end{array}$$

After raising everything to the power p ≥ 2,Footnote 4 taking the supremum over t ∈ [0, T] and then the expectation, we obtain

$$\displaystyle \begin{array}{llll} \mathbb{E}\left[ \displaystyle\sup_{t\in[0,T]}\left( e^{-\displaystyle\int_0^t \phi(s)ds}m_t\right)^p\right] & \leq C_p m_0^p + C_{p} \mathbb{E}\left[ \displaystyle\sup_{t\in[0,T]}\displaystyle\left |\int_0^te^{-\displaystyle\int_0^s\phi(r)dr}\psi(s)ds\right |{}^p\right] \\ & + C_p \mathbb{E}\left[ \displaystyle\sup_{t\in[0,T]}\left| \displaystyle\int_0^t e^{-\displaystyle\int_0^s\phi(r)dr} dD_s\right|{}^p\right] \end{array} $$
(27)

For the stochastic integral we use the Burkholder-Davis-Gundy inequality: for arbitrary p ≥ 2 and a martingale M t there exists a constant C p such thatFootnote 5

$$\displaystyle \begin{array}{llll} \mathbb{E}\left[ \displaystyle\sup_{t\in[0,T]}|M_t|{}^p\right] \leq C_p \mathbb{E}\left[ [M]_T^{p/2} \right] \end{array}$$

where [M]t is the quadratic variation of the martingale M t. In our case

$$\displaystyle \begin{array}{llll} M_t := \displaystyle\int_0^t e^{-\displaystyle\int_0^s\phi(r)dr} dD_s \end{array}$$

and then

$$\displaystyle \begin{array}{llll} {[}M{]}_t = \displaystyle\int_0^t e^{-2\displaystyle\int_0^s\phi(r)dr} d[D]_s = \displaystyle\int_0^t e^{-2\displaystyle\int_0^s\phi(r)dr} |\langle \bar{\omega}_s, \xi^1 \cdot \nabla \omega_s^1 - \xi^2 \cdot \nabla \omega_s^2 \rangle |{}^2ds. \end{array}$$

ThereforeFootnote 6

$$\displaystyle \begin{array}{llll} \mathbb{E}\left[ [M]_T^{p/2}\right] & = \mathbb{E}\left[\left( \displaystyle\int_0^T e^{-2\displaystyle\int_0^s\phi(r)dr} |\langle \bar{\omega}_s, \xi^1 \cdot \nabla \omega_s^1 - \xi^2 \cdot \nabla \omega_s^2 \rangle |{}^2ds\right)^{p/2}\right] \\ & \leq C_{p,T}\mathbb{E}\left[\displaystyle\int_0^T e^{-p\displaystyle\int_0^s\phi(r)dr} |\langle \bar{\omega}_s, \xi^1 \cdot \nabla \omega_s^1 - \xi^2 \cdot \nabla \omega_s^2 \rangle |{}^pds\right]\\ & \leq C_{p,T} \displaystyle\int_0^T \mathbb{E}\left[ \displaystyle\sup_{r\in[0,s]}e^{-p\displaystyle\int_0^r\phi(q)dq}\left(m_r^p + \tilde{Z}^p\right)\right] ds. \end{array}$$

Using these estimates in (27) we obtain

$$\displaystyle \begin{array}{llll} \mathbb{E}\left[ \displaystyle\sup_{t\in[0,T]}\left( e^{-\displaystyle\int_0^t \phi(s)ds}m_t\right)^p\right] & \leq C_p m_0^p + C_{p,T} \mathbb{E}\left[ \displaystyle\sup_{t\in[0,T]}\displaystyle\int_0^te^{-p\displaystyle\int_0^s\phi(r)dr}\psi(s)^pds \right] \\ & + C_{p,T} \displaystyle\int_0^T \mathbb{E}\left[\displaystyle\sup_{r\in[0,s]}e^{-p\displaystyle\int_0^r\phi(q)dq}\left( m_r^p + \tilde{Z}^p\right)\right]ds \end{array} $$
(28)

For the second term on the right hand side of (28) we use that, since Z is deterministic and by [8] the 2D Euler equation (3) has a unique global solution in \(\mathcal {W}^{k,2}(\mathbb {T}^2)\) for k ≥ 2, there exist \(\tilde {C}_{p}^1, \tilde {C}_{p}^2\) such that for all t ∈ [0, T]

$$\displaystyle \begin{array}{llll} \mathbb{E}\left[\displaystyle\sup_{s\in[0,t]}\psi(s)^p\right] &= \mathbb{E}\left[\displaystyle\sup_{s\in[0,t]}\left((C\|\omega_s^1\|{}_{k,2}^2 + C)Z + C\|\omega_s^1\|{}_{k,2}^2L\right)^p\right]\\ & \leq Z^p\mathbb{E}\left[\displaystyle\sup_{s\in[0,t]}(C\|\omega_s^1\|{}_{k,2}^2 + C)^p\right] +L^p\mathbb{E}\left[\displaystyle\sup_{s\in[0,t]}(C\|\omega_s^1\|{}_{k,2}^2)^p\right]\\ & \leq \tilde{C}_p^1 Z^p + \tilde{C}_p^2L^p. \end{array}$$

The same argument is used to control \(\displaystyle \int _0^T \mathbb {E}\left [\displaystyle \sup _{r\in [0,s]}e^{-p\displaystyle \int _0^r\phi (q)dq} \tilde {Z}^p \right ]ds \) in the third term of (28). Then

$$\displaystyle \begin{array}{llll} \mathbb{E}\left[ \displaystyle\sup_{t\in[0,T]} \left(e^{-\displaystyle\int_0^t \phi(s)ds}m_t\right)^p\right] & \leq C_{p,T}^1(m_0^p + Z^p +L^p) \\ &\quad + C_{p,T}^2 \displaystyle\int_0^T \mathbb{E}\left[ \displaystyle\sup_{r\in [0,s]}\left( e^{-\int_0^r\phi(q)dq}m_r\right)^p\right] ds. \end{array}$$

Then by Gronwall lemma

$$\displaystyle \begin{array}{llll} \mathbb{E}\left[\displaystyle\sup_{t\in[0,T]} \left(e^{-\displaystyle\int_0^t \phi(s)ds}m_t\right)^p \right] & \leq e^{\displaystyle\int_0^TC_{p,T}^2ds} \left(m_0^p + \displaystyle\int_0^T C_{p,T}^1(m_0^p + Z^p+L^p)ds \right) \\ & \leq e^{C(T)}\left( m_0^p + T(C_{p,T}^1(m_0^p + Z^p+L^p))\right). \end{array}$$

So we finally obtain that

$$\displaystyle \begin{array}{llll} &\mathbb{E}\left[ \displaystyle\sup_{t\in[0,T]}e^{-\gamma(t)}\|\omega_t^1-\omega_t^2\|{}_2^{2p}\right] \\ &\qquad \leq C_{p,T} \left( \|\omega_0^1 - \omega_0^2\|{}_2^{2p} + \|\xi^1 - \xi^2\|{}_2^{2p}+\|\xi^1-\xi^2\|{}_{1,2}^{2p}\right), \ \ \ \ p\geq 2 \end{array}$$

where

$$\displaystyle \begin{array}{llll} \gamma(t) := p\displaystyle\int_0^t\phi(r)dr. \end{array}$$

□

Lemma 3

Let \((\omega _t^1,\xi ^1)\) and \((\omega _t^2,\xi ^2)\) be two solutions of the 2D Euler equation with \(\bar {\omega }_t:= \omega _t^1 - \omega _t^2\) and \(\bar {\xi }:= \xi ^1 -\xi ^2.\) Then there exist constants C Footnote 7 such that the following estimates hold:

$$\displaystyle \begin{array}{llll} Q := |\langle \bar{\omega}_t, \xi^1\cdot\nabla\omega_t^1 - \xi^2\cdot\nabla\omega_t^2\rangle| \leq C\|\bar{\omega}_t\|{}_2^2 + C\|\omega_t^1\|{}_{k,2}^2\|\bar{\xi}\|{}_{2}^2. \end{array}$$
$$\displaystyle \begin{array}{llll} A := \langle \xi^1 \cdot \nabla\omega_t^1 - \xi^2 \cdot \nabla \omega_t^2, \xi^1 \cdot \nabla\omega_t^1 - \xi^2 \cdot \nabla \omega_t^2 \rangle \leq C \|\bar{\omega}_t\|{}_2^2 + C\|\omega_t^1\|{}_{k,2}^2 \|\bar{\xi}\|{}_2^2 \end{array}$$
$$\displaystyle \begin{array}{llll} |B| \leq (C\|\omega_t^1\|{}_{k,2}^2+C)\|\bar{\omega}_t\|{}_2^2 + C\|\bar{\xi}\|{}_2^2 + C\|\omega_t^1\|{}_{k,2}^2\|\bar{\xi}\|{}_{1,2}^2 \end{array}$$

where

$$\displaystyle \begin{array}{llll} B := \langle \bar{\omega}_t, \xi^1 \cdot \nabla \left(\xi^1\cdot\nabla\omega_t^1 \right) - \xi^2 \cdot \nabla \left(\xi^2\cdot\nabla\omega_t^2 \right) \rangle. \end{array}$$

and k > 4.

Proof

For the difference terms which include ξ 1 and ξ 2 we use that

$$\displaystyle \begin{array}{llll} \xi^1 \cdot \nabla\omega_t^1 - \xi^2 \cdot \nabla \omega_t^2 = \bar{\xi} \cdot \nabla\omega_t^1 + \xi^2 \cdot \nabla \bar{\omega}_t. \end{array}$$

We have

$$\displaystyle \begin{array}{llll} Q &= |\langle \bar{\omega}_t, \xi^1\cdot\nabla\omega_t^1 - \xi^2\cdot\nabla\omega_t^2\rangle| \\ & \leq |\langle \omega_t^1-\omega_t^2, (\xi^1-\xi^2)\cdot\nabla \omega_t^1 \rangle| + |\langle \omega_t^1-\omega_t^2, \xi^2\cdot\nabla(\omega_t^1-\omega_t^2)\rangle|\\ & \leq \frac{1}{2}\|\omega_t^1-\omega_t^2\|{}_2^2 + \frac{1}{2}\|\nabla\omega_t^1\|{}_{\infty}^2\|\xi^1-\xi^2\|{}_{2}^2 \\ & \leq \frac{1}{2}\|\bar{\omega}_t\|{}_2^2 + \frac{C}{2}\|\omega_t^1\|{}_{k,2}^2\|\bar{\xi}\|{}_{2}^2 \end{array}$$

with k ≥ 3, since the second scalar product is zero due to the fact that ∇⋅ ξ 2 = 0. Also

$$\displaystyle \begin{array}{llll} A &= \langle \xi^1 \cdot \nabla\omega_t^1 - \xi^2 \cdot \nabla \omega_t^2, \xi^1 \cdot \nabla\omega_t^1 - \xi^2 \cdot \nabla \omega_t^2 \rangle = \|\xi^1 \cdot \nabla\omega_t^1 - \xi^2 \cdot \nabla \omega_t^2\|{}_2^2 \\ & \leq \|(\xi^1 - \xi^2) \cdot \nabla\omega_t^1\|{}_2^2 + \|\xi^2 \cdot \nabla (\omega_t^1 - \omega_t^2)\|{}_2^2 \\ & \leq \|\xi^1 - \xi^2\|{}_2^2 \|\nabla\omega_t^1\|{}_{\infty}^2 + C \|\omega_t^1-\omega_t^2\|{}_2^2 \\ & \leq C\|\omega_t^1\|{}_{k,2}^2\|\bar{\xi}\|{}_2^2 + C \|\bar{\omega}_t\|{}_2^2 \end{array}$$

where k ≥ 3. For the higher order term we have

$$\displaystyle \begin{array}{llll} B & = \langle \omega_t^1 - \omega_t^2, \xi^1 \cdot \nabla \left(\xi^1\cdot\nabla\omega_t^1 \right) - \xi^2 \cdot \nabla \left(\xi^2\cdot\nabla\omega_t^2 \right) \rangle \\ & = \langle \omega_t^1 - \omega_t^2, (\xi^1 - \xi^2) \cdot \nabla (\xi^1 \cdot \nabla \omega_t^1) \rangle \\ & + \langle \omega_t^1 - \omega_t^2, \xi^2 \cdot \nabla \left( (\xi^1-\xi^2) \cdot \nabla \omega_t^1\right) \rangle \\ & + \langle \omega_t^1 - \omega_t^2, \xi^2 \cdot \nabla \left( \xi^2\cdot\nabla(\omega_t^1 - \omega_t^2)\right)\rangle \\ & =: a + b + c. \end{array}$$

Note that c is negative:

$$\displaystyle \begin{array}{llll} \langle \omega_t^1 - \omega_t^2, \xi^2 \cdot \nabla \left( \xi^2\cdot\nabla(\omega_t^1 - \omega_t^2)\right)\rangle & = - \langle \xi^2 \cdot \nabla(\omega_t^1 - \omega_t^2), \xi^2\cdot\nabla(\omega_t^1 - \omega_t^2) \rangle \\ & = -\|\xi^2 \cdot \nabla(\omega_t^1 - \omega_t^2)\|{}_2^2 \\ & \leq 0 \end{array}$$

so |B|≤|a| + |b|. We estimate |a| as follows:

$$\displaystyle \begin{array}{llll} |a| = |\langle \omega_t^1 -\omega_t^2, (\xi^1 -\xi^2)\cdot \nabla( \xi^1 \cdot \nabla \omega_t^1)\rangle| &\leq \frac{1}{2} \|\nabla(\xi^1\cdot\nabla\omega_t^1)\|{}_{\infty}^2\|\omega_t^1-\omega_t^2\|{}_2^2 + \frac{1}{2}\|\xi^1-\xi^2\|{}_2^2 \\ & \leq \frac{C}{2} \|\omega_t^1\|{}_{2,\infty}^2\|\omega_t^1-\omega_t^2\|{}_2^2 + \frac{1}{2}\|\xi^1-\xi^2\|{}_2^2 \\ & \leq \frac{C}{2} \|\omega_t^1\|{}_{k,2}^2\|\bar{\omega}_t\|{}_2^2 + \frac{1}{2}\|\bar{\xi}\|{}_2^2 \end{array}$$

with k > 4. Likewise, we estimate |b|:

$$\displaystyle \begin{array}{llll} |b| = |\langle \omega_t^1 - \omega_t^2, \xi^2 \cdot \nabla \left( (\xi^1-\xi^2) \cdot \nabla \omega_t^1\right) \rangle| & \leq \frac{1}{2}\|\omega_t^1 - \omega_t^2\|{}_2^2 + \frac{1}{2} \|\xi^2 \cdot \nabla \left( (\xi^1-\xi^2) \cdot \nabla \omega_t^1\right)\|{}_2^2 \\ & =: \frac{1}{2}\|\omega_t^1 - \omega_t^2\|{}_2^2 + \frac{1}{2}\mathcal{K}. \end{array}$$

Now

$$\displaystyle \begin{array}{llll} \mathcal{K} \leq \|\xi^2 \cdot \nabla(\xi^1-\xi^2) \cdot \nabla \omega_t^1\|{}_2^2 + \|\xi^2\cdot(\xi^1-\xi^2)\cdot\nabla(\nabla\omega_t^1)\|{}_2^2 := \mathcal{K}_1 + \mathcal{K}_2 \end{array}$$

where

$$\displaystyle \begin{array}{llll} \mathcal{K}_1 & \leq \|\xi^2\cdot\nabla\omega_t^1\|{}_{\infty}^2\|\nabla(\xi^1-\xi^2)\|{}_2^2 \\ & \leq C\|\omega_t^1\|{}_{1,\infty}^2\|\xi^1-\xi^2\|{}_{1,2}^2\\ & \leq C\|\omega_t^1\|{}_{k,2}^2\|\xi^1-\xi^2\|{}_{1,2}^2 \end{array}$$

and

$$\displaystyle \begin{array}{llll} \mathcal{K}_2 &\leq C\|\xi^2\cdot\nabla(\nabla\omega_t^1)\|{}_{4}^2\|\xi^1-\xi^2\|{}_4^2 \\ & \leq C\|\xi^2\cdot\nabla(\nabla\omega_t^1)\|{}_{1,2}^2\|\xi^1-\xi^2\|{}_{1,2}^2 \\ & \leq C\|\omega_t^1\|{}_{k,2}^2\|\xi^1-\xi^2\|{}_{1,2}^2 \end{array}$$

for k > 4. Then

$$\displaystyle \begin{array}{llll} \mathcal{K} \leq2 C\|\omega_t^1\|{}_{k,2}^2\|\bar{\xi}\|{}_{1,2}^2 \end{array}$$

and therefore

$$\displaystyle \begin{array}{llll} |b| \leq \frac{1}{2}\|\bar{\omega}_t\|{}_2^2 + C\|\omega_t^1\|{}_{k,2}^2\|\bar{\xi}\|{}_{1,2}^2 \end{array}$$

which gives

$$\displaystyle \begin{array}{llll} |B| \leq \left(\frac{C}{2}\|\omega_t^1\|{}_{k,2}^2+\frac{1}{2}\right)\|\bar{\omega}_t\|{}_2^2 + \frac{1}{2}\|\bar{\xi}\|{}_2^2 + C\|\omega_t^1\|{}_{k,2}^2\|\bar{\xi}\|{}_{1,2}^2. \end{array}$$

□

5 Numerical Results

In this section, we show the results we obtained for Example 1 in Sect. 3. We implemented the main equation (3) with added forcing and damping, on a unit square domain with doubly periodic boundary conditions,

$$\displaystyle \begin{array}{llll} d{\omega }_{t}+{\mathbf{u}}_{t}\cdot \nabla {\omega }_{t}dt+\xi \cdot \nabla {\omega }_{t}\circ dW_{t}= (Q - r\omega_t) dt \end{array} $$
(29)

where we chose r = 0.001 and \(Q(x) = 0.01 (\cos {}(8 \pi y) + \sin {}( 8 \pi x) )\). Note that, since the added forcing term is of bounded variation, (17) is unchanged for (29).

We considered a ξ whose parametric form with respect to the Fourier basis consists of only one α. The stream function of our chosen ξ is given by

$$\displaystyle \begin{array}{llll} \zeta(x, y) = \alpha \left(\cos{}(k_1 2\pi x)\cos{}(k_2 2\pi y) - \sin{}(k_1 2\pi x)\sin{}(k_2 2\pi y)\right). \end{array} $$
(30)

Note that

$$\displaystyle \begin{array}{llll} \zeta = \frac\alpha2(e^{i2\pi k\cdot x } + e^{-i2\pi k\cdot x}), \end{array} $$
(31)

and

$$\displaystyle \begin{array}{llll} \xi = i\alpha \pi (e^{i2\pi k\cdot x } - e^{-i2\pi k\cdot x})k^\perp. \end{array} $$
(32)

To discretise (29), we followed the methods documented in [4]—a mixed Finite Element method was used for the spatial derivatives, and an explicit strong stability preserving Runge-Kutta scheme of order 3 was used for the time derivative. We added the forcing and damping terms to help with maintaining the statistical homogeneity of the numerical solution, once it has reached a spun-up state from some set initial state. Our choice for the set initial state was

$$\displaystyle \begin{array}{llll} \omega(0,x,y) &= \sin{}(8\pi x)\sin{}(8\pi y) + 0.4 \cos{}(6\pi x)\cos{}(6 \pi y) \\&\quad + 0.3\cos{}(10 \pi x)\cos{}(4\pi y) + 0.02\sin{}(2\pi y) + 0.02\sin{}(2\pi x). \end{array} $$
(33)

Spatially, we chose the grid size 64 × 64 cells. We first spun-up the system until it reached a statistical equilibrium state. This statistical equilibrium state was then set as the initial condition for our experiment. Figure 1 shows a snapshot of the obtained initial condition. Over the spin-up phase, we used α = 0.000001 and \(k^\intercal =(2,4)\).

Fig. 1
figure 1

Snapshots of the numerical solution ω(t, x) to (29) at times t = 0 (left), and t = 1 (right)

Full size image

The time horizon for the experiment data was chosen to be the unit interval, i.e. we generated data ω ∗(t i, x) for 0 = t 0 < t 1 < ⋯ < t N = 1. See Fig. 1 for snapshots of ω ∗(0, x) and ω ∗(1, x). When generating the data, we used the larger value of α = 0.001. This was to avoid any possible numerical issuesFootnote 8 when we attempted to recover α from data.

Assuming we know in-advance the exact Fourier wavenumber k, the linear system for estimation reduces to

$$\displaystyle \begin{array}{llll} \widehat{[\omega]}_{t,N}(\mathbf{x}) := \displaystyle\sum_{i=1}^N(\omega_{t_i}(\mathbf{x}) - \omega_{t_{i-1}}(\mathbf{x}))^2 \approx \alpha^2 4 \pi^2 \ B(t,k,\mathbf{x}) {\mathfrak{e}}^{\prime}_k(\mathbf{x}) \end{array} $$
(34)

where

$$\displaystyle \begin{array}{llll} B(t,k,\mathbf{x}):= \displaystyle\int_0^t ( k^\perp \cdot \nabla\omega_s(\mathbf{x}))^2ds \end{array} $$
(35)

and

$$\displaystyle \begin{array}{llll} {\mathfrak{e}}^{\prime}_k(x,y) := \left( \cos{}(k_1 2\pi x)\sin{}(k_2 2\pi y)+\sin{}(k_12\pi x)\cos{}(k_2 2\pi y) \right)^2. \end{array} $$
(36)

Thus our estimate for α is given by

$$ \begin{array}{llll} \widehat{\alpha}_N^2 = \frac {1}{4\pi^2}\frac{\int_{\mathbb T^2} \widehat{[\omega]}_{t,N}(\mathbf{x}) d\mathbf{x} }{\int_{\mathbb T^2} B(t,k,\mathbf{x}){\mathfrak{e}}^{\prime}_k(\mathbf{x}) d\mathbf{x}}. \end{array} $$
(37)

Remark 4

In (37), we applied spatial averaging to stabilise estimation.

Remark 5

The assumption that we know k in advance is of course too strong from the applications viewpoint. The aim of this experiment is to test the strength of the pathwise approach under the assumption of “perfect knowledge”. If we cannot accurately recover α in this case, then getting a good estimate for α using the pathwise approach may be too difficult or impractical in more realistic scenarios.

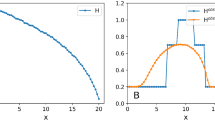
Figure 2 shows snapshots of \(\widehat {[\omega ]}_{t,N}(\mathbf {x})\) and \(B(t,k,\mathbf {x}){\mathfrak {e}}^{\prime }_k(\mathbf {x})\). We applied (37) for different values of N. In each case, the time integral that constitutes B(t, k, x) was approximated using a simple trapezoidal rule, for which the same N number of data snapshots were used. Figure 3 shows the results for the relative error

$$\displaystyle \begin{array}{llll} \mathrm{err}_N = \frac{|\alpha - \widehat{\alpha}_N|}{\alpha} \end{array} $$
(38)

for the different values of N. The results show that, in the worst case of N = 2500, the relative error was no greater than 0.89. This translates to an absolute error of range of 0.001 ± 0.00089. The best case was when all 200, 000 data samples were used to estimate α, the relative error in that case was 0.00135. This suggests convergence and stabilisation of the sum for \(\widehat {[\omega ]}_t\).

Fig. 2
figure 2

Shown on the left is a snapshot of the estimate \(\widehat {[\omega ]}_t\), which was computed using N = 200, 000 data samples. Shown on the right is a snapshot of the basis element \(B_t(k,x) \left ( \cos {}(k_1 2\pi x)\sin {}(k_2 2\pi y)+\sin {}(k_12\pi x)\cos {}(k_2 2\pi y) \right )^2\), which was approximated using the same N number of data samples

Full size image
Fig. 3
figure 3

The plot (in \(\log \log \) scale) shows the relative error errN defined in (38) as a function of N. errN was computed for N = 2500, 5000, 10, 000, 20, 000, 40, 000, 50, 000, 66, 667, 100, 000, 200, 000

Full size image

For future work, we aim to test the pathwise approach for cases in which we do not know the exact selection of basis elements for ξ. Further, we wish to extend and test these ideas on coarse grained PDE data and compare with the results that were obtained in [4] using previously developed calibration methods.