Basic Concepts of Radiation Biology

Abstract

Radiation biology is the study of the effects of ionizing radiation on biological tissues and living organisms. It combines radiation physics and biology. The purpose of this chapter is to introduce the terminology and basic concepts of radiobiology to create a better understanding of the ionizing radiation interactions with a living organism. This chapter firstly describes the different types of radiation, the sources, and the radiation interactions with matter. The basic concepts of radioactivity and its applications are also included. Ionizing radiation causes significant physical and chemical modifications, which eventually lead to biological effects in the exposed tissue or organism. The physical quantities and units needed to describe the radiation are introduced here. Eventually, a broad range of biological effects of the different radiation types are addressed. This chapter concludes with a specific focus on the effects of low doses of radiation.

FormalPara Learning Objectives

• To understand what radiation is, how the different types of radiation differ, and how the energy is transferred to matter

• To describe the natural and artificial sources of ionizing radiation to which we are exposed

• To understand the principles of radioactive decay, the production of artificial radioactive isotopes, and some important aspects of their environmental and clinical applications

• To describe the different dose quantities and units used to describe radiation

• To understand the concept of linear energy transfer (LET) and ionization clustering and how these are used to describe the relative biological effectiveness (RBE)

• To understand how ionizing radiation induces biological effects following energy deposition within biological tissues

• To understand the different types of health effects following different ionizing radiation doses and exposure scenarios

• To explain the factors influencing the results of low doses and introduction of the concept of targeted and non-targeted radiation effects

2.1 Physical and Chemical Aspects of Radiation Interactions with the Matter

2.1.1 Matter and Energy

There exists a wide variety of different types of particles in nature. These vary across those more commonly known, such as the constituents of atoms like electrons spinning around nuclei and protons and neutrons inside the nuclei. Particles generated through other particles’ decay and those which are the carriers of the fundamental electromagnetic, strong and weak nuclear, and gravitational force are also incredibly important in nature.

In physical science, a particle is characterized either as a localized entity which can be described by its own physical characteristics such as volume, density, and mass or as a wave, the latter being a less intuitive concept. Such dual nature of particles is named the wave-particle duality. The de Broglie wavelength associated with a particle is inversely proportional to its momentum, p, through the Planck constant, h:

$$ \lambda =\frac{h}{p}=\frac{h}{E/c}\left(\mathrm{photons}\right)=\frac{h}{m\cdot v}\left(\mathrm{particles}\kern0.17em \mathrm{with}\kern0.17em \mathrm{mass}\right). $$

(2.1)

When particles interact with objects much larger than the wavelength of the particles themselves, they show negligible interference effects. To get easily observable interference effects in the interaction of particles with matter, the longest wavelength of the particles and hence the smallest mass possible are needed. The wavelengths of high-speed electrons are comparable to the spacings between atomic layers in crystals. Therefore, this effect was first observed with electrons as diffraction, a characteristic wave phenomenon, in 1927 by C.J. Davisson and L.H. Germer [1] and independently by G.P. Thomson [2]. Such experiments established the wavelike nature of electron beams, providing support to the underlying principle of quantum mechanics. Thomson’s experiment of a beam of electrons that can be diffracted just like a beam of light or a water wave is a well-known case taught in basic courses of quantum mechanics [3].

For electromagnetic radiation for energies E = hc/λ of a few keV, the wavelength λ becomes comparable with the atomic size. At this energy range, photons can be practically considered as particles with zero mass and momentum p = E/c. Indeed, despite photons having no mass, there has long been evidence that electromagnetic radiation carries momentum. The photon momentum is, however, very small, since p = h/λ and h is very small [6.62606957 × 10⁻³⁴ (m² kg/s)], and thus it is generally not observed. Nevertheless, at higher energies, starting from hard X-rays (which have a small wavelength and a relatively large momentum), the effects of photon momentum can eventually be observed. They were observed by Compton, who was studying hard X-rays interacting with the lightest of particles, the electron. On a larger scale, photon momentum can have an effect if the photon flux is considerable and if there is nothing to prevent the slow recoil of matter due to the impinging and conservation of the total momentum. This may occur in deep space (a quasi-vacuum condition), and “solar” sails with low mass mirrors that would gradually recoil because of the impinging electromagnetic radiation are actually being investigated and tested to actually take spacecraft from place to place in the solar system [4,5,6].

While for photons the concept of wavelength is more intuitively directly related to the phenomena and excitations they can trigger in matter, for particles with mass (massive particles), the wavelength is usually too small to have a practical impact on our observation of interaction phenomena. Nevertheless, depending on the phenomenon or on the specific aspect one is looking at, it may be more convenient to consider the particles either as localized entities or in terms of waves.

Understanding the phenomenon of the passage of charged particles, in particular protons and other hadrons, heavy ions, electrons, and neutral particles, such as neutrons and photons, in matter has been a tempting and fascinating topic since the early development of quantum mechanics. The study of the passage of a particle through matter requires knowledge of the many interactions that govern the response of the target to the incoming (strong or weak) particle in the target itself. The number of these interactions is daunting, especially for the case of high-energy particles. In principle, to understand the types of possible particle-matter interactions and thus the response of the matter to radiation, it is more appropriate to consider the speed of the particle rather than the energy. The energy is less meaningful as the high energy of a heavy ion may be associated mostly to its mass, rather than purely to its speed. It is nevertheless common also to refer to the kinetic energy of the particle when looking at the induced interactions a particle can have when traveling through matter, distinguishing the particles with different mass. The interaction of a massive particle with matter can be understood by looking at Fig. 2.1, where the particle’s kinetic energy is plotted against the de Broglie wavelength, and the relevant dimensions of a nucleon, nucleus, electron orbitals, and water molecule (O–H distance) are reported. At high-projectile kinetic energies in the region of 1–10 GeV (reported are the cases of a proton, a neutron, and a ¹²C ion), the wavelength of the projectile is similar to the size of the nucleon, and hence the projectile is able to interact directly with the components of the single nucleons (quarks, gluons) in the nucleus of the target atom. At slightly lower kinetic energies (~1 MeV–1 GeV), the wavelength of the projectile becomes comparable to that of the nucleus of uranium, and thus the projectile can interact with the nucleons, but not with the constituents of the nucleons. This can cause fragmentation of the nucleus and generation of secondary species and decay particles that are emitted in the de-excitation of the nucleus, which is brought in an excited state by the impacting particle. Descending in kinetic energy, the wavelength of the incoming radiation on the order of the entire nucleus means that the impacting particle can interact with the entire nucleus but not with the nucleons. Further lower in energy and at increased wavelength, the incoming radiation has a wavelength of similar size to the electronic orbitals (reported here are lead orbitals), and still further of similar size to a water molecule, thus entering the regime of molecule-dominating behavior. It is thus clear that when spanning large energy windows, many different physical interactions take place with the target, which probe the different units of matter which are considered as elemental for different sub-disciplines of physics.

Fig. 2.1

Plot of the projectile kinetic energy vs. the de Broglie wavelength. The sizes of a nucleon, uranium nucleus, lead orbitals and water molecule are also reported. (Courtesy of Dr. Marc Verderi, Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, France)

It has to be stressed that in its path through matter, the primary particle can generate several secondary particles, such as electrons, by ionization and/or decay particles of excited nuclei in nuclear inelastic collisions. In the latter case, “daughter nuclei” are generated, which also act as projectiles interacting within the system. In the case of biological targets, primary radiation can generate ions, electrons, excited molecules, and molecular fragments (free radicals) that have lifetimes longer than approximately 10⁻¹⁰ s. The new species in turn travel and diffuse and start chemical reactions, the evolution of which is a main contributor to the effects at biological level.

Nowadays, apart from the well-known fields of the high-energy physics and nuclear science, radiation science is important in numerous sub-disciplines, such as ion beam therapy [7, 8], radiation protection in medicine [9] and nuclear facilities [10], development of risk assessment models for nuclear accidents [11], or radiation protection in deep space manned missions [12,13,14]. Apart from the effects on humans, parallel streams of research exist for the studies on radiation effects induced in plants, seeds, and animals, for the survival and adaptation around the Chernobyl site and even for the effects on small biological molecules of interest in studies on the search of life on other planets or their moons [15,16,17,18,19] (Box 2.1).

Box 2.1 Description of Particle Interactions

• The appropriateness of a description of particles as localized entities or as waves depends on the wavelength of the particle, the characteristics of the probed dimension of the target system, and the resulting phenomenon (change in the state of the target) which we are interested in.

• There exists a wide range of interactions that particles can induce in matter, from the interactions with quarks and gluons in high-energy collisions to excitations of electrons and vibrations in molecules which dominate at lower energies.

2.1.2 Electromagnetic Radiation

Electromagnetic radiation transfers energy without any atomic or molecular transport medium. According to the wave-particle duality of quantum physics, electromagnetic radiation can be described either as a wave or as a beam of energy quanta called photons.

To understand how electromagnetic radiation interacts with matter, we need to think of electromagnetic radiation as photons, and it is the energy of each photon, which determines how it interacts with matter. Figure 2.2 shows the spectrum of electromagnetic radiation. It is divided into radio waves, microwaves, infrared, (visible) light, ultraviolet (UV), and X- and γ-rays depending on the frequency and energy of the individual photons. Depending on the photon energy, the photon interaction with an atom can result in ionization, where an electron gets enough energy to leave the molecule/atom; excitations, where the electron gets the exact energy needed to move from an inner electron shell to an outer shell; or changes in the rotational, vibrational, or electronic valence configurations (Box 2.2).

Fig. 2.2

The electromagnetic spectrum (Created with BioRender)

Box 2.2 Ionizing Radiation

• It is not the total energy but the energy per photon which determines how the radiation interacts with matter.

• Ionizing radiation is the radiation with enough energy per photon to kick out one atomic electron.

Radiation can be divided into ionizing and nonionizing radiation. Ionizing radiation carries more than 10 eV, which is enough energy to break chemical bonds. Unlike ionizing radiation, nonionizing radiation does not have enough energy to remove electrons from atoms and molecules.

2.1.2.1 Nonionizing Electromagnetic Radiation

The UV spectrum is in the range of 3.1–124 eV. Even though the high-energy UV (UVC) can be ionizing, this is absorbed in the atmosphere and does not reach the Earth. Only UVA (3.10–3.94 eV) and UVB (3.94–4.43 eV) are transmitted through the atmosphere. UVB radiation has the energy to excite DNA molecules in skin cells. This can result in aberrant covalent bonds forming between adjacent pyrimidine bases, producing pyrimidine dimers. Most UV-induced pyrimidine dimers in DNA are removed by the process known as nucleotide excision repair, but unrepaired pyrimidine dimers have the potential to lead to mutations and cancer. UVA can induce production of reactive oxygen and reactive nitrogen species (ROS, RNS), which happens through interaction with chromophores such as nucleic acid bases, aromatic amino acids, NADH, NADPH, heme, quinones, flavins, porphyrins, carotenoids, 7-dehydrocholesterol, eumelanin, and urocanic acid [20]. ROS can induce ionizations in DNA. In summary, the UV light that reaches the Earth (UVA and UVB) has too low photon energies to induce direct ionization but can cause DNA instability through excitation (Box 2.3).

Box 2.3 Characteristics of UV—Radiation

• Ionizing UV radiation (UVC) is absorbed in the atmosphere.

• UVB can induce pyrimidine dimers in DNA.

• Both UVA and UVB can induce ROS, which in turn can induce DNA damage.

2.1.2.2 Ionizing Electromagnetic Radiation

An X-ray photon is emitted from an electron that is either slowed down or moves from one stationary state to another in an atom; a γ-photon is sent out by disintegration of an atomic nucleus. Except for the origin, from the physical perspective, there is no difference between X-ray and γ-photon radiation.

A photon can interact with matter by three different processes depending on its energy and the atomic number of the elements of the matter.

In the photoelectric effect, an atomic electron absorbs all the energy of the incoming photon and is emitted from the atom. Note that the photoelectric effect cannot occur with an electron that does not belong to an atom. This is because both energy and momentum need to be conserved, which cannot be achieved without an atom carrying the rest momentum.

The Compton effect implies, just like the photoelectric effect, that an electron is knocked out from an atom by transfer of energy from the photon. However, for the Compton effect, a secondary photon is also emitted, which preserves the momentum (Fig. 2.3). Therefore, the process may also apply to a nonatomic, or free, electron. The amount of energy transferred from the incident wave to the electron depends on the scatter angle as follows:

$$ {\lambda}^{\prime }-\lambda ={\lambda}_c\left(1-\cos \theta \right), $$

(2.2)

Fig. 2.3

The Compton process. The incident photon (γ-ray) interacts with an electron initially at rest resulting in a scattered photon (at angle θ) and electron (at angle Φ). The energy (E) and momentum (p) of the photon and electron before and after (marked with ′) scattering are given in the figure (Created with BioRender)

where ${\lambda}_c=\frac{h}{m_ec}$ is a constant denoted “the Compton wavelength for electrons” which equals the wavelength of a photon having the same energy as the rest-mass energy of the electron. Notice that maximum energy transfer to the electron is obtained with a scatter angle of 180° (backscatter), but it is not possible to transfer all the energy of the incoming photon to the electron (conservation of momentum).

As seen in Fig. 2.4, depending on the incoming photon energy, there will be a series of Compton processes, each with emission of an electron, followed by a photoelectric process in the end. The result of such a Compton track is an energy distribution of secondary electrons with many low-energy electrons but also a few with high energy. The high-energy electrons are important for the dose distribution in the irradiated material, because they transport energy away from the place of the primary photon interaction and deposit their energy further into the irradiated material.

Fig. 2.4

A typical example of a sequence of energy deposits. The energy of an original 1.25 MeV photon is deposited in five subsequent Compton processes with a final energy deposition in the form of a photoelectric process. The figure shows the mean range in water (dotted arrows) for the incoming photon and the reduced-energy photons emitted for each Compton process. The scale shown in the bottom left only applies to photons. The electron mean range is much shorter starting at about 2 mm going down to about 36 μm in the last Compton scattering (which is still larger than a typical cell diameter) (Created with BioRender)

Pair production occurs by the incoming photon interacting with the nuclear forces in the irradiated material resulting in an electron-positron pair. The rest energy of the two newly formed particles is 1.022 MeV, so the incoming photon must have higher energy than this for the process to occur. In body tissues and cells, more than 20 MeV in photon energy is required for pair production to dominate over the Compton processes.

The Compton process dominates in biological material for energies relevant for medical use of photons. However, the cross section (an expression of the probability of interaction) for each process also depends on the atomic number Z. The cross section is proportional to Z⁴ for photoelectric effect, Z for Compton effect, and Z² for pair production. Thus, the higher the effective atomic number, the lesser the importance of the Compton effect (Box 2.4).

Box 2.4 Interaction of Photon with Matter

• Electromagnetic radiation can ionize atoms/molecules through three different processes (photoelectric effect, Compton process, and pair production) depending on the photon energy and atomic number of the elements involved.

• The Compton process dominates in biological material for energies relevant for medical use of photons, but a Compton track ends with the photoelectric effect.

2.1.3 Particle Radiation

As described above, in physics, a particle is considered to be an object, which can be described through its properties including volume, density, and mass. In the context of particle radiation, two types of particles are defined: charged particles, such as electrons, protons, α-particles, or other ions and uncharged particles such as neutrons. In general, particle radiation can interact with matter through a number of different processes, where the frequency of occurrence depends on the particles’ mass, velocity, and charge. In the first type of the process called electronic interaction, the particle interacts with electrons in the atomic shell, and in the second, called nuclear interaction, the particle interacts with the atomic nuclei. All interactions can be considered as collisions between two masses, which can be either elastic or inelastic.

There are three types of electronic or Coulomb interactions, which can occur with or without energy loss from the incident particle. Elastic scattering of the particle in the atomic shell occurs with only neglectable energy transfer, as only the energy which needs to be transferred is that which is necessary to fulfill energy and momentum conservation. In this case, the incident particle is scattered and changes its direction. The two inelastic electronic processes are shown in Fig. 2.5 (left). The particle described through its atomic number z, its mass m, and its energy E is interacting with an atom of the matter characterized by the atomic number Z, the mass number A, and the density of the matter ρ. In the inelastic collision, the particle transfers energy to the hit electron. If sufficient energy is transferred, the electron will leave the atom, thus ionizing it. When the transferred energy is higher, the electron gets additional kinetic energy and can then itself act as particle radiation. If the energy is lower and fits the energy difference between two electron shells (the defined energies at which electrons “orbit”), the electron is excited, which means lifted to the higher shell. After a certain time, the electron falls back while emitting a photon with the energy corresponding to the energy difference between the shells.

Fig. 2.5

Visualization of the electronic interactions (left) and the nuclear interaction (right) of a particle with atomic number z, mass m, and energy E with matter with atomic number Z, mass number A, and density ρ (Created with BioRender)

In nuclear interactions, again three types can be defined. Firstly, elastic nuclear scattering, also called nuclear coulomb scattering, describes the elastic collision of a particle with the atomic nucleus. Here, the particle does not lose energy and only a deflection occurs (Fig. 2.5). In inelastic nuclear scattering, the particle is deflected and emits light, the so-called bremsstrahlung. Lastly, an interaction with the target nuclei itself is possible inducing nuclear reactions.

2.1.3.1 Charged Particle Radiation

Charged particle radiation describes high-energy massive particles such as electrons, protons , and other ions. These particles interact with matter through the described electronic or nuclear interactions. In each interaction, only a small amount of the total energy is transferred, and although the whole process of interaction is statistical in its nature, one can say that the particles stop more or less uniformly at a certain distance called the range. Furthermore, in each interaction, a certain angular deflection happens, which causes the particle to travel in a crooked path, and which effectively causes the incident particle beam to widen, while traversing a medium. The types of interactions can be described through the occurring energy loss and deflection of particle radiation in matter.

Ionizations and excitations, which occur in the electronic interactions, can be differentiated into soft and hard collisions. Interactions of the charged particle with the electrons in the outer atomic shell are called soft collisions, as the energy transfer is low (a few eV). The electrons, which are ionized, have a low energy and therefore emit all the energy in close proximity to the point of interaction. These soft collisions are responsible for approximately 50% of the total energy transfer of a particle. As the energy transfer of a single collision is very low, the particle velocity decrease is also low. But as a lot of these interactions occur, the slowing is, although of statistical nature, on average happening continuously. For particles which have a very high energy and thus velocity, the Cherenkov effect can occur. This effect describes the emittance of light, when a particle flies through matter with a velocity larger than the speed of light in this corresponding matter. This light is called Cherenkov radiation and can be seen as blue in the cooling water of nuclear reactors. The Cherenkov effect does not play a role in the effects of particle radiation on biological matter.

Coulomb interactions with the electrons of the inner shells are called hard collisions. Here, the electrons produced in ionizations have a higher energy and larger deflection angles compared to the ones from soft collisions. These electrons are called δ-rays, and they transfer their energy via soft collisions to the matter, thus spreading the energy distribution of an incident particle up to several μm distance to the incident particle track. This effect plays a major role in the microdosimetry.

Electronic interactions are the main contributors to the energy loss for high ion energies (see Fig. 2.6) but have a negligible deflection per collision.

Fig. 2.6

(a) Energy loss for protons (purple) and carbon (blue) ions depends on ion type and ion energy. For lower energies, the nuclear energy loss (dotted lines) starts to get an influence. At energies above ~0.0005 MeV/u for protons and ~0.005 MeV/u for carbon ions, the electronic energy loss is dominant (dashed lines) and the nuclear energy loss can be even neglected for higher energies. E/A is the energy divided by mass number. (b) Energy loss for a proton with initial energy of E_in = 200 MeV with a range in water of 256 mm on the left and for a carbon ion with initial energy of E_in = 375 MeV/u with a range in water of 251 mm on the right: at the end of range at a path length, the energy loss is increasing and rapidly goes to zero when the ion stops. The curve shape for the carbon ion is the same as for the proton but with a higher energy loss at all times. Energy losses are calculated via SRIM (SRIM—The Stopping and Range of Ions in Matter, J. Ziegler, http://www.srim.org/). (c) Stopping power of electrons depending on electron energy simulated using estar (https://physics.nist.gov/PhysRefData/Star/Text/ESTAR.html). (d) Energy loss of electrons in adipose tissue with penetration depth (inspired by Hazra et al. 2019) (licensed under CC-BY-4.0) [26]

Energy loss through elastic nuclear scattering as described above is only an important contribution to the total energy loss for ion energies below approximately 0.01 MeV/u. Here, the ions are already close to stopping and have a remaining range in the order of nanometers. For high ion energies (E > several 100 MeV/u), elastic and inelastic nuclear scattering are again mainly responsible for deflection but also for energy loss through emission of bremsstrahlung. There are also other mechanisms possible, happening quite rarely at the energies used in society, but which should be mentioned here [21, 22]. These are direct interactions with the nuclei, namely transfer reactions like stripping or pickup, where nucleons are transferred from or to the incident particle. Also charge exchange can happen, which is a combination of stripping and pickup, where a neutron of the particle is exchanged with a proton of the atom or vice versa. Also, fragmentation can occur, where the incident particle and/or the atomic nucleus break up into (more than two) fragments. And finally, fusion reactions can occur, where the incident particle is fused into the atomic nucleus and both together form a new nucleus.

2.1.3.1.1 Energy Loss and Range

The exact energy loss during an interaction is described through the so-called stopping power S and is made up of the collision S_col and the radiation S_rad stopping power [23]:

$$ S=\frac{\mathrm{d}E}{\mathrm{d}x}={S}_{\mathrm{col}}+{S}_{\mathrm{rad}}. $$

(2.3)

The collision stopping power is the energy loss through collisions along the track in matter. For high energies of the impacting particles, the collisional stopping power can be described by the known Bethe–Bloch formula, which is based on perturbation theory and can also incorporate relativistic corrections.

For protons or heavier ions, the collision power is

$$ {S}_{\mathrm{col}}={\left(\frac{\mathrm{d}E}{\mathrm{d}x}\right)}_{\mathrm{col}}=\rho \cdot 4\pi \cdot {r}_e^2\cdot {m}_o{c}^2\cdot \frac{Z}{u\cdot A}\cdot {z}^2\cdot \frac{1}{\beta^2}\cdot {R}_{\mathrm{col}}\left(\beta \right). $$

(2.4)

For electrons or positrons, this is

$$ {S}_{\mathrm{col}}={\left(\frac{\mathrm{d}E}{\mathrm{d}x}\right)}_{\mathrm{col}}=\rho \cdot 2\pi \cdot {r}_e^2\cdot {m}_o{c}^2\cdot \frac{Z}{u\cdot A}\cdot {z}^2\cdot \frac{1}{\beta^2}\cdot {R}_{\mathrm{col}}^{\ast}\left(\beta \right). $$

(2.5)

This formula includes the properties of the particle energy, charge number, and velocity characterized by m_oc², z², and β² and the properties of the matter density ρ, charge number Z, and mass number A. r_e is the classical electron radius and u the atomic mass unit. The terms R_col(β) and ${R}_{\mathrm{col}}^{\ast}\left(\beta \right)$ are called rest function for heavier particles or electrons and positrons, respectively. These are dimensionless quantities, which contain the complex energy and matter-dependent cross sections for collision stopping.

In practical use, especially in radiobiology, it is just important to know some proportionalities:

$$ {S}_{\mathrm{col}}\propto \rho \cdot \frac{Z}{A}\cdot {z}^2\cdot \frac{1}{v^2}. $$

(2.6)

The radiation stopping power does not play a role for protons and heavier particles, due to their heavy masses, but for electrons, which are more than three orders of magnitudes lighter.

The radiation stopping power for electrons is

$$ {S}_{\mathrm{rad}}={\left(\frac{\mathrm{d}E}{\mathrm{d}x}\right)}_{\mathrm{rad}}=\rho \cdot \frac{1}{u}\cdot {r}_e^2\cdot \alpha \cdot \frac{Z^2}{A}\cdot {E}_{\mathrm{tot}}\cdot \left({R}_{\mathrm{rad},n}+\frac{1}{Z}{R}_{\mathrm{rad},e}\right). $$

(2.7)

With E_tot the total energy of the electron and α the fine-structure constant. Again, dimensionless rest functions occur describing the cross sections for interactions with nuclei R_{rad, n} and electrons in the atomic shell R_{rad, e}.

For quantification in radiobiology, the detailed description of the stopping power is not used, as it would be too complicated, and the perturbation parts only contain a small correction. Conventionally, the linear energy transfer $\mathrm{LET}=\frac{\mathrm{d}E}{\mathrm{d}x}$ is used instead. The LET only takes electronic interactions into account. The difference between LET and electronic stopping lies in their origin. The electronic stopping is focused on the energy loss of the impacting particle, and it has a negative sign as it acts as a friction force. The LET has a positive sign, and it is the energy that the target sees deposited in itself; this “positive amount of energy” creates the nonequilibrium dynamics, which are the first radiation-induced effects. The LET and the electronic stopping are equal for big samples, which is the case in radiobiology. Therefore, the LET is the same as the electronic stopping, which can be looked up in programs such as pstar, astar, or SRIM [24, 25].

For protons and heavier ions at energies larger than ~0.01 MeV/u, the electronic energy loss is the dominant process, as can be seen in Fig. 2.6, whereas for low ion energies, the nuclear energy loss becomes dominant, validating the use of LET as the most appropriate measurement quantity for radiobiologically relevant energies of >1 MeV. The energy loss has a peak at

$$ v\approx {z}^{\frac{2}{3}}\cdot \frac{c}{137}\approx {z}^{\frac{2}{3}}\cdot 25\frac{\mathrm{keV}}{u}. $$

(2.8)

For even higher ion energies, the energy loss decreases again.

For a single collision, considering a maximum energy ΔE_max which can be transferred through electronic interactions is

$$ \Delta {E}_{\mathrm{max}}\approx 4\frac{m_e}{m}E. $$

(2.9)

With m_e being the electron mass, m the ion mass, and E the ion energy. For protons, this maximum energy transfer per collision is ΔE_{max, p} ≈ 0.2 % E_p. For carbon ions, it is even lower at ΔE_{max, C} ≈ 0.02 % E_C. Therefore, thousands of collisions are necessary before an ion stops, and the more energy it has lost, the slower it gets and therefore the interactions get closer together.

If one looks at the energy loss of an ion depending on the path length traveled in a target medium, a unique distribution is visible (Fig. 2.6b). The energy loss at the entrance is low and only slightly increasing with depth. Just in the last millimeters or even below, the energy loss sharply increases. After the peak, an even sharper decrease is visible until the ion stops only shortly after reaching the peak energy loss. This distribution is called the Bragg curve. Due to this distribution, a range of the particle can be defined, which is the average distance the ion travels before it stops. Due to the statistical nature of the interactions, the range can only be given as an average quantity. The ion range can be calculated as [23]:

$$ R\left({E}_{\mathrm{kin}}\right)=\int_0^{E_{\mathrm{kin}}}{\left(-\frac{\mathrm{d}E}{\mathrm{d}x}\right)}^{-1}\mathrm{d}E. $$

(2.10)

For example, for protons with therapy-relevant energies between approx. 10 MeV and 200 MeV, the range can be approximated to

$$ {R}_p\cong 19\ \mu \mathrm{m}\ {\left(\frac{E}{MeV}\right)}^{1.8}\mathrm{with}\;E=\frac{mc^2}{\sqrt{1-{\beta}^2}}. $$

(2.11)

The unique energy loss distribution, with a peak energy loss just at the end of range, gives particles a great advantage in tumor therapy compared to photons, as the tissue behind the tumor will not get irradiated at all, as explained in Chap. 6.

For low-energy electrons, the collision stopping power is the dominant process, whereas for higher energies, the radiation stopping power gets dominant (Fig. 2.6c). The energy loss distribution with penetration depth is due to the contribution of the radiation stopping power different to protons and heavier ions (Fig. 2.6d). There is no clear range visible, but after a small buildup, the maximum is reached, followed by a decrease, and with higher depth the energy loss will be zero; this is when the electron has stopped. The possible penetration depth and especially the maximum of energy loss are dependent on energy. This is relevant for therapy, where low-energy electrons are used to irradiate skin tumors, whereas for deeper lying tumors, higher energies are necessary (Box 2.5).

Box 2.5 Characteristics of Charged Particles

• Charged particles transfer their energy mainly through coulomb interactions with electrons and nuclei of the atoms of the matter.

• The energy loss of the particle can be described by the Bethe–Bloch formula of the stopping power.

• For ions, only collision stopping power plays a role, and for electrons also radiation stopping power.

• Ions have a defined range, where energy loss follows the Bragg curve.

2.1.3.1.2 Scattering and Deflection

The interaction of particles with matter is not only responsible for energy loss but also for a deflection of the incident particle. For the coulomb interactions with electrons, only negligible deflection occurs. The nuclear Coulomb interactions also give small deflections per collision. Furthermore, Rutherford scattering with the atomic nucleus can occur. Taking all the interactions into account, significant deflection of particles is common. This process is called multiple small-angle scattering. Additionally, the Rutherford scattering can lead to single large-angle scattering events, but this effect is very rare. The scattering of single ions leads to widening of the incident beam of particles with penetration depth. Due to the dominance of the multiple small-angle scattering, the lateral profile of the beam can be approximated by a Gaussian distribution. It is important to know that for larger lateral distances, the Gaussian distribution no longer holds, as the large-angle scattered ions are deflected in this region. But as already mentioned, this is a rare process and does not have an influence on the beam size. The lateral spread defined as the σ of the Gaussian distribution is $\sigma \propto \frac{z}{E_{\mathrm{kin}}}{x}^{\frac{3}{2}}$, with E_kin the kinetic energy of the particle, z the charge, and x the distance traveled (Box 2.6).

Box 2.6 Scattering of Particles

• Coulomb interactions are responsible for scattering of the particle.

• Multiple coulomb scattering leads to a deflection of the particle.

• Single Rutherford scattering with the atomic nuclei leads to large deflections, but these are very rare.

• An incident particle beam will have a Gaussian energy distribution profile in the lateral direction due to the statistical nature of scattering.

2.1.3.2 Neutron Radiation

The existence of the neutron as a component of the atom was first proposed by Rutherford in 1911, though it was Chadwick who in 1932 detected the particle as a result of experiments involving gamma irradiation of paraffin [27]. Advances in particle physics have led to our current understanding of hadronic matter which includes neutrons, such that the quark model of the neutron envisages the particle as consisting of two down quarks and an up quark (udd), as shown in Fig. 2.7.

Fig. 2.7

Quark structure of proton and neutron, with binding gluons shown (Created with BioRender)

The neutron differs from the proton (uud) by a single quark such that it has almost identical mass (m_n = 939.6 MeV/c², m_p = 938 MeV/c²) though the neutron has zero charge. It also differs further in that, while the proton is thought to be stable (current T_1/2 of ~10³⁸ years), the free neutron is unstable with a mean lifetime of approximately 879.6 s. While electrically neutral, the neutron does have a magnetic moment of approximately −1.93 ⌠N, where that for the proton is approximately 2.79 ⌠N (and where ⌠N is the nuclear magneton). As the neutron is a fermion, it has a spin of ½ [28].

Early experiments with neutrons relied upon their production in prototype nuclear reactors. Here, neutrons were classified according to their energies as thermal (E ~ 0.038 eV, on average associated with a Maxwell–Boltzmann distribution of particles at room temperature), slow (E < 0.1 MeV), fast (E > 10 MeV), or relativistic (with energies producing velocities of 0.1 c or above) [29].

Exploration of neutron interactions with matter has revealed that they have very complex energy cross sections, which vary substantially with the target material. However, the interactions may be broadly classified as elastic or inelastic interactions, with elastic collisions having a greater cross section at high neutron energies [29].

In elastic interactions, the neutron collides, typically, with a target nucleus, transferring some of its kinetic energy to the nucleus, which then recoils. It may be demonstrated that the maximum energy Q that a neutron of energy E_n and mass M may transfer to a recoil nucleus of mass m is given by [29].

$$ Q=\frac{4{mME}_n}{{\left(M+m\right)}^2}. $$

(2.12)

In general, one may observe a cosine-squared spatial distribution of recoil energies for nuclei, Q, from which the original energy of the neutron beam may be estimated [29]:

$$ Q={E}_n{\cos}^2\theta . $$

(2.13)

In inelastic scattering events, either the neutron can promote the nucleus of element X to an excited state, from which the nucleus itself decays by re-emitting the neutron with different energy and momentum [(n,n′) reactions], or, for neutrons with energy below 0.5 MeV, the nucleus absorbs (“captures”) the incident neutron, causing it to transmute to a new elementary state, Y, generally with the emission of some product projectile, b, such as a proton, alpha particle, or gamma ray. The latter nuclear reactions are written as

$$ X\left(n,b\right)Y, $$

(2.14)

where examples include ⁹Be(n,γ)¹⁰Be and ⁷⁵As(n,γ)⁷⁶As (radiative capture reactions).

The development of sources of neutrons for industrial purposes has been a highly complex undertaking. Spallation sources of neutrons, where a material is bombarded with a projectile particle and then emits a beam of neutrons, have existed for some time. However, these systems require acceleration of a projectile beam, which renders them costly from an energy-input perspective, though they produce highly intense beams which are useful in the imaging of materials, as well as for both breeding and burning of nuclear fuel. Most neutron beams are produced via collimation and focusing of neutron beams from nuclear reactors, for similar applications to those already highlighted, and importantly for therapeutic applications in medicine. The development of Wolter mirrors and lenses has provided the means to direct and focus beams of neutrons in a highly precise manner allowing for controlled therapeutic applications.

2.2 Sources and Types of Ionizing Radiation

Humans are continuously exposed to low levels of ionizing radiation from the surroundings as they carry out their normal daily activities; this is known as background radiation, which is present on Earth at all times [30]. In addition, we are exposed to ionizing radiation from artificial sources during medical examinations and treatments, during processing and using radioactive materials, and during operation of nuclear power plants or accelerators (Figs. 2.8 and 2.9). Below we provide a summary of the possible scenarios of exposure to natural and artificial radiation.

Fig. 2.8

Natural sources of ionizing radiation and their pathways (Figure from European Commission, Joint Research Centre—Cinelli, G., De Cort, M. & Tollefsen, T., European Atlas of Natural Radiation, Publication Office of the European Union [41]) (licensed under CC-BY-4.0)

Fig. 2.9

Worldwide average annual human exposure to ionizing radiation (from UNSCEAR (2008) Sources and effects of ionizing radiation) (Created with BioRender)

2.2.1 Natural Background Radiation

Natural radiation is all around us, and we receive it from the atmosphere, rocks, water, plants, as well as the food we eat (Fig. 2.8). Naturally occurring radioactive materials are present in the Earth’s crust; the floors and walls of our homes, schools, or offices; and food. Radioactive gasses are also present in the air we breathe. Our muscles, bones, and other tissues contain naturally occurring radionuclides [31]. Hence, our lives have evolved, and our bodies have adapted to the world containing considerable amounts of ionizing radiation. As per the United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR), terrestrial radiation, inhalation, ingestion, and cosmic radiation are the four foremost sources of public exposure to natural radiation.

• 1. Terrestrial Radiation: One of the major sources of natural radiation is the Earth’s crust, where the key contributors are the innate deposits of thorium, uranium, and potassium. These minerals are called primordial radionuclides and are the source of terrestrial radiation. These deposits discharge small quantities of ionizing radiation during the process of natural decay, and these minerals are found in building materials. Therefore, humans can get exposed to natural radiation both outdoors and indoors. These radiation levels can fluctuate substantially depending on the location. Traces of radioactive materials can be found in the body where nonradioactive and radioactive forms of potassium and other elements are metabolized in the same way [32].

• 2. Inhalation: Humans are exposed to inhalation of radioactive gasses that are formed by radioactive minerals found in soil and bedrock. For example, uranium-238, during its decay, produces radon (²²²Rn) which is an inert gas and thorium produces thoron (²²⁰Rn). These gasses get diluted to harmless levels when they traverse the Earth’s atmosphere. However, at times, these gasses escape through cracks in the building foundations, are trapped, and accumulate inside buildings where they are inhaled by the occupants (indoor living) [30].

• 3. Ingestion: Vegetables and fruits are grown in the soil and groundwater, which usually contain radioactive minerals. We ingest these minerals and subsequently are exposed to internal natural radiation. Carbon-14 and potassium-40 are naturally occurring radioactive isotopes which possess similar biological characteristics as their nonradioactive isotopes. These radioactive and nonradioactive elements are used not only in building our bodies but also in maintaining them. Therefore, such natural radioisotopes recurrently expose us to radiation [30].

• 4. Cosmic Radiation: Space is permeated by radiation, not only of electromagnetic type but also constituted by ionizing particles with mass. The electromagnetic radiation in space spans all wavelengths, from infrared to visible, from X-ray to gamma rays. In general, however, “space radiation” mostly refers to corpuscular radiation, which has three main sources:

  • (a) Galactic Cosmic Rays (GCRs): The GCRs constitute the slowly varying, low-intensity, and highly energetic radiation flux background in the universe, mostly associated with explosions of distant supernovae. The GCR spectrum consists of approximately 87% hydrogen ions (protons) and 12% helium ions (α-particles), with the remaining 1–2% of particles being HZE (high charge Z and energy) nuclei. The energies are between several tenths and 10 × 10 GeV/nucleon and more. GCRs directly hit the top of the Earth’s atmosphere, generating secondary particle showers. However, some direct GCRs and generated secondary particles infiltrate the Earth’s atmosphere reaching the ground. Such radiation gets absorbed by humans, and it thus constitutes a source of natural radiation exposure. Since at higher altitude the amount of atmosphere shielding us from incoming radiation is less, the higher we go in altitude, the higher dose we receive. For example, those living in Denver, Colorado (altitude of 5280 ft = about 1610 m), receive a higher annual radiation dose from cosmic radiation than someone living at sea level (altitude of 0 ft) [32]. GCR ions are a major health threat to astronauts for missions beyond the near-Earth environment and for interplanetary travel [33]. For Mars, the thin atmosphere combined with the absence of a planetary magnetic field essentially offers very little shielding from the incoming GCRs [34, 35]. Also, GCRs directly reach the surface of airless bodies such as the Moon [36].

  • (b) Radiation from the Sun: This consists of both low-energy particles flowing constantly from the Sun (the solar wind) and of solar energetic particles (SEPs), originating from transient intense eruptions on the Sun [37]. The solar wind is stopped by the higher layers of the atmosphere of our planet (and other celestial bodies with an atmosphere). SEPs come as huge injections and are composed predominantly of protons and electrons. Typical proton energies range from 10 to 100 of MeV. They are generally quite efficiently stopped in the Earth’s atmosphere, but some direct SEPs and their high flux of secondaries could eventually be dangerous for high-altitude/latitude flights and their crew [38] and for astronauts of the International Space Station (ISS) in extravehicular activities. Finally, SEPs can be a strong concern also for astronauts during interplanetary travel, such as a trip to Mars, even inside the spacecraft [39], or for humans on the surface of the Moon.

  • (c) Trapped Radiation: This consists of GCRs and SEPs and their secondaries trapped by the Earth’s magnetic field into the Van Allen radiation belts. Such belts comprise a stable inner belt of trapped protons and electrons (energies are between keV and 100 MeV) and a less stable outer electron belt. The inner Van Allen belt comes closest to the Earth’s surface, down to an altitude of 200 km, in a region just above Brazil. This area is named the South Atlantic Anomaly [40]. An increased flux of energetic particles exists in this region and exposes orbiting human missions to higher-than-usual levels of radiation (Box 2.7).

Box 2.7 Sources of Natural Radiation

The natural radiation to which we are continually exposed has its sources in:

• Cosmic radiation (the portion of it reaching the ground)

• Radiation from radioactive elements in rocks

• Radioactive gasses, generally at harmless concentration in the air but that can potentially also get trapped in building walls

• Food, grown in soil and groundwater, which can contain radioactive minerals

2.2.2 Artificial Radiation Sources

Nuclear power stations/plants use uranium to drive a fission reaction that heats water to produce steam. The latter drives turbines to produce electricity. During their normal activities, nuclear power plants release small amounts of radioactive elements, which can expose people to low doses of radiation. The water that passes through a reactor is processed and filtered to remove these radioactive impurities before being returned to the environment. Nonetheless, minute quantities of radioactive gasses and liquids are ultimately released to the environment. Such releases must be continuously monitored and are under the legislative framework of international organizations dealing with nuclear energy, such as the European Atomic Energy Community (EURATOM), established by one of the Treaties of Rome in 1958. Similarly, uranium mines and fuel fabrication plants release some radioactivity that contributes to the dose of the public [42]. The eventual release of radioactive materials should also be monitored and kept under established levels during the decommissioning of a nuclear power plant, from the shutdown of the reactor to the operation of radioactive waste facilities, and also including the short- and intermediate-term storage of spent nuclear waste to the transport to and storage in long-term geological disposal areas.

Technologically enhanced naturally occurring radioactive materials (TENORM): All minerals and raw materials contain radionuclides, commonly denoted as naturally occurring radioactive materials (NORM). When concentrations of radionuclides are increased by technological processes, the term technologically enhanced NORM (TENORM) is applicable. Coal-fired power stations, for example, emit an amount of radioactivity compared to or even higher (especially in the past) than nuclear power plants. Just for example, US coal-fired electricity generation in 2013 gave rise to 1100 tonnes of uranium and 2700 tonnes of thorium in coal ash. Other TENORM industries include oil and gas production, metallurgy, fertilizer (phosphate) manufacturing, building industry, and recycling [43].

Accelerators: The operation of accelerators, such as the Large Hadron Collider (LHC) at CERN for fundamental high-energy physics experiments, results in the production of radiation, in particular protons, because of the nuclear interactions between high-energy beams and accelerator components. Thus, the radiation levels around accelerators must be monitored continuously to ensure the protection and safety of the workers and of the public [44].

Radionuclide production facilities: Radionuclides are used worldwide in (a) medical imaging, fundamental to make correct diagnoses and provide treatments, in which radionuclides are injected into patients at low doses for functional imaging to detect diseases, and (b) therapy, in which radionuclides bound to other molecules or antibodies can be guided to a target tissue, for a local treatment of cancer. Facilities that produce radionuclides and facilities in which radionuclides are processed are reactors and particle accelerators. Radionuclides used in imaging and therapy are often beta or alpha emitters, or both. Thus, the facilities, reactors, and particle accelerators can present radiation hazards to workers and must be properly controlled and monitored, as is the case with the subsequent processing of radioactive material. Among the 238 research reactors in operation in 2017, approximately 83 were considered useful for regular radioisotope production [45]. Approximately 1200 cyclotrons worldwide were used to some extent for radioisotope production in 2015 [46]. The facilities must ensure the application of the requirements of the IAEA [47] (2014) intended to provide for the best possible protection and safety measures.

Hospitals: Daily, healthcare workers and patients are exposed to various diagnostic and therapeutic radiation sources [48, 49]. The radiation environment in different hospital departments (nuclear medicine, diagnostic radiology, radiotherapy, …) can be generated by different sources. Hospitals providing radionuclide-based treatments need to protect the staff involved and keep their dose within the acceptable levels. Similarly, the discharged patient must be monitored and measurements for protection purposes must be taken to keep dose to the public within acceptable levels. This may require hospitalization with isolation during the first hours or days of treatment [50, 51]. Waste should be minimized and segregated, and packages labeled and stored for decaying. Measures should also be in place for patients’ household waste related to, for example, urine. In a radiology department, the radiation emitted during fluoroscopic procedures is responsible for the greatest radiation dose to the medical staff. Radiation from diagnostic imaging modalities, such as mammography, computed tomography, and nuclear medical imaging, is a minor contributor to the cumulative dose incurred by healthcare personnel [52]. In radiotherapy departments, photons and electrons are mainly produced by linear accelerators. Rarely, cobalt sources are used to produce radiation. With the current safety regulations, radiotherapy staff will get almost no dose during normal operation. The same is true for modern brachytherapy machines, which are almost all after loading machines avoiding direct contact between the radioactive source and the operator.

Ion radiotherapy facilities: Most currently existing ion radiotherapy facilities use protons, with new facilities now being built for the acceleration of other ions, such as carbon. They are mostly cyclotrons or synchrotrons. For such facilities, the major issue is the massive production of neutrons. Ionizing radiation results from the passage of such neutrons through matter and from the radioactivity induced in exposed materials. In accelerator facilities, radioactivity is produced in the very material components, such as their beam delivery/shaping components, as well as in all the structural components and other materials in the facility. Induced radioactivity in treated patients could also reach considerable levels.

Nuclear bombs: Nuclear weapons have an explosive power deriving from the uncontrolled fission reaction of plutonium and uranium. This yields a large number of radioactive substances (isotopes) that are blown into the atmosphere. These radioactive isotopes gradually fall back to Earth. If a weapon is exploded near the Earth surface, radioactive fallout is formed in the vicinity of the burst point in a matter of tens of minutes to a couple of days (depending on the burst yield and the distance to the burst point); if a weapon is detonated aboveground (e.g., in Hiroshima and Nagasaki, the bombs exploded about 500 m above the ground level), local fallout is not formed but the radionuclides fall worldwide over a period of many years. Gamma-ray and neutron exposures leading to increased cancer incidence have been studied in the survivors of the atomic bombings in Japan since 1950 (the so-called Life Span Study, LSS, cohort), and currently all potentially suitable risk estimates are built on the excess risk from the LLS study [53]. Interestingly, the numerous tests of nuclear weapons performed by many countries since after World War II and the ensuing fallout have contributed minimally to the overall background radiation exposure (Box 2.8).

Box 2.8 Sources of Artificial Radiation

Artificial radiation sources are:

• Medical and radionuclide production facilities, accelerators for ion beam cancer therapy

• Technologically enhanced naturally occurring radioactive materials (TENORM)

• Nuclear power plants

• Accelerators for purely fundamental research in physics

2.3 Direct and Indirect Effects of Radiation

The interaction of ionizing radiation (IR) with matter leads to biological damage that can impair cell viability. Biological damage induced by IR arises from either direct or indirect action of radiation. Direct effects occur when IR interacts with critical target molecules such as DNA, lipids, and proteins, leading to ionization or excitation, which causes a chain of events that ultimately leads to the alteration of biomolecules. Indirect effects occur when IR interacts with water molecules, the major constituent of the cell. This reaction, called water radiolysis, generates high-energy species known as reactive oxygen species (ROS) that are highly reactive toward critical targets (cell macromolecules) and, when associated with reactive nitrogen species (RNS), lead to damage to the cell structure. Mechanism and critical targets for ionizing radiation to produce biological damage through direct and indirect effects are shown in Fig. 2.10. Damages to cell macromolecules may be multiple and are detailed in Chap. 3.

Fig. 2.10

Mechanism and critical targets for ionizing radiation to produce biological damage through direct and indirect effects (Created with BioRender)

2.3.1 Direct Effects of Radiation

Direct effects occur when the ionization takes place within a critical target with relevance to cell functions, such as DNA, lipids, and proteins. These effects are produced by both high and low linear energy transfer (LET) radiation. However, it is the predominant mode of action of high LET radiation such as alpha particles and neutrons, comprising about two-thirds of the radiation effects.

When critical molecules in the cell are directly hit by radiation, their molecular structure may be altered resulting in their functional impairment. While molecules from all cell organelles (including mitochondria, endoplasmic reticulum, or Golgi apparatus) may be hit, the nuclear DNA molecule has always been seen as the most critical target (because, unlike proteins, lipids, and carbohydrates, only a single copy of DNA is present in a cell) and was, therefore, the most thoroughly studied. The DNA damage produced by radiation includes base alterations, DNA–DNA cross-links, single- or double-strand breaks (SSB or DSB), or complex damages (described in Chap. 3).

2.3.2 Indirect Effects of Radiation

Indirect damages produced by IR in the cell macromolecules are mediated by ROS (resulting from water radiolysis) and by RNS (formed following the reaction of O₂ with endogenous nitric oxide). The indirect effects contribute to about two-thirds of the damages induced by low LET radiation (X-rays, gamma-rays, beta particles), which is explained by the fact that they are more sparsely ionizing compared to high LET radiation.

When radiation deposits energy in a biological tissue, it takes time until perceiving that an effect has occurred. The succession of the generation of events determines the four sequential stages that translate into the biological effects. These stages, with very different duration, are physical, physicochemical, chemical, and biological [54,55,56].

The physical stage is very transient, lasting less than 10⁻¹⁶–10⁻¹⁵ s, during which energy (kinetic if particles, or electromagnetic if waves) is transferred to the electrons of atoms or molecules, determining the occurrence of ionization and/or excitation. It is at this stage that ions are formed, which will initiate a sequence of chemical reactions that end up in a biological effect. In the case of water radiolysis (decomposition of water molecules due to IR), the ions H₂O⁺ and e⁻ are formed, as well as the excited water molecule (H₂O*) [54,55,56].

Very soon (10⁻¹² s) after the formation of these ions, the physicochemical stage begins, with their diffusion in the medium and consequent intermediate formation of oxygen and nitrogen radical species, i.e., atoms, molecules, or ions that have at least one unrepaired valence electron and hence are very reactive chemically. Following the example of water radiolysis, it is at this stage that Ḥ + HO^·, H₂ + 2HO, HO^· + H₃O⁺, HO^· + H₂ + OH⁻, and e⁻_aq are formed [55, 56], but also superoxide anion (O₂^·−) and hydrogen peroxide (H₂O₂). Peroxynitrite anion (ONOO⁻) is also formed following the reaction of O₂^·− with endogenous nitric oxide (NO). Together with peroxynitrous acid (ONOOH), nitrogen dioxide (NO₂^·), dinitrogen trioxide (N₂O₃), and others, they are referred to as RNS. The activation of the nicotinamide adenine dinucleotide phosphate (NADPH) oxidase, the mitochondrial electron transport chain (ETC), or the nitric oxide synthase by IR can also contribute to ROS/RNS generation.

In the next chemical stage, the formed radicals and ions recombine and interact with critical cellular organic molecules (DNA, lipids, proteins), inducing structural damages that will translate into disruption of the function of these molecules. Within the DNA molecule, possible chemical reactions with nitrogenous bases, deoxyribose, or phosphate group may result in breaks and recombinations with the consequent formation of abnormal molecules. Among ROS, OH, which has a strong oxidative potential, is a main contributor to cell damages. The chemical stage can last from 10⁻¹² s to a few seconds [55, 56]. ROS and RNS have also been largely implicated in the so-called non-targeted effects of IR (further discussed in Sect. 2.8.2).

Finally, the biological phase occurs, as a consequence of the spreading of chemical reactions involving various biological processes. The existence of more or less effective cellular damage repair mechanisms is responsible for the more or less belated appearance of biological effects and explains the possible long duration of this stage: from a few minutes to decades, depending on the type of radiation, the dose and dose rate, and the radiosensitivity of the irradiated tissue.

Differences in tissue radiosensitivity can be partially explained by the cellular antioxidant capacity, which may vary between cell types. Indeed, to counteract oxidative insults, cells have evolved several defense mechanisms that consist of enzymatic and nonenzymatic systems. When the amount of ROS/RNS exceeds the antioxidant capacity of the cells, a state of oxidative stress arises, characterized by a decreased pool of antioxidants and modifications in nucleic acids, lipids, and proteins. Oxidative stress can persist for much longer and extend far beyond the primary targets as well as can be transmitted to progeny of the inflicted cells. Responsible for this seems to be the continuous production of ROS and RNS, which can last for months.

2.3.3 Biological Damages Induced by Direct and Indirect Effects of Radiation on Cell Organelles

Virtually all cell molecules and organelles may be damaged by IR, with consequences for the cell function depending on the impact of the damage inflicted.

According to the radiobiology paradigm, a nucleus is regarded as the main target of IR due to the genetic information contained in the DNA. Therefore, damages to this molecule are considered the most critical ones for cell survival. While efficient repair mechanisms exist to preserve the genome integrity, IR may break bonds in purine and pyrimidine nitrogenous bases in the DNA (which may lead to mutations), SSBs or DSBs, cross-linking, and complex damages. Among these lesions, DSBs and complex damages are the most serious due to the difficulty of their repair. A thorough description of DNA lesions is provided in Chap. 3.

Mitochondria can also be subject to radiation damage, both directly and indirectly. These organelles may represent more than 30% of the total cell volume, and the mitochondrial circular DNA can suffer strand breaks, base mismatches, or even deletions of variable length. In this context, mitochondria constitute a major target of IR [57]. Besides the DNA, changes in mitochondrial morphology have also been observed [58]. Absorption of IR may lead to the enlargement of mitochondria and the increase in length and number of branches of the cristae [58, 59], rupture of the outer and inner membranes, as well as vacuolization and loss of the matrix. These alterations are accompanied by the decreased activity of the respiratory chain, with special emphasis on complexes I, II, and III, which are systematically referred to as especially sensitive to the direct effects of IR. Additionally, there is a decrease in the respiratory capacity driven by succinate and the ATP synthase, with a consequent impact on oxidative phosphorylation. The radiation-induced decrease in the rate of oxidative phosphorylation can recover over time, depending on the cell type [60, 61]. The electrons in the respiratory chain can leak during their transport and reduce oxygen molecules leading to the formation of superoxide anions, which are precursors of most ROS. Upon irradiation, the level of ROS produced in the mitochondria greatly increases, although under physiological conditions, it is already high.

Irradiation may also cause morpho-functional changes in the endoplasmic reticulum (ER). After exposure to IR, ER dilates, vesicles appear, and its cisternae break into fragments. In the case of rough endoplasmic reticulum, irradiation induces degranulation accompanied by transformation of the membrane-bound ribosomes into free organelles [59, 62].

Likewise, irradiation may also disorganize the structure of the Golgi apparatus due to the induced fragmentation and rearrangement of its cisterns. In view of the effects of IR on the endoplasmic reticulum-Golgi apparatus complex, the ensuing alterations in the synthesis and maturation of proteins in the irradiated cells come as no surprise. Lysosomes may also increase in number and volume in the irradiated cells, which is accompanied by upregulation of the enzymatic activity in these organelles [58, 59] (Box 2.9).

Box 2.9 Direct and Indirect Effects of Radiation

• Direct effects predominate after exposure to high LET radiation (e.g., alpha particles, neutrons).

• Exposure to low LET radiation (e.g., X-rays, gamma rays, beta particles) induces mostly indirect effects.

• Indirect effects are mediated by ROS/RNS produced during and after the radiolysis of water.

• Apart from nuclear DNA, other cellular molecules and organelles may be altered by IR, including mitochondrial DNA, plasma membrane lipids, endoplasmic reticulum, Golgi apparatus, and lysosomes.

2.4 Radioactivity and Its Applications

Radiation and radioactivity have been existing ever since the Earth was formed and long before life started to evolve. All living organisms on Earth are continuously exposed to both natural and artificial radioactivity, and without it, life in the present form would have not evolved. Since the first experiments with radioactivity, our understanding of this phenomenon has increased, and consequently, today radioactivity has numerous applications important to human life and health.

2.4.1 Radioactive Decay

2.4.1.1 Natural Radioactivity

The rate of decay of a radioactive source is proportional to the amount of the substance that is present at any given instant. Therefore, if the number of radioactive nuclei in a sample is N, then we may say the following:

$$ {\displaystyle \begin{array}{l}-\frac{\mathrm{d}N}{\mathrm{d}t}\propto N\\ {}\Rightarrow -\mathrm{d}N\propto N\cdot \mathrm{d}t,\\ {}\therefore -\mathrm{d}N=\lambda \cdot N\mathrm{d}t\end{array}} $$

(2.15)

where λ is the decay constant, which describes the rate of decay for a particular radioactive isotope.

If we integrate both sides of Eq. (2.15), we get the following more familiar equation:

$$ N={N}_0{e}^{-\lambda t}. $$

(2.16)

If we let the variable T_1/2 be the “half-life of the substance,” i.e., the time taken for the activity of the substance to reduce from its initial value to half of its initial value, then we may modify Eq. (2.16) as

$$ {\displaystyle \begin{array}{l}\frac{N_0}{2}={N}_0{e}^{-\lambda {T}_{1/2}}\\ {}\therefore {T}_{\frac{1}{2}}=\frac{\ln 2}{\lambda }=\frac{0.693}{\lambda}\end{array}} $$

(2.17)

The activity, A, of a given sample of a radioactive substance, i.e., the number of decays per second (in Bq), is given by the following equation:

$$ A(t)=\lambda \cdot N(t), $$

(2.18)

where calculations based on activities may be performed using Eqs. (2.2) and (2.3) above with the values of A inserted instead of N. The radioactivity of a sample is quoted in terms of the units of Curies, Ci (the radioactivity of a gram of ²²⁶Ra), where 1 Ci =3.7 × 10¹⁰ decays per second. This is more commonly quoted in terms of the S.I. unit the Becquerel, Bq, where 1 Bq = 1 decay per second. Therefore, 1 Ci = 3.7 × 10¹⁰ Bq (Box 2.10).

Box 2.10 The Activity of a Radioactive Substance

• The activity (A) of a radioactive substance is given in becquerel (1 Bq is the number of decays per second).

• The radioactivity of a sample can also be expressed in curies (Ci), where 1 Ci = 3.7 × 10¹⁰ Bq.

2.4.1.2 Radioactive Equilibrium

In nature, the abundance of the isotopes of certain radioactive nuclei depends on the abundance of their precursors, and the rate at which these precursors decay. Hence, the rate of production of each daughter nuclide of a certain radioactive isotope depends upon the rate at which its parent nuclide decays. All naturally occurring radioactive nuclides that are located below plutonium, ²³⁹Pu, in the periodic table are produced from the decay of just four parent (progenitor) isotopes: thorium (4n series), neptunium (4n + 1 series), uranium/radium (4n + 2), and actinium (4n + 3). Each of these nuclides then has a decay series or chain (see example in Fig. 2.11) with associated rates of decay at each step that determine the abundance of all other radionuclides in the universe.

Fig. 2.11

Uranium, ²³⁸U/radium, ²²⁶R (4n + 2) decay series. Radioactive decay series. (2020, September 8). [Retrieved August 16, 2021, from https://chem.libretexts.org/@go/page/86256 (open-source CC-BY textbook)]

The neptunium series is not observed in nature at the present time as ²³⁷Np, and all of its daughter nuclides have decayed since the birth of the universe, although the product of the series, bismuth ²⁰⁹Bi, is observed as a stable isotope in nature, pointing to the existence of the series at one time in the past. Each decay series begins with a radioactive isotope and ends with a stable daughter product. The parent isotopes of the isotopes at the beginning of the thorium, neptunium, and actinium series are produced as follows:

Th series: ²⁵²Cf → ²⁴⁸Cm → ® ²⁴⁴Pu → ® ²⁴⁰U → ® ²⁴⁰Np → ® ²⁴⁰Pu → ® ²³⁶U

Np series: ²⁴⁹Cf → ® ²⁴⁵Cm → ® ²⁴¹Pu → ® ²⁴¹Am → ® ²³⁷Np

Ac series: ²³⁹Pu → ® ²³⁵U

If we consider a hypothetical decay series as in Fig. 2.12, the three daughter isotopes of isotope A (namely isotopes B, C, D) are produced at different rates, each dependent on the decay constants of the isotope that is their parent. Say only N₀ atoms of A exist at time t = 0; then

$$ {N}_A={N}_0{e}^{-{\lambda}_A\kern0.1em t} $$

(2.19)

$$ \frac{\mathrm{d}{N}_B}{\mathrm{d}t}={\lambda}_A{N}_A-{\lambda}_B{N}_B $$

(2.20)

$$ \frac{\mathrm{d}{N}_C}{\mathrm{d}t}={\lambda}_B{N}_B-{\lambda}_C{N}_C. $$

(2.21)

From Eqs. (2.19) and (2.20):

$$ \frac{\mathrm{d}{N}_B}{\mathrm{d}t}+{\lambda}_B{N}_B={\lambda}_A{N}_0{e}^{-{\lambda}_At}. $$

(2.22)

Multiplying across by ${e}^{\lambda_Bt}$

$$ {\displaystyle \begin{array}{l}{e}^{\lambda_Bt}.\frac{\mathrm{d}{N}_B}{\mathrm{d}t}+{\lambda}_B{N}_B{e}^{\lambda_Bt}={N}_0{\lambda}_A{e}^{\left({\lambda}_B-{\lambda}_A\right)t}\\ {}\Rightarrow \frac{\mathrm{d}\left({N}_B{e}^{\lambda_Bt}\right)}{\mathrm{d}t}={N}_0{\lambda}_A{e}^{\left({\lambda}_B-{\lambda}_A\right)t}.\end{array}} $$

Integrating both sides then gives

$$ {N}_B{e}^{\lambda_Bt}={N}_0\frac{\lambda_A}{\lambda_B-{\lambda}_A}\left[{e}^{\left({\lambda}_B-{\lambda}_A\right)t}-1\right] $$

And multiplying across by ${e}^{-{\lambda}_Bt}$ gives

$$ {N}_B={N}_0\frac{\lambda_A}{\lambda_B-{\lambda}_A}\left({e}^{-{\lambda}_At}-{e}^{-{\lambda}_Bt}\right). $$

(2.23)

If the parent is very much shorter lived than the daughter, i.e., if λ_A > λ_B, we then have radioactive equilibrium (Fig. 2.12a). If the parent is longer lived than the daughter, then λ_A < λ_B and a particular case called transient equilibrium arises (Fig. 2.12b). In Fig. 2.12b, the daughter product C is stable and so no further decrease in activity occurs. Finally, secular equilibrium occurs when the parent is much longer lived than its daughter λ_A <<λ_B. In this case, Eq. (2.23) reduces to the following (also see Box 2.11)

$$ {\displaystyle \begin{array}{l}{N}_B={N}_0\frac{\lambda_A}{\lambda_B}\left({e}^{-{\lambda}_At}\right)\\ {}\therefore {N}_B={N}_0\frac{\lambda_A}{\lambda_B}.\end{array}} $$

(2.24)

Fig. 2.12

Hypothetical decay series involving four nuclides A, B, C, and D, with various different decay constants λ_A, λ_B, etc. (a) Radioactive equilibrium. (b) Transient equilibrium

Box 2.11 Natural Radioactivity

• The natural abundance of radionuclides is largely determined by the nuclear decay series of four parent nuclides, thorium, neptunium, uranium/radium, and actinium.

• Each decay series starts from an unstable radioactive parent isotope and ends with a stable daughter product.

• Various states of equilibrium can be reached depending on the relationship between the lifetime of the parent and daughter isotopes.

2.4.1.3 Artificial Radioactivity

Experiments demonstrating the production of radioactive nuclei in the laboratory were performed by Irène and Frédéric Joliot-Curie in 1934 through the bombardment of aluminum and boron atoms with alpha particles. Those scientists observed that positrons were produced long after the bombardment and neutron production had ceased. They postulated that radioactive isotopes of phosphorus and nitrogen had been produced, which decayed to silicon and carbon in the following reactions:

${\displaystyle \begin{array}{ll}\begin{array}{l}{}_{13}\mathrm{A}{\mathrm{l}}^{27}+{}_2\mathrm{H}{\mathrm{e}}^4\to {}_{15}\mathrm{P}^{30}+{\mathrm{n}}_0^1\\ {}{}_{15}\mathrm{P}^{30}\to {\beta_{-1}^0}^{+}+{}_{14}\mathrm{S}{\mathrm{i}}^{30}\end{array}& \begin{array}{l}{T}_{1/2}=150\\ {}\mathrm{seconds}\end{array}\\ {}\begin{array}{l}{}_5\mathrm{B}^{10}+{}_2\mathrm{H}{\mathrm{e}}^4\to {}_7\mathrm{N}^{13}+{\mathrm{n}}_0^1\\ {}{}_7\mathrm{N}^{13}\to {\beta_{-1}^0}^{+}+{}_6\mathrm{C}^{13}\end{array}& \begin{array}{l}{T}_{1/2}=600\\ {}\mathrm{seconds}\end{array}\end{array}}.$

Neither of the two radioactive isotopes of phosphorus and nitrogen produced in these reactions occurs in nature. The majority of the artificially produced isotopes are produced via the same bombardment as illustrated here, and most of them decay by the production of β⁺/βb⁻, the ratio of n/p in the nucleus determining which of the two reactions occurs.

Consider a situation where a nuclear reaction occurs by bombardment of nucleus X with particle a, producing a nucleus Y and another projectile particle b:

$$ X\left(a,b\right)Y. $$

(2.25)

Assuming that the rate of production, R, of Y is constant and its decay is also constant, then the infinitesimal change, dN, in the numbers of product atoms of Y over infinitesimal time, dt, is

$$ \mathrm{d}N=R\mathrm{d}t-\lambda N\mathrm{d}t, $$

(2.26)

where Rdt provides the number of nuclides of Y produced per unit time and λNdt the number decaying over this time period. We can then rearrange to obtain a differential equation for the system:

$$ \frac{\mathrm{d}N}{\mathrm{d}t}=R-\lambda N, $$

(2.27)

for which we can obtain a general solution for the number of nuclides of Y at any time t > 0:

$$ N(t)=\frac{R}{\lambda}\left(1-{e}^{-\lambda t}\right). $$

(2.28)

And since activity A = λN, we may obtain a relationship for the variation in activity with time as

$$ A(t)=R\left(1-{e}^{-\lambda t}\right). $$

(2.29)

We may use a Taylor expansion in e^-λt to then obtain

$$ A(t)=R\left(1-\left[1-\lambda t+\cdots \right]\right) $$

(2.30)

which allows a solution to be obtained for the special case where t << T_1/2 for the nuclide Y such that the following is true: (also see Box 2.12)

$$ A(t)\approx R\lambda t. $$

(2.31)

Box 2.12 Artificial Radioactivity

• In 1934, Irène and Frédéric Joliot-Curie demonstrated for the first time that artificial, i.e., not occurring in nature, radioactive nuclei can be produced.

• Artificial nuclides are produced by bombarding a nucleus (X) with a particle (a) resulting in the production of a new nucleus (Y) and a projectile particle (b).

2.4.1.4 Modes of Radioactive Decay

Unstable nuclei will transform spontaneously or artificially into an energetically more stable configuration by the emission of certain particles or electromagnetic radiation. This process, termed nuclear decay, is characterized by a parent nuclide (P) transforming into a daughter nuclide (D), which differs from the former in atomic number (Z), neutron number (N), and/or atomic mass number (A) [63]. The different types of nuclear decay are summarized in Table 2.1 (Box 2.13).

Table 2.1 Summary of the different types of nuclear decay

Box 2.13 Nuclear Decay

• During nuclear decay, unstable nuclei transform into an energetically more stable configuration by emission of certain particles or energy.

• Different modes of nuclear decay exist, each with their own mode of reaching this energetically stable configuration (Table 2.1).

2.4.2 The Chart of Nuclides

The term nuclide refers to an atom characterized by the number of protons and neutrons present in the nucleus. Nuclides can be sorted according to their number of protons and neutrons in a chart of nuclides. In contrast to the well-known periodic table, a chart of nuclides organizes the currently known radionuclides according to the number of protons and neutrons in their nucleus. Furthermore, it summarizes basic properties of these nuclides, such as atomic weights, decay modes, half-lives, and energies of the emitted radiations [64, 65].

In 2018, the tenth version of the Karlsruhe chart of radionuclides was published, containing nuclear data on 4040 experimentally observed nuclide ground states and isomers [66]. As mentioned earlier, this chart organizes data of currently known radionuclides according to the number of protons and neutrons present in their nucleus (Fig. 2.13a). Stable nuclides are shown in black, while the colored boxes indicate the decay mode of each nuclide (Fig. 2.13c). Data on individual nuclides can be found in the individual nuclide boxes (Fig. 2.13b). When a single nuclide has different decay modes, it is represented by different sizes of triangles, representing the branching ratios for each decay mode (Fig. 2.13b, ²²⁶Ac). A nuclide box can also be subdivided into different sections with a vertical line (Fig. 2.13b, ¹³⁵Cs). An undivided box refers to the ground state of a nuclide, while when subdivided, the right section corresponds to the ground state and the subsections on the left represent the nuclear isomers (nuclides with the same number of protons and neutrons in the nucleus, but a different energy). Nuclides with a black upper section in the nuclide box represent primordial nuclides, formed during the formation of terrestrial matter and still present on Earth due to their extremely long half-lives. For such nuclides, the upper section provides information on the isotopic abundance, while the lower section indicates decay modes and half-lives (Fig. 2.13b, ²³²Th) [66]. Radionuclide charts are available in printed or online versions.

Fig. 2.13

(a) Schematic representation of the complete Karlsruhe radionuclide chart. (b) Detailed representation of different radionuclide boxes. (c) Different colors of boxes representing the different decay modes, from left to right: stable isotope, proton emission (p), alpha decay (α), electron capture or beta-plus decay (ε or β+), isomeric transition (IT), beta-minus decay (β−), spontaneous fission (SF), cluster decay (CE), and neutron decay (n). [(Figure adapted from Soti et al., 2019) (licensed under CC-BY-4.0)]

A chart of nuclides can be used to investigate decay chains and nuclear reactions of different radionuclides. By following the specific decay rules of each type of nuclear decay, complete decay chains can be obtained manually. In a similar way, the chart can be used to obtain different activation and reaction products of nuclear reactions [66]. In this way, this chart can be of great assistance to obtain information on nuclear decay chains and isotope stability. It can help with both planning of experiments and interpretation of results [64, 65] (Box 2.14).

Box 2.14 Definition of a Nuclide

• A “nuclide” refers to an atom with a certain number of protons and neutrons in the nucleus.

• Nuclides can be sorted based on their characteristics in a nuclide chart.

• A nuclide chart can be used to investigate nuclear decay chains of different radionuclides.

2.4.3 Applications of Radioisotopes

The pioneering experiments performed by Wilhelm Conrad Roentgen (1895), Henri Becquerel (1896), and Marie and Pierre Curie (1898 and 1911) showed the potential of different radioactive elements. Over the decades to follow, radioisotopes have been applied in various fields, including medicine and food industry. In this section, some of the most common applications of radioisotopes will be discussed.

2.4.3.1 Radiometric Dating

Radiometric dating is a technique used to date materials such as rocks or fossils, in which trace radioactive impurities were selectively incorporated when these materials were formed. The method compares the abundance of a naturally occurring “parent” radioactive isotope within the material to the abundance of its decay products (“daughter isotopes”), arriving at a known constant rate of the decay process.

Today, there are more than 40 different radiometric dating techniques based on different parent-daughter isotope pairs (each with a different half-life) that are useful for dating various geological materials and samples of biological origins. The relative amounts of the parent and daughter isotopes can be measured by different chemical and mass spectrometric techniques. Table 2.2 lists some of the most commonly used isotope pairs in radiometric dating.

Table 2.2 Naturally occurring radioactive isotopes commonly used in radiometric dating [67]

One of the most well-known examples is the dating using radioactive ¹⁴C (half-life of 5730 years) formed by nuclear reactions in the atmosphere. The constantly produced ¹⁴C reacts with oxygen, leading to the formation of ¹⁴CO₂. This radioactive form of carbon dioxide is absorbed by plants via photosynthesis and will eventually become incorporated into all living organisms through the food chain. Once an organism dies, its metabolism stops, halting the incorporation of ¹⁴C. Therefore, by knowing the characteristic half-life and the ratio of ¹⁴C to the total carbon content, the age of the sample can be determined. The same principle applies to dating with the potassium-argon pair, which is commonly used to estimate the age of rocks, volcanic layers around fossils, and artifacts [68].

2.4.3.2 Sterilization by Gamma Irradiation

Sterilization is the complete killing or removal of all living organisms from a particular location or material. Several methods can be used to achieve sterilization, each with their own benefits and limitations. Irradiation with gamma rays (from a cobalt-60 or cesium-137 source, with a dose of around 15–25 kGy) is often used for the sterilization of medical products and pharmaceuticals, including implants, artificial joints, blood bags, and ointments. Sterilization by radiation has several benefits, the most important of which is that it can be used on heat-sensitive items that cannot be sterilized by other common methods such as autoclaving. It is also safer and cheaper because it can be done after the item is packaged. The sterile shelf life of the item is then practically indefinite provided that the seal is not broken. Indeed, it is estimated that irradiation technologies are used to sterilize almost half of the global supply of single-use medical products.

The use of gamma rays is, however, not strictly limited to the medical world. By irradiating food, we can significantly reduce their microbial burden, depending on the dose delivered. This prolongs the shelf life of the food in cases where microbial spoilage is the limiting factor. Some foods, e.g., herbs and spices, are irradiated at sufficient doses (5 kGy) to reduce the microbial counts by several orders of magnitude; such ingredients do not carry over spoilage or pathogenic microorganisms into the final product. It has also been shown that irradiation can delay the ripening of fruits or the sprouting of vegetables. Insect pests can be sterilized (be made incapable of proliferation) using irradiation at relatively low doses. The use of low-level irradiation can also be used as an alternative treatment to pesticides for fruits and vegetables that are considered hosts to a number of insect pests, including fruit flies and seed weevils. Food irradiation is currently permitted by over 50 countries, and the volume of food treated is estimated to exceed 500,000 metric tons annually worldwide [69].

2.4.3.3 Radioimmunoassays

Radioimmunoassays were first developed in the 1960s by Solomon Berson and Rosalyn Sussman Yalow for which they received the Nobel Prize in 1977. It was the first technique being able to determine hormone levels in blood. This type of in vitro assay can be used to measure the concentration of any antigen with very high sensitivity. To date, radioimmunoassays are among the most sensitive and specific laboratory tests employed by immunologists and other specialists. The general principle of an immunoassay is competition for binding to an antibody (Fig. 2.14). More specifically, the unlabeled antigen (sample) is incubated together with a fixed amount of the radiolabeled antigen and the antibody, resulting in competition between the unlabeled and labeled antigens for binding to the antibody. With increasing amounts of an unknown sample (unlabeled antigen), decreasing amounts of labeled antigen (tracer) will bind to the antigen [70]. The antibody–antigen complexes are separated from the free antigen by precipitation using a secondary antibody or chemical solutions. The antibody–antigen complexes are then measured in a scintillation counter. By running a set of standards, a standard curve is generated from which the concentration of the unknown sample can be calculated. The most commonly used radioisotopes for radioimmunoassays are iodine-125, iodine-131, and tritium (³H) [71] (Box 2.15).

Fig. 2.14

General principle of the radioimmunoassay (Created with BioRender)

Box 2.15 The Use of Radioisotopes

• Radioactive decay can be used as a natural clock to determine the age of different materials.

• The strong ionizing ability of gamma rays, along with their high penetration range, can be used for the killing or reduction of microorganisms in different items, ranging from medical to food products.

• The use of radioisotopes in immunoassays provides a very high level of sensitivity allowing the measurement of antigens in pictogram quantities.

2.4.3.4 Radionuclide Therapy

In radionuclide therapy (RNT), radioisotopes are administered to patients with cancer or other medical conditions. Particles emitted from the isotopes will deliver cytotoxic levels of radiation to target sites within the human body, resulting in destruction of the targeted tissue (Fig. 2.15).

Fig. 2.15

Schematic representation of the mechanism of action of radionuclide therapy. The blue line represents the path of ionizing radiation (Created with BioRender)

Three types of ionizing radiation can be used for radionuclide therapy (RTN), namely alpha and beta particles and Auger electrons (their most important characteristics are summarized in Fig. 2.16). The linear energy transfer (LET) and tissue particle range are the most important parameters to be considered for this type of therapy. Ideal therapeutic radionuclides have a short particle range so it only damages targeted tissue and a high LET so it deposits as much radiation as possible on its short path length. All of the above-listed particles fulfill these criteria to ensure lesion-specific damage.

Fig. 2.16

Schematic representation of the energy deposition of the ionizing radiation and tissue range of the different emission types used for targeted radionuclide therapy, being β⁻, α, and Auger electron emitters (Created with BioRender)

The major breakthrough for RNT was in 1946, when iodine-131 was first used for the treatment of thyroid cancer. In the following years, a large variety of other radionuclides were introduced for the treatment of different cancer types, palliation of bone pain due to metastases, and treatment of inflammatory processes such as rheumatoid arthritis [72]. This was followed by the development of the peptide receptor radionuclide therapy (PRRNT), utilizing low-molecular-weight radiolabeled peptides targeted at specific cell surface receptors which are very often upregulated on cancer cells. Lutathera^® (¹⁷⁷Lu-DOTA-TATE) was the first-in-class PRRNT drug to be formally approved (by the EMA in 2017 and the FDA in 2018) for the treatment of gastroenteropancreatic neuroendocrine tumors (GEP-NETs). The initial success of Lutathera^® led to the development of new radiopharmaceutical-based strategies for treating other cancer types. These include the PSMA-targeted radionuclide therapy for prostate cancer and radioimmunotherapy with nanobodies for glioblastoma (Table 2.3) (Box 2.16).

Table 2.3 Examples of radionuclides used for therapy (World Nuclear Association)

Box 2.16 Radionuclide Therapy

• In radionuclide therapy (RNT), radioisotopes are used to treat cancer or other medical conditions by administration of radiation sources to patients.

• Three types of radioisotopes can be used for RNT, namely alpha and beta particles and Auger electrons.

• The most important applications to date of RNT are iodine-131 for thyroid cancer, Lutathera^® for neuroendocrine tumors, and PSMA-targeted RNT for prostate cancer.

2.4.3.5 Clinical Diagnostics

Nuclear imaging techniques such as positron-emission tomography (PET) and single photon emission tomography (SPECT) are noninvasive procedures, which make use of radiolabeled probes to examine biological processes on the cellular or molecular levels in vivo. These techniques enable 3D visualization, quantification, and characterization of the target (enzyme, receptor, transporter, protein aggregates, etc.) under investigation [73]. For these purposes, the compounds are labeled with a radioisotope, with a fairly short half-life (T_1/2, min to days). Both PET and SPECT allow visualization and quantification of targets expressed in very low quantities (nano-to-femtomoles per milligram tissue) or detection of molecular aberrancies before phenotypical or morphological changes have occurred [74] (Fig. 2.17).

Fig. 2.17

Comparison of the SPECT (a) and PET (b) imaging techniques used for clinical diagnostic (adapted with permission of Hicks and Hofman, 2012) [75]

2.4.3.5.1 Single Photon Emission Tomography (SPECT)

SPECT makes use of the inherent decay properties of specific radionuclides, which decay with the emission of a photon (X-ray) (Hutton 2014).

The nuclides of choice are those which emit electromagnetic rays in the energy range of 100–200 keV. This is determined based on the absorption of the electromagnetic rays by the subject and the designated detector and is a trade-off between sensitivity and resolution. Low-energy rays are more easily absorbed by surrounding tissue (tissue not under investigation), leading to higher patient doses and less efficient detection. However, higher energy levels are not optimally detected (stopped) by the scintillation NaI crystals. Additionally, the half-life (T_1/2) of the radionuclide should be tailored to the conducted experiment.

A SPECT apparatus typically contains two cameras which rotate around the body of the patient and are focused on an area under investigation. The cameras contain a lead collimator to directionalize the incoming radiation. As such, only rays parallel to the holes of the collimator will reach the detector, and radiation coming from scatter or other tissues not under investigation will be absorbed less by the scintillation detector, leading to less interference in image reconstruction and in turn increase in the contrast and hence the resolution but decrease in the sensitivity significantly.

Compared to planar (2D) X-ray imaging, where the electromagnetic rays are projected on an imaging detector leading to reduced contrast of the tissue under investigation compared to the background, SPECT imaging provides a noninvasive 3D method to determine the accumulation of administered diagnostic radiopharmaceuticals [73]. The term tomography indicates the use of a combination of individual “slices” to generate a 3D image.

The most widely used SPECT radioisotope, ^99mTc, is metastable and decays via isomeric transition with emission of γ-rays of approximately 140 keV with a T_1/2 = 6 h. Further, ^99mTc is a radiometal that can be complexed by various chelators and can be incorporated into different ligands used in different investigations of a plethora of diseases (bone, heart, cancer, brain, liver). Another benefit of ^99mTc is the cost and the ease of acquirement via a ⁹⁹Mo/^99mTc generator.

Frequently clinically used radionuclides are depicted in Table 2.4.

Table 2.4 SPECT radionuclides [73, 76]

2.4.3.5.2 Positron-Emission Tomography (PET)

PET probes generally consist of a pharmaceutical vector molecule, which carries a coupled radionuclide to the target. Because of the radioactive decay, only a low mass amount of the tracer needs to be administered to the subject. As such, pharmaceutical or toxicological effects are avoided. The radioactive decay further enables highly sensitive detection of emitted γ-rays by a dedicated ring of detectors. PET allows to detect early molecular changes and follow-up of disease progression [74]. Typically, low atomic mass radioisotopes (C, N, O, F), with a rather short T_1/2 of minutes to hours, are coupled to the pharmaceutical vector. Additionally, these radioisotopes are commonly found in different small molecules and biomolecules, so they can be incorporated without changing the chemical structure of the compounds. Advances in radiolabeling techniques are continuously increasing the radiochemical and -pharmaceutical space, which allows for a more robust and quicker radiolabeling [77]. PET is increasingly used in the drug development stream, as it enables examination of pharmacodynamics, drug-target interaction, and dose occupancy [78].

Radionuclides with an excess of protons in their core will decay by conversion of a proton to a neutron with emission of a positron (β⁺, a positively charged electron) and a neutrino (ν, a quasi-massless particle) over which the decay energy is distributed to fulfill the quantum mechanical rule of conservation of energy and angular momentum. Based on the kinetic energy obtained from the decay, the β⁺ particle will travel a short distance (positron range, up to 0.5 cm for ¹⁸F, 1–2 cm for ¹¹C) and collides with an electron in the environment after which the masses of both are converted into energy in an annihilation event. Two γ-ray photons of 511 keV are emitted back-to-back over an angle of approximately 180°. These two γ-rays travel through the body and can be coincidentally detected by a ring of detectors (within a time interval of 10 ns), allowing to localize the imaginary “line of response” along which the annihilation event occurred. Many response lines can then be combined to determine the position of the PET radionuclide of which tissue concentrations can be derived. Compared to SPECT, thicker scintillation crystals are necessary to detect the higher γ-ray energy of 511 keV. These detectors typically consist of bismuth germanate (BGO) or lutetium oxyorthosilicate (LSO) and are more expensive compared to NaI crystals used in conventional SPECT and gamma counting. Hybrid imaging techniques such as PET/MRI and PET/CT allow a combination of morphological and functional imaging, where molecular and anatomical changes can be detected simultaneously with high accuracy. State-of-the-art PET technology research is investigating total-body PET with increased sensitivity (up to 40-fold) compared to normal PET scanners [79]. The worldwide workhorse of PET imaging is a radiolabeled glucose derivative, 2-[¹⁸F]fluoro-2-deoxy-d-glucose ([¹⁸F]FDG), which visualizes the glucose metabolism and is hence taken up and trapped in organs with extensive glucose metabolism such as brain and heart and aberrant growth. Because of this, [¹⁸F]FDG can be applied in the diagnostic imaging of cancer, inflammation, cardiology, and neurology [80]. [¹⁸F]FDG differs from glucose by the replacement of the hydroxyl moiety by ¹⁸F at C-2. This has consequences for the metabolization process of [¹⁸F]FDG and is depicted in Fig. 2.18. Both glucose and [¹⁸F]FDG are taken up by glucose transporters (Glut) and processed by glycolysis. Hexokinase will phosphorylate the C-6 OH-moiety of both molecules. As this brings a negative charge to the molecules, they will remain trapped inside the cell. Glucose is then further processed to fructose-6-phosphate by glucose-6-phosphate isomerase on the C-2 OH-moiety, and further metabolization will yield pyruvate. As [¹⁸F]FDG lacks the C-2 OH-moiety, further metabolization will not take place and the molecule will remain trapped in the cell until decay (T_1/2 = 109.7 min) of ¹⁸F to ¹⁸O, after which metabolization can resume.

Fig. 2.18

Metabolization of glucose and its radioactive analogue [¹⁸F]FDG (Created with BioRender)

PET radiopharmaceutical development has been favored over investigation into SPECT tracers over the last years. PET omits the use of mechanical collimation, replacing it with electronic collimation, increasing detector efficiency 100-fold compared to SPECT. The spatial resolution of PET is also higher with less influence of scattered photons. Attenuation correction is more efficient, and the imaging contrast is also better compared to SPECT [81]. A disadvantage of PET is the cost and the availability of PET radioisotopes, which need to be generated in a cyclotron (except for ⁶⁸Ga, which is generator based). Furthermore, the short T_1/2 of routinely used PET isotopes (carbon-11, fluorine-18, nitrogen-13, oxygen-15) requires production by an in-house cyclotron [82, 83].

Typical radionuclides, used for PET imaging, are listed in Table 2.5 (Box 2.17).

Table 2.5 PET radionuclides (Vermeulen et al. 2019)

Box 2.17 SPECT and PET

• SPECT and PET are noninvasive imaging techniques that allow to functionally diagnose different pathologies, including cancer, neurodegenerative diseases, and cardiovascular aberrations.

• SPECT and PET make use of radiolabeled drugs to specifically target aberrantly expressed receptors, enzymes, etc.

• SPECT makes use of the inherent γ- or X-ray decay of the used radioisotope, whereas the PET principle is based on the coincidental detection of the emission of 511 keV γ-rays, resulting from the annihilation of a β⁺ and an electron.

• The most frequently used SPECT radioisotope is ^99mTc, which can be incorporated in a plethora of vector molecules.

• The most widely used PET radiotracer is [¹⁸F]FDG, a radioactive glucose analogue.

2.5 Doses, Dose Rates, and Units in Radiation Protection

2.5.1 Dose and Absorbed Dose

Dose or absorbed dose is the mean energy imparted by ionizing radiation to a material.

Absorbed dose = dE/dm

where dE is the mean energy imparted by ionizing radiation and dm is the mass of the material.

The SI unit of dose is gray (Gy) and is defined as absorbed energy per unit of mass of tissue, given by one joule per kg. The old unit is rad, and the conversion is defined as 1 Gy = 100 rad [84].

2.5.2 Dose Rate

Dose rate is defined as the dose of ionizing radiation absorbed or delivered per unit time. It is measured in gray per hour.

The biological effect of a certain dose is dependent on its dose rate, known as the dose rate effect. The biologic effect of a given dose is reduced if the exposure time is extended, and so if the dose rate is lowered. This is due to repair of sublethal damage that occurs during long radiation exposure. It is also due to redistribution of cells in cell cycle and cell proliferation (see Chap. 5 for details).

On the contrary, inverse dose rate effect is observed when increased biologic effects of a given dose at lowering the dose rate occur. This only happens at a limited range of dose rates. This is attributed to progression of cells through the cell cycle and accumulation in the G2 cell cycle phase, which is a radiosensitive phase. Further lowering of the dose rate below this critical level leads to lowering of biologic effects as cells cross the G2 block and divide, leading to cell proliferation.

Importantly, dose rate reduction has a differential effect between most tumors or early-responding normal tissues and late-responding normal tissues. Late-responding normal tissues are more sensitive to dose rate changes, like changes in fraction size in external beam radiotherapy [85].

The dose rate of environmental exposure is low (around 0.1 μGy/min). Clinically, the concept of dose rate is utilized in brachytherapy. Accordingly, there are different categories such as

• 1. Ultralow dose rate (ULDR)—less than 0.4 Gy/h

• 2. Low dose rate (LDR)—0.4–2Gy/h

• 3. Medium dose rate (MDR)—2–12 Gy/h

• 4. High dose rate (HDR)—more than 12 Gy/h

Low-dose-rate irradiation can be considered as an extreme form of fractionation.

There is another entity called pulsed dose rate (PDR), which is used in brachytherapy. Dose and treatment time are prescribed for LDR, but radiation is delivered in a pulsed manner every 1–4 h in many small fractions. Contrastingly, in FLASH radiotherapy, an ultrahigh dose rate of more than 1,44,000 Gy/h is administered [86].

The biological effect will be explained in Chaps. 5 and 6 (Box 2.18).

Box 2.18 Definition of Dose and Dose Rate

• Dose or absorbed dose is the mean energy imparted by ionizing radiation to a material. The SI unit of dose is gray (Gy).

• Dose rate is defined as a dose of ionizing radiation absorbed or delivered per unit time. The SI unit of dose rate is gray/hour.

2.5.3 Units of Radiation Protection

2.5.3.1 Equivalent Dose

The interaction of radiation with matter or tissue is also influenced by the type of radiation. Some types of radiation produce different effects than others for the same amount of energy. This is because the pattern of dose distribution and the density of ionization events will be different. To account for these variations when describing human biological harm from radiation exposure, the “equivalent dose” is used. For example, for equal absorbed doses, neutrons may be 20 times as damaging as X-rays. The equivalent dose is the product of the absorbed dose averaged over the tissue or organ and the radiation weighting factor W_R particular for the type and energy of radiation involved. It is based on the absorbed dose to an organ, adjusted to account for the effectiveness of the type of radiation [85, 87]:

$$ {H}_T={w}_R{D}_T. $$

(2.32)

The SI unit of equivalent dose is sievert (Sv). The unit “rem” (roentgen equivalent in man) is also still used. One rem is equivalent to 0.01 Sv.

The radiation weighting factors recommended by the ICRP are shown in Table 2.6.

Table 2.6 Radiation weighting factors (ICRP 103)

If a mixture of radiation types is used, the equivalent dose is the sum of the individual doses of the various types of radiation, each multiplied by the corresponding weighting factor:

$$ {H}_T=\sum {w}_R{D}_T. $$

(2.33)

2.5.3.2 Effective Dose

The effective dose is the addition of equivalent doses to all organs, each adjusted to account for the sensitivity of the organ to radiation. If a body is uniformly exposed to radiation, the probability of biological effects is assumed to be proportional to the equivalent dose. However, various tissues react to ionizing radiation in different ways and have different sensitivity to radiation. The ICRP has introduced the tissue weighting factor (W_T), which represents the relative contribution of each tissue or organ to the total damage or “effect” resulting from uniform irradiation of the whole body [85, 87, 88] (Table 2.7).

Table 2.7 Tissue weighting factors (ICRP 103)

The effective dose is the product of the equivalent dose and the tissue weighting factor:

$$ E=\sum {w}_T{H}_T. $$

(2.34)

The SI unit of effective dose is sievert (Sv).

Despite differences in the sensitivity of tissue due to age and sex of the person, for the purpose of radiation protection, the values for tissue weighting factors are taken as constants and are applicable to the average population. The effective dose is a calculated quantity and not a physical, measurable quantity.

The effective dose is used to compare radiation exposure and risks between different radiation types and exposure modes and a total body exposure. According to the ICRP Publication 103, effective dose is to be used for “prospective dose assessment for planning and optimization in radiological protection, and retrospective demonstration of compliance for regulatory purposes.”

Annual dose limits for occupational and public exposure are given in terms of the annual effective dose.

2.5.3.3 Committed Equivalent Dose

In case of external irradiation, the absorbed dose is delivered at the time of exposure. In the case of internal irradiation, when radionuclides are taken into the body, the total absorbed dose is distributed over time as well as to different tissues in the body. The dose rate falls depending on the half-lives of the radionuclides. The committed equivalent dose considers the varying time distributions of dose delivery. The committed equivalent dose is calculated as the integral over 50 years of the equivalent dose in each tissue after intake of a radionuclide [85, 87].

2.5.3.4 Committed Effective Dose

This is the sum of the committed equivalent dose to the individual tissues or organs multiplied by their respective W_T.

2.5.3.5 Collective Equivalent Dose

The radiation doses discussed above relate to exposures of individuals. The collective equivalent dose is used to measure the total impact of a radiation exposure to a group or population. The collective equivalent dose is the product of the average equivalent dose to a population and the number of persons exposed. It is measured in man-sievert (man-Sv).

2.5.3.6 Collective Effective Dose

The collective effective dose allows a rough estimation of the potential health risks to a population after exposure to radiation. It is the product of the average effective dose to a population and the number of persons exposed. It is measured in man-sievert (man-Sv).

2.5.3.7 Collective Committed Effective Dose

If a population is exposed to internal exposure by radionuclides, the integral of the effective dose over 50 years is called the collective committed effective dose. It is measured in man-sievert (man-Sv) (Box 2.19).

Box 2.19 Definition of Units in Radiation Protection

• The effective dose is the product of the equivalent dose and the tissue weighting factor. The SI unit of effective dose is sievert (Sv).

• The equivalent dose is the product of the absorbed dose averaged over the tissue or organ and the radiation weighting factor W_R. The SI unit of equivalent dose is sievert (Sv).

2.6 Linear Energy Transfer and Relative Biological Effectiveness

2.6.1 Linear Energy Transfer

Ionizing radiation causes significant physical and chemical modifications, which eventually lead to biological effects in the exposed tissue. The amount of energy absorbed by the tissue (absorbed dose) and the rate at which such energy is deposited (dose rate and fractionation for clinical applications) play a critical role in determining the type and extent of the effects. However, other physical parameters can also affect the biological response. It is therefore necessary to introduce a radiation quality term to discriminate between different radiation types. Radiobiological data and models clearly point to the spatial distribution of energy deposition as a key radiation quality parameter. However, the stochastic nature of the interaction of radiation with matter prevents a comprehensive and unique description and measurements of the ionization patterns produced by the pathway of charged particles in matter. The alternative is, therefore, to define a suitable but inevitably incomplete characterization of radiation quality that will enable radiobiological predictions with sufficient accuracy.

The concept of linear energy transfer (LET), the amount of energy transferred per unit length, was introduced by Zirkle et al. [89] to account for the density of energy transfer occurring along the track of charged particles, including excitations and ionizations, until the particles reach the end of their range. LET values are generally reported in keV/μm. The symbol LET∞ (unrestricted LET) is used when all possible energy transfers are included, and also the energy deposition by particles that in principle exit the volume of interest. The LET∞ is numerically equivalent to electronic stopping power, i.e., the energy loss by the incoming particle (which may be a primary or a secondary particle) without any restrictions in energy and range. The formula for the electronic stopping power contains a negative sign as it is seen as the slowing force acting on charged particles, due to interaction with matter, resulting in loss of particle energy:

$$ S(E)=-\left(\mathrm{d}E/\mathrm{d}l\right)=-\mathrm{LET}\infty, $$

(2.35)

where S(E) is the stopping power, dl is the distance traversed by the particle, and dE is the mean energy loss due to collisions with energy transfers.

There is however a conceptual difference: the stopping power deals with the energy loss of the particle, while the LET∞ focuses on the energy deposition in the medium, and thus, the LET generally has an opposite sign. For large volumes, the electronic stopping and the LET∞ coincide (same absolute value), as for large volumes all the energy loss by the impacting particles is well likely deposited in the sample.

In radiobiology, the concept of “restricted LET” is mostly used. This is the locally transferred energy per unit length, with “locally” restricting to only the energy fraction, which leads to ionizations and/or excitations within the considered site. The remaining kinetic energy of particles leaving the site is excluded. This is particularly relevant for electrons since they may possess considerably long ranges. For example, for ions with E > 1000 MeV/μ, these electrons can have energies higher than 1 MeV. The lateral spread of the track is usually 100 s of nm, but for higher energies of the ions such as 1000 MeV/μ, this lateral spread can even be 1 cm.

According to the ICRU 1970, the linear energy transfer of charged particles in a medium is the quotient of dE by dl. Here, dE is less than some specified value Δ. The definition includes an energy cutoff rather than a range cutoff as this is of more practical use:

$$ {\mathrm{LET}}_{\Delta}={\left(\mathrm{d}E/\mathrm{d}l\right)}_{\Delta}. $$

(2.36)

It has become customary to specify a limit of energy deposition below which the deposition is considered to be local (energy restriction); 100 eV has been widely accepted, which corresponds to an electron range of about 5 nm. Electrons of longer ranges are called “δ electrons” or “δ rays.”

X-rays and gamma rays are considered low LET (sparsely ionizing) radiation types, while high-energetic protons, neutrons, and heavy charged particles are considered as high LET (densely ionizing) radiation. A proton can have high or low LET, depending on its energy. Although commonly high-energy protons have been considered low LET radiation, recently this has been questioned, starting a new “paradigm in radiation biology” [90]. For indirectly ionizing neutrons, LET refers to that of the secondary charged particles they produce. The value which is generally considered to mark the distinction between low and high LET is about 10 keV/μm.

As ionizing particles decelerate along their track, the LET decreases, leading to a LET distribution, and consequently two different LET average concepts can be defined. The “track average LET” is calculated by performing a weighted average considering the proportion of the total track length that is within specified LET intervals and assigning equal statistical weight to each unit of the track length. On the other hand, the “dose average LET” is a weighted average of the LET values taking into account the proportion of the energy that is deposited for each LET interval so equal statistical weight is assigned to each unit of the energy deposition. In the first approximation, the dose-averaged LET is more suitable as the radiation quality factors are based on such quantity.

Apart from ionizations and excitations, among which ionizations bring the highest contribution to electronic stopping over a wide range of energies [91], other mechanisms cause energy loss of the impinging particle and thus induce deposited energy. At energies below some few keV/μm of the traveling ion, also nuclear collisions can occur. Such elastic nuclear collisions (described by the concept of nuclear stopping), which cause displacement of atoms, can induce alteration and breaking of bonds, and thus also contribute to biological damage. For particles with high energy, inelastic nuclear collisions, where the impacting particle causes fragmentation of the nuclei generating daughter nuclei with emission of several secondary particles, can also occur. These loss mechanisms are not described by the concept of stopping. A significant loss of primary beam fluence is caused by such nuclear reactions. The inelastic nuclear cross section determines the number of particles left at a certain depth. For instance, for protons hitting a water target with an energy of 160 MeV, at the Bragg peak position, approximately 20% of the incident protons will be lost [92].

The Bragg curve represents the energy loss, in this case electronic stopping or LET, as a function of the distance through a stopping medium. The energy loss is characterized primarily by the square of the nuclear charge, Z, and the inverse square of the projectile velocity, β. This gives the Bragg curve its familiar shape, peaking at very low energies (Bragg peak), just before the projectile stops (Fig. 2.19). The stopping of charged particles increases with decreasing ion energy; in particular, around the Bragg peak, the stopping (or the LET) is maximum, near the very end of the particle’s range. Ions of the same specific energy (energy per nucleon) have a similar range, typically on the order of 10 μm at ~1 MeV/μ up to 1 mm at ~100 MeV/μ [25].

Fig. 2.19

Dose and LET distribution for proton beams of various energy in water (simulated using TOPAS MC)

Sparse energy deposition events along the track of a particle per unit of energy deposited appear to be less biologically damaging than “dense” deposition. The value of the LET that seems “optimal” for cell killing is in the range of 100 keV/μm. This is linked to the fact that the average separation of ionization events at this LET is about the same as the diameter (2 nm) of the DNA double helix, implying a higher probability of DSB, from the passage of a single particle. Clusters of lesions in the DNA molecule play a key role in biological damage [93] (Box 2.20).

Box 2.20 Definition of LET

• LET is a parameter that quantifies the amount of transferred energy per unit length.

• LET is reported in units of keV/μm.

• LET increases with the ion mass and with decreasing ion energy.

2.6.2 From Microdosimetry to Nanodosimetry: Spatial Pattern of Ionization Events

There is an intrinsic relationship between the quantities in dosimetry, e.g., absorbed dose (see Sect. 2.5), linked to the electronic stopping power, and quantities at the microscale and down to the nanoscale.

The study of the pattern of energy deposition at micrometer length scale is called microdosimetry [94]. In particular, microdosimetry studies the fluctuations and pattern of energy deposition in a micrometer-sized target, providing a comprehensive view of the energy deposition more detailed than the one given just by the LET alone. The measured spectra are distributions of energy depositions in the microscopic volume, which are a combination of several stochastic processes including the LET distribution, the track length distribution, the energy loss straggling (statistical fluctuation of energy loss along the particle track) of the primary particles, and the transport of energy by δ-rays [95]. Microdosimetric quantities are stochastic and therefore given in terms of particle interaction probabilities [95, 96]. The relevant quantities in microdosimetry are as follows:

• y: the lineal energy, which is defined as the energy imparted to matter in the microscopic volume by a single event divided by the mean chord length in that volume and the mean length of randomly oriented chords in a given convex volume

• f (y): the probability distribution of linear energy

• $\underline {y_F}=\int_0^{\infty } yf(y)\mathrm{d}y$: the first moment of f (y), also called the frequency mean lineal energy

• dy = yf (y)/$\underline {y_F}$: the dose distribution, which is important for obtaining the dose components of the microdosimetric spectrum

• • $\underline {y_D}=\int_0^{\infty }y\mathrm{d}(y)\mathrm{d}y$: the first moment of d (y), also called the dose mean lineal energy

2.6.3 Induced Biological Effects Depend on LET

2.6.3.1 Definition of RBE

Relative biological effectiveness (RBE) is a method to quantify and compare the biological damage of different types of radiation [97]. The RBE is a dimensionless quantity and can be described as a radiation quality index with regard to biological damage. Quantitatively, RBE is the ratio between the absorbed dose of a reference radiation type and the absorbed dose of the radiation type of interest, such that both the absorbed doses compared produce the same amount of a biological effect, known as isoeffect. The reference radiation is defined as a low LET radiation. Previously, the standard radiation used was 250 keV of X-ray; however, nowadays, it is more common to use as standard 1 MeV photons (from a cobalt-60 source). This means that RBE is 1, when cobalt-60 biological effect is compared with itself.

RBE guides in the selection of the weighting factors, which are required to define the effective dose (E) (Sect. 2.5). RBE varies with several factors described in detail later, namely LET, radiation dose, fractionation, dose rate, biological system, endpoint measured, and radiation quality.

$$ RBE=\frac{\mathrm{Absorbed}\kern0.17em \mathrm{dose}\kern0.17em \mathrm{of}\kern0.17em \mathrm{the}\kern0.17em \mathrm{standard}\kern0.17em \mathrm{radiation}\kern0.17em \mathrm{needed}\kern0.17em \mathrm{for}\kern0.17em \mathrm{an}\kern0.17em \mathrm{isoeffect}\ }{\mathrm{Absorbed}\kern0.17em \mathrm{dose}\kern0.17em \mathrm{of}\kern0.17em \mathrm{the}\kern0.17em \mathrm{test}\kern0.17em \mathrm{radiation}\kern0.17em \mathrm{needed}\kern0.17em \mathrm{for}\kern0.17em \mathrm{an}\kern0.17em \mathrm{isoeffect}\kern0.5em }. $$

(2.37)

2.6.3.2 Efforts to Develop Radiation Quality Factors and RBE Models Based on Nanodosimetry

Over the past decades, radiobiology and nanodosimetry studies have pointed out that the characteristic spatial distribution of energy deposition at the subcellular scale induced by different particles at different speed is a key aspect at the origin of the RBE of different radiation qualities [91]. Localized clusters of energy deposition within the DNA molecule play a critical role. The frequency and topological distribution of clustered lesions determine the effectiveness of the DNA repair mechanisms. Isolated lesions are more efficiently repaired, while for complex lesions, errors are more likely to occur in the repair, often leading to permanent damage [98]. One of the main aims of the radiation community is to develop models for the radiation quality factors, the RBE and cell survival, which are consistent with nanodosimetry. Several efforts have been done recently to (a) develop biologically relevant quantities based on nanodosimetry [99], in order to overcome the simplistic description of the quality factor as a (continuous) function of the sole LET; (b) develop new quality factors incorporating a formula that relates to densely and sparsely ionizing components of the radiation tracks and core track contributions and penumbra contributions [13]; (c) develop an RBE based on a radiation quality descriptor depending on energy deposition clustering [100]; (d) develop a cell damage/survival model based on the interactions between lesions at both the nanometer and micrometer scale [101]; and (e) perform a detailed analysis of the radial distribution of ionization cluster size distribution [102].

2.6.3.3 Colony Survival Assay and α/β Ratio

Prediction of radiobiological response is a major challenge in radiotherapy. Survival curves allow to determine the radiosensitivity of a cell line to different types of radiation, as well as to compare the response of one different cell type to one type of radiation. The linear-quadratic (LQ) model has been best validated by experimental and clinical data and describes the surviving fraction (SF) of cells as a function of radiation dose D: SF (D) = e^{−α.D − βD2}. It allows determining important biological parameters such as the survival fraction or the ratio α/β, which represents the intrinsic radiosensitivity. Cells with a higher α and β are more sensitive to radiation. The shape of the curves depends on the LET. Indeed, cells irradiated with the same dose of different LET induce different biological effects translated into different cell survivals. As the LET increases, the slope of the curve becomes steeper and straighter with less shoulder. This indicates a higher ratio of lethal to potentially lethal lesions or a less efficient repair of the high LET radiation damage. For the LQ representation, this is shown by a higher α/β ratio for high LET radiation. However, the lower the α/β ratio is (high β relative to α), the more curved the clonogenic curve is.

2.6.3.4 Limitations of the LET Concept

Although the LET is a common and useful parameter to quantify the distribution of absorbed radiation energy, there are considerable limitations, which need to be considered. The limitations in terms of using the LET for predicting biological effects are strongly related to the RBE models and have been discussed in previous sections. There are also caveats of more physical nature. In particular, LET measurements are complex, difficult to relate to clinical or radiobiological setups, and affected by several constraints particularly if LET distributions are to be reported rather than single LET values. Direct measurements of dE/dl can be attempted with very thin particle detectors (such that multiple interactions within the active volume rarely occur) with high-energy resolution and able to discriminate between secondary particles and photons. In this case, the energy loss (ΔE) by a particle passing through is related to the thickness of the detector (Δl). Ideally, detectors with different thickness would be employed and the energy detected plotted against the detector thickness from which the slope at the origin is extrapolated. The density of the sensitive material of the detector should also be considered to convert the measurements into water. This provides an estimation of the stopping power and therefore the LET∞. The development of several Monte Carlo-based codes has offered the possibility to quickly calculate LET values taking also into consideration the specific experimental settings.

The definition of the LET concept also implies that an average LET value may not always be adequate to describe the radiation quality to which biological samples are exposed. As mentioned, the LET changes significantly along the path of an individual charged particle and it is affected by the specific irradiation setup including any scattering conditions. Single LET values are suitable for “track segment” experiments where thin biological samples are exposed to mono-energetic charged particle beams. Even under such conditions, however, the energy loss by a charged particle over a cellular distance fluctuates and it can occasionally reach extreme high or low values, which are not well accounted for in an averaging process. Also, the angular deflection and the lateral extension of the particle tracks due to the finite range of δ-rays are in principle not taken into account in the LET concept. The restricted LET, which only includes energy transfer below a specified cutoff, can actually partially take into account the second point. However, a set of LET distributions that belong to different cutoff values would be needed, but still little information about the actual structure of particle tracks would be gained [103]. A quantitative evaluation has shown that the LET concept is quite inadequate for electrons; there are no sites sufficiently small to disregard the finite range of the electrons and simultaneously sufficiently large to disregard the lateral escape of δ-rays and the energy loss straggling [103].

Contrarily, for heavy ions, there are site sizes and particle energies for which the LET predicts adequately the energy deposition. LET increases approximately as the square of the ion charge, Z, and the inverse square of its velocity, v. On the other hand, the maximum range of the δ-ray electrons depends on the velocity of the particle but not its charge. Thus, the consideration of the sole LET of a particle is not sufficient for a description of the particle’s track structure, as two particles of identical LET but very different velocity and charge will have very different track structures [104].

2.6.4 Relative Biological Effectiveness Depends on Many Factors

2.6.4.1 LET

RBE increases as LET increases, up to a maximum LET value of about 100 keV/μm, and then decreases as LET increases (Fig. 2.20—RBE and LET) [97]. In general, high LET radiations allow the deposition of a given amount of energy over a shorter distance, being more efficient in producing biological effects than low LET radiations. In other words, low LET radiation creates sparse ionization, requiring more than one radiation track to pass through the cell and induce lethal biological damage, while high LET radiation is more effective, since one radiation track through the cell is enough to induce lethal biological damage. However, over 100 keV/μm, there are many “wasted” ionizations due to the very high ionization densities (number of ions per unit of path length). This phenomenon is the so-called overkilling and reflects the RBE declining for further increases in LET, for which biological effect is reduced since most of the energy is wasted.

Fig. 2.20

RBE variation with LET. RBE increases as LET increases, up to a maximum LET value of about 100 keV/μm. An “overkilling” effect is observed for higher LET values (Created with BioRender)

2.6.4.2 Radiation Dose

When determining RBE, it is important to understand that RBE values also depend on the radiation dose and, consequently, on the isoeffect level chosen for the comparison between radiation types [97]. For small radiation doses, RBE is particularly variable tending to increase. This is explained by the fact that at low doses, the difference in the biological damage induced by low and high LET radiation is huge; that is, high LET radiation is very effective in killing cells, while low LET radiation is ineffective in doing so. For high radiation doses, the difference between the effects induced by low and high LET radiation becomes smaller, considering that low LET radiation becomes more lethal. At very high doses, the RBE no longer depends on the dose.

2.6.4.3 Fractionation and LET

The shape of the cell survival curve determines the presence or absence of a fractionation effect. With repeated daily low-dose X-ray fractions, the shoulder curvature is repeated, and cell survival is increased relative to a single high-dose radiation fraction at equal total dose. As mentioned previously, the bending of the cell survival curve is described by the α/β ratio parameter of the LQ model equation. The principle of fractionation is the repeat of the shoulder of the cell survival curve. The broader the shoulder, the lower the α/β ratio and the higher the cell survival in fractionated irradiation, i.e., the higher the sparing effect. In other words, the straighter the curve is, the less the fractionation effect is. The cell survival curve of high LET irradiation such as alpha particles is a straight line (e.g., Fig. 2.22); hence, the effect of fractionation is lost. Fractionation of carbon ions does not influence its biological effectiveness.

The same effect is seen when the dose per fraction is reduced in vivo. While low LET X-ray irradiation shows—related to the α/β ratio of the LQ model—sparing effect with multiple low dose fractions, high LET irradiation does not show such typical fractionation sparing effect, as illustrated in Fig. 2.21 [105]. Figure 2.21 (left) shows large sparing, and thus an increased tolerance to low LET irradiation, for late-responding normal tissues (with a low α/β ratio such as the spinal cord and kidney) with decreasing dose per fraction, while early-responding normal tissues (e.g., jejunum) and tumors (e.g., fibrosarcoma), both characterized with a high α/β ratio in the LQ model, are marginally spared. With high LET neutron irradiation, very little normal tissue sparing of fractionation has been demonstrated (Fig. 2.21, right), neither for early-responding normal tissues and tumors nor for late-responding normal tissues. The current view is to use at least two high LET fractions to obtain some sparing and benefit from reoxygenation, but multiple fractions would not be further beneficial [106] (Box 2.21).

Fig. 2.21

Isoeffect curves as a function of total dose and the number of fractions for low LET X-rays or gamma rays (left) and high LET neutrons (right). See insert for explanation of symbols and curves. [Redrawn from Withers et al. [105] with permission]

Box 2.21 Fractionation and LET

• The higher the LET, the straighter the radiation–cell survival relationship, and the lower the sensitivity to dose fractionation.

• The RBE of high LET irradiation decreases with increasing dose or dose per fraction for both cells and tissues.

• Little normal tissue sparing after fractionated high LET irradiation: Few fractions are sufficient.

2.6.4.4 The Dose Rate

The dose rate is defined as the ratio of the radiation dose [Gy] to the duration of the radiation exposure [hour]. The spectrum of dose rates used in radiation oncology is broad: from low dose rate (LDR < 2 Gy/h) to ultrahigh dose rate (FLASH, >144.000 Gy/h). The dose rate of radiation exposure largely determines its RBE. Lowering the dose rate reduces the effectiveness of radiation in many ways. In terms of the 6 Rs of radiobiology, the dose rate affects the induction and repair of DNA damage and related clonogenic cell survival, cell cycle (re-)distribution and activation of cell cycle checkpoints, and cell repopulation and reoxygenation and likely influences the immune response as well. For a particular equal biological effect, a biological endpoint, lowering the dose rate relative to a reference radiation quality (usually high-dose-rate 250 keV X-rays), the RBE decreases (Fig. 2.22). The dose rate effect could also be defined with the dose reduction factor (DRF), also termed the dose recovery factor. The DRF indicates the ratio of the radiation dose to achieve an equal biological effect at specified dose rate and the dose at high dose rate. The term DRF is used by analogy with the dose enhancement factor or sensitizer enhancement ratio, to quantify a change toward steeper cell survival curves. With increasing dose rate, the DRF value is >1.

Fig. 2.22

Effects of the dose rate on clonogenic cell survival for a human melanoma cell line irradiated at dose rates of 1.6, 7.6, and 150 cGy/min. At equal biological effectiveness, e.g., 0.01 cell survival (broken line), high-dose-rate irradiation has larger relative biological effect than low-dose irradiation, resulting in a dose reduction of approximately 5 Gy, i.e., a DRF of 1.6 (12.8/7.7). Dotted lines: (A) no repair; (B) condition of full repair at infinitely low dose rate. (Figure adapted from Steel [107], with permission)

The increase in biological effectiveness with increasing dose rate applies to all tissues and organs and, importantly, discriminates between early-responding tumors and normal tissues and late-responding normal tissues. In late-responding normal tissues, characterized by a low α/β ratio of the LQ model, the increase of dose rate is more detrimental than for tumors and early-responding normal tissues with a high α/β ratio. Literature data show that, at ultrahigh dose rate in FLASH radiotherapy, this differential effect could be inverted [108]. This inverse effect could be explained by the oxygen depletion hypothesis, the DNA damage hypothesis, and the immune response hypothesis.

Box 2.22 Definition of Dose Rate and Dose Rate Effect

• Dose rate: radiation dose delivery per unit time (e.g., Gy/hour)

• Dose rate effect: decrease in biological effectiveness with decreasing dose rate

2.6.4.5 Biological System and Endpoints Measured

During the last decades, many tissues and cells were characterized by survival curves in response to different types of radiation, especially X-rays. They underlined a great variation of the RBE for all the biological systems studied. Indeed, large variable shoulder regions were observed in response to X-rays, whereas less variation was observed with neutrons, explaining that the RBE is different for each cell line. In response to heavy ions, the depth of the irradiation has also to be considered and explains in part the different RBE calculated for one cell line compared with X-rays.

While the physical and dosimetric aspects of radiobiology are well understood, the biological aspects such as the complex biological endpoints induced need further attention. The current estimates of RBE listed above depend on the biological system, but also depend on the detection methods used as it has been demonstrated that DNA damage and the resulting apoptotic responses vary greatly depending on the radiation quality in a tissue- and dose-dependent manner. Experimental data emerging from recent studies suggest that, for several endpoints of clinical relevance, the biological response is differentially modulated by particles compared to photons. However, up to date, only few studies have been performed to understand the differential response on the molecular and cellular levels between different radiation qualities.

2.6.4.6 Radiation Quality (Type of Radiation): Relation to Space

The biological effects of ionizing radiation relate strongly to the dose, dose rate, and quality of the radiation. To distinguish the different types of radiation, from low LET to high LET particle radiation, the quality factor Q (L) has been introduced. This factor reflects all cumulative knowledge on the dependence of the detrimental effects of radiation on physical characteristics and mainly LET (ionization density). Therefore, this factor can be used to multiply the absorbed dose (rad or gray) to obtain a quantity that expresses, on a common scale for all ionizing radiations, the biological damage (rem or sievert) to the exposed tissue. Although Q (L) has been superseded by the radiation weighting factor W_R in the definition of equivalent dose, it is still being used in calculating the operational dose equivalent quantities used for example in monitoring [109].

In order to encompass the dependence of biological effects to LET, many studies have been performed in order to measure RBE for a specific biological endpoint (usually reproductive cell death) for radiations of different LET [110]. In most cases, survival curves are evaluated assuming a linear-quadratic dose dependence of the induction of reproductive death of cells. The linear term accounts for damage from single particle tracks and the quadratic term for damage due to interaction of lesions from independent tracks. Although for many years 250 kVp X-ray was considered the standard reference radiation for the determination of RBE, the International Commission on Radiation Protection (ICRP) recommended in their 92nd report to use gamma rays of ⁶⁰Co as the reference radiation [111]. In both cases of low LET radiation, RBE is assumed to be equal to 1.0. When specific biological effects of high LET radiation (such as fast neutrons) on human cells are measured, the RBE ranges from about 3 to greater than 100 for various biological effects.

2.6.5 Oxygen Enhancement Ratio and LET

The oxygen effect is an important parameter in radiation therapy. Its influence on the tissue’s biological response (typically survival curves) will differ according to the radiation type used. This concept is represented by the oxygen enhancement ratio (OER).

The OER is a measure of the influence of the oxygen effect. It is defined as the ratio of radiation doses that produce the same biological effect in hypoxic compared to aerobic (well-oxygenated) conditions:

$$ OER=\frac{\mathrm{dose}\kern0.17em \mathrm{that}\kern0.17em \mathrm{produces}\;\mathrm{a}\;\mathrm{given}\kern0.17em \mathrm{biological}\kern0.17em \mathrm{response}\kern0.17em \mathrm{under}\kern0.17em \mathrm{hypoxic}\kern0.17em \mathrm{conditions}}{\mathrm{dose}\kern0.17em \mathrm{that}\kern0.17em \mathrm{produces}\kern0.17em \mathrm{the}\kern0.17em \mathrm{same}\kern0.17em \mathrm{biological}\kern0.17em \mathrm{response}\kern0.17em \mathrm{under}\kern0.17em \mathrm{aerobic}\kern0.17em \mathrm{conditions}} $$

The OER varies with the LET (ionization density) (Fig. 2.23). The OER decreases as the LET increases and approaches OER = 1 at LET ≈ 150 keV/μm, meaning that the level of oxygenation has little or no influence on the cell survival in case of high LET radiation (α particles, neutrons, and heavily charged particles). This is explained by the fact that high LET radiation mostly induces direct damage, which is not oxygen dependent. Therefore, high LET radiation is expected to lead to a better tumor control of hypoxic tumors compared to low LET radiation.

Fig. 2.23

OER as a function of LET (Created with BioRender)

It should be noted that these OER values were originally derived from in vitro experiments. Recently, the oxygen effect during carbon ion therapy was questioned due to low LET values in the spread-out Bragg peak, giving rise to a possible impact of oxygen on carbon ion treatment outcome [112]. In case of low LET radiation (X- and γ-rays, electrons), the OER increases and is in the range of 2.5–3.5, meaning that a 2.5–3.5 times higher dose is needed to achieve the same killing effect in hypoxic cells compared to normoxic cells. Indirect effects, relying on reactive oxygen species (ROS) production, are the dominant process associated with low LET radiation and explain the importance of oxygen for low LET radiation. Hypoxic regions within a tumor may therefore show radioresistance to low LET radiation. The OER has an intermediate value for neutrons. Based on this concept, a massive work on oxygen-based radiosensitization is being done and is discussed in Chap. 5.

2.7 Deterministic and Stochastic Effects

2.7.1 Introduction

The damage caused by ionizing radiation in the body can become clinically apparent as a number of different health effects. The type and severity of the effect are strongly dependent on dose and exposure conditions, but also on the health status of the exposed individual. For radiation protection purposes, and to ensure the safe use of radiation in society, the health effects of ionizing radiation exposure are classified into two types [113]:

Deterministic effects, which are also called tissue reactions, are those for which there is a defined threshold below which the effect is not expected to occur. In addition, the severity of the effect increases with dose. The acute radiation syndromes are examples of early effects following high doses. However, deterministic effects are not a synonym for acute effects, as some, e.g., fibrosis, can occur much later.

Stochastic effects have no threshold, and the occurrence of the effect is probabilistic, such that any exposure to ionizing radiation increases the risk of these effects. The severity of the effect is not related to the dose. Stochastic effects tend to manifest many years postexposure and include cancer and heritable effects.

2.7.2 Deterministic Effects or Tissue Reactions

2.7.2.1 Mechanisms of High-Dose Effects

High-dose penetrating radiation causes damage both to functional tissues and to stem cell compartments. In general, maintenance of health depends on a balance between loss and replacement of cells in many, but not all, organs and tissues of the body, reflecting physiological “wear and tear.”

Cellular damage is known to occur after exposing tissues to ionizing radiation. If the number of cells damaged is small relative to the total number of stem cells in the tissue, then the remaining stem cells can repopulate adequate numbers of functional cells. Consequently, there will be no obvious loss of tissue function. Conversely, if the stem cell population is reduced below a critical size, the tissue will cease to function efficiently, either transiently or permanently.

Organs and tissues differ in their sensitivity to radiation (Chap. 7), and the damage from radiation particularly affects the more radiosensitive cells, for example the lymphocytes in the lymphatic tissue, red bone marrow precursor cells, and crypt cells in the mucosal lining of the gastrointestinal tract.

Whether or not recovery will be possible will strongly depend upon the rate at which viable stem cells (that is, those cells undamaged or repaired) can repopulate the depleted stem cell population by self-renewal. The whole process of recovery is dependent upon feedback mechanisms stimulated by the body’s recognition of depleted functional cell numbers. Following exposure of a large proportion of or all of the body, the normal steady state of cellular regeneration for tissues throughout the body is interrupted: cells and tissues break down and cannot be replaced. This is the basis for the observed threshold for such deterministic effects or tissue reactions.

It is, however, very important to note that there is a variation in sensitivity among individuals in an exposed population with any particular dose and exposure scenario. This variation reflects differences in the ability of individuals to cope with radiation-induced cellular damage, which is influenced by the age and state of health of the individual at the time of irradiation [85].

2.7.2.2 Radiation Syndromes

When individuals are exposed to sufficiently high doses of acute, penetrating ionizing radiation, the acute radiation syndrome begins with the prodromal phase [114, 115]. Following this, there will be a latent period, which represents the time period between initial exposure and manifestation of full acute radiation syndrome (ARS) due to a lack of cell renewal, as described above. The severity of the initial prodromal effects, the time for their development, the timing and any symptoms experienced during the latent period, and the type and severity of the full manifestation of ARS are all dependent on the dose and exposure scenario. This is described in more detail in Fig. 2.24 (Box 2.23).

Fig. 2.24

Radiation syndrome phases (Created with BioRender)

Box 2.23 Symptoms of Exposure to Radiation

• The clinical signs and symptoms of high-dose radiation exposure are observed up to ~6 days after exposure (with a high degree of uncertainty). These come as soon as a few minutes after a very high dose.

• The symptoms of deterministic effects are dependent on dose (deterministic), with increased symptoms associated with higher doses.

• In general, individuals exhibit flu-like symptoms, vomiting, diarrhea, and headache. For doses in the region of:

  • 1–2 Gy, these are classified as “mild,” and we would expect 10–50% people vomiting, and others experiencing fatigue and weakness.

  • 2–4 Gy, these are classified as “moderate,” following which 70–90% people would be constantly vomiting, 2–6 h after exposure; 50% people would have a headache; 10–80% people would have a slight increase in body temperature.

  • 4–8 Gy, these are “severe,” following which ~100% of people would be vomiting <1 h after exposure; 50–80% people would have a headache; most others would have a constant fever <1 h after exposure; some people might lose consciousness or feel confused; 10% of individuals would have diarrhea 1–8 h after exposure.

  • 8 Gy, these are “very severe/lethal” (depending on the medical resources available); most people lose consciousness fairly quickly; temperature peak at about 41 °C is usually observed, and many patients would present with skin burns at these doses.

Following these initial signs and symptoms, for doses less than approximately 6 Gy, the latency period is generally fairly asymptomatic, and individuals usually start to feel a little better. Then, unless radiation has been identified as the cause of the observed prodromal symptoms, often nothing is done, because the symptoms can be mistaken for those of many other non-radiation-related illnesses. However, if ionizing radiation has been identified as a potential cause, differential white blood cell counts should be taken as a marker of the potential severity of the effects. A summary of the different types of ARS is given in Fig. 2.25.

Fig. 2.25

The dominant syndromes leading to death vary with dose and time postexposure. Therapy is possible for doses lower than approximately 8–10 Gy (depending on medical resources) (Created with BioRender)

2.7.2.2.1 Hematopoietic Effects

Following exposures greater than around 2 Gy, and with this syndrome dominating up to around 10 Gy, the fall in blood cell counts may result in death from septicemia or hemorrhage, due to bone marrow failure, unless the symptoms can be treated. When the bone marrow is acutely exposed to radiation, this causes hypoplasia, aplasia, and/or hemolysis of cells. This leads to a sudden and dose-dependent reduction in the stem cell population, and ultimately atrophy of the lymph nodes and spleen. Differentiating and maturing cells may initially be only marginally affected. Depletion of cellular components of blood leads to infection and hemorrhage.

The stem cell population may attempt to recover and, if successful, increasing numbers of granulocytes will appear in the blood about 3 weeks after exposure. Loss and recovery of blood platelet cell numbers follow a similar dose- and time-related pattern.

The severity of the radiation effect can be estimated based on differential white blood cell counts (neutrophils and lymphocytes). If neutrophil and lymphocyte levels are measured repeatedly following initial exposure (the half-life of circulating neutrophils is only about 6–8 h), this can give an indication of the likely severity of the ARS or other tissue effects: A large initial peak of neutrophils and a rapid drop-off could indicate a dose ~>5 Gy.

2.7.2.2.2 Gastrointestinal Effects

The mucosal crypt stem cells provide the protective mucosal cell lining of the intestinal tract wall. Due to the high turnover of these cells, particularly in the small intestine, damage to these cells results in a denudation of the gut surface as the epithelial cells are not replenished, within 5–10 days after exposure of the gastrointestinal tract to doses of radiation >1 Gy. Leakage of blood from damaged blood vessels into the gut then occurs, and blood appears in the feces. Simultaneously, translocation of normally harmless intestinal bacteria from the gut through the damaged blood vessels occurs, leading to infection. Once in the blood, these bacteria become pathogenic. Symptoms include severe bloody diarrhea, anemia, severe electrolyte disturbances, malnutrition, and sepsis.

This gastrointestinal syndrome is seen in individuals who have received acute doses to the gastrointestinal tract in excess of about 8–10 Gy.

2.7.2.2.3 Cerebrovascular Effects

With the traditional paradigm of the dependence of severity of response on cell turnover, it was thought for a long time that the effects in the brain, beyond direct cell killing, were minimal. However, we now know that ionizing radiation can otherwise affect the way the brain functions, e.g., through changes in mediation of substance release.

For doses to the brain >~15 Gy, swelling (edema) of the brain, cerebral death (breakdown of the nerve impulse pathways), and generalized shock lead to coma and death. At such high doses, this happens very quickly, with loss of consciousness followed by death within a few hours or days at most, before the wider systemic prodromal reaction can start.

At lower doses, the regulatory functions of the central nervous system (CNS) within the body are affected—either through vascular injury or through changes in how various neurotransmitters are released or by affecting the functioning of the brain itself. After whole-body exposure, the prodromal symptoms in the case of brain effects can also be detected as abnormalities on an electroencephalogram (EEG). This “neurovascular syndrome” tends to manifest around 10 Gy, and the vascular changes lead to hypertension, dizziness, confusion, impaired cognitive function, and neurological deficit later on. For cerebrovascular (and cardiovascular) effects, the assumed threshold is approximately 0.5 Gy.

It should be noted that multiple-organ dysfunction syndrome (MODS) can also occur—this is a clinical syndrome with the development of progressive and potentially reversible physiological dysfunction in two or more organs or organ systems induced by a variety of acute insults, like ionizing radiation.

2.7.2.3 Systemic and Late Effects

2.7.2.3.1 Pulmonary Effects

Cell proliferation is generally slower in the lung than in the hematopoietic or gastrointestinal systems; however, in the weeks and months following initial exposure, pulmonary effects may lead to death due to massive respiratory failure. Damage to the cells lining the alveoli may result in acute inflammation of the lungs (pneumonitis) at doses in the range of 5–15 Gy. This leads to pulmonary edema, which can result in adult respiratory distress syndrome and secondary bacterial and viral pneumonia. Pulmonary failure then occurs due to fibrosis as a direct result of the radiation itself or as a result of infection, between around 6 months and 2 years or more postexposure.

2.7.2.3.2 Local Radiation Injury

Local radiation injury (LRI) may be defined as a setting of signs and symptoms following local overexposure to ionizing radiation of the skin. Although sometimes called cutaneous radiation syndrome, this term applies better to skin manifestations in the context of ARS.

Skin injuries caused by the high initial dose occur initially as burning, itching, and acute pain coupled with very painful primary erythema (reddening of the skin). This is usually followed by edema, accumulation of fluid in the skin as a result of tissue damage. Cutaneous syndrome is usually characterized by a fairly short latency phase, but if edema occurs within a few hours, this will usually result in very severe ARS. After a few days, hair loss occurs and the skin starts to break down leading to ulceration and necrosis—tissue death occurs. Bacteria may use this as an entrance to the body ultimately followed by sepsis. Skin transplantation or amputation may be needed. As a late effect, telangiectasia and secondary erythema (and associated pain) can be very long lasting.

2.7.2.3.3 Fetal Effects

Evidence of the deterministic effects of radiation on the embryo and fetus is derived almost entirely from animal experiments. Extrapolation of the results of these studies can be used to predict the consequences of radiation exposure in humans.

The effects on the embryo depend on the time of exposure relative to its development. When the number of cells in the embryo is small (i.e., in the first 6 days of pregnancy) and the cells are not yet specialized, damage is frequently seen in animals as failure of the embryo to implant in the wall of the uterus. In humans, the only manifestation of this would be a late or missed menstrual period. However, evidence from in vitro human embryo research has shown that the survival of even one cell in the early embryo before implantation can allow normal development, since all the necessary genetic components are present in each cell of the embryo at this stage of development. The consequences of any of these cells carrying a point mutation are unknown, but the possibility of stochastic (genetic, heritable) effects occurring cannot be excluded.

Because of the lack of direct human evidence, it is useful to look in brief at the animal data. The data taken from animal experiments suggest that threshold doses in humans for radiological protection purposes are in the order of 0.05 Gy for reabsorption of preimplantation embryos; 0.05 Gy for minor skeletal abnormalities; 0.20 Gy for impaired fertility in the female; 0.2 Gy for functional disorders of the central nervous system; and between 0.20 and 0.50 Gy for serious skeletal abnormalities and growth retardation. Such information provides a basis for guidelines to ensure that pregnant women are adequately protected.

Brain development has been particularly well studied in animals. It is when neurons (the information-conducting cells in the brain) are developing and when they are migrating to their predetermined sites in the cerebral cortex that irradiation is most damaging. In humans, this corresponds to between 8 and 25 weeks postconception. Only a very small amount of human data exists. For example, data were published in 1984 from a relatively small study on intellectual disability in children exposed in utero following the atomic bombs dropped on Hiroshima and Nagasaki in 1945.

Intellectual disability is associated particularly with irradiation between the 8th and 15th weeks following conception. From these data, it has been estimated that the excess probability is about 40% per Gy; that is, at a dose of 1 Gy, 40 out of every 100 children exposed would be expected to experience severe intellectual disability. This compares with a background frequency of 0.8%. It is less marked between the 16th and 25th weeks, and no effect has been seen at other times of pregnancy.

The uncertainties at each measured dose point are extremely wide, because of the small numbers. Thus, the presence or absence of a threshold for developmental effects remains highly uncertain. However, school performance and IQ scores have been measured for children irradiated in utero, with a decrease of approximately 30 points at 1 Gy for children irradiated in the 8th to 15th week of pregnancy (but not before or after) [116].

2.7.2.3.4 Other Effects

A variety of additional effects can occur, but of particular note, ionizing radiation can also cause nephropathy, which is reduced renal function, leading to progressive scarring kidneys and ultimately failure months to years following exposure.

Other tissue effects may be seen many years postradiation exposure, for example cataract, which has an assumed threshold of approximately 0.5 Gy but which for low dose likely has a very long latency period. This topic is further considered in Chap. 8.

2.7.2.4 Dose-Response

The probability of detecting tissue reactions, characterized by loss of tissue function, in healthy individuals following exposure to radiation is non-existing in some tissues at doses of up to a few hundred mGy. In other tissues, the threshold of detection is above a few thousands of mGy. Above the threshold, the probability of a tissue reaction increases steeply in a sigmoid manner, with the severity of effect increasing linearly with dose. It is important to note that protracting the dose will result in a lower frequency of effects and less severe symptoms at a given dose compared with acute exposure [113, 117].

The range of doses associated with death from these syndromes after acute exposure to low linear energy transfer (LET) radiations is given in Table 2.8.

Table 2.8 Range of doses associated with death after exposure to low LET radiations

In an exposed population, there is a chance of death of approximately 5% of the population (5 persons dying in a population of 100) exposed to about 2 Gy or of about 50% without medical treatment (lethal dose, LD₅₀) within the dose range of 3–4 Gy. Most individuals would be expected to die at doses between about 6 Gy and 10 Gy, unless they receive treatment to prevent infection and bleeding. Above about 10 Gy, death is very likely, even after attempts to stimulate the bone marrow or bone marrow transfusion from a suitable donor. The risk of death thus also depends on the number of exposed individuals, and the available expertise and facilities for appropriate treatment, as discussed further in Chap. 7.

2.7.2.5 Mortality or Morbidity

High exposures do not always prove fatal, especially if the irradiation is nonuniform so that sufficient vital bone marrow stem cells are spared. Recent advances in immunology and in the administration of growth factors or cytokines to accidentally irradiated persons may rescue the bone marrow so that the hematopoietic syndrome might no longer be the limiting lethal condition. Matched stem cell transplantation is an alternative, provided that such stem cells are available at short notice. Death would then depend on whether damage to the lungs or intestine was sufficient to cause fatal pneumonitis or breakdown of the gut wall.

Table 2.9 shows proposed values of the LD₅₀ and/or ED₅₀ and 1% thresholds for a selection of the most important conditions of ARS (Table 2.10).

Table 2.9 Parameters for acute mortality (various sources including ICRP, 2007)

Table 2.10 Parameters for acute morbidity (various sources including ICRP, 2007)

2.7.3 Stochastic Effects

2.7.3.1 Cancer

Cancer develops in tissues through the accumulation of various mutations over several conceptual stages [118]. Initiation of the process can occur following exposure to various environmental agents including radiation, but further changes in neoplastic development require a complex interaction between various factors in the host and environment. For this reason, it is not possible to attribute causal relationships between a particular environmental agent (in this case, radiation exposure) and cancer in individuals [119]. Instead, attribution is made for increased cancer incidence in an exposed population over a known baseline rate either pre-exposure or in a nonexposed population. This attribution is expressed through risk estimates.

Present risk estimates for cancer following radiation exposure are based on a number of epidemiological studies, most notably the Life Span Study (LSS) of the Japanese atomic bomb survivors. The study is a gold standard against which the results of other studies on long-term radiation effect on humans are evaluated. In the latest analysis of mortality patterns between 1950 and 2003 [120] of the 50,234 deceased cohort members with dosimetric measurement data, there were 10,929 deaths from solid cancers and 695 deaths from hematological malignancies. Of these, 527 (4.8%) solid cancer deaths can be attributed to radiation exposure from the bomb in 1945. A dose-dependent increase in the rate of solid cancer deaths can be observed (Table 2.11).

Table 2.11 Observed and excess death from solid cancer and non-cancer diseases (adapted from Ozasa et al. 2012)

In the analysis of solid cancer incidence among the LSS population between 1958 and 2009 [53], the latest follow-up data of a cohort of 105,444 people who were alive without known history of cancer was presented. For a person exposed at age 30, the excess relative risk (ERR) for any cancer by the age of 70 was estimated to be 0.50 per Gy without adjusting for smoking. The dose-response was linear with an estimated ERR of 0.64 per Gy for females, but for males, a linear quadratic fit was observed instead, with ERR of 0.20 per Gy at 1 Gy and 0.010 per Gy at 0.1 Gy (Fig. 2.26).

Fig. 2.26

Smoking effects on solid cancer baseline rates. (a) Smoking ERR as a function of attained age for males (black curves) and females (gray curves). The solid curves represent lifelong smokers, while the dashed curves represent past smokers from the age at which they quit (shown are male past smokers quitting at age 50 years and female past smokers quitting at age 55 years). (b) Total smoking risk for current smokers, past smokers, and those who never smoked (thin solid curves) for males and females. The curves represent typical smoking histories. Male smokers started at age 20 years and smoked 20 cigarettes per day, while female smokers started at 30 years and smoked 10 cigarettes per day (reproduced with permission from Grant et al. © 2017 Radiation Research Society) [53]

At the moment, 0.1 Gy is the lowest dose for which the overall cancer risk from radiation exposure can be reliably estimated. Uncertainties from various factors such as limited statistical power, dosimetric uncertainties, and confounders begin to grow increasingly large and mask any possible effects in lower dose ranges or site-specific risk estimation. Unless properly addressed, these uncertainties distort the results and lead to erroneous estimation of risk [119].

2.7.3.2 Heritable Effects

Together with radiation-induced cancers, the hereditary effects of radiation are stochastic effects. By comparison with cancer, induced hereditary diseases are considered to be a minor component of the total stochastic disease risk due to radiation exposure of an individual or of the population generally.

There is little direct human evidence of hereditary effects; however, it is clear that ionizing radiation can cause mutations of the types seen in hereditary effects.

Multifactorial diseases are an additional class of effect, which combine heritable aspects in addition to influence from environmental factors. These include congenital abnormalities present at birth or chronic conditions, which appear later in life (Box 2.24).

Box 2.24 Classes of Mendelian Type Gene Mutations

There are three classes of Mendelian-type gene mutations , where genes are inherited from each parent:

• (a) Dominant conditions, where even in the heterozygote (a person inheriting one mutant and one normal gene), the abnormality is seen in the individual. Their effects in the homozygote (double dose of the mutant gene) are usually more severe, if not lethal. An example of a dominant gene condition is Huntington’s chorea (HC), which is characterized by nerve cell damage and changes in physical, emotional, and mental state. HC is caused by a faulty gene on chromosome 4.

• (b) Recessive conditions, which have an effect only when present in the homozygote (two genes with the same, disease-linked, mutation). Recessive disorders are usually rare, as the mutation would need to be inherited from both parents. However, some recessive genes even when present in a single dose, i.e., heterozygote accompanied by a dominant normal gene, do still confer slight deleterious effects. An example of a recessive gene disorder is cystic fibrosis, which is caused by mutations on a gene located on chromosome 7.

• (c) Sex-linked conditions, which involve genes located on the X chromosome. A large proportion of mutations that are inherited are related to the X chromosome. Since there is only one X chromosome in males, mutant genes here act as dominant genes in males who suffer, whereas they are masked in the female with two X chromosomes who act as carriers. Mutations in these genes will exert their effect in females only when present in homozygotes and therefore appear as a recessive condition. Half the male offspring of a carrier mother will suffer and half her female offspring will be carriers. Examples of sex-linked conditions are color-blindness and hemophilia.

2.8 Low-Dose Radiation Effects

2.8.1 What Is a “Low Dose”?

A low dose of irradiation can be defined as acute and chronic. An acute low dose is defined as less than 0.1 Gy (100 mGy), while a chronic low dose is defined as less than 6 mGy/h (or Sv equivalent). In this low-dose range, there are a variety of phenomena that dominate the dose-response relationship and lead to nonlinear and unpredictable outcomes.

2.8.1.1 What Are the Effects of a “Low Dose”?

A key finding in low-dose radiobiology is that the effects seen are not directly proportional to the dose received. Rather, there are a number of factors such as genetic background, age, gender, and lifestyle, which can modify the outcome. After higher doses, DNA strand breaks are the predominant cause of radiation effects, and these are more directly related to dose deposited in the tissue or cells. Figure 2.27 depicts the usual dose-response relationship with the low-dose region shown as of uncertain outcome. The expanded section shows the variety of factors and outcomes which can be expected.

Fig. 2.27

Usual dose-response relationship with the low-dose region shown as of uncertain outcome. (Figure from Kugathasan and Mothersill, 2022 [121])

2.8.1.2 What Are the Mechanisms Involved?

Mechanisms involved in non-targeted effects are described in Sect. 2.8.2, and low-dose hypersensitivity, hormesis, and adaptive response mechanisms are described in Chap. 3. Global mechanisms underlying LDR are mentioned here and include production of oxidative stress, mitochondrial and membrane channel changes, signaling to neighboring cells, release of exosomes carrying modified cargos, and changes in the proteome. It is important to recognize that these changes may be proactive damage responses and not harmful per se. Change does not necessarily equate with harm.

2.8.2 Targeted Effects

It is quite common that while a high dose/amount/rate of some medication or procedure is detrimental, a low dose is beneficial. Classical well-known examples include physical exercise (as opposed to forced labor), immunization (as opposed to virulent infection), and—directly related to biologically active radiation—controlled sun tanning (as opposed to sunburns and skin cancer caused by overexposure). Therefore, low-dose radiation effects may well be different from the effects of high doses. Actually, people have been using ionizing radiation for centuries: already, Herodotus and Hippocrates described healing properties of what we now know as radon springs. Radon treatment is considered to be a legitimate tool by mainstream medicine in Europe, especially for treating arthritis and other inflammatory diseases [122]. During the past four decades approximately, there has been a growing body of biological evidence regarding low-dose radiation effects. This evidence is concurrent with the shift in radiobiology from a DNA-centric view on radiation damage to a more systemic view that incorporates multi-level protection and nonlinear systems—adaptive response [123].

2.8.2.1 Adaptive Response

There is emerging evidence that low doses induce cellular and intercellular changes, which can lead to adaptive metabolic alterations. Adaptive responses against accumulation of damage—also of non-radiogenic origin—were also discovered [124]. Many studies demonstrated that radiation effects are far from linear [125]. Moreover, experimental, epidemiological, and ecological studies have shown that low doses of ionizing radiation can be beneficial to health [126, 127].

2.8.2.2 Hormesis

Beneficial low-dose effects of an agent that is harmful in high doses are called hormesis. Back in 1884, Hugo Schulz observed that low doses of many toxic agents, mercury and formaldehyde for example, enhanced the vitality of yeast cells. The term “hormesis” was introduced by John Ehrlich (also in the context of chemical toxicity) in 1942 [128]. The term “hormesis” is applied now to any kind of biphasic dose-response, i.e., when low doses of some agent are beneficial while higher doses are detrimental [128]. Physical exercise (as opposed to hard labor) is a typical example of hormetic response. According to the present knowledge, “hormetins”—agents inducing hormesis—include but are not limited to heat and oxidative stress, various food components, micronutrients, intermittent fasting, calorie restriction, etc. [129]. Radiation hormesis is the most thoroughly investigated among all hormesis-like phenomena.

Speaking about radiation hormesis, we should point out two somewhat different uses of the terms “hormesis” and “low dose.” Since radiation carcinogenesis is often considered as the single most important health hazard of ionizing radiation, radiation hormesis is usually understood in the narrow sense that low radiation doses may suppress cancer. In this narrow sense, curing arthritis or pneumonia is not viewed as a hormetic effect. Accordingly, there are two quite different meanings of the term “low dose.” In the context of radiation protection and many fields of radiobiology, “low dose” is understood to be 100 mGy or less as defined above. However, in the field of radiation therapy, the daily dose fraction is typically 2000 mGy and 6 weeks of therapy amounts to a total dose of 60,000 mGy—hence a single 1000 mGy dose to treat pneumonia may be regarded as a low dose [130].

2.8.2.3 HRS/IRR

Low-dose hyper-radiosensitivity (HRS) and induced radioresistance (IRR) describe a type of survival curve which has a dose range usually below 500 mGy acute dose, where the dose-response is significantly more radiosensitive than the overall fit to the higher dose points would suggest (see Fig. 2.28). The phenomenon is seen in a large variety of both tumor and normal cell lines and has been detected in human skin from patients [131]. It is seen following acute and fractionated irradiation meaning that it is likely to be relevant for radiotherapy and diagnostic radiology/medical imaging. It was first described by Lambin et al. (1993) and Marples and Joiner (1993) [132, 133]. The HRS phenomenon results in a significant reduction of clonogenic cell survival, increase in chromosome breaks, micronuclei, unrepaired DSB, or gene mutations after a single low dose in the range of 100–800 mGy. The maximal HRS effect is generally obtained at 200 mGy and corresponds to a biological effect equivalent to a dose 5–10 times higher. The mechanism of HRS/IRR is discussed in Chap. 3 (Box 2.25).

Fig. 2.28

Low-dose hyper-radiosensitivity (HRS) can be observed in a typical survival curve. The dashed line represents the linear-quadratic (LQ) model, while the solid line shows the induced repair (IR) model

Box 2.25 Low Dose Effects of Radiation

Dominant mechanisms below 100 mGy

Direct effects:

Low-dose hypersensitivity: Increased sensitivity to low-dose radiation which is not apparent at doses above 0.5 Gy.

Adaptive response: The ability of a low first dose of radiation to “protect” against the effects of a subsequent high dose.

Hormesis: Beneficial effects seen after low-dose exposure compared to unirradiated controls.

Non-targeted effects:

Bystander effects: One of the non-targeted effects defined as radiation-like effects seen in cells which did not get any energy deposition but which received signals from irradiated cells.

Genomic instability: Detection of non-clonal chromosomal damage or other DNA changes in distant progeny of cells which are genetically normal in the first postirradiation mitosis.

Lethal mutations: A form of genomic instability, detected as a permanently reduced plating efficiency of progeny cells which survived irradiation.

2.8.3 Non-targeted Effects

Non-DNA-targeted effects (NTE) refer to effects in cells, tissues, organs, or individuals which have not themselves received any radiation energy deposition but are in receipt of signals from irradiated entities. They include bystander effects, abscopal effects, clastogenic effects, genomic instability, and lethal mutations. Sometimes, adaptive responses and low-dose hypersensitivity are included as NTE, but although they can be induced by signaling in bystander cells, they are not strictly speaking NTE as they occur in directly exposed cells. Box 2.25 defines the terms. Box 2.25 shows the different effects observed in bystander cells and progeny cells compared to those seen in directly irradiated cells. The lists are the same showing that signaling can induce in bystanders most of the effects associated with low-dose direct radiation exposure. An NTE dose-response saturates in the low-dose region (Fig. 2.28). In general, increasing the dose beyond 0.5 Gy produces no additional NTE.

2.8.3.1 Bystander Effects

The United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR) defines bystander effect as a radiobiological effect that is transmitted from irradiated cells to neighboring unirradiated cells, generating biological alterations in the receiver cells that can influence the radiation-associated cancer risk [134]. As a communicative effect, bystander effects occur mainly at the primary site over a few millimeters or cellular diameters. This effect is mediated by the secretion of soluble factors or by signaling through gap junctions as well as through networks involving inflammatory cells of the microenvironment [135].

The term radiation-induced bystander effect (RIBE) is described as the ability of irradiated cells to transport manifestations of damage to other cells which were not directly targeted by irradiation. An irradiated cell sends out signals and induces response in nonirradiated neighboring cells. The intensity of the bystander response in nonirradiated cells is not necessarily proportional to the dose delivered to the irradiated cells and can occur even at low doses. The RIBE is highly dependent on the cell tissues concerned and the irradiation sources (such as radiation doses, LET, dose rates) and can influence the nature of the bystander factors secreted by irradiated cells, the intensity of the bystander response in nonirradiated cells, and the timing of the events in the bystander signaling [136]. This amplification can cause similar radiation-induced effects in cells not directly exposed to radiation and exhibit the heritable changes that include cellular damage, DNA damage, mutations, chromosomal aberrations, chromosomal instability, senescence, apoptosis, genomic instability, micronucleation, oncogenic transformations, etc. [136,137,139].

Some RIBEs can have deleterious effects, which involve the type of cell inducing the bystander signal after irradiation and the type of cells receiving these signals. Such effects can be determined by intercellular communication and level of amplification of original consequences of the event. Knowledge of the mechanism(s) by which non-targeted bystander effects are activated is still in its infancy and not well understood; however, it is believed that multiple pathways are involved in this phenomenon and also different cell types respond differently to bystander signaling.

RIBE is believed to be an incredibly complex phenomenon considering the involvement of sheer number of proteins, inorganic molecules, and cofactors. This effect encompasses a number of distinct signal-mediated effects (Figs. 2.29 and 2.30). Lately, communication of bystander signals between adjacent cells connected by gap junctions has been studied extensively. Signaling molecules are propagated through direct intercellular communication via gap junctions or through diffusible secretion in the surrounding environment of irradiated and bystander cells. Exosomes and signaling mRNAs also play a potential role in mediating bystander effect [140]. Exosomes can be released by bystander cells exposed to radiation-induced UV biophoton signals [141, 142], while miRNAs have a pivotal role in intercellular signaling between irradiated and bystander cells [143]. ROS and secondary messengers (such as nitric oxide), protein kinase, as well as cytokines (such as TGF-β and TNF-𝛼) are also considered to be involved in RIBE. Additionally, irradiated dying cells (predominantly from apoptotic rather than necrotic cells) release cell-free chromatin (cfCh) particles, which can integrate into genomes of surrounding healthy cells to induce extensive genomic instability (DNA damage) and inflammation [144]. In the absence of macrophages, cfCh shows direct involvement in the activation of H2AX by bystander cells. The bystander effect can be observed in different cell types with different endpoints.

Fig. 2.29

Probable players driving the non-targeted effects of radiation

Fig. 2.30

Factors involved in RIBE (created with BioRender)

2.8.3.2 Abscopal Effects on Normal Tissues

The term abscopal or out-of-field effect is an in vivo phenomenon in normal tissue that describes the occurrence of radiation-like damage in organs that have never been irritated. In other words, abscopal effects are bystander effects in vivo. Abscopal effects are known to occur after exposure to high or low doses of ionizing radiation in vivo and are often observed after high doses of targeted partial-body radiotherapy [145, 146]. The mediation of the effect is attributed to systemic factors such as the blood or the endocrine system [136, 146,147,149]. The immune system is also thought to play an important role. Experiments show that high levels of macrophage activation and neutrophil infiltration in mice are a consequence of radiation-triggered recognition and elimination of apoptotic cells [150]. The abscopal effect on normal tissue differs conceptually from the abscopal effect on tumors, which is often described in radiation oncology. The abscopal effect on tumors refers exclusively to systemic antitumor immune responses induced by radiotherapy alone or in combination with immunotherapy to only part of the tumor load. These antitumor immune responses are capable of completely eliminating primary tumors and unirradiated metastases in patients. For more information about the abscopal effect on tumors, see Chap. 5.

2.8.3.3 Clastogenic Factors

Clastogenic factors (CFs), potential biomarkers of a prooxidant state, are composed of endogenous lipid peroxidation products, cytokines such as necrosis factor alpha, unusual nucleotides, and other oxidants with chromosome-damaging properties. They are frequently noticed in the plasma of patients exposed to radiation [151]. Subsequently, it has been shown that CFs are not specific for irradiated subjects (Table 2.12), but are found in a variety of pathological conditions accompanied by oxidative stress. In both conditions, they can be considered as biomarkers of oxidative stress [152] as well as risk factors for carcinogenesis.

Table 2.12 Clastogenic factors (irradiation)

2.8.3.3.1 Occurrence and Formation of CF

The non-targeted effect is a dynamic complex response of epigenetic dysfunctions, DNA damage, and cell death in nonirradiated tissues as consequences of secretion of clastogenic factors—“chromosome breakage factors” from irradiated cells. The formation of these breakage factors (CF) with their chromosome-damaging actions is mediated by the superoxide anion radicals, which are regularly inhibited by exogenous superoxide dismutase (SOD). These free radicals are an initiator of a series of events leading to formation of clastogenic materials. In vitro experiments provide strong evidence for the role of O₂ in those cells exposed to superoxide-generating systems, such as the xanthine–xanthine oxidase reaction, a phorbol 12-myristate-13 acetate (PMA)-stimulated photodynamic reaction. The supernatant of these cells contains CF, while cell-free systems do not lead to CF formation. Studies of CFs originating from observations on the plasma from irradiated persons were shown to induce chromosomal aberrations when co-cultured with cells from unexposed persons (Fig. 2.31). However, this phenomenon is common in a large number of health defects as well [153].

Fig. 2.31

Clastogenic factors (created with BioRender)

2.8.3.3.2 Possible Mechanisms of Action of CF

TNF-𝛼 and inosine triphosphate (ITP) stimulate the production of superoxide by monocytes and neutrophils. The lipid peroxidation product, 4-hydroxynonenal, inhibits superoxide production; however, it has the capacity to decrease the activity of DNA polymerases by inactivating their sulfhydryl groups leading to genotoxic effects. Formation of CF often damages/changes the chromatid structure; which indicates that they are not immediate and occur late in the S phase or in the G2 phase of cell cycle where they have duplicated their chromatids. These chromosome-damaging effects can be detected by classical cytogenetic techniques.

Ionizing irradiation is known to have mutagenic and carcinogenic potential for the exposed host as it induces chromosomal aberrations in directly exposed cells.

2.8.3.4 Genomic Instability

Genomic instability (GI) is a hallmark of cancer cells, which includes variations of increased frequencies of base pair mutation, microsatellite instability (MSI), and chromosome instability (CIN) [154]. GI is a complex multiple-gene event marked during the development of some but not all cancers and also induced effectively by ionizing radiation. Radiation can provoke cellular communications eliciting a cascade of cellular events, which results in the destabilized genome in irradiated as well as unirradiated (bystander) cells. Radiation-induced genomic instability (RIGI) is observed in the progeny of irradiated cells as a delayed and elevated stochastic appearance of de novo chromosomal aberrations, gene mutations, and reproductive cell death [137, 155]. The effects of instability occur at a stable rate and are persistent in the postirradiation survivors for many generations.

Radiation-induced bystander effects are also involved in RIGI [156] due to contribution of indirect (by stimulating the reactive intermediates over many generations) and delayed effects (delayed DNA breakage, delayed reactivation of p53, delayed induction of various phenotypes) to cellular outcomes after radiation exposure. More detailed molecular studies on RIGI can provide deep insights into radiation-induced carcinogenesis (Box 2.26).

Box 2.26 Genomic Instability

• Genomic instability (GI), a characteristic of most cancers, is a complex multigene event and is often expressed by the appearance of chromosome aberrations many generations later.

• Microsatellite instability or chromosomal instability due to mutations in DNA repair genes or mitotic checkpoint genes is the underlying basis for GI in hereditary cancers.

• In sporadic (non-hereditary) cancers, GI occurs at least at the early stages of cancer development.

2.8.3.4.1 Potential Causes of RIGI

Biological effects of IR-induced GI are transmitted over several generations after irradiation via the progeny of surviving cells with delayed phenotypic expression, but not uniformly. Delayed manifestations of induced GI include delayed cell death, chromosomal instability, and mutagenesis.

The incidence of GI is significantly higher than that of conventional gene mutation, which eventually induces delayed reproductive death or delayed lethal mutations and increases the frequency of giant cells, micronuclei, senescence-like growth arrest, apoptosis, or necrosis in the progeny of surviving cells [157], suggesting that one of the potential initiators of RIGI is delayed cell death.

Exposure to sparse LET or dense LET radiation produces non-clonal chromosome aberrations (NCCAs), a highly significant feature for delayed chromosomal instability, genome heterogeneity, and complexity, in clonal descendants or stem cells that result in transmission of chromosome-type and chromatid-type aberrations to their progeny after irradiation [158].

Radiation may induce a type of GI in cells which results in an increased rate of spontaneous mutation that persists for many generations of cells. Clonal populations of cells surviving radiation exposure indicate such instability in a fraction of irradiated cells, which can persist longer over generations. Subpopulation of genetically unstable cells may arise from irradiated cells with a high frequency of even featureless minisatellite mutations [159], signifying the delayed appearance of certain mutational events in the progeny of irradiated cells.

2.8.3.4.2 Mechanism of RIGI

The mechanism of perpetuation in progeny populations is thought not only to be epigenetic but also to involve an excess generation of ROS over the course of time, cell-to-cell gap junction communication, dead and dying cells in the unstable population, and/or secreted factors from unstable cells (Fig. 2.32).

Fig. 2.32

Mechanisms involved in radiation-induced genomic instability (Created with BioRender)

2.8.3.4.3 Initiation of RIGI

DNA-damaging agents (such as X-rays, IR, restriction endonuclease Hinfl), radiomimetic drugs (bleomycin and neocarzinostatin), DNA DSBs, and DNA damage at the site of their decay are considered as effective initiators of RIGI. In some cases, sufficiently small or powerful environmental cues can directly exert their impact upon a cell’s DNA, which is a critical target for RIGI. DNA strand breaks, the most lethal lesions induced by IR, activate a number of cellular DDR signaling cascades such as the activation of DNA damage-sensing and early transduction pathways, cell cycle arrest, and DNA repair. To a certain degree, it could convert the initial sites of DNA DSBs to unforeseen structures and results in reorganized chromatin domains and a disrupted genome structure, evident as a mutation induction. Generation of gross chromosomal rearrangements, or multiple intrachromosomal aberrations, or DNA damage signatures is accountable for the initiation of GI.

2.8.3.4.4 Perpetuation

RIGI is transmitted through many generations after irradiation, suggesting that the memory of unrepaired DNA damage can be perpetuated over time by a number of processes involving ROS, communication through cell-to-cell gap junction, unstable dying cell population, and/or secreted factors from unbalanced cells. RIGI appears to be independent of the p53 status of the irradiated cells, but a number of genetic factors influence the expression of the unstable phenotype.

Radiation-induced DNA DSBs could cause nonlethal, “potentially unstable chromosome regions (PUCR)” and altered chromatin architecture within the nucleus through DNA repair, which are transmissible through the progeny of surviving cells for many generations after irradiation [160]. Indeed, though PUCRs are potentially unstable, they are capable of persisting for prolonged periods through bridge-breakage-fusion (BBF) cycle [161] and thus could be the regions susceptible for causing delayed DNA breakages [162], inducing telomere instability and delayed cell death.

PUCRs can possibly be reactivated by large deletions or abnormal positioning of telomeres, loss of nuclear matrix-attachment regions (MARs), translocations of the chromosomes, distorted nucleosome, and altered nuclear architecture, leading to upregulating or silencing gene transcription, delayed p53 reactivation, and delayed manifestation of GI in the progeny of surviving cells (Table 2.13).

Table 2.13 PUCR effects

2.8.3.4.5 Induction of Delayed Effects

IR-induced DSB repair defects predominantly persuade various delayed phenotypes, indicating that delayed DNA damage is associated with delayed phenotypes. It is expected that delayed DNA damage arising in the progeny of surviving cells activates the uniquely sensitive tumor suppressor p53 protein, a multifunctional, highly regulated, and promoter-specific transcription factor. It is known to depend on the kinase ATM, which acts via the downstream kinases Chk2/hCds1 and mediates phosphorylation of various nuclear proteins, including p53. Stabilized and activated p53 protein transactivates a variety of downstream gene products, which direct either a prolonged cell cycle arrest in G1, senescence-like growth arrest or an apoptotic pathway.

RIGI enhances the accumulation of genomic alterations, resultant of delayed unscheduled DNA breakage, which triggers deferred activation of p53 in the progeny of irradiated cells; however, RIGI can be induced in all cell types regardless of the presence and status of a p53 function. Reactivated PUCRs and delayed DNA breakage are directly or indirectly involved in the delayed expression of instability phenotypes (Box 2.27).

Box 2.27 Radiation-Induced Genomic Instability

• Radiation-induced genomic instability (RIGI) is characterized by an elevated and persistent rate in the accumulation of de novo genetic alterations in the progeny of irradiated cells after the initial insult.

• Delayed manifestations, e.g., chromosomal instability, mutational events, and cell death, are the potential initiators of RIGI for multiple generations following irradiation or exposure to DNA-damaging agents.

• Unirradiated progeny cells display phenotypic changes due to RIGI at delayed times after radiation of the parental cells.

• Along with changes in DNA, epigenetic aberrations may be involved in RIGI, suggesting that epigenetics may also be the link to understand the initiation and perpetuation of GI.

2.9 Exercises and Self-Assessment

• Q1. As seen in the figure below, the difference between the attenuated radiation, i.e., the radiation lost from the beam, and the absorbed dose is much larger for the energies where the Compton process dominates. Can you explain this?

  

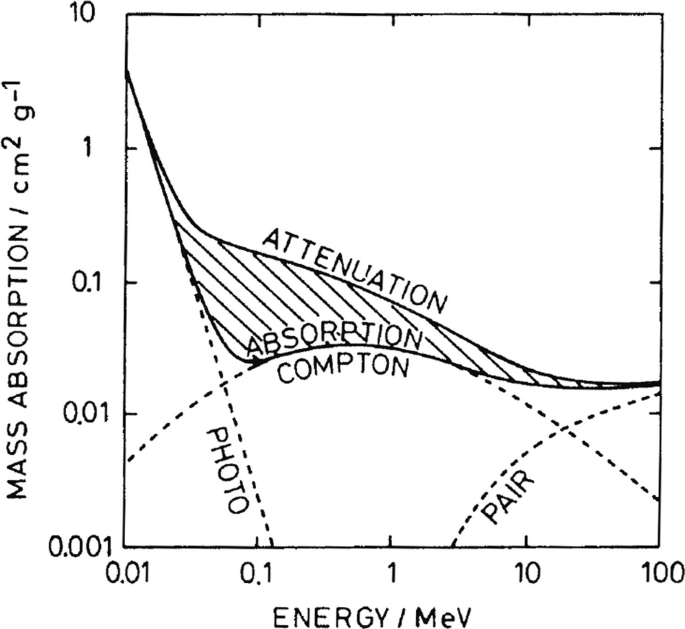
  Absorption and attenuation in water for photons with different energies [Figure from Kiefer, J. (1990). Biological radiation effects. Germany: Springer.]

• Q2. Can you tell why people living at high altitudes are more exposed to cosmic radiation? Can you tell which is the treatment at hospitals which is of most concern for radiation exposure?

• Q3. Which of the following is the most harmful to cells?

  • (a) H₂O₂

  • (b) H⋅

  • (c) OḤ

  • (d) e⁻_aq

• Q4. Name the four stages of indirect effects of ionizing radiation.

• Q5. Low LET radiation mostly induces direct effects: true or false?

• Q6. Fill in the missing items in the table (modes of radioactive decay).

  Mode of radioactive decay	Released particles	General reaction	Example
  α-Decay			92238U → 90234Th + 24He
  	Two fragment nuclei		100256Fm → 54140Xe + 46112Pd
  		ZAP → ZA − 1D + n0***	413Be → 412Be + n0***

• Q7. Describe the difference between the well-known periodic table and a chart of nuclides (chart of nuclides).

• Q8. The unit of effective dose is:

  • (a) Gy

  • (b) Sv

  • (c) Bq

  • (d) J

• Q9. The dose that takes into account both the quality of the radiation and the radiosensitivity of the tissue, and is thus a direct measure of the likelihood of developing cancer, is called:

  • (a) Absorbed dose

  • (b) Equivalent dose

  • (c) Effective dose

  • (d) Dose rate

• Q10. X-rays and beta particles have been given a radiation weighting factor of 1 because they produce:

  • (a) Virtually the same biological effect in tissue for equal absorbed doses

  • (b) No biological effect in tissues for equal absorbed doses

  • (c) Varying degrees of biological effect in body tissue for equal absorbed doses

  • (d) None of the answers above

• Q11. During flash radiotherapy, an ultralow dose rate is used. True or false?

• Q12. Arrange the following radiations in order of increasing LET in water:

  • (a) 5 MeV alpha particle

  • (b) 100 MeV carbon ion

  • (c) 10 MeV proton

  • (d) Cobalt-60 γ-rays

  • (e) 200 MeV iron ion

• Q13. Explain why high LET irradiation exerts a relatively larger RBE in the low-dose range.

• Q14. With decreasing dose rate, a discriminative biological effect can be obtained between late-responding normal tissues and tumors. Please explain.

• Q15. The consequences for human exposure to ionizing radiation can be classified into two categories—stochastic or deterministic effects/tissue reactions. Explain the reasoning behind this classification and describe the main features of these effects, giving examples.

2.10 Exercise Answers

• SQ1. The Compton process results in a secondary photon, which has its own track, and an electron, which may also have enough energy to move away from where the primary ionization took place. In both cases, some of the dose is deposited in a different position than where the energy was lost from the beam.

• SQ2. When going higher in altitude, the amount of atmosphere shielding us from incoming radiation is smaller than at the Earth’s surface. Thus, at higher altitudes, the “shielding” provided by the atmosphere against the incoming radiation from space is less efficient. Radionuclide-based treatments are the main concern in terms of radiation exposure at hospitals. There is the need to protect healthcare staff and to keep dose to caregivers and the public within the acceptable levels.

• SQ3. OḤ.

• SQ4. Physical, physicochemical, chemical, biological.

• SQ5. False.

  Mode of radioactive decay	Released particles	General reaction	Example
  α-Decay	Helium nucleus	ZAP → Z − 2A − 4P + 24He	92238U → 90234Th + 24He
  Spontaneous fission (SF)	Two fragment nuclei	ZAP → Z1A1D1 + Z2A2D2	100256Fm → 54140Xe + 46112Pd
  Neutron emission (NE)	Neutron	ZAP → ZA − 1D + n0***	413Be → 412Be + n0***

• SQ6. The periodic table organizes chemical elements by their respective atomic number, while a chart of nuclides organizes nuclides according to the number of protons (Y-axis) and neutrons (X-axis) present in the nucleus.

• SQ7. B.

• SQ8. C.

• SQ9. A.

• SQ10. False.

• SQ11. Cobalt-60 γ-rays (0.2 keV/μm) < 10 MeV proton (~5 keV/μm) < 5 MeV alpha particle (~100 keV/μm) < 100 MeV carbon ion (~200 keV/μm) < 200 MeV iron ion (>300 keV/μm).

• SQ12. The RBE is defined as the ratio of the high LET dose and the low LET reference dose (generally 250 kV X-rays) at isoeffect. The high LET dose-effect cell survival relation is a straight line over the full dose range. The low LET cell survival curve is however characterized by a broad shoulder in the low-dose range, followed by a straight, parallel steep downward curve in the higher dose range. Hence, the RBE in the low-dose range is higher than in the high-dose range.

• SQ13. Late-responding normal tissues (low alpha/beta ratio) are better spared than tumors and early-responding normal tissues (high alpha/beta ratio) by decreasing the dose rate. Lowering the dose rate can be considered as decreasing the “fraction size,” with larger sparing of late-responding normal tissues than of tumors, hence a therapeutic beneficial effect.

• SQ14. Deterministic effects or tissue reactions are those for which there is a threshold (varying between different effects), below which the effect is not seen. Above the threshold, the severity of the effect increases with dose. The syndromes of ARS are examples of deterministic effects.

  Stochastic effects are the probabilistic ones, for which there is no threshold—any increase in dose slightly increases the risk of the effect, and severity does not increase with increasing dose. Radiation cancers and genetic/hereditary effects are classified as stochastic effects.