Rotators and Snakes

Abstract

This lecture introduces various kinds of spin rotating devices used in present particle accelerators. They include Siberian Snakes used for polarization preservation and spin rotators used for creating a specific polarization orientation in experimental locations. Following the analysis of spin rotation in different types of magnets, approaches for designing spin rotating devices are discussed. Considerations for appropriate design choices of spin rotating devices in dependence on the beam energy are given. Examples of Snakes and spin rotators used in past accelerators as well as designs considered for future ones are presented.

This manuscript has been authored by Brookhaven Science Associates, LLC under Contract No. DE-SC0012704 with the U.S. Department of Energy. The United States Government and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes.

4.1 Spin Rotation Devices

When describing spin motion in a circular accelerator the central role belongs to periodical spin solution $\hat {\mathbf {n}}_{\mathbf {0}}$ on beam closed orbit:

$$\displaystyle \begin{aligned} \hat{\mathbf{n}}_{\mathbf{0}} (s) = \hat{\mathbf{n}}_{\mathbf{0}} (s+C) \end{aligned} $$

(4.1)

which is also called the stable spin direction. The importance of the vector $\hat {\mathbf {n}}_{\mathbf {0}} (s)$ comes from the fact that particle spin aligned along this vector repeats its direction on every turn. Particle spins not aligned with the vector $\hat {\mathbf {n}}_{\mathbf {0}}$ rotate around this vector, thus the spin projections on the vector $\hat {\mathbf {n}}_{\mathbf {0}}$ are preserved. This defines an observable beam polarization at a given location.

Let’s first consider a circular accelerator without any spin rotators. We assume that there is no magnet misalignments or magnet errors affecting the beam vertical orbit. Thus, the closed beam orbit is formed by vertical guiding field of dipole magnets and is in the horizontal plane everywhere. It is easy to see that in this case the periodical spin solution $\hat {\mathbf {n}}_{\mathbf {0}}$ is vertical at any ring azimuth s. And it remains vertical for any beam energy. Without betatron coupling the stable spin solution also remains vertical on a closed orbit for off-momentum particle, defined by the horizontal dispersion function. Obviously, this is very good case for controlling the polarization since one gets spin orientation at all energies parallel.

But often one needs to change the stable spin direction from vertical, which can be done by introducing non-vertical fields on the closed beam orbit in the accelerator. It affects the stable spin direction and makes it to deviate locally or globally from the vertical. Examples of such non-vertical fields are solenoid magnets having longitudinal field, or vertical bending magnets having a horizontal magnetic field. Various kinds of spin rotating devices utilizing non-vertical guiding fields are used in circular accelerators. They include:

• Siberian Snakes (or Full Snakes) which are used to prevent polarization loss when crossing spin resonances

• Partial Snakes which are used to improve the spin resonance crossing when Full Snakes are not feasible

• Spin Rotators around an experimental point to produce different from vertical beam polarization orientation at an experimental detector.

When working on design of a spin rotating device scientists and engineers become concerned with several design aspects. The spin rotating device should be compact in order to fit well into the accelerator lattice. It should produce sufficiently small orbit excursions. It also should have minimum effect on the beam optics and non-linear beam dynamics. Some of spin rotating devices have to operate in wide energy range.

In following description spin rotation matrices in the spinor presentation will be given for different types of magnets and spin rotating devices. We will use the spinor matrix form corresponding to right-handed convention for the spin rotation:

$$\displaystyle \begin{aligned} M = \exp[-i(\mathbf\sigma\cdot\mathbf b)\frac{\varphi}{2}] = I\cos{}(\varphi/2) - i (\mathbf\sigma\cdot\mathbf b)\sin{}(\varphi/2) \end{aligned} $$

(4.2)

where φ is the spin rotation angle around the rotation axis b (b is unit vector), and σ is a vector with components the Pauli matrices (Chap. 3).

4.2 Spin Rotation in Different Types of Accelerator Magnets

4.2.1 Spin Rotation in Solenoidal Field

First, we consider a solenoidal magnet which is a magnet with the longitudinally oriented magnetic field. In such magnet a particle which travels along the magnet axis preserves straight line trajectory. The spin rotates around longitudinal direction, hence the longitudinally oriented spin is preserved. The spin rotation angle around the longitudinal axis for a particle with the charge e, momentum p and anomalous magnetic moment G is defined by the field integral of solenoidal field:

$$\displaystyle \begin{aligned} \phi_{sp} = -(1+G)\frac{e}{p}\int B_{sol}\cdot ds \end{aligned} $$

(4.3)

If one would want to realize the spin rotation ϕ using the solenoidal magnet, the required field integral is:

$$\displaystyle \begin{aligned} B_{sol}\cdot L = \frac{\phi}{\pi} \frac{10.479}{1+G} p ({\mathrm{GeV}}/c) \end{aligned} $$

(4.4)

For 20 GeV/c protons (G = 1.79) to rotate spin by 180^∘ the field integral B_sol ⋅ L = 75.1 T⋅m is needed. For the electron beam (G = 0.00116)¹ having the same 20 GeV energy, the required field integral is considerably larger: B_sol ⋅ L = 209.3 T⋅m .

The major convenience of the spin rotator design based on solenoidal magnets is that the beam orbit is not distorted in this case. A disadvantage is that the field integral required for spin rotation is proportional to particle momentum. Thus, the use of these spin rotators is limited to the energies below 30 GeV.

The spinor transformation matrix for solenoidal field is written as:

$$\displaystyle \begin{aligned} M_{sol} = \cos{}(\phi_{sp}/2)-i\sigma_2 \sin{}(\phi_{sp}/2) \end{aligned} $$

(4.5)

4.2.2 Spin Rotation in Dipole Field

In a dipole magnet the magnetic field is orthogonal to the particle trajectory. The beam trajectory is curved. The spin equation becomes:

$$\displaystyle \begin{aligned} \frac{d\mathbf{S}}{ds} = -\frac{e (1+G\gamma)}{p}\; {\mathbf{B}}_{dip} \times \mathbf{S} \end{aligned} $$

(4.6)

The particle spin rotates around the magnetic field direction. But when considering the spin rotation angle resulting formulas depend on the coordinate frame. Often the laboratory frame, which has fixed orientation of coordinate axes, presents an appropriate coordinate frame for considering spin propagation. For instance, when considering a spin rotator with the particle orbit restored at the end of the rotator the laboratory frame is more convenient choice for design consideration. Resulting spin rotation angle in the laboratory frame can be written as:

$$\displaystyle \begin{aligned} \phi_{sp} = -(1+G\gamma)\frac{e}{p}\int B_{dip}\cdot ds = -(\frac{1}{\gamma}+G)\frac{e}{m\beta c}\int B_{dip}\cdot ds \end{aligned} $$

(4.7)

Let’s note that in this case for relativistic beams (γ >> 1) the spin rotation does not depend on the beam energy. It is all defined by the field integral.

Another coordinate frame that can be used is the accelerator frame which follows particle velocity rotation on the design closed orbit. The particle velocity vector remains constant in the accelerator frame. If one considers the spin rotation in a dipole magnet in such frame, the rotation of particle velocity is subtracted. It leads to the spin rotation proportional to the particle γ:

$$\displaystyle \begin{aligned} \phi_{sp} = G\gamma\frac{e}{p}\int B_{dip}ds = G\gamma\theta {} \end{aligned} $$

(4.8)

where θ is the velocity rotation angle. One obvious conclusion from the formula (4.8) is that in a ring with only vertical guiding field one turn spin rotation is 2πGγ, which defines the spin tune equal to Gγ .

4.2.3 Spin Rotation in Helical Dipole Field

As shown in Fig. 4.1 a helical dipole magnet is described by the following paraxial field (without magnet edges):

$$\displaystyle \begin{aligned} B_y = B_0 \cos ks , \,\,\,\,\,\, B_x = -B_0 \sin ks \end{aligned} $$

(4.9)

where

$$\displaystyle \begin{aligned} k = R\frac{2\pi}{\lambda} \end{aligned} $$

(4.10)

and λ is the helical twist period. Compared with common dipole the helical dipole has an additional parameter, the helicity R, which is equal to either +1 or -1.

Fig. 4.1

The fields in one period of helical dipole magnet

Actual helical field is intrinsically nonlinear. It also contains longitudinal off-axis component. For instance, if we limit consideration to second order terms in transverse coordinates, the helical field expressions become:

$$\displaystyle \begin{aligned} \begin{array}{rcl} B_x & =&\displaystyle -B_0\{[1+\frac{k^2}{8}(3x^2+y^2)]\sin{}(k s)-\frac{k^2}{4}x y\cos{}(k s)\} \\ B_y & =&\displaystyle B_0\{[1+\frac{k^2}{8}(x^2+3y^2)]\cos{}(k s)-\frac{k^2}{4}x y\sin{}(k s)\} \\ B_s & =&\displaystyle -B_0k \{x\cos{}(k s)+ y\sin{}(k s)\} \end{array} \end{aligned} $$

(4.11)

But, in most cases, when the particle trajectory stays close to the helical magnet axis, the evaluation of the spin and particle motion using the paraxial helical fields presents a quite good approximation.

Resolving the orbital motion in the paraxial approximation one gets following expressions for a particle trajectory:

$$\displaystyle \begin{aligned} \begin{array}{rcl} x(s) & =&\displaystyle -r (1 - \cos (ks)) + x_0 + x_0^\prime s, \\ y(s) & =&\displaystyle -r \sin (ks) + y_0 + (y_0^\prime + kr)s \end{array} \end{aligned} $$

(4.12)

The trajectory is a spiral with a shifted axis. The radius r of the spiral orbit is:

$$\displaystyle \begin{aligned} r = \frac{eB_0}{k^2p} =\frac{B_0 c}{k^2\beta} \frac{e}{E} \end{aligned} $$

(4.13)

If $x^{\prime }_0 = 0$ and $y^{\prime }_0 = 0$ the orbit is shifted after one helix period by:

$$\displaystyle \begin{aligned} \delta y = 2\pi R r {} \end{aligned} $$

(4.14)

as shown in Fig. 4.2. One can note that flipping simultaneously the sign of magnetic field and the helicity does not change the orbit shift.

Fig. 4.2

The beam orbit transformation through one period of helical dipole magnet

For evaluation of the spin motion it is convenient to use a coordinate frame, rotating around the longitudinal axis in which the vector of magnetic field remains constant. In the rotating coordinate frame the spin motion equation

$$\displaystyle \begin{aligned} \frac{d\mathbf{S}}{ds} = \tilde{\mathbf{W}}_{\mathbf{k}} \times \mathbf{S} \end{aligned} $$

(4.15)

has the spin precession vector $\tilde {\mathbf {W}}_{\mathbf {k}}$ with following components:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \tilde{W}_x & =&\displaystyle 0 \\ \tilde{W}_y & =&\displaystyle -\frac{e (1+G\gamma)}{p} B_0, \\ \tilde{W}_s & =&\displaystyle -k \end{array} \end{aligned} $$

(4.16)

Since the precession frequency is constant the spin motion is easily resolved. After one helix period the axes of rotating and laboratory frame coincide. From here one can find one period transformation of the spin vector in the laboratory frame. This transformation is characterized by the rotation angle ϕ_sp and the rotation axis b:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \phi_{sp} & =&\displaystyle 2\pi \sqrt{1+\chi^2} \end{array} \end{aligned} $$

(4.17)

$$\displaystyle \begin{aligned} \begin{array}{rcl} b_x & =&\displaystyle 0, \;\;\;\ b_y = -\frac{\chi}{\sqrt{1+\chi^2}}, \;\;\;\; b_s = -\frac{R}{\sqrt{1+\chi^2}}. \end{array} \end{aligned} $$

(4.18)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \chi & =&\displaystyle (G+1/\gamma) \frac{eB_0}{m\beta c|k|} \end{array} \end{aligned} $$

(4.19)

The helical dipole has an additional degree of freedom compared with the normal dipole: the helicity of helical twist R. That leads to four possible orientations of spin rotation axis of one period spin transformation, as shown in Fig. 4.3 with the same spin rotation angle ϕ_sp. Two of the axes orientations correspond to a positive shift of the beam orbit, while two others correspond to a negative shift. All this provides a good degree of flexibility when designing a spin rotator device consisting of several one period helical dipole modules. In addition, by rotating a helical dipole magnet around its longitudinal axis one can place the spin rotation axis in other planes, defined by the orientation of the magnetic field at the magnet entrance.

Fig. 4.3

Possible spin rotation axes of one turn spin transformation in a helical dipole magnet

4.2.4 Spin Rotation in Combined Electrical and Magnetic Field: Wien Filter

At very low energies an elegant way to realize spin rotation without distorting the beam orbit is given by the Wien filter. The Wien filter utilizes a combination of static transverse electrical and magnetic fields, oriented orthogonally to each other (Fig. 4.4). In order to have the beam trajectory straight the following condition relating electric and magnetic field values has to be satisfied:

$$\displaystyle \begin{aligned} \frac{\mathbf{E}\times \mathbf{v}}{c^2} = \frac{1-\gamma^2}{\gamma^2} B_\perp \end{aligned} $$

(4.20)

Fig. 4.4

The Wien filter exploits a combination of orthogonal electric and magnetic fields to rotate spin but keep the beam orbit not distorted

The spin rotation axis is defined by magnetic field direction. And the spin rotation angle is:

$$\displaystyle \begin{aligned} \varphi = \frac{e(1+G)}{\gamma^2\beta m c}\int B ds \end{aligned} $$

(4.21)

γ² dependence of the spin rotation limits using this device to very low energies. The required electrical field also becomes unreasonably large at kinetic beam energies above few MeV. The Wien filter is commonly used as a spin rotator for polarized particle sources.

4.3 Siberian Snakes

4.3.1 Main Properties of the Snakes

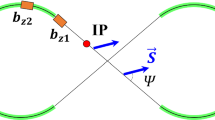
The Siberian Snake (or the Full Snake) is a spin rotating device which rotates particle spin by 180^∘ around some rotation axis (Fig. 4.5). The rotation axis is called the Snake axis and usually placed in horizontal plane. In the following we will consider only Snake with the Snake axis in the horizontal plane. The angle α_s characterizing the orientation of the Snake axis in the horizontal plane is called the Snake axis angle. We will count the value of α_s from the horizontal transverse axis.

Fig. 4.5

The spin transformation by a Siberian Snake

For the Siberian Snake having the Snake axis in the horizontal plane the spinor matrix is written as:

$$\displaystyle \begin{aligned} M_{snake} = -i (\sigma_1\cos\alpha_s + \sigma_2 \sin\alpha_s) \end{aligned} $$

(4.22)

Following two relations are very useful when analyzing spin transformation properties of an accelerator ring with Full Snakes.

• 1. Relation 1:

  $$\displaystyle \begin{aligned} M_{snake} = \exp(-i\alpha_s\sigma_3)\cdot(-i\sigma_1)\end{aligned} $$

  (4.23)

  This relation means that any Siberian Snake transformation can be presented as a rotation by 180^∘ around horizontal axis, followed by the rotation by 2α_s around vertical axis.

• 2. Relation 2:

  $$\displaystyle \begin{aligned} V(\phi) M_{snake} = M_{snake} V(-\phi) \end{aligned} $$

  (4.24)

  where V (ϕ) is the rotation about vertical axis by an angle ϕ:

  $$\displaystyle \begin{aligned} V(\phi) = \exp(-i\sigma_3 \frac{\phi}{2}) \end{aligned} $$

  (4.25)

Deriving these relations by exercising the spinor math we leave for the homework (see Exercise 4.6 in the Sect. 4.6).

Original Siberian Snake concept was invented by Derbenev and Kondratenko [1]. As you will see in the following the Siberian Snakes can be applied for two purposes. First is for controlling a direction of beam polarization in a particular location. For this purpose one Siberian Snake can be used. The second purpose is to prevent depolarization caused by spin resonance crossings when accelerating a particle beam in an accelerator ring. For this purpose, two Snakes (or, in general even number of Snakes) are usually considered. The invention of the Siberian Snake concept opened a way for achieving highly polarized proton beams at the energies of tens of GeV and higher.

4.3.2 Case of One Snake

We start with considering an accelerator ring with one Snake (Fig. 4.6). It is convenient to take the origin point of the ring azimuth in a ring location opposite to the Snake. Spin rotation in the arcs is described by the matrix V  which represents rotation around vertical axis by Gγπ. To evaluate one turn matrix the Relation 2 can be used:

$$\displaystyle \begin{aligned} M_{turn} = V(G\gamma\pi) M_{snake} V(G\gamma\pi) = M_{snake} V(-G\gamma\pi) V(G\gamma\pi) = M_{snake} \end{aligned} $$

(4.26)

arriving to the conclusion that one turn spin transformation matrix is the Snake matrix.

Fig. 4.6

The layout of a ring with one Snake

From here one can deduce the following properties for the accelerator ring with one Full Snake:

• The stable spin direction $\hat {\mathbf {n}}_{\mathbf {0}}$ at the ring azimuth opposite to the Snake is directed along the Snake axis.

• The stable spin vector $\hat {\mathbf {n}}_{\mathbf {0}}$ remains in the horizontal plane in the accelerator ring arcs.

• The spin rotation angle μ of the one turn matrix is equal to 180^∘. Therefore the spin tune is:

  $$\displaystyle \begin{aligned} u_{sp} = \frac{\mu}{2\pi} = \frac{\pi}{2\pi} = \frac{1}{2}\end{aligned} $$

  (4.27)

  Thus, the spin tune remains at constant value 1∕2 independently of the beam energy. This is a wonderful property which, as will be seen in following sections, is characteristic for accelerators with Full Snakes.

Main application of the single Snake configuration is related with producing the longitudinal polarization orientation for physics experiments. For this purpose, the Snake with longitudinal Snake axis has to be put at the ring azimuth opposite to the experimental detector. Such configuration was used in two electron accelerators, AmPS [2] in Amsterdam and the SHR ring [3] at MIT-Bates. They applied a single Siberian Snake to create the longitudinal polarization at the locations of internal targets.

The single Snake configuration can be also used for preventing depolarization during proton beam acceleration by avoiding spin resonance conditions, since the spin tune is held at fixed value 1∕2. But having the stable spin vector in horizontal plane creates the coupling with horizontal betatron motion. Another inconvenience is that the vector $\hat {\mathbf {n}}_{\mathbf {0}}$ has strong dependence on beam energy in the ring arcs. These issues can be resolved by using two Snakes.

4.3.3 Case of Two Snakes

Now we consider an arrangement with two Snakes placed at opposite azimuths of the accelerator ring (Fig. 4.7). The Snake axis angles of these Snakes are α_s1 and α_s2.

Fig. 4.7

The layout of a ring with two Snakes

Again for the analysis of the 2-Snake configuration properties one needs to start with calculating one-turn spin transformation matrix. For the ring azimuth right after the first Snake, one turn matrix calculation, using on the way both Relations 1 and 2, leads to:

$$\displaystyle \begin{aligned} \begin{array}{rcl} M_{turn} & =&\displaystyle M_{snake1} V(G\gamma\pi) M_{snake2} V(G\gamma\pi) = M_{snake1} M_{snake2} V(-G\gamma\pi) V(G\gamma\pi) \\ & =&\displaystyle M_{snake1} M_{snake2} = \exp(-i\alpha_{s1}\sigma_3)\cdot(-i\sigma_1) \exp(-i\alpha_{s2}\sigma_3)\cdot(-i\sigma_1) \\ & =&\displaystyle \exp(-i(\alpha_{s1}-\alpha_{s2})\sigma_3) (-\sigma_1^2) = \exp(-i(\alpha_{s1}-\alpha_{s2})\sigma_3) \end{array} \end{aligned} $$

(4.28)

From the one turn spin transformation matrix M_turn one can get two characteristic properties of two Snake configuration:

• Stable spin direction $\hat {\mathbf {n}}_{\mathbf {0}}$ is vertical in the ring arcs, pointing up in one half, and down on another.

• Spin tune is independent of particle energy and is defined by the Snake axis orientations:

  $$\displaystyle \begin{aligned} u_{sp} = \frac{2(\alpha_{s1}-\alpha_{s2})}{2\pi} = \frac{(\alpha_{s1}-\alpha_{s2})}{\pi} {} \end{aligned} $$

  (4.29)

For instance, to get the spin tune equal to 0.5, the Snake axes should be at 90^∘ angle to each other. And unlike the case with one Snake per ring, the 2-Snake configuration allows for any choice of the spin tune, not only 0.5 value. It should be noted that the energy independence of the spin tune is due to Snake placement at the opposite ring azimuths. The homework Exercise 4.6 in the Sect. 4.6 considers the effect of the Snake axis and bending angle errors on the spin tune.

With the stable spin oriented vertically at all energies the 2-Snake configuration is a preferable solution for accelerating polarized beams through the spin resonances.This configuration was implemented in RHIC for accelerating polarized protons from 25 GeV to 255 GeV energy [4]. Each RHIC ring contains two Snakes placed in opposite ring azimuths to each other (Fig. 4.8). The Snake axes of RHIC Snakes were chosen to be at 45 and 135^∘, that is symmetrical with respect to the longitudinal direction. According to (4.29) the spin tune is equal to 0.5 . Due to the Snakes polarized protons in RHIC have been accelerated to 255 GeV with minimal polarization loss. The polarization loss still happens due to high order resonances (so-called Snake resonances [5]). The resonance conditions for the Snake resonances are:

$$\displaystyle \begin{aligned} u_{sp} = N + m\cdot Q_{y}+ n\cdot Q_{x} \end{aligned} $$

(4.30)

Fig. 4.8

The scheme of RHIC setup for polarization. Each ring contains two Siberian Snakes. In addition, the spin rotators are used around experimental detectors

where N, m and n are arbitrary integers. The Snake resonances must be avoided by proper control of the betatron tune and betatron coupling. The analysis of the Snake resonances is beyond the scope of this lecture, but if you are interested in getting more information on them the following papers are recommended: [5,6,7]. The homework Exercise 4.6 in the Sect. 4.6 considers the Snake resonance values and the number of resonances for different spin tunes.

4.3.4 Case of Multiple Snakes

As the spin resonance strength increases with the beam energy, the increased number of Snakes may need to be employed in future high energy accelerators. Thus we consider the case of 2N Snakes distributed around the ring at azimuth θ₁, θ₂, …, θ_2N = 2π . Each Snake is characterized by its own Snake axis angle α_si and by the spin transformation matrix M_sn,i. Between the Snakes the spin rotates around vertical direction as the beam goes through the arcs which are presented by spin transformation matrices $V_{\theta _{i},\theta _{i-1}}$

Calculation of one turn matrix is a nice homework exercise (see Exercise 4.6 in the Sect. 4.6). The result of the exercise is:

$$\displaystyle \begin{aligned} \begin{array}{rcl} M_{turn} & =&\displaystyle M_{sn,2N} V_{\theta_{2N},\theta_{2N-1}} M_{sn,2N-1} V_{\theta_{2N-1},\theta_{2N-2}}\ldots M_{sn,1}V_{\theta_{1},\theta_{0}} \\ & =&\displaystyle \ldots \\ & =&\displaystyle V(\phi) = \exp(-i\sigma_3 \frac{\phi}{2}) {} \end{array} \end{aligned} $$

(4.31)

where the spin rotation angle ϕ depends on Snake location and Snake axis orientation:

$$\displaystyle \begin{aligned} \phi = G\gamma \sum_{i=1}^{2N} (-1)^{i-1}(\theta_{i}-\theta_{i-1}) + 2 \sum_{i=1}^{N} (\alpha_{s,2i}-\alpha_{s,2i-1}) \end{aligned} $$

(4.32)

From here the spin tune then is obtained as:

$$\displaystyle \begin{aligned} u_{sp} = \frac{G\gamma}{2\pi} \sum_{i=1}^{2N} (-1)^{i-1}(\theta_{i}-\theta_{i-1}) + \frac{1}{\pi} \sum_{i=1}^{N} (\alpha_{s,2i}-\alpha_{s,2i-1}) {} \end{aligned} $$

(4.33)

In order to avoid spin resonance conditions during beam acceleration one would want the spin tune to be independent of energy. The formula (4.33) shows that this can be achieved by allocating the Snakes around the ring so that the first term in (4.33) becomes 0. Then the spin tune value can be chosen by selecting proper orientations of Snake axes. Common approach is to have the spin tune at 0.5, providing maximum detuning from all first-order spin resonance conditions.

From (4.31) one can also deduce that the stable spin direction $\hat {\mathbf {n}}_{\mathbf {0}}$ is vertical in all arcs. Each Snake switches $\hat {\mathbf {n}}_{\mathbf {0}}$ direction from up to down, and vice versa.

Thus, with even number of Snakes one can maintain the vertical stable spin at all beam energies as well as have the spin resonances contained. If in locations of particle physics experiments a specific polarization orientation (often, longitudinal) is required, a pair of spin rotators can be installed, to convert the polarization orientation from the vertical to one required by the experiment, and then back to the vertical. This represents a general recipe for providing highly polarized beams at high energies for physics experiments.

4.4 Realization of Snakes and Spin Rotators

4.4.1 Solenoidal Snake and Spin Rotator

A Siberian Snake with longitudinal Snake axis can be simply constructed by using a solenoidal magnet. The required magnetic fields for 180^∘ spin rotation are:

• For electrons:

  $$\displaystyle \begin{aligned} B_{sol}\cdot L = 10.47 \cdot p ({\mathrm{GeV}}/c) \end{aligned} $$

  (4.34)

• For protons:

  $$\displaystyle \begin{aligned} B_{sol}\cdot L = 3.75 \cdot p ({\mathrm{GeV}}/c)\end{aligned} $$

  (4.35)

A notable advantage of solenoidal Snake is that the beam closed orbit is not affected by the Snake. But the longitudinal magnetic field introduces a betatron coupling which, in most cases, would require compensation. Since required magnetic field increases with the particle energy the energy range for solenoid-based Full Snake applications is limited to below 10–20 GeV.

A solenoidal Snake was used in IUCF 500 MeV Cooler Ring for Siberian Snake proof-of-principle experiments (1989–1997) [8]. The IUCF Snake used 2 T⋅m solenoid. The experiments provided a first observation that depolarizing resonances were overcome by the Snake, confirming the main principle of the Snake. High-order spin resonances, Snake resonances, have been also first observed during the IUCF Snake studies.

In following years the solenoidal Snakes were used in nuclear physics experiments in AmPS (Netherlands) [2] and MIT-Bates SHR (USA) [3] to create longitudinal polarization on internal targets. Beam energy in these accelerators was in 0.7–1 GeV range. For compensating betatron coupling the system of normal and skew-quadrupoles were incorporated into the solenoidal insertion as shown in Fig. 4.9. To make the Snakes as compact as possible the Snake solenoids were implemented as superconducting magnets.

Fig. 4.9

Solenoidal Snake coupling compensation scheme. SQ are skew-quadrupoles. QC is a normal quadrupole

A solenoidal magnet can be also used to realize a simple spin rotator. This is done by a combination of a solenoidal magnet and horizontally bending dipole. Spin transformation matrix for converting the vertical spin to longitudinal one is very simple:

$$\displaystyle \begin{aligned} M_{rot} = \exp (-i\pi\sigma_3/4) \exp (-i\pi\sigma_2/4) \end{aligned} $$

(4.36)

It requires 90^∘ spin rotation by the solenoid magnet accompanied by 90^∘ spin rotation by the horizontal bend. Similar rotator can be used also in transfer lines to convert the longitudinal beam polarization produced in a polarized electron source to the vertical one. One deficiency of such rotator is that it works perfectly only at one particular energy.

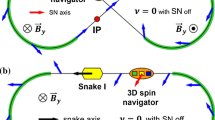
In order to operate in wide energy range the rotator scheme must use more than one solenoidal insertion. For instance, a general electron rotator scheme for EIC has to cover energy rage 6–18 GeV. In this case to convert vertical spin to longitudinal at the experimental location at all required energies a combination of two solenoidal insertions and two horizontal bending sections can be used. The schematic of such rotator is shown in Fig. 4.10. After passing the experiment location a similar combination of solenoidal and dipole magnets is used to convert the spin back to the vertical.

Fig. 4.10

The schematic layout of the electron spin rotator for EIC

The rotator system consideration using spin transformation matrices is a bit cumbersome in this case. But when one gets through it comes to the relations which define required solenoidal spin rotations φ_i as a function of spin rotation ψ₁ in dipole magnets:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \tan \varphi_1 & =&\displaystyle \pm \frac{\cos \psi_2}{\sqrt{-\cos (\psi_1 + \psi_2 ) \cos (\psi_1 - \psi_2 ) }} \end{array} \end{aligned} $$

(4.37)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \cos \varphi_2 & =&\displaystyle \cot \psi_1 \cot \psi_2 \end{array} \end{aligned} $$

(4.38)

From here the required solenoidal fields in all energy range can be found.

In order to properly integrate the solenoidal insertions into the electron ring lattice the optics of the solenoid insertion must satisfy two independent conditions:

• 1. Betatron coupling has to be compensated by the use of normal and skew quadrupoles.

• 2. Specific spin matching conditions have to be satisfied to minimize depolarization.

Realization detail for such solenoidal insertion will be considered in the lecture on spin matching.

4.4.2 Siberian Snake and Spin Rotator Based on Dipole Magnets

A Siberian Snake can be constructed using a sequence of alternating vertical (V ) and horizontal (H) bends, as shown in Fig. 4.11. Such design of the Siberian Snake was proposed by Steffen [9]. In more general form the Snake configuration can be written as:

$$\displaystyle \begin{aligned} (-H, -V, m\cdot H, 2V, -m\cdot H, -V, H).\end{aligned}$$

here m is a number more than 1 [10]. The design uses a special field symmetry with respect to the Snake center:

• the vertical field (H-bends) is anti-symmetric

  Fig. 4.11

  

  The schematic layout of Steffen’s Snake based on vertical and horizontal dipole magnets [6]

• the horizontal field (V -bends) is symmetric

Such symmetry makes the beam orbit restored at the Snake exit. It also results in the Snake axis lying in the horizontal plane. Then, by choosing fields of H and V  bending magnets one can setup the required spin rotation angle (180^∘ for the Full Snake) and a preferred direction of the Snake axis. Due to capability to select any Snake axis orientation such Snake configuration is called the continuous axis Snake.

From the analysis of the spin transformation matrix of this Snake one can derive that for getting 180^∘ spin rotation the following relation connecting spin rotations in horizontal (ψ_H) and vertical (ψ_V) bends must be satisfied:

$$\displaystyle \begin{aligned} \sin^2 \psi_H \sin^2 \psi_V = \frac{1}{2} \end{aligned} $$

(4.39)

Thus, this relation connects horizontal and vertical magnetic fields of the Snake magnets in order to realize the Full Snake. Using this relation and the Snake parameter plot shown in Fig. 4.12 one can select any Snake axis orientation in the horizontal plane and find corresponding set of magnetic fields.

Fig. 4.12

Dipole magnet Snake parameter plot defining the spin rotation in vertical bends required to get a particular Snake axis orientation [6]

The Snakes based on dipole magnets have following characteristics properties. First, required fields scale inversely proportionally to particle velocity, thus for relativistic beams the magnetic fields very weakly depend on the beam energy. Second, the orbit excursion changes inversely proportionally to the particle energy. And, at last, the required integrated magnetic field is generally in the range 15–35 T ⋅m, depending on the orientation of the Snake axis. Therefore this type of Snake is preferred at the high beam energy.

Unlike the Snake based on solenoidal magnets in the dipole magnet Snake the beam orbit makes excursion inside the Snake. Below 20 GeV the orbit excursion reaches tens of centimeters. But at the energies above 20 GeV the orbit excursion becomes reasonable. And while the required field of solenoidal Snake increases with the beam energy, the field of the dipole-based Snake is nearly constant at high energies. Thus, the Snake based on dipole magnets would be a good choice at the beam energies above 20 GeV.

The spin rotators based on dipole magnets were used in HERA [11]. HERA was the first e-p collider, operated with 27.5 GeV electrons and 920 GeV protons. The spin rotators were implemented for electron beam to produce longitudinal polarization at the experimental detectors. To this day it is the highest energy application of the spin rotators in electron accelerators. The HERA rotator was a sequence of three horizontal and three vertical bending magnets:

$$\displaystyle \begin{aligned} (V3, H3, V2, H2, V2, H1).\end{aligned}$$

Since the vertical orbit needs to be restored the fields of vertical bending magnets are connected by the relation:

$$\displaystyle \begin{aligned} V3 = -(V1+V2) \end{aligned} $$

(4.40)

Since the HERA spin rotators were for electron beam the rotator optics had to be designed to satisfy the spin matching conditions (see the lecture on spin matching). The vertical orbit excursion characteristic for rotators based on dipole magnets was addressed by placing some magnets off the horizontal plane to keep them centered on the beam orbit. But changing polarization direction at the experiments was challenging, since it required moving the magnets vertically to maintain the magnet alignment on the beam orbit.

4.4.3 Siberian Snake and Spin Rotator Based on Helical Magnets

The Siberian Snake can be created with four full twist helical dipole magnets, having vertically oriented field at the entrance of each helix [12]. Each magnet is characterized by the strength of magnetic field on the magnet axis B_i, the helical twist helicity R_i and the number of helical periods N_i. Similar to the continuous axis Snake based on dipole magnets one can identify symmetry conditions which automatically provide the beam orbit restoration and the Snake axis being in the horizontal plane. The symmetry conditions in the case of the helical magnets can be written by relating fields, helicities and numbers of helical periods of different Snake magnets:

$$\displaystyle \begin{aligned} B_1=-B_4; \,\,\, B_2 = -B_3; \,\,\, R_1 = R_4; \,\,\, R_2 =R_3; \,\,\, N_1 = N_4; \,\,\, N_2 =N_3. {} \end{aligned} $$

(4.41)

These conditions define the continuous axis helical Snake.

The Siberian Snakes based on the helical magnets have been implemented in collider RHIC in Brookhaven National Laboratory. In the RHIC Snake each helical magnet has one helical period. Fields of the Snake magnets can be found from the parameter plot that is obtained from the Snake spin transformation matrix. Figure 4.13 shows the parameter plot for RHIC Snake [4]. μ is the spin rotation angle. For the Full Snake μ = 180^∘ is needed (green curve). α_s is the Snake axis angle. (On this plot it is accounted from the longitudinal axis!). From this plot one can find helical fields (B₁, B₂) required to achieve given μ and α_s. Natural choice, applied in RHIC is to have one Snake axis at + 45^∘ with other Snake axis oriented at − 45^∘ with respect to longitudinal axis. Blue circles show possible parameter points for the 45^∘ Snake axis.

Fig. 4.13

Parameter plot defining the magnet strength of helical magnets for the RHIC Snake [4]

Figure 4.14 shows spin and orbit evolution through RHIC helical Snake at the injection energy (γ = 25). Since the orbit excursion reduces inversely proportionally to beam energy at the store energy (γ = 270) the maximum orbit deviation is just a couple of millimeters. Comparing the helical Snake with a Steffen Snake of similar total length one gets smaller resulting orbit excursion in the helical Snake. Some disadvantage of using helical magnets is related with the fact that their field is intrinsically non-linear. Because of this the effects of such spin rotators on particle dynamics has to be carefully considered. That includes betatron tune shifts and beta-function distortions induced by the helical Snakes. The homework Exercise 4.6 in the Sect. 4.6 compares several design options for the helical Siberian Snakes.

Fig. 4.14

Spin and orbit trajectories in RHIC helical Snake at γ = 25 [4]

The sequence of the four helical magnets can also be used to realize a spin rotator for transforming the vertical polarization at the rotator entrance into longitudinal polarization in the location of experimental detector. It was shown that most efficient scheme was one based on the helical magnets having horizontal field orientation at the magnet entrance [12]. Helical spin rotators were implemented in RHIC.

Stronger magnetic field makes the spin rotator or the Snake more compact and minimizes the beam orbit excursions inside the rotators. Because of this, superconducting magnet technology, using NbTi superconductor, has been used for building 4 T helical magnets for RHIC Snakes and spin rotators. Figure 4.15 shows the cross-sections of the helical magnets of RHIC spin rotators. The superconducting coil is surrounded by the iron collar. All magnet elements are cooled to 4.2 K by using liquid He. Since the orbit excursion gets larger at lower energies, the magnet aperture is defined at low energies. For instance, for RHIC the magnet aperture must be large enough to accommodate sufficiently large orbit excursion (∼2 cm) at RHIC injection energy 25 GeV.

Fig. 4.15

The cross-section of RHIC spin rotator helical magnets

4.5 Summary

Various types of spin rotating devices can be used in accelerator rings for different purposes. Among them the Siberian Snake represents an amazing device allowing polarization preservation when crossing numerous spin resonances during beam acceleration. Most efficient use of Snakes is in pairs (even number), with proper distribution of an accelerator ring. Proper selection of the Snake axis angle ensures spin tune 0.5. Even with Snakes one needs to be careful about depolarization, since there are higher order resonances, Snake resonances. And larger beam energies require larger number of the Snake pairs. Spin rotators also play very important role in accelerators which require longitudinally polarized beam at experimental detectors. Practical realization of Snakes and rotators depends on the energy of a particular accelerator. Dipole and helical dipole-based Snakes would be a proper choice at higher energies (>20 GeV); while solenoidal based Snakes more appropriate at lower energies (<20 GeV).

4.6 Homework Exercises

In this section several exercises referred throughout this Chapter are given together with their solutions.

Exercise 1 A general spinor transformation matrix has the form:

$$\displaystyle \begin{aligned} M = \exp[-i(\mathbf\sigma\cdot\mathbf b)\frac{\varphi}{2}] = I\cos{}(\varphi/2) - i (\mathbf\sigma\cdot\mathbf b)\sin{}(\varphi/2) \end{aligned} $$

(4.42)

where φ is the spin rotation angle and b is the rotation axis unit vector.

The matrix of the Siberian Snake with the Snake axis angle α_s is:

$$\displaystyle \begin{aligned} M_{snake} = -i (\sigma_1\cos\alpha_s + \sigma_2 \sin\alpha_s) \end{aligned} $$

(4.43)

And the matrix of spin rotation in the ring arcs, where the spin rotates around the vertical guiding magnetic field of dipole magnets is:

$$\displaystyle \begin{aligned} V(\phi) = \exp[-i(\sigma_3 \frac{\phi}{2})] = I\cos{}(\phi/2) - i (\sigma_3 \sin{}(\phi/2) \end{aligned} $$

(4.44)

where ϕ = Gγθ and θ is the arc bending angle.

Then, first, prove that the Snake matrix can be presented as the product of two consecutive rotations (around horizontal and vertical axes):

$$\displaystyle \begin{aligned} M_{snake} = \exp(-i\alpha_s\sigma_3)\cdot(-i\sigma_1) \end{aligned} $$

(4.45)

Second, prove the relation between arc and Snake matrices

$$\displaystyle \begin{aligned} V(\phi) M_{snake} = M_{snake} V(-\phi) \end{aligned}$$

Solution Please note, that there are different ways to prove these relations. Only one possible way is shown, as an example.

For proving the relation:

$$\displaystyle \begin{aligned} M_{snake} = \exp(-i\alpha_s\sigma_3)\cdot(-i\sigma_1) \end{aligned} $$

(4.46)

one could use the following properties of σ matrices:

$$\displaystyle \begin{aligned} \sigma_1\sigma_1 = I , \;\;\;\;\;\;\;\; \sigma_2\sigma_1 = -i \sigma_3 \end{aligned} $$

(4.47)

To prove the first relation one can follow this path:

$$\displaystyle \begin{aligned} \begin{array}{rcl} M_{snake} & =&\displaystyle -i(\sigma_1 \cos\alpha_s+\sigma_2 \sin\alpha_s) = -i(\sigma_1 \cos\alpha_s+\sigma_2\sigma_1^2 \sin\alpha_s) \\ & =&\displaystyle (\cos\alpha_s+\sigma_2\sigma_1 \sin\alpha_s)(-i\sigma_1) = (\cos\alpha_s -i\sigma_3\sin\alpha_s)(-i\sigma_1) \\ & =&\displaystyle \exp(-i \alpha_s \sigma_3 )(-i\sigma_1) \end{array} \end{aligned} $$

(4.48)

For proving the relation:

$$\displaystyle \begin{aligned} V(\phi) M_{snake} = M_{snake} V(-\phi) \end{aligned}$$

one could use the following properties of σ matrices:

$$\displaystyle \begin{aligned} \sigma_3\sigma_1 = -\sigma_1\sigma_3, \;\;\;\;\;\;\;\; \sigma_3\sigma_2 = -\sigma_2\sigma_3 \end{aligned} $$

(4.49)

Then this relation can be proved in following way:

$$\displaystyle \begin{aligned} \begin{array}{rcl} V(\phi)M_{snake} & =&\displaystyle (I\cos{}(\phi/2) - i\sigma_3 \sin{}(\phi/2))\cdot (-i)(\sigma_1 \cos\alpha_s+\sigma_2 \sin\alpha_s) \\ & =&\displaystyle (-i) [I\cos{}(\phi/2)(\sigma_1\cos\alpha_s+\sigma_2\sin\alpha_s) - \\ & -&\displaystyle i\sin{}(\phi/2)(\sigma_3\sigma_1 \cos\alpha_s+\sigma_3\sigma_2 \sin\alpha_s)] = \\ & =&\displaystyle (-i)[(\sigma_1\cos\alpha_s+\sigma_2\sin\alpha_s)\cdot I\cos{}(\phi/2) + \\ & +&\displaystyle i(\sigma_1\sigma_3 \cos\alpha_s+\sigma_2\sigma_3 \sin\alpha_s)\sin{}(\phi/2)] = \\ & =&\displaystyle (-i)(\sigma_1 \cos\alpha_s+\sigma_2 \sin\alpha_s)\cdot (I\cos{}(\phi/2) + i\sigma_3 \sin{}(\phi/2)) = \\ & =&\displaystyle M_{snake} V^{-1}(\phi) = M_{snake} V(-\phi) \end{array} \end{aligned} $$

(4.50)

Exercise 2 Consider a system of 2N Siberian Snakes placed at the azimuths θ₁, θ₂, …, θ_2N in an accelerator ring. Each Snake is characterized by its own Snake axis angle α_s,i.

Show that the one turn matrix is the matrix of the spin rotation around the vertical axis and confirm the spin tune expression (4.33):

$$\displaystyle \begin{aligned} \begin{array}{rcl} M_{turn} & =&\displaystyle M_{sn,2N} V_{\theta_{2N},\theta_{2N-1}} M_{sn,2N-1} V_{\theta_{2N-1},\theta_{2N-2}}\ldots M_{sn,1}V_{\theta_{1},\theta_{0}} \\ & =&\displaystyle \ldots \\ & =&\displaystyle V(\phi) = \exp(-i\sigma_3 \frac{\phi}{2}) \end{array} \end{aligned} $$

(4.51)

and

$$\displaystyle \begin{aligned} \phi = G\gamma \sum_{i=1}^{2N} (-1)^{i-1}(\theta_{i}-\theta_{i-1}) + 2 \sum_{i=1}^{N} (\alpha_{s,2i}-\alpha_{s,2i-1}) \end{aligned} $$

(4.52)

Solution Please note that there might be different ways to prove this relation. Only one possible way is shown, as an example.

Let’s note first that $V_{\theta _i, \theta _{i-1}} = V(G\gamma (\theta _i-\theta _{i-1}))$ Then, using the relation V (ϕ)M_snake = M_snakeV (−ϕ) one can consecutively exchange positions of Snake matrices

$$\displaystyle \begin{aligned} \begin{array}{rcl} M_{turn} & =&\displaystyle M_{sn,2N} V(G\gamma(\theta_{2N}-\theta_{2N-1})) M_{sn,2N-1} V(G\gamma(\theta_{2N-1}-\theta_{2N-2}))\ldots \\ & \ldots&\displaystyle M_{sn,1}V(G\gamma(\theta_{1}-\theta_{0})) = \\ & =&\displaystyle V(G\gamma(\theta_{2N-1}-\theta_{2N}))V(G\gamma(\theta_{2N-1}-\theta_{2N-2}))\ldots \\ & \ldots&\displaystyle V(G\gamma(\theta_{1}-\theta_{0}))M_{sn,2N}M_{sn,2N-1}\ldots M_{sn,1} = \\ & =&\displaystyle V(G\gamma[(\theta_{2N-1}-\theta_{2N})+(\theta_{2N-1}-\theta_{2N-2})+\ldots. \\ & \ldots&\displaystyle + (\theta_{1}-\theta_{0})]) M_{sn,2N} M_{sn,2N-1}\ldots M_{sn,1} = \\ & =&\displaystyle V(\varphi_1) M_{sn,2N} M_{sn,2N-1}\ldots M_{sn,1} \end{array} \end{aligned} $$

(4.53)

where

$$\displaystyle \begin{aligned} \varphi_1 = G\gamma \sum_{i=1}^{2N} (-1)^{i-1} (\theta_i - \theta_{i-1})\end{aligned} $$

(4.54)

On next step we transform the product of the Snake matrices:

$$\displaystyle \begin{aligned} \begin{array}{rcl} M_{sn,2N} M_{sn,2N-1}\ldots M_{sn,1} & =&\displaystyle \exp(-i \alpha_{s,2N} \sigma_3 )(-i\sigma_1) \exp(-i \alpha_{s,2N-1} \sigma_3 )(-i\sigma_1) \\ & \ldots&\displaystyle \exp(-i \alpha_{s,1} \sigma_3 )(-i\sigma_1) = \\ & =&\displaystyle \exp(-i \alpha_{s,2N} \sigma_3 ) \exp (i \alpha_{s,2N-1} \ldots \\ & \ldots&\displaystyle \exp(-i \alpha_{s,1} (-i\sigma_1)(-i\sigma_1) \ldots (-i\sigma_1) = \\ & =&\displaystyle \exp(-i (\alpha_{s,2N} -\alpha_{s,2N-1} +\ldots +\alpha_{s,1} ) \sigma_3 ) (-i\sigma_1)^{2N} \\ & =&\displaystyle V(\varphi_2) (-1)^N \end{array} \end{aligned} $$

(4.55)

where

$$\displaystyle \begin{aligned} \varphi_2 = 2 \sum_{i=1}^{N} (\alpha_{s,2i}-\alpha_{s,2i-1}) \end{aligned} $$

(4.56)

Finally:

$$\displaystyle \begin{aligned} \begin{array}{rcl} M_{turn} & =&\displaystyle V(\varphi_1) M_{sn,2N} M_{sn,2N-1}\ldots M_{sn,1} = (-1)^N V(\varphi_1) V(\varphi_2) = \\ & =&\displaystyle (-1)^N V(\varphi_1+ \varphi_2) = V(\phi) {} \end{array} \end{aligned} $$

(4.57)

where

$$\displaystyle \begin{aligned} \phi = \varphi_1 +\varphi_2 = G\gamma \sum_{i=1}^{2N} (-1)^{i-1} (\theta_i - \theta_{i-1}) + 2 \sum_{i=1}^{N} (\alpha_{s,2i}-\alpha_{s,2i-1}) \end{aligned} $$

(4.58)

Note, that factor (−1)^N in Eq. (4.57) can be dropped out since it increments ϕ by 2π.

Exercise 3 Consider a system of two Full Snakes separated precisely by 180^∘ bending angle. The Snake axes are chosen such that α_s,2 − α_s,1 = π∕2, so the spin tune is equal to one half.

• 1. Let’s assume that there is some error in the Snake axis orientation. Find a tolerance of the Snake axis angle to have the spin tune deviation less than 0.1.

• 2. Let’s assume that one Snake was placed imperfectly, shifted by 0.1^∘ of bending angle from the perfect location. Evaluate the spin tune shift when accelerating protons from 240 to 250 GeV.

Solution One can use the expression (4.33) for spin tune in the system with 2N Snakes. With only 2 Snakes the expression reads as:

$$\displaystyle \begin{aligned} \begin{array}{rcl} u_{sp} & =&\displaystyle \frac{G\gamma}{2\pi} [(\theta_1-\theta_2)+(\theta_1-\theta_0)]+ \frac{1}{\pi} (\alpha_{s,2}-\alpha_{s,1}) = \\ & =&\displaystyle \frac{G\gamma}{\pi} (\theta_1-\pi)+ \frac{1}{\pi} (\alpha_{s,2}-\alpha_{s,1}) \end{array} \end{aligned} $$

(4.59)

since θ₀ = 0 and θ₂ = 2π.

For perfectly placed Snakes (θ₁ = π) and with α_s,2 − α_s,1 = π∕2 the spin tune is ν_sp = 1∕2.

• 1. Let’s consider that one of the Snake axis (say, α_s,1) is shifted by δα_s,1. Corresponding change in the spin tune can be written as:

  $$\displaystyle \begin{aligned} u_{sp} = \frac{1}{\pi} (\pi/2 - \delta \alpha_{s,1}) \end{aligned} $$

  (4.60)

  Thus the spin tune shift is

  $$\displaystyle \begin{aligned} \delta u_{sp} = -\frac{1}{\pi} \delta \alpha_{s,1} \end{aligned} $$

  (4.61)

  From here, in order to have the spin tune shift less than 0.1, |δα_s,1| has to be less than 0.1π. That is the tolerance on |δα_s,1| is 0.314 rad (or 18^∘).

• 2. Now let’s consider that there is an error δθ in the bending angle between the Snakes. That is θ₁ = π + δθ The spin tune becomes

  $$\displaystyle \begin{aligned} u_{sp} = \frac{G\gamma}{\pi} (\delta \theta)+ 1/2. {} \end{aligned} $$

  (4.62)

For protons G = 1.79. Relativistic factor γ = 255.8 for 240 GeV, and γ = 266.5 for 250 GeV.

Then from the Eq. (4.62 ) the spin tune shifts corresponding to 0.1^∘ bending angle error can be calculated to be 0.254 at 240 GeV and 0.265 at 250 GeV, changing linearly with the beam energy between these two energies.

Exercise 4 Consider system of two Full Snakes separated by 180^∘ bending angle. The Snake axes are chosen such that α_s,2 − α_s,1 = π∕2. Spin tune for such system is 0.5.

Calculate vertical betatron tune values corresponding to the resonance conditions of 2nd, 3rd and 4th order spin resonances.

Next, consider that Snake axes were retuned to get the spin tune 0.25. Find the required orientation of the Snake axes and calculate vertical betatron tune values corresponding to the locations of 2nd, 3rd and 4th order spin resonances.

How does the number of the resonances compare in two cases?

Solution The general condition of the spin resonance between the spin tune ν_sp and vertical betatron tune Q_y is :

$$\displaystyle \begin{aligned} u_{sp} = N + m Q_y {} \end{aligned} $$

(4.63)

where N and m are arbitrary integer numbers. Absolute value of m defines the order of the resonance.

Let’s present Q_y as Q_y = [Q_y] + {Q_y} where [Q_y] is the integer part of the vertical betatron tune, and {Q_y} is the fractional part, which is between 0 and 1. For the fractional part of vertical betatron tune, using the Eq. (4.63) one gets:

$$\displaystyle \begin{aligned} \{Q_y\} = \frac{u_{sp} - N - m[Q_y]}{m} \end{aligned} $$

(4.64)

If the spin tune is equal to 1∕2, then resonance condition becomes:

$$\displaystyle \begin{aligned} \{Q_y\} = \frac{1 -2 N - 2m[Q_y]}{2m} = \frac{1+2*\tilde{N}}{2m} \end{aligned} $$

(4.65)

where $\tilde {N}$ is an arbitrary integer which gives {Q_y} between 0 and 1. From here the following table of high-order spin resonance values of {Q_y} can be compiled:

	m	Resonance {Qy}
2nd order	m = −2 or m = 2	1∕4, 3∕4
3rd order	m = −3 or m = 3	1∕6, 1∕2, 5∕6
4th order	m = −4 or m = 4	1∕8, 3∕8, 5∕8, 7∕8

Now let’s take the spin tune equal to 1∕4. As follows from the formula (4.29), to obtain this spin tune the Snake axis angles have to be in the relations:

$$\displaystyle \begin{aligned} \alpha_{s,2} - \alpha_{s,1} = \pi/4 \end{aligned} $$

(4.66)

The spin resonance condition in this case becomes:

$$\displaystyle \begin{aligned} \{Q_y\} = \frac{1 -4 N - 4m[Q_y]}{4m} = \frac{1+4*\tilde{N}}{4m} \end{aligned} $$

(4.67)

where $\tilde {N}$ is again an arbitrary integer which gives {Q_y} between 0 and 1. Then one gets the following table of high-order spin resonance values of {Q_y}:

	m	Resonance {Qy}
2nd order	m = −2 or m = 2	1∕8, 3∕8, 5∕8, 7∕8
3rd order	m = −3 or m = 3	1∕12, 3∕12, 5∕12, 7∕12, 9∕12, 11∕12
4th order	m = −4 or m = 4	1∕16, 3∕16, 5∕16, 7∕16, 9∕16, 11∕16, 13∕16, 15∕16

Comparing the results for ν_sp = 1∕2 and ν_sp = 1∕4 one can note that, beside different resonance locations, the total number of resonances of any order is twice smaller in the case of ν_sp = 1∕2. It happens because with ν_sp = 1∕2 high-order resonances are paired together. This can be considered as one of advantages of using ν_sp = 1∕2, since it provides a cleaner working point space for choosing the betatron tune.

Exercise 5 One needs to design a continuous axis Siberian Snake for a proton accelerator ring based on helical dipole modules. Three schemes have been proposed, which are summarized in the table:

	Scheme 1			Scheme 2			Scheme 3
	B 0	R	N	B 0	R	N	B 0	R	N
1st Helix	3.5T	+ 1	1	1.3T	+ 1	1	2.5T	+ 1	1
2nd Helix	− 1.1 T	+ 1	2	− 4 T	+ 1	1	− 2.5 T	+ 1	1
3rd Helix	1.1 T	+ 1	2	4 T	+ 1	1	2.4 T	− 1	1
4th Helix	3.5 T	+ 1	1	− 1.3 T	+ 1	1	− 2.4 T	− 1	1

All Snakes use helical magnets with twist period 2.4 m. N characterizes a number of helical twist periods in each magnet. Using the formula (4.14) for the orbit shift on one twist period, find the maximum orbit excursion inside each Snake design scheme at E = 25 GeV. Also, calculate the absolute total field integral for each design option. On the basis of these calculations and, may be, other considerations select a design scheme which you would recommend for the accelerator ring.

Solution From the orbit shift formula (4.14) one gets for the orbit shift on one helical period:

$$\displaystyle \begin{aligned} \Delta y = 2 \pi R r = \frac{2 \pi R B_0 c}{k^2 \beta} \frac{e}{E} = \frac{\lambda^2 R B_0 c}{2 \pi \beta} \frac{e}{E} \end{aligned} $$

(4.68)

For 25 GeV one then obtains:

$$\displaystyle \begin{aligned} \Delta y ({\mathrm{mm}}) \approx 11.0*R*B_0 (T) \end{aligned} $$

(4.69)

Then using values of B₀, R and N for three design options one can calculate Δy and y after each helix:

	Scheme 1		Scheme 2		Scheme 3
	Δy, mm	y, mm	Δy, mm	y, mm	Δy, mm	y, mm
1st Helix	38.5	38.5	14.3	14.3	27.5	27.5
2nd Helix	−24.2	14.3	−44.0	−29.7	−27.5	0
3rd Helix	24.2	38.5	44.0	14.3	26.4	26.4
4th Helix	−38.5	0	−14.3	0	−25.4	0

From there the maximum orbit excursion and the absolute field integral for every scheme can be summarized as:

	Max. Orbit |y|,	Total field integral,
	mm	T⋅m
Scheme 1	38.5	27.36
Scheme 2	29.7	25.44
Scheme 3	27.5	23.52

The Scheme 3 demonstrates smaller orbit excursion and smaller field integral than other two schemes. However, it does not satisfy symmetry conditions for field and twist helicities, required for the continuous axis Snake (4.41). Thus, the Scheme 2 would be a preferable choice. In fact, the Scheme 2 was realized at RHIC.