Non-degeneracy of the Local Minimizers

Abstract

In this section we prove the non-degeneracy of the solutions to the one-phase problem (2.1). Our main result is the following.

In this section we prove the non-degeneracy of the solutions to the one-phase problem (2.1). Our main result is the following:

FormalPara Proposition 4.1 (Non-degeneracy of the Solutions: Alt-Caffarelli [3])

Suppose that D is a bounded open set in $\mathbb {R}^d$ and u ∈ H ¹(D) is non-negative and minimizes the functional $\mathcal F_\Lambda$ in D, for some Λ > 0. Then, there is a constant κ > 0, depending on Λ and d, such that the following claim holds:

$$\displaystyle \begin{gathered} \mathit{If}\ B_r(x_0)\subset D \quad {and}\quad x_0\in\overline\Omega_u, \quad \mathit{\mbox{then}}\quad \|u\|{}_{L^\infty(B_r(x_0))}\ge \kappa r. \end{gathered} $$

The non-degeneracy holds in particular for functions satisfying the following optimality condition:

$$\displaystyle \begin{aligned} \mathcal F_\Lambda(u,\Omega)\le \mathcal F_\Lambda(v,\Omega)\quad \text{for every}\quad v\in H^1(\Omega)\quad \text{such that}\quad v\le u. \end{aligned} $$

(4.1)

For the sake of completeness, we notice that this optimality condition can also be expressed in a different way, at least when it comes to functions u, which are harmonic on their positivity set Ω_u. In fact, the following result is analogous to Lemma 3.3. Moreover, as in Lemma 3.3 (see Remark 3.4), we can suppose that all the test functions v in (4.1), (4.3) and (4.2) are non-negative.

FormalPara Lemma 4.2

Let D be a bounded open set in $\mathbb {R}^d$ and u ∈ H ¹(D) be a given non-negative function. Then the following are equivalent:

• (i) u satisfies the inwards minimality condition

  $$\displaystyle \begin{aligned} \mathcal F_\Lambda(u,D)\le \mathcal F_\Lambda(v,D)\quad & \mathit{\text{for every}}\quad v\in H^1(D)\quad \mathit{\text{such that}}\notag\\ & \qquad \qquad u-v\in H^1_0(D)\quad \mathit{\text{and}}\quad \Omega_u\supset\Omega_v.{} \end{aligned} $$

  (4.2)

• (ii) u is harmonic in Ω _u in the following sense:

  

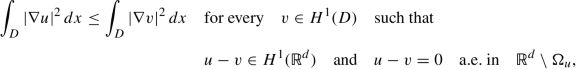  (4.3)

  and satisfies the minimality condition (4.1).

FormalPara Proof

The implication (i) ⇒ (ii) is immediate. In fact, (4.2) implies both (4.3) and (4.1). In order to prove that (ii) implies (i), we suppose that u satisfies (4.3) and (4.1) and we consider a (non-negative) function v ∈ H ¹(D) such that $u-v\in H^1_0(D)$ and Ω_u ⊂ Ω_v. As in the proof of Lemma 3.3, we consider the test functions u ∧ v and u ∨ v. Since u ∨ v = 0 on , the harmonicity of u (4.3) implies that

$$\displaystyle \begin{aligned} \int_D|\nabla u|{}^2\,dx\le \int_D|\nabla (u\vee v)|{}^2\,dx. \end{aligned}$$

On the other hand, we can use u ∧ v as a test function in (4.2). Thus

$$\displaystyle \begin{aligned} \int_D|\nabla u|{}^2\,dx+\Lambda |\Omega_u|\le \int_D|\nabla (u\wedge v)|{}^2\,dx+\Lambda |\Omega_{u\wedge v}|. \end{aligned}$$

Summing these inequalities and using that Ω_v = Ω_u∧v, we obtain

$$\displaystyle \begin{aligned} 2\int_D|\nabla u|{}^2\,dx+\Lambda |\Omega_u|& \le \int_D|\nabla (u\vee v)|{}^2\,dx+\int_D|\nabla (u\wedge v)|{}^2\,dx+\Lambda |\Omega_{u\wedge v}|\\ & = \int_D|\nabla u|{}^2\,dx+\int_D|\nabla v|{}^2\,dx+\Lambda |\Omega_{v}|, \end{aligned} $$

which concludes the proof of (4.1). □

FormalPara Remark 4.3 (On the Terminology: Inwards Optimality and Subsolutions; Outwards Optimality and Supersolutions)

We will often call the optimality conditions (4.2) and (3.1) inwards and outwards optimality condition, respectively. This is justified by the fact that the admissible test functions in (4.2) and (3.1) have positivity sets contained in or containing Ω_u. On the other hand, we will call (4.1) and (3.3) suboptimality condition and superoptimality condition, respectively, and the functions satisfying (4.1) and (3.3) will be called subsolutions and supersolutions. The terms inwards optimality and outwards optimality come from Geometric Analysis. The term subsolution was introduced in Shape Optimization by Bucur [8], originally to indicate inwards optimality with respect to shape functionals. The term supersolution appeared in the same context in several works (see for instance [51] and the references therein) to indicate outwards optimality. In the context of the functional $\mathcal F_\Lambda$, it seems more appropriate to use the terms subsolution and supersolution, when the condition is on the test functions, and the terms inwards and outwards, when the condition is on their (superlevel) sets. Nevertheless, being partially justified by Lemmas 3.3 and 4.2, we will often abuse this terminology by using subsolution and inwards-minimizing, and supersolution and outwards-minimizing as synonyms.

We will give two different proofs of the non-degeneracy. Lemma 4.4 is due to Alt and Caffarelli (see [3]), while Lemma 4.5 is due to David and Toro, it requires the function to be Lipschitz continuous, but the argument is more versatile and can be easily adapted, for instance, to the case of almost-minimizers of the functional $\mathcal F_\Lambda$ (see [19]).

FormalPara Lemma 4.4 (Non-degeneracy: Alt-Caffarelli)

Let $D\subset \mathbb {R}^d$ be a bounded open set. Suppose that u ∈ H ¹(D) satisfies the condition (4.1) and let x ₀ ∈ D. If $x_0\in \overline \Omega _u\cap D$ , then for every ball B _r(x ₀) ⊂ D, we have that $\|u\|{ }_{L^\infty (B_r(x_0))}\ge \Lambda ^{{1}/{2}}c_d\, r$ , where c _d > 0 is a dimensional constant.

FormalPara Proof

Without loss of generality we can suppose that x ₀ = 0 and that Λ = 1. For r > 0, let ϕ _r be the solution of

Then we have $\phi _r(x)=\phi _1\left (\frac {x}r\right )$, for every . We consider the function $\tilde u\in H^1_{loc}(\Omega )$ defined by

where $M_{2r}=\|u\|{ }_{L^{\infty }(B_{2r})}$. By the optimality of u in B _2r, we have that

$$\displaystyle \begin{aligned} \mathcal F_1(u,B_{2r})\le \mathcal F_1(\tilde u,B_{2r}), \end{aligned}$$

which means that

Since $\{u>0\}=\{\tilde u>0\}$ in , we get that

and so, we can estimate

Now, since

by the definition of $\tilde u$, we obtain

On the other hand, we have the following trace inequality

$$\displaystyle \begin{aligned} \int_{\partial B_r}u\,d\mathcal{H}^{d-1}& \le C_d\left(\int_{B_r}|\nabla u|\,dx+\frac 1r\int_{B_r}u\,dx\right)\\ & \le C_d\left(\int_{B_r}|\nabla u|{}^2\,dx+\left(1+\frac{M_r}r\right)\big|\{u>0\}\cap B_r\big|\right)\le C_d\left(1+\frac{M_r}r\right)\mathcal F_1(u,B_r). \end{aligned} $$

Thus, if $\mathcal F_1(u,B_r)>0$, then we have

$$\displaystyle \begin{aligned} 1\le C_d\left(1+\frac{M_r}r\right)\frac{M_{2r}}{2r}, \end{aligned}$$

which gives the claim. □

FormalPara Lemma 4.5 (Non-degeneracy: David-Toro)

Suppose that $D\subset \mathbb {R}^d$ is a bounded open set and $u:D\to \mathbb {R}$ is a non-negative Lipschitz continuous functions satisfying the optimality condition (4.1). Then, there is a constant κ ₀ > 0, depending on the dimension d, the Lipschitz constant $L=\|\nabla u\|{ }_{L^\infty (D)}$ and the constant Λ, such that:

FormalPara Proof

The proof is a consequence of the following three claims: Claim 1 Suppose that . Then,

$$\displaystyle \begin{aligned} u\le \kappa_1r\quad \text{on}\quad B_{\frac{r}2}(x_0)\quad \mathit{where}\quad \kappa_1=2^d\kappa_0. \end{aligned}$$

Claim 2 Suppose that u ≤ κ ₁ r on B _r∕2(x ₀). Then,

$$\displaystyle \begin{aligned} \big|\Omega_u\cap B_{\frac{r}2}(x_0)\big|\le \kappa_2|B_r|\quad \mathit{where}\quad \kappa_2=\frac{6L+9\kappa_1}\Lambda\,\kappa_1. \end{aligned}$$

Claim 3 Suppose that | Ω_u ∩ B _r∕2(x ₀)| ≤ κ ₂|B _r| and $\|u\|{ }_{L^\infty (B_{\frac {r}2}(x_0))}\le \kappa _1r$. Then, for every y ₀ ∈ B _r∕8(x ₀), there is $\rho \in \left [\frac {r}4,\frac {r}8\right ]$ such that

We first prove Claim 1. Let h be the harmonic extension of u in the ball B _r(x ₀). By the strong maximum principle, we have that u ≤ h on B _r(x ₀) (we notice that the optimality condition (4.1) trivially implies that the function u is subharmonic). On the other hand, the Poisson formula implies that

$$\displaystyle \begin{aligned} h(y)=\frac{r^2-|y|{}^2}{d\omega_d r}\int_{\partial B_r(x_0)}\frac{u(\zeta)}{|y-\zeta|{}^d}\,d\mathcal{H}^{d-1}(\zeta)\le 2^{d}\kappa_0 r, \end{aligned}$$

which gives Claim 1.

In order to prove Claim 2, we consider the function $\phi \in C^\infty _c(B_r)$ such that

$$\displaystyle \begin{aligned} 0\le \phi\le 1\quad \text{on}\quad B_r(x_0),\qquad \phi=1\quad \text{on}\quad B_{\frac{r}2}(x_0),\qquad |\nabla \phi|\le 3r^{-1}. \end{aligned}$$

Consider the competitor v = (u − κ ₁ rϕ)₊. Then, the optimality of u in B _r(x ₀) implies that

$$\displaystyle \begin{aligned} \Lambda |\Omega_u\cap B_{\frac{r}2}(x_0)|& \le \Lambda |\Omega_u\cap B_r(x_0)|-\Lambda |\Omega_v\cap B_r(x_0)|\le \int_{B_r(x_0)}|\nabla v|{}^2\,dx-\int_{B_r(x_0)}|\nabla u|{}^2\,dx\\ & \le \int_{B_r(x_0)}|\nabla (u-\kappa_1r\phi)|{}^2\,dx-\int_{B_r(x_0)}|\nabla u|{}^2\,dx\\ & \le 2\kappa_1r\int_{B_r(x_0)}|\nabla u|\,|\nabla\phi|\,dx+\kappa_1^2r^2\int_{B_r(x_0)}|\nabla\phi|{}^2\,dx\le \left(6\kappa_1L+9\kappa_1^2\right)|B_r|, \end{aligned} $$

which concludes the proof of Claim 2.

Let us now prove Claim 3. We first estimate

$$\displaystyle \begin{aligned} \int_{B_{\frac{r}2}(x_0)}u\,dx\le \|u\|{}_{L^\infty(B_{\frac{r}2}(x_0))}|\Omega_u\cap B_{\frac{r}2}(x_0)|\le \kappa_1 \kappa_2|B_r| r. \end{aligned} $$

Now, taking y ₀ ∈ B _r∕8(x ₀), we have , so there is ρ such that r∕8 ≤ ρ ≤ r∕4 and

$$\displaystyle \begin{aligned} \int_{\partial B_\rho(y_0)}u\,d\mathcal{H}^{d-1}\le \frac{8}{r}\int_{\frac{r}8}^{\frac{r}4}\int_{\partial B_s(y_0)}u\,d\mathcal{H}^{d-1}\,ds& \le \frac{8}{r}\int_{B_{\frac{r}2}(x_0)}u\,dx\\ & \le 8\kappa_1 \kappa_2|B_r|\le 8^{d+1}\kappa_1 \kappa_2\omega_d\rho^d, \end{aligned} $$

which concludes the proof of Claim 3.

We are now in position to conclude the proof of the lemma. We first notice that

$$\displaystyle \begin{aligned} \kappa_3\le 8^{d+1}\kappa_1\kappa_2\le 2^{7d+8}\frac{L+\kappa_0}{\Lambda}\kappa_0^2. \end{aligned}$$

Choosing

$$\displaystyle \begin{aligned} \kappa_0=\inf\left\{1,\frac{\Lambda}{(L+1)2^{7d+8}}\right\}, \end{aligned}$$

we get that κ ₃ ≤ κ ₀. In particular, if , then for any y ₀ ∈ B _r∕8(x ₀) there is a sequence ρ _j, j ≤ 1, such that $\displaystyle \frac {r}8\le \rho _1\le \frac {r}4$ and

In particular, this implies that u = 0 in B _r∕8(x ₀), which proves the claim. □