Abstract
The magic wand \(\mathbin {-\!\!*}\) (also called separating implication) is a separation logic connective commonly used to specify properties of partial data structures, for instance during iterative traversals. A footprint of a magic wand formula  is a state that, combined with any state in which A holds, yields a state in which B holds. The key challenge of proving a magic wand (also called packaging a wand) is to find such a footprint. Existing package algorithms either have a high annotation overhead or, as we show in this paper, are unsound.
is a state that, combined with any state in which A holds, yields a state in which B holds. The key challenge of proving a magic wand (also called packaging a wand) is to find such a footprint. Existing package algorithms either have a high annotation overhead or, as we show in this paper, are unsound.
We present a formal framework that precisely characterises a wide design space of possible package algorithms applicable to a large class of separation logics. We prove in Isabelle/HOL that our formal framework is sound and complete, and use it to develop a novel package algorithm that offers competitive automation and is sound. Moreover, we present a novel, restricted definition of wands and prove in Isabelle/HOL that it is possible to soundly combine fractions of such wands, which is not the case for arbitrary wands. We have implemented our techniques for the Viper language, and demonstrate that they are effective in practice.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others


1 Introduction
Separation logic [38] (SL hereafter) is a program logic that has been widely used to prove complex properties of heap-manipulating programs. The two main logical connectives that enable such reasoning are the separating conjunction \(*\) and the separating implication (more commonly known as the magic wand) \(\mathbin {-\!\!*}\), in combination with resource assertions which represent e.g. exclusive ownership of (and permission to access) particular heap locations. The separating conjunction expresses that two assertions prescribe ownership of disjoint parts of the heap, useful, for instance, to reason about aliasing or race conditions. More precisely, the assertion \(A*B\) holds in a program state \(\sigma \) if and only if \(\sigma \) can be split into two compatible program states \(\sigma _A\) and \(\sigma _B\) such that A and B hold in \(\sigma _A\) and \(\sigma _B\), respectively. In SL, heaps of program states are partial maps from locations to values; their domains represent heap locations exclusively owned. Two program states are compatible if (the domains of) their heaps are disjoint.
Intuitively, a magic wand  can be used to express the difference between the heap locations that B and A provide permission to access. The magic wand is useful, for instance, to specify partial data structures, where B specifies the entire data structure and A specifies a part that is missing [33, 41].
can be used to express the difference between the heap locations that B and A provide permission to access. The magic wand is useful, for instance, to specify partial data structures, where B specifies the entire data structure and A specifies a part that is missing [33, 41].  holds in a state \(\sigma _w\), if and only if for any program state \(\sigma _A\) in which A holds and that is compatible with \(\sigma _w\), B holds in the state obtained by combining the heaps of \(\sigma _A\) and \(\sigma _w\). Thus, if
holds in a state \(\sigma _w\), if and only if for any program state \(\sigma _A\) in which A holds and that is compatible with \(\sigma _w\), B holds in the state obtained by combining the heaps of \(\sigma _A\) and \(\sigma _w\). Thus, if  holds in a state, then so does B, analogously to the modus ponens inference rule in propositional logic.
holds in a state, then so does B, analogously to the modus ponens inference rule in propositional logic.
The magic wand has been shown to enable or greatly simplify proofs in many different cases [1, 9, 20, 21, 28, 33, 41, 42]. For instance, Yang [42] uses the magic wand to prove the Schorr-Waite graph marking algorithm. Dodds et al. [20] employ the wand to specify synchronisation barriers for deterministic parallelism. Examples using magic wands to specify partial data structures include tracking ongoing traversals of a data structure [33, 41], where the left-hand side of the wand specifies the part of the data structure yet to be traversed, or for specifying protocols that enforce orderly modification of data structures [21, 25, 28] (e.g. the protocol governing Java iterators). More recently, wands have been used for formal reasoning about borrowed references in the Rust programming language, which employs an ownership type system to ensure memory safety [1]. Magic wands concisely represent the remainder of a data structure from which a borrowed reference was taken, as well as reflecting back modifications to the part accessible via the reference. For example, consider a struct Point (represented by a SL predicate Point) with two fields x and y of type i32 (represented by the SL predicate i32). A Rust method that takes as input a Point p and returns a borrow of its field x is specified with the postcondition  , thus enabling the caller to regain ownership of the entire data structure Point(p).
, thus enabling the caller to regain ownership of the entire data structure Point(p).
The complexity of SL proofs has given rise to a variety of automatic SL verifiers that reduce the required proof effort. Given the usefulness of magic wands, it is important that such verifiers also provide automatic support for wands. However, reasoning about a magic wand requires reasoning about all states in which the left-hand side holds, which is challenging. It has been shown that a separation logic even without the separating conjunction (but with the magic wand) is as expressive as a variant of second-order logic and, thus, undecidable [6].
Two different approaches [3, 39] that provide partially-automated support are implemented in the verifiers Viper [34] and VerCors [2]. However, the approach implemented in VerCors [3] incurs significant annotation overhead, and the approach in Viper [39] suffers from a fundamental, previously undiscovered flaw that renders the approach unsound. Both approaches require user-provided package operations to direct the verifier’s proof search. Packaging a wand  expresses that the verifier should prove and subsequently record
expresses that the verifier should prove and subsequently record  . To package
. To package  the verifier must split the current state into two compatible states \(\sigma '\) and \(\sigma _w\) such that
the verifier must split the current state into two compatible states \(\sigma '\) and \(\sigma _w\) such that  holds in \(\sigma _w\). We call \(\sigma _w\) a footprint of the wand. After successfully packaging a wand, the verifier must disallow changes to \(\sigma _w\) to preserve the wand’s validity: the verifier packages the footprint into the wand.
holds in \(\sigma _w\). We call \(\sigma _w\) a footprint of the wand. After successfully packaging a wand, the verifier must disallow changes to \(\sigma _w\) to preserve the wand’s validity: the verifier packages the footprint into the wand.
The key challenge for supporting magic wands in automatic verifiers is to define a package algorithm that packages a wand. In VerCors’s package algorithm [3], a user must manually specify a footprint for the wand and the algorithm checks whether the wand holds in the specified footprint. This leads to a lot of annotation overhead. Viper’s current package algorithm [39] reduces this overhead significantly by automatically inferring a suitable footprint. Unfortunately, as we show in this paper, Viper’s current algorithm has a fundamental flaw that causes the algorithm to infer an incorrect footprint in certain cases, which may lead to unsound reasoning. We will explain the fundamental flaw in Sect. 2; it illustrates the subtlety of supporting this important connective.
Approach and Contributions. In this paper, we present a formal foundation for sound package algorithms, and we implement a novel such algorithm based on these foundations. Our algorithm requires the same annotation overhead as the prior, flawed Viper algorithm, which is (to our knowledge) the most automatic existing approach. We introduce a formal framework expressed via a novel package logic that defines the design space for package algorithms. The soundness of a package algorithm can be justified by showing that the algorithm finds a proof in our package logic. The design space for package algorithms is large since there are various aspects that affect how one expresses the algorithm including (1) which footprint an algorithm infers or checks (there are often multiple options, see Sect. 3), (2) the state model (which differs between different SL verifiers), and (3) restricted definitions of wands (for instance, to ensure each wand has a unique minimal footprint). Our package logic deals with (1) by capturing all sound derivations for the same wand. To deal with (2) and (3), our logic is parametric along multiple dimensions. For instance, the state model can be any separation algebra to support different SL extensions (e.g. fractional permissions [4]).
Our logic also supports parameters to restrict the allowed footprints for wands in systematic ways. Such restrictions are useful, for instance, in a logic supporting fractional permissions. Fractional permissions permit splitting ownership/resources into shared fragments which typically permit read access to the underlying data. However, as we show in Sect. 4, fractional parts of general magic wands cannot always be soundly recombined. Existing solutions for other connectives impose side conditions to enable sound recombinations [29], which are often hard to check automatically. We instead introduce a novel restriction of magic wands to avoid such side conditions and develop a corresponding second package algorithm again based on the formal framework provided by our package logic.
We make the following contributions:
-
We formalise a package logic that can be used as a basis for a wide range of package algorithms (Sect. 3). The logic has multiple parameters including: a separation algebra to model the states and a parameter to restrict the definition of a wand in a systematic way. We formally prove the logic sound and complete for any instantiation of the parameters in Isabelle/HOL [13].
-
We develop a novel, restricted definition of a wand (Sect. 4) and prove in Isabelle/HOL that this wand can always be recombined [14].
-
We implement sound package algorithms for both the standard and the restricted wand in the Viper verifier and justify their soundness directly via our package logic (Sect. 5). We evaluate both algorithms on the Viper test suite. Our evaluation shows that (1) our algorithms perform similarly well to prior work and correctly reject examples where prior work is unsound, and (2) our restricted wand definition is expressive enough for most examples.
Our Isabelle formalisation and the implementation of our new package algorithm are publicly available [13,14,15]. Further details are available in our accompanying technical report (TR hereafter) [16].
2 Background and Motivation
In this section, we present the necessary background for this paper. We use implicit dynamic frames [40] to represent SL assertions, since both existing automatic verifiers that support wands (VerCors and Viper) are based on it. There is a known strong correspondence between SL and implicit dynamic frames [36].
2.1 Implicit Dynamic Frames
Just like SL assertions, implicit dynamic frames (IDF hereafter) assertions specify not only value information, but also permissions to heap locations that are allowed to be accessed. To justify dereferencing a heap location, the corresponding permission is required, ensuring memory safety. IDF assertions specify permissions to locations and value information separately. An assertion  (an accessibility predicate) denotes permission to the heap location x.val, while
(an accessibility predicate) denotes permission to the heap location x.val, while  expresses that x.val contains value v. The separating conjunction in IDF enforces disjointness (formally: acts multiplicatively) with respect to resource assertions such as accessibility predicates; in particular, if
expresses that x.val contains value v. The separating conjunction in IDF enforces disjointness (formally: acts multiplicatively) with respect to resource assertions such as accessibility predicates; in particular, if  holds in a state, then x and y must be different (analogously to SL).
holds in a state, then x and y must be different (analogously to SL).
The main difference between IDF and SL is that SL does not allow general heap-dependent expressions such as x.val = v or x.left.right [40] to be specified separately from the permissions to the heap locations they depend on. The IDF assertion  must be expressed in SL via the points-to assertion
must be expressed in SL via the points-to assertion  , which also conveys exclusive permission to the location x.val. IDF supports heap dependent expressions within self-framing assertions: those which require permissions to all the heap locations on whose values they depend (e.g.
, which also conveys exclusive permission to the location x.val. IDF supports heap dependent expressions within self-framing assertions: those which require permissions to all the heap locations on whose values they depend (e.g.  is self-framing but x.val = v is not) [40].
is self-framing but x.val = v is not) [40].
The code on the left finds the leftmost leaf of a binary tree and includes specifications to prove memory safety. The predicate describing the permissions of a tree is defined on the right. The loop invariant uses a wand to summarise the permissions of the input tree excluding the tree not yet traversed. The blue operations are ghost operations to guide the verifier; we omit those specific to predicates. The package requires further hints in existing approaches, see App. J of the TR [16]. (Color figure online)
2.2 A Typical Example Using Magic Wands
Figure 1 shows a variation of an example from the VerifyThis competition [22]. The method leftLeaf iteratively computes the leftmost leaf of a binary tree (package and apply operations, shown in blue, should be ignored for now). The pre- and postconditions of leftLeaf are both Tree(x), which is a predicate instance used to specify all permissions to the fields of the tree rooted at x (the recursive definition of this predicate is on the right of Fig. 1). Proving this specification amounts to proving that leftLeaf is memory-safe and that the permissions to the input tree are preserved, enabling further calls on the same tree.
The key challenge when verifying leftLeaf is specifying an appropriate loop invariant. The loop invariant must track the permissions to the subtree rooted at y that still needs to be traversed, since otherwise dereferencing y.left in the loop body is not allowed. Additionally, the invariant must track all of the remaining permissions in the input tree rooted at x (the permissions to the nodes already traversed and others unreachable from y), since otherwise the postcondition cannot be satisfied. The former can be easily expressed with Tree(y). The latter can be elegantly achieved with a magic wand  . This wand promises
. This wand promises  if one combines the wand with
if one combines the wand with  . That is, the wand represents (at least) the difference between the permissions making up the two trees. Using SL’s modus-ponens-like inference rule (directed by the apply operation on line 13, explained next), one can show that the loop invariant entails the postcondition.
. That is, the wand represents (at least) the difference between the permissions making up the two trees. Using SL’s modus-ponens-like inference rule (directed by the apply operation on line 13, explained next), one can show that the loop invariant entails the postcondition.
2.3 Wand Ghost Operations
Automatic SL verifiers such as GRASShopper [37], VeriFast [24], VerCors, and Viper generally represent permissions owned by a program state in two ways: by recording predicate instances (such as Tree(x) in Fig. 1) and direct permissions to heap locations. Magic wand instances provide a third way to represent permissions and are recorded analogously. Verifiers that support them require two wand-specific ghost operations, which instruct the verifiers when to prove a wand and when to apply a recorded wand instance using SL’s modus-ponens-like rule.
A package ghost operation expresses that a verifier should prove a new wand instance in the current state and report an error if the proof attempt fails. To prove a new wand instance, the verifier must split the current state into two states  and
and  such that the wand holds in the footprint state
such that the wand holds in the footprint state  ; on success, permissions in the footprint are effectively exchanged for the resulting magic wand instance. We call a procedure that selects a footprint by splitting the current state a package algorithm. On lines 5 and 10 of Fig. 1, new wands are packaged to establish and preserve the invariant, respectively.
; on success, permissions in the footprint are effectively exchanged for the resulting magic wand instance. We call a procedure that selects a footprint by splitting the current state a package algorithm. On lines 5 and 10 of Fig. 1, new wands are packaged to establish and preserve the invariant, respectively.
The apply operation applies a wand  using SL’s modus-ponens-like rule if the verifier records a wand instance of
using SL’s modus-ponens-like rule if the verifier records a wand instance of  and A holds in the current state (and otherwise fails), exchanging these for the assertion B. The apply operation is directly justified by the wand’s semantics: Combining a wand’s footprint with any state in which A holds is guaranteed to yield a state in which B holds. For the apply operation on line 13 of Fig. 1, the verifier removes the applied wand instance and Tree(y), in exchange for the predicate instance Tree(x).
and A holds in the current state (and otherwise fails), exchanging these for the assertion B. The apply operation is directly justified by the wand’s semantics: Combining a wand’s footprint with any state in which A holds is guaranteed to yield a state in which B holds. For the apply operation on line 13 of Fig. 1, the verifier removes the applied wand instance and Tree(y), in exchange for the predicate instance Tree(x).
2.4 The Footprint Inference Attempt (FIA)
Package algorithms differ in how a footprint for the specified magic wand is selected. In VerCors [3], the user must manually provide the footprint and the algorithm checks whether the specified footprint is correct. In Viper’s current approach [39], a footprint is inferred. We explain and compare to the latter approach since it is the more automatic of the two; hereafter, we refer to its package algorithm as the Footprint Inference Attempt (FIA). Inferring a correct footprint is challenging due the complexity of the wand connective. In particular, we have discovered that, in certain cases, the FIA infers incorrect footprints, leading to unsound reasoningFootnote 1. The goal of this subsection is to understand the FIA’s key ideas, which our solution will build on, and why it is unsound.
In general, there may be multiple valid footprints for a magic wand  . The FIA attempts to infer a footprint which is as close as possible to the difference between the permissions required by B and A, taking as few permissions as possible while aiming for a footprint compatible with A (so that the resulting wand can be later applied) [39]. That is, the FIA includes only permissions in the footprint it infers that are specified by B and not guaranteed by A.
. The FIA attempts to infer a footprint which is as close as possible to the difference between the permissions required by B and A, taking as few permissions as possible while aiming for a footprint compatible with A (so that the resulting wand can be later applied) [39]. That is, the FIA includes only permissions in the footprint it infers that are specified by B and not guaranteed by A.
For a wand  , the FIA constructs an arbitrary state
, the FIA constructs an arbitrary state  that satisfies A (representing
that satisfies A (representing  symbolically). Then, the FIA tries to construct a state
symbolically). Then, the FIA tries to construct a state  in which B holds by taking permissions (and copying corresponding heap values) from
in which B holds by taking permissions (and copying corresponding heap values) from  if possible and the current state otherwise. If this algorithm succeeds, the (implicit) inferred footprint consists of the permissions that were taken from the current state. The FIA constructs
if possible and the current state otherwise. If this algorithm succeeds, the (implicit) inferred footprint consists of the permissions that were taken from the current state. The FIA constructs  by iterating over the permissions and logical constraints in B. For each permission, the FIA checks whether
by iterating over the permissions and logical constraints in B. For each permission, the FIA checks whether  owns the permission. If so, the FIA adds the permission to
owns the permission. If so, the FIA adds the permission to  and removes the permission from
and removes the permission from  . Otherwise, the FIA removes the permission from the current state or fails if the current state does not have the permission. For each logical constraint, the FIA checks that the constraint holds in
. Otherwise, the FIA removes the permission from the current state or fails if the current state does not have the permission. For each logical constraint, the FIA checks that the constraint holds in  as constructed so far. We show an example of the FIA correctly packaging a wand in App. A of the TR [16].
as constructed so far. We show an example of the FIA correctly packaging a wand in App. A of the TR [16].
Unsoundness of the FIA. We have discovered that for some wands  , the FIA determines an incorrect footprint for the magic wand. This unsoundness can arise when the FIA performs a case split on the content of the arbitrary state
, the FIA determines an incorrect footprint for the magic wand. This unsoundness can arise when the FIA performs a case split on the content of the arbitrary state  satisfying A. In such situations, the FIA infers a footprint for each case separately, making use of properties that hold in that case. For certain wands, this leads to different footprints being selected for each case, while none of the inferred footprints can be used to justify B in all cases, i.e. for all states
satisfying A. In such situations, the FIA infers a footprint for each case separately, making use of properties that hold in that case. For certain wands, this leads to different footprints being selected for each case, while none of the inferred footprints can be used to justify B in all cases, i.e. for all states  that satisfy A. As a result, the packaged wand does not hold in any of the inferred footprints, which can make verification unsound, as we illustrate below.
that satisfy A. As a result, the packaged wand does not hold in any of the inferred footprints, which can make verification unsound, as we illustrate below.
The wand  illustrates the problem. For this wand, every state
illustrates the problem. For this wand, every state  satisfying the left-hand side must have permission to x.f. However x.f may either point to y or z. If x.f points to y in
satisfying the left-hand side must have permission to x.f. However x.f may either point to y or z. If x.f points to y in  , then to justify the right-hand side’s second conjunct, the footprint must contain permission to y.g. Analogously, if x.f points to z in
, then to justify the right-hand side’s second conjunct, the footprint must contain permission to y.g. Analogously, if x.f points to z in  , then the footprint must contain permission to z.g. The wand’s semantics requires a footprint to justify the wand’s right-hand side for all states in which the left-hand side holds, and thus, a correct footprint must be able to justify both cases. Hence, the footprint must have permission to both y.g and z.g. However, the FIA’s inferred footprint is in effect the disjunction of these two permissions.
, then the footprint must contain permission to z.g. The wand’s semantics requires a footprint to justify the wand’s right-hand side for all states in which the left-hand side holds, and thus, a correct footprint must be able to justify both cases. Hence, the footprint must have permission to both y.g and z.g. However, the FIA’s inferred footprint is in effect the disjunction of these two permissions.
Packaging the above wand w using the FIA leads to unsound reasoning. After the incorrect package described above in a state with permission to x.f, y.g, and z.g, the assertion  can be proved since the FIA removes permission to either y.g or z.g from the current state, but not both. However, this assertion does not actually hold! According to the semantics of wands, w’s footprint must include permission to x.f or permission to both y.g and z.g, which implies that the assertion
can be proved since the FIA removes permission to either y.g or z.g from the current state, but not both. However, this assertion does not actually hold! According to the semantics of wands, w’s footprint must include permission to x.f or permission to both y.g and z.g, which implies that the assertion  is equivalent to false.
is equivalent to false.
The unsoundness of the FIA shows the subtlety and challenge of developing sound package algorithms. Algorithms that soundly infer a single footprint for all states in which the wand’s left-hand side holds must be more involved than the FIA. Ensuring their soundness requires a formal framework to construct them and justify their correctness. We introduce such a framework in the next section.
3 A Logical Framework for Packaging Wands
In this section, we present a new logical framework that defines the design space for (sound) package algorithms. The core of this framework is our package logic, which defines the space of potential algorithmic choices of a footprint for a particular magic wand. Successfully packaging a wand in a given state is (as we will show) equivalent to finding a derivation in our package logic, and any actual package algorithm must correspond to a proof search in our logic (if it is sound). In particular, we provide soundness (Theorem 1) and completeness (Theorem 2) results for our logic. We define a specific package algorithm with this logic at its foundation, inspired by the FIA package algorithm [39] (described in Sect. 2.4) but amending its unsoundness, resulting in (to the best of our knowledge) the first sound and relatively automatic package algorithm.
All definitions and results in this section have been fully mechanised [13] in Isabelle/HOL. Our mechanised definitions are parametric with the underlying verification logic in various senses: the underlying separation algebra is a parameter, the syntax of assertions is defined in a way which allows simple extension with different base cases and connectives, and the semantics of magic wands itself can be restricted if only particular kinds of footprint are desired in practice. As a specific example of the latter parameter, in Sect. 4 we define a novel restriction of magic wand footprints which guarantees better properties in combination with certain usages of fractional permissions; this is seamlessly supported by the general package logic presented here. Nonetheless, to simplify the exposition of this section, we will assume that any magic wand footprint satisfying the connective’s standard semantics is an acceptable result.
3.1 Footprint Selection Strategies
As we explained in Sect. 1, there is a wide design space for package algorithms; in particular, many potential strategies for finding a magic wand’s footprint exist and none is clearly optimal. Recall that a footprint is a state, and thus consists of permissions to certain heap locations as well as storing their corresponding values; for simplicity we identify a footprint by the permissions it contains.
For example, consider the following magic wand (using fractional permissions)  . Suppose this magic wand is to be packaged in a state where full permissions to both x.b and x.f are held, and the value of x.b is currently false. Two valid potential footprints are:
. Suppose this magic wand is to be packaged in a state where full permissions to both x.b and x.f are held, and the value of x.b is currently false. Two valid potential footprints are:
-
1.
Full permission to x.f. This is sufficient to guarantee the right-hand side will hold regardless of the value that x.b has by the time the wand is applied.
-
2.
Half permission to x.b. By including this permission, the fact that x.b is currently false is also included, and thus permission to x.f is not needed.
There is no clear reason to prefer one choice over the other: different package algorithms (or manual choices) might choose either. Our package logic allows either choice along with any of many less optimal choices, such as taking both permissions. On the other hand, as motivated earlier in Sect. 3.1, our package logic must (and does) enforce that a single valid footprint is chosen for a wand that works for each and every potential state satisfying its left-hand side.
3.2 Package Logic: Preliminaries
To capture different state models and flavours of separation logic, our package logic is parameterised by a separation algebra. For space reasons, we present here a simplified overview of this algebra, but all definitions (including our assertion semantics) are given in App. D of the TR [16] and have been mechanised. We consider a separation algebra [8, 19] where  is the set of states,
is the set of states,  is a partial operation that is commutative and associative, and
is a partial operation that is commutative and associative, and  , which corresponds to the empty state, is a neutral element for \(\oplus \). We write \(\succeq \) for the induced partial order of the resulting partial commutative monoid, and
, which corresponds to the empty state, is a neutral element for \(\oplus \). We write \(\succeq \) for the induced partial order of the resulting partial commutative monoid, and  iff
iff  is defined (i.e.
is defined (i.e.  and
and  are compatible). Finally, if
are compatible). Finally, if  , we define the subtraction
, we define the subtraction  to be the \(\succeq \)-largest state
to be the \(\succeq \)-largest state  such that
such that  .
.
We define our package logic for an assertion language with the following grammar: \(A = A{*}A \mid \mathcal {B} {\Rightarrow } A \mid \mathcal {B}\), where A ranges over assertions and \(\mathcal {B}\) over semantic assertions. To allow our package logic to be applied to a variety of underlying assertion logics, we distinguish only the two most-relevant connectives: the separating conjunction and an implication (for expressing conditional assertions). To support additional constructs of the assertion logic, the third type of assertion we consider is a semantic assertion, i.e. a function from  to Booleans. This third type can be instantiated to represent logical assertions that do not match the first two cases. In particular, assertions such as x.f = 5, acc(x.f), abstract predicates (such as Tree(x)) or magic wands can be represented as semantic assertions. This core assertion language can also be easily extended with native support for e.g. the logical conjunction and disjunction connectives; we explain in App. E of the TR [16] how to extend the rules of the logic accordingly.
to Booleans. This third type can be instantiated to represent logical assertions that do not match the first two cases. In particular, assertions such as x.f = 5, acc(x.f), abstract predicates (such as Tree(x)) or magic wands can be represented as semantic assertions. This core assertion language can also be easily extended with native support for e.g. the logical conjunction and disjunction connectives; we explain in App. E of the TR [16] how to extend the rules of the logic accordingly.
3.3 The Package Logic
We define our package logic to prescribe the design space of algorithms for deciding how, in an initial state  , to select a valid footprint (or fail) for a magic wand
, to select a valid footprint (or fail) for a magic wand  . The aim is to infer states
. The aim is to infer states  and
and  that partition
that partition  (i.e.
(i.e.  ) such that
) such that  is a valid footprint for
is a valid footprint for  (when combined with any compatible state satisfying A, the resulting state satisfies B). In particular, all permissions (and logical facts) required by the assertion B must either come from the footprint or be guaranteed to be provided by any compatible state satisfying A.
(when combined with any compatible state satisfying A, the resulting state satisfies B). In particular, all permissions (and logical facts) required by the assertion B must either come from the footprint or be guaranteed to be provided by any compatible state satisfying A.
Recall from Sect. 2.4 that the mistake underlying the FIA approach ultimately resulted from allowing multiple different footprints to be selected conditionally on a state satisfying A, rather than a single footprint which works for all such states. Our package logic addresses this concern by defining judgements in terms of the set of all states satisfying A; whenever any of these tracked states is insufficient to provide a permission required by B, our logic will force this permission to be added in general to the wand’s footprint (taken from the current state).
A witness set S is a set of pairs of states  ; conceptually, the first represents the state available for trying to prove B in addition to the current state; this is initially a state satisfying the wand’s left-hand side A. The second represents the state assembled (so-far) to attempt to satisfy the right-hand side B. We write \(S^1\) for the set of first elements of all pairs in a witness set S. A context \(\varDelta \) is a pair
; conceptually, the first represents the state available for trying to prove B in addition to the current state; this is initially a state satisfying the wand’s left-hand side A. The second represents the state assembled (so-far) to attempt to satisfy the right-hand side B. We write \(S^1\) for the set of first elements of all pairs in a witness set S. A context \(\varDelta \) is a pair  of a state and a witness set; here,
of a state and a witness set; here,  represents the (as-yet unused remainder of the) current state in which the wand is being packaged.
represents the (as-yet unused remainder of the) current state in which the wand is being packaged.
The basic idea behind a derivation in our logic is to show how to assemble a witness set in which all second elements are states satisfying B, via some combinations of: (1) moving a part of the first element of a pair in the witness set into the second, and (2) moving a part of the outer state  into all first elements of the pairs (this becomes a part of the wand’s footprint). The actual judgements of the logic are a little more complex, to correctly record any hypotheses (called path-conditions) that result from deconstructing conditional assertions in B.
into all first elements of the pairs (this becomes a part of the wand’s footprint). The actual judgements of the logic are a little more complex, to correctly record any hypotheses (called path-conditions) that result from deconstructing conditional assertions in B.
Configurations and Reductions. A configuration represents a current objective in our package logic: the part of the wand’s right-hand side still to be satisfied as well as the current state of a footprint computation. A configuration is a triple  , where B is an assertion, pc is a path condition (a function from
, where B is an assertion, pc is a path condition (a function from  to Booleans), and
to Booleans), and  is a context. Conceptually, B is the assertion still to be satisfied, pc represents hypotheses we are currently working under, and the context
is a context. Conceptually, B is the assertion still to be satisfied, pc represents hypotheses we are currently working under, and the context  tracks the current state and witness set, as described above.
tracks the current state and witness set, as described above.
A reduction is a judgement  , representing the achievement of the objective described via the configuration on the left, resulting in the final context on the right;
, representing the achievement of the objective described via the configuration on the left, resulting in the final context on the right;  is the new version of the outer state (and becomes the new current state after the package operation); whatever was removed from the initial outer state is implicitly the selected footprint state
is the new version of the outer state (and becomes the new current state after the package operation); whatever was removed from the initial outer state is implicitly the selected footprint state  . If a reduction is derivable in our package logic, this footprint
. If a reduction is derivable in our package logic, this footprint  guarantees that for all
guarantees that for all  , if
, if  , then
, then  satisfies \(\textit{pc}\Rightarrow B\). The condition
satisfies \(\textit{pc}\Rightarrow B\). The condition  ensures that the pair
ensures that the pair  actually corresponds to a state in which the wand can be applied given the chosen footprint
actually corresponds to a state in which the wand can be applied given the chosen footprint  , as we explain later. The package logic defines the steps an algorithm may take to achieve this goal.
, as we explain later. The package logic defines the steps an algorithm may take to achieve this goal.
We represent packaging a wand  in state
in state  by the derivation of a reduction
by the derivation of a reduction  , for some state
, for some state  and witness set \(S_1\). The path condition is initially true (we are not yet under any hypotheses). The initial witness set contains all pairs of a state
and witness set \(S_1\). The path condition is initially true (we are not yet under any hypotheses). The initial witness set contains all pairs of a state  that satisfies A and the empty state e, to which a successful reduction will add permissions in order to satisfy BFootnote 2. An actual algorithm need not explicitly compute this (possibly infinite) set, but can instead track it symbolically. If the algorithm finds a derivation of this reduction, it has proven that the difference between
that satisfies A and the empty state e, to which a successful reduction will add permissions in order to satisfy BFootnote 2. An actual algorithm need not explicitly compute this (possibly infinite) set, but can instead track it symbolically. If the algorithm finds a derivation of this reduction, it has proven that the difference between  and
and  is a valid footprint of the wand
is a valid footprint of the wand  , since the logic is sound (Theorem 1 below).
, since the logic is sound (Theorem 1 below).
Rules. Figure 2 presents the four rules of our logic, defining (via derivable reductions) how a configuration can be reduced to a context. There is a rule for each type of assertion B: Implication for an implication, Star for a separating conjunction, and Atom for a semantic assertion. The logic also includes the rule Extract, which represents a choice to extract permissions from the outer state and adds them to all pairs of states in the witness set. In the following, we informally write reducing an assertion to refer to the process of deriving (in the logic) that the relevant configuration containing this assertion reduces to some context.
To reduce an implication \(\mathcal {B} \Rightarrow A\), the rule Implication conjoins the hypothesis \(\mathcal {B}\) with the previous path condition, leaving A to be reduced. Informally, this expresses that satisfying \(pc \Rightarrow (b \Rightarrow A)\) is equivalent to satisfying \((pc \wedge b) \Rightarrow A\).
For a separating conjunction \(A_1 * A_2\), the Star rule expresses that both \(A_1\) and \(A_2\) must be reduced, in order to reduce \(A_1 * A_2\); permissions used in the reduction of the first conjunct must not be used again, which is reflected by the threading-through of the intermediate context \(\varDelta _1\).Footnote 3
The Atom rule specifies how to prove that all states in \(S^1\) (where S is the witness set) satisfy the assertion \(pc \Rightarrow \mathcal {B}\). To understand the premises, consider a pair  . If
. If  does not satisfy the path condition, i.e.
does not satisfy the path condition, i.e.  , then
, then  does not have to justify \(\mathcal {B}\), and thus the pair
does not have to justify \(\mathcal {B}\), and thus the pair  is left unchanged; this case corresponds to the set \(S_\bot \). Conversely, if
is left unchanged; this case corresponds to the set \(S_\bot \). Conversely, if  satisfies the path condition, i.e.
satisfies the path condition, i.e.  , then
, then  must satisfy \(\mathcal {B}\), and the corresponding permissions must be transferred from
must satisfy \(\mathcal {B}\), and the corresponding permissions must be transferred from  to
to  . Since some assertions may be satisfied in different ways, such as disjunctions, the algorithm has a choice in how to satisfy \(\mathcal {B}\), which might be different for each pair
. Since some assertions may be satisfied in different ways, such as disjunctions, the algorithm has a choice in how to satisfy \(\mathcal {B}\), which might be different for each pair  . This choice is represented by
. This choice is represented by  , which must satisfy \(\mathcal {B}\) and be smaller or equal to
, which must satisfy \(\mathcal {B}\) and be smaller or equal to  . We update the witness set by transferring
. We update the witness set by transferring  from
from  to
to  . This second case corresponds to the set \(S_\top \). Note that the Atom rule can be applied only if
. This second case corresponds to the set \(S_\top \). Note that the Atom rule can be applied only if  satisfies \(\mathcal {B}\), for all pairs
satisfies \(\mathcal {B}\), for all pairs  such that
such that  . If not, a package algorithm must either first extract more permissions from the outer state with the Extract rule, or fail.
. If not, a package algorithm must either first extract more permissions from the outer state with the Extract rule, or fail.
The \( Extract \) rule (applicable at any step of a derivation), expresses that we can extract permissions (the stateFootnote 4  ) from the outer state
) from the outer state  , and combine them with the first element of each pair of states in the witness set. Note that
, and combine them with the first element of each pair of states in the witness set. Note that  is removed from the witness set if
is removed from the witness set if  is not compatible with
is not compatible with  . In such cases, adding
. In such cases, adding  to
to  would create a pair in the witness set representing a state in which the wand cannot be applied. Consequently, there is no need to establish the right-hand side of the wand for this pair and our logic correspondingly removes it. Finally, the rule requires that we reduce the assertion A in the new context.
would create a pair in the witness set representing a state in which the wand cannot be applied. Consequently, there is no need to establish the right-hand side of the wand for this pair and our logic correspondingly removes it. Finally, the rule requires that we reduce the assertion A in the new context.
A package algorithm’s strategy is mostly reflected by how it uses the Extract rule. To package  from Sect. 3.1 one algorithm might use this rule to extract permission to x.f; another might use it to extract permission to x.b (if x.b had value false in the original state).
from Sect. 3.1 one algorithm might use this rule to extract permission to x.f; another might use it to extract permission to x.b (if x.b had value false in the original state).
Example of a Derivation. Let us now illustrate how these rules can be used to package the wand from Sect. 3.1,  . We omit the path condition since it is always the trivial condition \((\). Assume that the outer state
. We omit the path condition since it is always the trivial condition \((\). Assume that the outer state  is the addition of
is the addition of  , a state that contains permission to y.g and z.g, and
, a state that contains permission to y.g and z.g, and  .
.  is the initial witness set. We show below a part of a proof that
is the initial witness set. We show below a part of a proof that  is correct, and thus that
is correct, and thus that  is a correct footprint of the wand w (since
is a correct footprint of the wand w (since  ):
):

This derivation, which reflects the package algorithm that we will describe in Sect. 3.5, can be read from bottom to top and from left to right. Using the rule \( Star \), we split the assertion into its two conjuncts, acc(x.f) (on the left) and acc(x.f.g) (on the right). We then handle acc(x.f) using the rule \( Atom \). acc(x.f) holds in the first element of each pair of \(S_0\), since any state that satisfies the wand’s left-hand side owns x.f. Therefore, we use the rule \( Atom \) with a \( choice \) function that always chooses the relevant state with exactly full permission to x.f. \(S_1\) is the updated witness set where this permission to x.f has been transferred from the first to the second element of each pair of states. Next, we handle acc(x.f.g). We cannot do this directly using the rule \( Atom \) from \(S_1\). We know that, for each  , x.f.g evaluated in
, x.f.g evaluated in  is either y or z, but
is either y or z, but  owns neither y.g nor z.g. So, we transfer the permissions to both y.g and z.g from the outer state
owns neither y.g nor z.g. So, we transfer the permissions to both y.g and z.g from the outer state  to all states of \(S_1^1\), using the rule \( Extract \), which results in the context
to all states of \(S_1^1\), using the rule \( Extract \), which results in the context  ; \(\dagger \) represents the three other premises of the rule, namely
; \(\dagger \) represents the three other premises of the rule, namely  ,
,  , and \(S_2\)’s definition. Finally, we apply the rule \( Atom \) to prove
, and \(S_2\)’s definition. Finally, we apply the rule \( Atom \) to prove  , where the \( choice \) function chooses for each pair the corresponding state that contains full permission to x.f.g.
, where the \( choice \) function chooses for each pair the corresponding state that contains full permission to x.f.g.
3.4 Soundness and Completeness
We write \(\vdash \langle B, pc, \varDelta \rangle \rightsquigarrow \varDelta '\) to express that a reduction can be derived in the logic. As explained above, the goal of a package algorithm is to find a derivation of  . If it succeeds, then the difference between
. If it succeeds, then the difference between  and
and  is a valid footprint of
is a valid footprint of  , since our package logic is sound. In particular, we have proven the following soundness result in Isabelle/HOL:
, since our package logic is sound. In particular, we have proven the following soundness result in Isabelle/HOL:
Theorem 1
Soundness. Let B be a well-formedFootnote 5 assertion. If
-
1.
the set \(S_A\) contains all states that satisfy A. i.e.
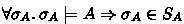 ,
, -
2.
 , and
, and -
3.
at least one of the following conditions holds:
-
(a)
B is intuitionistic
-
(b)
For all
 ,
,  contains no permission (i.e.
contains no permission (i.e.  )
)
-
(a)
then there exists a stable state  s.t.
s.t.  and
and  is a footprint of
is a footprint of  .
.
The third premise shows that, in an intuitionistic SL or in IDF, the correspondence between a derivation in the logic and a valid footprint of a wand is straightforward (case (a)). However, in classical SL, one must additionally check that all permissions in the witness set have been consumed (case (b)).
We have also proved in Isabelle/HOL that our package logic is complete, i.e. any valid footprint can be computed via a derivation in our package logic:
Theorem 2
Completeness. Let B be a well-formed (see footnote 5) assertion. If  is a stable footprint of
is a stable footprint of  , and
, and  , then there exists a witness set \(S'\) such that
, then there exists a witness set \(S'\) such that  .
.
3.5 A Sound Package Algorithm
We now describe an automatic package algorithm that corresponds to a proof search strategy in our package logic, and which is thus sound. To convey the main ideas, consider packaging a wand of the shape  .Footnote 6 Our algorithm traverses the assertion \(B_1 * \ldots * B_n\) from left to right, similarly to the FIA approach; this traversal is justified by repeated applications of the rule Star. Assume at some point during this traversal that the current context is
.Footnote 6 Our algorithm traverses the assertion \(B_1 * \ldots * B_n\) from left to right, similarly to the FIA approach; this traversal is justified by repeated applications of the rule Star. Assume at some point during this traversal that the current context is  . When we encounter the assertion \(B_i\), we have two possible cases:
. When we encounter the assertion \(B_i\), we have two possible cases:
-
1.
All states
 satisfy \(B_i\), which means that the permissions (or values) required by \(B_i\) are provided by the left-hand side of the wand. In this case, for each pair
satisfy \(B_i\), which means that the permissions (or values) required by \(B_i\) are provided by the left-hand side of the wand. In this case, for each pair  , we transfer permissions (and the corresponding values) to satisfy \(B_i\) from
, we transfer permissions (and the corresponding values) to satisfy \(B_i\) from  to
to  , using the rule Atom. Note that the transferred permissions might be different for each pair
, using the rule Atom. Note that the transferred permissions might be different for each pair  . This gives us a new witness set \(S'\), while the outer state
. This gives us a new witness set \(S'\), while the outer state  is left unchanged. We must then handle the next assertion \(B_{i+1}\) in the context
is left unchanged. We must then handle the next assertion \(B_{i+1}\) in the context  .
. -
2.
There is at least one pair
 such that \(B_i\) does not hold in
such that \(B_i\) does not hold in  . In this case, the algorithm fails if combining the permissions (and values) contained in the outer state with each
. In this case, the algorithm fails if combining the permissions (and values) contained in the outer state with each  is not sufficient to satisfy \(B_i\). Otherwise, we apply the rule Extract to transfer permissions from the outer state
is not sufficient to satisfy \(B_i\). Otherwise, we apply the rule Extract to transfer permissions from the outer state  to each state
to each state  in \(S^1\) such that \(B_i\) holds in
in \(S^1\) such that \(B_i\) holds in  . This gives us a new context
. This gives us a new context  . We can now apply the first case with the context
. We can now apply the first case with the context  .
.
4 Using the Logic with Combinable Wands
Extending SL with fractional permissions [4] is well-known to be useful for reasoning about heap-manipulating concurrent programs with shared state. In this setting, permission amounts are generalised to fractions \(0 \le p \le 1\). Reading a heap location is permitted if \(p > 0\), and writing if \(p = 1\), which permits concurrent reads and ensures exclusive writes. The assertion acc(x.f, p) holds in a state that has at least p permission to x.f. A permission amount \(p + q\) to a heap location x.f can be split into a permission amount p and a permission amount q, i.e.  , and these two permissions can be recombined, i.e.
, and these two permissions can be recombined, i.e.  .
.
This concept has been generalised [5, 7, 17, 23, 29] to fractional assertions \(A^p\), representing a fraction p of A. \(A^p\) holds in a state  iff there exists a state
iff there exists a state  in which A holds and
in which A holds and  is obtained from
is obtained from  by multiplying all permission amounts held by p [7, 29]; in this case, we write
by multiplying all permission amounts held by p [7, 29]; in this case, we write  . For example,
. For example,  , and
, and  (where Tree is the predicate defined in Fig. 1) expresses p permission to all nodes of the tree rooted in x.
(where Tree is the predicate defined in Fig. 1) expresses p permission to all nodes of the tree rooted in x.
Using fractional assertions, one might specify a function find, which searches a binary tree and yields a subtree whose root contains key key, as follows [7]:
 , in which ret corresponds to the return value of find. This postcondition is similar to the loop invariant in Fig. 1, except that it needs only a fraction p of Tree(x). A number of automatic SL verifiers, such as Caper [18], Chalice [31], VerCors [2], VeriFast [24], and Viper [34], support fractional assertions in some form.
, in which ret corresponds to the return value of find. This postcondition is similar to the loop invariant in Fig. 1, except that it needs only a fraction p of Tree(x). A number of automatic SL verifiers, such as Caper [18], Chalice [31], VerCors [2], VeriFast [24], and Viper [34], support fractional assertions in some form.
Combinable Assertions. While it is always possible to split an assertion \(A^{p+q}\) into \(A^p * A^q\), recombining \(A^p * A^q\) into \(A^{p+q}\) is sound only under some conditions, for example [29] if A is precise (in the usual SL sense [38]). We say that A is combinable iff the entailment \(A^p * A^q \models A^{p+q}\) holds for any two positive fractions p and q such that \(p + q \le 1\). As an example, acc(x.f) is combinable, but  is not because a state containing half permission to both x.f and x.g satisfies
is not because a state containing half permission to both x.f and x.g satisfies  , but not
, but not  . Combinable assertions are particularly useful to reason about concurrent programs, for instance, to combine the postconditions of parallel branches when they terminate [7].
. Combinable assertions are particularly useful to reason about concurrent programs, for instance, to combine the postconditions of parallel branches when they terminate [7].
However, a magic wand is in general not combinable, as we show below. This is problematic for SL verifiers; they cannot soundly combine wands, nor predicates that could possibly contain wands in their bodies. One way to prevent the latter is to forbid magic wands in predicate bodies entirely, but this limits the common usage of predicates to abstract over general assertions in specifications [35]. Another solution is to disallow combining fractional instances of a predicate if its body contains a wand, which means requiring additional annotations to “taint” such predicates transitively. This is overly restrictive for wands which are actually combinable and complicates reasoning about abstract predicate families [35].
To address this issue, we propose a novel restriction of the wand, called combinable wand (we use standard wand to refer to the usual, unrestricted connective). Unlike standard wands in general, a combinable wand is always combinable if its right-hand side is combinable. Thus, by only using combinable wands instead of standard wands, all assertions in logics such as those employed by VerCors and Viper can be made combinable without any of the other aforementioned restrictions regarding predicates. Section 5 shows that the restriction combinable wands impose is sufficiently weak for practical purposes. Finally, footprints of combinable wands can be automatically inferred by package algorithms built on our package logic. All results in this section have been proven in Isabelle/HOL.
Standard Wands are Not Combinable in General. Even if B is combinable, the standard wand  is, in general, not. As an example, the wand
is, in general, not. As an example, the wand  is not combinable, because \(w^{0.5} * w^{0.5} \not \models w\). To see this, consider two states
is not combinable, because \(w^{0.5} * w^{0.5} \not \models w\). To see this, consider two states  and
and  , containing full permissions to only x.f and x.g, respectively. Both states are valid footprints of w, i.e.
, containing full permissions to only x.f and x.g, respectively. Both states are valid footprints of w, i.e.  (because
(because  is incompatible with all states that satisfy the left-hand side) and
is incompatible with all states that satisfy the left-hand side) and  (because
(because  entails the right-hand side). Thus, by definition,
entails the right-hand side). Thus, by definition,  and
and  . However,
. However,  , i.e. a state with half permission to both x.f and x.g, is not a valid footprint of w, and thus \(w^{0.5} * w^{0.5} \not \models w\).
, i.e. a state with half permission to both x.f and x.g, is not a valid footprint of w, and thus \(w^{0.5} * w^{0.5} \not \models w\).
Intuitively, w is not combinable because one of its footprints,  , is incompatible with the left-hand side of the wand, but becomes compatible when the footprint is scaled down to a fraction. After scaling, the wand no longer holds trivially, and the footprint does not necessarily establish the right-hand side.
, is incompatible with the left-hand side of the wand, but becomes compatible when the footprint is scaled down to a fraction. After scaling, the wand no longer holds trivially, and the footprint does not necessarily establish the right-hand side.
To make this intuition more precise, we introduce the notion of scalable footprints. For a state  , we define
, we define  to be the set of copies of
to be the set of copies of  multiplied by any fraction \(0 < \alpha \le 1\), i.e.
multiplied by any fraction \(0 < \alpha \le 1\), i.e.  . A footprint
. A footprint  is scalable w.r.t. a state
is scalable w.r.t. a state  iff either (1)
iff either (1)  is compatible with all states from
is compatible with all states from  , or (2)
, or (2)  is compatible with no state in
is compatible with no state in  . A footprint is scalable for a wand
. A footprint is scalable for a wand  iff it is scalable w.r.t. all states that satisfy A. Intuitively, this means that the footprint does not “jump” between satisfying the wand trivially and having to satisfy the right-hand side. In the above example,
iff it is scalable w.r.t. all states that satisfy A. Intuitively, this means that the footprint does not “jump” between satisfying the wand trivially and having to satisfy the right-hand side. In the above example,  is a scalable footprint for w, but
is a scalable footprint for w, but  is not.
is not.
Making Wands Combinable. The previous paragraphs show that, even if B is combinable, the standard wand  is in general not combinable because it can be satisfied by non-scalable footprints. Therefore, we define a novel restricted interpretation for wands that forces footprints to be scalable, in the following sense. The restricted interpretation of a wand accepts all scalable footprints, and transforms non-scalable footprints before checking whether they actually satisfy the wand. We call a wand with this restricted interpretation a combinable wand, and write
is in general not combinable because it can be satisfied by non-scalable footprints. Therefore, we define a novel restricted interpretation for wands that forces footprints to be scalable, in the following sense. The restricted interpretation of a wand accepts all scalable footprints, and transforms non-scalable footprints before checking whether they actually satisfy the wand. We call a wand with this restricted interpretation a combinable wand, and write  to differentiate it from the standard wand
to differentiate it from the standard wand  .
.
For standard wands, any state  is a footprint of
is a footprint of  iff, for all states
iff, for all states  that satisfy A,
that satisfy A,  . We obtain the definition of combinable wands by replacing
. We obtain the definition of combinable wands by replacing  with a (possibly smaller) state
with a (possibly smaller) state  that is scalable w.r.t.
that is scalable w.r.t.  .
.  is defined as
is defined as  if no state in
if no state in  is compatible with any
is compatible with any  ; in that case, condition (2) of scalable footprints holds for
; in that case, condition (2) of scalable footprints holds for  w.r.t.
w.r.t.  . Otherwise,
. Otherwise,  is obtained by removing just enough permissions from
is obtained by removing just enough permissions from  to ensure that all states in
to ensure that all states in  are compatible with
are compatible with  , which ensures that condition (1) holds for
, which ensures that condition (1) holds for  w.r.t.
w.r.t.  .
.
To formally define  , we fix a concrete separation algebra (formally defined in App. G of the TR [16]), whose states are pairs \((\pi , h)\) of a permission mask \(\pi \), which maps heap locations to fractional permissions, and a partial heap h, which maps heap locations to values.
, we fix a concrete separation algebra (formally defined in App. G of the TR [16]), whose states are pairs \((\pi , h)\) of a permission mask \(\pi \), which maps heap locations to fractional permissions, and a partial heap h, which maps heap locations to values.
Definition 1
Let \((\pi _A, h_A)\) and \((\pi _w, h_w)\) be two states, and let \(\pi '_w\) be the permission mask such that  . Then
. Then

The combinable wand  is then interpreted as follows:
is then interpreted as follows:

The following theorem (proved in Isabelle/HOL) shows some key properties of combinable wands.
Theorem 3
Let B be an intuitionistic assertion.
-
1.
If B is combinable, then
 is combinable.
is combinable. -
2.
 .
. -
3.
If A is a binary assertion, then
 and
and  are equivalent.
are equivalent.
Property 1 expresses that combinable wands constructed from combinable assertions are combinable, which enables verification methodologies underlying tools such as VerCors and Viper to support flexible combinations of wands and predicates (as motivated at the start of this section). Property 2 implies that  , that is, combinable wands can be applied like standard wands. Property 3 states that combinable wands pose no restrictions if the left-hand side is binary, that is, if it can be expressed without fractional permissions (formally defined in App. G of the TR [16]). For example, the predicate Tree(x) from Fig. 1 is binary, which implies that the wands
, that is, combinable wands can be applied like standard wands. Property 3 states that combinable wands pose no restrictions if the left-hand side is binary, that is, if it can be expressed without fractional permissions (formally defined in App. G of the TR [16]). For example, the predicate Tree(x) from Fig. 1 is binary, which implies that the wands  and
and  are equivalent. This property is an important reason for why combinable wands are expressive enough for practical purposes, as we further evidence in Sect. 5.
are equivalent. This property is an important reason for why combinable wands are expressive enough for practical purposes, as we further evidence in Sect. 5.
Footprints of combinable wands can be automatically inferred by algorithms built on our package logic. We explain (along with examples) in App. H of the TR [16] how to lift the package logic presented in Sect. 3 to handle alternative definitions of allowable footprints such as the restrictions imposed by Definition 1.
5 Evaluation
We have implemented package algorithms for the standard wands and combinable wands in a custom branch of Viper’s [34] verification condition generator (VCG). Both are based on the package logic described in Sect. 3, adapted to the fractional permission setting. Both algorithms automate the proof search strategy outlined in Sect. 3.5. Viper’s VCG translates Viper programs to Boogie [32] programs. It uses a total-heap semantics of IDF [36], where Viper states include a heap and a permission mask (tracking fractional permission amounts). The heap and mask are represented in Boogie as maps; we also represent witness sets as Boogie maps.
We evaluate our implementations of the package algorithms on Viper’s test suite and compare them to Viper’s implementation of the FIA as presented in Sect. 2.4. Our key findings are that our algorithms (1) enable the verification of almost all correct package operations. (2) correctly report package operations that are supposed to fail (in contrast to the FIA), and (3) have an acceptable performance overhead compared to the FIA. Moreover, interpreting wands as combinable wands as explained in Sect. 4 has only a minor effect on the results, but correctly rejects attempts to package a non-combinable wand. This finding suggests that verifiers could improve their expressiveness by allowing flexible combinations of wands and predicates with only a minor completeness penalty.
For our evaluation, we considered all 85 files in the test suite for Viper’s VCG with at least one package operation. From these 85 files, we removed 29 files containing features that our implementation does not yet support. 28 of these 29 files require proof scripts to guide the footprint inference, which are orthogonal to the concerns of this paper (see App. J of the TR [16] for details).
Table 1 gives an overview of our results. These confirm that our algorithms for standard and combinable wands (S-Alg and C-Alg) do not produce false negatives, that is, are sound. In contrast, the FIA does verify an incorrect program (which is similar to the example in Sect. 2.4). While this is only a single unsound example, it is worth emphasing that (a) it comes from the pre-existing test suite of the tool itself, (b) the unsoundness was not known of until our work, and (c) soundness issues in a program verifier are critical to address; we show how to achieve this.
Compared with the FIA, our implementation reports a handful of false positives (spurious errors). For S-Alg, 3 out of 5 false positives are caused by missing features of our implementation (such as remembering a subset of the permissions that are inside predicate instances when manipulating predicates); these features could be straightforwardly added in the future. The other 2 false positives are caused by S-Alg’s strategy. In one, the only potential footprint prevents the wand from ever being applied; although technically a false positive, it seems useful to reject the wand and alert the user. The other case is due to a coarse-grained heuristic applied by S-Alg that can be improved.
C-Alg reports the expected result in 48 benchmarks. Importantly, it correctly rejects one wand that indeed does not hold as a combinable wand. 5 of the 8 false positives are identical to those for S-Alg. In the other three benchmarks, the wands still do hold as combinable wands, but further extensions to C-Alg are required to handle them due to technical challenges regarding predicate instances. Once these extensions have been implemented, C-Alg will be as precise as S-Alg, indicating that comparable program verifiers could switch to combinable wands to simply enable sound, flexible combinations with predicates.
To evaluate performance, we ran each of the three implementations 5 times on each of the 56 benchmarks on a Lenovo T480 with 32 GB of RAM and a i7-8550U 1.8 GhZ CPU, running on Windows 10. We removed the slowest and fastest time, and then took the mean of the remaining 3 runs. The FIA takes between 1 and 11 seconds per benchmark. On average, S-Alg is 21% slower than the FIA. For 46 of the 56 examples, the increase is less than 30%, and for 3 examples S-Alg is between a factor 2 and 3.4 slower. The overhead is most likely due to the increased complexity of our algorithms, which track more states explicitly and require more quantified axioms in the Boogie encoding. C-Alg is on average 10% slower than S-Alg. We consider the performance overhead of our algorithms to be acceptable, especially since wands occur much more frequently in our benchmarks than in average Viper projects, as judged by existing tests and examples. More representative projects will, thus, incur a much smaller slow-down.
6 Related Work
VerCors [2] and Viper [34] are to the best of our knowledge the only automatic SL verifiers that support magic wands. Both employ package and apply ghost operations. VerCors’ package algorithm requires a user to manually specify a footprint whereas Viper infers footprints using the FIA, which is unsound as we show in Sect. 2.4. Our package algorithm is as automatic as the FIA but is sound.
Lee and Park [30] develop a sound and complete proof system for SL including the magic wand. Moreover, they derive a decision procedure from their completeness proof for propositional SL. However, more expressive versions of SL (that include e.g. predicates and quantifiers) are undecidable [6] and so this decision procedure cannot be directly applied in the logics employed by program verifiers.
Chang et al. [11] define a shape analysis that derives magic wands  of a restricted form (A and B cannot contain general imprecise assertions); our package logic does not impose such restrictions, which rule out some useful kinds of wands. For example, A may be a data structure with a read-only part expressed via existentially-quantified fractional permissions or A may contain the necessary permission to invoke a method, which may be an arbitrary assertion. In follow-up work, Chang and Rival [10] present a restricted “inductive” magic wand. Footprints of inductive wands are expressed via a finite unrolling of an inductive predicate defining B until the permissions in A are revealed. Such wands are useful to reason about data structures with back-pointers such as doubly-linked lists.
of a restricted form (A and B cannot contain general imprecise assertions); our package logic does not impose such restrictions, which rule out some useful kinds of wands. For example, A may be a data structure with a read-only part expressed via existentially-quantified fractional permissions or A may contain the necessary permission to invoke a method, which may be an arbitrary assertion. In follow-up work, Chang and Rival [10] present a restricted “inductive” magic wand. Footprints of inductive wands are expressed via a finite unrolling of an inductive predicate defining B until the permissions in A are revealed. Such wands are useful to reason about data structures with back-pointers such as doubly-linked lists.
Iris [26] provides a custom proof mode [27] for interactive SL proofs in Coq [12]. Separation logics expressed in Iris support wands and are more expressive than those of automatic SL verifiers at the cost of requiring more user guidance. Packaging a wand in the proof mode requires manually specifying a footprint and proving that the footprint is correct. While tactics can be used in principle to automate parts of this process, there are no specific tactics to infer footprints.
Fractional assertions have been used in various forms [5, 7, 17, 23, 29]. Le and Hobor [29] allow combining two fractional assertions \(A^p\) and \(A^q\) only if A is precise in the SL sense (i.e. A describes the contents of the heaps in which it holds precisely). To avoid requiring A to be precise, Brotherston et al. [7] introduce nominal labels for assertions. If an assertion is split into two fractional assertions, then the same fresh label can be associated with both parts to indicate that they were split from the same assertion.
Two fractional assertions with the same label can be combined. However, this solution has not been implemented and does not deal with packaging wands. Our solution also avoids requiring that an assertion is precise and allows combining assertions even if they were not split from the same assertion. Instead of introducing labels, we introduce a light restriction that ensures that wands are always combinable. As a result, assertions containing combinable wands but no other potentially imprecise connectives (such as disjunction) are combinable. In particular, all assertions employed in verifiers such as VerCors and Viper can be made combinable thanks to our work.
7 Conclusion
We presented a package logic that precisely characterises sound package algorithms for automated reasoning about magic wands. Based on this logic, we developed a novel package algorithm that is inspired by an existing approach, but is sound. Moreover, we identified a sufficient criterion for wands to be combinable, such that they can be used flexibly in logics with fractional permissions, and presented a package algorithm for combinable wands. We implemented our solutions in Viper and demonstrated their practical usefulness. The soundness and completeness of our package logic, as well as key properties of combinable wands are all proved in Isabelle/HOL. As future work, we plan to extend the implementation of the two package algorithms described in Sect. 5 by porting various features of the pre-existing FIA implementation. Moreover, we will use our package logic to develop another algorithm for Viper’s symbolic-execution verifier.
Notes
- 1.
This unsoundness might not be observable in restricted logics, but it is in Viper (see App. B of the TR [16]) and the rich logics supported by existing verification tools.
- 2.
If B is intuitionistic, this can be simplified to only the \(\succeq \)-minimal states that satisfy A. B is intuitionistic [38] iff, if B holds in a state
 , then B holds in any state
, then B holds in any state 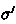 such that
such that  . In intuitionistic SL or in IDF, all assertions are intuitionistic.
. In intuitionistic SL or in IDF, all assertions are intuitionistic. - 3.
The order in the premises is unimportant since \(A_1 * A_2\) and \(A_2 * A_1\) are equivalent.
- 4.
We explain formally in App. D of the TR [16] the notion of a stable state, which is a technicality of our general state model; in standard SL, all states are stable.
- 5.
- 6.
In App. I of the TR [16], we also show how our package algorithm handles implications.
References
Astrauskas, V., Müller, P., Poli, F., Summers, A.J.: Leveraging Rust types for modular specification and verification. In: OOPSLA (2019)
Blom, S., Darabi, S., Huisman, M., Oortwijn, W.: The VerCors tool set: verification of parallel and concurrent software. In: Polikarpova, N., Schneider, S. (eds.) IFM 2017. LNCS, vol. 10510, pp. 102–110. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66845-1_7
Blom, S., Huisman, M.: Witnessing the elimination of magic wands. Int. J. Softw. Tools Technol. Transfer 17(6), 757–781 (2015). https://doi.org/10.1007/s10009-015-0372-3
Boyland, J.: Checking interference with fractional permissions. In: Cousot, R. (ed.) SAS 2003. LNCS, vol. 2694, pp. 55–72. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-44898-5_4
Boyland, J.T.: Semantics of fractional permissions with nesting. TOPLAS 32(6), 1–33 (2010)
Brochenin, R., Demri, S., Lozes, E.: On the almighty wand. Inf. Comput. 211, 106–137 (2012)
Brotherston, J., Costa, D., Hobor, A., Wickerson, J.: Reasoning over permissions regions in concurrent separation logic. In: Lahiri, S.K., Wang, C. (eds.) CAV 2020. LNCS, vol. 12225, pp. 203–224. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-53291-8_13
Calcagno, C., O’Hearn, P.W., Yang, H.: Local action and abstract separation logic. In: LICS (2007)
Cao, Q., Wang, S., Hobor, A., Appel, A.W.: Proof pearl: magic wand as frame (2019). https://arxiv.org/abs/1909.08789
Chang, B.E., Rival, X.: Relational inductive shape analysis. In: POPL (2008)
Chang, B.-Y.E., Rival, X., Necula, G.C.: Shape analysis with structural invariant checkers. In: Nielson, H.R., Filé, G. (eds.) SAS 2007. LNCS, vol. 4634, pp. 384–401. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74061-2_24
Coq Development Team, T.: The Coq Reference Manual, version 8.10 (2019). Available electronically at http://coq.inria.fr/documentation
Dardinier, T.: Formalization of a framework for the sound automation of magic wands. AFP, May 2022. https://isa-afp.org/entries/Package_logic.html
Dardinier, T.: A restricted definition of the magic wand to soundly combine fractions of a wand. AFP, May 2022. https://isa-afp.org/entries/Combinable_Wands.html
Dardinier, T., Parthasarathy, G., Weeks, N., Müller, P., Summers, A.J.: Sound automation of magic wands (artifact) (2022). https://doi.org/10.5281/zenodo.6526611
Dardinier, T., Parthasarathy, G., Weeks, N., Summers, A.J., Müller, P.: Sound automation of magic wands (extended version) (2022). https://arxiv.org/abs/2205.11325
Dinsdale-Young, T., Dodds, M., Gardner, P., Parkinson, M.J., Vafeiadis, V.: Concurrent abstract predicates. In: D’Hondt, T. (ed.) ECOOP 2010. LNCS, vol. 6183, pp. 504–528. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14107-2_24
Dinsdale-Young, T., da Rocha Pinto, P., Andersen, K.J., Birkedal, L.: Caper. In: Yang, H. (ed.) ESOP 2017. LNCS, vol. 10201, pp. 420–447. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54434-1_16
Dockins, R., Hobor, A., Appel, A.W.: A fresh look at separation algebras and share accounting. In: Hu, Z. (ed.) APLAS 2009. LNCS, vol. 5904, pp. 161–177. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10672-9_13
Dodds, M., Jagannathan, S., Parkinson, M.J.: Modular reasoning for deterministic parallelism. In: POPL (2011)
Haack, C., Hurlin, C.: Resource usage protocols for iterators. JOT 8(4), 55–83 (2009)
Huisman, M., Klebanov, V., Monahan, R.: VerifyThis 2012 - a program verification competition. STTT 17(6), 647–657 (2015)
Jacobs, B., Piessens, F.: Expressive modular fine-grained concurrency specification. In: POPL (2011)
Jacobs, B., Smans, J., Philippaerts, P., Vogels, F., Penninckx, W., Piessens, F.: VeriFast: a powerful, sound, predictable, fast verifier for C and Java. In: NFM (2011)
Jensen, J., Birkedal, L., Sestoft, P.: Modular verification of linked lists with views via separation logic. JOT 10, 1–20 (2011)
Jung, R., Krebbers, R., Jourdan, J., Bizjak, A., Birkedal, L., Dreyer, D.: Iris from the ground up: a modular foundation for higher-order concurrent separation logic. JFP 28, e20 (2018)
Krebbers, R., et al.: MoSeL: a general, extensible modal framework for interactive proofs in separation logic. In: ICFP (2018)
Krishnaswami, N.R.: Reasoning about iterators with separation logic. In: SAVCBS (2006)
Le, X.-B., Hobor, A.: Logical reasoning for disjoint permissions. In: Ahmed, A. (ed.) ESOP 2018. LNCS, vol. 10801, pp. 385–414. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89884-1_14
Lee, W., Park, S.: A proof system for separation logic with magic wand. In: POPL (2014)
Leino, K.R.M., Müller, P., Smans, J.: Verification of concurrent programs with Chalice. In: Aldini, A., Barthe, G., Gorrieri, R. (eds.) FOSAD 2007-2009. LNCS, vol. 5705, pp. 195–222. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03829-7_7
Leino, K.R.M.: This is Boogie 2, June 2008. https://www.microsoft.com/en-us/research/publication/this-is-boogie-2-2/
Maeda, T., Sato, H., Yonezawa, A.: Extended alias type system using separating implication. In: TLDI (2011)
Müller, P., Schwerhoff, M., Summers, A.J.: Viper: a verification infrastructure for permission-based reasoning. In: Jobstmann, B., Leino, K.R.M. (eds.) VMCAI 2016. LNCS, vol. 9583, pp. 41–62. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49122-5_2
Parkinson, M., Bierman, G.: Separation logic and abstraction. In: POPL (2005)
Parkinson, M.J., Summers, A.J.: The relationship between separation logic and implicit dynamic frames. Log. Methods Comput. Sci. 8(3:01), 1–54 (2012). https://doi.org/10.1007/978-3-642-35182-2_8
Piskac, R., Wies, T., Zufferey, D.: GRASShopper–complete heap verification with mixed specifications. In: Ábrahám, E., Havelund, K. (eds.) TACAS 2014. LNCS, vol. 8413, pp. 124–139. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54862-8_9
Reynolds, J.C.: Separation logic: a logic for shared mutable data structures. In: LICS (2002)
Schwerhoff, M., Summers, A.J.: Lightweight support for magic wands in an automatic verifier. In: ECOOP (2015)
Smans, J., Jacobs, B., Piessens, F.: Implicit dynamic frames: combining dynamic frames and separation logic. In: ECOOP (2009)
Tuerk, T.: Local reasoning about while-loops. In: VS-Theory (2010)
Yang, H.: An example of local reasoning in bi pointer logic: the Schorr-Waite graph marking algorithm. In: SPACE (2001)
Acknowledgement
This work was partially funded by the Swiss National Science Foundation (SNSF) under Grant No. 197065.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this paper
Cite this paper
Dardinier, T., Parthasarathy, G., Weeks, N., Müller, P., Summers, A.J. (2022). Sound Automation of Magic Wands. In: Shoham, S., Vizel, Y. (eds) Computer Aided Verification. CAV 2022. Lecture Notes in Computer Science, vol 13372. Springer, Cham. https://doi.org/10.1007/978-3-031-13188-2_7
Download citation
DOI: https://doi.org/10.1007/978-3-031-13188-2_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-13187-5
Online ISBN: 978-3-031-13188-2
eBook Packages: Computer ScienceComputer Science (R0)







 ,
, , and
, and ,
,  contains no permission (i.e.
contains no permission (i.e.  )
) satisfy
satisfy  , we transfer permissions (and the corresponding values) to satisfy
, we transfer permissions (and the corresponding values) to satisfy  to
to  , using the rule Atom. Note that the transferred permissions might be different for each pair
, using the rule Atom. Note that the transferred permissions might be different for each pair  . This gives us a new witness set
. This gives us a new witness set  is left unchanged. We must then handle the next assertion
is left unchanged. We must then handle the next assertion  .
. such that
such that  . In this case, the algorithm fails if combining the permissions (and values) contained in the outer state with each
. In this case, the algorithm fails if combining the permissions (and values) contained in the outer state with each  is not sufficient to satisfy
is not sufficient to satisfy  to each state
to each state  in
in  . This gives us a new context
. This gives us a new context  . We can now apply the first case with the context
. We can now apply the first case with the context  .
. is combinable.
is combinable. .
. and
and  are equivalent.
are equivalent. , then B holds in any state
, then B holds in any state  such that
such that  . In intuitionistic SL or in IDF, all assertions are intuitionistic.
. In intuitionistic SL or in IDF, all assertions are intuitionistic.