Abstract
Auto2 is a recently introduced prover for the proof assistant Isabelle. It is designed to be both highly customizable from within Isabelle, and also have a powerful proof search mechanism. In this paper, we apply auto2 to the verification of imperative programs. We describe the setup of auto2 for both stages of the proof process: verification of a functional version of the program, and refining to the imperative version using separation logic. As examples, we verify several data structures, including red-black trees, interval trees, priority queues, and union-find. We also verify several algorithms making use of these data structures. These examples show that our framework is able to verify complex algorithms efficiently and in a modular manner.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others

1 Introduction
Verification of imperative programs has been a well-studied area. While work on separation logic addressed the main theoretical issues, verification in practice is still a tedious process. Even if we limit to the case of sequential programs with relatively simple memory-allocation patterns, verification is still difficult when a lot of mathematical reasoning is required to justify the underlying algorithm. Such reasoning can quickly go beyond the ability of automatic theorem provers. Proof assistants such as Isabelle and Coq provide an environment in which human users can guide the computer through the proof. However, such a process today often requires a lot of low-level reasoning with lists, sets, etc, as well as dealing with details of separation logic. We believe much work can still be done to provide more automation in this area, reducing the amount of time and expertise needed to perform verifications, with the goal of eventually making verification of complex algorithms a routine process.
The auto2 prover in Isabelle is introduced by the author in [28]. Its approach to automation in proof assistants is significantly different from the two main existing approaches: tactics and the use of external automatic theorem provers (as represented by Sledgehammer in Isabelle). Compared to Sledgehammer, auto2 is highly customizable: users can set up new reasoning rules and procedures at any point in the development of a theory (for example, our entire setup for separation logic is built outside the main auto2 program). It also works directly with higher-order logic and types available in Isabelle. Compared to tactics, auto2 uses a saturation-based search mechanism, that is closer to the kind of search performed in automatic theorem provers, and from experience has been more powerful and stable than the backtracking approach usual in the tactics framework.
In this paper, we apply auto2 to the verification of imperative programs. We limit ourselves to sequential programs with relatively simple memory-allocation patterns. The algorithms underlying the programs, however, require substantial reasoning to justify. The verification process can be roughly divided into two stages: verifying a functional version of the program, and refining it to an imperative version using separation logic.
The main contributions of this paper are as follows.Footnote 1
-
We discuss the setup of auto2 to provide automation for both stages of this process. For the verification of functional programs, this means automatically proving simple lemmas involving lists, sets, etc. For refining to the imperative program, this means handling reasoning with separation logic.
-
Using our setup, we verify several data structures including red-black trees, interval trees, priority queues, and union-find. We also verify algorithms including Dijkstra’s algorithm for shortest paths and a line-sweeping algorithm for detecting rectangle intersection. These examples demonstrate that using our approach, complex algorithms can be verified in a highly efficient and modular manner.
We now give an outline for the rest of the paper. In Sect. 2, we give an overview of the auto2 prover. In Sect. 3, we discuss our setup of auto2 for verification of functional programs. In Sect. 4, we review the Imperative HOL framework in Isabelle and its separation logic, which we use to describe and verify the imperative programs. In Sect. 5, we discuss our setup of auto2 for reasoning with separation logic. In Sect. 6, we briefly describe each of the case studies, showing some statistics and comparison with existing verifications. Finally, we review related work in Sect. 7, and conclude in Sect. 8.
2 Overview of the auto2 Prover
The auto2 prover is introduced in [28]. In [29], several additional features are described, in an extended application to formalization of mathematics. In this section, we summarize the important points relevant to this paper.
Auto2 uses a saturation-based proof search mechanism. At any point during the search, the prover maintains a list of items, which may be derived facts, terms that appeared in the proof, or some other information. At the beginning, the statement to be proved is converted into contradiction form, and its assumptions form the initial state. The search ends successfully when a contradiction is derived. In addition to the list of items, the prover also maintains several additional tables, three of which will be described below.
2.1 Proof Steps
Proof steps are functions that produce new items from existing ones. During the development of an Isabelle theory, proof steps can be added or removed at any time. At each iteration of the proof search, auto2 applies the current list of proof steps to generate new items. Each new item is given a score and inserted into a priority queue. They are then added to the main list of items at future iterations in increasing order of score. The score is by default computed from the size of the proposition (smaller means higher priority), which can be overriden for individual proof steps.
Adding new proof steps is the main way to set up new functionality for auto2. Proof steps range from simple ones that apply a single theorem, to complex functions that implement some proof procedure. Several proof steps can also work together to implement some proof strategy, communicating through their input and output items. We will see examples of all these in Sects. 3 and 5.
2.2 Rewrite Table
Among the tables maintained by auto2, the most important is the rewrite table. The rewrite table keeps track of the list of currently known (ground) equalities. It offers two main operations: deciding whether two terms are equivalent, and matching up to known equalities (E-matching). The latter is the basic matching function used in auto2: whenever we mention matching in the rest of the paper, it is assumed to mean E-matching using the rewrite table.
We emphasize that when a new ground equality is derived, auto2 does not use it to rewrite terms in the proof state. Instead, the equality is inserted into the rewrite table, and incremental matching is performed on relevant items to discover new matches.
2.3 Property and Well-Formedness Tables
We now discuss two other important tables maintained by auto2: the property table and the well-formedness table.
Any predicate (constant of type  ) can be registered as a property during the development of a theory. During the proof, the property table maintains the list of properties satisfied by each term appearing in the proof. Common examples of predicates that we register as properties include sortedness on lists and invariants satisfied by binary search trees.
) can be registered as a property during the development of a theory. During the proof, the property table maintains the list of properties satisfied by each term appearing in the proof. Common examples of predicates that we register as properties include sortedness on lists and invariants satisfied by binary search trees.
For any function, we may register certain conditions on its arguments as well-formedness conditions of that function. Common examples include the condition  for the term
for the term  , and
, and  for the term
for the term  (
( ’th element of the list
’th element of the list  ). We emphasize that registering well-formedness conditions is for the automation only, and does not imply any modification to the logic. During the proof, the well-formedness table maintains the list of well-formedness conditions that are known for each term appearing in the proof.
). We emphasize that registering well-formedness conditions is for the automation only, and does not imply any modification to the logic. During the proof, the well-formedness table maintains the list of well-formedness conditions that are known for each term appearing in the proof.
The property and well-formedness tables allow proof steps to quickly lookup certain assumptions of a theorem. We call assumptions that can be looked-up in this way side conditions. We will see examples of these in Sect. 3.1, and another important application of the well-formedness table in Sect. 3.2.
2.4 Case Analysis
The need for case analysis introduces further complexities. New case analysis is produced by proof steps, usually triggered by the appearance of certain facts or terms in the proof. We follow a saturation-based approach to case analysis: the list of cases (called boxes) is maintained as a part of the proof state, and derivation in all boxes are performed in parallel. More precisely, every item (and entry in the tables) is assigned to some box, according to the set of additional assumptions needed to derive that item. When a contradiction is derived in a box with additional assumption P, the fact \(\lnot P\) is added to its parent box. The proof finishes only if a contradiction is derived in the initial box (with no additional assumptions).
2.5 Proof Scripts
Auto2 defines its own language of proof scripts, which is similar to, but independent from the Isar proof language in Isabelle. The main differences between auto2 and Isar are that auto2 scripts do not contain names of tactics (all subgoals are proved using auto2), labels for intermediate goals, or names of previous theorems.
Examples of auto2 scripts are given in Sect. 3.4. We explain the basic commands here (all commands in auto2 scripts begin with an  sign, to distinguish them from similar Isar commands).
sign, to distinguish them from similar Isar commands).
-
 : prove the intermediate goal P. Afterwards, make P available in the remainder of the proof block.
: prove the intermediate goal P. Afterwards, make P available in the remainder of the proof block. -
 : prove the current goal with additional assumption P. Afterwards, make \(\lnot P\) available in the remainder of the proof block.
: prove the current goal with additional assumption P. Afterwards, make \(\lnot P\) available in the remainder of the proof block. -
 : here
: here  must be a fresh variable. Prove the intermediate goal
must be a fresh variable. Prove the intermediate goal  . Afterwards, create variable x and make fact P(x) available in the remainder of the proof block.
. Afterwards, create variable x and make fact P(x) available in the remainder of the proof block. -
 : create a new proof block. That is, instead of proving the subgoal in the previous command directly using auto2, prove it using the commands between
: create a new proof block. That is, instead of proving the subgoal in the previous command directly using auto2, prove it using the commands between 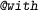 and
and  .
. -
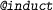 ,
, 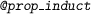 , etc: commands for several types of induction. Each type of induction has its own syntax, specifying which variable or proposition to apply induction on. We omit the details here.
, etc: commands for several types of induction. Each type of induction has its own syntax, specifying which variable or proposition to apply induction on. We omit the details here.
3 Verification of Functional Programs
Proofs of correctness of functional programs involve reasoning in many different domains, such as arithmetic, lists, sets, maps, etc. The proof of a single lemma may require results from more than one of these domains. The design of auto2 allows automation for each of these domains to be specified separately, as a collection of proof steps. During the proof, they work together by communicating through the common list of items and other tables maintained by the prover.
In this section, we discuss our setup of auto2 for verification of functional programs. It is impossible to describe the entire setup in detail. Instead, we will give some examples, showing the range of functionality that can be supported in auto2. At the end of the section, we give an example showing the strength of the resulting automation.
We emphasize that the aim here is not to implement complete proof procedures, or to compete with highly-optimized theory solvers for efficiency. Instead, we simply aim for the prover to consistently solve tasks that humans consider to be routine. Since we are in an interactive setting, we can always ask the user to provide intermediate goals for more difficult proof tasks.
3.1 Simple Proof Steps
Most of the proof steps added to auto2 apply a single theorem. Such proof steps can be added easily to auto2 (for example, a forward reasoning rule can be added by setting the  attribute to a theorem). We describe some basic examples in this section.
attribute to a theorem). We describe some basic examples in this section.
Forward and Backward Reasoning. The most basic kind of proof steps apply a theorem in the forward or backward direction. For example, the theorem

is added as a forward proof step. This proof step looks for pairs of facts in the form  and
and  (using E-matching, same below). For every match, it outputs the fact
(using E-matching, same below). For every match, it outputs the fact  as a new item (to be added to the main list of items at a future iteration).
as a new item (to be added to the main list of items at a future iteration).
In contrast, the theorem

should be added as a backward proof step. This proof step looks for facts of the form  (equivalently, goal to prove
(equivalently, goal to prove  ). For every match, it looks for the assumption
). For every match, it looks for the assumption  in the property table, and
in the property table, and  in the well-formedness table (it is the well-formedness condition of the subterm
in the well-formedness table (it is the well-formedness condition of the subterm  ). If both side conditions are found, the proof step outputs fact
). If both side conditions are found, the proof step outputs fact  (equivalently, goal to prove
(equivalently, goal to prove  ).
).
Another type of proof step adds a new fact for any term matching a certain pattern. For example, for the theorem

the corresponding proof step looks for terms of the form  . For every match, it looks for the assumption
. For every match, it looks for the assumption  in the well-formedness table, and output
in the well-formedness table, and output  if the assumption is found. This particular setup is chosen because assumptions of the form
if the assumption is found. This particular setup is chosen because assumptions of the form  appears frequently in practice.
appears frequently in practice.
Rewrite Rules. Rewrite rules form another major class of proof steps. They add new equalities to the rewrite table, usually after matching the left side of the equality. As an example, consider the theorem for evaluation of list update:

The corresponding proof step looks for terms of the form  . For every match, it looks for the assumption
. For every match, it looks for the assumption  in the well-formedness table (this is the well-formedness condition of
in the well-formedness table (this is the well-formedness condition of  ). If the assumption is found, the proof step outputs the equality. When the equality is pulled from the priority queue at a later iteration, it is added to the rewrite table.
). If the assumption is found, the proof step outputs the equality. When the equality is pulled from the priority queue at a later iteration, it is added to the rewrite table.
For the theorem evaluating the length of list update:

we add a slightly different proof step: it produces the equality whenever it finds the term  , without waiting for
, without waiting for  to appear. This can be justified by observing that it is useful to know the length of any list appearing in the proof, as it is mentioned in the assumptions of many theorems.
to appear. This can be justified by observing that it is useful to know the length of any list appearing in the proof, as it is mentioned in the assumptions of many theorems.
Generating Case Analysis. Another class of proof steps generate case analysis on seeing certain terms or facts in the proof state. For example, there is a proof step that looks for terms of the form  , and creates case analysis on
, and creates case analysis on  for every match.
for every match.
Case analysis may also be created to check well-formedness conditions. Usually, when we register a well-formedness condition, auto2 will look for the condition in the list of items during the proof. However, sometimes it is better to be more proactive, and try to prove the condition whenever a term of the given form appears. This is achieved by creating a case analysis with the condition as the goal (or equivalently, with the negation of the condition as the assumption).
3.2 Normalization of Natural Number Expressions
In this section, we give an example of a more complex proof step. It compares expressions on natural numbers by normalizing both sides with respect to addition and subtraction.
Mathematically, the expression \(a-b\) on natural numbers is undefined if \(a<b\). In Isabelle (and many other proof assistants), it is simply defined to be zero. This means many equalities involving subtraction on natural numbers that look obvious are in fact invalid. Examples include \(a-b+b=a\), which in Isabelle is false if \(a<b\).
This substantially complicates normalization of expressions on natural numbers involving subtraction. In general, normalization of such an expression agrees with intuition as long as the expression is well-formed, in the sense of Sect. 2.3. Following the terminology in [29, Sect. 3.3], we say a well-formed term is a term together with a list of theorems justifying its well-formedness conditions, and a well-formed conversion is a function that, given a well-formed term, returns an equality rewriting that term, together with theorems justifying well-formedness conditions on the right side of the equality. Well-formed conversions can be composed in the same way as regular conversions (rewriting procedures). In particular, we can implement normalization for expressions on natural numbers with respect to addition and subtraction as a well-formed conversion.
This is in turn used to implement the following proof step. Given any two terms s, t of type  involving addition and subtraction, look for their well-formedness conditions in the well-formedness table. If all well-formedness conditions for subtraction are present, normalize s and t using the well-formed conversion. If their normalizations are the same, output the equality \(s = t\). Such proof steps, when combined with proof scripts, allow the user to rapidly perform arithmetic manipulations.
involving addition and subtraction, look for their well-formedness conditions in the well-formedness table. If all well-formedness conditions for subtraction are present, normalize s and t using the well-formed conversion. If their normalizations are the same, output the equality \(s = t\). Such proof steps, when combined with proof scripts, allow the user to rapidly perform arithmetic manipulations.
3.3 Difference Logic on Natural Numbers
Difference logic is concerned with propositions of the form \(a\le b + n\), where n is a constant. A collection of such inequalities can be represented as a directed graph, where nodes are terms and weighted edges represent inequalities between them. A collection of inequalities is contradictory if and only if the corresponding graph contains a negative cycle, which can be determined using the Bellman-Ford algorithm.
In auto2, we implement difference logic for natural numbers using special items and proof steps. While less efficient than a graph-based implementation, it is sufficient for our purposes, and also interacts better with other proof steps. Each inequality on natural numbers is represented by an item of type  , which contains a triple
, which contains a triple  recording the terms on the two sides and the difference. The transitivity proof step looks for pairs of items of the form
recording the terms on the two sides and the difference. The transitivity proof step looks for pairs of items of the form  and
and  , and produces the item
, and produces the item  for each match. The resolve proof step looks for items of the form
for each match. The resolve proof step looks for items of the form  , where
, where  is less than zero, and derives a contradiction for each match.
is less than zero, and derives a contradiction for each match.
3.4 Example
As an example, we show a snippet from the functional part of the verification of the union-find data structure. Union-find is implemented on an array  , with
, with  equal to
equal to  if
if  is the root of its component, and the parent of
is the root of its component, and the parent of  if otherwise.
if otherwise.  denotes the root of the component containing
denotes the root of the component containing  . The compress operation is defined as:
. The compress operation is defined as:

The main properties of  are stated and proved using auto2 as follows:
are stated and proved using auto2 as follows:

The only hints that needs to be provided by the human to prove these lemmas are how to apply the induction (specified using the  command). By comparison, in the AFP library [14], the corresponding proofs require 20 tactic invocations in 42 lines of Isar text.
command). By comparison, in the AFP library [14], the corresponding proofs require 20 tactic invocations in 42 lines of Isar text.
4 Imperative HOL and Its Separation Logic
In this section, we review some basic concepts from the Imperative HOL framework in Isabelle and its separation logic. See [3, 13, 14] for details.
4.1 Heaps and Programs
In Imperative HOL, procedures are represented as Haskell-style monads. They operate on a heap (type  ) consisting of a finite mapping from addresses (natural numbers) to natural numbers, and a finite mapping from addresses to lists of natural numbers (in order to support arrays). Values of any type
) consisting of a finite mapping from addresses (natural numbers) to natural numbers, and a finite mapping from addresses to lists of natural numbers (in order to support arrays). Values of any type  can be stored in the heap as long as one can specify an injection from
can be stored in the heap as long as one can specify an injection from  to the natural numbers. This means records with multiple fields, such as nodes of a search tree, can be stored at a single address. Along with native support for arrays, this eliminates any need for pointer arithmetic.
to the natural numbers. This means records with multiple fields, such as nodes of a search tree, can be stored at a single address. Along with native support for arrays, this eliminates any need for pointer arithmetic.
The type of a procedure returning a value of type  is given by
is given by

The procedure takes as input a heap h, and outputs either  for failure, or
for failure, or  , where r is the return value and \(h'\) is the new heap. The
, where r is the return value and \(h'\) is the new heap. The  function for sequencing two procedures has type
function for sequencing two procedures has type

Imperative HOL does not have native support for while loops. Instead, basic applications use recursion throughout, with properties of recursive procedures proved by induction. We will follow this approach in our examples.
4.2 Assertions and Hoare Triples
The type partial heap is defined by  . The partial heap (h, as) represents the part of the heap h given by the set of addresses as.
. The partial heap (h, as) represents the part of the heap h given by the set of addresses as.
An assertion (type  ) is a mapping from
) is a mapping from  to
to  , that does not depend on values of the heap outside the address set. The notation \((h, as) \vDash P\) means “the assertion P holds on the partial heap (h, as)”.
, that does not depend on values of the heap outside the address set. The notation \((h, as) \vDash P\) means “the assertion P holds on the partial heap (h, as)”.
Some basic examples of assertions are:
-
 : holds for all valid partial heaps.
: holds for all valid partial heaps. -
 : the partial heap is empty.
: the partial heap is empty. -
\(\uparrow (b)\): the partial heap is empty and b (a boolean value) holds.
-
\(p\mapsto _ra\): the partial heap contains a single address pointing to value a.
-
\(p\mapsto _axs\): the partial heap contains a single address pointing to list xs.
The separating conjunction on two assertions is defined as follows:
This operation is associative and commutative, with unit  . Existential quantification on assertions is defined as:
. Existential quantification on assertions is defined as:
Assertions of the form \(\uparrow (b)\) are called pure assertions. In [14], conjunction, disjunction, and the magic wand operator on assertions are also defined, but we will not use them here.
A Hoare triple is a predicate of type

defined as follows:  holds if for any partial heap (h, as) satisfying P, the execution of c on (h, as) is successful with new heap \(h'\) and return value r, and the new partial heap \((h',as')\) satisfies Q(r), where \(as'\) is as together with the newly allocated addresses.
holds if for any partial heap (h, as) satisfying P, the execution of c on (h, as) is successful with new heap \(h'\) and return value r, and the new partial heap \((h',as')\) satisfies Q(r), where \(as'\) is as together with the newly allocated addresses.
From these definitions we can prove the Hoare triples for the basic commands, as well as the frame rule

In [14], there is further setup of a tactic sep_auto implementing some level of automation in separation logic. We do not make use of this tactic in our work.
5 Automation for Separation Logic
In this section, we discuss our setup of auto2 for separation logic. The setup consists of a collection of proof steps working with Hoare triples and entailments, implemented in around 2,000 lines of ML code (including specialized matching for assertions). While knowledge of auto2 is necessary to implement the setup, we aim to provide an easy-to-understand interface, so that no knowledge of the internals of auto2, or of details of separation logic, is needed to use it for concrete applications.
5.1 Basic Approach
Our basic approach is to analyze an imperative program in the forward direction: starting at the first command and finishing at the last, using existing Hoare triples to analyze each line of the procedure. To simplify the discussion, suppose the procedure to be verified consists of a sequence of commands \(c_1; \ldots ; c_n\). Let \(P_0\) be the (spatial) precondition of the Hoare triple to be proved.
To reason about the procedure, we use existing Hoare triples for \(c_1, \ldots , c_n\) (these may include the induction hypothesis, if some of \(c_i\) are recursive calls). We write each Hoare triple in the following standard form:

Here  is the spatial part of the precondition, specifying the shape of the heap before the command, and
is the spatial part of the precondition, specifying the shape of the heap before the command, and  is the pure part of the precondition, specifying additional constraints on the abstract values (we assume that all variables appearing in \(a_i\) also appear in \(p_i\) or c). The assertions
is the pure part of the precondition, specifying additional constraints on the abstract values (we assume that all variables appearing in \(a_i\) also appear in \(p_i\) or c). The assertions  and
and  (depending on the return value r and possibly new data-variables \(\mathbf {x}\)) are the spatial and pure parts of the postcondition. They provide information about the shape of the heap after the command, and constraints on abstract values on that heap.
(depending on the return value r and possibly new data-variables \(\mathbf {x}\)) are the spatial and pure parts of the postcondition. They provide information about the shape of the heap after the command, and constraints on abstract values on that heap.
Applying the Hoare triple for \(c_1\) involves the following steps:
-
1.
Match the pattern c with the command \(c_1\), instantiating some of the arbitrary variables in the Hoare triple.
-
2.
Match the spatial part of the precondition with \(P_0\). This is the frame-inference step: the matching is up to the associative-commutative property of separating conjunction, and only a subset of factors in \(P_0\) need to be matched. Each match should instantiate all remaining arbitrary variables in the Hoare triple.
-
3.
Generate case analysis (discussed at the end of Sect. 3.1) to try to prove each of the pure conditions \(a_i\).
-
4.
After all pure conditions are proved, apply the Hoare triple. This creates new variables for the return value r and possible data variables \(\mathbf {x}\). The procedure is replaced by \(c_2;\dots ;c_n\) and the precondition is replaced by
 . The pure assertions \(b_1,\dots ,b_l\) in the postcondition are outputed as facts.
. The pure assertions \(b_1,\dots ,b_l\) in the postcondition are outputed as facts.
On reaching the end of the imperative program, the goal reduces to an entailment, which is solved using similar matching schemes as above.
5.2 Inductively-Defined Assertions
Certain assertions, such as those for linked lists and binary trees, are defined inductively. For example, the assertion for binary trees (with a key-value pair at each node) is defined as follows:

Here  is an assertion stating that the memory location p contains a functional data structure t. The term
is an assertion stating that the memory location p contains a functional data structure t. The term  represents a functional binary tree, where
represents a functional binary tree, where  and
and  are subtrees, while the term
are subtrees, while the term  represents a record on the heap, where
represents a record on the heap, where  and
and  are pointers. When working with inductively-defined assertions like this, the heap can be divided into spatial components in several ways. For example, a heap satisfying the assertion
are pointers. When working with inductively-defined assertions like this, the heap can be divided into spatial components in several ways. For example, a heap satisfying the assertion

also satisfies the assertion

The former considers the heap as three components, while the latter considers it as one component.
We follow the policy of always using assertions in the more expanded form (that is, (1) instead of (2)). This means matching of assertions must also take into account inductive definitions of assertions, so that the assertion (1) will match the pattern  as well as (for example) the pattern
as well as (for example) the pattern  . This is realized by maintaining a list of inductive definitions of assertions in the theory, and have the special matching function for assertions refer to this list during matching.
. This is realized by maintaining a list of inductive definitions of assertions in the theory, and have the special matching function for assertions refer to this list during matching.
5.3 Modularity
For any data structure, there are usually two levels at which we can define assertions: the concrete level with definition by induction or in terms of simpler data structures, and the abstract level describing what data the structure is supposed to represent.
For example, in the case of binary trees, the concrete assertion  is defined in the previous section. At the abstract level, a binary tree represents a mapping. The corresponding assertion
is defined in the previous section. At the abstract level, a binary tree represents a mapping. The corresponding assertion  is defined by:
is defined by:

where  is the mapping corresponding to the binary tree t with key-value pairs at each node. For each operation on binary trees, we first prove a Hoare triple on the concrete assertion
is the mapping corresponding to the binary tree t with key-value pairs at each node. For each operation on binary trees, we first prove a Hoare triple on the concrete assertion  , then use it to derive a second Hoare triple on the abstract assertion
, then use it to derive a second Hoare triple on the abstract assertion  . For example, for the insertion operation, we first show:
. For example, for the insertion operation, we first show:

where  is the functional version of insertion on binary trees. Using this Hoare triple, and the fact that
is the functional version of insertion on binary trees. Using this Hoare triple, and the fact that  preserves sortedness and behaves correctly with respect to
preserves sortedness and behaves correctly with respect to  , we prove
, we prove

Similarly, for tree search, the Hoare triple on the concrete assertion is:

This Hoare triple, along with properties of  , is used to prove the Hoare triple on the abstract assertion:
, is used to prove the Hoare triple on the abstract assertion:

After the Hoare triples for  are proved, the definition of
are proved, the definition of  , as well as the Hoare triples for
, as well as the Hoare triples for  , can be hidden from auto2 by removing the corresponding proof steps. This enforces modularity of proofs: auto2 will only use Hoare triples for
, can be hidden from auto2 by removing the corresponding proof steps. This enforces modularity of proofs: auto2 will only use Hoare triples for  from now on, without looking into the internal implementation of the binary tree.
from now on, without looking into the internal implementation of the binary tree.
5.4 Example
With the above setup for separation logic, auto2 is able to prove the correctness of the imperative version of compression in union-find after specifying how to apply induction (using the  command):
command):

Note that the imperative procedure performs full compression along a path, rather than a single compression for the functional version in Sect. 3.4. By comparison, the corresponding proof in the AFP requires 13 tactic invocations (including 4 invocations of  ) in 34 lines of Isar text.
) in 34 lines of Isar text.
6 Case Studies
In this section, we describe the main case studies performed to validate our framework. For each case study, we describe the data structure or algorithm that is being verified, its main difficulties, and then give comparisons to existing work. Statistics for the case studies are summarized in the following table. On a laptop with two 2.0 GHz cores and 16 GB of RAM, it takes auto2 approximately 14 min to process all of the examples.
#Imp | #Def | #Thm | #Step | Ratio | #LOC | |
|---|---|---|---|---|---|---|
Union-find | 49 | 7 | 26 | 42 | 0.86 | 244 |
Red-black tree | 270 | 27 | 83 | 173 | 0.64 | 998 |
Interval tree | 84 | 17 | 50 | 83 | 0.99 | 520 |
Rectangle intersection | 33 | 18 | 31 | 111 | 3.36 | 417 |
Indexed priority queue | 83 | 10 | 53 | 84 | 1.01 | 477 |
Dijkstra’s algorithm | 44 | 19 | 62 | 150 | 3.41 | 549 |
The meaning of the fields are as follows:
-
#Imp is the number of lines of imperative code to be verified.
-
#Def is the number of definitions made during the verification (not counting definitions of imperative procedures).
-
#Thm is the number of lemmas and theorems proved during the verification.
-
#Step is the number of “steps” in the proof. Each definition, lemma, and intermediate goal in the proof script counts as one step (so for example, a lemma proved with one intermediate goal counts as two steps). We only count steps where auto2 does some work, omitting for example variable definitions.
-
Ratio: ratio between #Step and #Imp, serving as a measure of the overhead of verification.
-
#LOC: total number of lines of code in the theories (verification of functional and imperative program). This can be used to make approximate comparisons with other work.
6.1 Union-Find
Our verification follows closely that in the AFP [14]. As in the example in the AFP, we do not verify that the array containing the size of components has reasonable values (important only for performance analysis). Two snippets of auto2 proofs are shown in previous sections. Overall, we reduced the number of lines in the theory by roughly a half. In a further example, we applied union-find to verify an algorithm for determining connectivity on undirected graphs (not counted in the statistics).
6.2 Red-Black Tree
We verified the functional red-black tree given by Okasaki ([21], for insertion) and Kahrs ([18], for deletion). Both functional correctness and maintenance of invariants are proved. We then verified an imperative version of the same algorithm (imperative in the sense that no more memory is allocated than necessary). This offers a stringent test for matching involving inductively defined assertions (discussed in Sect. 5.2). For the functional part of the proof, we used the technique introduced by Nipkow [19] for proving sortedness and proper behavior on the associated maps using the inorder traversal as an intermediary.
Functional red-black tree has been verified several times in proof assistants [2, 19]. The imperative version is a common test-case for verification using automatic theorem provers [17, 22,23,24]. It is also verified “auto-actively” in the SPARK system [9], but apparently not in proof assistants such as Coq and Isabelle.
6.3 Interval Tree and Rectangle Intersection
Interval tree is an augmented data structure, with some version of binary search tree serving as the base. It represents a set of intervals S, and offers the operation of determining whether a given interval i intersects any of the intervals in S. See [8, Sect. 14.3] for details. For simplicity, we verified interval tree based on an ordinary binary search tree.
As an application of interval trees, we verify an algorithm for detecting rectangle intersection (see [8, Exercise 14.3-7]). Given a collection S of rectangles aligned to the x and y axes, one can determine whether there exists two rectangles in S that intersect each other using a line-sweeping algorithm as follows. For each rectangle \([a,b]\times [c,d]\), we create two operations: adding the interval [a, b] at time c, and removing it at time d. The operations for all rectangles are sorted by time (breaking ties by putting insertion before deletion) and applied to an initially empty interval tree. There is an intersection if and only if at some point, we try to insert an interval which intersects an existing interval in the tree. Formal verification of interval trees and the line-sweeping algorithm for rectangle intersection appear to be new.
6.4 Indexed Priority Queue and Dijkstra’s Algorithm
The usual priority queue is implemented on one array. It supports insertion and deleting the minimum. In order to support decreasing the value of a key (necessary for Dijkstra’s algorithm), we need one more “index” array recording locations of keys. Having two arrays produce additional difficulty in having to verify that they stay in sync in all operations.
The indexed priority queue is applied to verify a basic version of Dijkstra’s algorithm. We make several simplifying assumptions: the vertices of the graph are natural numbers from 0 to \(n-1\), and there is exactly one directed edge between each ordered pair of vertices, so that the weights of the graph can be represented as a matrix. Since the matrix is unchanged during the proof, we also do not put it on the heap. Nevertheless, the verification, starting from the definition of graphs and paths, contains all the essential ideas of Dijkstra’s algorithm.
The indexed priority queue and Dijkstra’s algorithm are previously verified using the refinement framework in [12, 20]. It is difficult to make precise comparisons, since the approach used in the refinement framework is quite different, and Dijkstra’s algorithm is verified there without the above simplifying assumptions. By a pure line count, our formalization is about 2-3 times shorter.
7 Related Work
This paper is a continuation of the work in [28, 29]. There is already some verification of imperative programs in [28]. However, they do not make use of separation logic, and the examples are quite basic. In this paper, we make full use of separation logic and present more advanced examples.
The refinement framework, introduced by Lammich in [13], can also be used to verify programs in Imperative-HOL. It applies refinement and data abstraction formally, verifying algorithms by step-wise refinement from specifications to concrete implementations. It has been used to verify several advanced graph algorithms [11, 15, 16]. Our work is independent from the refinement framework. In particular, we use refinement and data abstraction only in an ad-hoc manner.
Outside Imperative-HOL, there are many other frameworks based on tactics for automating separation logic in proof assistants. Examples include [1, 4,5,6,7, 14, 27]. As discussed in the introduction, our framework is implemented on top of the auto2 prover, which follows a quite different approach to automation compared to tactics.
Finally, there are many systems for program verification using automatic theorem provers. The main examples include [10, 25, 26]. The basic approach is to generate verification conditions from user-supplied annotations, and solve them using SMT-based provers. Compared to such systems, we enjoy the usual advantages of working in an interactive theorem prover, including a small trusted kernel, better interaction when proving more difficult theorems, and having available a large library of mathematical results.
8 Conclusion
In this paper, we described the setup of the auto2 prover to provide automation for verification of imperative programs. This include both the verification of a functional version of the program, and refining it to the imperative version using separation logic. Using our framework, we verified several data structures and algorithms, culminating in Dijkstra’s shortest paths algorithm and the line-sweeping algorithm for detecting rectangle intersection. The case studies demonstrate that auto2 is able to provide a great deal of automation in both stages of the verification process, significantly reducing the length and complexity of the proof scripts required.
Notes
- 1.
Code available at https://github.com/bzhan/auto2.
References
Appel, A.: Tactics for separation logic, January 2006. http://www.cs.princeton.edu/~appel/papers/septacs.pdf
Appel, A.: Efficient verified red-black trees (2011). http://www.cs.princeton.edu/~appel/papers/redblack.pdf
Bulwahn, L., Krauss, A., Haftmann, F., Erkök, L., Matthews, J.: Imperative functional programming with Isabelle/HOL. In: Mohamed, O.A., Muñoz, C., Tahar, S. (eds.) TPHOLs 2008. LNCS, vol. 5170, pp. 134–149. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-71067-7_14
Cao, J., Fu, M., Feng, X.: Practical tactics for verifying C programs in Coq. In: Leroy, X., Tiu, A. (eds.) CPP 2015, pp. 97–108 (2015)
Charguéraud, A.: Characteristic formulae for the verification of imperative programs. In: ICFP, pp. 418–430. ACM (2011)
Chlipala, A.: Mostly-automated verification of low-level programs in computational separation logic. In: PLDI 2011, pp. 234–245 (2011)
Chlipala, A., Malecha, G., Morrisett, G., Shinnar, A., Wisnesky, R.: Effective interactive proofs for higher-order imperative programs. In: Proceedings of the 14th ACM SIGPLAN International Conference on Functional Programming (ICFP 2009), pp. 79–90, August 2009
Cormer, T.H., Leiserson, C.E., Rivest, R., Stein, C.: Introduction to Algorithms, 3rd edn. MIT Press, Cambridge (1989)
Dross, C., Moy, Y.: Auto-active proof of red-black trees in SPARK. In: Barrett, C., Davies, M., Kahsai, T. (eds.) NFM 2017. LNCS, vol. 10227, pp. 68–83. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-57288-8_5
Filliâtre, J.-C., Paskevich, A.: Why3 — Where programs meet provers. In: Felleisen, M., Gardner, P. (eds.) ESOP 2013. LNCS, vol. 7792, pp. 125–128. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37036-6_8
Lammich, P.: Verified efficient implementation of Gabow’s strongly connected component algorithm. In: Klein, G., Gamboa, R. (eds.) ITP 2014. LNCS, vol. 8558, pp. 325–340. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08970-6_21
Lammich, P.: Refinement based verification of imperative data structures. In: Avigad, J., Chlipala, A. (eds.) CPP 2016, pp. 27–36 (2016)
Lammich, P.: Refinement to imperative/HOL. In: Urban, C., Zhang, X. (eds.) ITP 2015. LNCS, vol. 9236, pp. 253–269. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-22102-1_17
Lammich, P., Meis, R.: A separation logic framework for imperative HOL. In: Archive of Formal Proofs, November 2012. http://afp.sf.net/entries/Separation_Logic_Imperative_HOL.shtml. Formal proof development
Lammich, P., Sefidgar, S.R.: Formalizing the Edmonds-Karp algorithm. In: Blanchette, J.C., Merz, S. (eds.) ITP 2016. LNCS, vol. 9807, pp. 219–234. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-43144-4_14
Lammich, P., Tuerk, T.: Applying data refinement for monadic programs to Hopcroft’s algorithm. In: Beringer, L., Felty, A. (eds.) ITP 2012. LNCS, vol. 7406, pp. 166–182. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32347-8_12
Le, Q.L., Sun, J., Chin, W.-N.: Satisfiability modulo heap-based programs. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016, Part I. LNCS, vol. 9779, pp. 382–404. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-41528-4_21
Kahrs, S.: Red-black trees with types. J. Funct. Program. 11(4), 425–432 (2001)
Nipkow, T.: Automatic functional correctness proofs for functional search trees. In: Blanchette, J.C., Merz, S. (eds.) ITP 2016. LNCS, vol. 9807, pp. 307–322. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-43144-4_19
Nordhoff, B., Lammich, P.: Formalization of Dijkstra’s algorithm. Archive of Formal Proofs, January 2012. https://www.isa-afp.org/entries/Dijkstra_Shortest_Path.html
Okasaki, C.: Red-black trees in a functional setting. J. Funct. Program. 9(4), 471–477 (1999)
Pek, E., Qiu, X., Madhusudan, P.: Natural proofs for data structure manipulation in C using separation logic. In: PLDI 2014, pp. 440–451 (2014)
Piskac, R., Wies, T., Zufferey, D.: Automating separation logic with trees and data. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 711–728. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08867-9_47
Qiu, X., Garg, P., Ştefănescu, A., Madhusudan, P.: Natural proofs for structure, data, and separation. In: PLDI 2013, pp. 231–242 (2013)
Leino, K.R.M.: Dafny: an automatic program verifier for functional correctness. In: Clarke, E.M., Voronkov, A. (eds.) LPAR 2010. LNCS (LNAI), vol. 6355, pp. 348–370. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17511-4_20
Jacobs, B., Piessens, F.: The VeriFast program verifier. Technical report CW-520, Department of Computer Science, Katholieke Universiteit Leuven, Belgium, August 2008
Tuerk, T.: A separation logic framework for HOL. Technical report UCAM-CL-TR-799, University of Cambridge, Computer Laboratory, June 2011
Zhan, B.: AUTO2, a saturation-based heuristic prover for higher-order logic. In: Blanchette, J.C., Merz, S. (eds.) ITP 2016. LNCS, vol. 9807, pp. 441–456. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-43144-4_27
Zhan, B.: Formalization of the fundamental group in untyped set theory using auto2. In: Ayala-Rincón, M., Muñoz, C.A. (eds.) ITP 2017. LNCS, vol. 10499, pp. 514–530. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66107-0_32
Acknowledgements
The author would like to thank Adam Chlipala, Peter Lammich, and Tobias Nipkow for discussions and feedback during this project, and to the referees for their helpful comments. For the first half of this project, the author was at MIT and was supported by NSF Award No. 1400713. During the second half, the author is at TU Munich, and is supported by DFG Koselleck grant NI 491/16-1.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
<SimplePara><Emphasis Type="Bold">Open Access</Emphasis> This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.</SimplePara> <SimplePara>The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.</SimplePara>
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Zhan, B. (2018). Efficient Verification of Imperative Programs Using Auto2. In: Beyer, D., Huisman, M. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2018. Lecture Notes in Computer Science(), vol 10805. Springer, Cham. https://doi.org/10.1007/978-3-319-89960-2_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-89960-2_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89959-6
Online ISBN: 978-3-319-89960-2
eBook Packages: Computer ScienceComputer Science (R0)





 : prove the intermediate goal P. Afterwards, make P available in the remainder of the proof block.
: prove the intermediate goal P. Afterwards, make P available in the remainder of the proof block. : prove the current goal with additional assumption P. Afterwards, make
: prove the current goal with additional assumption P. Afterwards, make  : here
: here  must be a fresh variable. Prove the intermediate goal
must be a fresh variable. Prove the intermediate goal  . Afterwards, create variable x and make fact P(x) available in the remainder of the proof block.
. Afterwards, create variable x and make fact P(x) available in the remainder of the proof block. : create a new proof block. That is, instead of proving the subgoal in the previous command directly using auto2, prove it using the commands between
: create a new proof block. That is, instead of proving the subgoal in the previous command directly using auto2, prove it using the commands between 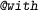 and
and  .
.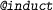 ,
, 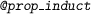 , etc: commands for several types of induction. Each type of induction has its own syntax, specifying which variable or proposition to apply induction on. We omit the details here.
, etc: commands for several types of induction. Each type of induction has its own syntax, specifying which variable or proposition to apply induction on. We omit the details here. : holds for all valid partial heaps.
: holds for all valid partial heaps. : the partial heap is empty.
: the partial heap is empty. . The pure assertions
. The pure assertions