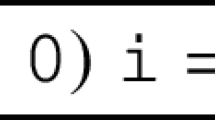Abstract
Many problems in program verification, Model Checking, and type inference are naturally expressed as satisfiability of a verification condition expressed in a fragment of First-Order Logic called Constrained Horn Clauses (CHC). This transforms program analysis and verification tasks to the realm of first order satisfiability and into the realm of SMT solvers. In this paper, we give a brief overview of how CHCs capture verification problems for sequential imperative programs, and discuss CHC solving algorithm underlying the Spacer engine of SMT-solver Z3.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
First Order Logic (FOL) is a powerful formalism that naturally captures many interesting decision (and optimization) problems. In recent years, there has been a tremendous progress in automated logic reasoning tools, such as Boolean SATisfiability Solvers (SAT) and Satisfiability Modulo Theory (SMT) solvers. This enabled the use of logic and logic satisfiabilty solvers as a universal solution to many problems in Computer Science, in general, and in Program Analysis, in particular. Most new program analysis techniques formalize the desired analysis task in a fragment of FOL, and delegate the analysis to a SAT or an SMT solver. Examples include deductive verification tools such as Dafny [30] and Why3 [13], symbolic execution engines such as KLEE [7], Bounded Model Checking engines such as CBMC [10] and SMACK [9], and many others.
In this paper, we focus on a fragment of FOL called Constrained Horn Clauses (CHC). CHCs arise in many applications of automated verification. They naturally capture such problems as discovery and verification of inductive invariants [4, 18]; Model Checking of safety properties of finite- and infinite-state systems [2, 23]; safety verification of push-down systems (and their extensions) [4, 28]; modular verification of distributed and parameterized systems [17, 19, 33]; and type inference [35, 36], and many others.
Using CHC, developers of program analysis tools can separate the process of developing a proof methodology (also known as generation of Verification Condition (VC)) from the algorithmic details of deciding whether the VC is correct. Such a flexible design simplifies supporting multiple proof methodologies, multiple languages, and multiple verification tasks with a single framework. Today, there are multiple effective program verification tools based on the CHC methodology, including a C/C++ verification framework SeaHorn [18], a Java verification framework JayHorn [25], and an Android information flow verification tool HornDroid [8], a Rust verification framework RustHorn [31], Solidity verification tools SmartACE [37] and Solidity Compiler Model Checker [1]. Many more approaches utilize CHC as part of a more general verification solution.
The idea of reducing program verification (and model checking) to FOL satisfiability is well researched. A great example is the use of Constraint Logic Programming (CLP) [24] in program verification, or the use of Datalog for pointer analysis [34]. What is unique is the application of SMT-solvers in the decision procedure and lifting of techniques that have been developed in Model Checking and Program Verification communities to the uniform setting of satisfiabilty of CHC formulas. In the rest of this paper, we show how verification problems can be represented in CHCs (Sect. 2), and describe key algorithms behind Spacer [27], a CHC engine of the SMT solver Z3 [32] that is used to solve them (Sect. 3).
2 Logic of Constrained Horn Clauses
In this section, we give a brief overview of Constrained Horn Clauses (CHC). We illustrate an application of CHC to verification of a simple imperative program with a loop.
The logic of Constrained Horn Clauses is a fragment of FOL. We assume that the reader is familiar with the basic concepts of FOL, including signatures, theories, and models. For the purpose of this presentation, let \(\varSigma \) be some fixed FOL signature and \(\mathcal {A}\) be an FOL theory over \(\varSigma \). For example, \(\varSigma \) is a signature for arithmetic, including constants 0, and 1, and a binary function \(\cdot + \cdot \), and \(\mathcal {A}\) the theory of Presburger arithmetic. A Constrained Horn Clause (CHC) is an FOL sentence of the form:
where V is the set of all free variables in the body of the sentence, \(\{p_i\}_{i=1}^{k}\) and h are uninterpreted predicate symbols (in the signature), \(\{X_i\}_{i=1}^{k}\) and X are first-order terms, and p(X) stands for application of predicate p to a list of terms X.
A CHC in Eq. (1) can be equivalently written as the following clause:
where all free variables are implicitly universally quantified. Note that in this case only h appears positively, which explains why these are called Horn clauses. We write \(\mathrm {CHC}(\mathcal {A})\) to denote the set of all sentences in FOL modulo theory \(\mathcal {A}\) that can be written as a set of Constrained Horn Clauses. A sentence \(\varPhi \) is in \(\mathrm {CHC}(\mathcal {A})\) if it can be written as a conjunction of clauses of the form of Eq. (1).
A \(\mathrm {CHC}(\mathcal {A})\) sentence \(\varPhi \) is satisfiable if there exists a model \(\mathcal {M}\) of \(\mathcal {A}\) extended with interpretation for all of the uninterpreted predicates in \(\varPhi \) such that \(\mathcal {M}\) satisfies \(\varPhi \), written \(\mathcal {M} \models \varPhi \). In practice, we are often interested not in an arbitrary model, but a model that can be described concisely in some target fragment of FOL. We call such models solutions. Given an FOL fragment \(\mathcal {F}\), an \(\mathcal {F}\)-solution to a \(CHC(\mathcal {A})\) formula \(\varPhi \) is a model \(\mathcal {M}\) such that \(\mathcal {M} \models \varPhi \) and interpretation of every uninterpreted predicate in \(\mathcal {M}\) is definable in \(\mathcal {F}\). Most commonly, \(\mathcal {F}\) is taken to be either a quantifier free or universally quantified fragment of arithmetic \(\mathcal {A}\), often further extended with arrays.
Example 1
To illustrate the definitions above consider a C program of a simple counter shown in Fig. 1. The goal is to verify that the assertion at the end of the program holds on every execution. To verify the assertion using the principle of inductive invariants, we need to show that there exists a formula Inv(x) over program variable x such that (a) it is true before the loop, stable at every iteration of the loop, and guarantees the assertion when the loop terminates. Since we are interested in partial correctness, we are not concerned with the case when the loop does not terminate. This principle is naturally encoded as three Constrained Horn Clauses, shown in the in Fig. 1. The uninterpreted predicate \( Inv \) represents the inductive invariant. The program is correct, hence the CHCs are satisfiable. The satisfying model extends the theory of arithmetic with the following definitions of \( Inv \):
The CHCs also have a solution in the quantifier free theory of Linear Integer Arithmetic. In particular, \( Inv \) can be defined as follows:
where the notation function with argument x and body \(\varphi \).
The CHCs in this example can be expressed as an SMT-LIB script, shown in Fig. 2, and solved by Spacer engine of Z3. Note that the script uses some Z3-specific extensions, including logic HORN and several option that disable pre-processing (which is not necessary for such a simple example).
\(\square \)
CHCs from Fig. 1 in SMT-LIB format.
Example 2
Figure 3 shows a similar program, however, with a function
 that abstracts away the increment operation. The corresponding CHCs are also shown in Fig. 3. There are two unknowns, \( Inv \) that represents the desired inductive invariant, and \( Inc \) that represents the summary (i.e., pre- and post-conditions, or an over-approximation) of the function
that abstracts away the increment operation. The corresponding CHCs are also shown in Fig. 3. There are two unknowns, \( Inv \) that represents the desired inductive invariant, and \( Inc \) that represents the summary (i.e., pre- and post-conditions, or an over-approximation) of the function
 . Since the program still satisfies the assertion, the CHCs are satisfiable, and have
. Since the program still satisfies the assertion, the CHCs are satisfiable, and have
The corresponding SMT-LIB script is shown in Fig. 4. \(\square \)
Example 3
In this last example, consider a set of CHCs shown in Fig. 5. They are similar to CHCs in Fig. 1, with one exception. These CHCs are unsatisfiable. There is no interpretation of \( Inv \) to satisfy them. This is witnessed by a refutation – a resolution proof – shown in Fig. 6. The corresponding SMT-LIB script in shown in Fig. 7. \(\square \)
3 Solving CHC Modulo Theories
The logic of CHC can be seen as a convenient modelling language. That is, it does not restrict or impose a preference on a decision procedure used to solve the problem. In fact, a variety of solvers and techniques are widely available, including Spacer [28] (that is available as part of Z3), FreqHorn [12], and ELDARICA [22]. There is also an annual competition, CHC-COMPFootnote 1, to evaluate state-of-the-art solvers. In the rest of this section, we give a brief overview of the algorithm underlying Spacer.
CHCs from Fig. 3 in SMT-LIB format.
Spacer is an extension and generalization of SAT-based Model Checking algorithms to CHC modulo SMT-supported theories. On propositional transition systems, Spacer behaves similarly to IC3 [6] and PDR [11], and can be seen as an adaptation of these algorithms. For other first-order theories, Spacer extends Generalized PDR of Hoder and Bjørner [21].
Given a CHC system \(\varPhi \), Spacer works by iteratively looking for a bounded derivation of \(\mathrm {false}\) from \(\varPhi \). It explores \(\varPhi \) in a top-down (or backwards) direction. Each time Spacer fails to find a derivation of a fixed bound N, the reasons for failure are analyzed to derive consequences of \(\varPhi \) that explain why a derivation of \(\mathrm {false}\) must have at least \(N+1\) steps. This process is repeated until either (a) \(\mathrm {false}\) is derived and \(\varPhi \) is shown to be unsatisfiable, (b) the consequences form a solution to \(\varPhi \), thus, showing that \(\varPhi \) satisfiable, or (c) the process continues indefinitely, but continuously ruling out impossibility of longer and longer refutations. Thus, even though the problem is in general undecidable, Spacer always makes progress trying to show that \(\varPhi \) is unsatisfiable or that there is no short proof of unsatisiability.
Spacer is a procedure for solving linear and non-linear CHCs. For convenience of the presentation, we restrict ourselves to a special case of non-linear CHCs that consists of the following three clauses:
where, X is a set of free variables, \(X' = \{x' \mid x \in X\}\) and \(X^o = \{x^o \mid x \in X\}\) are auxiliary free variables, \( Init \), \( Bad \), and \( Tr \) are FOL formulas over the free variables (as indicated), and P is an uninterpreted predicate. Recall that all free variables in each clause are implicitly universally quantified. Thus, the only unknown to solve for is the uninterpreted predicate P. We call these three clauses a safety problem, and write \(\langle Init (X), Tr (X, X^o, X'), Bad (X) \rangle \) as a shorthand to represent them. It is not hard to show that satisfiability of arbitrary CHCs is reducible to a safety problem. Thus, this simplification does not lose generality. In practice, Spacer directly supports more complex CHCs with multiple unknown uninterpreted predicates.
Refutation proof for CHCs in Fig. 5.
CHCs from Fig. 5 in SMT-LIB format.

Before presenting the algorithm, we need to introduce two concepts from logic: Craig Interpolation and Model Based Projection.
Craig Interpolation. Given two formulas \(A[\vec {x},\vec {z}]\) and \(B[\vec {y},\vec {z}]\) such that \(A \wedge B\) is unsatisfiable, a Craig interpolant \(I[\vec {z}] = \textsc {Itp}(A[\vec {x},\vec {z}], B[\vec {y}, \vec {z}])\), is a formula \(I[\vec {z}]\) such that \(A[\vec {x}, \vec {z}] \Rightarrow I[\vec {z}]\) and \(I[\vec {z}] \Rightarrow \lnot B[\vec {y},\vec {z}]\). We further require that the interpolant is a clause. Intuitively, the interpolant I captures the consequences of A that are inconsistent with B. If A is a conjunction of literals, the interpolant can be seen as a semantic variant of an UNSAT core.
Model Based Projection. Let \(\varphi \) be a formula, \(U \subseteq Vars (\varphi )\) a subset of variables of \(\varphi \), and P a model of \(\varphi \). Then, \(\psi = \textsc {Mbp}(U, P, \varphi )\) is a model based projection if (a) \(\psi \) is a monomial, (b) \( Vars (\psi ) \subseteq Vars (\varphi ) \setminus U\), (c) \(P \models \psi \), (d) \(\psi \Rightarrow \exists V \cdot \varphi \). Intuitively, an MBP is an under-approximation of existential quantifier elimination, where the choice of the under-approximation is guided by the model.
We present Spacer [27] as a set of rules shown in Algorithm 1. While the algorithm is sound under any order on application of the rules, it is easy to see that only some orders lead to progress. Since solving CHCs even over LIA is undecidable, we are only concerned with soundness and progress, and do not discuss termination. The algorithm is based on the core principles of IC3 [5], however, it differs significantly in the details. The rules Unreachable and Reachable detect termination, either by discovering an inductive solution, or by discovering existence of a refutation, respectively. Unfold increases the exploration depth, and Candidate constructs a new proof obligation based on the current depth and the set \( Bad \) of bad states. Successor computes additional reachable states, that is, an under-approximation of the model of the implicit predicate P. Note that it used Model Based Projection to under-approximate forward predicate transformer. The rules MustPredecessor and MayPredecessor compute a new proof obligation that precedes an existing one. MustPredecessor does the computation based on existing reachable states, while MayPredecessor makes a guess based on existing over-approximation of P. In this case, MBP is used again, but now to under-approximate a backward predicate transformer. The rule NewLemma computes a new over-approximation, called a lemma, of what is derivable about P in \(i+1\) by blocking a proof obligation. This is very similar to the corresponding step in IC3. Note, however, that interpolation is used to generalize the learned lemma beyond the literals of the proof obligation. ReQueue allows pushing blocked proof obligations to higher level, and Push allows pushing and inductively generalizing lemmas.
Spacer was introduced in [27]. Extension for convex linear arithmetic (i.e., discovering convex and co-convex solutions) is described in [3]. Support for quantifier free solutions for CHC over the combined theories of arrays and arithmetic is described in [26]. Extension for quantified solutions, which are necessary for establishing interesting properties when arrays are involved is described in [20]. More recently, the interpolation for lemma-generalization has been replaced by more global guidance [14]. This made Spacer competitive with other data-driven approaches that infer new lemmas based on numerical values of blocked counterexamples. Machine Learning-based inductive generalization has been suggested in [29]. The solver has also been extended to support Algebraic Data Types and Recursive Functions [16]. Work on improving support for bit-vectors [15] and experimenting with support for uninterpreted functions is ongoing.
Notes
References
Alt, L., Blicha, M., Hyvarinen, A., Sharygina, N.: SolCMC: solidity compiler’s model checker. In: Proceedings of CAV 2022 (2022)
Beyene, T.A., Popeea, C., Rybalchenko, A.: Efficient CTL verification via horn constraints solving. In: Gallagher, J.P., Rümmer, P. (eds.) Proceedings 3rd Workshop on Horn Clauses for Verification and Synthesis, HCVS@ETAPS 2016, Eindhoven, The Netherlands, 3rd April 2016. EPTCS, vol. 219, pp. 1–14 (2016). https://doi.org/10.4204/EPTCS.219.1
Bjørner, N., Gurfinkel, A.: Property directed polyhedral abstraction. In: D’Souza, D., Lal, A., Larsen, K.G. (eds.) VMCAI 2015. LNCS, vol. 8931, pp. 263–281. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46081-8_15
Bjørner, N., Gurfinkel, A., McMillan, K., Rybalchenko, A.: Horn clause solving for program verification. In: Proceedings of a Symposium on Logic in Computer Science celebrating Yuri Gurevich’s 75th Birthday (2015)
Bradley, A.R.: SAT-based model checking without unrolling. In: Jhala, R., Schmidt, D. (eds.) VMCAI 2011. LNCS, vol. 6538, pp. 70–87. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-18275-4_7
Bradley, A.R.: IC3 and beyond: incremental, inductive verification. In: CAV, p. 4 (2012)
Cadar, C., Dunbar, D., Engler, D.R.: KLEE: unassisted and automatic generation of high-coverage tests for complex systems programs. In: Draves, R., van Renesse, R. (eds.) 8th USENIX Symposium on Operating Systems Design and Implementation, OSDI 2008, December 8–10, 2008, San Diego, California, USA, Proceedings, pp. 209–224. USENIX Association (2008). http://www.usenix.org/events/osdi08/tech/full_papers/cadar/cadar.pdf
Calzavara, S., Grishchenko, I., Maffei, M.: Horndroid: practical and sound static analysis of android applications by SMT solving. CoRR abs/1707.07866 (2017). http://arxiv.org/abs/1707.07866
Carter, M., He, S., Whitaker, J., Rakamaric, Z., Emmi, M.: SMACK software verification toolchain. In: Dillon, L.K., Visser, W., Williams, L. (eds.) Proceedings of the 38th International Conference on Software Engineering, ICSE 2016, Austin, TX, USA, May 14–22, 2016 - Companion Volume, pp. 589–592. ACM (2016). https://doi.org/10.1145/2889160.2889163
Clarke, E., Kroening, D., Lerda, F.: A tool for checking ANSI-C programs. In: Jensen, K., Podelski, A. (eds.) TACAS 2004. LNCS, vol. 2988, pp. 168–176. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24730-2_15
Eén, N., Mishchenko, A., Brayton, R.K.: Efficient implementation of property directed reachability. In: Bjesse, P., Slobodová, A. (eds.) International Conference on Formal Methods in Computer-Aided Design, FMCAD 2011, Austin, TX, USA, October 30–November 02 2011, pp. 125–134. FMCAD Inc. (2011). http://dl.acm.org/citation.cfm?id=2157675
Fedyukovich, G., Prabhu, S., Madhukar, K., Gupta, A.: Solving constrained horn clauses using syntax and data. In: Bjørner, N.S., Gurfinkel, A. (eds.) 2018 Formal Methods in Computer Aided Design, FMCAD 2018, Austin, TX, USA, October 30–November 2 2018, pp. 1–9. IEEE (2018). https://doi.org/10.23919/FMCAD.2018.8603011
Filliâtre, J.-C., Paskevich, A.: Why3–where programs meet provers. In: Felleisen, M., Gardner, P. (eds.) ESOP 2013. LNCS, vol. 7792, pp. 125–128. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37036-6_8
Vediramana Krishnan, H.G., Chen, Y.T., Shoham, S., Gurfinkel, A.: Global guidance for local generalization in model checking. In: Lahiri, S.K., Wang, C. (eds.) CAV 2020. LNCS, vol. 12225, pp. 101–125. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-53291-8_7
Govind V. K., H., Fedyukovich, G., Gurfinkel, A.: Word level property directed reachability. In: Proceedings of the 39th International Conference on Computer-Aided Design. ICCAD 2020, Association for Computing Machinery, New York, NY, USA (2020). https://doi.org/10.1145/3400302.3415708
Govind V. K., H., Shoham, S., Gurfinkel, A.: Solving constrained horn clauses modulo algebraic data types and recursive functions. Proc. ACM Program. Lang. 6(POPL), 1–29 (2022). https://doi.org/10.1145/3498722
Grebenshchikov, S., Lopes, N.P., Popeea, C., Rybalchenko, A.: Synthesizing software verifiers from proof rules. In: Vitek, J., Lin, H., Tip, F. (eds.) ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2012, Beijing, China - 11–16 June 2012, pp. 405–416. ACM (2012). https://doi.org/10.1145/2254064.2254112
Gurfinkel, A., Kahsai, T., Komuravelli, A., Navas, J.A.: The SeaHorn Verification Framework. In: Kroening, D., Pasareanu, C.S. (eds.) Computer Aided Verification - 27th International Conference, CAV 2015, San Francisco, CA, USA, July 18–24, 2015, Proceedings, Part I. Lecture Notes in Computer Science, vol. 9206, pp. 343–361. Springer (2015). https://doi.org/10.1007/978-3-319-21690-4<errorl="336" c="Missing dollar" />20, http://dx.doi.org/10.1007/978-3-319-21690-4_20
Gurfinkel, A., Shoham, S., Meshman, Y.: SMT-based verification of parameterized systems. In: Zimmermann, T., Cleland-Huang, J., Su, Z. (eds.) Proceedings of the 24th ACM SIGSOFT International Symposium on Foundations of Software Engineering, FSE 2016, Seattle, WA, USA, 13–18 November 2016, pp. 338–348. ACM (2016). https://doi.org/10.1145/2950290.2950330
Gurfinkel, A., Shoham, S., Vizel, Y.: Quantifiers on demand. In: Lahiri, S.K., Wang, C. (eds.) ATVA 2018. LNCS, vol. 11138, pp. 248–266. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-01090-4_15
Hoder, K., Bjørner, N.: Generalized property directed reachability. In: Cimatti, A., Sebastiani, R. (eds.) SAT 2012. LNCS, vol. 7317, pp. 157–171. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31612-8_13
Hojjat, H., Rümmer, P.: The ELDARICA horn solver. In: Bjørner, N.S., Gurfinkel, A. (eds.) 2018 Formal Methods in Computer Aided Design, FMCAD 2018, Austin, TX, USA, October 30–November 2 2018, pp. 1–7. IEEE (2018). https://doi.org/10.23919/FMCAD.2018.8603013
Hojjat, H., Rümmer, P., Subotic, P., Yi, W.: Horn clauses for communicating timed systems. In: Bjørner, N.S., Fioravanti, F., Rybalchenko, A., Senni, V. (eds.) Proceedings First Workshop on Horn Clauses for Verification and Synthesis, HCVS 2014, Vienna, Austria, 17 July 2014. EPTCS, vol. 169, pp. 39–52 (2014). https://doi.org/10.4204/EPTCS.169.6
Jaffar, J., Lassez, J.L.: Constraint logic programming. In: POPL, pp. 111–119 (1987)
Kahsai, T., Rümmer, P., Sanchez, H., Schäf, M.: JayHorn: a framework for verifying Java programs. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016. LNCS, vol. 9779, pp. 352–358. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-41528-4_19
Komuravelli, A., Bjørner, N., Gurfinkel, A., McMillan, K.L.: Compositional verification of procedural programs using horn clauses over integers and arrays. In: Kaivola, R., Wahl, T. (eds.) Formal Methods in Computer-Aided Design, FMCAD 2015, Austin, Texas, USA, 27–30 September 2015, pp. 89–96. IEEE (2015)
Komuravelli, A., Gurfinkel, A., Chaki, S.: SMT-based model checking for recursive programs. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 17–34. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08867-9_2
Komuravelli, A., Gurfinkel, A., Chaki, S., Clarke, E.M.: Automatic abstraction in SMT-based unbounded software model checking. In: CAV, pp. 846–862 (2013)
Le, N., Si, X., Gurfinkel, A.: Data-driven optimization of inductive generalization. In: Formal Methods in Computer Aided Design, FMCAD 2021, New Haven, CT, USA, 19–22 October 2021, pp. 86–95. IEEE (2021). https://doi.org/10.34727/2021/isbn.978-3-85448-046-4_17
Leino, K.R.M.: Developing verified programs with Dafny. In: Brosgol, B., Boleng, J., Taft, S.T. (eds.) Proceedings of the 2012 ACM Conference on High Integrity Language Technology, HILT 2012, 2–6 December 2012, Boston, Massachusetts, USA, pp. 9–10. ACM (2012). https://doi.org/10.1145/2402676.2402682
Matsushita, Y., Tsukada, T., Kobayashi, N.: Rusthorn: CHC-based verification for rust programs. ACM Trans. Program. Lang. Syst. 43(4), 15:1–15:54 (2021). https://doi.org/10.1145/3462205
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Popeea, C., Rybalchenko, A., Wilhelm, A.: Reduction for compositional verification of multi-threaded programs. In: Formal Methods in Computer-Aided Design, FMCAD 2014, Lausanne, Switzerland, 21–24 October 2014, pp. 187–194. IEEE (2014). https://doi.org/10.1109/FMCAD.2014.6987612
Smaragdakis, Y., Balatsouras, G.: Pointer analysis. Found. Trends Program. Lang. 2(1), 1–69 (2015). https://doi.org/10.1561/2500000014
Tan, B., Mariano, B., Lahiri, S.K., Dillig, I., Feng, Y.: SolType: refinement types for arithmetic overflow in solidity. Proc. ACM Program. Lang. 6(POPL), 1–29 (2022). https://doi.org/10.1145/3498665
Toman, J., Siqi, R., Suenaga, K., Igarashi, A., Kobayashi, N.: ConSORT: context- and flow-sensitive ownership refinement types for imperative programs. In: ESOP 2020. LNCS, vol. 12075, pp. 684–714. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-44914-8_25
Wesley, S., et al.: Verifying solidity smart contracts via communication abstraction in SmartACE. In: Finkbeiner, B., Wies, T. (eds.) VMCAI 2022. LNCS, vol. 13182, pp. 425–449. Springer, Cham (2022). https://doi.org/10.1007/978-3-030-94583-1_21
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this paper
Cite this paper
Gurfinkel, A. (2022). Program Verification with Constrained Horn Clauses (Invited Paper). In: Shoham, S., Vizel, Y. (eds) Computer Aided Verification. CAV 2022. Lecture Notes in Computer Science, vol 13371. Springer, Cham. https://doi.org/10.1007/978-3-031-13185-1_2
Download citation
DOI: https://doi.org/10.1007/978-3-031-13185-1_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-13184-4
Online ISBN: 978-3-031-13185-1
eBook Packages: Computer ScienceComputer Science (R0)