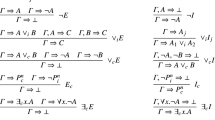Leśniewski’s Ontology – Proof-Theoretic Characterization

Abstract

The ontology of Leśniewski is commonly regarded as the most comprehensive calculus of names and the theoretical basis of mereology. However, ontology was not examined by means of proof-theoretic methods so far. In the paper we provide a characterization of elementary ontology as a sequent calculus satisfying desiderata usually formulated for rules in well-behaved systems in modern structural proof theory. In particular, the cut elimination theorem is proved and the version of subformula property holds for the cut-free version.

1 Introduction

The ontology of Leśniewski is a kind of calculus of names proposed as a formalization of logic alternative to Fregean paradigm. Basically, it is a theory of the binary predicate $\varepsilon$ understood as the formalization of the Greek ‘esti’. Informally a formula $a\varepsilon b$ is to be read as “(the) a is (a/the) b”, so in order to be true a must be an individual name whereas b can be individual or general name. In the original formulation Leśniewski’s ontology is the middle part of the hierarchical structure involving also the protothetics and mereology (see the presentation in Urbaniak [20]). Protothetics, a very general form of propositional logic, is the basis of the overall construction. Its generality follows from the fact that, in addition to sentence variables, arbitrary sentence-functors (connectives) are allowed as variables, and quantifiers binding all these kinds of variables are involved. Similarly in Leśniewski’s ontology, we have a quantification over name variables but also over arbitrary name-functors creating complex names. In consequence we obtain very expressive logic which is then extended to mereology. The latter, which is the most well-known ingredient of Leśniewski’s construction, is a theory of parthood relation, which provides an alternative formalization of the theory of classes and foundations of mathematics.

Despite of the dependence of Leśniewski’s ontology on his protothetics, we can examine this theory, in particular its part called elementary ontology, in isolation, as a kind of first-order theory of $\varepsilon$ based on classical first-order logic (FOL). Elementary ontology, in this sense, was investigated, among others, by Słupecki [17] and Iwanuś [7], and we follow this line here. The expressive power of such an approach is strongly reduced, in particular, quantifiers apply only to name variables. One should note however that, despite of the appearances, it is not just another elementary theory in the standard sense, since the range of variables is not limited to individual names but admits general and even empty names. Thus, name variables may represent not only ‘Napoleon Bonaparte’ but also ‘an emperor’ and ‘Pegasus’. This leads to several problems concerning the interpretation of quantifiers in ontology, encountered in the semantical treatment (see e.g. Küng and Canty [8] or Rickey [16]). However, for us the problems of proper interpretation are not important here, since we develop purely syntactical formulation, which is shown to be equivalent to Leśniewski’s axiomatic formulation.

Taking into account the importance and originality of Leśniewski’s ontology it is interesting, if not surprising, that so far no proof-theoretic study was offered, in particular, in terms of sequent calculus (SC). In fact, a form of natural deduction proof system was applied by many authors following the original way of presenting proofs by Leśniewski (see, e.g. his [9,10,11]). However this can hardly be treated as a proof-theoretic study of Leśniewski’s ontology but only as a convenient way of simplifying presentation of axiomatic proofs. Ishimoto and Kobayashi [6] introduced also a tableau system for part of (quantifier-free) ontology – we will say more about this system later.

In this paper we present a sequent calculus for elementary ontology and focus on its most important properties. More specifically, in Sect. 2 we briefly characterise elementary ontology which will be the object of our study. In Sect. 3 we present an adequate sequent calculus for the basic part of elementary ontology and prove that it is equivalent with the axiomatic formulation. Then we prove the cut elimination theorem for this calculus in Sect. 4. In the next section we focus on the problem of extensionality and discuss some alternative formulations of ontology and some of its parts, as well as the intuitionistic version of it. Section 6 shows how the basic system can be extended with rules for new predicate constants which preserve cut elimination. The problem of extension with rules for term constants is discussed briefly in Sect. 7. A summary of obtained results and open problems closes the paper.

2 Elementary Ontology

Roughly, in this article, by Leśniewski’s elementary ontology we mean standard FOL (in some chosen adequate formalization) with Leśniewski’s axiom LA added. For more detailed general presentation of Leśniewski’s systems one may consult Urbaniak [20] and for a detailed study of Leśniewski’s ontology see Iwanuś [7] or Słupecki [17]. In the next section we will select a particular sequent system as representing FOL and investigate several ways of possible representation of LA in this framework.

We will consider two languages for ontology. In both we assume a denumerable set of name variables. Following the well-known Gentzen’s custom we apply a graphical distinction between the bound variables, which will be denoted by x, y, z, ... (possibly with subscripts), and the free variables usually called parameters, which will be denoted by a, b, c, .... These are the only terms we admit, and both kinds will be called simply name variables. The basic language $L_o$ consists of the following vocabulary:

• connectives: $\lnot , \wedge , \vee , \rightarrow$;

• first-order quantifiers: $\forall , \exists$;

• predicate: $\varepsilon$.

As we can see, in addition to the standard logical vocabulary of FOL, the only specific constant is a binary predicate $\varepsilon$ with the formation rule: $t\,\varepsilon \,t'$ is an atomic formula, for any terms $t, t'$. In what follows we will use a convention: instead of $t\,\varepsilon \,t'$ we will write $tt'$. The complexity of formulae of $L_o$ is defined as the number of occurrences of logical constants, i.e. connectives and quantifiers. Hence the complexity of atomic formulae is 0.

The language $L_p$, considered in Sect. 6, adds to this vocabulary a number of unary and binary predicates: $D, V, S, G, U, =, \equiv , \approx , \bar{\varepsilon }, \subset , \nsubseteq , A, E, I, O$.

In $L_o$ and $L_p$ we have name variables, which range over all names (individual, general and empty), as the only terms. However Leśniewski considered also complex terms built with the help of specific term-forming functors. We will discuss briefly such extensions in the setting of sequent calculus in Sect. 7 and notice important problems they generate for decent proof-theoretic treatment.

The only specific axiom of elementary ontology is Leśniewski’s axiom LA:

$\forall xy(xy \leftrightarrow \exists z(zx)\wedge \forall z(zx\rightarrow zy) \wedge \forall zv(zx\wedge vx\rightarrow zv))$

LA$^\rightarrow$, LA$^\leftarrow$ will be used to refer to the respective implications forming LA, with dropped outer universal quantifier. Note that:

Lemma 1

The following formulae are equivalent to LA:

• 1. $\forall xy(xy \leftrightarrow \exists z(zx\wedge zy)\wedge \forall zv(zx\wedge vx\rightarrow zv))$

• 2. $\forall xy(xy \leftrightarrow \exists z(zx\wedge zy \wedge \forall v(vx\rightarrow vz)))$

• 3. $\forall xy(xy \leftrightarrow \exists z(\forall v(vx\leftrightarrow vz)\wedge zy))$

We start with the system in the language $L_o$, i.e. with $\varepsilon$ (conventionally omitted) as the only specific predicate constant added to the standard language of FOL.

3 Sequent Calculus

Elementary ontology will be formalised as a sequent calculus with sequents $\varGamma \Rightarrow \varDelta$ which are ordered pairs of finite multisets of formulae called the antecedent and the succedent, respectively. We will use the calculus G (after Gentzen) which is essentially the calculus G1 of Troelstra and Schwichtenberg [19]. All necessary structural rules, including cut, weakening and contraction are primitive. The calculus G consists of the rules from Fig. 1:

Fig. 1.

Calculus G

Let us recall that formulae displayed in the schemata are active, whereas the remaining ones are parametric, or form a context. In particular, all active formulae in the premisses are called side formulae, and the one in the conclusion is the principal formula of the respective rule application. Proofs are defined in a standard way as finite trees with nodes labelled by sequents. The height of a proof $\mathcal{D}$ of $\varGamma \Rightarrow \varDelta$ is defined as the number of nodes of the longest branch in $\mathcal{D}$. $\vdash _k \varGamma \Rightarrow \varDelta$ means that $\varGamma \Rightarrow \varDelta$ has a proof of the height at most k.

G provides an adequate formalization of the classical pure FOL (i.e. with no terms other than variables). However, we should remember that here terms in quantifier rules are restricted to variables ranging over arbitrary names (including empty and general). This means, in particular, that quantifiers do not have an existential import, like in standard FOL.

Let us call G+LA an extension of G with LA as an additional axiomatic sequent. The following hold:

Lemma 2

The following sequents are provable in G+LA:

$ab\Rightarrow \exists x(xa)$

$ab\Rightarrow \forall x(xa\rightarrow xb)$

$ab \Rightarrow \forall xy(xa\wedge ya\rightarrow xy)$

$\exists x(xa), \forall x(xa\rightarrow xb), \forall xy(xa\wedge ya\rightarrow xy)\Rightarrow ab$

The proof is obvious. In fact, these sequents together allow us to derive LA so we could use them alternatively in a characterization of elementary ontology on the basis of G.

G+LA is certainly an adequate formalization of elementary ontology in the sense of Słupecki and Iwanuś. However, from the standpoint of proof theoretic analysis it is not an interesting form of sequent calculus and it will be used only for showing the adequacy of our main system called GO.

To obtain the basic GO we add the following four rules to G:

(R) $\dfrac{aa, \varGamma \Rightarrow \varDelta }{ab, \varGamma \Rightarrow \varDelta }$         (T) $\dfrac{ac, \varGamma \Rightarrow \varDelta }{ab, bc, \varGamma \Rightarrow \varDelta }$         (S) $\dfrac{ba, \varGamma \Rightarrow \varDelta }{ab, bb, \varGamma \Rightarrow \varDelta }$

(E) $\dfrac{da, \varGamma \Rightarrow \varDelta , dc \quad dc, \varGamma \Rightarrow \varDelta , da \quad ab, \varGamma \Rightarrow \varDelta }{cb, \varGamma \Rightarrow \varDelta }$

where d in (E) is a new parameter (eigenvariable), and a, b, c are arbitrary.

The names of rules come from reflexivity, transitivity, symmetry and extensionality. In case of (R) and (S) it is a kind of prefixed reflexivity and symmetry ($ab\rightarrow aa, bb\rightarrow (ab\rightarrow ba))$. Why (E) comes from extensionality will be explained later.

We can show that GO is an adequate characterization of elementary ontology.

Theorem 1

If G+LA $\vdash \varGamma \Rightarrow \varDelta$, then GO $\vdash \varGamma \Rightarrow \varDelta$.

Proof

It is sufficient to prove that the axiomatic sequent LA is provable in GO.

$(\Rightarrow \wedge )$ with:

yields LA$^\rightarrow$ after $(\Rightarrow \rightarrow )$. A proof of the converse is more complicated (for readability and space-saving we ommited all applications of weakening rules necessary for the application of two- and three-premiss rules; this convention will be applied hereafter with no comments):

It is routine to prove LA.    $\square$

Note that to prove LA$^\rightarrow$ the rules (R), (T), (S) were sufficient, whereas in order to derive the converse, (E) alone is not sufficient - we need (T) again.

Theorem 2

If GO $\vdash \varGamma \Rightarrow \varDelta$, then G+LA $\vdash \varGamma \Rightarrow \varDelta$.

Proof

It is sufficient to prove that the four rules of GO are derivable in G+LA.

For (T):

where the leftmost leaf is provable in G+LA (Lemma 2).

For (S):

where the leftmost leaf is provable in G+LA (Lemma 2). By cut with the premiss of (S) we obtain its conclusion.

For (R):

where $S := \exists x(xa), \forall xy(xa\wedge ya\rightarrow xy), \forall x(xa\rightarrow xa)\Rightarrow aa$ and all leaves are provable in G+LA (Lemma 2); in particular S is the fourth sequent with b replaced with a. By cut with $\Rightarrow \forall x(xa\rightarrow xa)$ and the premiss of (R) we obtain its conclusion.

Since (R), (T), (S) are all derivable in G+LA we use them in the proof of the derivability of (E) to simplify matters. Note first the following three proofs with weakenings omitted:

and

By three cuts with $\exists x(xa), \forall x(xa\rightarrow xb), \forall xy(xa\wedge ya\rightarrow xy)\Rightarrow ab$ and contractions we obtain a proof of $S := \forall x(xa\leftrightarrow xc), cb \Rightarrow ab$. Then we finish in the following way:

Note that to prove derivability of (E) we need in fact the whole LA. We elaborate on the strength of this rule in Sect. 5.    $\square$

4 Cut Elimination

The possibility of representing LA by means of these four rules makes GO a calculus with desirable proof-theoretic properties. First of all note that for G the cut elimination theorem holds. Since the only primitive rules for $\varepsilon$ are all one-sided, in the sense that principal formulae occur in the antecedents only, we can easily extend this result to GO. We follow the general strategy of cut elimination proofs applied originally for hypersequent calculi in Metcalfe, Olivetti and Gabbay [13] but which works well also in the context of standard sequent calculi (see Indrzejczak [5]). Such a proof has a particularly simple structure and allows us to avoid many complexities inherent in other methods of proving cut elimination. In particular, we avoid well known problems with contraction, since two auxiliary lemmata deal with this problem in advance. Note first that for GO the following result holds:

Lemma 3 (Substitution)

If $\vdash _k \varGamma \Rightarrow \varDelta$, then $\vdash _k \varGamma [a/b] \Rightarrow \varDelta [a/b]$.

Proof

By induction on the height of a proof. Note that (E) may require similar relettering like $(\exists \Rightarrow )$ and $(\Rightarrow \forall )$. Note that the proof provides the height-preserving admissibility of substitution.    $\square$

Let us assume that all proofs are regular in the sense that every parameter a which is fresh by side condition on the respective rule must be fresh in the entire proof, not only on the branch where the application of this rule takes place. There is no loss of generality since every proof may be systematically transformed into a regular one by the substitution lemma. The following notions are crucial for the proof:

• 1. The cut-degree is the complexity of cut-formula $\varphi$, i.e. the number of connectives and quantifiers occurring in $\varphi$; it is denoted as $d\varphi$.

• 2. The proof-degree ($d\mathcal{D}$) is the maximal cut-degree in $\mathcal{D}$.

Remember that the complexity of atomic formulae, and consequently of cut- and proof-degree in case of atomic cuts, is 0. The proof of the cut elimination theorem is based on two lemmata which successively make a reduction: first on the height of the right, and then on the height of the left premiss of cut. $\varphi ^k, \varGamma ^k$ denote $k > 0$ occurrences of $\varphi , \varGamma$, respectively.

Lemma 4 (Right reduction)

Let $\mathcal{D}_1 \vdash \varGamma \Rightarrow \varDelta , \varphi$ and $\mathcal{D}_2 \vdash \varphi ^k, \varPi \Rightarrow \varSigma$ with $d\mathcal{D}_1, d\mathcal{D}_2 < d\varphi$, and $\varphi$ principal in $\varGamma \Rightarrow \varDelta , \varphi$, then we can construct a proof $\mathcal{D}$ such that $\mathcal{D} \vdash \varGamma ^k, \varPi \Rightarrow \varDelta ^k, \varSigma$ and $d\mathcal{D} < d\varphi$.

Proof

By induction on the height of $\mathcal{D}_2$. The basis is trivial, since $\varGamma \Rightarrow \varDelta , \varphi$ is identical with $\varGamma ^k, \varPi \Rightarrow \varDelta ^k, \varSigma$. The induction step requires examination of all cases of possible derivations of $\varphi ^k, \varPi \Rightarrow \varSigma$, and the role of the cut-formula in the transition. In cases where all occurrences of $\varphi$ are parametric we simply apply the induction hypotheses to the premisses of $\varphi ^k, \varPi \Rightarrow \varSigma$ and then apply the respective rule – it is essentially due to the context independence of almost all rules and the regularity of proofs, which together prevent violation of side conditions on eigenvariables. If one of the occurrences of $\varphi$ in the premiss(es) is a side formula of the last rule we must additionally apply weakening to restore the missing formula before the application of the relevant rule.

In cases where one occurrence of $\varphi$ in $\varphi ^k, \varPi \Rightarrow \varSigma$ is principal we make use of the fact that $\varphi$ in the left premiss is also principal; for the cases of contraction and weakening it is trivial. Note that due to condition that $\varphi$ is principal in the left premiss it must be compound, since all rules introducing atomic formulae as principal are working only in the antecedents. Hence all cases where one occurrence of atomic $\varphi$ in the right premiss would be introduced by means of (R), (S), (T), (E) are not considered in the proof of this lemma. The only exceptions are axiomatic sequents $\varGamma \Rightarrow \varDelta , \varphi$ with principal atomic $\varphi$, but they do not make any harm.    $\square$

Lemma 5 (Left reduction)

Let $\mathcal{D}_1 \vdash \varGamma \Rightarrow \varDelta , \varphi ^k$ and $\mathcal{D}_2 \vdash \varphi , \varPi \Rightarrow \varSigma$ with $d\mathcal{D}_1, d\mathcal{D}_2 < d\varphi$, then we can construct a proof $\mathcal{D}$ such that $\mathcal{D} \vdash \varGamma , \varPi ^k \Rightarrow \varDelta , \varSigma ^k$ and $d\mathcal{D} < d\varphi$.

Proof

By induction on the height of $\mathcal{D}_1$ but with some important differences. First note that we do not require $\varphi$ to be principal in $\varphi , \varPi \Rightarrow \varSigma$ so it includes the case with $\varphi$ atomic. In all these cases we just apply the induction hypothesis. This guarantees that even if an atomic cut formula was introduced in the right premiss by one of the rules (R), (S), (T), (E) the reduction of the height is done only on the left premiss, and we always obtain the expected result. Now, in cases where one occurrence of $\varphi$ in $\varGamma \Rightarrow \varDelta , \varphi ^k$ is principal we first apply the induction hypothesis to eliminate all other $k-1$ occurrences of $\varphi$ in premisses and then we apply the respective rule. Since the only new occurrence of $\varphi$ is principal we can make use of the right reduction lemma again and obtain the result, possibly after some applications of structural rules.    $\square$

Now we are ready to prove the cut elimination theorem:

Theorem 3

Every proof in GO can be transformed into cut-free proof.

Proof

By double induction: primary on $d\mathcal{D}$ and subsidiary on the number of maximal cuts (in the basis and in the inductive step of the primary induction). We always take the topmost maximal cut and apply Lemma 5 to it. By successive repetition of this procedure we diminish either the degree of a proof or the number of cuts in it until we obtain a cut-free proof.    $\square$

As a consequence of the cut elimination theorem for GO we obtain:

Corollary 1

If $\vdash \varGamma \Rightarrow \varDelta$, then it is provable in a proof which is closed under subformulae of $\varGamma \cup \varDelta$ and atomic formulae.

So cut-free GO satisfies the form of the subformula property which holds for several elementary theories as formalised by Negri and von Plato [14].

5 Modifications

Construction of rules which are deductively equivalent to axioms may be to some extent automatised (see e.g. Negri and von Plato [14], Braüner [1], or Marin, Miller, Pimentel and Volpe [12]). Still, even the choice of the version of (equivalent) axiom which will be used for transformation, may have an impact on the quality of obtained rules. Moreover, very often some additional tuning is necessary to obtain rules, which are well-behaved from the proof-theoretic point of view. In this section we will focus briefly on this problem and sketch some alternatives.

In our adequacy proofs we referred to the original formulation of LA, since rules (R), (T), (S) correspond directly in a modular way to three conjuncts of LA$^\rightarrow$. Our rule (E) however, is modelled not on LA$^\leftarrow$ but rather on the suitable implication of variant 3 of LA from Lemma 1. As a first approximation we can obtain the rule:

$\dfrac{\varGamma \!\!\Rightarrow \varDelta , \exists z(\forall v(va\leftrightarrow vz)\wedge zb)}{ \varGamma \Rightarrow \varDelta , ab}$

which after further decomposition and quantifier elimination yields:

$\dfrac{da, \varGamma \!\!\Rightarrow \varDelta , dc \quad dc, \varGamma \!\!\Rightarrow \varDelta , da \quad \varGamma \Rightarrow \varDelta , cb }{\varGamma \Rightarrow \varDelta , ab}$

(where d is a new parameter) which is very similar to (E) but with some active atoms in the succedents. This is troublesome for proving cut elimination if ab is a cut formula and a principal formula of (R), (S) or (T) in the right premiss of cut. Fortunately, (E) is interderivable with this rule (it follows from the rule generation theorem in Indrzejczak [5]) and has the principal formula in the antecedent.

It is clear that if we focus on other variants then we can obtain different rules by their decomposition. In effect note that instead of (E) we may equivalently use the following rules based directly on LA, or on variants 2 and 1 respectively:

$(E_{LA})$ $\dfrac{da, \varGamma \!\!\Rightarrow \varDelta , db \quad da, ea, \varGamma \!\!\Rightarrow \varDelta , de \quad ab, \varGamma \Rightarrow \varDelta }{ca, \varGamma \Rightarrow \varDelta }$

$(E_2)$ $\dfrac{da, \varGamma \!\!\Rightarrow \varDelta , dc \quad da, \varGamma \!\!\Rightarrow \varDelta , cd \quad ab, \varGamma \Rightarrow \varDelta }{ca, cb, \varGamma \Rightarrow \varDelta }$

$(E_1)$ $\dfrac{da, ea, \varGamma \!\!\Rightarrow \varDelta , de \quad ab, \varGamma \Rightarrow \varDelta }{ca, cb, \varGamma , \Rightarrow \varDelta }$

where d, e are new parameters (eigenvariables).

Note, that each of these rules, used instead of (E), yields a variant of GO for which we can also prove cut elimination. However, as we will show by the end of this section, (E) seems to be optimal. Perhaps, the last one is the most economical in the sense of branching factor. However, since its left premiss directly corresponds to the condition $\forall xy(xa\wedge ya\rightarrow xy)$ it introduces two different new parameters to premisses which makes it more troublesome in some respects. In fact, if we want to reduce the branching factor it is possible to replace all these rules by the following variants:

$(E')$ $\dfrac{da, \varGamma \!\!\Rightarrow \varDelta , dc \quad dc, \varGamma \!\!\Rightarrow \varDelta , da}{cb, \varGamma \Rightarrow \varDelta , ab}$

$(E_{LA}')$ $\dfrac{da, \varGamma \!\!\Rightarrow \varDelta , db \quad da, ea, \varGamma \!\!\Rightarrow \varDelta , de }{ca, \varGamma \Rightarrow \varDelta , ab}$

$(E_2')$ $\dfrac{da, \varGamma \!\!\Rightarrow \varDelta , dc \quad da, \varGamma \!\!\Rightarrow \varDelta , cd }{ca, cb, \varGamma \Rightarrow \varDelta , ab }$

$(E_1')$ $\dfrac{da, ea, \varGamma \!\!\Rightarrow \varDelta , de }{ca, cb, \varGamma \Rightarrow \varDelta , ab}$

with the same proviso on eigenvariables d, e. Their interderivability with the rules stated first is easily obtained by means of the rule generation theorem too. These rules seem to be more convenient for proof search. However, for these primed rules cut elimination cannot be proved in the constructive way, for the reasons mentioned above, and it is an open problem if cut-free systems with these rules as primitive are complete.

We finish this section with stating the last reason for choosing (E). Let us explain why (E), the most complicated specific rule of GO, was claimed to be connected with extensionality. Consider the following two principles:

$WE \,\,\forall x(xa\leftrightarrow xb)\rightarrow \forall x(ax\leftrightarrow bx)$

$WExt \,\,\forall x(xa\leftrightarrow xb)\rightarrow \forall x(\varphi (x, a)\leftrightarrow \varphi (x, b))$

where $\varphi (x, a)$ denotes arbitrary formula with at least one occurrence of x (not bound by any quantifier within $\varphi$) and a.

Lemma 6

WE is equivalent to WExt.

Proof

That WE follows from WExt is obvious since the former is a specific instance of the latter. The other direction is by induction on the complexity of $\varphi$. In the basis there are just two cases: $\varphi (x, a)$ is either xa or ax; the former is trivial and the latter is just WE. The induction step goes like an ordinary proof of the extensionality principle in FOL.    $\square$

Lemma 7

In G (E) is equivalent to (WE).

Proof

Note first that in G the following sequents are provable:

• $\forall x(ax\leftrightarrow cx), cb\Rightarrow ab$

• $\forall x(xa\leftrightarrow xc), da\Rightarrow dc$

• $\forall x(xa\leftrightarrow xc), dc\Rightarrow da$

we will use them in the proofs to follow.

For derivability of (E):

where $\mathcal{D}$ is a proof of $\forall x(xa\leftrightarrow xc) \Rightarrow \forall x(ax\leftrightarrow cx)$ from WE and the rightmost sequent is provable. The endsequent by cut with $ab, \varGamma \Rightarrow \varDelta$ yields the conclusion of (E).

Provability of WE in G with (E):

In the same way we prove $\forall x(xa\leftrightarrow xc), ab \Rightarrow cb$ which by $(\Rightarrow \leftrightarrow )$, $(\Rightarrow \forall )$ and $(\Rightarrow \rightarrow )$ yields WE.

   $\square$

This shows that we can obtain the axiomatization of elementary ontology by means of LA$^\rightarrow$ and WE (or WExt). Also instead of LA$^\rightarrow$ we can use three axioms corresponding to our three rules (R), (S), (T). Note that if we get rid of (E) (or WE) we obtain a weaker version of ontology investigated by Takano [18]. If we get rid of quantifier rules we obtain a quantifier-free version of this system investigated by Ishimoto and Kobayashi [6].

On the basis of the specific features of sequent calculus we can obtain here for free also the intuitionistic version of ontology. As is well known it is sufficient to restrict the rules of G to sequents having at most one formula in the succedent (which requires small modifications like replacement of $(\leftrightarrow \Rightarrow )$ and $(\Rightarrow \vee )$ with two variants having always one side formula in the succedent) to obtain the version adequate for the intuitionistic FOL. Since all specific rules for $\varepsilon$ can be restricted in a similar way, we can obtain the calculus GIO for the intuitionistic version of elementary ontology. One can easily check that all proofs showing the adequacy of GO and the cut elimination theorem are either intuitionistically correct or can be easily changed into such proofs. The latter remark concerns these proofs in which the classical version of $(\leftrightarrow \Rightarrow )$ required the introduction of the second side formula into succedent by $(\Rightarrow W)$; the intuitionistic two versions of $(\leftrightarrow \Rightarrow )$ do not require this step.

6 Extensions

Leśniewski and his followers were often working on ontology enriched with definitions of special predicates and name-creating functors. In this section we focus on a number of unary and binary predicates which are popular ontological constants. Instead of adding these definitions to GO we will introduce predicates by means of sequent rules satisfying conditions formulated for well-behaved SC rules. Let us call $L_p$ the language of $L_o$ enriched with all these predicates and GOP, the calculus with the additional rules for predicates. The definitions of the most important unary predicates are:

• $Da := \exists x(xa) \quad Va := \lnot \exists x(xa)$

• $Sa := \exists x(ax) \quad Ga := \exists xy(xa\wedge ya\wedge \lnot xy)$

D, V, S, G are unary predicates informing that a is denoting, empty (or void), singular or general. D and S are Leśniewski’s ex and ob respectively. He preferred also to apply sol(a) which we symbolize with U (for unique):

$Ua := \forall xy(xa\wedge ya\rightarrow xy)$ [or simply $\lnot Ga$]

The additional rules for these predicates are of the form:

$(D\Rightarrow )$$\dfrac{ba, \varGamma \!\!\Rightarrow \varDelta }{Da, \varGamma \!\!\Rightarrow \varDelta }$    $(\Rightarrow D)$$\dfrac{\varGamma \!\!\Rightarrow \varDelta , ca}{\varGamma \!\!\Rightarrow \varDelta , Da}$    $(S\Rightarrow )$$\dfrac{ab, \varGamma \!\!\Rightarrow \varDelta }{Sa, \varGamma \!\!\Rightarrow \varDelta }$

$(\Rightarrow S)$$\dfrac{\varGamma \!\!\Rightarrow \varDelta , ac}{\varGamma \!\!\Rightarrow \varDelta , Sa}$   $(V\Rightarrow )$$\dfrac{\varGamma \!\!\Rightarrow \varDelta , ca}{Va, \varGamma \!\!\Rightarrow \varDelta }$    $(\Rightarrow V)$$\dfrac{ba, \varGamma \!\!\Rightarrow \varDelta }{\varGamma \!\!\Rightarrow \varDelta , Va}$

where b is new and c arbitrary in all schemata.

$(G\Rightarrow )$$\dfrac{ba, ca, \varGamma \!\!\Rightarrow \varDelta , bc}{Ga, \varGamma \!\!\Rightarrow \varDelta }$      $(\Rightarrow G)$$\dfrac{\varGamma \!\!\Rightarrow \varDelta , da \varGamma \!\!\Rightarrow \varDelta , ea de, \varGamma \Rightarrow \varDelta }{\varGamma \!\!\Rightarrow \varDelta , Ga}$

$(\Rightarrow U)$$\dfrac{ba, ca, \varGamma \!\!\Rightarrow \varDelta , bc}{\varGamma \!\!\Rightarrow \varDelta , Ua}$      $(U\Rightarrow )$$\dfrac{\varGamma \!\!\Rightarrow \varDelta , da \varGamma \!\!\Rightarrow \varDelta , ea de, \varGamma \Rightarrow \varDelta }{Ua, \varGamma \!\!\Rightarrow \varDelta }$

where b, c are new, and d, e are arbitrary parameters.

The binary predicates of identity, (weak and strong) coextensiveness, nonbeing b, subsumption and antysubsumption are defined in the following way:

• $a=b := ab\wedge ba \quad \quad \,\,\, a\bar{\varepsilon }b := aa \wedge \lnot ab$

• $a\equiv b := \forall x(xa\leftrightarrow xb) \,\,\,\, a\subset b := \forall x(xa\rightarrow xb)$

• $a\approx b := a\equiv b \wedge Da \quad \, a \nsubseteq b := \forall x(xa\rightarrow \lnot xb)$

Finally note that Aristotelian categorical sentences can be also defined in Leśniewski’s ontology:

• $aAb := a\subset b\wedge Da \,\,\, aEb := a\nsubseteq b \wedge Da$

• $aIb := \exists x(xa\wedge xb) \,\,\, aOb := \exists x(xa\wedge \lnot xb)$

The rules for binary predicates:

$(=\Rightarrow )$$\dfrac{ab, ba, \varGamma \Rightarrow \varDelta }{ a=b, \varGamma \Rightarrow \varDelta }$                     $(\Rightarrow =)$$\dfrac{\varGamma \Rightarrow \varDelta , ab \varGamma \Rightarrow \varDelta , ba}{\varGamma \Rightarrow \varDelta , a=b}$

$(\equiv \Rightarrow )$$\dfrac{\varGamma \Rightarrow \varDelta , ca, cb ca, cb, \varGamma \Rightarrow \varDelta }{a\equiv b, \varGamma \Rightarrow \varDelta }$   $(\Rightarrow \equiv )$$\dfrac{da, \varGamma \Rightarrow \varDelta , db db, \varGamma \Rightarrow \varDelta , da}{\varGamma \Rightarrow \varDelta , a\equiv b}$

$(\approx \Rightarrow )$ $\dfrac{da, \varGamma \Rightarrow \varDelta , ca, cb ca, cb, da, \varGamma \Rightarrow \varDelta }{a\approx b, \varGamma \Rightarrow \varDelta }$

$(\Rightarrow \approx )$ $\dfrac{da, \varGamma \Rightarrow \varDelta , db db, \varGamma \Rightarrow \varDelta , da \varGamma \Rightarrow \varDelta , ca}{\varGamma \Rightarrow \varDelta , a\approx b}$

$(\bar{\varepsilon }\Rightarrow )$$\dfrac{aa, \varGamma \Rightarrow \varDelta , ab}{ a\bar{\varepsilon }b, \varGamma \Rightarrow \varDelta }$                     $(\Rightarrow \bar{\varepsilon })$$\dfrac{\varGamma \Rightarrow \varDelta , aa ab, \varGamma \Rightarrow \varDelta }{\varGamma \Rightarrow \varDelta , a\bar{\varepsilon }b}$

$(\subset \Rightarrow )$$\dfrac{{\varGamma \Rightarrow \varDelta , ca cb, \varGamma \Rightarrow \varDelta }}{a\subset b, \varGamma \Rightarrow \varDelta }$           $(\Rightarrow \subset )$$\dfrac{da, \varGamma \Rightarrow \varDelta , db }{\varGamma \Rightarrow \varDelta , a\subset b}$

$(\nsubseteq \Rightarrow )$$\dfrac{\varGamma \Rightarrow \varDelta , ca \varGamma \Rightarrow \varDelta , cb }{a\nsubseteq b, \varGamma \Rightarrow \varDelta }$           $(\Rightarrow \nsubseteq )$$\dfrac{da, db, \varGamma \Rightarrow \varDelta }{\varGamma \Rightarrow \varDelta , a\nsubseteq b}$

$(A\Rightarrow )$$\dfrac{da, \varGamma \Rightarrow \varDelta , ca cb, da, \varGamma \Rightarrow \varDelta }{aAb, \varGamma \Rightarrow \varDelta }$   $(\Rightarrow A)$$\dfrac{da, \varGamma \Rightarrow \varDelta , db \varGamma \Rightarrow \varDelta , ca}{\varGamma \Rightarrow \varDelta , aAb}$

$(E\Rightarrow )$$\dfrac{da, \varGamma \Rightarrow \varDelta , ca da, \varGamma \Rightarrow \varDelta , cb }{aEb, \varGamma \Rightarrow \varDelta }$   $(\Rightarrow E)$$\dfrac{da, db, \varGamma \Rightarrow \varDelta \varGamma \Rightarrow \varDelta , ca}{\varGamma \Rightarrow \varDelta , aEb}$

$(I\Rightarrow )$$\dfrac{da, db, \varGamma \Rightarrow \varDelta }{ aIb, \varGamma \Rightarrow \varDelta }$                     $(\Rightarrow I)$$\dfrac{\varGamma \Rightarrow \varDelta , ca \varGamma \Rightarrow \varDelta , cb}{\varGamma \Rightarrow \varDelta , aIb}$

$(O\Rightarrow )$$\dfrac{da,\varGamma \Rightarrow \varDelta , db}{ aOb, \varGamma \Rightarrow \varDelta }$                     $(\Rightarrow O)$$\dfrac{\varGamma \Rightarrow \varDelta , ca cb, \varGamma \Rightarrow \varDelta }{\varGamma \Rightarrow \varDelta , aOb}$

where d is new and c arbitrary (but c can be identical to d in rules for $\approx , A, E$).

Proofs of interderivability with equivalences corresponding to suitable definitions are trivial in most cases. We provide only one for the sake of illustration. The hardest case is $\approx$.

and

by $(\Rightarrow \wedge )$ yield one part. For the second:

where the left and the middle premiss are obviously provable by means of $(\forall \Rightarrow ), (\leftrightarrow \Rightarrow )$. We omit proofs of the derivability of both rules in GO enriched with the axiom $\Rightarrow \forall x(xa\leftrightarrow xb)\wedge \exists x(xa)\leftrightarrow a\approx b$.

We treat all these predicates as new constants hence their complexity is fixed as 1, in contrast to atomic formulae, which are of complexity 0. Of course we can consider ontology with an arbitrary selection of these predicates according to the needs. Accordingly we can enrich GO also with arbitrary selection of suitable rules for predicates. All the results holding for GOP are correct for any subsystem. Let us list some important features of these rules and enriched GO:

• 1. All rules for predicates are explicit, separate and symmetric, which are usual requirements for well-behaved rules in sequent calculi (see e.g. [5]). In this respect they are similar to the rules for logical constants and differ from specific rules for $\varepsilon$ which are one-sided (in the sense of having principal formulae always in the antecedent).

• 2. All these new rules satisfy the subformula property in the sense that side formulae are only atomic.

• 3. The substitution lemma holds for GO with any combination of the above rules.

• 4. All rules are pairwise reductive, modulo substitution of terms,

We do not prove the substitution lemma, since the proof is standard, but we comment on the last point, since cut elimination holds due to 3 and 4. The notion of reductivity for sequent rules was introduced by Ciabattoni [2] and it may be roughly defined as follows: A pair of introduction rules $(\Rightarrow \star )$, $(\star \Rightarrow )$ for a constant $\star$ is reductive if an application of cut on cut formulae introduced by these rules may be replaced by the series of cuts made on less complex formulae, in particular on their subformulae. Basically it enables the reduction of cut-degree in the proof of cut elimination. Again we illustrate the point with respect to the most complicated case. Let us consider the application of cut with the cut formula $a\approx b$, then the left premiss of this cut was obtained by:

where c is new and d is arbitrary. And the right premiss was obtained by:

where e is new and f is arbitrary.

By the substitution lemma on the premisses of $(\Rightarrow \approx ), (\approx \Rightarrow )$ we obtain:

• 1. $fa, \varGamma \Rightarrow \varDelta , fb$

• 2. $fb, \varGamma \Rightarrow \varDelta , fa$

• 3. $da, \varPi \Rightarrow \varSigma , fa, fb$

• 4. $da, fa, fb, \varPi \Rightarrow \varSigma$

and we can derive:

where $\mathcal{D}$ is a similar proof of $fa, \varGamma , \varPi \Rightarrow \varDelta , \varSigma$ from $\varGamma \Rightarrow \varDelta , da$, 4 and 1 by cuts and contractions. All cuts are of lower degree than the original cut. It is routine exercise to check that all rules for predicates are reductive and this is sufficient for proving Lemma 4 and 5 for GOP. As a consequence we obtain:

Theorem 4

Every proof in GOP can be transformed into cut-free proof.

Since the rules are modular this holds for every subsystem based on a selection of the above rules.

7 Conclusion

Both the basic system GO and its extension GOP are cut-free and satisfy a form of the subformula property. It shows that Leśniewski’s ontology admits standard proof-theoretical study and allows us to obtain reasonable results. In particular, we can prove for GO the interpolation theorem using the Maehara strategy (see e.g. [19]) and this implies for GO other expected results like e.g. Beth’s definability theorem. Space restrictions forbid to present it here. On the other hand, we restricted our study to the system with simple names only, whereas fuller study should cover also complex names built with the help of several name-forming functors. The typical ones are the counterparts of the well-known class operations definable in Leśniewski’s ontology in the following way:

$a\bar{b} := aa \wedge \lnot ab \quad a(b\cap c) := ab \wedge ac \quad a(b\cup c) := ab \vee ac$

It is not a problem to provide suitable rules corresponding to these definitions:

$(-\Rightarrow ) \,\, \dfrac{ aa, \varGamma \Rightarrow \varDelta , ab}{ a\bar{b}, \varGamma \Rightarrow \varDelta } \qquad \qquad \quad \,\, (\Rightarrow -) \,\, \dfrac{ab, \varGamma \Rightarrow \varDelta \quad \varGamma \Rightarrow \varDelta , aa}{\varGamma \Rightarrow \varDelta , a\bar{b}}$

$(\cap \Rightarrow ) \,\, \dfrac{ab, ac, \varGamma \Rightarrow \varDelta }{ a(b\cap c), \varGamma \Rightarrow \varDelta } \qquad \quad (\Rightarrow \cap ) \,\, \dfrac{\varGamma \Rightarrow \varDelta , ab \quad \varGamma \Rightarrow \varDelta , ac}{\varGamma \Rightarrow \varDelta , a(b\cap c)}$

$(\cup \Rightarrow ) \,\, \dfrac{ab, \varGamma \Rightarrow \varDelta \quad ac, \varGamma \Rightarrow \varDelta }{ a(b\cup c), \varGamma \Rightarrow \varDelta } \qquad \quad (\Rightarrow \cup ) \,\, \dfrac{\varGamma \Rightarrow \varDelta , ab, ac }{\varGamma \Rightarrow \varDelta , a(b\cup c)}$

Although their structure is similar to the rules provided for predicates in the last section, their addition raises important problems. One is of a more general nature and well-known: definitions of term-forming operations in ontology are creative. Although it was intended in the original architecture of Leśniewski’s systems, in the modern approach this is not welcome. Iwanuś [7] has shown that the problem can be overcome by enriching elementary ontology with two axioms corresponding to special versions of the comprehension axiom but this opens a problem of derivability of these axioms in GO enriched with special rules.

There is also a specific problem with cut elimination for GO with added complex terms and suitable rules. Even if they are reductive (and the rules stated above are reductive, as a reader can check), we run into a problem with quantifier rules. If unrestricted instantiation of terms is admitted in $(\Rightarrow \exists ), (\forall \Rightarrow )$ the subformula property is lost. One can find some solutions for this problem, for example by using two separated measures of complexity for formula-makers and term-makers (see e.g. [3]), or by restricting in some way the instantiation of terms in respective quantifier rules (see e.g. [4]). The examination of these possibilities is left for further study.

The last open problem deserving careful study is the possibility of application for automated proof-search and obtaining semi-decision procedures (or decision procedures for quantifier-free subsystems) on the basis of the provided sequent calculus. In particular, due to modularity of provided rules, one could obtain in this way decision procedures for several quantifier-free subsystems investigated by Pietruszczak [15], or by Ishimoto and Kobayashi [6].