On Monotonicity Detection in Simplicial Branch and Bound over a Simplex

Abstract

The concept of exploiting proven monotonicity for dimension reduction and elimination of partition sets is well known in the field of Interval Arithmetic Branch and Bound (B &B). Part of the concepts can be applied in simplicial B &B over a box. The focus of our research is here on minimizing a function over a lower simplicial dimension feasible set, like in blending and portfolio optimization problems. How can monotonicity be detected and be exploited in a B &B context? We found that feasible directions can be used to derive bounds on the directional derivative. Specifically, Linear Programming can be used to detect the sharpest bounds.

This paper has been supported by The Spanish Ministry (RTI2018-095993-B-I00) in part financed by the European Regional Development Fund (ERDF).

1 Introduction

Monotonicity considerations to remove subsets and to reduce dimension has a long tradition in Interval Arithmetic based branch and bound, see [4, 8]. The basic property is to be able to remove interior boxes where the function is monotone over the box and to reduce the dimension with respect to monotone components when a box facet is at the boundary of the search space.

Ideas of monotonicity were not investigated in the simplicial branch and bound overview book [10]. More recently, [2, 3, 5, 6] extended monotonicity considerations towards simplicial partition sets. One of the main observations is that if the function to be minimized, f, is monotonically increasing in a direction from a facet of a simplicial partition set S towards its opposite vertex, then S can be reduced to F and consequently, we have a simplicial dimension reduction. As was shown in [2], if F is not border, i.e. not included in one of the faces of the feasible set with the same dimension, then S can be removed from consideration.

The latter question is mainly convenient if the feasible set is a box, as considered in traditional simplicial B &B. However, if the feasible set is a simplex with a dimension lower than that of the function to be minimized, the determination of monotonicity and of a facet being border is more challenging. The focus of this paper is mainly on these research questions. How to demonstrate monotonicity and how to capture that a facet is border.

To investigate these question, Sect. 2 introduces mathematical properties of monotonicity over simplicial sets. Section 3 then discusses some special cases together with LP and MIP models to find monotone directions. Section 4 describes how to keep track of border facets, while Sect. 5 summarises our findings.

2 Mathematical Notation and Properties

2.1 Notation

We consider the minimization of a continuously differentiable function $f:\mathbb R^n\rightarrow \mathbb R$, over a feasible set $\varDelta$, which is an $p-$simplex, i.e. $\varDelta :={{\,\mathrm{conv}\,}}(\mathcal W)$ is defined by a set of $p+1$ affine independent vectors that serve as vertices

$$\begin{aligned} \mathcal W:=\{v_0,\ldots ,v_{p}\}\subset \mathbb R^n, p<n. \end{aligned}$$

(1)

The idea is to find or enclose all global minimum points of

$$\begin{aligned} \min f(x),x\in \varDelta . \end{aligned}$$

(2)

The consideration of $n-$dimensional functions over $m<n$ lower dimensional simplicial feasible area appears for instance in blending problems [1]. Our context is that of a branch and bound algorithm to enclose all minimum points of f on $\varDelta$. In contrast to the algorithms described in [10], the used partition sets are $m-$simplices S, where $m\le p$. This means $S:={{\,\mathrm{conv}\,}}(\mathcal V)$ with $\mathcal V$ a set of $m+1=|\mathcal V|$ vertices. The branch and bound algorithm works with a set $\Lambda$ of partition sets, which as a whole include all global minimum points.

Although we usually limit our context to the use of longest edge bisection, where the longest edge (v, w) of a partition set S is bisected using mid-point $x:=\frac{v+w}{2}$, we pose the monotonicity question in a larger context where any partition method may be used, as described in [7]. The set of evaluated points that serve as vertices of the partition sets is denoted by X. Specifically, we focus on dimension reduction due to monotonicity considerations, where a set $\mathcal V$ of vertices of $m-$simplex S is reduced to $\mathcal V\setminus \{v\}$ and S is replaced by one (or more) of its facets $F:={{\,\mathrm{conv}\,}}(\mathcal V\setminus \{v\})$ for some $v \in \mathcal V$. Notice that F is an $(m-1)$-simplex. It may be clear that for $m=0$, the $0-$simplex $S={{\,\mathrm{conv}\,}}(\{v\})$ is an individual point and does not have faces. Its dimension cannot be reduced.

The centroid of $m-$simplex $S= {{\,\mathrm{conv}\,}}(\{v_0,v_1,\ldots ,v_m\})$ is given by $c:=\frac{1}{m+1}\sum _{j=0}^m v_j$ and the relative interior is defined by

$$\begin{aligned} {{\,\mathrm{rint}\,}}(S)=\{x=\sum _j\lambda _jv_j, \lambda _j>0, j=0,\ldots ,m,\sum _{j=0}^m \lambda _j=1\}. \end{aligned}$$

(3)

The relative boundary of a simplex S is defined by removing the relative interior from it. Given a simplicial partition set S, we are interested in whether its (simplicial) facets F are border with respect to the feasible set $\varDelta$. In general, we can define a simplex to be border with respect to a simplicial feasible set.

Definition 1

Given p-simplex feasible area $\varDelta$. An $m-$simplex S with $m<p$ is called border with respect to $\varDelta$ if there exists an m-simplex face $\varphi$ of $\varDelta$, such that $S\subseteq \varphi$.

One of the main questions is how to determine whether a facet of a simplex is border in a numerically efficient way. Border facets and the concept of monotonicity are used to reject a simplex or to reduce its simplicial dimension.

Relevant information is an enclosure G of the gradient $\nabla f(x)\subseteq G:=[\underline{G},\overline{G}], \forall x \in S$. Interval vector G can be calculated by Interval Automatic Differentiation over the interval hull of a simplex S, see [9, 11]. Now consider directional vector d as the difference between two points in S, then the corresponding directional derivative $d^T\nabla f(x)$ is also included in the inner product

$$\begin{aligned} {d^TG}=\left[ \underline{d^TG},\overline{d^TG}\right] = \left[ \sum _{i=1}^{n} \min \{d_i\underline{G}_i, d_i \overline{G}_i\}, \sum _{i=1}^{n} \max \{d_i\underline{G}_i, d_i \overline{G}_i\}\right] . \end{aligned}$$

(4)

2.2 Mathematical Properties on Monotonicity

The monotonicity is based on directional derivative bounds of (4). Notice that condition $0\notin G$ is necessary to have monotonicity, but not sufficient. The question is which direction d to consider. The most general result for an $m-$simplex is the following.

Proposition 1

Let $S\subseteq \varDelta$ be an $m-$simplex with gradient enclosure G. If $\exists \ x,y\in S$, such that direction $d=x-y$ has corresponding directional derivative bounds (4) with $0\notin [\underline{d^TG},\overline{d^TG}]$ then ${{\,\mathrm{rint}\,}}(S)$ does not contain a global minimum point of (2).

Proof

Consider $z\in {{\,\mathrm{rint}\,}}(S)$. As z is in the relative interior, there exists a feasible direction d in which lower function values can be found, i.e. $\exists \varepsilon \in \mathbb R$ small enough, such that $z+\varepsilon d \in S$ and $f(z+\varepsilon d)<f(z)$. So z cannot be a minimum point of f.    $\square$

The elaboration for an algorithm depends on the choice of the direction d and the way to compute it.

Corollary 1

Let $S\subseteq \varDelta$ be an $m-$simplex as partition set in a branch and bound algorithm with corresponding gradient enclosure G. If the conditions of Proposition 1 apply and S has no border facets, then S can be rejected.

The argument is that the relative boundary of S may contain a global minimum point, but the same point is enclosed in the relative boundary of another partition set.

Given that the minimum is not in ${{\,\mathrm{rint}\,}}(S)$, we have to decide which of the facets to focus on. In [2], we made use of the following property in the design of a specific algorithm.

Proposition 2

Given $m-$simplex $S={{\,\mathrm{conv}\,}}(\mathcal V)$ with centroid c and a facet F generated by removing vertex v from $\mathcal V$. Consider direction $d=v-c$. If $\underline{d^TG}>0$, then the facet F contains all minimum points in S, i.e. ${{\,\mathrm{argmin}\,}}_{x\in S}f(x)\subseteq F$.

Practically, this means that S can be replaced by F if $\underline{d^TG}>0$. However, a similar reasoning applies as in Corollary 1; if F is a non-border facet, then simplex S can be removed from further consideration in a branch and bound context. The idea is again that faces of F may contain the minimum. However, because we are dealing with a partition, the same points are also included in other simplicial partition sets.

Fig. 1.

Three partition sets generated by bisection, using bisection points $x_3$ and $x_4$. We focus on monotone directions in S.

Example 1

For the illustration of the concept, consider the simplices in Fig. 1. It shows three partition sets generated by bisection, using bisection points $x_3$ and $x_4$. Consider $S={{\,\mathrm{conv}\,}}(\mathcal V)$ with $\mathcal V=\{v_1,x_3,x_4\}$, where we assume that the orange direction provides a monotonously increasing direction. According to Proposition 1, the interior of S does not contain a global minimum point. Let the blue direction provide a direction $d=v-c$ for which the lower bound of (4) is positive for facet $F={{\,\mathrm{conv}\,}}(\mathcal V\setminus \{v\})$ with $v=x_4$. According to Proposition 2, facet $F={{\,\mathrm{conv}\,}}(\{v_1,x_3\})$ contains all minimum points on S. Now, the border considerations show that we even can remove S, as there is another partition set at its left, that encloses all minimum points.

There are two questions we address in this paper.

• Is there a way to show that a direction d in which f is monotonic on S exists?

• The direction $d=v-c$ for a facet F may not be monotonically increasing, but can there be another direction from facet F to vertex v?

3 Cases of Directional Derivatives

To prove that there exists a monotone direction in an $m-$simplex, at least we should have $0\notin G$. This is a necessary, but not sufficient condition for an $m-$simplex, $m<n$. To prove that such a direction exists, according to Proposition 1, we need to find a direction $d=x-y$, with $x,y \in S$ corresponding to a positive lower bound of the directional derivative

$$\begin{aligned} 0 < \underline{d^TG} = \sum _{i=1}^{n} \min \{d_i\underline{G}_i, d_i \overline{G}_i\}. \end{aligned}$$

(5)

Finding such a direction can be done by searching for the steepest monotone direction $\max _{d} \underline{d^TG}$. Consider the terms $z_i=\min \{d_i\underline{G}_i, d_i \overline{G}_i\}$. This means we can write $\underline{d^TG}=\sum _{i=1}^{n} z_i$. If we fix one of the point $x \in S$ in $d=x-y$, then the term $z_i(y)=\min \{(x_i-y_i)\underline{G}_i, (x_i-y_i) \overline{G}_i\}$ is a concave function in y, as it is the minimum of two affine functions. Therefore, the lower bound on the directional derivative $\underline{g}(y):=\underline{(x-y)^TG}$ is a concave function being the sum of concave terms. Similarly, it can be shown that the upper bound $\overline{g}$ on the directional derivative is a convex function. We will illustrate this with an example and then show how an LP problem can be formulated to find a maximum of $\underline{g}(y)$.

Fig. 2.

Shape of concave $\underline{g}(y)=\underline{g}(\lambda v_1+(1-\lambda )v_2$ as function of $\lambda$ in orange and convex $\overline{g}$ in purple (Color figure online).

Example 2

Consider a simplex $S={{\,\mathrm{conv}\,}}(\mathcal V)$ with $\mathcal V=\{v_0,v_1,v_2\}$ in $\mathbb R^6$ with $v_0=0, v_1=(1,-2,3,-4,5,6)^T$ and $v_2=(0,3,-2,5,-4,-5)^T$. In $d=x-y$, we take as fixed point $x=v_0$ and vary y over the edge between $v_1$ and $v_2$ as suggested in Proposition 2, so $y=\lambda v_1+(1-\lambda )v_2, 0\le \lambda \le 1$. Figure 2 sketches the oncave piece-wise linear shape of $\underline{g}$ as function of $\lambda$ and the convex shape of $\overline{g}$.

Looking for the existence of a positive value of $\underline{d^TG}$ for some direction d, we can fix x to the centroid in the directional vector, i.e. $d=c-y$. The maximization of concave piece-wise linear function $\underline{g}(y)$ over $y\in S$ can be formulated as the following LP problem.

$$\begin{aligned} \begin{aligned}&\max \sum _{i=1}^n z_{i} \\ {{\,\mathrm{\quad s.t. \quad }\,}}&z_{i}\le (c_i-y_i)\underline{G}_i,\ i=1,\ldots ,n\\&z_{i}\le (c_i-y_i)\overline{G}_i,\ i=1,\ldots ,n\\&\sum _{j=1}^m \lambda _j=1 \\&y=\sum _{j=0}^m\lambda _jv_j\\&\lambda _j\ge 0, j=0,\ldots ,m \end{aligned} \end{aligned}$$

(6)

If there is no monotone direction, then $y=c$ and $\sum _{i=1}^m z_{i}=0$.

Example 3

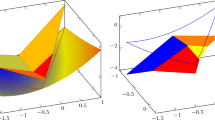
For the illustration of the concept, consider the 2-simplex S defined by three vertices $\mathcal V=\{(4,0,1)^T, (0,0,0)^T, (3,2,1)^T\}$ in 3-dimensional space, projected in 2D for Fig. 3. Its centroid is given by $\frac{1}{3}(7,2,2)^T$. Now let the bounds of the gradient be given by $\underline{G}=(-3,1,0)^T$ and $\overline{G}=(1,2,1)^T$. For none of the directions $d=v_j-c$, we have that lower bound $\underline{d^TG}$ is positive. Running the LP (6) provides us with a positive directional derivative bound of $\frac{2}{3}$ for the point $y=(\frac{7}{3}, 0, \frac{7}{12})^T$. The monotone direction $c-y$ is drawn by an orange arrow in Fig. 3. This means that f is monotone on S. This illustrates that checking a finite number of directions over the simplex is not necessarily sufficient to prove that f is monotone. The LP (6) provides a numerical proof of f being monotone over S or not. Notice again that $y=c$ is a feasible solution of the LP yielding an objective function value of zero as soon as monotonicity cannot be proven.

Fig. 3.

2D image of the 2-simplex S. The point y provides a positive lower bound on the directional derivative in direction $d=c-y$.

Following the line of reasoning of the example, according to Proposition 1, we can conclude that simplex S can be replaced by its facets. Now at least one of the facets is of interest, although that cannot be concluded by only considering the directions $d=v-c$ for this specific example. The question is now whether there is a monotone direction from a vertex v to a point y on the facet $F={{\,\mathrm{conv}\,}}(\mathcal V\setminus \{v\})$ for which $d=v-y$ has a positive lower bound on the directional derivative $\underline{d^TG}>0$. If such direction can be found, according to a similar reasoning as in Proposition 2, the minimum of the simplex is in F.

To answer the question whether such a direction would exist, we can solve the following LP for a specific facet F maximizing the lower bound of a directional derivative. Consider now the ordered vertex set $\mathcal V:=\{v_0, v_1,\ldots ,v_m\}$ and the vertex set of F given as $\{v_1,\ldots ,v_m\}:=\mathcal V\setminus \{v_0\}$. Focusing on the direction $v_0-y$ with $y=\sum _{j=1}^m \lambda _jv_j$, we can demonstrate that there is a (maximum) positive directional derivative, if it exists, by solving the LP

$$\begin{aligned} \begin{aligned}&\max \sum _{i=1}^n z_{i} \\ {{\,\mathrm{\quad s.t. \quad }\,}}&z_{i}\le \underline{G}_i (v_{0i}-y_i),\ i=1,\ldots ,n\\&z_{i}\le \overline{G}_i (v_{0i}-y_i),\ i=1,\ldots ,n\\&\sum _{j=1}^m \lambda _j=1 \\&y=\sum _{j=1}^m \lambda _jv_{j} \\&\lambda _j\ge 0, j=1,\ldots ,m. \end{aligned} \end{aligned}$$

(7)

If the result is positive, we have proven all minima of f over S are on F.

Example 4

We can now show how LP (7) is working, following the illustration in Fig. 3 for facet $F={{\,\mathrm{conv}\,}}\{v_0,v_1\}$. Although the lower bound on the directional derivative of $d=v_2-c$ is not positive, the LP will provide a solution $y=(3, 0, \frac{3}{4})^T$ with an objective function value of 2. The corresponding direction is also illustrated with an arrow between $(3, 0, \frac{3}{4})^T$ and $v_2$ in Fig. 3.

In a procedure for searching for such a facet, in the worst case we need to solve LP (7) $m+1$ times. Instead, we might solve only one Mixed Integer Programming problem (MIP) where a binary variable $\delta _j$ selects the facet corresponding to the most positive directional derivative.

$$\begin{aligned} \begin{aligned}&\max \sum _{i=1}^n z_{i} \\ {{\,\mathrm{\quad s.t. \quad }\,}}&z_{i}\le \underline{G}_i d_i,\ i=1,\ldots ,n\\&z_{i}\le \overline{G}_i d_i,\ i=1,\ldots ,n\\&\sum _{j=0}^m \lambda _j=1 \\&d = \sum _{j=0}^m \delta _jv_j -\sum _{j=0}^m\lambda _j v_{j}\\&\sum _{j=0}^m \delta _j = 1.\\&\lambda _j\ge 0, j=0,\ldots ,m\\&\delta _j\in \{0, 1\}, j=0,\ldots ,m \end{aligned} \end{aligned}$$

(8)

MIP (8) can be used to replace LP problem (7) if such a monotonously increasing direction towards one of the vertices exists. If this is not the case, the solution is 0 with the direction $d=0$. However, there still may exist an increasing direction according to LP (6).

Example 5

For our example in Fig. 3 with $S={{\,\mathrm{conv}\,}}\{v_0,v_1,v_2\}$ the MIP (8) finds indeed the positive objective function value of $\sum _{i=1}^n z_{i}$, stating that the facet corresponding to $\delta _2=1$ provides the maximum derivative lower bound.

The two steps, looking whether a monotone direction exists and identifying which facet contains all the minima (if any), can also be done in one step. Thus, instead of solving LP (6) and (7) $m+1$ times (or MIP (8)), we can solve directly one MIP as follows. Let $d=x-y$, where $x,y\in S$, so $x=\sum _{j=0}^m \lambda _j v_j$ and $y=\sum _{j=0}^m \mu _j v_j$. Consider direction $d=x-y=\sum _{j=0}^m (\lambda _j-\mu _j)v_j$.

$$\begin{aligned} \begin{aligned}&\max \sum _{j=0}^m \delta _j \\ {{\,\mathrm{\quad s.t. \quad }\,}}&z_{i}\le \underline{G}_i d_i,\ i=1,\ldots ,n\\&z_{i}\le \overline{G}_i d_i,\ i=1,\ldots ,n\\&\sum _{j=0}^m \lambda _j=1 \\&\sum _{j=0}^m \mu _j=1 \\&d = \sum _{j=0}^m (\lambda _j-\mu _j)v_j\\&\sum _{i=1}^n z_{i} \ge \varepsilon \\&\mu _j+1 \ge 2\delta _j \quad \forall j=1,\ldots , m\\&\sum _{j=0}^m \delta _j \le 1.\\&\mu _j, \lambda _j\in \left[ 0, 1\right] , j=1,\ldots ,m\\&\delta _j\in \{0, 1\}, j=1,\ldots ,m \end{aligned} \end{aligned}$$

(9)

A solution with $\mu _k=1$ and $\mu _j= 0, j\ne k$ represents a direction d pointing to vertex $v_k$. A solution with $\lambda _k=1$ and $\lambda _j=0, j\ne k$ represents a direction pointing from vertex $v_k$. We connect $\mu _j$ with binary variables $\delta _j$ such that $\delta _j=1$ implies $\mu _j=1$. The inequality $\sum _{i=1}^n z_{i} \ge \varepsilon$ with $\varepsilon >0$ assures d is a monotone direction. Moreover, it forces $\mu \ne \lambda$, because otherwise $z=0$ as well. If no monotone direction exists, (9) has no feasible solution.

The objective is to maximize the sum of $\delta _j$, meaning that we aim at finding a monotone direction with $\mu _k=1$ corresponding to $\delta _k=1$. In this case, we know that facet $F={{\,\mathrm{conv}\,}}(\mathcal{V}\setminus \{v_k\})$ contains all minima according to Proposition 2. If the objective is zero, there is no facet containing all the minima, i.e. there is no $\delta _k=1$, but there is a monotone direction d.

Example 6

Following our example in Fig. 3 with $S={{\,\mathrm{conv}\,}}\{v_0,v_1,v_2\}$ the MIP (9) finds the positive objective function value 1 for $\sum _{i=1}^n z_{i}$, stating that the facet corresponding to $\delta _2=1$ provides a positive directional derivative for $d=v_2-v_0$. Notice, that this direction is not the maximum directional derivative, but still positive, which is the main question.

Interestingly, solving the LP-s and MIP-s in Matlab, the necessary time for this example was counter-intuitive: LP (6) 0.521, LP (7) 0.033, while MIP (9) 0.048 s.

We investigated whether the counter-intuitive result of a smaller solution time for the MIP than for the LP is a general trend. Therefore, we compared the solution time and effectiveness of formulations (6), (7), (8) and (9). We took 447 simplices from a branch and bound process over the functions Hartman 3, 4 and 6 that, as the name suggests, have dimension 3, 4 and 6. We have used the routines linprog and intlinprog in Matlab setting IntegerTolerance to 1e−6 and ConstraintTolerance to 1e−8. The result is given in Table 1.

Table 1. Time and effectiveness of the LP and MIP formulations

In each line of the table we give for the LP and MIP formulations the percentage of the effectiveness measured as proven monotonicity. For instance, for problem Hartman 3, LP (6) proved in 81.6% that there is a monotone directional derivative.

We can prove there is a monotone decreasing direction from any facet by solving LP (7) for all vertices, or by solving any of the MIP-s once. Comparing the formulations, LP (7) is the strongest, while MIP (9) is the weakest due to the $\varepsilon$ in its formulations, which is hard to set together with the tolerances. The percentage development shows that, as the found monotone directions are less and less solving LP (7), MIP (8) and MIP (9), and the percentage where the best results are not found goes up in the same order.

Surprisingly, the average computing time is the smallest for MIP (8), followed by MIP (9) or LP (6), and the slowest is LP (7). The latter is no surprise as in that case we added up the time needed to solve LP (7) for all facets, or until it found a monotone decreasing direction from a facet.

4 Keeping Track of Border Facets

Fig. 4.

Faces of the feasible set with bisection points $x_3$ and $x_4$.

For a box constrained feasible set, finding the border status of a partition set is relatively easy, as it is determined by lower and upper bounds on the components and the correspondence with the simplicial partition sets. To determine the border status of a given facet in a simplicial feasible set, we use a labelling system to find out which minimum dimensional face of $\varDelta$ the F is included in. This is done by assigning to each face $\varphi$ of feasible set $\varDelta ={{\,\mathrm{conv}\,}}(\mathcal W)$ a label $\mathcal B(\varphi )$, starting with the vertex faces labeled $\mathcal B(v_j)=0...010...0$ where the only 1 is the jth bit, for $j=0,\ldots ,n$. Each face $\varphi$, which is a convex combination of vertices $\mathcal{V}\subseteq \mathcal{W}$, the corresponding bit-string $\mathcal B(\varphi )$ has a value 1 for each vertex $v\in \mathcal{V}$ in the same position as in $\mathcal B(v)$. For instance, in Fig. 4, the edge $(v_1,v_2)$ has label 011, and the simplex $\varDelta$ has label 111. In fact, for an m-simplex face $\varphi$ of the feasible set, its label is given by the bitwise OR operation (BitOr) of the label of all its vertices. The complete face graph is given in Fig. 5 for a 4-vertex simplex.

In a bisection refinement, the label can easily be determined. After bisecting the original set of vertices $\mathcal W$, we store the bisection points in set X. For instance in Fig. 4, we have $X=\{v_0, v_1, v_2, x_3, x_4\}$. We label all generated points $x\in X$, which serve as vertices for the partition sets. The label of point x is the same as the label of the minimum dimensional face $\varphi$ of the feasible set x is in. For instance, the label of $x_3$ is 101, the same as the label of face ${{\,\mathrm{conv}\,}}(v_0,v_2)$. During bisection, a new vertex $x=\frac{v+w}{2}$ gets label $\mathcal B(x)={\textbf {BitOr}} (\mathcal B(v),\mathcal B(w)).$

Fig. 5.

Face graph for a 3-simplex. Binary boxed labels for each face.

Given an $m-$simplex $S={{\,\mathrm{conv}\,}}(\mathcal V)$, the question is what is the label of the (smallest dimensional) face $\varphi$ it is included in. This is determined by the label $\mathcal B(\varphi )={\textbf {BitOr}} (\mathcal B(\mathcal V))$, to be interpreted as a bitor on all its vertex labels. The number of ones of a bitstring $\mathcal B(\varphi )$ is denoted by $|\mathcal B(\varphi )|$, giving the number of vertices of $\varphi$. According to Definition 1, $m-$simplex S is border if there exists an $m-$simplex face $\varphi$ of the feasible set including S ($m<p$).

Proposition 3

Given $m-$simplex $S={{\,\mathrm{conv}\,}}(\mathcal V)$ with $m<p$, if $|{\textbf {BitOr}} (\mathcal B(\mathcal V))|=m+1$, then simplex S is border.

Proof

Consider the face $\varphi$, which is the minimal dimensional face containing S, i.e. label $\mathcal B(\varphi )={\textbf {BitOr}} (\mathcal B(\mathcal V))$. As $|{\textbf {BitOr}} (\mathcal B(\mathcal V))|=m+1$, we have $|\mathcal B(\varphi )|=m+1$, thus $\varphi$ is an $m-$simplex. Therefore, S is enclosed by an $m-$simplex face of the feasible set and thus is border.

For example in Fig. 4, the edge $(x_3,v_2)$ is border, as $|{\textbf {BitOr}} (\mathcal B(\{x_3,v_2\}))|=|{\textbf {BitOr}} (101,001)|=|101|=2$ corresponding to face ${{\,\mathrm{conv}\,}}(\{v_0,v_2\})$. In contrast, edge $(x_3,x_4)$ is not border, because $|{\textbf {BitOr}} (\mathcal B(\{x_3,x_4\}))|=|111|=3\ne 2$. In fact, the minimum dimensional face it is included in, is $\varDelta$ itself.

5 Conclusions

The interest in monotonicity in simplicial branch and bound is relatively recent. Given bounds on the gradient, the essential idea is that we have to check bounds on the directional derivative for a feasible direction related to the simplicial dimension of a partition set. In this paper, we show that the determination of monotonicity of a function over a simplicial partition set can be done by solving an LP problem. Moreover, it is possible for a facet to find the highest lower bound based on a specific LP. The outcome determines, whether it is possible to reduce the dimension of the simplicial partition set or to decide to remove it from further consideration. Several steps can be combined by solving a specific MIP problem.

For the decision on the removal of a simplex, it is relevant whether a facet is border with respect to the feasible set. For a box constrained feasible set this is relatively easy. This paper shows that by consistently labeling points that serve as vertices, it is possible to determine a facet is border or not.

In our future work, we implement the LP type of tests in a simplicial branch and bound framework to investigate whether the number of generated simplices is decreasing compared to an algorithm, where one direction is tested per facet.