1 Introduction

Phase change processes in clouds are one of the most important driving factors of precipitation, such as rain or snow, and have a great influence on our daily weather. The understanding of these processes is crucial for the development of weather and climate models and of reliable weather forecasts [40]. Especially the small scales, such as droplets and their interactions in the atmosphere, strongly affect the behaviour of the macroscopic systems [5, 39]. However, there is still a lack of knowledge regarding the processes in clouds at high altitude [28, 62]. Within these, a range of phenomena are encountered which in turn are responsible for the evolution of the water cycle [64]. Among them are the freezing of supercooled droplets, collision and coalescence events, evaporation and sublimation processes, droplet growth due to condensation, or the formation of larger structures, such as snow or hail [25]. Acquiring a deeper understanding of those events as well as developing new models and strategies was the aim of this study.

The main focus is put on the behaviour of droplets in extreme conditions, particularly at low temperatures. In high altitudes, where the atmosphere cools down to less than \(-40 \, {{}^{\circ }\text {C}}\) [77], liquid droplets are still present in a metastable state, which is termed supercooled. In an unsaturated ambiance evaporation processes can occur, whereas when the surrounding air is oversaturated condensation takes place. If droplets cool down even further, droplet freezing inevitably begins. Two different types of freezing processes exist. On the one hand, homogeneous freezing, when a sufficiently large nucleus is spontaneously generated, and on the other hand heterogeneous freezing, where a seed particle initiates the solidification [75]. In an analogous way, depending on the ambient conditions, the frozen droplets can subsequently grow even further due to deposition or decrease in size because of sublimation. The growth of ice strongly depends on the pressure and temperature boundary conditions in the surrounding and various crystallized structures can evolve [7].

In order to investigate supercooled droplets under extreme ambient conditions and to study the mentioned phase change processes, experimental and numerical methods are deployed in this work. The combination of both allows precise insight into the physics of droplets. Furthermore, the synergy of numerical simulations and experiments can provide detailed information about the phase change processes. The present work represents a summary of multiple studies within the third funding phase of the subproject B1 of the Collaborative Research Centre SFB-TRR 75. To classify the complete compilation and outcome of the project, a brief overview of previous works concerning phase change processes of droplets is given in the following. It is split into experimental and numerical studies and subdivided into the respective characteristics of phase change.

Many numerical studies focusing on multiphase flows exist in literature. Two approaches are prevalent, which are front-tracking [72] and front-capturing methods[20, 60]. A classification of both can be found in [33]. When dealing with evaporation, a lot of numerical approaches in the literature provide deep insight into its mechanisms [14, 18, 19, 46, 47, 68, 73]. The most promising approaches, which are also able to deal with complex three-dimensional structures as well as extreme conditions, are conducted using the Volume-of-Fluid (VOF) method [49, 58, 78]. The same accounts for investigations of solidification and melting processes, where auspicious results were obtained with this method in [32] and within the SFB-TRR 75 [42, 44]. Nevertheless, various other approaches exist, particularly for investigating crystal growth of water [1, 8, 10, 59, 67, 74]. In contrast to evaporation or freezing, numerical studies regarding sublimation are rare in literature. Besides large-scale investigations [30, 64] for geophysical models only a few small-scale approaches exist [27, 45, 70].

Various experiments were reported that study the supercooled environment in clouds. These were conducted in wind tunnels and cloud chambers, among others [38, 66]. In order to study the phase change of droplets more closely, experiments with single droplets were conducted. Several experimental studies have been performed on the evaporation of droplets under ambient conditions in electrodynamic traps [24, 26] and by means of acoustic levitation [48] as well as on the evaporation of droplets at low Reynolds numbers [79]. Only few literature can be found concerning the investigation of the evaporation of supercooled water droplets (SWD) [51, 71]. More broadly investigated is the behaviour of ice crystals which included experimental studies on evaporation and melting of different shapes of ice crystals [36], sublimation [35, 65] and growth of ice crystals [65]. Furthermore, sublimation experiments with frozen droplets or spheres were conducted [52, 70]. Several works have focused on the freezing of droplets. The probabilities of freezing on contact was investigated [2] as well as heterogeneous nucleation and contact freezing of levitated droplets [13, 23, 37]. Additionally, studies were performed to determine the nucleation time and freezing behaviour of SWDs [11, 29, 52, 61].

The following sections will outline the numerical and experimental investigations of the evaporation, sublimation and freezing of droplets within the subproject B1 of the Collaborative Research Centre SFB-TRR 75.

2 Experimental Methods

2.1 Experimental Setup

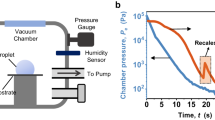
The experiments are conducted with an optical levitation setup as described in Roth et al. [52] and Ruberto et al. [56]. The stable optical trapping through radiation pressure was first investigated by Ashkin [4]. Figure 1 shows the setup of the cooling chamber as well as the optical setup. A laser beam focused by a lens is directed through the levitation chamber. The droplet is levitated above the focus and the position of the droplet within the chamber can be varied when the lens is moved. The laser has a wavelength of 532 nm, that is hardly absorbed by water, so the droplet does not heat up during the experiments. The chamber can be cooled down to –40 \({}^{\circ }\text {C}\) by a cryostat. A U-shaped temperature profile develops in the chamber, that is qualitatively shown in Fig. 1 next to the experimental setup. Droplets were trapped in the region of constant temperature. As the droplet is cooled down to a metastable state, it is important to use purified water so that it does not freeze due to impurities. In order to avoid pollution of the atmosphere inside the chamber and convection from outside, a very slow flow of dry nitrogen (99,999%) passes through the chamber. It is controlled by precise mass flow meters. The volume flow rate is variable but chosen such that only low Reynolds numbers are reached. This flow is needed for achieving steady conditions in the chamber, so that evaporated mass from the droplet can be transported out and no saturation is reached inside the chamber. To study phase-change behaviours with different relative humidities, the nitrogen can be humidified in an appropriate setup. These conditions, relative humidity and temperature, are monitored before and after the experiment.

The droplets are produced by a droplet-on-demand generator which is driven by a piezo-electric ceramic. Recently, the in-house built generator was exchanged with a commercial one [69] which allows for more controllable conditions and increased repeatability for future experiments. As the droplet is levitated, it has to fall into the test chamber along the centre of the laser beam. Thus, the generator is mounted onto two precise linear position stages. The position of the levitated droplet is monitored by a position sensitive device (PSD). A second PSD sensor is mounted alongside the first. It monitors the split-beam of the scattered light after a Wollaston prism which will show the depolarisation of the light due to the freezing of the droplet. Once the droplet is levitated, the measurement starts with a delay in order to ensure that the droplet attained the ambient temperature.

Fig. 1
figure 1

adapted from [55]

Left side: Schematic of the experimental setup, indicating the temperature profile along the chamber height. Right side: Optical setup to record the light scattering and shadowgraphy and signal path,

Full size image

2.2 Observation Techniques

The droplet inside the test chamber can be observed by two techniques. When the laser reaches the droplet, the light scatters. This light scattering in the forward hemisphere is recorded by a CCD line camera and is shown in Fig. 2. The light is collected by a lens in the focal plane of the camera so that a specific scattering angle is recorded on the same camera pixel. The recorded intensity distribution is converted to intensity over scattering angle. The scattering image is dependent on the droplet diameter which will show a smaller fringe spacing and higher number of maxima for a larger droplet diameter [15]. The following equation was used to determine the droplet diameter, D, for evaporating droplets [15]

$$\begin{aligned} D = \frac{2~\lambda }{\Delta \Theta }\left( cos\left( \frac{\Theta }{2}\right) + n~sin\left( \frac{\Theta }{2}\right) ~\left[ 1+ n^2-2 n~cos\left( \frac{\Theta }{2}\right) \right] ^{1/2}\right) ^{-1} \end{aligned}$$
(1)

in which n is the refractive index, \(\lambda \) the laser wavelength in m, \(\Theta \) the camera mounting angle in \({}^{\circ }\) and \(\Delta \Theta \) the angular fringe distance in \({}^{\circ }\). The refractive index was derived from a correlation as a function of the laser wavelength \(\lambda \) and the fluid temperature [16, 56]. The fringe distance is averaged over several maxima of a line. The accuracy of the measurements is about \(\pm 2{\%}\) for droplet diameters in the range of \(20~{\upmu \text {m}}< D <60~{\upmu \text {m}}\) [56]. Below 20\(\upmu \)m, the accuracy decreases as the intensity of the maxima is lower and, therefore, the noise increases. As mentioned above, the number of maxima decreases for lower droplet diameters which leads to larger uncertainties in \(\Delta \Theta \) [56]. As mentioned above, the number of maxima decreases for lower droplet diameters which leads to larger uncertainties in \(\Delta \Theta \) [56]. It is important that the image of the line camera is not overexposed as the position of the maxima is then lost [55]. The line camera was triggered with a frequency of 5000 Hz and for a period of 12s. This method is mainly used for the observation of evaporating droplets and derivation of the evaporation rate. When the droplet freezes, the scattering image shows a dramatic difference and the pattern of the maxima becomes more indistinct and chaotic. Nevertheless, it was still possible to derive the sublimation rate from the scattering images by adapting the evaluation code. As mentioned above, the moment of freezing is detected by an increase of intensity on the PSD sensor after the Wollaston Prism. As the scattering image is chaotic, the droplet is also observed by shadowgraphy. A LED illuminates the droplet and the shadow is recorded by a CCD camera with a frequency of 2 Hz and a magnification of \(M = 36.4\) [54]. The size of the droplet can be derived from the shadow images by image processing. An algorithm identifies the size of the area of the shadow by the number of pixels that the droplet comprises or a circle can be computed that fits the area around the droplet. From the area and the circle around the droplet, its size and the decrease in diameter over time can be derived.

Fig. 2
figure 2

Light scattering recorded from a SWD, which froze at \(t= 0~{\text {s}}\). The intensity signal is plotted over the camera pixel

Full size image

3 Numerical Methods

All developed methods and conducted numerical investigations are done using the in-house software package Free Surface 3D (FS3D) [12]. This Direct Numerical Simulation (DNS) code is based on the mentioned VOF method and solves the incompressible Navier-Stokes equations on a Marker and Cell (MAC) grid. In addition, the energy equation is included, which is mandatory when dealing with phase change processes. The interface reconstruction is achieved by applying the Piecewise Linear Interface Calculation (PLIC) scheme. The code is highly parallelized using MPI as well as OpenMP and is run on the High-Performance Computing Center (HLRS) in Stuttgart. Main focus from the numerical side is put on the three types of phase change: solidification, sublimation, and evaporation. The introduced new developed methods and approaches are based on works of Reitzle et al. [44, 45] (solidification and sublimation) as well as Reutzsch et al. [49] (evaporation).

3.1 Conservation Equations

For all phase change algorithms the basic equations are similar. Several assumptions are made, such as neglecting radiation and viscous dissipation, pure substances, Newtonian insoluble fluids, and local thermodynamic equilibrium at the interface. Furthermore, a Fickian diffusion model is used for the diffusive fluxes. The mass conservation for every species j reads

$$\begin{aligned} \frac{\partial (\rho _{p}^{j})}{\partial t} + \nabla \cdot (\rho _{p}^{j} {\textbf {u}}) = \nabla \cdot (\bar{\rho } \mathfrak {D} \nabla \! X^j) \, , \end{aligned}$$
(2)

with the partial density \(\rho _{p}\), average density \(\bar{\rho }\), velocity \({\textbf {u}}\), diffusion coefficient \(\mathfrak {D}\), and the mass fraction X. For an incompressible, pure fluid within a Eulerian one-field formulation it simplifies to \(\nabla \cdot {\textbf {u}} = 0\). This can be used to formulate the momentum balance equation in differential form as

$$\begin{aligned} \frac{\partial (\rho {\textbf {u}})}{\partial t} + \nabla \cdot (\rho {\textbf {u}} \otimes {\textbf {u}}) = -\nabla p + \nabla \cdot {\textbf {S}} + \rho {\textbf {g}} \, , \end{aligned}$$
(3)

where p denotes the pressure, \({\textbf {S}} = \mu \left( \nabla {\textbf {u}} + (\nabla {\textbf {u}})^T \right) \) the viscous part of the stress tensor with the dynamic viscosity \(\mu \), and \({\textbf {g}}\) the gravitational acceleration. Finally, the energy equation reads

$$\begin{aligned} \frac{\partial }{\partial t}\left( \rho c_p T \right) + \nabla \cdot \left( \rho c_p T {\textbf {u}} \right) = \nabla \cdot \left( \lambda \nabla T \right) + \dot{q}''' \, . \end{aligned}$$
(4)

Therein, \(c_p\) is the specific heat capacity at constant pressure, T the temperature, \(\lambda \) the thermal heat conductivity, and \(\dot{q}'''\) a volumetric heat source. A two-field approach is used where an energy equation is solved for each phase. The balance equations are coupled at the interface with jump conditions as additional constraints in multiphase flows. In the following, we distinguish between the continuous phase \(\left( ^\textrm{c}\right) \) and the disperse phase \(\left( ^\textrm{d}\right) \). In addition, whenever necessary, a further differentiation is made regarding the phase change cases solidification (\(\textrm{so}\)), sublimation (\(\textrm{su}\)), and evaporation (\(\textrm{ev}\)). The mass jump condition can be written as

$$\begin{aligned} \dot{m}'' = \rho ^\textrm{c} \left( {\textbf {u}}^{\textrm{c}} - {\textbf {u}}_{\mathrm {\Gamma }} \right) \cdot {\textbf {n}}_\Gamma = \rho ^\textrm{d} \left( {\textbf {u}}^{\textrm{d}} - {\textbf {u}}_{\mathrm {\Gamma }} \right) \cdot {\textbf {n}}_\Gamma \, , \end{aligned}$$
(5)

with the area-specific mass source \(\dot{m}''\), the interface velocity \({\textbf {u}}_{\mathrm {\Gamma }}\) and the respective normal vector \({\textbf {n}}_\Gamma \). The disperse phase represents the solid for solidification and sublimation, and analogously the liquid for evaporation cases. The continuous phase is synonymous considered to the gaseous phase \(\left( ^\textrm{gp}\right) \) for sublimation and evaporation, and to the liquid phase for solidification. For sublimation and evaporation, the gaseous phase can be split further into inert gas \(\left( ^\textrm{g}\right) \) and vapour \(\left( ^\textrm{v}\right) \) and the interface velocity can be derived from the mass source (see [45]) as

$$\begin{aligned} V_\Gamma = -\frac{\rho ^\textrm{gp}_\Gamma }{\rho ^\textrm{d}} \mathfrak {D} \frac{1}{1-X^\textrm{v}} \nabla X^\textrm{v} \cdot {\textbf {n}}_\Gamma . \end{aligned}$$
(6)

Note that in order to evaluate the term \(\nabla X^\textrm{v} \cdot {\textbf {n}}_\Gamma \) information about the condition at the interface need to be known. For sublimation processes, an expression for the solid-gaseous equilibrium was derived [43, 45], whereas for evaporation the saturation condition for the pure substance was used. The momentum jump condition simplifies to the well-known Young-Laplace equation

$$\begin{aligned} p^{\textrm{d}} - p^{\textrm{c}} = \kappa \sigma \, , \end{aligned}$$
(7)

where \(\kappa \) represents the interface curvature and \(\sigma \) the surface tension. The energy balance across the interface (see [43] for the contained simplifications and assumptions) yields

$$\begin{aligned} \dot{m}'' \Delta {h} = -\lambda ^{\textrm{c}} \Delta T^{\textrm{c}} \cdot {\textbf {n}}_\Gamma -\lambda ^{\textrm{d}} \Delta T^{\textrm{d}} \cdot {\textbf {n}}_\Gamma \, , \end{aligned}$$
(8)

with the specific latent heat \(\Delta {h}\), which obviously differs for all cases.

For solidification processes, containing liquid \(\left( ^\textrm{l}\right) \) and solid \(\left( ^\textrm{s}\right) \), the character of growth is of greater interest. The surface energy density determines strongly the morphology of a crystal. The boundary condition for the energy is computed with the Gibbs-Thomson equation in this case. Considering the anisotropic mean curvature \(H_\Gamma \) that contains information about the (possibly anisotropic) surface energy densities it reads

$$\begin{aligned} T_\Gamma&= T_m \left[ 1 - \frac{1}{\rho \Delta {h}^\textrm{s}} \left( \sigma _0 H_\Gamma \right) \right] \nonumber \\&+ \frac{ \left( c_p^\textrm{l} - c^\textrm{s} \right) T_\Gamma }{\Delta {h}^\textrm{s}} \left[ T_\Gamma \ln \left( \frac{T_\Gamma }{T_m} \right) - \left( T_m -T_\Gamma \right) \right] \, , \end{aligned}$$
(9)

with the interface temperature \(T_\Gamma \), melting temperature \(T_m\), and latent heat of fusion \(\Delta {h}^\textrm{s}\). For detailed information the reader is referred to [45]. The energy equation for solidification at the interface, also known as Stefan condition, can be derived as

$$\begin{aligned} \dot{m}'' \left[ \Delta {h}^\textrm{s} - \left( c_p^\textrm{l} - c^\textrm{s} \right) \left( T_m - T_\Gamma \right) \right] = -\lambda ^{\textrm{l}} \Delta T^{\textrm{l}} \cdot {\textbf {n}}_\Gamma +\lambda ^{\textrm{s}} \Delta T^{\textrm{s}} \cdot {\textbf {n}}_\Gamma \, . \end{aligned}$$
(10)

Note that terms of higher order were neglected in this formulation. For the precise modelling of the local thermodynamic equilibrium at the interface, the anisotropic surface energy density, and a detailed derivation of all boundary conditions the reader is referred to already mentioned studies [44, 45, 49].

3.2 Numerical Approach

The complete basic numerical scheme of the used code is described in great detail in the work of Rieber [50] and several extensions are given by many other authors e.g. [12, 17, 41, 58]. Thus, only a brief overview of the necessary approaches is given here. Due to the formulation of the VOF method, additional scalar variables \(f_i\) are introduced, which contain information about the volume fraction within each cell. They are defined as

$$\begin{aligned} f_i({{\textbf {x}}},t) = {\left\{ \begin{array}{ll} 0 &{} \text {in the continuous phase,}\\ ]0;1[ &{} \text {in interface cells,}\\ 1 &{} \text {in the disperse phase.} \end{array}\right. }\end{aligned}$$
(11)

Depending on the phase, \(f_i\) describes the fraction of the liquid (\(f_1\)), the vapour (\(f_2\)), or the solid (\(f_3\)) phase. Due to the one-field character of the VOF method, material properties can be expressed using just one equation. Considering all volume fractions the density, for instance, reads

$$\begin{aligned} \rho ({{\textbf {x}}},t) = \sum _{i=1}^{3}f_i({{\textbf {x}}},t) \rho _{p,i} + \left( 1 - \sum _{i=1}^{3}f_i({{\textbf {x}}},t)\right) \rho ^\textrm{g} \, . \end{aligned}$$
(12)

The densities \(\rho _{p,i}\) refer to the partial densities of the liquid, vapour, and solid phase. The transport of the VOF variables is done via the equation

$$\begin{aligned} \frac{\partial f_i}{\partial t} + {\textbf {u}} \cdot \nabla f_i = 0 \, . \end{aligned}$$
(13)

Note that diffusion is additionally considered for the transport of the vapour phase inside the inert gas. Advection is done using an operator-splitting technique [63], where the three dimensional transport is achieved by three single one-dimensional steps. Details regarding the necessary divergence corrections steps can be found in [50]. The fluxes are obtained in interfacial cells using the PLIC algorithm.

Furthermore, for phase change processes the movement of the interface is interpreted as a consequence of a flux. In contrast to previous approaches [42, 58] this leads to more stable simulations as well as circumvents complex redistribution. Hence, the movement of the interface is done using an additional transport equation, which reads

$$\begin{aligned} \frac{\partial f_i}{\partial t} + \nabla \cdot \left( f_i {\textbf {u}}_\Gamma \right) = f_i \nabla \cdot {\textbf {u}}_\Gamma \, . \end{aligned}$$
(14)

The velocity field at the interface \({\textbf {u}}_\Gamma \) is related to the local interfacial velocity via \(V_\Gamma ={\textbf {u}}_\Gamma \cdot {\textbf {n}}_\Gamma \). For the evaluation of the fluxes a geometrical unsplit advection scheme is applied [44]. The gradients of volume fractions, which serve as the basis to derive the interface velocity, are obtained by means of second order finite differences coupled with a tridiagonal interpolation scheme [42].

Taking the definition of the density and substituting it into the continuous and disperse part and considering the global mass conservation, an expression for the volume conserving velocity \({\textbf {u}}_\textrm{vol}\) depending on the mass source \(\dot{m}'''\) can be derived as

$$\begin{aligned} \nabla \cdot {\textbf {u}}_\textrm{vol} = \dot{m}''' \left( \frac{1}{\rho ^\textrm{c}} - \frac{1}{\rho ^\textrm{d}} \right) \, . \end{aligned}$$
(15)

Note that in case of solidification the difference in densities of the phases is neglected and, hence, a solenoidal velocity field is retained. For evaporation the possible movement of the liquid interface also has to be considered for the convective step. A mass averaged velocity is necessary which is a consequence of the solution of the momentum equations. Two methods to obtain the velocities for the gaseous and liquid phase were developed by Reutzsch et al. [49]. The basic idea is to split the parts into the respective amounts of vapour and inert gas and connect them with the mass source term. An averaging with the volume fractions as well as a more precise approach using cell wetting is proposed.

The momentum equations are solved in several steps. The detailed procedure is described in [50]. In a first step, the convective part is handled using the before mentioned operator-splitting method. The viscous part is discretized using central differences and a pressure projection scheme is applied in order to obtain a solenoidal velocity field [9]. For rigid bodies, which are relevant for solidification and sublimation cases, further treatment is necessary (see [42]).

The diffusive parts are solved using the newly developed approach by Reitzle et al. [45]. The energy equation is solved for all phase change processes, using a two-field approach in order to gain more precise values at the interface [43, 57]. Diffusive mass transfer is only considered for the vapour field in sublimation or evaporation simulations. The basic idea is to set Dirichlet boundary conditions on the sharp interface for the concentration fields. The gradient is obtained by an accurate geometrical approach evaluating an inverse distance interpolation scheme in the vicinity of neighbouring cells. The resulting system of linear equations is finally solved with a Red-Black Gauss-Seidel algorithm.

The convective part of the energy equation is again solved using the splitting algorithm in a semi-implicit formulation. A TVD-limiter from van Leer [76] is used in order to interpolate the values onto the cell edges. The fluxes are obtained in a similar way as the VOF variables.

Fig. 3
figure 3

Simplified sequence of steps for all considered phase change processes

Full size image

3.3 Solution Procedure

Due to the complexity of the code the complete time integration scheme is not presented here and the reader is referred to the afore mentioned literature for a detailed description. In general, it is possible to use first or second order accurate schemes within FS3D.

An abstracted, simplified sequence of steps for all possible phase change processes is shown in Fig. 3. Note that the depicted procedure gives only a rough overview and several steps are summed up within one sub–item. The new methods developed within this project dealing with solidification, sublimation, and evaporation were validated extensively. Due to the high complexity, multi-stage procedures were applied in order to validate not only the single terms and routines, but also their interactions for all kinds of setups. The respective simulations, evaluations and comparisons to experimental results or analytical models are not presented here. They can be found e.g. in the works of Reitzle et al. [43,44,45] and Reutzsch et al. [49] along with the complete, detailed description of all routines.

Fig. 4
figure 4

Temporal evolution of the solid particle represented by partly opaque PLIC surfaces

Full size image

4 Results

4.1 Solidification Simulation

A three dimensional simulation for the hexagonal anisotropic growth of a water crystal has been conducted successfully. It is described in detail in [44], a short summary is presented in the following. The initial setup contains a spherical seed with a radius \(r_0 = 8.206 \, {\upmu \text {m}}\) slightly larger than the stable radius in a liquid water environment with a supercooling of \(\Delta T = 10 \, {\text {K}}\). The cubic domain has a dimension of \(30 r_0\), where a Dirichlet boundary condition for the temperature is applied at a sphere with a radius of \(15 r_0\) in order to minimize the influence of the cubic domain. The material properties of the solid were evaluated at the melting temperature, the liquid properties were taken at a reference temperature \(T = T_\infty \), where \(T_\infty \) denotes the ambient temperature. In addition, a slight rotation of the prismal energy was set to ensure that no dendrite is directly aligned with any coordinate axis. The temporal evolution of the crystal growth from the spherical seed is shown in Fig. 4. In addition, the three-dimensional ice crystal after \(t = 1.2 \, {\upmu \text {s}}\) is depicted in Fig. 5. The hexagonal structure as well as constrictions of the crystal in the prismal planes are clearly visible. This behaviour is also observed in literature (cf. [6]). Furthermore, it leads to the evolution of crystal forms, such as capped-cylinders or hollow needles.

Fig. 5
figure 5

Rendered visualization based on PLIC surface data at \(t=1.2 \, {\upmu \text {s}}\)

Full size image
Fig. 6
figure 6

Comparison of experimentally (dots) and numerically (triangles) obtained rates of sublimation \(\beta \) over relative humidity \(\Phi _{\text {ice}}\) with respect to ice. A linear fit (solid line) to the experimental results was calculated using a forced constraint \(\beta (\Phi _{\text {ice}}={100\,\mathrm{\%}}) = 0\). The uncertainties in the experiments in the vertical direction incorporate the \({95\,\mathrm{\%}}\) confidence level, whereas the uncertainty in the horizontal direction is due to the accuracy of the humidity sensor

Full size image

4.2 Sublimation Simulations and Experimental Results

Investigations concerning sublimation of frozen droplets were conducted numerically and experimentally. A detailed description of the numerical setup as well as the test chamber is given in [45]. An ice particle at \(236.15 \, {\text {K}}\) with a diameter of \(50 \, {\upmu \text {m}}\) in a slow air flow was investigated. Sublimation rates were measured and simulated at varying ambient humidity \(\Phi \) and compared subsequently. The material properties for all components were obtained from literature [3, 31, 53]. A numerical setup with a spatial resolution of \(512^3\) grid cells was chosen that represents a small part of the experimental test chamber. The experiments were conducted at relative humidities with respect to ice of \(\Phi _{\text {ice}{1}}=66\%\), \(\Phi _{\text {ice}{2}}=69\%\), and \(\Phi _{\text {ice}{3}}=70\%\). The results were obtained by averaging at least 10 independent measurements. Again, detailed values are presented in [45]. Whereas the experiments could not be conducted at a broad range of humidity, the simulations were performed between 0 and \(80\%\). The sublimation rates \(\beta _\textrm{su}\) are compared and results are shown in Fig. 6. One can clearly see that there is a linear trend of the sublimation rate as was already assumed in literature (e.g. [70]). The comparison of numerical and experimental results shows that the numerical model is able to predict the sublimation rates very well. The remaining differences occur probably due to uncertainties in the boundary conditions and the remaining simplifications in the numerical model. The maximum sublimation rate at \(0\%\) was found as \(\beta _{\Phi =0} = 19.87 \, \upmu \textrm{m}\,\textrm{s}^{-2}\).

The experiments were conducted at around \(T_\infty = 236 \, {\text {K}}\) which was the temperature at which homogeneous nucleation occurred. At this temperature, it proved difficult to control and measure the humidity as the conditions inside the chamber were already supersaturated with the residual humidity and the humidities in Fig. 6 resulted from freezing at the chamber entry. Moreover, the accuracy of the humidity sensor was not high at such low temperatures and no dew point monitors could be used due to space restrictions in the chamber.

In Fig. 7, shadow images of a first liquid and then frozen droplet are shown. In the experiments, when the droplet froze, it deformed and a spike appeared on the outside of the droplet. In literature, it is reported that this spike can eject ice particles or in case of larger droplets, the droplet can shatter due to high pressure inside [21, 66]. This is a very important process in cloud formation [22]. In comparison, the droplet is also shown after 120s when it is reduced in size and the spike has disappeared due to sublimation. The measurements of the ambient conditions and sublimation rate include some uncertainties. For the temperature, it was \(\pm ~ \Delta T_\infty = 0.4{\text {K}}\) and \(\pm ~ \Delta \phi = 4{\%}\) for the humidity over ice. The uncertainty in the sublimation rate was determined as the standard error of the mean with a 95% confidence interval.

Fig. 7
figure 7

Time evolution of a levitated drop from the liquid to the frozen state showing a spike. After 120 s, the droplet shrank and the spike disappeared due to sublimation, leaving the droplet almost shperical again

Full size image

4.3 Evaporation Simulations and Experimental Results

A similar procedure as for the before mentioned sublimation investigation was applied for the evaluation of evaporation of supercooled droplets. The experimental setup is described in detail by Ruberto et al. [55] whereas further information about the numerics can be found in Reutzsch et al. [49]. In contrast to sublimation, the control of the ambient conditions of the experimental setup was easier. Therefore, it was possible to conduct an expanded systematic study on the evaporation rates. Supercooled droplets were levitated at various temperature regimes. In addition, the ambient humidity could be varied in a larger range. Hence, measurements between \(T_\infty =253.15 \, {\text {K}}\) and \(T_\infty =268.15 \, {\text {K}}\) have been performed with a humidity between \(25\%\) and up to \(95\%\) and the corresponding evaporation rates \(\beta _\textrm{ev}\) were measured. The new evaporation model was applied to perform comparative simulations. The numerical setup was adapted to the experiments and is shown schematically in Fig. 8. The domain, consisting of the levitated droplet, an air flow from the left side, as well as several boundary conditions, has a resolution of \(512\times 256\times 256\) cells. Thus, the droplet is resolved with about 26 cells per diameter. Material properties were taken from the literature (cf. Sect. 4.2).

Fig. 8
figure 8

Numerical setup. The droplet, air flow, and the respective boundary conditions are highlighted

Full size image
Fig. 9
figure 9

Experimental and numerical results at temperatures \(T_\infty =268.15\), \(T_\infty =263.15\), and \(T_\infty =253.15\) with varying humidity \(\Phi \). The symbols represent the averaged measurements and simulations, respectively, the linear fits of the experiments are additionally highlighted with lines

Full size image

The results of the experiments as well as the simulations are depicted in Fig. 9. For three different ambient temperatures in the test chamber at \(T_\infty =268.15\, {\text {K}}\), \(T_\infty =263.15\, {\text {K}}\), and \(T_\infty =253.15\, {\text {K}}\) several points were measured and simulations have been conducted. The humidities, as mentioned before, were varied. In the frame of the numerical investigation, even a complete dry atmosphere, as well as a saturated ambiance were set up and simulated for each case. The experimental linear fit for all temperatures is also depicted with the respective lines. The results are in very good agreement for all cases. The maximum deviation between the linear fits and the simulations is about \(5\%\). In addition, a comparison with the well known \(D^2\)-law [34] is promising. Worth mentioning is that also an older evaporation model of the authors was able to predict similar evaporation rates [55, 56]. However, the current evaporation model was mainly developed to cope with all ranges of extreme ambient condition, even with higher evaporation rates and strong surface deformations. The latter problems cannot be described with our previous models.

There are several uncertainties in the measurements. In case of the temperature the uncertainties originate from the accuracy of the thermocouple, an uncertainty due to the droplet position in the chamber and the stability of the ambient temperature in the chamber [54]. Furthermore, a mean value as well as the standard error of the mean (SEM) were calculated from the measurements of the ambient conditions in the chamber for all of the measurements of a set temperature. This gave an uncertainty in the temperature of \(\Delta T_\infty \approx 0.4 {\text {K}}\). The SEM for the humidity was low and the uncertainty stems mostly from the probe with \(\Delta \Phi = \pm 6\%\) or lower. The SEM of the evaporation rate was calculated with a Student’s factor for a 95\(\%\) confidence interval [54].

5 Conclusions

The investigation of phase changes of and in supercooled droplets is of fundamental interest for the understanding of the processes in clouds at high altitudes and the development of modern climate models. The focus in this work lies on the phase transitions evaporation, sublimation, and freezing. Due to the metastable state of supercooled droplets, the extreme conditions and the complexity of this topic, several approaches to increase the knowledge within this field were considered and multiple studies have been conducted: On the one hand, numerical models were developed, which are capable of dealing with all three phase transitions mentioned above. These newly developed methods, which comprise fully consistent treatments of the processes, were summarized and the solution procedures were collated in a neat arrangement for the first time. On the other hand, experimental investigations were performed simultaneously. An experimental setup was built, which traps single droplets through optical levitation. The test chamber is able to realise conditions far below the freezing point of water and, thus, emulate the temperature encountered in clouds at high altitudes. Sublimation and evaporation rates of frozen and supercooled droplets were measured. Subsequently, they were compared with the simulation results gained by means of the developed numerical methods. The experimental and numerical results showed a very good agreement.