1 Introduction

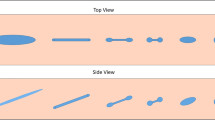
Dynamic wetting of a solid surface by impacting liquid droplets has gained a lot of attention due to its practical relevance in agriculture, coating, painting, ink-jet printing, etc.. [13, 17, 20, 53, 60]. When a droplet impacts on a solvophobic surface, it can deposit, splash (disintegrate), or rebound depending on liquid and solid properties [29]. After a droplet touches a surface, it spreads laterally. The spreading of Newtonian droplets is generally governed by their initial kinetic energy (impact velocity), the viscous energy dissipation of the liquid, and the surface tension of the droplet. Dimensionless Reynolds, Re = \(\rho v D/\eta \), and Weber numbers, We = \(\rho v^2 D/\gamma \), characterise the balance between them, where \(\rho \), v, D, \(\eta \), and \(\gamma \) refer to the droplet mass density, the impact velocity, the initial droplet diameter, the shear viscosity of the liquid, and the droplet surface tension, respectively [1, 29, 38, 50]. For a droplet of small Re, much energy is dissipated by liquid viscosity, which leads to a small droplet diameter at maximum spreading. A small We refers to large surface tension, also resulting in small droplet diameter. The spreading is followed by splashing or retraction depending on the surface energy compared to the remaining kinetic energy. If the liquid-vapor surface tension is not large enough to store the remaining kinetic energy, the droplet splits into several sub-droplets. Otherwise, the droplet retracts as it minimises its surface area. The retraction of Newtonian droplets is controlled by the initial kinetic energy, the capillary force and the viscous dissipation, which is quantified by the dimensionless capillary number, Ca = \(\eta v / \gamma \). A large Ca denotes a stronger viscous effect compared to an elastic effect of the surface, thus it makes the retraction velocity slow. The retraction is also affected by frictional energy dissipation at the liquid-solid interface, which is characterised either by surface wettability or the solid-liquid interfacial tension. As the latter is not easy to measure experimentally, equilibrium or dynamic contact angles are widely adopted in its place. If the kinetic energy is not sufficiently dissipated during the retraction, the remaining particle momentum is diverted to the surface normal, which results in droplet rebound (Fig. 1).

Fig. 1
figure 1

Schematic description of droplet impact process. A droplet first spreads laterally after touching the surface. After reaching maximum spreading, it retracts back to recover its spherical shape. If the initial kinetic energy is not fully dissipated, it rebounds off the surface

Full size image

A droplet impacting on a solvophobic surface is very likely to bounce off it as the frictional energy dissipation at the liquid-solid interface during spreading and retraction is small. The unwanted droplet rebound may lead to reduced productivity in many industrial processes including coating, painting and printing [2, 35, 57]. In agriculture, it is a challenging problem to suppress the bouncing of pesticide sprays for better efficiency without a large modification of the solution composition [62]. Among several strategies to suppress droplet rebound from a solvophobic surface [26, 30, 58], polymer additives are well-established. The first observation was that a few hundreds ppm of polyethylene oxide (PEO) in water suppresses the rebound when a droplet impacts on a hydrophobic leaf [6, 36, 54]. A droplet of an aqueous polymer solution in the dilute regime well below the overlap concentration has a liquid-vapor surface tension and the shear viscosity very similar to that of a pure water droplet, but it is able to suppress the rebound [4]. Since only considering We and Ca cannot explain the phenomenon, other, non-Newtonian properties are necessary to explain it.

Over three decades, scientists put efforts to find the mechanism of the polymer-induced anti-rebound. Many observations showed that the retraction velocity of a polymer-solution droplet is slower than that of a pure solvent droplet, but this has been interpreted in many different ways. In this article, we review some physical concepts of the existing explanations, and we provide a molecular picture of the droplet impact process in order to elucidate the polymer effect on the rebound using dissipative particle dynamics simulations.

1.1 Dynamic Surface Tension

An early attempt held the dynamic liquid-vapor surface tension of a droplet responsible for the rebound suppression. Mourougou-Candoni et al. [37] performed a droplet impact experiment of a surfactant solution onto a hydrophobic flat surface, and interpreted the different dynamics, particularly during retraction, in terms of the dynamic surface tension. Newtonian droplets have a homogeneous liquid-vapor interface, thus the surface tension under any deformation remains the same or very close to its equilibrium value. In contrast, a small amount of surfactant is heterogeneously distributed in the droplet, and the molecules are localised on a quickly expanding or shrinking surface. As the droplet is deformed, a surfactant molecule needs time to diffuse onto the new surface. The rate of the surfactant diffusion to the surface, typically called adsorption kinetics, depends on the type of surfactants and the deformation rate. Surfactants with fast adsorption kinetics quickly diffuse to the surface during spreading, so the dynamic surface tension at maximum spreading becomes small, leading to a low retraction force. The adsorption kinetics also affects the reduction of the surface tension during retraction. The slow retraction due to the small surface tension causes a fast reorganisation of surfactant molecules on the surface during retraction, leading to a further decrease of the surface tension. Therefore, surfactants having fast adsorption kinetics are expected to suppress the droplet rebound.

A later work done by Crooks et al. [16] followed a similar idea of the dynamic surface tension, but under restricted conditions. They found that the fluid’s hydrodynamics is different for the droplet impact from that in the maximum bubble pressure method (MBPM) which is a measurement technique for the dynamic surface tension. They alleged that the mechanism of the dynamic surface tension does not work below the critical micelle concentration of the surfactant when hydrodynamics critically influences to the surfactant diffusion. However, above the critical micelle concentration, demicellisation quickly supplies the surfactants to the surface. Because this process is not much affected by hydrodynamics, the dynamic surface tension observed from MBPM could explain the different retraction and rebound upon impact.

The idea of the reduced surface tension, however, cannot explain the rebound suppression by a polymer additive, e.g., PEO in water, as PEO has a very slow adsorption kinetics [24]. Moreover, a small amount of surface-stabilising surfactants substantially reduces an equilibrium surface tension, provoking fragmentation or splashing of the droplet after spreading, which worsens the problems beyond the droplet rebound in many applications.

Fig. 2
figure 2

A typical schematic of shear (black) and elongational (blue) viscosities as a function of deformation rate of polymeric materials. A red line indicates an average polymer extension in the steady state as a function of the elongation flow rate

Full size image

1.2 Elongational Viscosity

When an elongational deformation is applied to a polymeric material, the polymer stretches in the direction of the elongation. The stretched polymer is entropically and sometimes energetically, too, unfavourable compared to its average equilibrium conformation. The tendency to recover its equilibrium coiled conformation generates a pulling force against elongation. If a polymer solution is deformed by flow, the polymer is elongated in the flow direction. As a consequence, the first normal stress difference, \(N_1=\sigma _{zz}-\sigma _{xx}\), becomes negative, where \(\sigma _{zz}\) and \(\sigma _{xx}\) refer to the diagonal stress tensor components in flow and in perpendicular directions, respectively. The elongational viscosity characterises the viscous energy dissipation by the first normal stress under elongation, written as \(\eta _\text {e}=-N_1/\dot{\epsilon }\), where \(\dot{\epsilon }\) indicates the elongational flow rate. For moderate flow rates, the restoring force of the polymer is purely entropic and the elongational viscosity is strongly related to the amount of stretch of the polymer chains (Fig. 2). Due to the finite extensibility of chains, the elongational viscosity saturates at high elongation rates. The finite extensibility of the polymer also makes it difficult to measure experimentally the elongational viscosity of a dilute polymer solution since the fluid easily breaks up under the large deformation. Figure 2 shows a typical dependence of the elongational viscosity of shear-thinning polymeric materials on the deformation rate. At low deformation rates, materials follow Newtonian behaviour with the relation \(\eta _\text {e}=3\eta \) [9]. At high deformation rates, however, the Trouton ratio defined by the ratio between elongational and shear viscosities, \(\eta _\text {e}/\eta \), raises to up to \(10^4\) for polymer solutions [47].

The concentration dependence of the elongational viscosity of polymer solution is stronger than of the shear viscosity. Even for dilute polymer solutions far below the overlap concentration, the elongational viscosity increases rapidly with increasing polymer concentration as the stretching amount is very sensitive to the elongation rate, while the shear viscosity is not [48]. The strongly concentration-dependent, non-Newtonian property made it an attractive candidate explanation for the slow droplet retraction caused by a tiny amount of polymer.

Bergeron et al. [3] proposed a relation between the reduction of the retraction velocity and the elongational viscosity of the fluid. They found that the retraction of a 100 ppm aqueous PEO droplet impacting on a hydrophobic spin-coated glass plate is five times slower than that of a pure water droplet, and consequently, the droplet does not rebound. The elongational viscosity was obtained using an opposing nozzle rheometer, and also by fitting the normal stress under shear with the finite extensible nonlinear elastic polymer (FENE-P) constitutive equation [9]. The authors claimed that the normal stress differences due to the elongated chains are the main channel for the additional energy dissipation during retraction. The capillary number typically governing the retraction velocity of Newtonian droplets also works for polymer solution droplets when it is re-written in terms of the elongational viscosity replacing shear viscosity, Ca = \(v_\text {ret}\eta _\text {e}/3\gamma \).

A controversy about this work, however, debated the effect of the elongational viscosity being applied only to the retraction, but not to the spreading. In their publication, even for an impacting velocity high enough to make the liquid flow rate much faster than the polymer relaxation rate (We > 1), the elongational viscous energy dissipation does not occur during the spreading, and the maximum spreading diameter does not change [6]. Furthermore, the calculated elongation is incorrect because the flow velocity is divided by the thickness of the droplet instead of the length of the droplet along the elongation direction, which is, by definition, a shear rate. The correct elongation rate would be an order of magnitude smaller than that reported, thus it is no longer constant with varying flow rate, and its accuracy is no longer reliable. The discrepancy of \(\eta _\text {e}\) of the same material in different publications from the same group also made it even more controversial [6, 34].

Recently, non-Newtonian liquid properties originating from polymer stretching were again studied in an experiment by Dhar et al. [18]. They impacted an aqueous solution droplet of polyacrylamid on a superhydrophobic surface, and observed the critical impact velocity above which the rebound is suppressed. It turned out to decrease with increasing polymer concentration. They argued that a deformation rate of the fluid faster than the rate of polymer relaxation, achieved by the high impact velocity, is necessary for the additional energy dissipation during retraction. Although the fact that the additional energy dissipation by non-Newtonian behaviour of the droplet suppresses the droplet rebound aligns with the idea of Bergeron et al. [3], it would rather have to be interpreted as the behaviour of a non-Newtonian droplet whose shear viscosity is higher than that of a pure water droplet, because they used droplets of high polymer concentration and also the shear rate is used for the critical Weissenberg number.

While many simulations of the impact Newtonian droplets using molecular dynamics [23, 31], dissipative particle dynamics [56, 61], and numerical solutions of the Eulerian droplet model [14] have been published, very few studied dilute polymer solution droplets using field-based simulations of the FENE-Chilcott-Rallison (FENE-CR) model [28, 49]. This model can control non-Newtonian viscoelasticity of a droplet by an extra stress tensor, keeping the solvent viscosity constant. A study by Izbassarov et al. [28] found an enhanced rebound tendency of the viscoelastic droplet compared to a Newtonian one, when its equilibrium contact angle ranges from 50 to 120\(^\circ \). This result is opposed to many experimental findings of polymer-induced rebound suppression, which implies that elongational energy dissipation is not the source of rebound suppression. A later work by Tembely et al. [49] reproduced the rebound suppression of a viscoelastic droplet on a super-hydrophobic surface with an equilibrium contact angle of 154\(^\circ \). Unfortunately, molecular mechanisms or its physical origins are completely missing in this publication. Furthermore, the FENE-CR model showed that the behaviour during spreading, i.e. a maximum spreading factor defined by the maximum diameter divided by the initial droplet diameter, is also affected by viscoelastic properties, which is contrary to experimental observations.

The idea of the energy dissipation by non-Newtonian elongational viscosity receded from the mainstream, since several experiments provided evidence against it. Rozhkov et al. [40] performed an experiment of PEO solution droplets of various concentrations impacting on a small disk-like object whose diameter is comparable to the droplet’s diameter. The purpose of impacting droplet on a very small object is to minimise the effect of surface wettability (liquid-surface interaction) on the droplet dynamics. They found that the maximum spreading factor and the retraction velocity do not depend on the PEO concentration, but that the shape of the spreading droplet does, which ruled out the possible role of the elongational viscosity as the source of energy dissipation during spreading and retraction. Another impact experiment of polymer solution droplets on a heated surface in which the liquid-surface interaction is negligible due to the vapor film above the surface (Leidenfrost phenomenon) also showed that polymer concentration does not alter the rebound tendency [4].

Fig. 3
figure 3

a Beads-on-a-spring structure in 5g/L PEO solution. Temporal evolution of the flatness factor \(\zeta \), height divided by lateral radius, for b pure water and c 10g/L polymer solution droplets. d The damping coefficient and e the spring constant obtained by fitting data with the equation of a damped harmonic oscillator. Reprinted with permission from [15]. Copyright (2018) @ American Chemical Society

Full size image

The fluid behaviour caused by polymer elongation was recently revisited in a different aspect by Chen et al. [15]. This work performed a droplet impact experiment of a dilute aqueous PEO solution on a superhydrophobic glass surface coated with cellulose stearoyl ester. They found a “beads-on-a-string” structure which is a thin liquid filament between the droplet and the substrate, when the droplet jumped from the surface. The filament can be thinner and longer before breaking up for higher polymer concentrations, and it applies an elastic elongation force against the rebound (Fig. 3a). Analysis of the droplet-height oscillation by fitting it with the equation for a damped harmonic oscillator (flatness factor, \(\xi \)) shows a higher damping coefficient and a higher spring constant for higher polymer concentration (Fig. 3b–e). The formation of a thin neck in the course of the hopping was also observed in another experiment [18]. Although only macroscopic images were given without any molecular evidence, these works suggested a possible role of the elongation force of polymer not only during retraction, but also during the hopping stage after retraction.

1.3 Friction on Three Phase Contact Line

Most recently, the focus moved to more local effects of polymer additives, especially to their effect on the three-phase contact line (TPL). A study done by Bartolo et al. [2] showed an experiment of a polyacrylamid-solution droplet impacting on a hydrophobic parafilm surface. They stated that the additional energy dissipation by the normal stress at the TPL under the applied shear, which is known to increase quadratically with increasing shear rate, reduces the retraction velocity of the droplet. They also ruled out the possible roles of liquid-surface interaction and the polymer adsorption on the surface leading to the energy dissipation at the TPL. The established lubricant equation for thin films states that, for large dynamic contact angles, the retraction velocity is inversely proportional to the square root of the normal stress at the TPL. When the surface-adsorption effect is ignored as the authors intended, this statement is, however, contrary to the elastic effect of the elongation force from a molecular point of view. The net force due to the normal stress by elongation pulls the TPL in the same direction as the capillary force, which would have increased the retraction velocity. Furthermore, the typical shear rate of droplets of dilute polymer solution during retraction, calculated as the retraction speed divided by the height of the droplet, is of the order of \(10^2\)s\(^{-1}\). At this shear rate, the first normal stress difference of a bulk dilute polymer solution is negligible, as given by their experimental data. The polymer concentration in their experiments is above the overlap concentration. Therefore, influences other than the first normal stress, such as the shear viscosity and the surface tension cannot be simply ruled out as main contributors to the rebound suppression.

The most widely accepted explanation for the polymer-induced rebound suppression in recent years is the additional friction on the moving TPL. Using particle image velocimetry, Bertola et al. showed that the average velocities of all molecules inside droplets of rebounding water and non-rebounding polymer solution are quantitatively similar to each other even during retraction [42,43,44]. The main velocity difference is found locally at the TPL. The energy dissipation by the additional friction, which is quantified by the slip distance during the first contact angle oscillation, increases with polymer concentration. They also visualised stained \(\gamma \)-DNA added to a droplet which deposits behind the receding contact line (Fig. 4a). This finding directly indicates the change of surface properties by the polymer.

Their statement was also supported by the observation of dynamic contact angles [5,6,7, 45]. The apparent contact angle of the polymer solution droplet at the beginning of the retraction is much smaller than that of the water droplet, even though their behaviour during spreading is identical (Fig. 4b) [7]. The dynamic contact angle varying with the contact line velocity is interpreted either by viscous bending of the liquid-vapor interface in a mesoscopic region or by the kinetics of molecular adsorption/desorption to the surface [11]. Especially, the latter, often called Molecular Kinetic Theory (MKT) of dynamic wetting, explains contact angle dependence on the velocity of the TPL in terms of the surface wettability (an equilibrium contact angle). Therefore, the reduced contact angle during the retraction together with the decreasing retraction velocity can be interpreted by the additional friction by polymer on the TPL. It was also found that the concentration of polymer and the impact velocity affect the retraction as shown in Fig. 4c. The increasing polymer concentration leads to a decrease of the contact angle and in the TPL velocity, which is indicative of the increased friction on the TPL.

It is worth noting that the increasing impact velocity (We) also decreases the contact angle and the TPL velocity, implying a large effective friction against the TPL movement. This result is consistent with the experiment by Dhar et al. [18] who interpreted the behaviour in a different way using the polymer relaxation time with respect to the shear rate. The same tendency was observed in another experiment for an impacting water droplet with PEO and nanoparticle additives [59]. This work argued that the impact velocity mainly affects the amount of polymer adsorption on the surface during spreading. For a high enough impact velocity, the droplet is highly deformed and then polymer accumulates on the substrate, which in turn, generates a strong friction at the liquid-solid interface. They showed, as an analogy to the decreasing contact angle during retraction, an increasing advancing contact angle upon impact on a tiled surface with the increasing impact velocity. However, again, no molecular evidence was provided in these works, which makes it difficult to find a concrete mechanism covering the impact dynamics of various types of material.

Fig. 4
figure 4

a Fluorescence microscope image of \(\gamma \)-DNA left behind on the surface after the droplet has retracted. Reprinted figure with permission from [43]. Copyright (2010) @ American Physical Society. b Apparent contact angle and the spreading factor of 50ppm aqueous PEO solution impacting on the hydrophobic surface. Inset shows the definition of the apparent contact angle. c The minimum dynamic apparent contact angle for different polymer concentration and the different impact velocity. Reprinted figures from [7]. Copyright (2015) with permission from Elsevier. d Syringe-driven flow (square) water and (triangle) PEO solution droplets at flow rate 485 µL/s\(^{-1}\). Reprinted with permission from [45]. Copyright (2014) @ American Chemical Society

Full size image

Another experiment obtained the dependency of the contact line velocity on the dynamic contact angle from a different experimental setup, so called forced dewetting [45]. This work measured the dynamic contact angle of a polymer solution droplet under the syringe-driven flow where the retraction velocity can be imposed by the rate of liquid suction (Fig. 4d). They found that the contact angle of the polymer solution droplet during the retraction is substantially smaller than that of a water droplet at the same retraction velocity. Furthermore, it continuously decreases as the TPL recedes with a constant velocity, which indicates an increasing frictional force in the course of retraction.

To establish the relation between the polymer concentration and the rebound tendency with the concept of the additional friction, a semimperical energy balance equation was derived [27]. The equation shows the excess rebound energy in terms of the spreading factor, the equilibrium contact angle, and the capillary number. However, the capillary number used is written in terms of the shear viscosity of the polymer solution which, in the authors’ intention, directly contributes to the additional energy dissipation at the TPL. Therefore, the behaviour of a dilute polymer solution, specifically the experimental observation of the polymeric effect only acting on the retraction not on the spreading, can not be explained by this model.

1.4 A Summary of the State of the Art

To sum up, the rebound suppression by a small amount of polymer additive has been explained broadly by different physical concepts: the dynamic surface tension depending on the adsorption kinetics, the elongation effect of the stretched polymer, and the additional friction on the three-phase contact line by polymer adsorption. The dynamic surface tension turned out to be inappropriate for the dilute polymer solution since it leads to a significantly reduced equilibrium surface tension, which is not found for dilute polymer solutions. The elongational viscosity was also debated, since the experiments with negligible surface-liquid interactions showed almost the same retraction behaviour irrespective of the presence of polymer in the droplet. However, a few works have focused on the different role of the elongation force as an elastic response, in which the liquid filament of the polymer solution actually pulls the droplet back when it tries to jump from the substrate. The concept most widely accepted in recent years is the additional friction on the TPL induced by polymer adsorbed on a surface. This idea was supported by the visible presence of a polymer deposit behind the receding contact line, and the substantial reduction of the receding contact angle for a polymer solution. Although the experimental findings clearly point out the increased friction on the TPL as the polymer contribution to the rebound suppression, a comprehensive understanding with a clear molecular picture is still incomplete, which raises the need of molecular simulation studies.

2 Elongation Force of Stretched Polymer during Hopping

Recently, we examined how the elastic force of elongated polymer reduces the rebound tendency using particle-based multi-body dissipative particle dynamics (MDPD) simulations [32]. This method allows mesoscale simulations with correct hydrodynamics using a soft-core interaction potential [21, 22, 25]. In particular, the density-dependent attractive force in MDPD makes it possible to sample phase coexistence for one-component systems, which is necessary for the droplet impact simulation [52]. Different adsorptivity of solvent and polymer beads to surface beads were suspected as a physical origin of the polymer effect as many experimental observations imply. The strength of the pairwise attractive force in MDPD is given by the amplitude of a function which decays linearly with the distance between two beads, i.e. \(F=A(1-r/r_\text {c})\), where A, r, and \(r_\text {c}\) refer to the amplitude, the distance between two beads, and the cutoff distance beyond which the force is zero, respectively. A similar but shorter-ranged term accounts for pairwise repulsion. The repulsive potential parameters for all pairs are identical. We varied A between different bead types to model the different adsorptivity. Our choice of A for different pairs mimics a good solvent condition of the polymer solution, a solvophobic and polymerphilic surface with equilibrium contact angles of 155°  for a pure solvent droplet, and of 83 ° for a pure polymer droplet. We investigated polymer-solution droplets for different polymer molecular weights and concentrations, where the concentration is always far below the overlap concentration. The zero-shear viscosity and the equilibrium liquid-vapor surface tension of the fluids were calculated separately. They turned out to be almost identical irrespective of the polymer content in this regime, where the Reynolds and the Weber numbers are Re = 35–42 and We = 78–81.

Fig. 5
figure 5

a The most probable outcomes are shown for different polymer molecular weight (\(N_\textrm{p}\)) and concentration (\(x_\textrm{p}\)). Two outcomes for a given \(N_\textrm{p}\) and \(x_\textrm{p}\) (for example, deposition and partial rebound for \(N_\textrm{p}\) = 20, \(x_\textrm{p}\) = 0.015) indicate that two outcomes are equally probable out of five independent trajectories. The black dashed line on the graph is a rough boundary between rebound and deposition. b Simulation snapshots of the outcome of deposition by polymer necking from side view. Solvent and substrate particles are coloured in cyan and yellow, respectively. Each polymer strand is depicted in different colour. Reprinted with permission from [32]. Copyright (2021) @ American Chemical Society

Full size image

The droplets (total number of particles = \(4\times 10^4\)) were shot towards the surface with a velocity \(v_\text {imp}\) = 2 (in DPD reduced unit). We observed four characteristic outcomes of rebound, complete rebound (R), partial rebound (P), deposition (D) and deposition by necking (N), at different polymer composition (Fig. 5a). A higher polymer concentration and a larger molecular weight tend to suppress the rebound. Especially close to the boundary between rebound and deposition, a thin liquid filament, mainly composed of polymer chains, is observed which is in agreement with experimental images by high speed cameras [15, 18, 27]. On the molecular level, as the polymer preferably adsorbs on the surface, one of its ends is pinned on the surface and the other end is immersed in the droplet jumping from the surface. Owing to the elastic elongation force of the stretched polymer originating from the tendency to recover its coiled structure, the polymer pulls the droplet back to the surface, leading to droplet deposition. A similar morphology of the liquid filament for viscoelastic polymer solutions has been observed not only in droplet impact experiments [15, 18, 27] but also in different experimental systems [19, 41, 46, 51] such as a droplet pinch-off in a T-shaped microfluidic junction [41]. In particular, the highly stretched polymer conformation within the “neck” is confirmed by a fluorescence image, which is a clear indication of the polymer contribution to the elasticity of the fluid.

Fig. 6
figure 6

a Spreading factor as a function of time for droplets of different outcomes: complete rebound (R), partial rebound (P), deposition (D) and deposition by necking (N). The vertical dashed line indicates the beginning of a hopping stage. b Hopping velocity versus the maximum value of the number of adsorbed polymer beads for different \(N_\textrm{p}\) and \(x_\textrm{p}\). Each \(v_\textrm{hop}\) is obtained from each trajectory in which the droplet rebounds. Fitted linear functions for each \(N_\textrm{p}\) (\(v_\textrm{hop}=-sn_\textrm{ads,max}+c\)) are represented by dashed lines, where the fitted s are given in the legend. Reprinted with permission from [32]. Copyright (2021) @ American Chemical Society

Full size image

The time evolution of the spreading factor in Fig. 6a shows that the maximum spreading factor does not depend on droplet properties as expected from similar Re and We numbers. Interestingly, all simulated droplets show almost identical retraction velocities, calculated by the slope of the spreading factor versus time during the retraction. This is contrary to many experimental observations in which the rebound suppression is attributed to a reduced retraction velocity. Our simulation rather showed that the polymer adsorption is more relevant for rebound suppression. The maximum number of adsorbed polymer beads during the whole impact, \(n_\text {ads,max}\), is strongly (almost linearly) correlated with the hopping (rebound) velocity (Fig. 6b). A droplet of higher polymer concentration and larger molecular weight shows more polymer adsorption, which eventually leads to rebound suppression. The concentration effect on the polymer adsorption is obvious as more chains in the filament apply a stronger elastic force to the droplet. The observation that longer polymers suppress the rebound more effectively for droplets at the same \(n_\text {ads,max}\) can be understood by the fact that a longer polymer can exert the restoring force for longer time as the filament can be stretched longer [19].

This simulation work provided a clear picture of the so-called, slow hopping mechanism, induced by the elastic effect of the elongated polymer whose one end is pinned on the surface. However, the identical retraction velocity for different droplets observed in this work does not mean that slow hopping is the only mechanism responsible for the rebound suppression. Other scenarios like the slow retraction may prevail under different choice of simulation parameters (see the next section). This work rather states that the elongation force of polymer and the polymer-containing thin filament can be one reason of the rebound suppression by polymer additives.

3 Increasing the Contact Line Friction by Adsorbed Polymer

3.1 Slow Retraction and Adsorbed Polymer

Our recent study using MDPD simulations of impacting droplet reproduced a second mechanism coexisting with the slow hopping, the so-called slow retraction mechanism [33]. It is a function of the polymer-solvent attraction strength, \(|A_\mathrm {P/W}|\) (Fig. 7). In Fig. 7a, the retraction velocity initially decreases substantially (\(|A_\mathrm {P/W}|<90\)), leading to rebound suppression (blue squares) as \(|A_\mathrm {P/W}|\) increases. However, if \(|A_\mathrm {P/W}|\) increases further beyond 90, the retraction velocity again increases due to complete deposition of the polymer behind the receding contact line. Moreover, the slow retraction velocity of \(|A_\mathrm {P/W}|\) >150 is similar to that at \(|A_\mathrm {P/W}|=50\). Thus, on its own, it can not suppress the droplet rebound without elongation force during the hopping stage. This indicates the coexistence of two mechanisms, the slow-hopping and the slow-retraction mechanisms.

Fig. 7
figure 7

a The average retraction velocity of impacting droplets at different polymer-surface attraction strength, \(|A_\mathrm {P/W}|\). Black and blue points indicate rebounding and depositing droplets, respectively. b Retraction velocity of individual trajectory as a function of the number of adsorbed polymer beads at the beginning of the hopping stage. Dashed lines indicate the linear fitting of \(v_\text {ret}\) with \(n_\text {ads,hop}\). Difference symbols represent different molecular weight. c Height and d the number of adsorbed polymer beads as a function of time for different impact velocities. Simulations snapshot of droplets at maximum spreading for \(v_\text {imp}=0.6\) is given in the inset of (c)

Full size image

We found that the retraction velocity is correlated, again, with the number of adsorbed polymer beads on the surface. As more polymer beads adsorb, the retraction is slowed down (Fig. 7b). The influence of the molecular weight on the retraction velocity is not as strong as on the hopping resistance (Fig. 6b). A noticeable difference in this work, which uses larger droplets (total number of particles = \(10^5\)) than the former study [32], is that the retraction velocity at \(|A_\mathrm {P/W}|=30\) is also reduced despite the same simulation parameters except for the droplet size. This is attributed to the small surface-to-volume ratio of the large droplet in which the larger fraction of the solid-liquid interface is covered by polymer at the same bulk concentration.

The contribution of the adsorbed polymer to the slow retraction velocity is also confirmed by droplet impact simulations at different impact velocities. We found that the critical polymer concentration necessary to suppress the rebound decreases with increasing impact velocity, which is in agreement with experiments [18, 59]. The authors of the experiments stated that the shear rate being faster than the polymer relaxation is a key factor of the rebound suppression. However, our simulation provided a molecular picture completely different from this interpretation: the amount of adsorbed polymer determined by the impact velocity is a key of the slow retraction (inset of Fig. 7c). We found that a smaller height of the laterally expanded droplet enables more polymer adsorption since the diffusion path from solution to surface is shorter (Fig. 7c and d). Such impact velocity-dependent rebound suppression was also shown in recent molecular dynamics simulation study [55]. Therefore, a droplet of low polymer concentration needs high impact velocity and strong droplet deformation into the thin pancake-like morphology in order to transfer a large amount of polymer to the surface.

Fig. 8
figure 8

A scatter plot of the \(-\cos \theta _d\) as a function of \(v_\textrm{ret}\) for a pure solvent droplet, a polymer solution droplet with \(A_\mathrm {P/W}=-30\), and a polymer solution droplet with \(A_\mathrm {P/W}=-90\). Dashed lines represent fitted functions with line. Inset shows a simulation snapshot of the liquid particles on the first layer from the surface for 2500 ppm polymer solutions in the middle of the retraction stage

Full size image

3.2 Dynamic Contact Angle during Retraction

According to the Molecular Kinetic Theory (MKT) of dynamic wetting, the friction on the moving contact line determines the relation between its velocity and the dynamic contact angle [8, 10]. In this theory, the velocity of the moving contact line, \(v_\text {cl}\), is calculated from the frequency of a random molecular displacement to the next nearest adsorption site, \(\kappa _0\), thus it is given by

$$\begin{aligned} v_\text {cl}=2\kappa _0\lambda \sinh \Big (\frac{\gamma (\cos \theta _0 -\cos \theta _\text {d})}{2nkT}\Big )\text{, } \end{aligned}$$
(1)

where \(\gamma \), \(\lambda \), \(\theta _0\), \(\theta _\text {d}\), and n refer to the liquid-vapor surface tension, the distance between the adsorption sites, the equilibrium contact angle, the dynamic contact angle and the number of adsorption sites per unit area, respectively. k is the Boltzmann constant and T is the temperature. When the system is close to equilibrium or to the steady state, so as \(v_\text {cl}\) is close to zero, Eq. (1) reduces to

$$\begin{aligned} v_\text {cl}=\frac{\kappa _0\lambda }{nkT}\gamma (\cos \theta _0 -\cos \theta _\text {d})\text{. } \end{aligned}$$
(2)

On the right hand side of Eq. (2), \(\Big ( \frac{\kappa _0 \lambda }{nkT} \Big ) ^{-1}\) is often defined as \(\zeta _\text {cl}\), the coefficient of effective friction on the contact line. When the friction is strong (large \(\zeta _\text {cl}\)), \(\cos \theta _\text {d}\) depends strongly on \(v_\text {cl}\).

The additional friction by adsorbed polymer during retraction is, therefore, quantified by the relation between the dynamic contact angle (\(\theta _\textrm{d}\)) and the retraction velocity (\(v_\textrm{ret}=v_\textrm{cl}\)). Figure 8 shows a scatter plot of \(-\cos \theta _d\) as a function of \(v_\textrm{ret}\) for a pure solvent droplet (black squares), a polymer solution droplet with moderate polymer-surface attraction strength (\(A_\mathrm {P/W}=-30\), red circles), and a polymer solution droplet with strong polymer-surface attraction strength (\(A_\mathrm {P/W}=-90\), blue triangles). If we fit the data approximately with a line, the slope of the line increases as \(|A_\mathrm {P/W}|\) increases. For the pure solvent droplet, the slope is small which means that \(\kappa _0\) is large and the friction, \(\zeta _\text {cl}\), is small. Larger slopes are found for stronger polymer-surface attractions, which implies a larger effective friction on the contact line. A simulation snapshot in the inset of Fig. 8 shows that the adsorbed polymer becomes more concentrated near the contact line as the contact line recedes during retraction. This is attributed to the slower surface diffusivity of polymers compared to solvent molecules. Therefore, even a tiny amount of polymer accumulates near the contact line during retraction, which leads to the substantial reduction of the retraction velocity.

4 Conclusions

We reviewed the state-of-the-art of the possible physical origins of the rebound suppression of an impacting droplet from a solvophobic surface by a small amount of polymer additive. We discussed several physical concepts, such as the dynamic surface tension, the additional energy dissipation by non-Newtonian elongational viscosity, the elastic force of the stretched polymer and the additional friction on the receding contact line. The explanation based on the dynamic surface tension and the elongational energy dissipation have become less persuasive, since contradictory evidence was reported. The additional friction on the contact line during retraction became more popular, but still lacked a comprehensive understanding. Our MDPD simulations traced the rebound suppression to both the slowing of droplet hopping by the restoring force of stretched polymer, and to the slowing of the droplet retraction by an additional friction on the contact line provided by the polymer adsorbed on the surface. Both mechanisms coexist over a wide range of simulation parameters, but the slow-retraction mechanism is prevailing for large droplets and for strong attraction between polymer and surface. Increasing the polymer adsorption by changing its polymer concentration, its molecular weight, or its interactions with the surface, stimulates both mechanisms; thus, the rebound is suppressed. Evidence of the additional friction on the receding contact line is inferred from the relation between the dynamic contact angle and the contact line velocity, as the slope of the fitted line is proportional to the friction.

The molecular mechanism can be roughly summarised: After impact, the droplet expands sideways. During this spreading phase, the flow is unhindered by the polymer, since its concentration is low enough to leave both the fluid viscosity and its surface tension unchanged. At the same time, however, polymer equilibrates between solvation and surface adsorption. This equilibration is aided by a shorter diffusion path, i.e. a flatter, more spread-out droplet, which in turn is brought about by a higher impact velocity. The adsorbed polymer, however, strongly influences the second phase, retraction. When the fluid is driven by its surface tension to retract, the polymer is unable to follow quickly enough due to its slow mobility on the surface. It remains partially attracted to the surface. Its other parts are dissolved in the solvent, which is as we recall, a good solvent. In its effort to stay solvated, it exerts a thermodynamic force, akin to an osmotic pressure, on the solvent molecules. Since, due to its slowness, the polymer is enriched near the contact line, the force counteracts the retraction of the contact line. This contact-line friction makes some of the kinetic energy of the droplet dissipate. In phase three, hopping, the remaining kinetic energy is converted. Hopping is opposed by polymer chains that are attached to the surface with one end and dissolved in the solvent with the other. The chains stretch, as the droplet is trying to detach, and at a large enough concentration, they prevent hopping.

Our simulation studies clearly confirmed the qualitative origin of the polymer-induced anti-rebound on the molecular level. A quantitative understanding of the rebound tendency as a function of polymer composition is still poor since droplet impact is an extremely non-equilibrium process and not even close to the steady state. We expect that the physics of the moving contact line upon droplet impact can be quantitatively analysed by simulations of a capillary bridge under steady shear [12, 39] which give the velocity-angle relation of the contact line with better statistics. The effect of elastic elongation force of stretched polymer can also be studied by dynamics of polymer solution droplets, e.g., the droplet impact on wired surface [46], and a droplet detachment simulation from polymer-tethered surfaces.