1 Introduction

The transmission and distribution of electric power relies on its components, which are specifically designed to withstand various different environmental stresses like rain, snow, UV-light and extreme temperatures for many years [13, 15]. The efficiency and reliability of the system mainly depends on the performance of the individual components within the system. High-voltage insulators are used to insulate the high-voltage potential present on the line conductor from the ground potential of the pylons. Nowadays, more and more composite insulators are used due to their advantages compared to glass or ceramic insulators [39]. Composite insulators are typically made out of a fibre-glass rod covered by weather sheds consisting of silicone rubber. The most important advantages are the high robustness, the lowered weight and the hydrophobic surface properties, which prevents the formation of a liquid layer on the surface [39]. Any contamination of the insulators surface might increase the surface conductivity and, thus, lead to undesired creeping currents on the surface, which significantly affect the efficiency of the system. The hydrophobic surface properties of composite insulators prevent the formation of conductive liquid layers on the surface and cause the formation of single sessile droplets instead. Even though the hydrophobicity of the silicone rubber is an advantage with respect to creeping currents, the formation of sessile droplets causes electrically critical points directly at the three-phase contact line. Due to the different electric and dielectric properties of the involved materials, namely air, water and silicone rubber, the electric field is suppressed or completely vanishes inside the water droplet. Furthermore, the electric field strength in the material with the lowest relative permittivity (air) is significantly enhanced. Hence, the breakdown strength of air might be locally exceeded resulting in the formation of partial discharges [51]. The presence of partial discharges is associated with locally increased temperatures and the generation of UV-light, which contribute to an accelerated aging of the silicone rubber [2, 12]. To ensure a reliable and efficient power transmission and distribution the aging behavior of composite insulators caused by sessile droplets has to be investigated in detail. This behavior comprising the general behavior of water droplets under the impact of an electric field and various conditions as well as the corresponding partial discharge inception is experimentally investigated in this work. During the last twelve years various different influencing factors such as surface properties, droplet volume, droplet-droplet interaction, electric field strength, type of electric field, frequency of electric field, electric charge and orientation of the substrate were investigated. In collaboration with the Institute for Accelerator Science and Electromagnetic Fields (TEMF) of the Technical University of Darmstadt the experimental results are extended by numerical simulations.

Based on the knowledge of the general behavior of water droplets under the impact of electric fields, which highly affects the shape and motion of the droplets, the impact of high electric fields on ice nucleation is investigated. High-voltage insulators operated in cold regions might be affected by accreted ice [9]. The ice accretion causes an altered shape of the insulators and might also lead to a conductive impurity layer on the surface [10]. In addition, a large amount of ice can lead to bridging of the weather sheds causing a decreased insulation distance eventually resulting in flashovers [11]. Besides the impact on the electrical properties the ice accretion leads to additional static and dynamic loads on the pylons, which might cause a collapse of the pylons in the worst case [9]. While the general behavior of water droplets under cold conditions or under the influence of electric fields was already intensively investigated [1, 3, 7, 14, 36, 43, 49, 50, 55, 57], the impact of electric fields on ice nucleation is controversially discussed in literature [5, 6, 8, 16, 29,30,31, 37, 40, 41, 44, 47, 48, 52,53,54, 56]. However, the strong interaction of the droplets and the electric fields under ambient conditions leads to the suggestion that also ice nucleation is significantly affected by strong electric fields. To determine the impact of electric fields on ice nucleation an experimental setup has been developed, and several experiments under different conditions with respect to the type, strength and frequency of the electric field are performed.

The aim of this work is to enhance the knowledge about droplets under the impact of strong electric fields under well-defined conditions. The main focus is to determine the underlying physical mechanisms to be able to predict and control the behavior of the droplets. Hence, the presented work aids the development of theoretical models for the forecast of the aging of high-voltage insulators or the prediction of ice nucleation of water droplets under the impact of electric fields.

The following sections briefly summarize the results of the progress of the project but mainly focus on the most recent results. The chapter is divided into two main sections, which present the results of the experiments of droplets at ambient temperature and the nucleation behavior of droplets under low temperature conditions affected by different types of electric fields.

2 Sessile Droplets in Electric Fields Under Normal Ambient Conditions

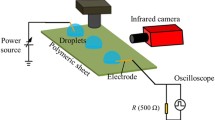
The general behavior of sessile droplets under the impact of strong electric fields is investigated using a generic insulator model. The specimen is made out of a typical high-voltage insulation material, such as silicone rubber or epoxy, containing two embedded brass electrodes. The electric field strength is evaluated at the droplets position in absence of the droplet. In case of alternating or transient electric fields the amplitude or the maximum field strength is used to characterize the electric field strength. The generated electric field is tangentially aligned to the substrate surface because tangentially aligned electric fields are known to have the largest impact on the droplet [45]. In addition, tangentially aligned electric fields reproduce the electrical situation at the surface of a high-voltage insulator very accurately. Different types of electric fields, namely constant, alternating and transient electric fields are generated by different high-voltage sources connected to one of the electrodes, while the other electrode is grounded. The general behavior of the droplets is investigated using shadowgraphy and a high-speed camera. Prior to each experiment the substrate surface is cleaned using anti-static wipes soaked with isopropanol to remove surface contamination such as dust and to minimize surface charges [28]. The droplets are generated either with a conventional pipette or using an automated high precision syringe to ensure a well-defined droplet volume. The electric charge of the droplets can be actively controlled by using a grounded needle to produce uncharged droplets or a droplet charger, similar to [4], to generate charged droplets. A single droplet is placed on the center of the specimen without touching the surface to prevent the generation of surface charges.

2.1 General Droplet Behavior

The behavior of sessile droplets mainly depends on the type of the applied electric field. To determine the influence of each type of electric field, three-different types are used, namely constant, alternating and transient electric fields. For each type different influencing factors such as strength and frequency of the electric field are investigated. The following sections shortly summarize the outcome of the different experiments. A more detailed description of the experiments and the results can be found in the corresponding publications.

2.1.1 Constant (Time-Invariant) Electric Fields

Constant (time-invariant) electric fields are identified to affect the behavior of a sessile droplet [32]. The forces generated by the electric field causes an elongation of the droplet. The droplet always moves towards the negative electrode. The contact line facing the positive electrode is pinned during this motion. However, after reaching a certain deformation a jumping motion towards the positive electrode is observed. The position of the droplet on the insulator is changed, and the droplet adapts to a new equilibrium shape. The principal behavior of a droplet under the influence of a constant electric field is shown in Fig. 1. The volume of the droplets is identified to influence the motion of the droplets. The smaller the volume of the droplets, the shorter is the elongation process compared to larger droplets.

Fig. 1
figure 1

Principal motion of a sessile droplet under the impact of a constant electric field. Reprinted (adapted) figure with permission from [32] under the Creative Common License (CC-BY-NC-ND 3.0 International)

Full size image

2.1.2 Alternating Electric Fields

While constant electric fields lead to deformations of the droplets, alternating electric fields cause an oscillation of the droplets. The behavior of the droplets mainly depends on the electric field strength but is also influenced by the e.g. the droplet volume, electric charge or wetting properties of the substrate. For low electric field strengths the droplet only oscillates, and the three-phase contact line is static and does not move. Increasing the electric field strength leads to larger oscillation amplitudes finally resulting in a movement of the three-phase contact line if the contact angles exceed the advancing contact angle. In the following the main focus lies on the droplet oscillation, which depends on the droplet volume, strength of the electric field as well as the frequency of the electric field. The principal motion of a droplet under the impact of an alternating electric field oscillating in the first three resonance modes is shown in Fig. 2. The motion of the droplets is affected by the frequency of the electric field and is different for each resonance mode. While droplets in first resonance mode are periodically leaning sideways, which results in a principal motion tangentially aligned to the substrate, higher resonance modes cause a stretching and compression cycle of the droplet perpendicular to the substrate. For hydrophobic substrates the resonance frequency of the droplet is well described by the resonance frequencies of a free droplet [46]. The characteristic frequencies of the droplet depend on the droplet volume. The larger the droplet volume, the lower is the frequency of the corresponding resonance mode.

Fig. 2
figure 2

One cycle of the first three modes for \(n=2,3,4\) of uncharged drops. a Example of Mode 1 (\(n=2\)) of a 20 \(\upmu \)l droplet at 27 Hz and \(\hat{E}=3.81~\)kV/cm, b example of Mode 2 (\(n=3\)) of a 30 \(\upmu \)l droplet at 23 Hz and \(\hat{E}=4.67~\)kV/cm and c example of Mode 3 (\(n=4\)) of a 60 \(\upmu \)l droplet at 48 Hz and \(\hat{E}=7.37~\)kV/cm. Reprinted (adapted) figure with permission from [20], Copyright 2020 by the American Physical Society

Full size image

Besides the frequency of the electric field and the droplet volume, the electric charge of the droplet is identified to have a significant influence on the droplet motion [19, 20]. Generally, uncharged droplets are assumed to oscillate with twice the frequency of the applied voltage because the electric field causes a force proportional to the square of the electric field. Thus, a sinusoidal voltage leads to \(f_\textrm{d}\propto \hat{E}^2\propto 1-\cos {(2\omega t)}\), where \(f_\textrm{d}\) is the oscillation frequency of the droplet, \(\hat{E}\) the amplitude of the electric field strength, t the time and \(\omega \) the pulsatance of the applied voltage. In contrast, a charged droplet should oscillate with the same frequency as that of the applied voltage because of the Coulomb force (\(f_\textrm{d}\propto \hat{E}\propto \sin {(\omega t)}\)) acting on the droplet. Whether the droplet oscillates with the same or twice the frequency of the applied voltage depends on the droplet volume, the amount of charge present on the droplet and the applied electric field strength, which define the predominant force. The droplet oscillates with the same frequency if the amount of charge present on the droplet is high enough to cause a sufficiently large Coulomb force. However, the charge on a droplet is limited by the Rayleigh charge [42], so that sufficiently high electric field strengths will always force the droplet to oscillate with twice the frequency of the electric field. Note that the transition between the different oscillation frequencies is continuous, because of the different forces simultaneously act on the droplet. The performed experiments revealed the amount of charge necessary to cause a change of the behavior depending on the droplet volume, electric charge, electric field strength and resonance mode. While this behavior is observed for droplets oscillating in resonance mode two or higher, a different behavior is observed for droplets oscillating in first resonance mode. Independently of the amount of charge present on the droplet, the droplet always behaves like a charged droplet and oscillates with the same frequency of the applied voltage. Hence, the behavior of a droplet oscillating in first resonance mode is not changed by the presence of charges. In contrast, the oscillation behavior in higher resonance modes can be actively controlled by the electric field strength, the droplet volume, the frequency of the electric field and the electric charge on the droplet. Especially, small droplets are highly affected by the presence of electric charges. Consequently, the electric charge has a significant impact on the motion of the droplets and has to be taken into account whenever an electric field is present. Corresponding numerical simulations of the droplet motion for specific conditions can be found in [38].

2.2 Transient Electric Fields

Fig. 3
figure 3

Side view time series of a sessile water droplet (\(V=50\,\upmu \)l) surrounded by air and exposed to a switching impulse voltage (\(\hat{E}=18.43\,\)kV/cm) under ambient conditions [23] (Creative Common License (CC-BY-NC-ND 4.0 International)

Full size image

In addition to constant and alternating electric fields, the behavior of single and multiple droplets under the impact of transient electric fields are investigated [25]. Standard lightning and switching impulse voltages (\(1.2/50\,\upmu \)s and \(250/2500\,\upmu \)s) as defined by IEC 60060 are used to generate well-defined transient electric fields. The general behavior of a droplet under the impact of a standard switching impulse voltage is shown in Fig. 3. The force generated by the electric field is mainly concentrated at the three-phase contact line, and causes an outward motion of the contact line. The footprint of the droplet is increased and small disturbances are initiated, which propagate as surface waves on the droplet. The disturbances generated at both sides of the droplet interact as soon as they reach the top of the droplet and result in large droplet oscillations. In case of standard lightning impulse the general behavior is similar, but the impact of the electric field is much smaller. The movement of the contact line and the amplitude of the oscillations are barely visible on the high-speed videos. Hence, the standard switching impulse voltages have a larger impact on droplets compared to standard lightning impulse voltages. While the initial impact of the electric field, namely the increase of the footprint, usually does not lead to coalescence of neighbouring droplets, the droplet oscillation might cause droplet coalescence depending on droplet volume and droplet-droplet distance. However, for small droplet-droplet distances (\(h_\mathrm {d-d}<1\,\)mm) the initial increase of the footprint can lead to coalescence of the neighboring droplets. The interaction of nearby droplets is investigated in more detail, and a region map is generated to determine the behavior of the droplets depending on the droplet-droplet distance, the droplet volume, electric field strength and impulse type [25]. While sufficiently high electric field strengths and small droplet-droplet distances always lead to droplet coalescence in case of standard switching impulse voltages, droplet coalescence under the impact of standard lightning impulse voltage also depends on the droplet volume. Small droplets (droplet volume \(V_\textrm{d}<40\,\upmu \)l) do not interact even for small droplet-droplet distances of \(h_\mathrm {d-d}\approx 1\,\)mm. However, large droplets might coalesce depending on the electric field strength and the droplet-droplet distance.

Consequently, the behavior of the droplets clearly depends on the type and characteristic time constants of the electric field. The characteristic time scales of the standard switching impulse are much larger compared to those of standard lighting impulse voltages, as defined by IEC 60060. Thus, the electric field is present for a longer time, which leads to a larger macroscopic motion, potentially resulting in coalescence.

2.3 Partial Discharge Inception Field Strength

As already mentioned the electric field is significantly enhanced near the three-phase contact line. The local field enhancement can lead to a field strength locally exceeding the breakdown strength of air resulting in the generation of partial discharges. The associated generation of UV-light and locally high temperatures contribute to the accelerated aging of composite insulators [2, 17, 18]. To determine the various influencing factors and the impact of different boundary conditions, the partial discharge inception field strength is investigated under various different conditions. The partial discharge inception field strength is determined for different types of electric fields [32, 35], droplet volumes [32,33,34], surface orientations [32, 34] and wetting properties of the substrate [32, 34]. In addition, the impact of the conductivity of the droplet [34], the electric charges and the oscillation of the droplet are investigated [27].

Generally, partial discharges are identified to occur directly at the three-phase contact line as shown in Fig. 4. The UV-light generated by the partial discharges is used to visualize the location of the partial discharges with high resolution. The UV-light is colored in magenta and is superimposed to the daylight image of the droplet. Due to the forces generated by the electric field, the shape of the droplet is altered and takes a complex form. The occurrence of partial discharges mainly depends on the shape of the droplet, so that the partial discharges are only observed at specific locations at the contact line. The partial discharges are mainly located at conical tips of the droplet as shown in Fig. 4b. Especially, at this location the curvature of the interface is low and, thus these locations are more prone to generate partial discharges because of a significantly increased electric field strength. The partial discharge inception field strength depends on the type of electric field. For constant electric fields the critical partial discharge inception is determined for different droplet volumes [35]. Generally, the generation of partial discharges is observed to be independent of the polarity of the applied potential. The higher the electric field strength, the higher is the measured partial discharge impulse.

Fig. 4
figure 4

Exemplary images of a water droplets with superimposed image of UV-camera to visualize the partial discharges (colored in magenta). a Water droplet with \(V_\textrm{d}=20\,\upmu \)l in side view for \(\hat{E}=9.02\,\)kV/cm and b in top view for \(\hat{E}=9.63\,\)kV/cm. Reprinted (adapted) figure with permission from [21], Copyright 2021 by the American Physical Society

Full size image

In addition to constant electric fields, the inception field strength is investigated under the impact of alternating electric fields. The inception field strength is identified to depend on various influencing factors. An increasing droplet volume generally leads to a decreasing inception field strength for partial discharges [34]. Due to the fact that the water droplets used for the experiments can be assumed as perfect conductors for low frequencies (\(f<1000\,\)Hz for the given liquid), a change of the conductivity revealed a negligible effect on the inception field strength [32]. This assumption is valid as long as the charge relaxation time of the liquid \(\tau _\textrm{el}\) is much lower than the characteristic time of the electric field \(\tau _E\). In contrast, the frequency of the electric field and the wettability of the substrate have a significant influence on the inception of partial discharges. The lower the contact angle of the single sessile droplets (the better the wettability of the substrate), the lower is the inception field strength for partial discharges. Hence, the inception field strength of sessile water droplets on silicone rubber is higher compared to epoxy resin. The presence of electrical charges also influences the inception field strength [27]. The higher the amount of charges present on the droplet, the lower is the inception field strength of partial discharges. Besides the already mentioned influencing factors, the inception field strength is determined for the first three resonance modes [27]. The higher the frequency of the electric field i.e. the higher the resonance mode, the higher is the inception field strength of partial discharges. Additionally, the surface inclination and the presence of further droplets affect the generation of partial discharges. Especially, nearby droplets can significantly reduce the partial discharge inception field strength [27].

The combination of constant and alternating electric fields revealed that the inception field strength of partial discharges can be further lowered by the presence of a superimposed constant electric field compared to an alternating electric field [35].

Simulation results of the partial discharge inception field strength are performed by [38]. Based on the performed experiments the inception field strength is estimated and compared to measured values. The generation of partial discharges is affected by various influencing factors and very sensitive to changes of the boundary conditions.

3 Ice Nucleation Under the Impact of Electric Fields

The presence of an electric field impacts the behavior of a sessile water droplet under normal ambient conditions. Due to the fact that the electric field significantly affects the mechanical and electrical behavior of a droplet under ambient conditions, it is assumed that the electric field might also affect additional physical mechanisms like ice nucleation. There is an ongoing discussion in literature as shown in Sect. 1 whether ice nucleation can be affected by electric fields or not. In the scope of this work an experimental setup called SAPPHIRE is developed to investigate the impact of electric fields on ice nucleation in more detail [27]. The temperature as well as the electric field are precisely controlled to determine even small influences of the electric field on ice nucleation. Different types of electric fields, namely constant, alternating and transient electric fields, are used to determine the impact of various influencing factors such as the electric field strength, frequency of the electric field and type of the electric field. The electric field strength is evaluated at the droplets position in absence of the droplets. In case of alternating or transient electric fields, the amplitude of the electric field is used to characterize the electric field strength. Furthermore, the variety of experimental conditions is assumed to improve the understanding of the underlying physical mechanisms.

A droplet ensemble consisting of 40 droplets with well-controlled volumes are cooled with a constant cooling rate or hold at a constant temperature. Ice nucleation inside the individual droplets is observed with a video camera and identified by the vanishing glare point during the freezing of the droplets. To generate a sufficient number of nucleation events the same droplet ensemble is used several times to ensure well-defined boundary conditions and to rule out any influence of changed contamination inside the droplets. Hence, for the investigation of each parameter like the electric field strength a fixed droplet ensemble is used. The droplets are exposed to several freezing and thawing cycles resulting in a large number of nucleation events. The impact of the electric field is determined by a comparison of the different experiments with and without an electric field present. Subsequently, the results for the different types of electric fields are shortly summarized and exemplary results are shown.

Fig. 5
figure 5

Liquid fraction \(N_\textrm{l}/N_0\), where \(N_\textrm{l}\) is the number of liquid droplets at a certain temperature \(\vartheta \) and \(N_0\) is the number of initially liquid droplets, depending on the droplet temperature \(\vartheta \) for different electric field strengths |E|. Republished with permission of/from [26]; permission conveyed through Copyright Clearance Center, Inc

Full size image

3.1 Constant (Time-Invariant) Electric Fields

The impact of constant (time-invariant) electric fields on ice nucleation is extensively studied in [22, 26]. The same set of droplets is exposed to various freezing and thawing cycles while the electric field strength is continuously increased up to a value of \(E=9.76\,\)kV/cm. Using the same set of droplets ensures that the contamination and the position of the droplets do not affect ice nucleation because any influence present is constant for all cycles. The droplets are cooled at a constant rate of \(\dot{T}=5\,\)K/min. The nucleation events and the associated temperatures are used to analyze the impact of a constant electric field on ice nucleation. Based on the freezing events droplet survival curves are generated, which correlate the liquid fraction \(N_\textrm{l}/N_0\), where \(N_\textrm{l}\) is the number of liquid droplets at a certain temperature \(\vartheta \) and \(N_0\) is the number of initially liquid droplets, and the droplet temperature \(\vartheta \). The comparison of the survival curves generated under different conditions reveals the impact of the electric field on ice nucleation. Exemplary results are shown in Fig. 5. Survival curves depending on the electric field strength are presented. Low electric field strengths \(E<6.50\,\)kV/cm do not influence ice nucleation as shown by the almost perfect accordance of the different survival curves [26]. However, increasing the electric field strength (\(E\ge 9.76\,\)kV/cm) leads to a survival curve shifted to higher temperatures [26]. The individual droplets freeze at a higher temperature so that ice nucleation is promoted by the electric field. Nevertheless, the impact is rather small. To quantify the increase of the nucleation temperature, the mean nucleation temperature \(\vartheta _{0.5}\) can be used. The mean nucleation temperature is the temperature associated to \(N_\textrm{l}/N_0=0.5\) and, thus characterizes the temperature necessary to cause half of the ensemble to be frozen. The increase of the temperature is always correlated to the run without an electric field. In case of a constant electric field the largest increase of the nucleation temperature is observed at \(E=9.76\,\)kV/cm and yields approximately \(\Delta \vartheta \approx 1\,\)K [26]. Consequently, ice nucleation can be influenced by the constant electric fields, but the influence is rather small and might be masked by other influencing factors such as the measurement uncertainty of the temperature or the stochastic nature of ice nucleation.

Even though ice nucleation is a stochastic process, the performed experiments revealed a singular nucleation behavior of the droplets in absence of an electric field. Due to the fact that the same droplet ensemble is used for the different freezing and thawing cycles the nucleation temperature of each droplet can be compared to the previous and subsequent runs. In absence of an electric field, the nucleation temperature of the individual droplets is almost constant and suggests that ice nucleation is mainly influenced by the ice nucleation particles inside the droplets and their characteristic temperature [26]. Therefore, the experimental data is described very well by the singular nucleation model.

In summary, the experiments revealed a rather small influence of constant electric fields on nucleation. However, the used procedure is capable to reveal even small influences with good accuracy.

3.2 Alternating Electric Fields

In addition to constant electric fields, the impact of alternating electric fields is investigated with respect to the electric field strength and the frequency [24]. Similar to the investigation of the impact of constant electric fields, a fixed droplet ensemble is used to investigate the impact of each influencing parameter such as the electric field strength or frequency. The droplet ensemble containing up to 40 droplets is cooled at a constant cooling rate of \(\dot{T}=5\,\)K/min. To generate a large number of nucleation events the same ensemble is used to perform several freezing and thawing cycles. Overall a minimum of 55 droplets is used for analyzing the behavior of the droplets. The occurring nucleation events are correlated to the actual nucleation temperature and analyzed using droplet survival curves. Exemplary results are given by the droplet survival curves shown in Fig. 6. The liquid fraction \(N_\textrm{l}/N_0\) depending on the droplet temperature \(\vartheta \) for various electric field strengths \(\hat{E}\) is presented. While small electric field strengths (\(\hat{E}<3.34\,\)kV/cm) have an almost negligible influence on ice nucleation, larger electric field strengths (\(\hat{E}\ge 3.34\,\)kV/cm) significantly influence ice nucleation. The impact of the electric field on ice nucleation is twofold. First, the general shape of the droplet survival curves is altered from the typical ‘S’-like shape. Second, individual droplets are forced to freeze at higher temperatures, so that the temperature of the first freezing event is significantly increased. Hence, the temperature range of ice nucleation is increased. Generally, the impact of the electric field increases with increasing electric field strength. The impact of an alternating electric field can be quantified by the mean nucleation temperature \(\vartheta _{0.5}\). The maximum change of the mean nucleation temperature is observed for \(\hat{E}=7.16\,\)kV/cm and yields \(\Delta \vartheta _{0.5}\approx 10\,\)K. However, for \(N_\textrm{l}/N_0<0.5\) the change of the characteristic nucleation temperature is even higher. Even though the temperature of individual droplets is increased, the lowest freezing temperature is almost constant independent of the applied electric field. Hence, the electric field does not influence all droplets in the same manner. A more detailed analysis of the individual nucleation events revealed that not all droplets are affected by the electric field. Consequently, the impact of an alternating electric field is of singular rather than stochastic nature. Due to the fact that the number of droplets affected by the electric field increases with increasing electric field strength, it seems that each droplet is associated with a characteristic electric field strength necessary to influence ice nucleation. To reveal if additional influencing factors (besides the electric field strength) also have a singular impact on ice nucleation, the singular and stochastic behavior of the nucleation events is analyzed in more detail with respect to the temperature and time. The analysis revealed that the individual droplet can be characterized by a specific nucleation temperature according to the singular nucleation model. However, stochastic processes still play a role, which is shown by the scatter of the experimental data. Even though ice nucleation is a time dependent process, the electric history of the droplets does not influence the outcome of the experiments. Hence, a previously applied electric field does not influence the actual nucleation behavior at a different electric field strength. Ice nucleation is only affected on a small time scale and the boundary conditions present at the time instant of nucleation.

Fig. 6
figure 6

Liquid fraction \(N_\textrm{l}/N_0\), where \(N_\textrm{l}\) is the number of liquid droplets at a certain temperature \(\vartheta \) and \(N_0\) is the number of initially liquid droplets, depending on the droplet temperature \(\vartheta \) for different electric field strengths \(\hat{E}\) (\(f=50\,\)Hz). Reprinted (adapted) figure with permission from [24], Copyright 2021 by the American Physical Society

Full size image

Besides the magnitude of the electric field strength, its frequency has large influence on the nucleation behavior. Specific frequencies to promote ice nucleation are identified (\(f=100\,\)Hz or \(f=110\,\)Hz for the given setup). Thus, the macroscopic motion, namely the oscillation of the droplets seems to have a large impact on the nucleation behavior. However, the influence of the electric field on ice nucleation is not completely understood yet.

Compared to constant electric fields, the impact of alternating electric field is significantly increased. Individual droplets are highly affected by the electric field, so that ice nucleation is promoted by the presence of the electric field.

Fig. 7
figure 7

Frozen fraction \(N_\textrm{f}/N_0\) depending on the degree of supercooling \(\Delta T\) under the impact of standard lightning impulse voltages generating an electric field strength of E [23] (Creative Common License (CC-BY-NC-ND 4.0 International)

Full size image

3.3 Transient Electric Fields

In contrast to the investigation of constant and alternating electric fields, the impact of transient electric fields is determined at constant temperature. The droplet ensemble is cooled to a constant temperature. Afterwards the electric field is applied and the number of frozen droplets is analyzed. To determine the impact of different types of transient electric fields standard lightning and standard switching impulse voltages are used to investigate the nucleation behavior. A more detailed overview is given by [23]. Exemplary results for an ensemble exposed to standard lightning impulse voltage are shown in Fig. 7. The frozen fraction \(N_\textrm{f}/N_0\), where \(N_\textrm{f}\) is the number of frozen droplets at the temperature \(\vartheta \) and \(N_0\) is the number of initially liquid droplets, depending on the degree of supercooling \(\Delta T\) and the electric field strength \(\hat{E}\) is shown. The electric field strength corresponds to the highest electric field strength present while the electric field is applied. While low electric field strength (\(\hat{E}<9.78\,\)kV/cm) does not affect ice nucleation, i.e. does not cause any droplet to freeze, higher electric field strength have an impact on ice nucleation. The higher the electric field strengths, the higher is the frozen fraction depending on the degree of supercooling. Note that the frozen fraction is always analyzed at \(t=1.5\,\)s after the electric field is applied for comparison reasons and to ensure that the nucleation event is caused by the electric field rather than by the stochastic nature of ice nucleation. Electric field strengths higher than \(\hat{E}=19.56\,\)kV/cm lead to a completely frozen ensemble at least for a supercooling of \(\Delta T=20\,\)K. Comparing the impact of standard lightning and standard switching impulse voltage reveals that the impact of standard switching impulse voltage is higher, i.e. the number of frozen droplets is increased for the same degree of supercooling and applied electric field strength. However, the influence of an electric field strength of \(\hat{E}=6.52\,\)kV/cm is also almost negligible for standard switching impulse voltages. In contrast, the mean freezing temperature \(\vartheta _{0.5}\) can be significantly increased for both impulse types. The highest change of the mean freezing temperature can be observed at high electric field strength and yields \(\Delta \approx 6\,\)K.

Not only the impact of standard switching impulse voltage on ice nucleation is higher compared to standard lightning impulse voltage but also the macroscopic behavior of the droplets. While standard switching impulse voltages lead to significant droplet oscillations, the standard lightning impulse voltages have an almost negligible impact for the investigated electric field strength. As a conclusion the impact of the electric field might be associated with the motion of the droplets. Nevertheless, even in case of small droplet oscillations, the electric field does influence the nucleation behavior. However, the physical mechanism affecting ice nucleation is not completely understood yet, because no general model is available to describe the influence of electric field on ice nucleation.

The freezing of the individual droplets is not always observed during the highest electric field strength but also after the electric field has already completely decayed. The moment of nucleation of the individual droplets with respect to the application of the electric field covers several orders of magnitude (from milliseconds to seconds). Hence, ice nucleation is clearly a time dependent process. However, the stochastic nature of the process can only be observed on a small time scale. A larger time scale might mask the stochastic nature of ice nucleation and causes a singular behavior.

Generally, transient electric fields can be used to actively affect ice nucleation. The presence of sufficiently high electric fields significantly promotes ice nucleation and increases the nucleation temperature of the individual droplets.

4 Conclusions

The behavior of sessile droplets is highly affected by the presence of electric fields. The impact of the electric field mainly depends on the type of the electric field but is also influenced by other factors such as droplet volume or electric field strength. Generally, the electric field causes oscillations or deformations of the droplet and might even lead to an enhanced surface wetting. In addition to the mechanical phenomena, the interaction of a sessile water droplet and the electric field causes a field enhancement at the three-phase contact line of the droplet. The locally enhanced electric field causes the formation of partial discharges, which contribute to an accelerated aging of the insulators. In the scope of this work the main influencing factors of the electrical and mechanical phenomena are investigated in detail. Especially, the electric charge is identified to have a large impact on the mechanical and electrical behavior of the droplet and might have been underestimated in many other investigations performed in the past and reported in literature. In addition, droplet volume, strength, frequency and type of the electric field as well as the electrical and geometrical properties of the experimental setup clearly affect the motion of the droplets and the formation of partial discharges.

The electric field does not only impact the mechanical and electrical behavior of a droplet under normal ambient conditions but also additional physical mechanisms like ice nucleation. The developed experimental setup called SAPPHIRE allows the investigation of ice nucleation of sessile and emulsified droplets under well-defined conditions with respect to temperature and electric field strength. While constant electric fields are identified to have a rather small impact on ice nucleation, alternating and transient electric fields significantly promote ice nucleation. The nucleation temperature of individual droplets can be notably increased by the presence of an electric field. The nucleation temperature of each droplet is not only associated with a characteristic temperature, as defined by the singular nucleation model, but also by a characteristic electric field strength necessary to cause an impact on ice nucleation. Hence, the impact of an electric field can also be of singular rather than stochastic nature. Generally, the presence of an electric field can clearly promote ice nucleation and can be actively used to force ice nucleation.

The experimental work performed in this work is expanded by numerical simulations performed by Institute for Accelerator Science and Electromagnetic Fields of the Technical University of Darmstadt. The results enhance the knowledge of the behavior of water droplets under the impact of electric fields, which might be the origin for the development of more advanced prediction models for the inception of partial discharges of sessile water droplet or the icing of high-voltage insulators.