Interaction of Drops and Sprays with a Heated Wall

Abstract

Spray-wall interactions take place in many technical applications such as spray cooling, combustion processes, cleaning, wetting of surfaces, coating and painting, etc. The outcome of drop impact onto hot surfaces depends on a variety of parameters like for example material and thermal properties of the liquid and wall, substrate wetting properties, surrounding conditions which determine the saturation temperature, spray impact parameters and surface temperature. The aim of the current project is to improve knowledge of the underlying physics of spray-wall interactions. As an important step towards spray impact modeling first a single drop impact onto hot substrates is considered in detail. Various regimes of single drop impact, such as thermal atomization, magic carpet breakup, nucleate boiling and thermosuperrepellency, observed at different wall temperatures, ambient pressures and impact velocities, have been investigated experimentally and modelled theoretically during the project period. The heat flux, an important parameter for spray cooling, has been modeled not only for single drop impacts but also for sprays within many regimes. The models show a good agreement with experimental data as well as data from literature.

1 Introduction

The impact of drops with a solid surface is a widely studied phenomenon of interest not only for engineering applications, but also in many other fields, even extending into the natural and life sciences. However, the particular situation of impact onto a hot surface is much more specific and especially for surfaces at high temperatures, the heat transfer and thermodynamics of the wall-fluid interaction begin to significantly influence the hydrodynamics of drop impact, making the physics much more complex and challenging to predict. On the other hand, this is a common and key phenomenon, in particular for spray cooling, but also for many other applications. During the course of this project extending from 2010 until 2021, the strategy has been to investigate single drop impact onto hot surfaces under varying ambient conditions (pressure, surface temperature, etc.), with the aim to first develop models which are more physics-based then existing models, to describe the hydrodynamics and thermodynamics of the interaction. Once having developed these models, the next step is to extend these to the case of higher drop flux densities, eventually reaching conditions typical of spray impact onto hot surfaces. The overarching aim is to provide reliable models and predictive tools for design of such systems, in dependence of the boundary and operating conditions at hand. In many respects this goal has been achieved and both past results and on-going research will be summarized below.

It is not possible to recap all of the research conducted within the framework of this project and carried out at the Institute of Fluid Mechanics and Aerodynamics at the Technical University of Darmstadt, and therefore a selection has been made as to which topics to highlight. Nevertheless, more details can be found in the extensive literature published during the course of the project [3,4,5,6,7, 9, 14, 17, 22, 25].

Principally however, it is important to distinguish the boundary conditions imposed on any particular problem and these must also be reflected in the experimental, numerical and theoretical treatment of the problem. Although this statement appears trivial, it is of particular significance to the present physical problem, since the question immediately arises whether the hot surface is in an equilibrium state, for instance constant temperature or heat flux, or whether the surface is continually being cooled during interaction with liquid drops. This is important in two respects. For one, the material properties of the liquid are temperature dependent and if the surface changes temperature over time, this must be accounted for in the hydrodynamic treatment of the problem. Second, the problem may be a conjugate heat transfer problem, depending on the time scales involved, in which case also the thermal boundary layer and heat flux within the surface become an integral and very influential part of the problem. To the most extent, the results presented in Sect. 2 will relate to the case of the surface being in thermal equilibrium; however, also the case of transient cooling has been extensively investigated and the reader is referred to the appropriate literature for more details [27]. In Sect. 3 transient cooling of the substrate will also be addressed.

2 Heat Transfer Models in Various Drop Impact Regimes

This chapter begins with an overview of drop-wall regimes according to wall temperature and then proceeds with two sections addressing the selected cases of nucleate boiling and the strategy of extending single drop results to spray-wall interaction.

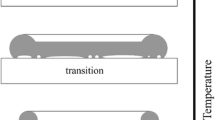
The impact of a drop onto a hot wall is usually subdivided into regimes according to the heat flux achieved at the wall, which is immediately reflected in the hydrodynamic behaviour upon impact and on total lifetime of the drop before complete evaporation. Figure 1 summarizes typical impact outcomes with representative photographs (on the left side) and a pictorial representation of the liquid/wall contact encountered in each regime (on the right side). The heat flux associated with each regime is given in Fig. 2, whereby the exact demarcation and definition of regime boundaries can vary among authors. In the framework of this study a main achievement was to capture the heat flux in theoretical expressions for each of the various regimes dependent on the material and operating parameters. This then allowed estimation of the drop lifetime. One such expression, that for nucleate boiling, will be described below in the following section. More details of these expressions and their derivation can be found in the respective publications for: drop deposition [3]; nucleate boiling [5]; thermal atomization [4, 22]; and film boiling [6].

Fig. 1

(Adapted from [7], with permission of Springer, Copyright 2018)

Thermally induced outcomes/regimes of drop impact onto a hot substrate. Left, from top to bottom: a drop deposition ($T_{w0}=120^{\,\circ }$C, $V_0=1.5$ m/s, $D_0=2.2$ mm), b drop dancing ($T_{w0}=170^{\,\circ }$C, $V_0=0,7$ m/s, $D_0=2.2$ mm), c thermal atomization ($T_{w0}=260^{\,\circ }$C, $V_0=1.7$ m/s, $D_0=2.2$ mm), d drop rebound ($T_{w0}=280^{\,\circ }$C, $V_0=0.7$ m/s, $D_0=2.2$ mm). Right, sketches of the typical mechanisms of the boiling regimes.

Fig. 2

(Adapted from [27], with permission of Cambridge University Press, Copyright 2019)

Measured heat flux $\dot{q}$ as a function of surface temperature $T_i$.

2.1 Drop Impact in the Nucleate Boiling Regime

At the instant of drop impact, heat begins to flow from the substrate to the drop; in the substrate this is pure conduction. The overall energy balance of heat transfer from the evaporating sessile drop and the heat flux from the substrate is given by

$$\begin{aligned} \int _0^{t_c} A_c(t) \dot{q}(t) ~\textrm{d} t = \rho _l L \frac{\pi D_0^3}{6} \end{aligned}$$

(1)

where $t_c$ is the contact time until the entire drop is evaporated, $A_c$ is the contact area, $\dot{q}$ is the heat flux density at the solid/liquid interface, $D_0$ is the initial drop diameter, $\rho _l$ and L are the density and the latent heat of evaporation of the liquid, respectively.

At the first instant of drop contact a thermal boundary layer develops in the substrate. The thickness of the thermal boundary layer is $h_\textrm{bl}\sim \sqrt{\alpha _w t}$, where $\alpha _w$ is the thermal diffusivity of the wall material. Since the thickness of the boundary layer is much smaller than the drop diameter, the heat conduction in the substrate can be approximated by a one-dimensional model. The temperature at the solid/liquid interface is not uniform. It is influenced by the appearance and growth of the bubbles initiated by heterogeneous nucleation at the substrate surface. The temperature at the contact line of each bubble is equal to the saturation temperature. The bubble contact lines move on the substrate, since the bubble diameter changes in time: periodically increasing due to evaporation until the drop detaches [10]. The wall superheat $\Delta T = T_w - T_\textrm{sat}$ required for nucleation is in the order of 10 K. Therefore, to roughly estimate the heat flux it is possible to approximate the interface temperature by the saturation temperature, $T_\textrm{sat}$ for $T_0-T_\textrm{sat}\gg 10$ K.

Fig. 3

(Reprinted from [5], with permission of American Physical Society, Copyright 2017)

Sketch of the temperature distribution within the solid material due to the contact of the liquid to the substrate. The solid/liquid interface is located at $z=0$.

The geometry and the definition of the coordinate system are shown schematically in Fig. 3. At $t=0$ the liquid is placed in contact with a semi-infinite wall $z<0$ at the initial temperature $T_0$. The heat conduction equation in the wall,

$$\begin{aligned} \frac{\partial T_w}{\partial t} - \alpha _w \frac{\partial ^2 T_w}{\partial z^2}=0, \end{aligned}$$

(2)

has to be solved subject to the boundary conditions

$$\begin{aligned} T_w=T_\textrm{sat}\quad \textrm{at}\quad z=0;\quad T_w\rightarrow T_0\quad \textrm{at}\quad z\rightarrow \infty , \end{aligned}$$

(3)

where $T_w(z,t)$ is the temperature in the wall region. The similarity solution of Eqs. (2)–(3) is well-known [21]

$$\begin{aligned} T_w(z, t)= T_\textrm{sat}+( T_{0}-T_\textrm{sat}) {\text {erf}}{\left( \frac{z}{2\sqrt{\alpha _w t}}\right) }. \end{aligned}$$

(4)

The heat flux density at the solid/liquid interface can be expressed with the help of Eq. (4) as

$$\begin{aligned} \dot{q}(t)\equiv \left. \lambda _w \frac{\partial T_w}{\partial z} \right| _{z=0}=\frac{e_w \Delta T_w}{\sqrt{\pi } \sqrt{t}}, \end{aligned}$$

(5)

where $\lambda _w$ is the thermal conductivity of the wall material, $e_w$ is the thermal effusivity $e_w=\sqrt{\lambda _w \rho _w c_p}$, and $\Delta T_w=T_{0}-T_\textrm{sat}$ is the overall temperature difference in the wall (see Fig. 3).

The contact area $A_c(t)$ changes during drop spreading and receding. However, since the contact time $t_c$ in the nucleate boiling regime is much longer than the observed impact time ($t_{imp}\sim D_0/V_0$, where $V_0$ is the impact velocity), the contact area can be estimated in the form

$$\begin{aligned} A_c\approx k_w \pi D_0^2, \end{aligned}$$

(6)

where the coefficient $k_w$ is determined primarily by the surface structure and wettability. The coefficient $k_w$ accounts also for the effective drop growth due to bubble expansion. This coefficient is of order unity and can be determined from the experiments. Substituting expressions (4), (5) and (6) into the energy balance Eq. (1) yields

$$\begin{aligned} t_{c}=\pi \left[ \frac{\rho _l L^{*} D_0}{12 k_w e_w \Delta T_w}\right] ^2. \end{aligned}$$

(7)

It is important to note that the obtained dependence $t_{c} \sim \Delta T_w^{-2}$ is in good agreement with the experimental results. Introducing the scaled wall temperature and dimensionless time in the form

$$\begin{aligned} \Theta =\frac{T_0-T_\textrm{sat}}{T_\textrm{sat}-T_l},\quad \tau =\frac{t}{\pi } \left[ \frac{12 e_w \left( T_\textrm{sat}-T_l\right) }{\rho _l L^{*} D_0}\right] ^2, \end{aligned}$$

(8)

allows the contact time to be given in dimensionless form

$$\begin{aligned} \tau _{c}=\frac{1}{k_w^2\,\Theta ^2}. \end{aligned}$$

(9)

Fig. 4

(Reprinted from [5], with permission of American Physical Society, Copyright 2017)

Dimensionless contact time from this study for water drops and existing literature data [1, 8, 15, 26] as a function of dimensionless time, in comparison with the theoretical prediction defined in (9) and in Eq. (17) in [5]. The initial drop diameter in the experiments ranges from 2.1 to 4.6 mm and the wall materials are aluminum, carbon steel and stainless steel.

The contact times from this study and those found in literature from Abu-Zaid [1], Buchmüller [8], Itaru and Kunihide [15] and Tartarini et al. [26] are compared with the theoretical prediction (9) in Fig. 4. The agreement is good for all the cases when the adjustable coefficient is set to $k_w=1.6$. This parameter is the same for all the substrates used in the experiments, since their wettability properties are similar.

2.2 From Drop Impact to Spray Impact in the Film Boiling Regime

In this section the application of heat flux expressions for single drops to the case of sprays will be addressed for the particular condition of film boiling. In Sect. 3.4 the transition from drops to sprays will be examined for other heat transfer regimes. In film boiling a vapour layer arises between the liquid and hot wall such that the heat flux reduces to very low levels, as indicated in Fig. 2. This leads to the hydrodynamic behavior pictured in Fig. 1d, in which drops rebound completely from the surface. Thus, the heat transfer is only momentary and through the vapour layer. In [6] an expression for the total heat transferred during an impact event has been theoretically derived and experimentally validated. Accordingly, this amount can be expressed as:

$$\begin{aligned} Q_\textrm{single} = \frac{4.63 D_0^{5/2} G\,e_\textrm{w}\left( T_0-T_\textrm{sat}\right) }{ V_0^{1/2}\left( K+2 G \right) } \end{aligned}$$

(10)

where $D_0$ and $V_0$ are the drop diameter and velocity upon impact, $T_0$ and $T_{\text {sat}}$ are the wall temperature and liquid saturation temperature, $e_w$ is the thermal effusivity of the wall material and G and K are given by the relations:

$$\begin{aligned} K=\sqrt{(B-G)^2+\frac{4 G}{\sqrt{\pi }}}-B- G, \end{aligned}$$

(11)

with

$$\begin{aligned} G=\frac{\sqrt{\pi } \lambda _\textrm{v} \rho _\textrm{f} L }{2\left( T_0-T_\textrm{sat}\right) e_\textrm{w}^2}; \quad B=\frac{\sqrt{5} \left( T_\textrm{sat}-T_{D_0}\right) e_\textrm{f} }{\sqrt{\pi } \left( T_0-T_\textrm{sat}\right) e_\textrm{w}}. \end{aligned}$$

(12)

In the case of sparse sprays, each drop and its associated heat transfer would be independent of all other drop impacts, since the drops immediately leave the surface. Thus the heat flux can be computed as the superposition of many individual drops. However, at higher mass fluxes of drops, the probability of drops interacting with one another must be taken into consideration, which can be done on the basis of Poisson statistics. Once drop interaction occurs, for instance the spreading of one drop interacts with the spreading of a neighbour drop (in time and space), then a decrease in the overall heat flux must be accounted for, as outlined in [3]. Doing this, and using previous results for the spreading diameter and time of single drops given in [28], the heat flux coefficient for dense sprays can now be obtained

$$\begin{aligned} \alpha _\textrm{ht} = 8.85 \chi \frac{\dot{m} G\,e_\textrm{w}\left( T_0-T_\textrm{sat}\right) }{\rho _\textrm{f}\Delta T \left( K+2 G \right) D_0^{1/2} V_0^{1/2}}\eta _\textrm{wet}, \end{aligned}$$

(13)

where $\eta _\textrm{wet}$ is the correction factor for the relative wetted area estimated using the assumption of randomly distributed drop impacts on the the substrates in space and time, which can be described by the Poisson distribution. The cumulative wetted area $\gamma$ on the surface

$$\begin{aligned} \gamma = \frac{2.1\dot{m}}{\rho _\textrm{f} V_0} \left( 1+0.36 \textrm{We}^{0.48}\right) ^2 \end{aligned}$$

(14)

is expressed accounting for the superposition of all the drops impacting onto a unit area per unit time. Here $\dot{m}$ is the mass flux in the spray and $\rho _f$ is the fluid density. The Weber number is defined as $We=\rho _f V_0 D_0^2/\sigma$, where $\sigma$ is the surface tension. Therefore, the correction factor which accounts for the drop interactions at the substrate is

$$\begin{aligned} \eta _\textrm{wet}=\frac{1-e^{-\gamma }}{\gamma }. \end{aligned}$$

(15)

The dimensionless constant $\chi$ accounts for the heat flux during the later stages of drop spreading, which is not considered in the present analysis. Since the heat flux density sharply reduces at large times, the value of $\chi$ should be approximately unity. The coefficient $\chi$ can be estimated by fitting to the experimental data.

This expression proves to predict very well past measurement of the heat transfer coefficient for dense sprays impacting on substrates at temperature above the Leidenfrost point. This is illustrated in Fig. 5. In the left plot of this figure, using a coefficient $\chi =3.2$ derived by fitting to the data from [18] and kept constant for all other comparisons, excellent agreement is found between theory and experiments for the heat transfer coefficient. Similarly, good agreement is found for varying operating conditions, in particular for largely differing average drop sizes and velocities, as shown in the right plot of Fig. 5.

Fig. 5

(Adapted from [6], with permission of Elsevier, Copyright 2017)

Heat transfer coefficient for water spray in the film boiling regime as a function of the mass flux densities of the spray $\dot{m}$. Comparison of the theoretical prediction (Eq. (13)) with existing experimental data from: Left plot—[2, 12, 16, 19, 29] for approximately the same operational conditions: $\Delta T = 700\,^\circ \textrm{C}$, $D_0 = 350 \,\upmu$m, $V_0 = 14$ m/s; Right plot—for $\Delta T=700\,^\circ \textrm{C}$, $D_0=350 \,\upmu$m, $V_0=14$ m/s from [29] and $\Delta T=550\,^\circ \textrm{C}$, $D_0=18 \,\upmu$m, $V_0=27$ m/s from [18]

3 Measurement of the Heat Flux

The focus of the current work is placed on the measurement of the heat flux during single drop impacts and the transfer of these results to sprays. Therefore single drop experiments as well as drop chain experiments have been performed.

3.1 Experimental methods

The experimental setup comprises a drop generator, an impact target embedded in a heating system, a high-speed video system for viewing from the side and a high-speed mid-wave infrared (MWIR) camera system to measure the emitted infrared radiation of the hot surface during drop impact. The experimental setup is shown in Fig. 6. Drops with a diameter of $D_0 =2.2\,{\text {mm}}$ drip off a needle. The needle is fed with double-distilled water. By applying a constant volume flow a drop chain is generated with a drop frequency of $0.9\,{\text {Hz}}$ up to $5.7\,{\text {Hz}}$. The impact velocity can be varied in the range of 0.4–$2\,{\text {m}}\,\,{\text {s}}^{-1}$ by changing the height of the needle above the impact surface.

Fig. 6

Sketch of the experimental setup with the drop generator (1), sapphire window with CrN PVD coating (2) or metal substrate (3) as impact target, heating system (4), high-speed IR camera (5), thermocouples (6), high-speed camera with telecentric lens (7) and telecentric background light source (8)

The drops impact onto a interchangeable hot surface. An IR transparent sapphire substrate is used as an impact target, enabling measurement of the surface temperature during drop impact with a high temporal and spatial resolution. The sapphire window has a thickness of $3\,{\text {mm}}$. The upper surface of the window is coated with a $600\,{\text {nm}}$ thick CrN PVD layer. The coating is highly infrared emissive, while the sapphire window is transparent for MWIR radiation. The window is placed in a heater with optical access in the center. The heating system controls the temperature of the sapphire window from 100 to $400\,{}^{\circ }{\text {C}}$. The emitted infrared radiation from the CrN coating is captured from below using a high-speed MWIR camera. An in-situ calibration is performed to calculate the surface temperature based on the measured radiation and to take optical errors into account.

Different metal substrates of aluminium (EN AW 7075), copper (CW004A) and stainless steel (1.4841) have been used in the experiments as the impact substrates. The impact surface of the metal substrates are mirror polished. The metal substrates can be heated up to $550\,{}^{\circ }{\text {C}}$. The temperature of the substrate is measured with thermocouples type J, placed $1\,{\text {mm}}$ below the surface. The stainless steel target is equipped with 11 thermocouples to measure the temperature distribution inside the substrate during the impact of a drop chain.

The drop impact is observed from the side using a high-speed camera and with background lighting (shadowgraphy).

For the single drop experiments the substrate is heated to a certain surface temperature. After the system reaches steady state, the single drop experiments are performed. The side view observations are used to measure the impact parameters and residence time of the drops on the surface and to observe the drop impact regime. The IR camera is used to measure the temperature distribution close to the liquid-solid interface.

The drop impact lowers the contact temperature at the liquid-solid interface, leading to a three-dimensional temperature gradient inside the substrate. The temperature gradient inside is described by the heat conduction equation

$$\begin{aligned} \frac{\partial T_\textrm{w}}{\partial t} - \alpha _\textrm{w} \frac{\partial ^2 T_\textrm{w}}{\partial z^2} = 0 \end{aligned}$$

(16)

where $T_w$ is the wall temperature, t is time and $\alpha _{w}$ the thermal diffusivity of the wall.

The heat flux removed during a single drop impact is obtained by numerically solving the heat conduction equation inside the sapphire substrate. In Fig. 7 the mesh of the numerical calculation is shown. Close to the liquid-solid interface, the temperature gradient is very steep, thus, the mesh is refined in this area. The temperature distribution captured by the IR camera is used as a boundary condition at the upper surface. All other boundaries are considered to be adiabatic. The heat conduction equation is solved using the computational fluid dynamic solver OpenFOAM, as described in [13, 23].

Fig. 7

Computational mesh of the sapphire window. The mesh is refined closer to the impact surface. The temperature distribution, measured by the IR camera, is used as a boundary condition on the upper side

For the drop chain experiments the substrate is initially heated up to $550\,{}^{\circ }{\text {C}}$. After the system reaches steady state, the heater is switched off and the drop chain is applied to the surface. The impacting drop chain causes a transient cooling of the substrate and a growing thermal boundary layer, as described by Eq. (16). The thermal boundary is measured inside the stainless steel target using the thermocouples. Based on the thermal gradient orthogonal to the surface, the heat flux removed from the substrate is calculated using an analytical solver provided by Woodfield et al. [30].

The temporal resolution of the thermocouples is significantly lower than that of the IR camera. For this reason the IR camera is used to measure the heat flux removed from single drops. Since the resistance of sapphire against thermal shocks is limited, it is not possible to resolve the transient heat transfer during the impact of the drop chain or during spray cooling of a sapphire window. For this reason a combination of both described measurement techniques is used, depending on the scope of the experiment.

3.2 Heat Flux During a Single Drop Impact

The heat flux removed from a substrate by single impacting droplets is addressed in the following section. The three drop impact phenomena, drop deposition with and without nucleate boiling and thermal atomization, have been observed using single drop experiments on the sapphire window. First the heat flux within the single regimes is described. Afterwards a two-dimensional heat flux model is introduced, valid for thermal atomization.

3.2.1 Observations

Drop evaporation The heat flux removed from a hot surface depends on the drop impact regime. For low surface superheat the drop deposits on the surface and evaporates slowly without nucleate boiling. Figure 8 illustrates the heat flux removed from a hot surface during a drop impact in this regime. The initial surface temperature is $123\,{}^{\circ }{\text {C}}$. The impacting drop leads to a temperature drop in the newly wetted area, causing a strong temperature gradient inside the substrate and a high heat flux removed from the substrate. The highest heat flux can be observed in the newly wetted areas and close to the three-phase contact line. After some time an ongoing convection can be observed inside the sessile drop, leading to heat flux rates comparable to the heat flux at the three-phase contact line.

Fig. 8

Heat flux measurements during drop impact on a sapphire substrate at $123\,{}^{\circ }{\text {C}}$ with an impact velocity of $0.34\,{\text {m}}\,{\text {s}}^{-1}$. The drop deposits and slowly evaporates without nucleate boiling

Nucleate boiling At higher surface temperatures the drop deposition is accompanied by nucleate boiling. Figure 9 shows the heat flux during a drop impact onto a $166\,{}^{\circ }{\text {C}}$ hot surface in the nucleate boiling regime. Small areas with stronger temperature drops and high heat flux are observed, especially in newly wetted areas. The heat flux is less uniform compared to the drop evaporation regime. At later times the heat flux becomes more uniform, while a high heat flux at the three-phase contact line of growing bubbles remains. Early after the drop impact only small droplets and bubbles can be observed from the side. This leads to the assumption that many small microbubbles lead to the high, irregular heat flux at the beginning.

Fig. 9

Heat flux measurements during drop impact onto a sapphire substrate at $166\,{}^{\circ }{\text {C}}$ with an impact velocity of $0.45\,{\text {m}}\,{\text {s}}^{-1}$. The drop deposits and nucleate boiling can be observed

Thermal atomization At high surface temperatures the drop impacts and the drop rebounds or the drop atomizes. The heat flux measurements in this thermal atomization regime is shown in Fig. 10 for a drop impact onto a $345\,{}^{\circ }{\text {C}}$ hot surface. The thermal atomization regime is characterized by initial direct contact between the liquid and solid, leading to strong ongoing nucleate boiling with many small secondary droplets. Starting from the rim, the lamella starts to levitate away from the surface. The heat flux distribution in Fig. 10 shows a very high heat flux at the beginning. Later the heat flux decreases. After $2.05\,{\text {ms}}$ the area of a high heat flux decreases, while the drop is still spreading. The decreasing heat flux area indicates that the liquid lamella, starting from the rim, has detached from the surface.

Fig. 10

Heat flux measurements during drop impact in the thermal atomization regime. The sapphire substrate has a initial surface temperature of $345\,{}^{\circ }{\text {C}}$. The drop impacts with an impact velocity of $1.15\,{\text {m}}\,{\text {s}}^{-1}$

The heat flux inside the substrate is described by Eq. (16). Since the liquid and solid are in direct contact in the thermal atomization regime, the contact temperature at the interface is assumed to be at the liquid saturation temperature, while the substrate is still wetted. A thermal boundary layer grows inside the solid material as well as inside the liquid. Both are described by $\sqrt{\alpha t}$, with $\alpha$ being the thermal diffusivity of the solid material or liquid. An exact solution of this problem is provided in [20, 21]. The heat flux removed from the substrate is obtained in the form

$$\begin{aligned} \dot{q}(r,t) = \frac{e_l e_w (T_{w0} - T_{l0})}{(e_l + e_w \mathcal {J}(Pr)) \sqrt{\pi t} \sqrt{1 - \bar{r}^2}} \end{aligned}$$

(17)

in which $e_w$ is the thermal effusivity of the wall, $e_l$ the thermal effusivity of the liquid, $T_{w0}$ the initial temperature of the wall, $T_{l0}$ the initial temperature of the liquid. The factor $\bar{r}$ is the dimensionless radius

$$\begin{aligned} \bar{r} = r/a(t), \quad a(t) \approx \sqrt{D_0 V_0 t} \end{aligned}$$

(18)

with a being the contact radius.

Figure 11 compares the analytic model of Eq. (17) to the experimental data shown in Fig. 10 for $r = 0$. The analytic model exhibits good agreement with the experimental data. After $3.5\,{\text {ms}}$ the liquid lamella levitates and the boundary condition and model are no longer valid.

Fig. 11

Heat flux of a drop impact in the thermal atomization regime. The drop impacted with $1.15\,{\text {m}}\,{\text {s}}^{-1}$ at the $345\,{}^{\circ }{\text {C}}$ hot substrate. The line shows the analytic model of Eq. (17) in the center of the lamella ($r = 0$) as a function of time. The stars show the experimental data

In Fig. 12 the spatial distribution of heat flux is shown for $t =1.377\,{\text {ms}}$ after the impact, again a comparison between the analytical model and the experimental data. The experimental data is averaged over all cells with the same distance from the center of the lamella. The error bars represent the scatter by one standard deviation. In the center the experimental data exhibit a higher heat flux with low scatter. From $r =0.5\,{\text {mm}}$ to $1.5\,{\text {mm}}$ the heat flux and scatter of the experimental data is higher. This is caused by the strong nucleate boiling in this area, leading to a higher heat flux compared to the pure conduction as assumed in Eq. (17). From $r \approx 1.6\,{\text {mm}}$ onward the experimental data shows a decrease of heat flux, since the lamella starts to levitate, beginning form the rim. For $r = a$ the analytical model has a singularity, which is non-physical.

Fig. 12

Heat flux of a drop impact in the thermal atomization regime. The impact velocity is $1.15\,{\text {m}}\,{\text {s}}^{-1}$ and the initial surface temperature $345\,{}^{\circ }{\text {C}}$. The line shows the analytic model of Eq. (17) $1.377\,{\text {ms}}$ after impact as a function of the radius. The experimental data are averaged over the radius and the error bars indicate one standard deviation of the measured fluctuations

The experimental measured heat flux is in most cases higher then the predicted heat flux by conduction. This indicates that the liquid is in contact with the substrate without any isolating vapour layer, even if the surface temperature is very high.

3.3 Thermosuperrepellency

The transition between different drop impact regimes is important information for modeling as well as for applications. The onset of drop rebound is an important transition, since it indicates that a vapour layer between the drop liquid and the hot substrate has been established, lowering the removable heat flux.

Figure 13 shows the residence time of single drops impacting onto a hot stainless steel target. At low surface temperatures, the impacting drops are in the drop deposition regime. The residence time $t_{\text {deposit}}$ in the drop deposition regime is described in [5]. The experimental data exhibit good agreement with the model of the residence time. With increasing substrate temperature, more liquid is ejected by secondary droplets or rebound. The residence time decreases faster then described by the model. Above a certain transition temperature $\Delta T^* = T^* - T_\textrm{sat}$, the residence time remains constant, since most of the drop liquid rebounds. The residence time is comparable with the natural oscillation time of drops [11]

$$\begin{aligned} t_\sigma \approx \sqrt{\frac{\rho D_0^3}{\sigma }} = \frac{D_0 We^{1/2}}{V_0}. \end{aligned}$$

(19)

Fig. 13

Drop residence time on the hot substrate depending on the substrate superheat $\Delta T_{w0} = T_{w0} - T_\textrm{sat}$. The residence time remains constant for temperatures above $T^*$

The same behaviour can be observed for drop impacts on all substrate materials within this study. Vapour rivulets or clusters are visible from top view observations of drop impacts onto hot aluminium above $\Delta T^*$, as shown in Fig. 14a. A similar behaviour can be observed from IR measurements, in which large clusters with a low heat flux can be observed, during drop impact onto a hot sapphire window, as shown in Fig. 14b. The occurrence of large vapour clusters can be described by the percolation of single bubbles within the lamella, as shown in Fig. 14c and described in [25]. The remaining wetted area, which is not covered by vapour, is described by $\epsilon _c \approx 0.32$. The heat removed from the surface goes into the evaporation of the liquid. This leads to

$$\begin{aligned} \rho h_\textrm{res} L^* \epsilon '(t) = -\dot{q} , \end{aligned}$$

(20)

where $\rho$ is the liquid density, $h_\textrm{res}$ is the height of the liquid lamella $L^*$ is the sensible heat $c_\text {p}(T_\text {sat} - T_\text {l0})$ and latent heat of liquid evaporation, $c_p$ is the specific heat capacity and $\epsilon$ is the wetted area. The height of the liquid lamella is described by $h_\textrm{res} \approx 0.79 D_0 Re^{-2/5}$. Solving the differential Eq. (20) and assuming $t = t_\sigma$ leads to a temperature superheat of

$$\begin{aligned} \Delta T = b \frac{D_0^{1/4} L^*\rho ^{3/4}\sigma ^{1/4}}{e_w Re^{2/5}}, \end{aligned}$$

(21)

with $b = 0.48$. This assumption is only valid as long as the drop impact is surface tension dominated or $We < 2.5 \, Re^{2/5}$.

Fig. 14

(Adapted from [25])

a Vapour rivulets from top view observations during drop impacts onto a $200\,{}^{\circ }{\text {C}}$ hot aluminium substrate. b Similar clusters of low and high heat flux areas can be observed from IR measurements of drop impacts onto a hot sapphire window in the drop rebound regime. c Exemplary cluster of discs as described by percolation theory.

In the case of fast and small droplets the relevant time for the drop rebound is defined by the time in which the viscous boundary layer reaches the top of the lamella, which is $t_{\nu } = \frac{D_0 Re^{1/5}}{V_0}$. Solving the differential Eq. (20) and assuming $t = t_\nu$ leads to

$$\begin{aligned} \Delta T_{\nu } = \frac{\rho \sqrt{\nu } L^*}{e_w}. \end{aligned}$$

(22)

Fig. 15

(Reprinted from [25])

Comparison of the thermosuperrepellency threshold temperature $\Delta T^* = T^* - T_\textrm{sat}$ with the models given in a Eq. (21) and b Eq. (22).

In Fig. 15 the experimental data of spray cooling experiments and single drop experiments are compared to the scales shown in Eqs. (21) and (22). Figure 15a shows how the experimental data of single drop impacting with different drop impact velocities onto different substrate materials scale well with the model of Eq. (21). Figure 15b shows experimental data from literature and in-house data and how they correlate with Eq. (22).

3.4 Drop Chain Impact

The single drop experiments on a hot substrate are generic experiments and a major simplification of spray-wall interactions. To transfer the knowledge from single drop experiments to spray-wall interaction it is necessary to increase the complexity towards drop/drop interactions, like in drop chains. Monodisperse drop chain impacts onto a hot substrate are used in the following as a generic one-dimensional spray. The drop chain experiments allow to study single drop impacts onto the substrate in greater detail, while measuring the overall heat flux during the cooling of the substrate. This combination will allow to transfer knowledge of single drop experiments to spray cooling.

In Fig. 16a an exemplary drop chain experiment is shown. The substrate is heated up to $550\,{}^{\circ }{\text {C}}$, the heater is switched off and a drop chain with a frequency of $f_c = 0.8\,{\text {Hz}}$ is applied. Each drop impact causes a strong temperature drop, as shown in the detailed view (insert). After the drop rebounds or evaporates the substrate is dry and the surface temperature increases again. Even for higher drop chain frequencies of $f_c = 5.19$ Hz the drops do not interact or accumulate in the drop rebound regime. The wetting increases for lower surface temperatures, leading to a higher amplitude of the temperature drop. At even lower surface temperatures the substrate is continuously wetted, leading to weaker temperature oscillations. In Fig. 16b the corresponding heat flux is shown. The black shaded area corresponds to the oscillations of the heat flux caused by the temperature drop of each drop impact. In the detailed view (insert) the heat flux of three single drop impacts is shown. After a strong temperature drop and high heat flux, the surface is dry and reheats. The red dashed line indicates the average heat flux, while the green dashed line shows one standard deviation of heat flux fluctuations, valid as an indicator of the oscillation amplitude. At early times the heat flux oscillations are low, since a vapor layer insulates the drop from the substrate. The heat flux oscillations increase significantly as soon as the surface is wetted, since the contact temperature is significantly lower. The oscillations as well as the standard deviation increases. In addition, the average heat flux increases slightly. For even lower surface temperatures the residence time of the drops increase and the drops start to interact until they accumulate and the substrate is uniformly wetted with a continuous liquid film. Due to the liquid film, the contact temperature and heat flux oscillates less, while the average heat flux continues to rise.

Fig. 16

(Adapted from [24])

a The surface temperature during transient cooling by a monodisperse drop chain. The insert view shows three single drop impacts at a high surface temperature. b The corresponding heat flux. The red dashed line shows the moving average, while the green dashed line indicates one standard deviation of the fluctuations. In the insert the heat flux caused by three single drop impacts is shown.

Fig. 17

Heat flux as a function of the wall superheat for different drop chain frequencies $f_c$, but similar impact parameters (Reynolds number)

Several parameters of sprays can be varied, which potentially influence the heat flux during spray cooling. One of the parameters is the mass flux in a spray or in the case of an one-dimensional drop chain the frequency of drops. Figure 17 compares the average heat flux for different drop chain frequencies $f_c$. At high surface temperatures the heat flux scales linearly with $f_c$, since no interaction of drops can be observed. With lower surface temperature the heat flux does not scale linearly anymore with $f_c$. The heat flux removed per drop decreases with increasing $f_c$.

3.5 Conclusion

The focus of this experimental and theoretical study is the impact of single drops and sprays onto hot substrates over a wide range of ambient conditions as well as substrate materials. It is motivated by many technical applications, mainly related to spray cooling. The topic is highly interdisciplinary. It includes hydrodynamics of drop impact and spreading, thermodynamics of boiling and evaporation, diagnostic techniques of sprays and drops, and mathematical modeling of the basic phenomena.

The research strategy is built on the accurate investigation and theoretical modeling of a single drop impact and its further application to the chain of drops impact and spray cooling.

During the first period, the outcome of single drop impacts onto hot surfaces has been characterized regarding the ambient conditions. The main drop impact regimes, drop deposition, drop dancing, thermal atomization and drop rebound have been identified and described. The heat flux as the key interest of cooling technologies has been modeled on a physical base, for single phase cooling, as well as nucleate boiling in the drop deposition regime, thermal atomization and drop rebound based on film boiling. Additionally, the model of the heat flux in the film boiling regime is transferred from single drop to spray impact at a hot surface, which allows prediction of the heat transfer during spray cooling in film boiling. All models are validated with the performed experiments and showed a good agreement within the single regimes.

The main focus of the last project period is the accurate study of the temperature distribution in the substrate during the impact. The wall temperature and local heat flux is measured with a high temporal and spatial resolution. A model of the local heat flux distribution is shown for the thermal atomization regime with good agreement between the model and experimental data. The thermosuperrepellency phenomena has been identified as a thermodynamic regime which is accompanied by nucleate boiling and leading vapor percolation and partial drop rebound at temperatures much smaller than the real Leidenfrost point.

Finally the cooling effects of a chain of liquid drops are characterized to better understand the transient cooling of a substrate by multiple droplets.