High Resolution Measurements of Heat Transfer During Drop Impingement onto a Heated Wall

Abstract

Drop impact on a hot surface heated above the saturation temperature of the fluid plays an important role in spray cooling. The heat transferred from the wall to the fluid is closely interrelated with drop hydrodynamics. If the surface temperature is below the Leidenfrost temperature, the heat transport strongly depends on the transport phenomena in the vicinity of the three-phase contact line. Due to extremely high local heat flux, a significant fraction of the total heat flow is transported through this region. The local transport processes near the three-phase contact line, and, therefore, the total heat transport, are determined by the wall superheat, contact line velocity, system pressure, fluid composition, surface structure and physical properties on the wall. The effect of the aforementioned influencing parameters on fluid dynamics and heat transport during evaporation of a single meniscus in a capillary slot are studied in a generic experimental setup. The hydrodynamics and evolution of wall heat flux distribution during the impact of a single drop onto a hot wall are also studied experimentally by varying the impact parameters, wall superheat, system pressure, and wall topography. In addition, the fluid dynamics and heat transport behavior during vertical and horizontal coalescence of multiple drops on a heated surface are studied experimentally.

1 Introduction

Spray cooling is one of the most efficient methods for heat removal in applications, which range from the cooling of electronic devices to metal quenching. Heat transfer by spray cooling is governed by the transport processes during the impact of multiple drops onto a hot surface (see Fig. 1, right). Understanding the multiple drop impacts necessitates a detailed investigation of transient processes accompanying the single drop impact (see Fig. 1, middle).

Fig. 1

Sketch of spray cooling process (right), evaporating liquid drop (middle) and three-phase contact line (left)

In a non-isothermal drop impact, the wall temperature affects both the hydrodynamics and heat transport. According to [2, 3, 16], five heat transfer regimes can be distinguished: (i) evaporation below the onset of bubble nucleation, which is also known as the film evaporation [16]; (ii) nucleate boiling; (iii) transition boiling; (iv) thermal atomization; and (v) film boiling. The impact regime is determined by the impact Reynolds and Weber numbers, properties of the substrate and the liquid, and wall temperature.

Numerical simulations [11, 12, 21] and experimental studies [8, 11] reveal that, if the drop impinges an impermeable and rigid substrate in drop deposition (in the absence of splashing and bouncing phenomena) and film evaporation regimes, its evolution can be subdivided into three subsequent phases: (i) the drop spreading phase, in which the contact line advances radially outwards due to action of inertia; (ii) the drop receding phase, in which the contact line moves inwards due to surface tension; and (iii) the phase of sessile drop evaporation, in which the drop is at a state of mechanical equilibrium. During all three phases, heat is transferred by conduction, convection, and evaporation. The contribution of each of these heat transfer mechanisms differs during the various phases. In many spray cooling regimes, the multiple impacting drops wet isolated parts of the surface. In these cases, the cooling efficiency significantly depends on the cumulative length of the contact lines which separate the wetted parts from dry patches [26]. This can be explained by strong heat flux maxima existing in the vicinity of the three-phase contact lines [13,14,15, 22] (see Fig. 1, left). Herbert et al. [11] and Batzdorf [21] have shown by numerical simulation of a drop impact and evaporation on a heated wall that the heat transported in the proximity of the three-phase contact line amounts to almost $50\%$ of the total heat transfer during the sessile drop evaporation phase.

If the spray is not extremely dilute, the heat transport during spray cooling is governed not by the impacts of separate drops onto a hot wall, but by an interaction of multiple impacting drops with each other or with a liquid film covering the wall. The heat transport mechanisms related to interaction between the drops on hot walls are very complex and not yet sufficiently understood. In order to reduce the complexity pertinent to the spray impact at applications-relevant conditions, the interactions drops can be studied in generic configurations, such as interaction between several drops simultaneously impacting onto different locations [1, 20] or an interaction between drops successively impacting onto the same location [5, 7, 9, 10, 17].

The present work aims at enhancing the understanding of non-isothermal drop–wall interactions in an atmosphere of a pure vapor and at a wall superheat (the difference between the temperature of the wall and the saturation temperature) below 18 K. A special attention is paid to detailed investigation of the the contact line movement and heat transfer in the vicinity of the contact line. High resolution experimental studies have been performed for two configurations: single meniscus evaporation in a capillary gap, and impact of one drop or multiple drops onto a hot substrate. A parameter study has been conducted, in which, among others, the wall superheat and impact parameters have been systematically varied. The experimental results, together with a predictive model described in Chapter “Numerical Simulation of Heat Transfer and Evaporation During Impingement of Drops onto a Heated Wall”, contribute to better insights into the mechanisms of spray cooling and potential improvements of spray cooling systems.

2 Experimental Method

This section outlines the experimental apparatus employed for the single meniscus and the drop impact studies followed by a brief description of the data reduction and measurement uncertainties. The single meniscus experiment is designed in such a manner that allows a specific and generic investigation of the heat transfer phenomena in the direct vicinity of a moving three-phase contact line. The drop impact experiments, on the other hand, are designed to study the hydrodynamics and heat transfer phenomena on the larger and fully dynamic drop impact scale.

2.1 Experimental Setups

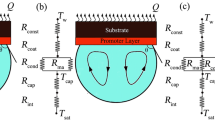
Figures 2 and 3 demonstrate the core parts of the single meniscus evaporation and drop impact experimental setups, respectively. The core component of both setups are sealed temperature-controlled test cells filled with pure vapor. Both setups utilize a high-temperature thermostat to pass heated liquid through the thermalization channels drilled in the walls of the cells to establish and control the fluid temperature and accordingly the system pressure.

The refrigerant FC-72 has been used as a working fluid. This refrigerant possesses a relatively low saturation temperature at atmospheric pressure ($56.6^{\,\circ }$C), which, together with the dielectric property of FC-72, makes it suitable for thermal management of electronic devices. Prior to filling the test cell with the working fluid, the non-condensable gases were extracted from the liquid using a degassing setup described in [22]. Afterward, the gas in cell was evacuated and filled with the degassed working fluid to establish pure saturation conditions.

Fig. 2

Schematic of single meniscus experimental setup

Fig. 3

Schematic of drop impact experimental setup

In the single meniscus experimental setup (see Fig. 2), a single meniscus is formed in a vertical flat gap between the heater plate and a copper plate kept at the system set-point temperature. The meniscus can be moved in a direction normal to the straight contact line by a volume shift in the stainless steel bellows controlled by the stepper motor. This allows the investigations of advancing (wetting) and receding (dewetting) contact lines.

In the experimental setup for investigation of drop impact (Fig. 3), the drops are generated by pumping the working fluid from a reservoir into the cell using a syringe pump. The drop size at the moment of detachment is governed by the balance between the gravity and surface tension forces and is therefore highly reproducible. To vary the impact velocity and the drop impact diameter, the height of the needle over the substrate and the needle diameter have been varied, respectively. In this study, the investigations are not limited to single drop impingement. Multiple drops are created by either variation of the dispensing volume flow rate of the pump (successive drop impingement) or by mounting an additional syringe pump unit parallel to the main unit (simultaneous drop impingement).

In both setups, a high-speed black/white camera is placed at the side of the cell for optical observation of the moving meniscus or of the dynamic drop shape evolution during its impact. The B/W images are post–processed in order to determine the liquid–vapor interface velocity and the apparent contact angle during single meniscus evaporation experiments, as well as the drop diameter, impact velocity, and time difference between two impacts during drop impact experiments.

An infrared (IR) camera having high spatial resolution and high frame rate is employed to record the temperature field at the solid–fluid interface. The spatial resolution of the IR camera is 29.27 $\upmu$m/pixel and the frame rate is 1 kHz. During the drop impact experiments, in order to fit the largest drop or two simultaneously impacting drops in the field of view (FOV) of the IR camera, its spatial resolution has been set to 40.82 $\upmu$m/pixel. After the experimental run was finished, the IR signal has been calibrated in-situ versus temperature for each pixel within FOV. The calibration has been accomplished by pressing a copper block with a known temperature against the substrate and recording IR images for different temperatures.

The heated substrate is comprised of an IR-transparent CaF$_2$ glass plate with a thickness of 4 mm coated with a 400-nm-thick chromium nitride (CrN) black layer with high emissivity and a 400-nm-thick chromium layer, which is used for Joule heating. These layers are deposited by employing the physical vapor deposition method [25]. The thermal diffusivity of the substrate material is close to the thermal diffusivity of the stainless steel alloys, which find application in many technical systems. The input heat flux and accordingly the wall superheat have been varied through the electrical power delivered to the chromium layer.

2.2 Data Reduction

The time-dependent distribution of the heat flux at the interface between the solid substrate and the working fluid is the central outcome of the experimental investigations. The heat flux distribution at the solid–fluid interface is computed from the transient temperature field recorded with the IR camera. This is done by solving a transient three-dimensional equation of heat conduction within the substrate. The heat conduction equation is solved using the finite volume method. The details of the above procedure for determination of heat flux distribution and its accuracy are discussed in [8, 22].

In single meniscus evaporation experiments, the heat flux field has been averaged along the horizontal direction, and the resulting heat flux line profile along the vertical direction has been analyzed. The contact line position has been determined by searching for the local maximum of the heat flux line profile.

In drop impact experiments, the impact diameter, impact velocity, and time interval between the impact of drops are derived by post-processing of B/W images. The drop diameter is computed by applying a three-dimensional volume integration method. This method is based on the fact that the images of the drops which are captured by the black/white camera with a telecentric lens are orthogonal projections of the drop. The position of the contact line is derived via post-processing of the IR images. It has been assumed that the drops are symmetric in respect to the vertical axis. The effect of deviations from symmetry is marginal. The total heat flow at each time instant is calculated by integrating the heat flux over the whole footprint of the drop. The details of data reduction are given in [8].

2.3 Measurement Uncertainties

The uncertainties of the measured temperature arise from the noise level of the chip detector within the infrared camera. This noise level, which is also known as the noise-equivalent temperature difference (NETD), depends both on the temperature and on the optical setup. The NETDs values reported by the IR camera manufacturers are valid for a certain given temperature level. The noise-equivalent heat flux difference (NEHFD) related the heat flux uncertainty can be computed on the basis of NETD. The methods applied for determination of NETD and NEHFD for different temperatures are described in [22]. The uncertainty of the total heat flow is determined both by the uncertainties of the evaluation of the boundaries of the drop footprint and by the uncertainty of the the heat flux field. The drop footprint uncertainty is governed by the size of two pixels of the infrared image. The maximum uncertainty of the total heat flow occurs at the instant of maximal drop spreading. The vapor temperature inside the cell has been measured with an uncertainty of 0.6 K.

3 Results and Discussion

This section briefly addresses the main outcomes obtained from single meniscus experiments based on [22]. Subsequently, the results of single drop impact and multiple drops impact experiments are reviewed in detail.

3.1 Single Meniscus Experiment

Figure 4 shows the temperature field (left), heat flux field (middle), and the corresponding temperature and heat flux line profiles (right) during the evaporation of a single meniscus. The temperature minimum and heat flux maximum in the vicinity of the three-phase contact line can be explained by an extremely small local thickness of the liquid film, which leads to a very low local thermal resistance of this film.

The influence of contact line velocity and movement direction on heat transport has been investigated. The heat flux peak at the spreading contact line has been found to be up to twice as high as at the receding case. The peak heat flux increases with an increase in the advancing contact line velocity. This is due to the stronger micro-convection close to the contact line. This effect is absent for a receding contact line, resulting in the independence of the heat flux peak from the velocity [22].

Fig. 4

Temperature field (left), heat flux field (middle), and temperature and heat flux line profiles (right) at $\Delta T= 3.4$ K and p $= 0.57$ bar

The increasing system pressure leads to a decrease in the heat flux peak near the contact line for static, advancing, and receding contact lines. This is explained by the reduction in latent heat of vaporization at elevated pressures.

The heater substrate has been coated with a nanofiber mat generated through electrospinning of 5 wt$\%$ polyacrylonitrile solution (PAN; M$_{\text {w}} = 150$ kDa) in N,N-dimethylformamide (DMF) to investigate the influence of surface structure. It has been found that the local heat flux in proximity of a stationary apparent contact line increases by $60\%$ if the substrate is coated by the nanofiber mat. In the case of a receding meniscus, the heat transfer is enhanced due to formation of an extended region, in which the pores within the nano-textured mat are partially filled with evaporating liquid [4].

A mixture of FC-3284 and FC-84 fluids has been used to study the influence of fluid composition on the local heat flux. It has been shown that in binary mixtures the local evaporation rate and heat flux peak are lower compared to the pure fluids. This effect can be explained by the influence of the mixture on the phase equilibrium, the local variation of the evaporation rates of various components and the local differences in concentration.

3.2 Drop Impact Experiment

This section contains the results corresponding to the impact of a single drop (Sect. 3.2.1) and multiple drops (Sect. 3.2.2) onto a heated surface.

Fig. 5

B/W images and heat flux fields during the impact of a drop onto a heater for 25 ms after impact (Re = 1450, We = 34, D$_0 = 0.93$ mm, u$_0= 0.44$ m s$^{-1}$, $\Delta T= 9.5$ K, and p $= 0.9$ bar) [8]

3.2.1 Single Drop Impact Experiment

This section addresses the influence of wall superheat, impact velocity, drop size, system pressure, and surface structure on hydrodynamics and heat transport during a single drop impact onto a heated surface. The side view of the drop captured by the B/W camera at different time instants and the temporal evolution of the heat flux distribution at the solid–fluid interface determined from the IR images are presented in Fig. 5. At the initial stages of impact, the maximal heat flux is detected at the center of the drop footprint. At this stage, a high, uniform heat flux around the central part of the footprint decreases radially outwards near the drop periphery. The heat is transported from the wall to the fluid mainly by conduction and convection. At t $= 4$ ms, shortly before the drop reaches its maximum spreading radius, the highest local heat flux is observed near the contact line. Starting from this instant, the heat flux in proximity of the contact line is larger than near the the center, indicating that the evaporation in the vicinity of the contact line is an important heat transfer mechanism at this stage. At t $= 7$ ms, the contact line radius reaches its maximum and (i) the drop spreading phase ends. Then, (ii) the drop receding phase begins and the contact line moves inwards until t $= 25$ ms. From this moment on, the drop reaches a state at which the drop footprint stays approximately constant, corresponding to (iii) the sessile drop evaporation phase. A qualitatively similar evolution of the contact line radius and heat flux distribution have been observed over the entire parameter range.

Influence of Wall Superheat

The experimental results and numerical predictions of the contact line radius, R$_{\text {cl}}$, and the heat flow, $\dot{Q}$, for different wall superheats ranging from 6.9 to 17.2 K are shown in Fig. 6a and b, respectively. As depicted in Fig. 6a, increasing wall superheat leads to a decrease in maximum contact line radius and the duration of spreading and receding phases. This can be explained by the higher evaporation rate in proximity of the three-phase contact line and concomitant higher apparent contact angle [18]. Increasing the wall superheat leads to stronger oscillations before the beginning of the sessile drop evaporation phase. In addition, the drop footprint radius at the sessile drop evaporation phase decreases with increasing of the superheat. The experimental findings have been compared with numerical predictions showing a good agreement [8]. The heat transfer increases with increasing wall superheat, but the dependence is weaker than linear. The deviation between the measured and numerically predicted heat flow can be attributed to the limited spatial resolution of the IR camera.

Fig. 6

Temporal evolution of the a contact line radius and b heat flow during the impact of a single drop onto a bare heater for various wall superheats (Re $= 1450$, We $= 34$, D$_0 = 0.93$ mm, u$_0= 0.44$ m s$^{-1}$, and p $= 0.9$ bar) [8]

Influence of Drop Impact Velocity

Figures 7a and b show the experimental and numerical results on the contact line radius and heat flow for the impact velocities range from 0.33 to 0.57 m s$^{-1}$.

Fig. 7

Temporal evolution of the a contact line radius and b heat flow during the impact of a single drop onto a bare heater for various impact velocities ($1073\le$ Re $\le 1905$, $20\le$ We $\le 59$, D$_0 = 0.93$ mm, $\Delta T= 6.3$ K, and p $= 0.9$ bar) [8]

The higher impact velocities and accordingly spreading velocities lead to the shorter duration of the spreading phase and the larger maximum contact line radius. The maximal contact line radius determined from these experimental data scales as $R_{\text {cl,max}} \propto u_{0}^{0.208}$. This is in good agreement with the scaling $R_{\text {cl,max}} \propto u_{0}^{0.2}$ based on the balance between the initial kinetic energy and the viscous dissipation for isothermal impacts [12].

Increasing impact velocity leads to prolongation of the receding phase. The final radius of the sessile drop reached at the beginning of the sessile drop evaporation phase does not depend on the impact velocity. The shape of the sessile drop is determined by the balance between the surface tension and gravity (depending on the Bond number) for the given drop volume and static contact angle.

During the spreading phase, the heat flow reaches its maximum earlier with increasing the impact velocity. Heat flow increases with the impact velocity during both spreading and receding phases. However, the maximum of heat flow appears at a higher dimensionless time [8]. At the sessile drop evaporation phase, the heat flow, as well as the drop shape, is independent of the impact velocity. Experimental and simulation data are in good qualitative and quantitative agreement [8].

Influence of Drop Size

The experimental and numerical data on the contact line radius and heat flow during the impact of liquid drops with sizes ranging from 0.97 to 1.60 mm are depicted in Fig. 8a and b, respectively. In these experiments, the spatial resolution of the IR camera is set to 40.82 $\upmu$m/pixel. This leads to lower measurement accuracy and a larger deviation between experimental and simulated curves.

Fig. 8

Temporal evolution of the a contact line radius and b heat flow during the impact of a single drop onto a bare heater for various impact diameters ($1520\le$ Re $\le 2500$, $37\le$ We $\le 61$, u$_0= 0.44$ m s$^{-1}$, $\Delta T= 6.9$ K, and p $= 0.9$ bar) [8]

Fig. 9

Temporal evolution of the a contact line radius and b heat flow during the impact of a single drop onto a bare heater for various system pressures ($1220\le$ Re $\le 1530$, $23\le$ We $\le 53$, D$_0= 0.94$ mm, u$_0= 0.34$ m s$^{-1}$, and $\Delta T= 6.5$ K)

It can be seen in Fig. 8a that the impact of larger drops is accompanied by the prolongation of both drop spreading and receding phases. Additionally, the maximum spreading radius strongly increases with the increase of the drop diameter. The heat flow during all phases increases with the increase of drop diameter, one of the reasons being the increased wetted area (see Fig. 8b).

Influence of System Pressure

Figure 9a, and b present the temporal evolution of the contact line radius and heat flow during drop impact at reduced pressures (ratios of system pressure and critical pressure) ranging from 0.05 to 0.5, respectively. As depicted in Fig. 9a, the maximum of the contact line radius is similar for all four pressures. However, the duration of the spreading and particularly receding phases is increased at elevated pressures. This is attributed to the slight decrease of kinetic energy due to the lower liquid density and a significant decrease of surface tension caused by an increase in cell pressure. The drop footprint during the sessile drop evaporation phase decreases with increasing pressure. This is due to the decrease in latent heat of vaporization, which leads to a higher evaporation rate in proximity of the three-phase contact line and a higher apparent contact angle. The observed behavior agrees qualitatively with the numerical results of Schlawitschek [24].

The maximum heat flow decreases with increasing pressure, which can be attributed to the decreasing thermal effusivity of the liquid. The heat flow during the sessile drop evaporation phase also decreases with increasing pressure (see Fig. 9b). This can be explained by a decrease in latent heat of vaporization at elevated pressures, which is supported by the results of the single capillary slot experiment.

Influence of Surface Structure

This section is devoted to the influence of a porous coating on hydrodynamics and heat transport during a single drop impact onto a heated surface. To generate a porous coating, the heater substrate is covered with a nanofiber mat with a thickness of 22 $\upmu$m consisting of randomly oriented nanofibers generated through electrospinning of 5 wt$\%$ polyacrylonitrile solution (PAN; M$_{\text {w}} = 150$ kDa) in N,N-dimethylformamide (DMF). The mat thickness was measured using confocal microscopy.

Fig. 10

Heat flux fields for a duration of 17 ms after the impact of a drop onto a bare (top) and nanofiber-coated (bottom) heater (Re $= 1500$, We $= 37$, D$_0 = 0.95$ mm, u$_0= 0.45$ m s$^{-1}$, and $\Delta T= 14.6$ K)

An exemplary temporal evolution of heat flux distribution evaluated from the IR images in the presence and absence of nanofiber mat is presented in Fig. 10. Similar to the bare surfaces, inertia force leads to drop spreading over the nanofiber-coated surface at the early stages of impact. However, the spreading velocity is slower compared to the uncovered substrate. In addition, the heat flux during the spreading phase is significantly lower for the coated surface compared to the bare surface. After the maximal spreading radius is reached, the contact line remains pinned. The receding phase is suppressed. Moreover, spots of high heat flux appear at the periphery of the wetted region.

The presence of a nanofiber mat prevents direct contact between the liquid and the heater surface at the early stages of impact. The cold liquid impacts first onto the top surface of the hot nanofiber mat and is decelerated. The vapor entrapped inside the pores in between the Cr surface and the bulk liquid plays the role of heat-insulating layer. This phenomenon, which is referred to as the “skeletal” Leidenfrost effect, weakens the heat flux tremendously [27]. The drop cools down the nanofibers first, and heat is removed from the heater mainly through the nanofiber skeleton. At this stage, the heat transport is determined by the thermal conductivity of the nanofibers, which is $0.02{-}0.05$ W m$^{-1}$ K$^{-1}$ [23].

Fig. 11

Temporal evolution of the a contact line radius and b heat flow during the impact of a single drop onto a bare and a nanofiber-coated heater (D$_0 = 0.95$ mm, p $= 0.9$ bar, h$_{\text {mat}}= 22$ $\upmu$m, for scenario (I): Re $= 1920$, We $= 60$, u$_0= 0.58$ m s$^{-1}$ and $\Delta T= 9.6$ K; for scenario (II): Re $= 1500$, We $= 37$, u$_0= 0.45$ m s$^{-1}$, and $\Delta T= 7.0$ K)

After several milliseconds, two scenarios might occur depending on wall superheat and impact velocity. Scenario (I): the liquid drop penetrates entirely through the pores of the nanofiber mat and reaches the solid heater surface. This phenomenon takes place at low wall superheats and high impact velocities and leads to the appearance of multiple regions of high heat flux. Scenario (II): the vapor entrapped inside the pores seems to prevent direct contact of the liquid with the substrate. In this scenario, the low kinetic energy of the impacting drop prevents the liquid drop from displacing the generated vapor inside the pores of the nanofiber mat radially outwards. Therefore, the heat flux around the center of the impact location stays at a low level.

Figure 11a and b compare the contact line radius and heat flow between scenarios (I) and (II) during drop impact onto a heater covered with nanofiber mat. For better comparability of the results, the data for drop impact onto a bare heater at the same impact parameters and wall superheats are plotted in the same figures.

If the heater is covered with a nanofiber mat, the drop evolution, regardless of the scenario, starts from an initial inertia-driven drop spreading, which is in both cases slower than for the bare substrates. Furthermore, the surface tension-driven receding phase observed for the drops on bare substrates is suppressed for both scenario (I) and scenario (II). The drop evolution in scenario (I) is characterized by a faster initial spreading and by a slow decreasing of the footprint radius after reaching the maximal spreading, which can be attributed to the effect of evaporation. Scenario (II) is characterized by a slower initial spreading velocity. At t $= 14$ ms, the spreading velocity decreases considerably. It is suggested that imbibition is responsible for the second spreading phase, which is not completed after 250 ms. The dynamics of second spreading phase is strongly affected by the wettability of the fibers. Initially (during the spreading and a large part of the receding phase for the drops on a bare substrate) the total heat flow on the bare substrate is significantly higher than on the coated substrate. However, starting from the time instant about 25 ms after the impact (sessile drop evaporation phase for drops on a bare substrate) the heat flow on a coated substrate is higher than that on a bare substrate. This can be attributed to the larger footprint of the drop. In scenario (I), the heat flow transported from the heated wall in this phase is very high. We assume that this is explained by the intensive evaporation of liquid at multiple liquid-solid contact spots appearing after the penetration of liquid through the mat. The fast evaporation at this phase leads to the observed slight shrinkage of the drop footprint.

3.2.2 Multiple Drop Impact Experiment

The present section addresses the cumulative effect of the impact of multiple drops onto a heated wall. With this objective, the hydrodynamic and heat transport behavior during vertical and horizontal coalescence of multiple drops on a heated surface is presented.

Vertical Coalescence

Figure 12 shows the side view of the drop recorded by the B/W camera and the temporal evolution of the heat flux distribution obtained by post-processing of the IR images. The behavior of the drop shape and heat flux for the first drop follows the trend presented in Sect. 3.2.1. At t $= 102$ ms, the second drop impacts vertically onto the first drop. It is clearly seen on the side view images that, similar to the findings reported in literature [5, 17], the impact of the second drop is followed by swelling up of the bottom part of this drop (t $= 102$ ms), by formation of a crown (t $= 103$ ms) and by increasing of the footprint of the combined drop (from t $= 103$ ms to t $=120$ ms). The heat flux within the drop footprint rises shortly after the impact of the second drop (t $= 103$ ms). However, the level of maximal heat flux measured after the impact of the first drop (t $= 4$ ms) is not reached. This is caused by the pre-cooling of the substrate by the first drop and by the fact that the direct contact between the liquid drop and the substrate is prevented due to the presence of the liquid layer on the substrate. At the time instants t $= 105$ ms and t $= 106$ ms two ring-shaped regions of high heat fluxes can be observed: the radius of the first region is close to the contact radius of the first drop prior to the second impact; the second region is at the contact line of the combined drop.

Fig. 12

B/W images and heat flux fields for vertical coalescence of two successive drops impinging onto a bare heater (Re $= 2160$, We $= 64$, D$_0 = 1.14$ mm, u$_0= 0.54$ m s$^{-1}$, $\Delta T= 7.6$ K, p $= 0.9$ bar, and f $= 10$ Hz [7]

As presented in Chapter “Numerical Simulation of Heat Transfer and Evaporation During Impingement of Drops onto a Heated Wall”, the formation of the inner ring with high heat flux can be explained by the locally low thickness of the liquid film, which corresponds to the low local thermal resistance of the liquid layer. Moreover, a high local flow velocity in this region is observed, which leads to extensive mixing of the liquid. The spreading phase is followed by the receding phase (starting at t $= 120$ ms), in which the contact line radius decreases. Finally, the sessile drop evaporation phase is reached. The footprint area of the combined drop at this stage is larger than that after the impact of the first drop, which is explained by a bigger volume contained in the combined drop.

Figure 13a and b illustrate the contact line radius and heat flow following the impacts of four successive drops with the frequency of 10 Hz, respectively. The contact line radius and the heat flow are shown as functions of time elapsed after the last impact event. As depicted in Fig. 13a, the duration of the spreading phase, and particularly, the receding phase, increases after each impact. Additionally, the maximum contact line radius rises after the second and the third impacts. This behavior, which is in qualitative agreement with the findings of Guggilla et al. [9], can be explained by the larger mass of the liquid wetting the substrate. The relative increase of the maximum spreading radius is less significant after the third impact, and the maximum spreading radius after the fourth impact stays the same as after the third one. At the end of the receding phase following each impact, oscillations of contact radius and heat flow are observed, whereas the oscillation frequency increases and its amplitude decreases with the increasing sequential number of drop.

Despite a lower maximal heat flux during the spreading phase initiated by the second impact, the maximum heat flow increases with increasing of the drop sequential number (see Fig. 13b). This is associated with the larger footprint of the drop (see Fig. 13a), which effect is more significant than a decrease of the heat flux. A weak increase in the maximum heat flow is observed after the third impact. The maximum heat flow after the fourth impact is nearly the same as after the third impact, in agreement with the trend of maximum spreading radius. The oscillations in the heat flow before the onset of the sessile drop evaporation phase are caused by the oscillations of the contact line radius.

Fig. 13

Temporal evolution of the a contact line radius and b heat flow during the vertical coalescence of four successive drops impinging onto a bare heater (Re $= 2160$, We $= 64$, D$_0 = 1.14$ mm, u$_0= 0.54$ m s$^{-1}$, $\Delta T= 12.4$ K, p $= 0.9$ bar, and f $= 10$ Hz) [7]

Horizontal Coalescence

Figure 14 shows the side view of the drop recorded with the high-speed B/W camera and heat flux distribution, which was determined by postprocessing of the IR images, at different time instants after the nearly simultaneous impact of two drops. In this experiment, the difference in impact time between two drops is about 1 ms, which corresponds to the time resolution of the camera recordings. The wall superheat and the spacing parameter, e, which is the ratio of the distance between the impact locations to the drop diameter, are set to 7.3 K and 2.15, respectively. Similar to single drop impact, high local and overall heat fluxes are transferred to the liquid in the first few milliseconds when both drops spread over the heated surface.

At the time interval between 2 and 3 ms after the beginning of recording, the rims of both drops come into contact, and the coalescence of the drops starts. A stagnation flow is formed at the position where two spreading fronts meet. As a result, the liquid flow is redirected sidewards and upwards, which leads to the emergence of a bump between the drops (t $= 3$ ms). A similar phenomena has been observed in [1, 19, 20]. The wetted area and the heat flux distribution far from the region where the droplet coalescence takes place are not influenced by the interaction between the drops. Similar to the single drop impact, a region with high heat fluxes in proximity of the three-phase contact line of the combined drop can be examined. The spreading process of the combined drop ends due to the dissipation of kinetic energy (t $= 8$ ms). The combined drop then starts to shrink, driven by the surface tension force. From this time on, low heat flux at the liquid–solid interface is observed everywhere, apart from the apparent three-phase contact line. After some time (t $= 60$ ms), the combined drop reaches the equilibrium state, forming a single sessile drop.

Fig. 14

B/W images and heat flux fields during the horizontal coalescence of two drops over a bare heater (Re $= 1750$, We $= 50$, D$_0 = 0.93$ mm, u$_0= 0.53$ m s$^{-1}$, $\Delta T= 7.3$ K, p $= 0.9$ bar, and e $= 2.15$) [6]

Figure 15a and b present the the heat flow and cumulative heat transport as functions of time during the nearly simultaneous impact of two drops onto a heated surface for different spacing parameters. The impact with spacing parameters of 1.18 and 2.15 result in horizontal drop coalescence over the heater substrate. The spacing parameter of $\infty$ stands for the impact of two drops that are so far from each other that no interactions takes place between them. The corresponding heat flow is equivalent to twice the heat flow of a single drop impact. The experimental results show that the heat flow is not affected by the presence of a neighbouring drop as long as the the wetted regions corresponding to these drops stay separated from each other. Once the drops start to coalesce, the heat flow during the spreading and receding phases of e $= 2.15$ is relatively similar to the case of two independent drops (e $\rightarrow \infty$). However, for the case e $= 1.18$ the heat flow during the spreading phase (including the maximal heat flow) is lower, and during the receding phase, is higher than for e $\rightarrow \infty$ and e $= 2.15$. These results are in good agreement with the numerical simulations presented in [1].

Fig. 15

Temporal evolution of the a heat flow and b cumulative heat flow during simultaneous impact of two drops onto a bare heater for various spacing parameters; e $\rightarrow \infty$ represents the non-coalescence case (Rec $= 1750$, We $= 50$, D$_0 = 0.93$ mm, u$_0= 0.53$ m s$^{-1}$, $\Delta T= 7.3$ K, and p $= 0.9$ bar) [6]

At the late stages of the impact in which a single sessile drop is formed, the heat flow through the liquid–solid interface transferred to the combined drop is independent of the spacing parameter and is lower compared to the case of two independent drops. This observation is attributed to the smaller cumulative liquid–solid contact area and shorter cumulative length of the three-phase contact line of the combined sessile drop compared to two sessile drops with the same cumulative volume.

4 Conclusions

This study is devoted to experimental investigations on fluid dynamics and heat transport during the impact of a single drop and multiple drops onto a heated surface. In addition, transport phenomena associated with a single evaporating contact line under well-controlled conditions have been studied in a dedicated experimental environment. In the scope of this work, the influences of wall superheat, contact line velocity and its direction, system pressure, fluid composition, and surface structure on fluid dynamics and heat transport during moving contact line and drop impact were investigated.

The experimental results of single drop impact revealed that increasing the wall superheat, impact velocity, and drop diameter, as well as decreasing system pressure, results in increased heat flow to the drop after the impingement. The maximum spreading radius after impingement increases with the increase of impact velocity and impact diameter and decreases with the increase of wall superheat and system pressure. The experimental results at atmospheric pressure were compared against the available numerical model developed in [11, 21]. A good agreement between measurements and model predictions was observed. In addition, the impact of a drop onto a surface with a porous coating is accompanied by lower heat flow at the early stages of impact, while it leads to enhancement of the heat flow at the late stages of impact. The heat flow enhancement is due to the large solid–liquid contact area caused by the drop pinning effect. A significant heat transfer enhancement has been observed for the scenario in which the kinetic energy of the drop was sufficient to completely penetrate through the coating.

The last part of this study focuses on the impingement of multiple drops onto a moderately heated wall as an important step towards understanding the mechanisms of spray cooling. Hydrodynamics and heat transport behavior during vertical and horizontal coalescence of multiple drops over a heated surface are addressed. The investigations revealed that the solid–liquid contact area, and, accordingly, heat flow, rise after successive impacts. Horizontal drop coalescence leads to lower heat flow in comparison to non-coalescence cases, especially during the sessile drop evaporation phase.