Numerical Simulation of Heat Transfer and Evaporation During Impingement of Drops onto a Heated Wall

Abstract

In this study, hydrodynamics and heat transport during the impact of single and multiple drops onto a hot wall are studied numerically. The heat transfer in the vicinity of the three-phase contact line, where solid, liquid and vapour meet, contributes significantly to the global heat transfer. The microscale processes in the region of the three-phase contact line are analysed using a lubrication approximation. The results in the form of correlations are integrated into an overall model. The impingement of drops on a macro scale is simulated using a numerical model developed within the OpenFOAM library. The influence of dimensionless parameters, i.e., the Reynolds, Weber, Bond, Prandtl and Jakob numbers, as well as the influence of pressure, on the transport phenomena is discussed. The analysis of the influence of drop frequency and substrate thickness during the vertical coalescence and the influence of the drop spacing during the horizontal coalescence of drops on the hot surface complete the study. The results contribute to a better understanding of the complex mechanisms of spray cooling.

1 Introduction

Spray cooling is a very promising technology for the cooling of electronic devices. The hydrodynamic and heat transport processes that occur during the impact of a spray onto a hot wall are very complex. The first step towards an understanding of spray cooling mechanisms is the investigation of single and multiple drops impacting onto hot walls. The impact of single and multiple drops onto hot walls is also relevant to numerous additional industrial applications, such as falling-film evaporators, drop impingement onto steam turbine blades, metal quenching and direct-fuel injection [17, 18].

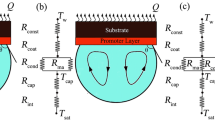
If a drop impacts onto a superheated wall, strong temperature gradients and extremely high local heat fluxes occur in the vicinity of the three-phase contact line, where solid, liquid and vapour meet. The hydrodynamics and heat transport at the macroscopic scale are influenced by the transport processes in the vicinity of the three-phase contact line. To understand the complex mechanisms during the drop impact, it is necessary to analyse the processes occurring at both the micro and the macro scales (see Fig. 1).

Fig. 1

Different length scales of relevant hydrodynamic and heat transport processes during the impact of a spray onto a superheated wall

Comprehensive reviews of current experimental, numerical and analytical studies on the impact of a single drop onto non-heated walls are presented in [14, 19, 21, 23, 27]. Depending on the impact parameters, material properties and surface roughness, six characteristic impingement scenarios have been identified: drop deposition, prompt splash, corona splash, receding breakup, and partial and full rebound. If the wall is heated above the saturation temperature, the outcome additionally depends strongly on the wall superheat. Liang and Mudawar [17] identified four distinct scenarios: film evaporation, nucleate boiling, transition boiling and film boiling. Additionally, Breitenbach et al. [4] identified the thermal atomization regime. The focus of the present work is on the drop impingement at moderate Reynolds, Weber and Jakob numbers in the drop deposition and film evaporation regimes. Evaporation into a pure vapour atmosphere is considered.

In this study, numerical simulations are used to study the impact of single and multiple drops onto a hot wall with special consideration of the processes in the vicinity of the three-phase contact line (micro region). The hydrodynamic and heat transport processes in the micro region are analysed by means of a one-dimensional lubrication model and direct numerical simulations. On the macro scale, hydrodynamics and heat transfer during the drop impact over a wide range of dimensionless parameters are studied. Both a compressible and an incompressible solver are used to study the drop impact at different pressures. Furthermore, the influence of substrate thickness and drop frequency during the vertical coalescence of multiple successive impacting drops is analysed. Lastly, the horizontal coalescence of two simultaneously impacting drops is studied. The numerical results are compared with experimental results (see Gholijani et al. in this volume).

2 Overview of the Numerical Model

The impact phenomena considered in this study take place on a millimetre scale. The transport processes in the micro region are determined on a submicrometre scale. This scale difference necessitates a modular modelling approach, in which the micro region phenomena are considered separately, and the results are incorporated into the macroscale model (see Fig. 1) in the form of correlations. A lubrication approximation is used to simulate the micro region, and computational fluid dynamics simulations are used for the overall macroscale model. Additionally, a full-scale numerical simulation of the micro region has been used to determine the validity limits of the lubrication approximation for the micro region description. Beyond the applicability limits of the lubrication approximation, the full-scale numerical simulation can be used for the description of transport processes in the micro region.

Most simulations presented here use the refrigerant perfluorohexane (FC-72) at saturation conditions as a working fluid. The drop impinges onto a superheated calcium fluoride glass ($\textrm{CaF}_2$), allowing the simulation results to be directly linked and compared with associated experimental results (see Gholijani et al. in this volume).

3 Modelling of the Micro Region

In this section, the micro region model in the framework of one-dimensional lubrication theory is briefly described and results using this model are presented. The influence of governing parameters on the output of the micro region model is analysed. Furthermore, a direct full-scale numerical simulation of the micro region is performed.

3.1 One-Dimensional Lubrication Model

Potash and Wayner [20] assumed in their concept of the contact line in an evaporating perfectly wetting liquid that a thin adsorbed film of fluid molecules covers the apparently dry wall (see Fig. 1). They suggested that the heat and mass flow at the apparent contact line are determined by the film thickness distribution in a micro region, or the region between the adsorbed film with thickness $\delta _\textrm{ad}$ and the macroscopic meniscus. Stephan and Busse [26] have used the micro region approach to predict the evaporation rate from a groove at the heat pipe evaporator. Herbert et al. [12] and Schlawitschek [24] extended this model to account for the contact line velocity within a moving reference frame, the effect of recoil pressure, and the Kapitza resistance (a thermal resistance at the solid–liquid interface). A detailed and comprehensive description as well as the discussion of the assumptions made during the derivation of this model can be found in [1, 24]. Steady-state, incompressible Navier-Stokes equations and the energy conservation equation are used to model the micro region. By using the one-dimensional lubrication approximation, a system of four coupled first order ordinary, non-linear differential equations can be derived.

Fig. 2

Influence of the contact line velocity $u_\textrm{cl}$ and wall superheat $\Delta T$ on the apparent contact angle $\theta$ (left) and integrated heat flux $\dot{Q}_\textrm{mic}$ (right). The Kapitza resistance is neglected in this study [1]

Thermal resistances at the solid–liquid interface ($R_\textrm{Kap}$), within the liquid ($R_\textrm{liq}$) and at the liquid–vapour interface ($R_\textrm{int}$) are taken into account. Furthermore, the effect of the augmented capillary pressure, which includes the vapour recoil and the disjoining pressure, is included. The model allows for the computation of the apparent contact angle $\theta$, the film thickness distribution, and the integrated heat flux $\dot{Q}_\textrm{mic}$ as functions of the wall superheat, $\Delta T = T_\textrm{w,mic} - T_\textrm{sat}$, and the contact line velocity $u_\textrm{cl}$. The model is restricted to perfectly wetting fluids and small contact angles.

3.2 Influence of Contact Line Velocity and Local Wall Superheat

The integrated heat flux and the apparent contact angle predicted by the one-dimensional lubrication model of the micro region are depicted in Fig. 2 as functions of contact line speed and local wall superheat. The apparent contact angle increases with increasing wall superheat. This can be explained by the increasing evaporation rate, which is balanced by the enhanced liquid flow from the macroscopic meniscus. The enhanced flow is possible due to the higher film thickness gradients. The numerical predictions agree well with the experimentally observed static contact angle of less than $3^\circ$ under isothermal conditions and about $35^\circ$ for a wall superheat of $\Delta T = {10\,\textrm{K}}$ [12]. The increasing wall superheat also leads to an increase in integrated heat flux. The apparent contact angle increases with the contact line speed. This can be explained by the fact that, in the reference frame fixed at the advancing contact line, the moving wall transports liquid out of the micro region. The pressure difference between the macroscopic meniscus and the adsorbed layer is fixed by the wall superheat. As a result, the required liquid flow rate from the macroscopic meniscus is reached by an increase in the cross-sectional area. The concomitant increase in film thickness and of the thermal resistance of the liquid layer leads to a decrease in integrated heat flux.

3.3 Influence of Material Properties and Pressure

It can be observed in Fig. 3 that the contact angle and integrated heat flux in the micro region are very sensitive to changes in material properties. Material properties might change with changing pressure or by using a different fluid. The variation of liquid viscosity $\nu _\textrm{l}$ and thermal conductivity $k_\textrm{l}$ by an order of magnitude or more has a strong influence both on the apparent contact angle and integrated heat flux. However, this is only relevant if a different fluid is chosen, since these properties only moderately depend on pressure. In contrast, the saturated vapour density $\rho _\textrm{v}$, surface tension $\sigma$ and latent heat of vaporisation $\Delta h_\textrm{v}$ strongly depend on the ambient pressure and have a strong influence on the apparent contact angle as well as the integrated heat flux. Furthermore, the figure illustrates that small changes in material properties resulting from possible measurement uncertainties have a weak influence on the apparent contact angle and integrated heat flux.

Fig. 3

Sensitivity of the apparent contact angle $\theta$ (left) and integrated heat flux $\dot{Q}_\textrm{mic}$ (right) in dependency of the material properties $\phi$, exemplary for a static contact line and a wall superheat of $\Delta T = {5\,\textrm{K}}$. Solid lines indicate a variation within the available data range in the literature; dashed lines indicate additional variations [24]

The influence of the ambient pressure on the apparent contact angle and integrated heat flux is shown in Fig. 4 and can be attributed to the change in the material properties. For static and receding contact lines, the apparent contact angle increases with pressure. For advancing contact lines, a local minimum of the apparent contact angle at approximately ${1\,\textrm{bar}}$ is predicted. One of the significant factors affecting the increasing contact angle with pressure is the decreasing surface tension. The integrated heat flux depends on pressure non-monotonically. This behaviour is determined by a combined effect of simultaneously changing different material properties. In particular, the integrated heat flux decreases with increasing thermal resistance, which is a combination of the resistance at the liquid–vapour interface, the resistance of the liquid layer and the Kapitza resistance. The influence of pressure on the total average thermal resistance as well as on its components is illustrated in Fig. 5. For low pressures the thermal resistance at the liquid–vapour interface dominates, and at high pressures the thermal resistance within the liquid dominates. The Kapitza resistance has been calculated by Han et al. [10] for the combination of FC-72 and chromium using molecular dynamics simulations. It has been found that the Kapitza resistance is independent of pressure in the relevant range and is small compared to the total resistance over the entire pressure range. The total thermal resistance reaches a minimum in the pressure range corresponding to the maximum integrated heat flux.

Fig. 4

Influence of the pressure p on the apparent contact angle $\theta$ (left) and integrated heat flux $\dot{Q}_\textrm{mic}$ (right) for a receding, static and advancing contact line [24]

Fig. 5

Different thermal resistances of the micro region averaged over the length of the micro region for different pressures, exemplary for a static contact line and a wall superheat of $\Delta T = {5\,\textrm{K}}$ [24]

3.4 Full-Scale Numerical Simulation of the Transport Processes in the Micro Region

Stationary, incompressible, three-dimensional Navier-Stokes equations and the energy balance equation are solved numerically using the OpenFOAM library. The momentum balance contains terms accounting for adhesion forces. Gravity is neglected. In contrast to the one-dimensional lubrication model, the full scale numerical model is valid for apparent contact angles up to $90^\circ$. For larger apparent contact angles, the computational domain and the boundary conditions would have to be changed. A complete description of the numerical model can be found in [1, 3].

In [3], results of the direct numerical simulation are analysed and compared with results from the one-dimensional lubrication model. A parabolic velocity profile and a nearly linear temperature profile within the micro region for moderate wall superheats is shown in the results of the direct numerical simulation. The calculated apparent contact angle and integrated heat flux agree well with the results from the one-dimensional lubrication model up to the apparent contact angle of $40^\circ$. However, the direct numerical simulation predicts slightly higher heat flux values than the one-dimensional lubrication model, especially at high wall superheats. It has been shown that the deviation between the results of the full-scale numerical simulations and the lubrication model are mainly attributed to the assumption of one-dimensional heat conduction.

The errors in the evaluation of integrated heat flux are acceptable for moderate apparent contact angles, and the use of the lubrication approximation is justified, taking into account the significant reduction of computational efforts in comparison with the full-scale numerical simulation.

In addition, the full-scale numerical simulation has been used to study the micro region evaporation on a nanostructured wall consisting of periodically arranged cubes with a side length of ${5\,\textrm{nm}}$. This side length is comparable to the adsorbed film thickness. A part of the evaporating film near the curvilinear non-evaporating adsorbed film is shown in Fig. 6. In [3], it is shown that the apparent contact angle is slightly smaller for the structured wall than for the smooth wall. However, almost no change in the integrated heat flow is observed. Hence, for a static contact line, the structure of the wall can be neglected, as long as the length scale of the structure is on the order of the adsorbed film layer or smaller. More details on the investigation of the micro region using the full-scale numerical simulations can be found in [1, 3].

Fig. 6

Reprinted from [3] with permission from ASME

Streamlines and temperature profile in the micro region close to the adsorbed film layer for a static contact line and a wall superheat of $\Delta T = {5\,\textrm{K}}$ on a nanostructured wall.

4 Macroscale Model

In this section, a macroscale model for simulation of a single drop impact onto a smooth, hot wall is presented. The numerical model developed within the OpenFOAM library is based on the interFoam solver. Hydrodynamics and heat transport phenomena are described, and the influence of dimensionless parameters and of system pressure on transport processes is analysed. Second, the macroscale model is applied to study the impact of multiple drops and their coalescence on a smooth, hot wall. Illustrative videos for different drop impact scenarios can be found in [25].

4.1 Model Description

The numerical model is based on the works of Kunkelmann [15] and Batzdorf [1]. Batzdorf [1] has applied the model to the description of the drop impact onto a smooth, hot wall. For a complete, comprehensive overview of the solver for incompressible flow, the reader is referred to [1]. More information on the solver for compressible flow developed by Schlawitschek [24] is given in Sect. 4.2.3.

It is shown in associated experiments in [6, 7] that no three-dimensional effects (like splash) are observed for the investigated parameter range. Hence, a static, structured 2D axis-symmetric grid with local grid refinement at the solid-fluid interface is chosen. Only for the case of the horizontal coalescence (Sect. 4.3.2), a dynamically refined 3D grid is chosen. In Fig. 7 the computational domain and the boundary conditions are illustrated.

Fig. 7

Computational domain and boundary conditions for the 2D axis-symmetric grid. The opening angle of the wedge is $5^\circ$. A thermal boundary layer in the vapour region close to the wall is initialised prior to the simulation. Dimensions of the domain are chosen such that boundary conditions do not influence the drop impingement process [1]

The governing equations in the fluid region describe the conservation of mass, momentum and energy. Source terms ($\Sigma _\textrm{V}$, $\Sigma _\textrm{e}$) are added to the mass and energy equations to account for heat and mass transfer at the interface. Gravitational and surface tension forces ($\rho \boldsymbol{g}$, $\boldsymbol{f_\sigma }$) are included in the momentum equation. The system of transport equations has the form:

$$\begin{aligned} \nabla \cdot \boldsymbol{u} = \Sigma _\textrm{V} \end{aligned}$$

(1)

$$\begin{aligned} \rho \left[ \frac{\partial {\boldsymbol{u}}}{\partial t} + \left( \boldsymbol{u} \cdot \nabla \right) \boldsymbol{u} \right] = \nabla \cdot \left[ - p - \frac{2}{3} \upmu \left( \nabla \cdot \boldsymbol{u} \right) \boldsymbol{\textrm{I}} + \mu \left( \nabla \boldsymbol{u} + \left( \nabla \boldsymbol{u} \right) ^\textsf{T} \right) \right] + \rho \boldsymbol{g} + \boldsymbol{f}_\mathrm {\sigma } \end{aligned}$$

(2)

$$\begin{aligned} \frac{\partial \left( \rho c T \right) }{\partial t} + \nabla \cdot \left( \rho c \boldsymbol{u} T \right) = \nabla \cdot \left( k \nabla T \right) + \Sigma _\textrm{e} \end{aligned}$$

(3)

In the solid region, only the energy conservation equation is solved:

$$\begin{aligned} \frac{\partial \left( \rho c T \right) }{\partial t} = \nabla \cdot \left( k \nabla T \right) \end{aligned}$$

(4)

An explicit Dirichlet-Neumann algorithm is used to couple the solid and fluid regions. The volume-of-fluid method is used to track the interface. An additional compressive term counteracting the numerical diffusion is included in the transport equation for the volume fraction field F:

$$\begin{aligned} \frac{\partial F}{\partial t} + \nabla \cdot \left( \boldsymbol{u} F \right) + \nabla \cdot \left[ c_\textrm{F} |\boldsymbol{u}| |\boldsymbol{n}_\textrm{int}| \left( 1 - F \right) F \right] = \Sigma _\textrm{v} F \end{aligned}$$

(5)

By considering the iso-surface of $F = 0.5$, the interface is reconstructed continuously. The evaporation model was developed by Kunkelmann and Stephan [16] and further developed by Herbert et al. [12]. At the interface, the saturation temperature is assumed to hold for both liquid and vapour. Temperature gradients normal to the interface are used to calculate the heat fluxes. The method developed by Hardt and Wondra [11] is used to enhance numerical stability. The results of the one-dimensional lubrication model of the micro region introduced in Sect. 3.1 are incorporated into the macroscale simulation using parametrised regressions to accurately calculate the contact angle $\theta$, integrated heat flux $\dot{Q}_\textrm{mic}$ and film thickness $\delta$ in dependency of wall superheat $\Delta T$ and contact line velocity $u_\textrm{cl}$ in the range of ${5\,\textrm{K}} \le \Delta T \le {20\,\textrm{K}}$ and ${-0.1\,\mathrm{m s^{-1}}} \le u_\textrm{cl} \le {2\,\mathrm{m s^{-1}}}$, respectively.

4.2 Single Drop Impact

A detailed description and validation of the model describing the single drop impact onto a smooth, hot wall at ambient pressure, including the mesh independence study, is given in [1].

4.2.1 Basic Hydrodynamic and Heat Transport Phenomena

The numerical prediction of the evolution of spreading radius $R_\textrm{cl}$ and of solid-drop heat flow $\dot{Q}$, which is validated by comparison with experimental data, is shown in Fig. 8. Details of the experimental setup and procedure can be found in [5, 12]. The impingement process can be divided into three phases: spreading phase (I), receding phase (II) and sessile drop phase (III). The kinetic energy of the impacting drop leads to quick spreading on the surface. Kinetic energy is then partly converted into surface energy and partly dissipated. After reaching the maximum contact line radius, surface tension forces the drop to recede, and the kinetic energy rises again. After the receding phase, the drop oscillates around its stationary state with decreasing amplitude.

During the spreading phase, the heat flow is dominated by convection due to high spreading velocities. The maximum heat flow is reached before the maximum contact line radius due to decreasing spreading velocities. The role of evaporation increases during the receding phase. Especially at low velocities, the evaporation at the three-phase contact line can contribute up to 50% of the overall heat transfer [12].

Fig. 8

Contact line radius $R_\textrm{cl}$ (left) and heat flow $\dot{Q}$ (right) over time for the impact of a single drop ($D_0 = {0.977\,\textrm{mm}}$, $u_0 = {0.584\,\mathrm{m s^{-1}}}$) onto a smooth, hot wall ($\Delta T = {17.4\,\textrm{K}}$, $\dot{q}_\textrm{heater} = {9500\,\mathrm{W m^{-2}}}$). The total heat flow describes the heat transferred from the wall to the drop, the evaporation heat flow describes the heat transfer by evaporation, and the contact line heat flow describes the heat transfer in the vicinity of the three-phase contact line [1]

Fig. 9

Exemplary heat transfer paths during the a spreading phase and b receding phase. The thickness of the paths shows the proportion of the heat transferred. The corresponding isotherms with a spacing of $\Delta T = {2\,\textrm{K}}$ and streamlines are shown in a moving reference frame close to the contact line [1]

The role of heat transfer mechanisms during the spreading and receding phases is illustrated in Fig. 9. During the spreading phase, the vortex in the vicinity of the apparent contact line transports the cold liquid towards the wall. This enhances the convective heat transport. During the receding phase, the vortex changes its direction and transports hot liquid from the wall to the liquid–vapour interface. This effect leads to a decrease in the convective transport and to the enhancement of evaporation.

Fig. 10

Influence of Reynolds ($Re = \rho _\textrm{l} D_0 u_0 \mu _\textrm{l}^{-1}$, left) and Weber ($We = \rho _\textrm{l} D_0 u_0^2 \sigma ^{-1}$, right) numbers on the spreading ratio ($S = D_\textrm{cl} D_0^{-1}$) and dimensionless heat ($E^* = 6 Q ( \pi \rho _\textrm{l} D_0^3 h_\textrm{lv} )^{-1}$) for the single drop impact onto an isothermal, hot wall ($\Delta T = {10\,\textrm{K}}$). Results are obtained by changing the initial drop diameter $D_0$, impact velocity $u_0$ and gravitational acceleration g, and keeping all other dimensionless numbers constant [1]

4.2.2 Influence of Dimensionless Parameters

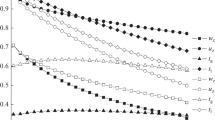
In this section, the influence of dimensionless parameters, i.e., the Reynolds ($Re$), Weber ($We$), Bond ($Bo$), Prandtl ($Pr$) and Jakob ($Ja$) numbers, on the evolution of the spreading ratio (the relation between the drop footprint diameter and the initial drop diameter, S) and the evolution of dimensionless cumulative heat transported from the solid to the drop, $E^*$, during the single drop impact onto a hot wall, is presented. Detailed discussions of the results can be found in [1, 13]. The significant influence of the Reynolds number on the maximum spreading shown in Fig. 10 is attributed to the competition between the inertial and friction forces during the spreading phase. The amplitude of drop oscillations before reaching the mechanically stable sessile shape increases with increasing $Re$. An increase in the Weber number leads to significant prolongation of the receding phase, since the role of surface tension, which is the driving force for the drop receding, decreases in comparison to inertia with increasing $We$.

Despite an increase in the maximum spreading ratio and thus the wetted area, the dimensionless cumulative heat decreases with increasing $Re$, since increasing $Re$ at constant $We$ corresponds to larger drop volume (the denominator in the definition of $E^*$). Increasing $We$ leads to decreasing $E^*$ during the spreading phase and increasing $E^*$ during the receding phase, which decelerates with increasing $We$.

Higher Bond numbers lead to higher maximal spreading and enhanced heat transfer. Increasing the Prandtl number increases the spreading ratio as well, but leads to a decrease in cumulative heat transfer. Increasing the Jakob number by increasing the wall superheat leads to an increase in the apparent contact angle and, consequently, to a decrease in the maximum spreading ratio and deceleration of the receding phase. The transferred heat increases with increasing Jakob numbers. The dependence of dimensionless parameters on the maximum spreading ratio and dimensionless heat transfer has been summarised in the form of correlations [1].

4.2.3 Influence of Ambient Pressure

The analysis in this work is limited to reduced pressures of up to $P^* = p p_\textrm{crit}^{-1}=0.5$. The solver of the macroscale model has been extended to account for compressibility effects and validated by Schlawitschek [24]. The governing equations in the fluid region (Eq. 1–3) have been modified: a source term has been added to the mass conservation equation to account for compressibility effects; the momentum and energy balance equations have been modified to account for the variable density. The density is calculated with a linearised Peng-Robinson equation of state. A complete, comprehensive description of the compressible solver is given in [24].

In the study on low and high ambient pressure presented in Fig. 11, all impact parameters are kept constant. The Reynolds, Weber, Bond and Jakob numbers increase with increasing pressure, while the Prandtl number decreases with increasing pressure. The maximum spreading ratio slightly increases with increasing pressure, which can be attributed to the dominant role of the Reynolds number. The dimensionless cumulative heat increases with increasing pressure, although the dimensional cumulative heat decreases with increasing pressure [24]. However, the drop mass and the latent heat of evaporation, which constitute the denominator in the definition of $E^*$, decrease at higher pressures stronger than Q. Further details related to the influence of pressure on hydrodynamics and heat transfer during single drop impingement onto a hot surface can be found in [24].

Fig. 11

Influence of low (left) and high (right) ambient pressure ($P^* = p p_\textrm{crit}^{-1}$) on the spreading ratio ($S = D_\textrm{cl} D_0^{-1}$) and dimensionless heat ($E^* = 6 Q ( \pi \rho _\textrm{l} D_0^3 h_\textrm{lv} )^{-1}$) for the single drop impact ($D_0 = {1.0241\,\textrm{mm}}$, $u_0 = {0.2735\,\mathrm{m s^{-1}}}$) onto an isothermal, hot wall ($\Delta T = {10\,\textrm{K}}$) [24]

4.3 Multiple Drop Impact

In the spray cooling process, many drops impact successively and simultaneously onto a hot wall. The interaction between the drops governs the hydrodynamics and heat transport phenomena during spray cooling. In this chapter, the vertical and horizontal coalescence of drops over a hot surface are studied numerically.

4.3.1 Vertical Coalescence

In this section, the impingement of chains of drops with identical impact parameters onto the same location is studied numerically. The predicted evolution of the contact line radius for the case of an impact of consequent drops onto a sessile drop has been compared with experimental results and shows good agreement (see Fig. 12). The experimental setup and procedure are described in [6, 7]. After the impact and coalescence of two drops, the combined drop spreads. The maximum spreading radius increases with each subsequent drop impact, and the oscillations preceding the sessile drop phase are more pronounced with each subsequent drop impact.

Fig. 12

Contact line radius $R_\textrm{cl}$ and heat flow $\dot{Q}$ from the wall to the drop over time for four successively impacting drops ($D_0 = {1.14\,\textrm{mm}}$, $u_0 = {0.54\,\mathrm{m s^{-1}}}$) onto a smooth, hot wall ($\Delta T = {9.8\,\textrm{K}}$, $\dot{q}_\textrm{heater} = {2900\,\mathrm{W m^{-2}}}$)

In Fig. 13, the snapshots of drop shape, wall temperature and wall heat flux distributions at two time instants (the first around one millisecond after the impact of second drop and the second close to end of the spreading phase) are shown. During the advanced spreading phase, several rings of high heat flux are observed in both experiments and simulations. The inner ring-shaped high heat flux region can be explained by the formation of a wave-like flow within the liquid leading to enhanced convective mixing of the liquid.

Fig. 13

Comparison between experiments (exp.) and simulations (sim.) of temperature (T) and heat flux ($\dot{q}$) fields at the drop footprint as well as the side (exp.) and cross-sectional (sim.) views during the vertical coalescence onto a sessile drop ($D_0 = {1.14\,\textrm{mm}}$, $u_0 = {0.54\,\mathrm{m s^{-1}}}$, $\Delta T = {9.8\,\textrm{K}}$, $\dot{q}_\textrm{heater} = {2900\,\mathrm{W m^{-2}}}$)

Guggilla et al. [8] reported a lower heat flow peak during the impact of a drop onto a sessile drop compared to the first drop impact. In their experimental work, a ${25\,\mathrm{mm}}$ thin steel foil heated by electrical current was used as a substrate, and the impact frequency was 20 drops per minute. In contrast, Gholijani et al. [6] reported a higher heat flow peak after each consequent impact; their experiments were performed with a heated, ${4\,\textrm{mm}}$ thick calcium fluoride substrate, and the drop frequency was varied between 6 and ${10\,\textrm{Hz}}$. To explain this apparent contradiction, the developed numerical model has been used to study the influence of the substrate thickness on heat transfer by using identical thermal properties of the substrate (see Fig. 14). For the thick substrate, the input heat flux in the experiments of $\dot{q}_\textrm{heater} = {2900\,\mathrm{W m^{-2}}}$ is chosen such that the dry substrate maintains a constant surface temperature. However, non-constant surface temperatures are expected when imposing this input heat flux to the thin substrate. Hence, for the thin substrate, a heated ($\dot{q}_\textrm{heater} = {2900\,\mathrm{W m^{-2}}}$) and unheated ($\dot{q}_\textrm{heater} = {0\,\mathrm{W m^{-2}}}$) substrate is studied numerically. The corresponding input heat flux to maintain a constant surface temperature on the dry, thin substrate is expected to be somewhere between these two limits. As shown in Fig. 14, the substrate temperature decreases significantly after the first drop impingement due to the low thermal inertia of the thin substrate. As a result, the second drop spreads, depending on the input heat flux of the heater, either on a warmer or a cooler surface. Hence, the peak in the heat flow of the second drop can be significantly higher or lower than the peak of the first drop. Further numerical studies reveal that this effect is more pronounced for lower impact frequencies. Similar conclusions have been drawn in a numerical study by Guggilla et al. [9].

Fig. 14

Left: Comparison of radial temperature profiles on the wall surface at the time just prior to the drop impact onto a sessile drop ($D_0 = {1.14\,\textrm{mm}}$, $u_0 = {0.54\,\mathrm{m s^{-1}}}$). A thick substrate (${4\,\textrm{mm}}$) is compared to a thin substrate (${24\,\mathrm{mm}}$), both heated ($\Delta T = {9.8\,\textrm{K}}$, $\dot{q}_\textrm{heater} = {2900\,\mathrm{W m^{-2}}}$) and unheated ($\Delta T = {9.8\,\textrm{K}}$, $\dot{q}_\textrm{heater} = {0\,\mathrm{W m^{-2}}}$). Right: Corresponding heat flow from the wall to the drop

Finally, the effect of the time interval between the first and the second impact on spreading radius and heat flow has been studied and compared with the impact of a single drop with double volume. The interval between the impacts has been chosen in such a way that the second drop impacts onto the first drop during the spreading, receding and sessile phases. As shown in Fig. 15, the highest maximal spreading radius is observed for the impact during the spreading phase of the first drop and the lowest for the impact during the receding phase. The flow field within the first drop at the instant of impact of the second drop has a significant influence on the spreading behaviour. The highest heat is transferred during the impact in the spreading phase. For all other studied cases, almost the same heat is transferred at ${150\,\textrm{ms}}$ after the impact of the first drop.

Fig. 15

Contact line radius $R_\textrm{cl}$ and cumulative heat flow Q from the wall to the drop over time for the impact of the second drop during different impingement phases of the initial drop ($D_0 = {1.14\,\textrm{mm}}$, $u_0 = {0.54\,\mathrm{m s^{-1}}}$, $\Delta T = {9.8\,\textrm{K}}$, $\dot{q}_\textrm{heater} = {2900\,\mathrm{W m^{-2}}}$). In the figure showing the radius, time $t = {0\,\textrm{s}}$ is set as the time just before the collision with the first drop or the wall occurs

Furthermore, a drop chain consisting of five drops impacting during the spreading phase of the previous drop has been studied. It has been found that the drop chain transfers more heat than a single drop of a fivefold volume.

4.3.2 Horizontal Coalescence

For spray cooling, in addition to the vertical coalescence, the horizontal coalescence is also of great importance. The simultaneous impact of two identical drops onto two close locations of a hot substrate and the subsequent horizontal coalescence has been simulated using a structured 3D grid. Due to the symmetry of the geometry, the computational domain includes only a half of a droplet. A dynamic mesh refinement with load balancing [22] has been used to refine the mesh locally near the moving interface.

Figure 16 shows the impact of two drops with a small spacing onto a smooth, hot wall. Shortly after the collision of the drops’ spreading fronts ($t = {2\,\textrm{ms}}$), an uprising planar jet forms between the drops. Afterwards (starting at $t = {3\,\textrm{ms}}$), a sideward flow of liquid leads to the thickening of a neck between the drops. The liquid flow far away from the location of collision is not influenced by the presence of a second drop. Later, the jet collapses and the two drops form a single sessile drop.

Fig. 16

Reprinted from [2] with permission from Elsevier

Horizontal coalescence of two drops with a spacing of $e = d / D_0 = 1.5$. d denotes the initial distance between the centres of the drops.

For different spacing parameters e, Fig. 17 shows that the heat flow from the wall deteriorates as soon as the drops coalescence in comparison to the case of two non-interacting drops. After the coalescence event, both the wetted area and the local flow velocity decrease resulting in a lower heat transfer compared to the case of two non-interacting drops. Hence, the outcome of the simultaneous impact of two drops strongly depends on the spacing between the drops. More details on the numerical investigation of the horizontal coalescence and a comparison with an analytical model can be found in [1, 2].

Fig. 17

Total heat flow $\dot{Q}$ from the wall to the drop over time during the horizontal coalescence of two drops with different spacing parameters $e = d / D_0$. d denotes the initial distance between the centres of the drops. $e \rightarrow \infty$ labels the simultaneous impact of two non-interacting drops [1]

5 Conclusions

The numerical study of the impact of single and multiple drops onto hot walls significantly contributes to the understanding of the complex hydrodynamic and heat transport processes during spray cooling. In this study, the drop impact has been studied at moderate Reynolds, Weber and Jakob numbers in the drop deposition and film evaporation regime.

Almost 50% of the global heat transfer can be observed in the vicinity of the evaporative three-phase contact line. A one-dimensional lubrication model describes the hydrodynamic and heat transport processes in a micro region at the three-phase contact line. The results from this model are in good agreement in the chosen parameter range with results from a full-scale direct numerical simulation of the micro region.

A numerical model developed within the OpenFOAM library is used to study the drop impact on a macro scale. The results of the micro region model have been incorporated into the macroscale model in the form of correlations. It has been found that convective heat transfer is dominant during the spreading phase of the drop. However, during the receding and sessile drop phases, evaporation at the liquid–vapour interface and at the three-phase contact line play the main role. An extensive parameter study of the governing dimensionless numbers, i.e., the Reynolds, Weber, Bond, Prandtl and Jakob numbers, has been performed. The influence of pressures on hydrodynamics and heat transfer behaviour has been studied. Finally, the impact of multiple drops on the hot surface has been studied. The drop frequency is found to have a major influence on hydrodynamics and heat transport during the impingement process. Furthermore, it is shown that during the vertical coalescence of two successive impacting drops the peak in the heat flow can either be higher or lower for the second drop in comparison to the first drop, in dependency on the substrate thickness. The outcome of the horizontal coalescence of two simultaneously impacting drops is determined by the spacing between the drops.