Abstract
Our Earth is a complex system. By monitoring the integrated geodetic-geodynamic processes, we can understand its sub-systems and geographical distribution of its resources. With the development of space techniques and artificial satellites, satellite geodesy era started, e.g., it became possible to observe a wide range of processes, occurring both on and below the Earth's surface. Such observations can be exploited not only in environmental activities, but also in societal activities like natural disasters monitoring. Thus, satellite geodesy can bring great benefits to “Climate action”, one of the 17 sustainable development goals of the United Nation: we can estimate the ice-sheet mass balance and study the impact of climate change by monitoring sea levels. This paper aims to investigate the possible implementation of cold atom sensors for future satellite gravity missions, which would improve our current knowledge of the Earth’s gravity field and contribute into the sustainable environmental management.
Graphical Abstract

You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
- Earth observation
- Satellite geodesy
- Gradiometry
- Cold atom interferometer
- Climate action
- Sustainable environmental management
1 Introduction
The Earth’s gravity field is the result of mass distribution in the Earth’s system, which includes the solid Earth, oceans, atmosphere, ice, land, as well as the biosphere. Mass redistribution and transport in any of the Earth’s subsystems cause gravity field variations. Thus, continuous monitoring of the Earth’s gravity and its changes is important for studies on climate changes, hydrology, sea level changes, solid Earth phenomena (Fig. 1). These variations can be measured both on the Earth surface and from the space. Data from gravity surveys on the Earth surface allow us to map the gravity field with high resolution, but these data are inhomogeneous and have a different level of precision depending on the data availability and used instruments. Such issue can be overcome by using satellite-based observations which provide a uniform coverage of the Earth and map its gravity field in a very homogeneous way.
Contribution of satellite geodesy in the Earth observation. Adapted from [14]
The aim of satellite gravity missions is to refine the Earth’s gravity field model, monitor and model the static and/or the time-variable gravity field variation. The static gravity field represents the spatial variations in the gravity field, generated by the density inhomogeneities inside Earth, representing the geological processes acted over the geological time scale. Such observations can contain information on the presence of sediment basins, magmatic intrusions, volcanic deposits, metamorphic rock lineaments. At larger scale, they represent density contrasts associated with mantle convection or plate tectonics, tied to long term dynamical processes within the Earth. On the other hand, the time-variable gravity field is the expression of the variations that occur much more rapidly due to various tidal, oceanic, atmospheric, hydrological, glaciological, and tectonic processes. Measurement of such temporal variations can reveal the effect of mega earthquakes and monitor crustal deformation. Besides, ice masses carry a significant gravity signal and time-variable gravity solutions are fundamental for studies on ice-sheet mass variations and their impact on climate [25].
In the first decade of the new millennium, three successful satellite missions (Fig. 2) were launched:
Dedicated satellite gravity missions. Adapted from [12]
-
1.
CHAMP (Challenging Mini-satellite Payload): to observe both the gravity field and magnetic field from a low altitude orbit [28].
-
2.
GRACE (Gravity Recovery and Climate Experiment): to map the variations of Earth’s gravity by measuring the changes in the inter-satellite distance [31].
-
3.
GOCE (Gravity field and steady Ocean Circulation Explorer): to determine the static gravity field: geoid, the equipotential reference surface, and gravity anomalies with unprecedented accuracy and spatial resolution [9].
These missions delivered plenty of data to the scientific communities and space agencies and, of course, achieved spectacular science results, but our current knowledge of the Earth’s system is still limited. Thus, the sustained observation of the Earth’s gravity field is required to overcome this shortcoming. The geophysical and societal impact and objectives of future gravity missions with respect to GRACE and GOCE have been studied, e.g., in the framework of the Global Geodetic Observing System (GGOS) Working Group for Satellite Missions [25]. Recently, a GRACE-FO (Gravity Recovery and Climate Experiment Follow-On) mission was launched in 2018 [15] (Fig. 2). It is continuing and will continue the work of previous GRACE twin in monitoring the water movement around the planet to detect the changes in amount of water in large lakes and rivers, soil moisture, ice sheets and glaciers, and in sea level caused by the water transfer from continental areas to the ocean [10].
Currently, ongoing studies such as NGGM (Next Generation Gravity Mission) are also being carried out for the long-term monitoring of the Earth’s gravity field with high temporal and spatial resolution [13]. One of recent NGGM studies investigated its capability to detect the earthquake gravity signatures, including those from active tectonics and inter-seismic deformation [3]. It was proved that this new application of NGGM can be used to also detect the gravity signatures of those processes responsible for the earthquake generation, thus contributing to seismic hazard studies.
2 Spaceborne Cold Atom Gradiometer for Future Gravity Mission
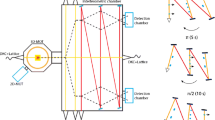
Quantum sensors based on atom interferometry have evolved rapidly in the last few decades. Thanks to their excellent long-term stability and accuracy level, such sensors have demonstrated the potential to enable the inertial and gravity sensing payloads and have been used for a wide range of practical applications from oil and minerals exploration to defense, from civil engineering to space [1]. Future improvements of the GOCE mission concept can be achieved by going beyond the technology of electrostatic gravity gradiometers and taking advantage of a new generation of quantum sensors. Carraz et al. [4] proposed the concept of a new spaceborne cold atom gradiometer for high-sensitivity measurements of all diagonal elements of the gravity gradient tensor and the full spacecraft angular velocity. A gradiometer in one given direction (e.g., the radial one) can be obtained by measuring the acceleration of two clouds of cold atoms (at mK) separated by a certain distance. At the same time, this instrument allows to measure the rotation angle around the axis perpendicular to the plane of motion of the atom clouds. Several studies of European Space Agency (ESA) [7, 23, 33] investigated the performance of an innovative gradiometer and technological developments required for further space applications. The power spectral density of the gradiometer noise is flat at low frequencies in contrast to the spectrally colored noise of the electrostatic accelerometers (Fig. 3). The sensitivity of the ground-based atom gradiometers can reach a few tens of E/Hz1/2 [30], while a spaceborne cold atom gradiometer can provide the sensitivity of few mE/Hz1/2 [4], where 1 E = 10−9 s−2. Thanks to its spectral characteristics, this instrument might allow to meet the requirements of a future mission dedicated to the observation of both the time-variable gravity field (like GRACE) and the static field (like GOCE).
One of possible schemes of a cold atom gradiometer has been proposed and implemented in the framework of the MOCASS (Mass Observation with Cold Atom Sensors in Space) study, performed by Italian universities and research institutions under the Italian Space Agency (ASI) contract [22, 27, 29]. A similar concept also has been exploited in the “Cold Atom Inertial Sensors: Mission Application (CAI)” study, carried out by Thales Alenia Space Italia under ESA contract [23]. In the former, the gradiometer capability to detect and monitor various geophysical phenomena was assessed, considering different gradiometer configurations, whereas the latter focused more on the possible payload of a single-arm gradiometer and the mission architecture, addressing the required accommodation resources and technological developments. Other main differences between two studies were in the simulation scenarios, as well as in the characteristics of the gradiometer noise (see again Fig. 3).
3 Data Analysis
In both studies, the gradiometer performance was evaluated by using numerical simulations, processing the simulated data by space-wise approach. The main idea behind this approach [18] is to filter the noise and estimate the spherical harmonic coefficients of the geopotential model by exploiting the spatial correlation of the Earth’s gravity field. Theoretically, it could be done by a global collocation solution, modelling the signal covariance as a function of spatial distance, and the noise covariance as a function of time distance. It would allow to filter together data that are close in space but far in time, thus overcoming the problems related to the strong time correlation of the observation noise. However, such a unique collocation solution is computationally unfeasible due to the huge amount of data to be processed for this type of satellite missions [24]. Indeed, the dimension of the system to be solved in this case would be equal to the number of input data. Hence, the space-wise approach (Fig. 5) was implemented as a multi-step collocation procedure consisting of:
-
1.
Wiener filtering [26], applied to the data along the orbit to reduce the highly time correlated noise of the gradiometer.
-
2.
Interpolation of filtered data to obtain values over spherical grids at mean satellite altitude, by applying collocation to local patches of data [20].
-
3.
Spherical harmonic (SH) analysis of gridded data by numerical integration [5] to retrieve the geopotential coefficients.
In the case of the cold atom gradiometer, time correlation arises also from the atom interferometer integrator or transfer function [32], which is shown in Fig. 4a. This means that the MOCASS or CAI gradiometer does not provide point-wise observations like in GOCE and, therefore, the Wiener filter was generalized to a Wiener deconvolution filter (Fig. 4b).
In the general GOCE scheme, the procedure is iterated till convergence to recover the signal frequencies cancelled by the Wiener filter along the orbit and to correct the rotation from the gradiometer to the local orbital reference frame (LORF) [19]. For MOCASS and CAI simulations, no iterations were implemented due to the prevailing white behavior of the noise spectrum of the cold atom gradiometer and to the assumption that the spacecraft (and therefore the gradiometer) is kept aligned with the LORF. The simplified flow-chart in Fig. 5 without iterations allowed higher speed in computations and hence the possibility to analyze several case studies.
4 Simulation Scenario
The numerical simulations were performed considering the parameters reported in Table 1. In the case of MOCASS study, 20 different simulation scenarios were implemented, whereas only 3 scenarios were considered in CAI study. For all simulated scenarios, the estimation errors were computed using Monte Carlo (MC) techniques as an exact error covariance propagation is not feasible [21].
The MC strategy consisted in simulating a set of spherical harmonic model coefficients \({T}_{\mathcal{\ell}\mathcal{m}}\) of the anomalous potential T of degree \(\mathcal{\ell}\) and order m, then computing average and sample error covariances of the corresponding solutions. The coefficient error variances of the reference model EIGEN-6C4 [11] were used to generate MC samples. This means that the sample data are equal to EIGEN-6C4 on average, but differ from it by a variation, related to the EIGEN-6C4 error variances. A higher number of samples would be recommendable to get more accurate error estimates; however, the choice was driven by the need of limiting the computational burden. The error rms of the estimated coefficients \({\hat{T}}_{\mathcal{\ell}\mathcal{m}}\) was computed as:
5 Simulation Results
Let us consider 2-month MOCASS solutions in high orbit in terms of error degree variances (Fig. 6). For comparison, the error of the GOCE_TIM_R1 model [25] and the error of the average of two GRACE monthly solutions [17], corresponding to the same data period of the GOCE_TIM_R1 model, are reported here.
The best performance can be achieved when working with:
-
1.
Tzz component or a pair of Tyy and Tzz in the case of a mission with a nadir-pointing satellite.
-
2.
Tyy component or a pair of Tyy and Tzz in the case of a mission with an inertial-pointing satellite.
In these “optimal” scenarios, MOCASS observations allow for an improvement with respect to GOCE at all spherical harmonic degrees and with respect to GRACE at higher harmonic degrees (approximately above 35–40). At lower harmonic degrees, the GRACE estimates remain better than the MOCASS ones. Also, it must be underlined that this kind of comparison is a general indication of how well the MOCASS mission would perform with respect to GOCE and GRACE; in fact, the quality of real mission solutions depends on various factors such as the processing method or model version.
Consequently, the same comparison was done with CAI error curves, considering 2-month-solutions, which revealed that:
-
1.
Tzz component shows the best performance, the error curves for Txx and Tyy components show a quite similar performance.
-
2.
In the “optimal” case, CAI shows improvement with respect to GOCE at degrees above 15, and with respect to GRACE at higher degrees (above 60).
-
3.
Degradation of CAI with respect to MOCASS at all spherical harmonic degrees is due to the higher noise level of the CAI gradiometer, which in turn depends on the more accurate modelling of the interactions between the gradiometer and the spacecraft.
The results can also be compared in terms of gravity anomaly (Δg) cumulative error at ground level (Table 2):
-
1.
Static gravity field: the commission error of the optimal MOCASS (in high orbit) and CAI solutions was computed at degree \(\mathcal{\ell}\) = 200, which corresponds to spatial resolution of about 100 km. For a fair comparison, the corresponding cumulative error of the GOCE solutions (the time-wise solution of GOCE Release 1 (R1) and GOCE Release 5 (R5) [2]), is also reported.
-
2.
Time-variable gravity field: the commission error of the optimal MOCASS (in high orbit) and CAI solutions, including the GRACE one (ITSG-Grace2014k) [16], was computed at the maximum degree \(\mathcal{\ell}\) = 45. It was due to the signal power, which is so lower that a higher accuracy is required for the signal detection, at the cost of a lower spatial resolution.
Here, the GOCE R1 solution corresponds to a time span of 2 months, whereas GOCE (TIM R5) and GRACE (ITSG-Grace2014k) solutions have been rescaled for the corresponding number of months.
6 Conclusion
Since 2014 the cold atom technology and instrument architecture have been further investigated for space application. So far, some achievements were obtained in operating atomic quantum sensors in the real-space environment, one of which is the Cold Atom Laboratory (CAL) [8]. It was successfully installed on the International Space Station in 2018 and serves as an experiment in the use of laser-cooled atoms for future quantum sensors. Recently, worldwide laboratories and research institutes have been investigating the idea of exploiting cold atom sensors for future satellite gravity missions [6]. Of course, designing such a mission is not only a technological challenge, but also represents complex trade-offs at the system and mission level.
The data simulation and analysis for two studies of future gravity missions, namely the MOCASS and CAI studies, were described in this paper. In both missions, the satellite would fly in a low orbit (GOCE-like) and carry onboard a gradiometer built by exploiting the ultra-cold atom technology. First estimates show that MOCASS and CAI gradiometer can improve the GOCE gradiometer performance in the mapping of the Earth’s gravity field with high accuracy. Regarding the case of time-variable gravity field recovery, MOCASS and CAI error estimates show an improvement with respect to GRACE at higher degrees. Particularly, another fundamental part of MOCASS study was to evaluate the significance of the mission for the improvement in the detection and monitoring of geophysical phenomena, estimating the progress that could be achieved. For this purpose, different phenomena were simulated by geophysicists: deglaciation in High Mountains of Asia (HMA), mountain building processes (tectonic), continental hydrology, and volcanic eruptions leading to growing seamounts [27]. The simulation results showed that MOCASS observations could:
-
1.
increase the detectability of small trends in the glacier ice mass in the HMA region and improve the studies of seamounts;
-
2.
detect smaller areas subject to deglaciation in HMA;
-
3.
map the complex tectonic deformation in the HMA with higher resolution.
Summarizing all the above mentioned aspects, it can be said that a cold atom interferometry is a promising maturing technology that could be implemented in future gravity missions to improve the measuring accuracy. A new gravity mission with such an innovative sensor may have great potential for enabling sustained observation of the Earth’s gravity field and detecting and monitoring geophysical phenomena. For instance, by monitoring the sea levels, we can estimate the ice sheet mass balance and deglaciation rates and study the impact of climate change. Eventually, it may contribute into sustainable environmental management, and play a crucial role for achieving one of the sustainable development goals “Climate action”.
References
Bongs, K., Holynski, M., Vovrosh, J., et al.: Taking atom interferometric quantum sensors from the laboratory to real-world applications. Nat. Rev. Phys. 3, 814 (2021). https://doi.org/10.1038/s42254-021-00396-1
Brockmann, J.M., Zehentner, N., Höck, E., et al.: EGM_TIM_RL05: An independent geoid with centimeter accuracy purely based on the GOCE mission. Geophys. Res. Lett. 41(22), 8089–8099 (2014). https://doi.org/10.1002/2014GL061904
Cambiotti, G., Douch, K., Cesare, S., et al.: On earthquake detectability by the next-generation gravity mission. Surv. Geophys. 41, 1049–1074 (2020). https://doi.org/10.1007/s10712-020-09603-7
Carraz, O., Siemes, C., Massotti, L., et al.: A spaceborne gravity gradiometer concept based on cold atom interferometers for measuring Earth’s gravity field. Microgravity Sci. Technol. 26, 139–145 (2014). https://doi.org/10.1007/s12217-014-9385-x
Colombo, O.L.: Numerical methods for harmonic analysis on the sphere. Technical report N. 310, Department of Geodetic Science and Surveying, The Ohio State University, Columbus, Ohio (1981)
Devani, D., Maddox, S., Renshaw, R., et al.: Gravity sensing: cold atom trap onboard a 6U CubeSat. CEAS Space 12, 539–549 (2020). https://doi.org/10.1007/s12567-020-00326-4
Douch, K., Wu, H., Schubert, C., et al.: Simulation-based evaluation of a cold atom interferometry gradiometer concept for gravity field recovery. Adv. Space Res. 61(5), 1307–1323 (2018). https://doi.org/10.1016/j.asr.2017.12.005
Elliott, E.R., Krutzik, M.C., Williams, J.R., et al.: NASA’s cold atom lab (CAL): system development and ground test status. npj Microgravity 4, 16 (2018). https://doi.org/10.1038/s41526-018-0049-9
European Space Agency.: Steady-state ocean circulation mission. ESA SP 1233(1), 217 (1999)
Frappart, F., Ramillien, G.: Monitoring groundwater storage changes using the gravity recovery and climate experiment (GRACE) satellite mission: a review. Remote Sens. 10(6), 829 (2018). https://doi.org/10.3390/rs10060829
Förste, C., Bruinsma, S. L., Abrikosov, O., et al.: EIGEN-6C4: the latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ potsdam and GRGS toulouse. GFZ Data Serv. (2014). https://doi.org/10.5880/ICGEM.2015.1
Gruber, T., Beutler, G., Fecher, T., et al.: Earth gravity field determination from space—A computational challenge. In: LRZ Linux-Cluster Workshop (2008)
Haagmans, R., Siemes, C., Massotti, L., et al.: ESA’s next-generation gravity mission concepts. Rend. Lincei Sci. Fis. Nat. 31, 15–25 (2020). https://doi.org/10.1007/s12210-020-00875-0
Ilk, K.H., Flury, J., Rummel, R., et al.: Mass transport and mass distribution in the Earth system. In: Contribution of the New Generation of Satellite Gravity and Altimetry Missions to Geosciences, 2nd edn, GOCE Projektbüro TU München, GFZ Potsdam (2005)
Kornfeld, R.P., Arnold, B.W., Gross, M.A., et al.: GRACE-FO: the gravity recovery and climate experiment follow-on mission. J. Spacecr. Rockets 56(3), 931–951 (2019). https://doi.org/10.2514/1.A34326
Mayer-Gürr T., Zehentner N., Klinger B., Kvas A.: ITSG-Grace2014: a new GRACE gravity field release computed in Graz. In: GRACE Science Team Meeting (GSTM), Potsdam (2014)
Mayer-Gürr, T., Behzadpour, S., Ellmer, M., et al.: ITSG-Grace2016: monthly and daily gravity field solutions from GRACE. GFZ. (2016). https://doi.org/10.5880/icgem.2016.007
Migliaccio, F., Reguzzoni, M., Sansò, F.: Space-wise approach to satellite gravity field determination in the presence of coloured noise. J. Geod. 78, 304–313 (2004). https://doi.org/10.1007/s00190-004-0396-z
Migliaccio, F., Reguzzoni, M., Sansò, F., and Zatelli, P.: GOCE: Dealing with large attitude variations in the conceptual structure of the space-wise approach. In: Proceedings of the 2nd International GOCE user Workshop. Frascati, Rome, Italy, ESA SP-569 (2004)
Migliaccio, F., Reguzzoni, M., Sansò, F., Tselfes, N.: On the use of gridded data to estimate potential coefficients. In: Proceedings of the 3rd International GOCE user Workshop, pp. 311–318. Frascati, Rome, Italy, ESA SP-627 (2007)
Migliaccio, F., Reguzzoni, M., Sansò, F., Tselfes, N.: An error model for the GOCE space-wise solution by monte carlo methods. In: Sideris, M.G. (eds) Observing our Changing Earth. International Association of Geodesy Symposium, p. 133. Springer, Berlin, Heidelberg (2009). https://doi.org/10.1007/978-3-540-85426-5_40
Migliaccio, F., Reguzzoni, M., Batsukh, K., et al.: MOCASS: a satellite mission concept using cold atom interferometry for measuring the earth gravity field. Surv. Geophys. 40, 1029–1053 (2019). https://doi.org/10.1007/s10712-019-09566-4
Mottini, S., Anselmi, A. (2019). Cold atom inertial sensor: mission applications (CAI). Summary report. Thales Alenia Space
Pail, R., Bruinsma, S., Migliaccio, F., et al.: First GOCE gravity field models derived by three different approaches. J. Geod. 85(11), 819–843 (2011). https://doi.org/10.1007/s00190-011-0467-x
Pail, R., Bingham, R., Braitenberg, C., et al.: Science and user needs for observing global mass transport to understand global change and to benefit society. Surv. Geophys. 36, 743–772 (2015). https://doi.org/10.1007/s10712-015-9348-9
Papoulis, A.: Probability, Random Variables and Stochastic Processes. McGraw-Hill (1984)
Pivetta, T., Braitenberg, C., Barbolla, D.F.: Geophysical challenges for future satellite gravity missions: assessing the impact of MOCASS mission. Pure Appl. Geophys. 178, 2223–2240 (2021). https://doi.org/10.1007/s00024-021-02774-3
Reigber, C., Schwintzer, P., Luhr, H.: The CHAMP geopotential mission. Boll. di Geofis. Teor. ed Appl. 40(3–4), 285–289 (1999)
Reguzzoni, M., Migliaccio, F., Batsukh, K.: Gravity field recovery and error analysis for the MOCASS mission proposal based on cold atom interferometry. Pure Appl. Geophys. 178, 2201–2222 (2021). https://doi.org/10.1007/s00024-021-02756-5
Sorrentino, F., Bodart, Q., Cacciapuoti, L., et al.: Sensitivity limits of a Raman atom interferometer as a gravity gradiometer. Phys. Rev. A. 89, 023607 (2014)
Tapley, B.D., Bettadpur, S., Watkins, M., Reigber, C.: The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 31(9) (2004). https://doi.org/10.1029/2004GL019920
Tino G.M., Kasevich M.A.: Atom interferometry. In: Proceedings of the International School of Physics “Enrico Fermi”. vol. 188. ISBN: 978-1-61499-447-3 (print), 978-1-61499-448-0 (online) (2014)
Trimeche, A., Battelier, B., Becker, D., et al.: Concept study and preliminary design of a cold atom interferometer for space gravity gradiometry. Class. Q. Gravity 36(21), 215004 (2019). https://doi.org/10.1088/1361-6382/ab4548
Acknowledgements
I would like to acknowledge my supervisors prof. Federica Migliaccio and prof. Mirko Reguzzoni for their continuous support and guidance throughout this work. The MOCASS study has been funded under Italian Space Agency contract N. 2016-9-U-0 “Proposal of a satellite mission and sensor concept based on advanced atom interferometry accelerometers for high resolution monitoring of mass variations on and below the Earth surface”. The CAI study has been funded under European Space Agency contract N. 4000117930/16/NL/FF/gp.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this chapter
Cite this chapter
Batsukh, K. (2022). Cold Atom Interferometry in Satellite Geodesy for Sustainable Environmental Management. In: Antonelli, M., Della Vecchia, G. (eds) Civil and Environmental Engineering for the Sustainable Development Goals. SpringerBriefs in Applied Sciences and Technology(). Springer, Cham. https://doi.org/10.1007/978-3-030-99593-5_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-99593-5_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-99592-8
Online ISBN: 978-3-030-99593-5
eBook Packages: EngineeringEngineering (R0)